Dynamical diquarks in the ${\varvec{\gamma ^{(*)} p\rightarrow N(1535)\frac{1}{2}^-}}$ transition

Abstract

The $\gamma ^{(*)}+p \rightarrow N(1535) \tfrac{1}{2}^-$ transition is studied using a symmetry-preserving regularisation of a vector$\,\otimes \,$vector contact interaction (SCI). The framework employs a Poincaré-covariant Faddeev equation to describe the initial and final state baryons as quark+diquark composites, wherein the diquark correlations are fully dynamical, interacting with the photon as allowed by their quantum numbers and continually engaging in breakup and recombination as required by the Faddeev kernel. The presence of such correlations owes largely to the mechanisms responsible for the emergence of hadron mass; and whereas the nucleon Faddeev amplitude is dominated by scalar and axial-vector diquark correlations, the amplitude of its parity partner, the $N(1535) \tfrac{1}{2}^-$, also contains sizeable pseudoscalar and vector diquark components. It is found that the $\gamma ^{(*)}+p \rightarrow N(1535) \tfrac{1}{2}^-$ helicity amplitudes and related Dirac and Pauli form factors are keenly sensitive to the relative strengths of these diquark components in the baryon amplitudes, indicating that such resonance electrocouplings possess great sensitivity to baryon structural details. Whilst SCI analyses have their limitations, they also have the virtue of algebraic simplicity and a proven ability to reveal insights that can be used to inform more sophisticated studies in frameworks with closer ties to quantum chromodynamics.

Appendices

Appendix A: Electromagnetic interaction vertices

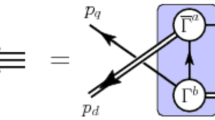
To calculate the baryon elastic and transition currents considered herein, the vertices in Fig. 2 must be specified, i.e. the momentum-dependent photon+quark and photon+diquark interaction form factors.

1.1 Appendix A.1: Photon+quark vertex – S1

The primary element throughout is the dressed photon+quark vertex, which takes the following form when using the SCI:

$$\begin{aligned} \varGamma _\mu ^\gamma (Q) = \frac{Q_\mu Q_\nu }{Q^2} \gamma _\nu + \varGamma _\mu ^{\mathrm{T}}(Q)\,, \end{aligned}$$

(A.1)

with $Q=p_f-p_i$, where $p_{f,i}$ are the outgoing, incoming quark momenta, , , and [45, 51]:

(A.2)

Here [51]

$$\begin{aligned} P_{\mathrm{T}}(Q^2)&= \frac{1}{1+K_\gamma (Q^2)}\,, \end{aligned}$$

(A.3a)

$$\begin{aligned} K_\gamma (Q^2)&= \frac{4\alpha _{\mathrm{IR}} Q^2}{3\pi m_G^2} \int _0^1 d\alpha \,\alpha (1-\alpha )\,\bar{\mathcal{C}}_1(\omega (\alpha ,\varDelta ^2)), \end{aligned}$$

(A.3b)

where the mass-scale $m_G=0.5\,$GeV when $\alpha _{IR}$ has the value in Table 1, $\omega (\alpha ,Q^2) = M^2 + \alpha (1-\alpha ) Q^2$,

$$\begin{aligned} \overline{{\mathcal {C}}}_1(\sigma )&= \varGamma (0,\sigma \tau _{\mathrm{ir}}^2) - \varGamma (0,\sigma \tau _{\mathrm{uv}}^2), \end{aligned}$$

(A.4)

with $\varGamma (\alpha ,y)$ being the incomplete gamma-function. The dressing function in Eq. (A.3) is depicted in Fig. 9.

Fig. 9

Photon+quark vertex dressing function in Eq. (A.3). As in any symmetry preserving treatment of photon+quark interactions, $P_{\mathrm{T}}(Q^2)$ exhibits a pole at $Q^2= -m_\rho ^2$. Moreover, $P_{\mathrm{T}}(Q^2 = 0) = 1 = P_{\mathrm{T}}(Q^2 \rightarrow \infty )$

The second term in Eq. (A.2) expresses the fact that owing to DCSB a dressed light-quark has a large anomalous electromagnetic moment (DqAMM) [84, 85]. With $\zeta =1/3$, we reproduce all form factor results in Ref.  [45]. Our value for $\zeta$ is smaller than that used therein because Ref.  [45] omitted this contribution when computing the $0^+ \leftrightarrow 1^+$ diquark transition form factor. To illustrate the sensitivity of calculated observables to the DqAMM, we typically show results obtained with $\zeta \in [0,0.5]$, highlighting those obtained using $\zeta =1/3$.

1.2 Appendix A.2: Elastic photon+diquark vertices – S2

Using the SCI, all photon+diquark vertices can be calculated following the pattern described in Ref.  [53]. Herein, therefore, we will only present the results. To begin, the elastic $\gamma \, 0^{\pm } \rightarrow 0^\pm$ vertices take the following form ($2K=p_f+p_i$):

$$\begin{aligned} \varLambda _\mu ^\pm (p_f,p_i) = K_\mu F^{0^\pm }(Q^2)\,. \end{aligned}$$

(A.5)

The scalar functions can be computed; and on the domain $Q^2\in [0,10\,\mathrm{GeV}^2]$ they are accurately interpolated using the following [1, 2] Padé approximant:

$$\begin{aligned} F^{0^\pm }(s=Q^2) = \frac{a_0^\pm + a_1^\pm s }{1+b_1^\pm s + b_2^\pm s^2 }, \end{aligned}$$

(A.6)

with the interpolation coefficients listed in Table 3. The results are drawn in Fig. 10.

Table 3 Interpolation coefficients to be used in Eq. (A.6) for each respective elastic photon+diquark form factor. All form factors are dimensionless, so each coefficient has the mass-dimension required to cancel that of the associated $Q^2\,(\mathrm{GeV}^2)$ factor

Fig. 10

Elastic photon+(pseudo)scalar-diquark form factors: $F^+(Q^2)$ – solid red curve; and $F^-(Q^2)$ – dashed blue curve. There is practically no sensitivity to the DqAMM in these $J=0$ systems

Elastic electromagnetic form factors involving $1^\pm$ diquark correlations can be expressed as follows:

$$\begin{aligned} \varLambda _{\mu \alpha \beta }^\pm (p_i,p_f) = \sum _{j=1}^3 T_{\mu \alpha \beta }^{(j)}(K,Q)\, F_j^\pm (Q^2), \end{aligned}$$

(A.7)

where

(A.8)

(A.9)

(A.10)

Our calculated results are accurately interpolated using a [1, 2] Padé approximant of the form in Eq. (A.6) with the coefficients in Table 3. Depicted in Fig. 11, the form factors are similar to those of a vector meson [53] and, as in that case, the magnetic form factor $G_M = -F_2$. The DqAMM has an observable impact on the elastic electromagnetic form factors of these $J=1$ systems.

Fig. 11

Upper panel – A. Elastic photon+pseudovector-diquark form factors: $F_1(Q^2)$ – solid red; $F_2(Q^2)$ – dashed blue; and $F_3(Q^2)$ – dot-dashed green. In each case, the shaded areas show the response to variation of the DqAMM strength, $\zeta \in [0,0.5]$, around the highlighted $\zeta =1/3$ curves. Lower panel – B. Elastic photon+vector-diquark form factors with legend as in A

1.3 Appendix A.3: Photon-induced diquark transition vertices – S3

Diagram S3 in Fig. 2 represents five electromagnetically induced diquark transition vertices: scalar$\,\leftrightarrow \,$pseudovector; pseudoscalar$\,\leftrightarrow \,$vector; scalar$\,\leftrightarrow \,$vector; pseudoscalar$\,\leftrightarrow \,$pseudovector; and pseudovector$\,\leftrightarrow \,$vector.

The first two involve like-parity diquarks in the initial and final states and have the following simple structure:

$$\begin{aligned} \varLambda _{\mu \rho }^{1^\pm 0^\pm }(p_f,p_i) = \frac{1}{m_1^\pm }\epsilon _{\mu \rho \alpha \beta } Q_\alpha p_{f\beta } F^\pm (Q^2). \end{aligned}$$

(A.11)

Our calculated results are accurately interpolated by a [1, 2] Padé approximant in the form of Eq. (A.6) with the coefficients given in Table 4. They are drawn in Fig. 12. Plainly, the DqAMM has a noticeable impact on both vertices and the $\gamma 0^- \rightarrow 1^-$ transition form factor is typically larger in magnitude than that describing $\gamma 0^+ \rightarrow 1^+$. The latter feature has little impact, however, because the nucleon contains practically no negative-parity diquarks.

Fig. 12

Form factors for photon induced transition between: scalar-diquark and pseudovector-diquark, $\gamma ^{(*)} 0^+ \rightarrow 1^+$ – solid red curve; and pseudoscalar-diquark and vector-diquark, $\gamma ^{(*)} 0^- \rightarrow 1^-$ – dashed blue curve. In each case, the shaded areas show the response to variation of the DqAMM strength, $\zeta \in [0,0.5]$, around the highlighted $\zeta =1/3$ curves

Table 4 Interpolation coefficients to be used in Eq. (A.6) for each photon-induced diquark transition form factor. There are two exceptions: [2, 3] Padé approximants are required to accurately represent the $\gamma ^{(*)} 1^+ \rightarrow 0^-$, $\gamma ^{(*)} 0^+ \rightarrow 1^-$ transitions. In each of these cases there are two additional coefficients for both of the functions involved, Eq. (A.12). $\gamma ^{(*)} 1^+ \rightarrow 0^-$: $a_2 = 0.267$, $b_3 = 0.029$ ($F_1$); and $a_2 = -0.019$, $b_3 = 0.348$ ($F_2$). $\gamma ^{(*)} 1^- \rightarrow 0^+$: $a_2 = 0.227$, $b_3 = 1.852$ ($F_1$); and $a_2 = 0.051$, $b_3 = 2.449$ ($F_2$). All form factors are dimensionless, so each coefficient has the mass-dimension required to cancel that of the associated $Q^2\,(\mathrm{GeV}^2)$ factor

The next two transitions involve opposite parity diquarks: $\gamma 1^\pm \rightarrow 0^\mp$. They are characterised by two form factors [86]:

$$\begin{aligned} \varLambda _{\mu \rho }^{\mp \pm }(p_i,p_f) = \sum _{j=1}^2 T_{\mu \rho }^{(j)}(p_i,p_f) F_j^{\mp \pm }(Q^2) \,, \end{aligned}$$

(A.12)

where

$$\begin{aligned} T_{\mu \rho }^{(1)}(p_i,p_f)&= \frac{m_{1^\pm }}{\mathcal {D}} \big [\varOmega \;\mathcal {P}^{T}_{\mu \rho }(p_f) \nonumber \\&-\mathcal {P}^{T}_{\mu \nu }(p_f)p_{i\nu }(p_{f\rho }(p_f\cdot p_i)-m_{1^\pm }^2 p_{i\rho }) \big ] \,, \end{aligned}$$

(A.13a)

$$\begin{aligned} T_{\mu \rho }^{(2)}(p_i,p_f)&= \frac{m_{1^\pm }}{\mathcal {D}} \mathcal {P}^{T}_{\mu \nu }(p_f)p_{i\nu }\big [(p_f\cdot p_i)(p_f+p_i)_{\rho } \nonumber \\&- m_{0^\pm }^{2}p_{f\rho }-m_{1^\pm }^{2}p_{i\rho } \big ], \end{aligned}$$

(A.13b)

with $\varOmega = (p_i \cdot p_f)^2- p_i^2 p_f^2$ and $\mathcal {D} = \varOmega , m_{1^-}^4$ for the $\gamma 1^+ \rightarrow 0^-$ and $\gamma 1^-\rightarrow 1^+$ cases, respectively.

Accurate interpolations of the computed results for these form factors are provided by [2, 3] Padé approximants with the coefficients described in Table 4. They are illustrated in Fig. 13. Evidently, $F_1$ is dominant in both cases and the $0^+\leftrightarrow 1^-$ transition form factors exhibit greater sensitivity to the DqAMM.

Fig. 13

Upper panel – A. $\gamma ^{(*)} 1^+ \rightarrow 0^-$ transition form factors, Eq. (A.12): $F_1(Q^2)$ – solid red; and $F_2(Q^2)$ – dashed blue. Lower panel – B. $\gamma ^{(*)} 1^- \rightarrow 0^+$ transition form factors with legend as in A. In each case, the shaded areas show the response to variation of the DqAMM strength, $\zeta \in [0,0.5]$, around the highlighted $\zeta =1/3$ curves

The final transition is $\gamma 1^- \rightarrow 1^+$, a complete description of which requires three form factors:

$$\begin{aligned} \varLambda _{\mu \alpha \beta }^{1^+1^-}(K,Q) = \sum _{j=1}^3 T_{\mu \alpha \beta }^{(j)}(K,Q) \, F_j^{1^+1^-}(Q^2), \end{aligned}$$

(A.14)

where

$$\begin{aligned} T_{\mu \alpha \beta }^{(1)}(K,Q)&= m_{1^-} \, \frac{\epsilon _{\mu \rho \sigma \gamma }(p_{i}-p_{f})_{\gamma }}{4\sqrt{2}\varOmega } \nonumber \\&\quad \times (p_{i}+p_{f})_{\sigma } \, \big [2m_{1^-} \, \mathcal {P}_{\lambda \alpha }^{\bot }(p_{i}) \, p^{f}_{\lambda } \, \mathcal {P}_{\rho \beta }^{\bot }(p_{f}) \nonumber \\&\quad +2m_{1^+} \, \mathcal {P}_{\lambda \beta }^{\bot }(p_{f}) \, p^{i}_{\lambda } \, \mathcal {P}_{\rho \alpha }^{\bot }(p_{i}) \big ] \,, \end{aligned}$$

(A.15a)

$$\begin{aligned} T_{\mu \alpha \beta }^{(2)}(K,Q)&= m_{1^-} \, \frac{\epsilon _{\mu \rho \sigma \gamma }(p_{i}-p_{f})_{\gamma }}{4\sqrt{2}\varOmega } \nonumber \\&\quad \times (p_{i}+p_{f})_{\sigma } \big [2m_{1^-} \, \mathcal {P}_{\lambda \alpha }^{\bot }(p_{i}) \, p^{f}_{\lambda } \, \mathcal {P}_{\rho \beta }^{\bot }(p_{f}) \nonumber \\&\quad -2m_{1^+} \, \mathcal {P}_{\lambda \beta }^{\bot }(p_{f}) \, p^{i}_{\lambda } \, \mathcal {P}_{\rho \alpha }^{\bot }(p_{i}) \big ] \,, \end{aligned}$$

(A.15b)

$$\begin{aligned} T_{\mu \alpha \beta }^{(3)}(K,Q)&= \frac{\epsilon _{\mu \rho \sigma \gamma }(p_{i}-p_{f})_{\gamma }}{4\sqrt{2}\varOmega } \nonumber \\&\quad \times \big (-4\varOmega \, \mathcal {P}_{\rho \alpha }^{\bot }(p_{i}) \, \mathcal {P}_{\sigma \beta }^{\bot }(p_{f}) \nonumber \\&\quad + (p_{i}+p_{f})_{\sigma } [(p_{i}^{2}-p_{f}^{2}+Q^{2}) \, p_{f \lambda } \, \mathcal {P}_{\lambda \alpha }^{\bot }(p_{i}) \, \mathcal {P}_{\rho \beta }^{\bot }(p_{f}) \nonumber \\&\quad + (p_{i}^{2}- p_{f}^{2}-Q^{2}) \, p_{i \lambda } \, \mathcal {P}_{\lambda \beta }^{\bot }(p_{f}) \, \mathcal {P}_{\rho \alpha }^{\bot }(p_{i})]\big ) \;. \end{aligned}$$

(A.15c)

This case requires that one evaluate the two possible orderings of incoming/outgoing diquarks in order to guarantee that the vertex $\varLambda _{\mu \alpha \beta }^{1^+1^-}(K,Q)$ is symmetric under the simultaneous interchanges $p_i \leftrightarrow p_f$, $\alpha \leftrightarrow \beta$.

Fig. 14

Photon induced $1^+ \leftrightarrow 1^-$ transition form factors, Eq. (A.14): $F_1(Q^2)$ – solid red; $F_2(Q^2)$ – dashed blue; and $F_3(Q^2)$ – dot-dashed green. The shaded band shows the response to variation of the DqAMM strength, $\zeta \in [0,0.5]$, around the highlighted $\zeta =1/3$ curves

The calculated form factors are drawn in Fig. 14. Accurate interpolations of the results are provided by [1, 2] Padé approximants with the coefficients listed in Table 4. The DqAMM has only a marginal impact on these transition form factors.

Appendix B: Nucleon elastic and transition form factors

In our SCI quark+diquark picture of baryons, each elastic and transition form factor can be divided into two separate contributions: photon strikes quark; and photon strikes diquark. Thus, one may rewrite Eq. (11) as follows:

$$\begin{aligned}&\varGamma _\mu ^{BA}(P_f,P_i) \nonumber \\&\quad = \sum _{I=S1,S2,S3}\int _l \varLambda _+^B(P_f) \varLambda _\mu ^I(l;P_f,P_i) \varLambda _+^A(P_i)\,, \nonumber \\&\quad =: \int _l \varLambda _+^B(P_f) \left[ \sum _r \mathcal {Q}_\mu ^{(j)} + \sum _{s,t} \mathcal {D}_\mu ^{(s,t)} \right] \varLambda _+^A(P_i) \nonumber \\ \end{aligned}$$

(B.1)

where $BA= ++$, $--$, $-+$, as before, $\int _l$ is our SCI regularisation of the four-dimensional integral; and $\mathcal {Q}_\mu ^{(r)}$ is a diagram in which the photon strikes a quark with a diquark spectator, labelled by $r=0^+,1^+,0^-,1^-$, whereas $\mathcal {D}_\mu ^{(s,t)}$ indicates a diagram with a quark spectator to a diquark interaction $s\leftrightarrow t$, $s,t=0^+,1^+,0^-,1^-$.

1.1 Appendix B.1: Photon strikes quark

This contribution has the general form

$$\begin{aligned} \mathcal {Q}^{(r)}_\mu= & {} q_r \int _l {\bar{\psi }}_{(m)}^{f(r)} S(l_f^+)\varGamma _\mu ^\gamma (Q) S(l_i^+) \psi _{(m)}^{i(r)} \varDelta ^{(r)}(-l),\nonumber \\ \end{aligned}$$

(B.2)

where $l_{f,i}^\pm = \pm l + P_{f,i}$, $P_{f,i}^2=-M_{f,i}^2$, with $M_{f,i}$ being the masses of the baryons involved, and $Q^2=(P_f-P_i)^2$. Here, referring to Eq. (3), $\psi _{(m)}^{i(r)}$ denotes that part of the Faddeev amplitude for the indicated baryon that is associated with component-m of the diquark type r bystander; and $q_r$ is the charge of the struck quark in units of the positron charge. Depending on r, the diquark propagator may have Lorentz indices that are contracted with those of the Faddeev amplitude, also suppressed:

$$\begin{aligned} \varDelta ^{0^\pm }(K)= & {} \frac{1}{K^2+m_{0^\pm }^2}\;, \end{aligned}$$

(B.3)

$$\begin{aligned} \varDelta ^{1^\pm }_{\mu \nu }(K)= & {} \frac{1}{K^2+m_{1^\pm }^2}\left( \delta _{\mu \nu }+\frac{\delta _\mu \delta _\nu }{m_{1^\pm }^2} \right) \,. \end{aligned}$$

(B.4)

It is worth providing some details here on the $\varGamma _\mu ^{-+}=\gamma ^{(*)} p \rightarrow N^*(1535)\,\tfrac{1}{2}^-$ transition. Suppose $r=0^+$, then $q_r=2/3$, $m=1$, and

(B.5)

The $r=0^-$ case is obvious by analogy.

Consider next the case $r=1^+$. Then $m=1,2$,

(B.6a)

(B.6b)

In these expressions: , which means $q_{1^+}^1=-1/3$; and , $q_{1^+}^2=2/3$. We work in the isospin-symmetry limit; so, as noted following Eq. (4), . Hence, the terms in this $1^+$-spectator contribution combine as follows:

(B.7)

etc. Namely, they cancel.

Following this pattern, the contribution to Eq. (B.1) connected with the vector diquark bystander is readily constructed. Since this is an isoscalar diquark, there is no cancellation in this case.

Consider now Eq. (5b). Observe that the initial state nucleon has practically no pseudoscalar or vector diquark content; and we have just seen that the contributions from pseudovector-diquark bystanders cancel amongst themselves. Consequently, regarding the $\gamma ^{(*)} p \rightarrow N^*(1535)\,\tfrac{1}{2}^-$ transition, only the $0^+$ diquark spectator diagram can make a material contribution.

The calculation of any given contribution is completed by using a Feynman parametrisation to combine denominators, followed by evaluation of the four-dimensional integral following usual SCI procedures. An explicit example may be found in Ref.  [45].

1.2 Appendix B.2: Photon strikes diquark

For this class of processes, the general expression is:

$$\begin{aligned} \mathcal {D}^{(s,t)}_\mu&= q_{ts} \int _l {\bar{\psi }}^{f(t)}_{(m)} S(l) \psi ^{i(s)}_{(m)} \varDelta ^{t}(l_f^-) \varLambda _{\mu }(l_f^-,l_i^-) \varDelta ^{s}(l_i^-) \;, \end{aligned}$$

(B.8)

where $\varLambda _\mu$ corresponds to the appropriate photon-diquark vertex in Appendix A and, as above, the diquark propagator and Faddeev amplitude component may have contracted Lorentz indices.

Focusing again on $\gamma ^{(*)} p \rightarrow N^*(1535)\,\tfrac{1}{2}^-$, using the $\gamma 0^+ \rightarrow 1^+$ transition as an example and referring to Eq. (3), one has $q_{ts}=q_{\{ud\}}=1/3$,

(B.9a)

(B.9b)

where $\varLambda _{\lambda \alpha }^{1^+0^+}$ is given in Eq. (A.11). All other cases are equally straightforward.

Again, the evaluation of any given contribution is completed by following the procedures established in Ref.  [45].