Dynamical gravastars from the interaction between scalar fields and matter

Abstract

Gravastars are configurations of compact singularity-free gravitational objects which are interesting alternatives to classical solutions in the strong gravitational field regime. Although there are no static star-like solutions of the Einstein–Klein–Gordon equations for real scalar fields, we show that dynamical gravastars solutions arise through the direct interaction of a scalar field with matter. Two configurations presented here show that, within the internal zone, the scalar field plays a role similar to a cosmological constant, while it decays at large distances as the Yukawa potential. Like classical gravastars, these solutions exhibit small values of the temporal metric component near a transitional radial value, although this behaviour is not determined by the de Sitter nature of the internal space-time, but rather by a slowly-varying scalar field. The scalar field-matter interaction is able to define trapping forces that rigorously confine the polytropic gases to the interior of a sphere. At the surface of these spheres, pressures generated by the field-matter interaction play the role of “walls” preventing the matter from flowing out. These solutions predict a stronger scattering of the accreting matter with respect to Schwarzschild black holes.

1 Introduction

The detection of gravitational waves by merging compact objects [1] and the imaging of the environment around the supermassive compact object M87$^*$ [2] has spawned renewed attention to alternative solutions to the classic central singularities in collapsed matter structures [3] beyond General Relativity [4]. However, current observations cannot, as yet, disentangle effects associated with the properties of the accretion flow from the ones produced by a strong gravitational field [5].

One of the most attractive alternatives are gravitational-vacuum stars (gravastars), first proposed in references [6,7,8] as an extension of Bose–Einstein condensates in gravitational systems, and which constitute a broad class of solutions which do not require exotic new physics as they are supported by negative pressure and present no singularities or event horizons. Arbitrarily compact, they typically have an internal region described by a de Sitter space-time which is matched at the horizon by an external Schwarzschild metric. The matter is concentrated at the boundary, which shows infinite surface tension, appear to be dynamically stable [9], and might match the observed lensed images around M87$^*$ [10].

The present work identifies a new type of such solutions, which we call dynamical gravastars because the role of the de Sitter space in repelling matter away from the origin of coordinates is played here by a scalar field, a more dynamical object than the cosmological constant in the de Sitter space. The search for such solutions was first suggested by [11,12,13,14], and in [11, 12] it was argued that the Einstein–Klein–Gordon (EKG) equations can be solved exactly in the interior of a sphere with a scalar field configuration interacting with gravity. There is a singularity at certain critical radius, and outside this spherical zone, the solution is exactly the Schwarzschild space-time with a zero value of the scalar field. These solutions, however, were found in the sense of the Colombeau-Egorov generalized functions, which are still in a clarification stage regarding its connections with real physical solutions [15, 16]. If the solution advanced in [11, 12] is shown to have a physical meaning it could furnish a further example against the validity of the Penrose Conjecture [17]. Within this framework, there are solutions in which matter could be trapped in an interior spherical region, outside of which the field reduces gradually (but within a relatively short distance) to the classical Schwarzschild space-time with a vanishing scalar field [18].

Further, in [13, 14, 19] it was argued that the existence of a static solution of the EKG equations became allowed thanks to the assumed interaction of the scalar field with matter. Although the structure resulted not to be closely resembling a neat gravastar, the discussion suggested the possibility of obtaining further similar solutions.

Here we consider physical systems constituted by a real scalar field interacting with matter in two different forms: an elastic solid and a polytropic gas. An important and already mentioned element of the model is that the scalar field is considered interacting with the energy density, as it is relevant for reaching boson star solutions [13, 14]. In the two cases studied, this interaction is implemented assuming that the source of the scalar field is proportional to the particular matter energy density under consideration. The Lagrangian also includes quadratic terms in the source, which are incorporated ensuring a positive-definite energy density at any point of the space-time.

First we write the Einstein–Klein–Gordon equations for the two forms of matter in terms of the scalar field source J(r), the energy density $\varepsilon (r)$ and the pressure P(r). Second, the solutions must have configurations where the matter is rigorously confined within a spherical region, and we formulate criteria for the existence of solutions with trapped matter configurations.

Numerical solutions of the equations for each type of matter are found and all the field configurations show an internal region within which all the matter of the system is exactly constrained to be inside a sphere of radius $r_{b}$, at which point the pressure falls to zero.

The first type of dynamical gravastar solution is associated with matter defined by an elastic body with a constitutive relation between energy density and pressure of the form $\varepsilon (p)=\varepsilon _{0}+\sigma p^{2}$, where the energy density grows with the square of the pressure. The interaction between the scalar field and matter is implemented by an assumed proportionality of the energy density $\varepsilon (p(r))$ with the sources of the scalar field J(r). In this example, the equation coming from the Bianchi identity (which implements the mechanical equilibrium condition for this system) allows for solutions showing a jump-like reduction of the pressure to zero values at some radial point. Therefore, this solution describes a spherical elastic body with a boundary with the vacuum in the external region. The scalar field decays in the faraway radial region like the exponential Yukawa potential.

The second dynamical gravastar solution is to a polytropic gas with a constitutive relation of the form $p(r)= e^{-\gamma } \varepsilon (r)^{\gamma }$. This case represents a gas of particles, and we expect that the solutions might show a smooth decay of the pressure and density as the radius increases. Surprisingly, we find that in addition to smooth solutions, there are configurations in which the gas is rigorously “trapped” within a spherical region by the interaction with the scalar field. Again the equation associated to the Bianchi relations might develop impulsive force densities acting like solid walls preventing particles of the gas from flowing outside a trapped spherical region.

The satisfaction of the existence criteria are checked for each of the two types of solutions.

The two solutions presented here strongly suggest the possibility of having regions in which the metric closely approaches one with horizons, but not quite reaching the limit to change its signature for travellers passing though this region. That is, the space-time does not unavoidably show self-trapped trajectories, attracting all the bodies to a central singularity. In the external region, the solution is close to the Schwarzschild space-time. These results argue, therefore, for the existence of solutions of the EKG equations for interacting matter and scalar fields, which truly constitute dynamical gravastars alternatives to the classical solutions.

In Sect. 2, we present the general system of EKG equations including direct interaction between matter and a scalar field, which are derived in Appendix A. Sect. 3 gives the general equations corresponding to matter exactly confined within a spherical region of radius $r_{b}$ , and their numerical solutions are given Sect. 4 for elastic bodies. The satisfaction of the solvability condition is checked. Section 5 presents solutions associated to a polytropic gas trapped by the interaction with the scalar field inside a central spherical region, and the corresponding satisfaction of the solvability condition verified. The results are summarised in Sect. 6.

2 The EKG equations including a field-matter interaction

The field equations to be solved are very close in form to the ones considered in [13], but we also derive them in Appendix A for clarity. In their general form, that is, without specifying the scalar field sources $J\,(r)$ and the constitutive relation between the energy $\varepsilon (r)$ and pressure P(r), the EKG equations are derived in Appendix A as expressions (A.23)–(A.26). Reproduced here, they are

$$\begin{aligned} E_{ekg}^{(1)}(r)= & {} {\frac{u_{,r}(r)}{r}}-{\frac{1-u(r)}{r^{2}}}\nonumber \\&+\frac{1}{2}\left( u(r){\varPhi _{,r}(r)}^{2}+\left( \varPhi (r)+J(r)\right) ^{2}\right) \nonumber \\&+\,\varepsilon (r)=0, \end{aligned}$$

(1)

$$\begin{aligned} E_{ekg}^{(2)}(r)= & {} \frac{u(r)}{v(r)}\frac{v_{,r}(r)}{r}-{\frac{1-u(r)}{r^{2}}} \nonumber \\&+\frac{1}{2}\left( -u(r){\varPhi _{,r}(r)}^{2}+\left( \varPhi (r) +J(r)\right) ^{2}\right) \nonumber \\&-\,P(r)=0, \end{aligned}$$

(2)

$$\begin{aligned} E_{ekg}^{(3)}(r)= & {} P_{,r}(r)+\left( \varepsilon (r)+P(r)\right) \frac{v_{,r}(r)}{2v(r)}\nonumber \\&-\left( J(r)+\varPhi (r)\right) J_{,r}(r)=0, \end{aligned}$$

(3)

$$\begin{aligned} E_{ekg}^{(4)}(r)= & {} J(r)+{\varPhi }(r)-u(r)\text { }{\varPhi }^{\prime \prime }(r) \nonumber \\&-{\varPhi }^{\prime }(r)\left( \frac{u(r)+1}{r} \right. \nonumber \\&\left. -\frac{r}{2}\left( {\varPhi }(r)+J(r)\right) ^{2}+\frac{\varepsilon (r)-P(r)}{2}\right) =0, \end{aligned}$$

(4)

The first two are the Einstein equations associated to the temporal and radial diagonal components of the mixed tensor Einstein equations. The third relation is the Bianchi identity defined by the exact vanishing of the covariant divergence of the energy momentum tensor. Physically, it represents the mechanical equilibrium of the system. Finally, the fourth equation is the Klein–Gordon equation in the curved space-time defined by the scalar and normal matter. We recall here the various notations employed below for the radial derivatives of a function f(r):

$$\begin{aligned} \frac{df(r)}{dr}=f_{r}(r)=f^{\prime }(r). \end{aligned}$$

We solve these equations adopting constitutive relations between the energy corresponding to an elastic body and to a polytropic gas. In the two situations the interaction between matter and the sources of the real scalar field is implemented assuming a proportionality between the scalar field sources and the energy density of the form

$$\begin{aligned} J(r) \; = \; \alpha \text { }\varepsilon (r). \end{aligned}$$

(5)

3 Gravastars and EKG equations including matter

In this section we search for general solutions of the EKG equations above (1–4) including the interaction between the scalar field and matter. Specifically, we search for solutions resulting in a spherical gravastar-like configuration where the distribution of matter drastically ends at a radial distance $r_{b}$. Outside this region, when $r>r_{b}$, the matter is absent.

Let us consider the scalar field sources and energy density in Eqs.  (1)–(4) to satisfy

$$\begin{aligned} J(r)&=\overline{J}(r)\text { }\theta (r_{b}-r), \end{aligned}$$

(6)

$$\begin{aligned} \varepsilon (r)&=\overline{\varepsilon }(r)\text { }\theta (r_{b}-r), \end{aligned}$$

(7)

$$\begin{aligned} P(r)&=\overline{P}(r)\text { }\theta (r_{b}-r). \end{aligned}$$

(8)

That is, the scalar field sources, the energy density and pressure are assumed to vanish for radii larger than $r_{b}$, outside the body.

Note that the proportionality between the scalar field source and energy density functions conveys the interaction between the scalar field and matter through

$$\begin{aligned} \overline{J}(r)=\overline{\varepsilon }(r), \end{aligned}$$

which is be valid for the two types of matter considered in the following sections.

For the region (0,  $r_{b})$ the EKG equations in terms of the field solutions in this neighborhood $u_{i}(r),v_{i}(r),\varPhi _{i}(r)$ and P(r), take the form

$$\begin{aligned}&\frac{1}{r}{\frac{du_{i}(r)}{dr}}-{\frac{1-u_{i}(r)}{r^{2}}} \nonumber \\&\quad = -\frac{1}{2}\left( u_{i}(r)\left( \frac{d{\varPhi }_{i}}{dr}{(r)}\right) ^{2}+\left( \varPhi _{i}(r)+\overline{J} (r)\right) ^{2}\right) -\overline{\varepsilon }(r), \end{aligned}$$

(9)

$$\begin{aligned}&\frac{1}{r}\frac{u_{i}(r)}{v_{i}(r)}\frac{dv_{i}(r)}{dr}-{\frac{1-u_{i} (r)}{r^{2}}} \nonumber \\&\quad = -\frac{1}{2}\left( -u_{i}(r)\left( \frac{d{\varPhi }_{i}}{dr}{(r)}\right) ^2 +\left( \varPhi _{i}(r)+\overline{J}(r)\right) ^{2}\right) +\overline{P}(r), \end{aligned}$$

(10)

$$\begin{aligned}&0 =\frac{d\overline{P}(r)}{dr}+\left[ \varepsilon (r)+\overline{P}(r)\right] \frac{1}{2v_{i}(r)}\frac{dv_{i}(r)}{dr} \nonumber \\&\quad - \left[ \overline{J}(r)+\varPhi _{i}(r)\right] \frac{d}{dr}\overline{J}(r), \end{aligned}$$

(11)

$$\begin{aligned}&\quad \overset{}{\text { }\ \overline{J}}(r)+{\varPhi }_{i}(r)-u_{i}(r)\text { }{\varPhi } _{i}^{\prime \prime }(r) = {\varPhi }_{i}^{\prime }(r)\left[ \frac{u_{i}(r)+1}{r} \right. \nonumber \\&\quad \left. -r\text { }\left( \frac{{\varPhi }_{i}(r)^{2}}{2}+\overline{J}(r){\varPhi }_{i} (r)+\frac{\overline{J(}r)^{2}}{2}+\frac{\overline{\varepsilon }(r)-\overline{P}(r)\text { }}{2}\right) \right] . \nonumber \\ \end{aligned}$$

(12)

Next, for radial values larger than $r_{b}$, that is, in the interval $(r_{b},\infty )$ we consider the same set of Eqs.  (1)–(4), but where the scalar field sources, energy density and pressure vanish exactly

$$\begin{aligned}&\frac{1}{r}{\frac{du_{e}(r)}{dr}}-{\frac{1-u_{e}(r)}{r^{2}}} \nonumber \\&\quad = -\frac{1}{2}\left( u_{e}(r)\left( \frac{d{\varPhi }_{e}}{dr}(r)\right) ^{2}+\varPhi _{e}(r)^{2}\right) , \end{aligned}$$

(13)

$$\begin{aligned}&\quad \frac{1}{r}\frac{u_{e}(r)}{v_{e}(r)}\frac{dv_{e}(r)}{dr}-{\frac{1-u_{e} (r)}{r^{2}}} \nonumber \\&\qquad = -\frac{1}{2}\left( -u_{e}(r)\left( \frac{d{\varPhi }_{e}}{dr}(r)\right) ^{2}+\varPhi _{e}(r)^{2}\right) , \end{aligned}$$

(14)

$$\begin{aligned}&\quad 0 = 0 \end{aligned}$$

(15)

$$\begin{aligned}&\quad {\varPhi }_{e}(r)-u_{e}(r)\text { }{\varPhi }_{e}^{\prime \prime }(r) \nonumber \\&\qquad = {\varPhi } _{e}^{\prime }(r)\left( \frac{u_{e}(r)+1}{r}-r\frac{{\varPhi }_{e}(r)^{2}}{2}\right) . \end{aligned}$$

(16)

Here the fields $u_{e}(r), v_{e}(r), \varPhi _{e}(r)$ indicate the solutions of the above equations. Note that in this zone, the Bianchi identity is automatically satisfied.

We now define an ansatz for the solution of the EKG equations we seek along the whole radial axis as

$$\begin{aligned} u(r)&=u_{i}(r)\text { }\theta (r_{b}-r)+u_{e}(r)\text { }\theta (r-r_{b}), \end{aligned}$$

(17)

$$\begin{aligned} v(r)&=v_{i}(r)\text { }\theta (r_{b}-r)+u_{e}(r)\text { }\theta (r-r_{b}), \end{aligned}$$

(18)

$$\begin{aligned} {\varPhi }(r)&={\varPhi }_{i}\text { }\theta (r_{b}-r)+{\varPhi }_{e}(r)\text { } \theta (r-r_{b}), \end{aligned}$$

(19)

$$\begin{aligned} {P}(r)&={\overline{P}(r)}\text { }\theta (r_{b}-r), \end{aligned}$$

(20)

$$\begin{aligned} \varepsilon (r)&=\overline{\varepsilon }(r)\text { }\theta (r_{b}-r), \end{aligned}$$

(21)

$$\begin{aligned} J(r)&=\overline{J}(r)\text { }\theta (r_{b}-r). \end{aligned}$$

(22)

That is, the solution is assumed to coincide with the fields $u_{i} (r),v_{i}(r),\varPhi _{i}(r)$ and P(r) for points within the internal interval (0,  $r_{b})$. In the external region $(r_{b},\infty )$ the solution is chosen to be given by the external solution $u_{e}(r)$, $v_{e}(r)$, $\varPhi _{e}(r)$.

3.1 Criteria for solutions

To find gravastar-like solutions for the two forms of matter considered, we use the criterion employed in the theory of generalised functions. In our case, it can stated as follows: The system of differential equations $E_{ekg}^{(n)}(r)=0,$ for $n=1,2,3,4$ defined in Eqs.  (1)–(4) are solved by the fields $u(r),v(r),\varPhi (r),P(r),\varepsilon (r)$ and J(r) specified in (17)–(22), if all the integrals

$$\begin{aligned} \int _{0}^{\infty }dr\ \varOmega (r)\text { }E_{ekg}^{(n)}(r)=0,\text { }\ n=1,2,3,4, \end{aligned}$$

vanish for any arbitrarily-chosen test function $\varOmega (r)$ pertaining to $C^{\infty }.$

3.2 The general solution for trapped matter region

Let us first consider the equations $E_{ekg}^{(n)}(r)=0, \, n=1,2,4,$  that is, excluding for the moment the Bianchi identity equation. In these three equations there appear no derivatives of the suddenly-changing quantities $P(r),\varepsilon (r)$ or J(r) at the point $r_{b}$. Let us then assume that we determine the above-defined fields $u_{i}(r), v_{i}(r), \varPhi _{i}(r), P(r), \varepsilon (r)$ and J(r) that effectively solve the set of internal equations (9)–(12) in the entire interval $(0,r_{b})$, in a way that the three fields $u_{i}(r)$, $v_{i}(r)$, $\varPhi _{i}(r)$ have well-defined finite limits

$$\begin{aligned} \lim _{r\rightarrow rb}u_{i}(r_{b})&=u_{i}(r_{b}), \end{aligned}$$

(23)

$$\begin{aligned} \lim _{r \rightarrow rb}v_{i}(r)&=v_{i} (r_{b}), \end{aligned}$$

(24)

$$\begin{aligned} \lim _{r \rightarrow rb}\varPhi _{i}(r)&=\varPhi _{i}(r_{b}), \end{aligned}$$

(25)

$$\begin{aligned} \lim _{r \rightarrow rb}\varPhi ^{\prime }_{i}(r)&=\varPhi ^{\prime }_{i}(r_{b}), \end{aligned}$$

(26)

at the radial point $r_{b}.$

If the above conditions are met, let us also assume that the set of equations for the external zone (13)–(16) can also be solved in an external interval $\ (r_{b},\infty ),$ by fixing the ending values of the interior solution at $r_{b}:$ $u_{i}(r_{b}),$ $v_{i}(r_{b}),\varPhi _{i} (r_{b})$ and $\varPhi _{i}^{\prime }(r_{b})$ as initial values for the Eqs. (13)–(16) in the external region. These conditions at $r_{b},$ then impose the continuity for the general solution of the quantities u(r), v(r), $\varPhi (r)$ plus the continuity of the derivative of the scalar field $\varPhi ^{\prime }(r),$ which can be fixed because the Klein–Gordon equation is the only one of second order.

Consider now the entire radial axis as the union of small vicinities $(r_{b}-\delta ,r_{b}+\delta )$ of the point $r_{b}$ and the two interior and external intervals $(0,r_{b}-\delta )$ and $(r_{b}+\delta ,\infty ).$ Then, the three equations can be written as

$$\begin{aligned}&\int _{0}^{\infty }dr\, \varOmega (r)\,E_{ekg}^{(n)}(r) =\int _{0}^{r_{b}-\delta }dr\ \varOmega (r)\,E_{ekg}^{(n)}(r) \\&\qquad +\int _{r_{b}-\delta }^{r_{b}+\delta }dr\, \varOmega (r)\,E_{ekg}^{(n)}(r)+ \int _{r_{b}+\delta }^{\infty }dr\ \varOmega (r)\text { }E_{ekg}^{(n)}(r)\\&\quad = \int _{r_{b}-\delta }^{r_{b}+\delta }dr\ \varOmega (r)\text { }E_{ekg} ^{(n)}(r)=0,\; \; n=1,2,4, \end{aligned}$$

in which the integrals over the intervals $(0,r_{b}-\delta )$ and $(r_{b}+\delta ,\infty )$ identically vanish because the internal and external fields satisfy the corresponding equations in such regions.

For the remaining integral is helpful to consider the definitions of the ansatz for the three fields

$$\begin{aligned} u(r)&=u_{i}(r)\text { }\theta (r_{b}-r)+u_{e}(r)\text { }\theta (r-r_{b}), \end{aligned}$$

(27)

$$\begin{aligned} v(r)&=v_{i}(r)\text { }\theta (r_{b}-r)+u_{e}(r)\text { }\theta (r-r_{b}), \end{aligned}$$

(28)

$$\begin{aligned} {\varPhi }(r)&={\varPhi }_{i}\text { }\theta (r_{b}-r)+{\varPhi }_{e}(r)\text { } \theta (r-r_{b}), \end{aligned}$$

(29)

around the transition point $r_{b}$. It can be noted that only up to the first derivatives of u(r) , v(r), and up to the second one of $\phi (r)$ appear in the three equations $E_{ekg}^{(n)}(r)=0$   $n=1,2,4$. However, the only first derivatives involved of the continuous u(r) and v(r) can not introduce any unbounded quantity in the interval $(r_{b}-\delta ,r_{b}+\delta )$ due to the imposed continuity conditions. Further, the fact that the first derivative of the scalar field is continuous defines that the only second derivative of the equations, which appears in the Klein-Gordon equation, again is unable to introduce an unbounded term in the remaining integral.

Therefore, since $\delta$ is completely arbitrary, taking the limit $\delta \rightarrow 0$ shows the three equations are satisfied

$$\begin{aligned} \int _{0}^{\infty }dr\ \varOmega (r)E_{ekg}^{(n)}(r)=0, \quad n=1,2,4. \end{aligned}$$

(30)

For the third equation, that is, the Bianchi identity, we decompose again the entire radial axis in the union of small vicinity $(r_{b}-\delta ,r_{b}+\delta )$ of the point $r_{b}$ and the two interior and external intervals $(0,r_{b}-\delta )$ and $(r_{b}+\delta ,\infty ).$ The condition for a solution of the third equation takes the form

$$\begin{aligned}&\int _{0}^{r_{b}-\delta }dr\ \varOmega (r)E_{ekg}^{(3)}(r) \\&\quad \, + \int _{r_{b}-\delta }^{r_{b}+\delta }dr\ \varOmega (r)\text { }E_{ekg}^{(3)}(r)+ \int _{r_{b}+\delta }^{\infty }dr\ \varOmega (r)\text { }E_{ekg}^{(3)}(r) = 0,\\&\quad \int _{r_{b}-\delta }^{r_{b}+\delta }dr\ \varOmega (r)\text { }E_{ekg}^{(3)}(r) = 0, \end{aligned}$$

also because the interior and exterior fields, by construction, solve the four equations in the internal and external zones. Therefore, the integration range is reduced to the interval of arbitrary width $2\,\delta .$

The remaining integral also can be rewritten as

$$\begin{aligned} 0&=\int _{r_{b}-\delta }^{r_{b}+\delta }dr\ \varOmega (r)\text { }\left( \left( \varepsilon (r)+P(r)\right) \frac{1}{2v(r)}\frac{dv(r)}{dr}\right) +\nonumber \\&\int _{r_{b}-\delta }^{r_{b}+\delta }dr\ \varOmega (r)\text { }\bigg ( P^{\prime }(r)-J^{\prime }(r)\left( J(r)+{\varPhi }(r)\right) \bigg ) . \end{aligned}$$

(31)

The first integral vanishes because the interval width $2 \,\delta$ is arbitrary and the integrand is a bounded function, since all the quantities entering are finite. The remaining integral is considered for the case in which the source $J(r)=-g$ $\varepsilon (r)$ is not constant as a function of the radius.

In this case let us assume that the constitutive relations and the expression determining the interaction of the scalar field and matter take the forms

$$\begin{aligned} \varepsilon \left( p(r)\right)&= \; f(p(r)) \,, \end{aligned}$$

(32)

$$\begin{aligned} J(r)&= \; - g\text { }\varepsilon (r) \, . \end{aligned}$$

(33)

Then, the integral (31) can be transformed to the form

$$\begin{aligned} 0&=\int _{r_{b}-\delta }^{r_{b}+\delta }dr\, \varOmega (r)\,\bigg ( P^{\prime }(r)-J^{\prime }(r)(J(r)+{\varPhi }(r))\bigg ) \nonumber \\&=\int _{r_{b}-\delta }^{r_{b}+\delta }dr\, \varOmega (r)\,P^{\prime }(r)\left( 1+g\big (-g\text { }\varepsilon (r)+{\varPhi }(r)\big )\frac{\partial f(p)}{\partial p}\right) . \end{aligned}$$

(34)

In the integrand of the integral, it can be noted that if the pressure suddenly vanishes at $r=r_{b}$ the integral does not vanish as required, unless the function

$$\begin{aligned} Z(r)=1+g\bigg (-g\text { }\varepsilon (r)+{\varPhi }(r)\bigg )\frac{\partial f(p)}{\partial p}, \end{aligned}$$

(35)

also reduces to zero at $r_{b}$.

For the third equation to be satisfied there is an additional boundary condition for the ansatz to become a solution in the form

$$\begin{aligned} 1+g\bigg (-g\text { }\varepsilon (r)+{\varPhi }(r)\bigg )\frac{\partial f(p)}{\partial p} =0. \end{aligned}$$

(36)

In addition, for the solubility to hold it becomes also necessary to check that the behaviour of $P^{\prime }(r)$ in the neighborhood of the boundary is not able to invalidate the vanishing of the integral (31). This verification will be done in what follows for each of the two problems considered.

We then arrive to the solution we were seeking: assuming that the interior and exterior solutions can be obtained, that the fields u,  v,  ${\varPhi }$ and ${\varPhi }^{\prime }$ can be made continuous at the point $r_{b}$ and also that the function $1+g (-g \varepsilon (r)+{\varPhi }(r))\frac{\partial }{\partial p}f(p)$ might also be fixed to vanish at the point $r_{b}$, the proposed ansatz solution also satisfies the four EKG equations including matter interacting with the scalar field.

In the next two sections we find numerical solutions satisfying the above conditions for the two types of matter being trapped in the central zone: an elastic solid and a polytropic gas.

4 The elastic body gravastar

The corresponding numerical solution of the Eqs. (1)–(4) for matter as an elastic body assumes that the interaction between the scalar field and matter is reflected in the adopted proportionality between the energy density and scalar field sources $J(r)=g \varepsilon (r).$

The energy density at the interior point is now defined as

$$\begin{aligned} \varepsilon (r)&=\varepsilon _{0}+\sigma \text { }P(r)^{2}\\&=f(P), \end{aligned}$$

(37)

which reflects that the energy density of the body has a minimum at zero pressure and grows quadratically with the pressure. Therefore, we are interested in describing a spherical elastic body whose extension ends at the radius $r_{b}.$

For the evaluation of the searched solution satisfying the conditions required in Sect. 3, we simply follow the procedure described in the previous section. After solving the equations in the interior region, the radial value $r_{b}$ is determined finding the roots of the function Z(r) which in this case is

$$\begin{aligned} Z(r)&=1+g\left( -g\text { }\varepsilon (r)+{\varPhi }(r)\right) \frac{\partial }{\partial P}f(P), \end{aligned}$$

(38)

$$\begin{aligned} J(r)&=\alpha \text { }\varepsilon (r)=\alpha (\varepsilon _{0}+\sigma \text { } P(r)^{2}). \end{aligned}$$

(39)

Equations (9)–(11) and (13)–(15) are initially solved for $r<r_{b}$ and $r>r_{b},$ respectively, and then an iterative procedure described below is implemented to find a solution showing a Yukawa-like behaviour for the scalar field in the distant regions.

The initial conditions for the equations are chosen at a point very close to origin $r=\varDelta$, and they are fixed in the form

$$\begin{aligned} \varPhi (\varDelta )&=1, \end{aligned}$$

(40)

$$\begin{aligned} \varPhi ^{\prime }(\varDelta )&=0, \end{aligned}$$

(41)

$$\begin{aligned} u(\varDelta )&=1, \end{aligned}$$

(42)

$$\begin{aligned} v(\varDelta )&=0.0085, \end{aligned}$$

(43)

$$\begin{aligned} P(\varDelta )&=0.2, \end{aligned}$$

(44)

$$\begin{aligned} \varDelta&=0.000001. \end{aligned}$$

(45)

The proportionality constants defining the interaction between scalar field and matter and the elastic body constitutive relation were fixed to the values

$$\begin{aligned} \alpha&=3, \end{aligned}$$

$$\begin{aligned} \varepsilon _{0}&=0.931116, \end{aligned}$$

(46)

$$\begin{aligned} \sigma&=3. \end{aligned}$$

(47)

As it noted above, the solutions require a procedure for adjusting the parameters. Assuming the values of the parameters given above, the scalar field solutions at large radial distances might appear by example, positive (negative) at large radii. In this case increasing (decreasing) of the $\varepsilon _{0}$ parameter, it is always possible to attain solutions for which the scalar field tends to show negative (positive) values at large radii. This property implies an iterative procedure, in which the scalar field of the arising solution can be made to decrease exponentially at large radial values.

Fig. 1

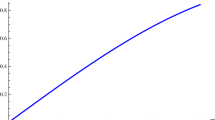
Radial dependence of u(r) and v(r) which define the metric. The top figure shows u(r) as the curve tending to unity at the origin of coordinates and v(r) as the one approaching a much smaller value at the origin. The bottom figure shows the same curves in detail at the boundary. Note that the potential v(r) exhibits a maximum at the origin. Therefore, in this case the gravitational potential decreases away form the center. This is a behaviour similar to the classical gravastars solutions [6,7,8]

Figure 1 (top) shows the dependence of the radial diagonal component of the countervariant metric u(r),  in common with the temporal component of the covariant metric. The metric rapidly tends to be closely similar to the Schwarzschild one in the external zone, resembling the structure of the classical solutions of this type [6,7,8]. The solution shows a structure very similar to a gravastar, as the minimum of u(r) is very close to zero. In addition, the gravitational potential exhibits a maximum at the centre of symmetry just as in the usual vacuum stars.

Fig. 2

The radial dependence of the scalar $\phi (r)$ for the elastic body solution shows a decay at infinity with an exponential Yukawa-like dependence

The temporal component of the covariant metric, shown in detail in Fig. 1 (bottom), also approaches zero at the surface of the body. However, in this case, this field slightly increases to a maximum at the origin. As before, in the external regions the radial behaviour of u(r) and v(r) tends to approach one to another (mainly related by a multiplicative constant). This describes the fact that the external zone asymptotically tends to be the Minkowski spacetime in the distant regions.

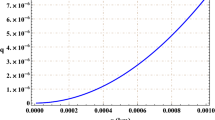
The scalar field behaviour is shown in Fig. 2, and tends to rapidly decrease in the external region approaching the exponential behaviour of the Yukawa potential.

The resulting radial dependence of the pressure in the elastic body is illustrated in Fig. 3. As in the previous solution, the pressure grows as the radial position tends to the centre of symmetry and drastically reduces to zero at the boundary of the elastic body at the radial position $r_{b}.$

Fig. 3

The pressure of the configuration tends to contract the elastic body increasingly as the symmetry centre is approached. However, this behaviour is curious, because the gravitational potential decreases when moving away form the centre, attracting the matter to the boundary. This property means that since the forces determined by the field-matter interaction oppose the repulsing gravitational forces and overcome them, they lead to a net contraction. Since the parameters can be varied, this property can be different for other sets of values

4.1 Solvability condition: elastic body

Let us inspect now in more detail the behavior of $P^(r)$ around the boundary, which is illustrated in Fig. 3. The pressure rapídly tends to vanish at $r_b$ and its derivative becomes negatively large in approaching the boundary from the left. For studying the degree of increasing of this derivative, we can write the following expression for P(r) in the border region

$$\begin{aligned} P(r)= P_{int}(r) \, \theta (r_b -r), \end{aligned}$$

(48)

where $P_{int}(r)$ defines the values of the pressure for points being at the interior of the boundary at which it reduces to zero. But, it is possible rewrite this expression in the form

$$\begin{aligned} P(r)= P_{int}(r_b)\, \theta (r_b -r)+ (P_{int}(r)- P_{int}(r_b)) \, \theta (r_b -r),\nonumber \\ \end{aligned}$$

(49)

in which $P_{int}(r_b)$ is the limit $r \rightarrow r_b^{-}$ of the internal pressure. For the present case of the elastic body, $P_{int}(r_b)=0$, because the pressure tends to zero at the left of $r_b$. However, for the next to be considered polytropic gas example, it will be a finite constant. Now, taking the radial derivative of P(r) and multiplying by the function Z(r), we can write for the factor $Z(r)P^{\prime }(r)$ in the integrand of the condition (34), the expression

$$\begin{aligned} Z(r)\, P^{\prime }(r)= & {} -P_{int}(r_b)\, Z(r) \, \delta (r- r_b )-(P_{int}(r) \nonumber \\&- P_{int}(r_b))\, Z(r) \, \delta (r_b -r) \nonumber \\&+ P^{\prime }_{int}(r) \, Z(r) \, \theta (r_b -r). \end{aligned}$$

(50)

The remaining factor in the integrand in (34) is $\varOmega (r)$ which is an infinitely differentiable bounded function.

Fig. 4

The bottom curve is the radial dependence of the factors $Z(r)\, P^{\prime }(r)$ associated to the integrand in (34), shown in a close vicinity of $r_b$. It can be seen that in the limit $r \rightarrow r_b^{-}$ this quantity is finite. Therefore, the integration vanishes when the width $2 \delta$ of the region approaches zero. This result verifies the satisfaction of the solvability condition. The plot at the top illustrates the values of the pressure P(r) which suddenly reduces to zero at $r_b$

The first term in (49) is the product of the function Z(r) by the Dirac Delta function $\delta (r- r_b)$, with support in $r_b$. But, since Z(r) has a zero at $r_b$, this term leads to a zero contribution to the integral in (34). The second term is also proportional to the same Dirac Delta function, but as multiplied by the product of two factors both having a zero at $r_b$. Thus, this contribution also leads to a vanishing addition in (34). The last term in (49) is proportional to a step-like function times the factor $P^{\prime }_{int}(r) Z(r)$, in which Z(r) has a zero at $r_b$. But, $P^{\prime }_{int}(r)$ rapidly grows when $r \rightarrow r_b^{-}$. However, the plot of this third term is shown in the Fig. 4 showing that the limit $r \rightarrow r_b^{-}$ of the product is finite. Therefore, as the size of the integration interval $2 \delta$ in (34) tends to zero, the examined contribution of the third term also vanishes, which checks the satisfaction of the solvability condition (34).

It should be noted that the equation of motion associated to the Bianchi identify corresponds to a mechanical equilibrium of these systems. This equation is particularly relevant in defining the required boundary conditions, and thus determining the concentrated pressures which act over the boundary in this elastic body case. The internal pressure of matter suddenly jumps at the radius $r_{b}$ to zero values at vacuum for $r > r_{b}$ and Fig. 5 shows the zero crossing of the function Z(r) which determines $r_{b}$.

To conclude this section, it is of interest to note that the boundary pressures which appear here can be expected to be present in the just-discussed elastic body. This is because parts of the solids are not expected to detach from the body at a free boundary. However, in the next section we discuss the case of a polytropic gas, which is expected to occupy, through diffusion processes, all the volume accessible to it. In this case a force also appears, purely determined by the interaction of the scalar field with matter, and which also confines the gas to the interior of a spherical region.

Fig. 5

The function $\mathrm {Crit(r)}=-Z(r) / (2\sigma g^2)$ for the case of the elastic body which determines the value of $r_{b}$ at which it vanishes

5 The polytropic gas gravastar

The method for deriving this solution is similar to one used in the previous section. First, Eqs. (9)–(11) and (13)–(15) are solved by imposing continuity boundary conditions.

Fig. 6

The two metric functions. As before, u(r) is the curve approaching the value of unity at the origin. The gravitational potential v(r) in this case decreases towards the origin, and hence the gravitational pressure contributes to increasingly compressing the gas when approaching the origin

Similarly, the value of $r_{b}$ is determined finding the root with respect to the radial coordinate of the function

$$\begin{aligned} Z(r)&=1+g\text { }(-g\text { }\varepsilon (r)+{\varPhi }(r))\frac{\partial }{\partial P}f(P), \end{aligned}$$

(51)

$$\begin{aligned} J(r)&= -g \text { }\varepsilon (r), \end{aligned}$$

(52)

$$\begin{aligned} P(r)&=\exp (-\gamma )\text { }\varepsilon (r)^{\gamma }, \end{aligned}$$

(53)

$$\begin{aligned} f(P)&=\exp (1)\text { }P^{\frac{1}{\gamma }} \end{aligned}$$

(54)

$$\begin{aligned} \gamma&=7.13571\\ g&=0.897102, \end{aligned}$$

(55)

where (52) is the constitutive relation between the energy and pressure of a polytropic gas and (55) is the constant defining the matter and scalar field interaction defined by relation (51).

The iterative process of varying the parameters (in this case the absolute value of the constant $\alpha$) is performed step by step to reach a solution which shows a scalar field decaying as the Yukawa potential at large radii.

Fig. 7

The scalar field in this case also shows the bell-like behaviour as a function of radius, which again tends to the Yukawa potential form at large distances

As remarked at the end of the previous section, an interesting question in connection with the polytropic gas case is the following. Up to what extent a solution exists showing the gas completely trapped within a spherical region with the boundary surface at $r=r_{b}$? The elastic solid situation can be expected to show a vanishing pressure at the outside because the body is a solid-like one, but the polytropic gas could perhaps not have the gas fully confined to a spherical region.

Fig. 8

Radial dependence of the pressure for the polytropic gas system. For this type of matter, and the chosen parameters, the pressure increases as the distance to the boundary becomes smaller. This is at variance with the case of the elastic body, as shown in Fig. 3

In fact the polytropic gas also shows solutions in which the gas is rigorously confined within a spherical region of radius $r_{b}$.

As discussed in the case of the elastic body, the initial conditions were fixed at a point $r=\varDelta$ such that

$$\begin{aligned} \varPhi (\varDelta )&=0.65, \end{aligned}$$

(56)

$$\begin{aligned} \varPhi ^{\prime }(\varDelta )&=0, \end{aligned}$$

(57)

$$\begin{aligned} u(\varDelta )&=1, \end{aligned}$$

(58)

$$\begin{aligned} v(\varDelta )&=0.2, \end{aligned}$$

(59)

$$\begin{aligned} \varepsilon (\varDelta )&=2, \end{aligned}$$

(60)

$$\begin{aligned} \varDelta&=0.000001. \end{aligned}$$

(61)

Fig. 9

The Z(r) function (after being multiplied by a constant) for the polytropic gas system, which defines $r_{b}$ as the radius when it reaches the zero value

The quantities u(r), v(r), $\varPhi$, P(r), $\varepsilon (r)$ and Z(r) are shown in Figs. 6, 7, 8 and 9. These solutions for a the polytropic gas show a behaviour similar to the previously-discussed ones of elastic bodies. In both of them a sudden change at the boundary of the pressure to a zero value at vacuum is present and the space-time tends to be the Schwarzschild one at large distances, after a rapid transition in which the scalar field decreased. The asymptotic behaviour of the scalar field in the two cases is a Yukawa-like exponential.

5.1 Solvability condition: polytropic gas

Let us check the satisfaction of the solvability condition for the polytropic gas solution. The P(r) radial dependence near the boundary is depicted in Fig. 8. At difference with the case of the elastic body, the pressure shows a drastic jump to a zero value after $r_b$. However, it also exhibit a large increase in its derivative as $r \rightarrow r_{b}^{-}$.

Exactly in the same form as it was done in the past section, by taking (for this polytropic gas solution) the radial derivative of P(r) and multiplying by the corresponding function Z(r), again the factor $Z(r)P^{\prime }(r)$ in the integrand of the condition (34), can be written as follows

$$\begin{aligned} Z(r)\, P^{\prime }(r)= & {} -P_{int}(r_b)\, Z(r) \, \delta (r- r_b )-(P_{int}(r) \nonumber \\&- P_{int}(r_b))\, Z(r) \, \delta (r_b -r) \nonumber \\&+ P^{\prime }_{int}(r) \, Z(r) \, \theta (r_b -r), \end{aligned}$$

(62)

where all the appearing quantities now take their values as associated to the polytropic gas solution in this section.

Fig. 10

The plot shows the radial dependence of the factors $Z(r)\, P^{\prime }(r)$ defining the integrand in (34). It shows that the limit $r \rightarrow r_b^{-}$ the product is finite. Thus, the integral vanishes when the width $2 \delta$ of the integration region tends to zero. This result checks the satisfaction of the solvability condition

In the first term in (62), at variance with the case of the elastic body situation $P_{int}$ (which is the left side limit of the pressure at $r_b$ ) is not vanishing. However, the factor Z(r) of the Dirac Delta function $\delta (r- r_b)$, has its zero at $r_b$. Thus, this term again leads to a zero addition to the integral in (34). The second term, in identical form as what a happens in the previous case, is proportional to the Dirac Delta function, times the product of two factors having a zero at $r_b$. Therefore, this term again furnishes a vanishing contribution in (34). Finally, the last term (62) becomes proportional to a step-like function times the factor $P^{\prime }_{int}(r) Z(r)$, in which Z(r) has a zero at $r_b$, although $P^{\prime }_{int}(r)$ largely increases if $r \rightarrow r_b^{-}$. The plot of this term is illustrated in the Fig. 10. The picture indicates that the limit $r \rightarrow r_b^{-}$ of the considered product becomes finite. Thus, since the size of the integration interval $2 \delta$ in (34) tends to vanish, the third term contribution to the solvability condition is zero. This completes the checking of the solvability for the polytropic gas.

As final remark, it is an interesting and unexpected outcome that the case of a polytropic gas also presents wall-like forces which rigorously confine the gas within the interior of a spherical region. This result is a direct consequence of the assumed interaction between the scalar field with matter: the concentrated impulsive forces determined by the interaction terms in the fourth divergence of the energy momentum tensor are the confining forces acting like a spherical “wall” over the gas of particles.

This matter-scalar field interaction is implemented by the sources of the scalar field which are proportional to the matter energy density. That is, the confining forces over the polytropic gas matter are generated by the interaction of the scalar field with matter.

6 Summary

We have found new examples of gravastar-like field configurations in General Relativity which are solutions of the EKG equations including matter. Their existence is allowed by the presence of a direct interaction between the scalar field and matter. Within the internal zone, the scalar field plays a role similar to a cosmological constant, and the solutions can be considered as dynamically-generated gravastars. The metrics have a region in which its temporal component take values close to zero near a radial distance $r_{b}$. For larger radial values the metric tensor rapidly tends to the Schwarzschild case. The configurations considered show a scalar field behaving as the Yukawa potential at large radii and the scalar field-matter interaction is able to define trapping forces that rigorously confine the polytropic gases to the interior of a sphere. In the surface of these spheres, pressures generated by the field-matter interaction play the role of “walls” preventing the matter from flowing out.

Finally, it is useful to remark that the relevance of the interaction of matter with the scalar field suggests the possible important role of string theory for the constituency of such structures. This idea comes from the fact that the Yukawa interaction of the scalar moduli fields with fermion matter fields makes completely natural the presence of such interactions in field theory approximations of string theory [20, 21].

It will be interesting to investigate in detail image formation under these configurations even under simplified accretion disc physics, such as the analysis carried out in [5]. Due to the structure of these dynamical gravastars, we expect that they will show evidence for a stronger scattering of the accreting matter than the one found in Schwarzschild black holes. This possibility comes from the presence of matter directly at the entrance of the captured beams in the interior regions [22]. Finally, the connections of the solutions with the ongoing searches for field configurations describing primordial black holes is also of interest, and it is planned to be investigated [23,24,25,26,27,28].

Appendix A: The general field equations

In this Appendix we reproduce for bookkeeping reasons the derivation of the Einstein–Klein–Gordon equations that were presented in [13].

The physical system includes matter defined by a scalar field and usual matter showing a constitutive relation expressing the energy density as a general function of the pressure.

The metric is associated to the squared proper time interval

$$\begin{aligned} ds^{2}&= v (\rho ){dx^{0}}^{2}-u(\rho )^{-1}d\rho ^{2}-\rho ^{2}(sin^{2}\theta d\varphi ^{2}+d\theta ^{2}) \, , \end{aligned}$$

(A.1)

$$\begin{aligned} x^{0}&=ct\, , \; \; \; x^{1}=\rho \, , \; \; \; x^{2} = \varphi \, ,\; \; \; x^{3}\equiv \theta \, . \end{aligned}$$

(A.2)

The Einstein tensor $G_{\mu \nu }$ in terms of functions u, v and the radial variable $\rho$ can be evaluated as

$$\begin{aligned} {G_{0}^{0}}&={\frac{u^{\prime }}{\rho }}-{\frac{1-u}{\rho ^{2}}}, \end{aligned}$$

(A.3)

$$\begin{aligned} G_{1}^{1}&={\frac{u}{v}}{\frac{v^{\prime }}{\rho }}-{\frac{{1-u}}{\rho ^{2}} } \, , \end{aligned}$$

(A.4)

$$\begin{aligned} {G_{2}^{2}}&={G_{3}^{3}} ={\frac{u}{2v}}{v^{\prime \prime }}+{\frac{uv^{\prime }}{4v}\left( \frac{u^{\prime }}{u}-\frac{v^{\prime }}{v}\right) }\nonumber \\&+{\frac{u}{2\rho }\left( \frac{u^{\prime }}{u}+\frac{v^{\prime }}{v}\right) } \, . \end{aligned}$$

(A.5)

In what follows we use various notations for a derivative of a function f(x) as

$$\begin{aligned} \frac{df(x)}{dx}=f_{,x}(x) \, = \, f^{\prime }(x) \, . \end{aligned}$$

The physical system interacting with gravity is considered to be made of a scalar field and a material body, both with spherical symmetry. The scalar field is also assumed to interact linearly with an external source associated with it. Further, the source field is considered to be proportional to the body energy density. This assumption introduces the interaction of the scalar field with matter. It should be noted that in most of the former studies of the EKG equations including matter the substance had not been considered as directly interacting with the field [29,30,31,32,33,34,35].

The action of the field takes the form

$$\begin{aligned} {S}_{mat-\phi } \, = \, \int L\sqrt{-g}d^{4}x \, , \end{aligned}$$

(A.6)

with a Lagrangian density given by

$$\begin{aligned} {L}\, = \, {\frac{1}{2}}\left( g^{\alpha \beta }{\phi }_{,\alpha }{\phi }_{,\beta }+m^{2}{\phi }^{2}+2\text { }j(\rho )\text { }\phi +j^{2}(\rho )\right) \, . \end{aligned}$$

(A.7)

This Lagrangian determines an energy momentum of the form

$$\begin{aligned} (T_{mat-\phi })_{\mu }^{\nu } \, = \, -\frac{\delta _{\mu }^{\nu }}{2}\left( g^{\alpha \beta }{\phi }_{,\alpha }{\phi }_{,\beta }+m^{2}{\phi }^{2}+2\text { }j(\rho )\text { }\phi +j^{2}(\rho )\right) \, , \end{aligned}$$

which can be added to the energy momentum tensor of the matter [36]:

$$\begin{aligned} (T_{e,p})_{\mu }^{\nu }\, = \, p\,\delta _{\mu }^{\nu }-u^{\nu }u_{\mu }(p+\varepsilon ) \, , \end{aligned}$$

(A.8)

so as to write the total energy momentum tensor as

$$\begin{aligned} T_{\mu }^{\nu }&=-\frac{\delta _{\mu }^{\nu }}{2}\left( g^{\alpha \beta }{\phi }_{,\alpha }{\phi }_{,\beta }+m^{2}{\phi }^{2}+2j(\rho )\text { }\phi +j^{2}(\rho )\right) \nonumber \\&\text { \ \ \ }+g^{\alpha \nu }{\phi }_{,\alpha }{\phi }_{,\mu }+p \, \delta _{\mu }^{\nu }-u^{\nu }u_{\mu }(p+e) \, . \end{aligned}$$

(A.9)

Since static field configurations are being searched for, the four-velocity reduces to the form in the local rest system at any spatial point

$$\begin{aligned} u^{\mu }(t,r)=(1,0,0,0) \, . \end{aligned}$$

(A.10)

After these definitions, the Einstein equations for the considered system can be written as usual

$$\begin{aligned} G_{\mu }^{\nu }=G\,\, T_{\mu }^{\nu } \, , \end{aligned}$$

(A.11)

in which both tensors are diagonal and the gravitational constant has the value

$$\begin{aligned} G \, = \, 8\pi \; l_{P}^{2} \, , \end{aligned}$$

(A.12)

in terms of the Planck length $l_{P}=1.61\times 10^{-36}$ m.

The non-vanishing Einstein equations determined by the diagonal terms take the form

$$\begin{aligned}&{\frac{u^{\prime }}{\rho }}-{\frac{1-u}{\rho ^{2}}} \nonumber \\&\quad =-G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}+m^{2}\phi ^{2}+2 j \phi +j^{2}\right) +\varepsilon \right] \, ,\nonumber \\&\quad {\frac{u}{v}}{\frac{v^{\prime }}{\rho }}-{\frac{{1-u}}{\rho ^{2}}} \nonumber \\&\quad =G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}-m^{2}\phi ^{2}-2 j \phi -j^{2}\right) +p\,\right] \, ,\nonumber \\&\quad {\frac{\rho ^{2}u}{2}}{v^{\prime \prime }}+\frac{\rho ^{2}}{4}u\text { }v^{\prime }\left( {\frac{{u}^{\prime }}{u}-}\frac{{v}^{\prime }}{v}\right) +\frac{\rho }{2}u\text { }v^{\prime } \nonumber \\&\quad =G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}+m^{2}\phi ^{2}+2j \phi +j^{2}\right) +p\,\right] \, ,\nonumber \\&\quad {\frac{\rho ^{2}u}{2}}{v^{\prime \prime }}+\frac{\rho ^{2}}{4}u v^{\prime }\left( {\frac{{u}^{\prime }}{u}-}\frac{{v}^{\prime }}{v}\right) +\frac{\rho }{2}u v^{\prime } \nonumber \\&\quad =G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}+m^{2}\phi ^{2}+2 j \phi +j^{2}\right) +p\,\right] \, . \end{aligned}$$

(A.13)

These are four equations, the last two of which are identical. Thus, there are three independent Einstein equations in the problem. However, the third and the equivalent fourth one can be substituted by a simpler relation which comes from the Bianchi identities [36]:

$$\begin{aligned} G_{\mu \text { };\text { }\nu }^{\nu }=0, \end{aligned}$$

(A.14)

where the semicolon indicates the covariant derivative of the tensor $G_{\mu \text { }}^{\nu }.$ After assuming the Einstein equations (A.11) are satisfied, the $G_{\mu }^{\nu }$ tensor in (A.14) can be substituted by the energy momentum tensor $T_{\mu }^{\nu }$ leading to the relation

$$\begin{aligned} -(\phi +j)\text { }j^{\prime }+p^{\prime }+\frac{v^{\prime }}{2v}(p+e)=0, \end{aligned}$$

(A.15)

which are dynamical equations for the energy, the pressure and the scalar field, substituting the two equivalent Einstein equations being associated to the two angular directions, related to the mechanical equilibrium of the system.

The last of the equations of movement for the system is the Klein-Gordon one for the scalar field. It can be obtained by imposing the vanishing of the functional derivative of the action $S_{mat-\phi }$ with respect to the field

$$\begin{aligned} \frac{\delta S_{mat-\phi }}{\delta \phi (x)}&\equiv \frac{\partial }{\partial x^{\mu }}\frac{\partial L}{\partial \phi _{,\mu }}-\frac{\partial L}{\partial \phi }\nonumber \\&\equiv \frac{1}{\sqrt{-g}}\frac{\partial }{\partial x^{\mu }}(\sqrt{-g} g^{\mu \nu }\phi _{,\nu })-m^{2}\phi -j\nonumber \\&=0, \end{aligned}$$

(A.16)

a relation that after using the temporal and radial Einstein equations in (A.11) can be written in the form

$$\begin{aligned}&j(\rho )+m^{2}\phi (\rho )-u(\rho )\text { }\phi ^{\prime \prime }(\rho ) \, \nonumber \\&\quad = \phi ^{\prime }(\rho )\left( \frac{u(\rho )+1}{\rho }-\rho \text { }G\text { }\left( \frac{m^{2}\phi (\rho )^{2}}{2}+j(\rho )\text { }\phi (\rho ) \right. \right. \nonumber \\&Q\left. \left. + \frac{j(\rho )^{2}}{2}+\frac{e(\rho )-p(\rho )}{2}\right) \right) . \end{aligned}$$

(A.17)

Therefore, the relevant EKG equations for the problem can be reduced to

$$\begin{aligned}&{\frac{u^{\prime }(\rho )}{\rho }}-{\frac{1-u(\rho )}{\rho ^{2}}} \\&\quad = -\,G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}(\rho )+m^{2}\phi (\rho )^{2}+2j(\rho )\phi (\rho )+j(\rho )^{2}\right) +e(\rho )\right] \, ,\\&\quad {\frac{u(\rho )}{v(\rho )}}{\frac{v^{\prime }(\rho )}{\rho }}-{\frac{{1-u}(\rho )}{\rho ^{2}}} \, \\&\quad = G\left[ \frac{1}{2}\left( u\phi _{,\rho }^{2}(\rho )-m^{2} \phi (\rho )^{2}-2\text { }j(\rho )\text { }\phi (\rho )-j(\rho )^{2}\right) +p(\rho )\,\right] , \\&\quad j(\rho )+m^{2}\phi (\rho )-u(\rho )\text { }\phi ^{\prime \prime (\rho )} \\&\quad =\phi ^{\prime }(\rho )\left( \frac{u(\rho )+1}{\rho }-\rho \text { }G\text { }\left( \frac{m^{2}\phi (\rho )^{2}}{2}+j\text { }(\rho )\phi (\rho )\nonumber \right. \right. \\&\quad \left. \left. +\frac{j(\rho )^{2}}{2}+\frac{e(\rho )-p(\rho )}{2}\right) \right) ,\\&\quad 0 \, = \\&\quad -\left( \phi (\rho )+j(\rho )\right) \text { }j^{\prime }(\rho )+p^{\prime }(\rho )+\frac{v^{\prime }(\rho )}{2v}\left( p(\rho )+e(\rho )\right) \, . \end{aligned}$$

In order to reduce the number of parameters in the equations, let us define a new radial variable, scalar field and other parameters as follows

$$\begin{aligned} r&=m\rho , \end{aligned}$$

(A.18)

$$\begin{aligned} \varPhi (r)&=\sqrt{8\pi }l_{p}\phi (\rho ) \, , \end{aligned}$$

(A.19)

$$\begin{aligned} J(r)&=\frac{\sqrt{8\pi }l_{p}}{m^{2}}j(\rho ) \, , \end{aligned}$$

(A.20)

$$\begin{aligned} \text { }\varepsilon (r)&\equiv \frac{8\pi l_{p}^{2}}{m^{2}}e(\rho ) \, , \end{aligned}$$

(A.21)

$$\begin{aligned} P^{*}(r)&=\frac{8\pi l_{p}^{2}}{m^{2}}p(\rho ) \, . \end{aligned}$$

(A.22)

With the new notation the working equations become

$$\begin{aligned}&{\frac{u_{,r}(r)}{r}}-{\frac{1-u(r)}{r^{2}}} \, \nonumber \\&\quad = -\frac{1}{2}\left( u(r){\varPhi _{,r}(r)}^{2}+\varPhi (r)^{2}+2J(r)\varPhi (r)+J(r)^{2}\right) \nonumber \\&\quad -\varepsilon (r), \end{aligned}$$

(A.23)

$$\begin{aligned}&\frac{u(r)}{v(r)}\frac{v_{,r}(r)}{r}-{\frac{1-u(r)}{r^{2}}} \, \nonumber \\&\quad = -\frac{1}{2}\left( -u(r){\varPhi _{,r}(r)}^{2}+\varPhi (r)^{2}+2J(r)\varPhi (r)+J(r)^{2})\right. \nonumber \\&\quad \left. -P^{*}(r)\right) , \end{aligned}$$

(A.24)

$$\begin{aligned}&0 \, = \nonumber \\&P^{*\prime }(\rho )+\left( \varepsilon (r)+P^{*}(r)\right) \frac{v_{,r}(r)}{2v(r)}-\left( J(r)+\varPhi (r)\right) J_{,r}(r), \end{aligned}$$

(A.25)

$$\begin{aligned}&J(r)+{\varPhi }(r)-u(r)\text { }{\varPhi }^{\prime \prime }(r) \nonumber \\&\quad = {\varPhi }^{\prime }(r)\left( \frac{u(r)+1}{r}-r\text { }\left( \frac{{\varPhi }(r)^{2}}{2}+J(r){\varPhi }(r) \right. \right. \nonumber \\&\quad \left. \left. +\frac{J(r)^{2}}{2}+\frac{\varepsilon (r)-P^{*}(r)}{2}\right) \right) . \end{aligned}$$

(A.26)

In order to simplify the notation, the same letters u and v have been used to indicate the metric components in the new variables. That is we write $u(r)=u(\rho )$ and $v(r)=v(\rho )$ in spite of the fact that functional forms of the two letters can not be equal. This should not create confusion.