Geodesic motion around a supersymmetric $\hbox {AdS}_5$ black hole

Abstract

In this article the geodesic motion of test particles in the spacetime of a supersymmetric $\hbox {AdS}_5$ black hole is studied. The equations of motion are derived and solved in terms of the Weierstrass $\wp$, $\sigma$, and $\zeta$ functions. Effective potentials and parametric diagrams are used to analyze and characterize timelike, lightlike, and spacelike particle motion and a list of possible orbit types is given. Furthermore, various plots of orbits are presented.

1 Introduction

The famous anti-de Sitter/conformal field theory (AdS/CFT) correspondence provides a relation between gravity and quantum field theory, in particular, Maldacena [1, 2] connected compactifications of string theory on anti-de Sitter to a conformal field theory. Therefore, black holes that are asymptotically anti-de Sitter are very interesting to study.

A few years after Kerr [3] presented an asymptotically flat rotating black hole, Carter [4] came up with the first rotating asymptotically anti-de Sitter black hole. In five dimensions Hawking et al. [5] found an AdS black hole with two rotation parameters. Five dimensional AdS black holes are especially interesting since the $\hbox {AdS}_5$/$\hbox {CFT}_4$ correspondence is very well understood and CFT can be described as ${\mathscr {N}}=4$ SU(N) super Yang-Mills theory. One of the first supersymmetric $\hbox {AdS}_5$ black hole solutions were found by Gutowski and Reall [6]. They considered the minimal $D=5$ gauged supergravity theory described in [7] and found an asymptotically $\hbox {AdS}_5$ black hole parameterized by its mass, charge, and two equal angular momenta. Many more black hole solutions in supergravity theories were found, see, e.g., [8].

The motion of test particles is a useful tool to study black holes in various theories of gravity. The solutions of the equations of motion can be applied to calculate observable quantities like the shadow of a black hole or the periastron shift of a bound orbit. Geodesics also provide information on the structure of a spacetime. In the framework of AdS/CFT, geodesics correspond to two-point correlators [9]. In particular, spacelike geodesics with both endpoints on the boundary (i.e., escape orbits of particles with imaginary rest mass) are related to the eikonal approximation of holographic two-point functions. CFT correlators describe observables on the AdS boundary.

The Hamilton–Jacobi formalism represents an efficient method to derive the equations of motion for test particles. In the four-dimensional Kerr spacetime, Carter [4] showed that the Hamilton–Jacobi equation for test particles separates. The resulting equations of motion can be solved analytically in terms of elliptic functions. In higher dimensions, or in spacetimes with a cosmological constant, the analytical solutions of the geodesic equations often require hyperelliptic functions [10,11,12,13,14,15]. The geodesics in a rotating supersymmetric black hole spacetime were analyzed in [16, 17], where the complete analytical solution of the geodesics equations in the supersymmetric Breckenridge–Myers–Peet–Vafa (BMPV) [18] spacetime was presented. Here we will study the geodesic motion of test particles around the supersymmetric, asymptotically $\hbox {AdS}_5$ black hole of Gutowski and Reall [6].

The article is structured as follows. We derive the equations of motion in Sect. 2 and give a complete classification of the geodesics in Sect. 3. In Sect. 4 we solve the equations of motion analytically in terms of the Weierstrass $\wp$, $\sigma$, and $\zeta$ functions. Finally we present some example plots of the orbits in Sect. 5 and conclude in Sect. 6.

2 The supersymmetric $\hbox {AdS}_5$ black hole

Gutowski and Reall [6] found a one-parameter family of supersymmetric $\hbox {AdS}_5$ black holes. The metric is given by

$$\begin{aligned} \begin{aligned} {\mathrm{d}}{s^2}&=-{f}^{2}{{\mathrm{d}}{t}}^{2}-2{f}^{2}\varPsi {{\mathrm{d}}{t}}\sigma _L^3 +{U(R)}^{-1}{{\mathrm{d}}{R}}^{2}\\&\quad +\frac{{R}^{2}}{4}\left[ (\sigma _L^1)^2+(\sigma _L^2)^2 +\varLambda (R)(\sigma _L^3)^2\right] , \end{aligned} \end{aligned}$$

(1)

where the $\sigma _L^i$ can be expressed in terms of the Euler angles $(\theta ,\phi ,\psi )$ as

$$\begin{aligned} \sigma _L^1&=\sin \phi {\mathrm{d}}{\theta }-\cos \phi \sin \theta {\mathrm{d}}{\psi }, \end{aligned}$$

(2a)

$$\begin{aligned} \sigma _L^2&=\cos \phi {\mathrm{d}}{\theta }+\sin \phi \sin \theta {\mathrm{d}}{\psi },\end{aligned}$$

(2b)

$$\begin{aligned} \sigma _L^3&={\mathrm{d}}{\phi }+\cos \theta {\mathrm{d}}{\psi }, \end{aligned}$$

(2c)

and the metric functions are

$$\begin{aligned} f&=1-\frac{R_{0}^{2}}{{R}^{2}},\end{aligned}$$

(3)

$$\begin{aligned} \varPsi&=-\frac{\varepsilon {R}^{2}}{2l}\left( 1+{\frac{2R_{0}^{2}}{{R}^{2}}} +{\frac{3R_{0}^{4}}{2{R}^{2}\left( {R}^{2}-R_{0}^{2}\right) }}\right) ,\end{aligned}$$

(4)

$$\begin{aligned} U&=\left( 1-\frac{R_0^{2}}{{R}^{2}}\right) ^{2}\left( 1+\frac{2R_0^{2}}{{l}^{2}} +\frac{{R}^{2}}{{l}^{2}}\right) ,\end{aligned}$$

(5)

$$\begin{aligned} \varLambda&=1+\frac{R_0^{6}}{{l}^{2}{R}^{4}}-\frac{R_0^{8}}{4{l}^{2}{R}^{6}}. \end{aligned}$$

(6)

The Maxwell potential is

$$\begin{aligned} A=\frac{\sqrt{3}}{2}\left[ \left( 1-\frac{R^2}{R_0^2}\right) {\mathrm{d}}{t} +\frac{\varepsilon R_0^4}{4lR^2}\sigma _L^3\right] . \end{aligned}$$

(7)

Here $R_0$ is the radial coordinate of the black hole’s degenerate horizon, $\varepsilon =\pm 1$ is the sign of its angular momentum, and l is the AdS radius. Note that $\varepsilon$ can be absorbed into l, consequently, in the following analysis of the geodesics we set $\varepsilon =1$ but examine the geodesic motion for arbitrary sign of l.

It can be shown that the solution is asymptotically $\hbox {AdS}_5$, by using the coordinate transformation $\phi '=\phi +\frac{2\varepsilon }{l}t$, see [6]. It has the $R\times S^3$ Einstein universe as its conformal boundary and the $S^3$ has the radius l. Boundary as well as bulk time translations are generated by $\frac{\partial }{\partial t}$. However, as for all rotating AdS black holes, there is another timelike Killing vector field in the bulk

$$\begin{aligned} V=\frac{\partial }{\partial t}+\frac{2\varepsilon }{l}\frac{\partial }{\partial \phi '}\,. \end{aligned}$$

(8)

If V is used to generate time translations, we are working in a co-rotating frame and there is no ergoregion. If, on the other hand, $\frac{\partial }{\partial t}$ generates time translations, then an ergoregion exists.

The metric (1) is characterized by its conserved quantities associated with symmetries of the conformal boundary, which was shown for asymptotically AdS spacetimes of dimension $D\ge 4$ by Ashtekar and Das [19]. In this case, the black hole’s conserved quantities can be defined by an Ashtekar and Das mass

$$\begin{aligned} M=\frac{3\pi R_0^2}{4G}\left( 1+\frac{3R_0^2}{2l^2} +\frac{2R_0^4}{3l^4}\right) , \end{aligned}$$

(9)

an angular momentum with respect to $\phi '=\phi +\frac{2\varepsilon }{l}t$ of

$$\begin{aligned} J'=\frac{3\varepsilon \pi R_0^4}{8Gl}\left( 1+\frac{2R_0^2}{3l^2}\right) , \end{aligned}$$

(10)

a vanishing angular momentum with respect to $\psi$, an energy of

$$\begin{aligned} E=M+\frac{3\pi l^2}{32G}, \end{aligned}$$

(11)

and a charge of

$$\begin{aligned} Q=\frac{\sqrt{3}\pi R_0^2}{2G}\left( 1+\frac{R_0^2}{2l^2}\right) . \end{aligned}$$

(12)

We then obtain

$$\begin{aligned} M-\frac{2}{l}| J'|= \frac{\sqrt{3}}{2}|Q| \end{aligned}$$

(13)

and therefore the solution saturates the BPS bound, see also [6]. Note that the conserved charges by Ashtekar and Das are only correct for a special class of solutions, where the non-normalizable modes of all matter fields vanish and the Ricci curvature of the boundary metric also vanishes, unless $D\le 4$. In [20] the authors present well defined conserved charges for general asymptotically AdS black holes in the presence of matter.

The solution (1) has a smooth event horizon at $R=R_0$ and the spatial geometry of the horizon is a squashed $S^3$

$$\begin{aligned} {\mathrm{d}}{s_3^2}=\frac{R_0^2}{4}\left[ \left( {\sigma _L^1}''\right) ^{2} +\left( {\sigma _L^2}''\right) ^{2} +\left( 1+\frac{3R_0^2}{4l^2}\right) \left( {\sigma _L^3}''\right) ^{2}\right] , \end{aligned}$$

(14)

where the ${\sigma _L^i}''$ are defined as the $\sigma _L^i$ with $\phi ''=\phi +\frac{4f^2\varPsi }{R^2U}r$ instead of $\phi$. Behind the event horizon there is a curvature singularity at $R=0$ surrounded by a region of closed timelike curves [6].

2.1 The equations of motion

We use the Hamilton–Jacobi formalism to obtain the equations of motion for test particles in the spacetime of a supersymmetric black hole. To solve the Hamilton–Jacobi equation of an uncharged particle

$$\begin{aligned} -2\frac{\partial S}{\partial \tau }=g^{\mu \nu }\frac{\partial S}{\partial x^\mu }\frac{\partial S}{\partial x^\nu }, \end{aligned}$$

(15)

we make the ansatz for the action S

$$\begin{aligned} S=\frac{1}{2}\delta \tau -Et+L\phi +J\psi +S_R(R)+S_\theta (\theta )\,. \end{aligned}$$

(16)

Here E is the particle’s conserved energy, L and J are its conserved angular momenta along $\phi$ and $\psi$, respectively, $\tau$ is an affine parameter along the geodesic, and $\delta$ is equal to 0 for light, equal to 1 for particles of positive mass, and equal to $-1$ for particles of imaginary mass. The case $\delta =-1$ corresponds to spacelike geodesics and is of relevance for AdS/CFT if the geodesics’ endpoints are on the boundary $R\rightarrow \infty$. This is discussed in more detail in Sect. 3.4.

Using this ansatz and the metric (1), the Hamilton–Jacobi Eq. (15) becomes

$$\begin{aligned} \begin{aligned} -\delta&=\frac{-R^2\varLambda E^2}{\left( 4\Phi ^2f^2+R^2\varLambda \right) f^2} +\frac{8\Phi EL}{4\Phi ^2f^2+R^2\varLambda }\\&\quad +\frac{\left( 16\Phi ^2\cos ^2\theta f^2 +4\varLambda \cos ^2\theta R^2+4R^2\sin ^2\theta \right) L^2}{ R^2\sin ^2\theta \left( 4\Phi ^2f^2+R^2\varLambda \right) }\\&\quad -\frac{8\cos \theta JL}{R^2\sin ^2\theta }{+}\frac{4J^2}{R^2\sin ^2\theta } {+}\frac{4}{R^2}\left( \frac{\partial S_\theta }{\partial \theta }\right) ^{2} {+}U\left( \frac{\partial S_R}{\partial r}\right) ^{2}. \end{aligned} \end{aligned}$$

(17)

One can separate the Hamilton–Jacobi Eq. (15) by terms in R and $\theta$ in

$$\begin{aligned} \begin{aligned}&\delta R^2-\frac{R^4\varLambda E^2}{\left( 4\Phi ^2f^2+R^2\varLambda \right) f^2} +\frac{8R^2\Phi EL}{4\Phi ^2f^2+R^2\varLambda }\\&\quad +\frac{4R^2L^2}{4\Phi ^2f^2+R^2\varLambda }+R^2U\left( \frac{\partial S_R}{\partial r}\right) ^{2}=K \end{aligned} \end{aligned}$$

(18)

and

$$\begin{aligned} -\frac{4\cos ^2\theta L^2}{\sin ^2\theta }+\frac{8\cos \theta JL}{\sin ^2\theta } -\frac{4J^2}{\sin ^2\theta }-4\left( \frac{\partial S_\theta }{\partial \theta }\right) ^{2}=K. \end{aligned}$$

(19)

Here we introduced K as a separation constant known as the Carter [21] constant. Now we can solve Eq. (18) for $\frac{\partial S_R}{\partial r}$ and Eq. (19) for $\frac{\partial S_\theta }{\partial \theta }$, which can then be used to substitute the functions $S_R$ and $S_\theta$ in the ansatz (16) (no need to actually compute the integrals here). Finally, the equations of motion can be deduced with a variational method; the derivatives of the action S with respect to the constants of motion can be set to zero.

With the help of the Mino [22] time $\gamma$ given by $R^2{\mathrm{d}}{\gamma }={\mathrm{d}}{\tau }$ to remove the factor $R^2$ from all equations and the substitution $r=R^2$, this yields five differential equations of motion

$$\begin{aligned} \left( \frac{{\mathrm{d}} r}{{\mathrm{d}} \gamma }\right) ^{2}= & {} \text {P}(r), \end{aligned}$$

(20)

$$\begin{aligned} \left( \frac{{\mathrm{d}} \theta }{{\mathrm{d}} \gamma }\right) ^{2}= & {} \varTheta (\theta ), \end{aligned}$$

(21)

$$\begin{aligned} \frac{{\mathrm{d}} \phi }{{\mathrm{d}} \gamma }= & {} -l{\frac{2E{r}^{2}+(2E-Ll)r+Ll-E}{({l}^{2}+r+2)(r-1)}}\nonumber \\&-\frac{\cos \theta }{\sin ^2\theta }\left( J-L\cos \theta \right) , \end{aligned}$$

(22)

$$\begin{aligned} \frac{{\mathrm{d}} \psi }{{\mathrm{d}} \gamma }= & {} \frac{1}{\sin ^2\theta }\left( J-L\cos \theta \right) , \end{aligned}$$

(23)

$$\begin{aligned} \frac{{\mathrm{d}} t}{{\mathrm{d}} \gamma }= & {} \frac{(4E{l}^{2}+2Ll){r}^{3}+(4E-3Ll)r+Ll-E}{4({l}^{2}+r+2)(r-1)^{2}}.\nonumber \\ \end{aligned}$$

(24)

The polynomial $\text {P}$ and the function $\varTheta$ are

$$\begin{aligned} \text {P}= & {} -4{\frac{\delta {r}^{4}}{{l}^{2}}}+4\left( {E}^{2}+{\frac{EL}{l}} -\delta -\frac{1}{4}{\frac{K}{{l}^{2}}}\right) {r}^{3}\nonumber \\&+\left( -{L}^{2}-K+8\delta +12{\frac{\delta }{{l}^{2}}}\right) {r}^{2}\nonumber \\&+2\left( {L}^{2}-3{\frac{EL}{l}}+K-2\delta +2{\frac{{E}^{2}}{{l}^{2}}} +\frac{3}{2}{\frac{K}{{l}^{2}}}-4{\frac{\delta }{{l}^{2}}}\right) r\nonumber \\&-{L}^{2}+2{\frac{EL}{l}}-K-{\frac{{E}^{2}}{{l}^{2}}}-2{\frac{K}{{l}^{2}}}, \end{aligned}$$

(25)

$$\begin{aligned} \varTheta= & {} K-\frac{1}{\sin ^2\theta }\left( J-L\cos \theta \right) ^2. \end{aligned}$$

(26)

To simplify the equations of motion, dimensionless quantities were introduced by scaling with $R_0$

$$\begin{aligned} R&\rightarrow R_0R\,,&t&\rightarrow R_0t\,,&\tau&\rightarrow R_0\tau \,,&l&\rightarrow R_0l, \nonumber \\ L&\rightarrow \frac{1}{4}R_0L\,,&J&\rightarrow \frac{1}{4}R_0J\,,&K&\rightarrow \frac{1}{4}R_0^2K\,. \end{aligned}$$

(27)

This was achieved by setting $R_0=1$ and canceling factors of 4 in front of L, J, and K for convenience.

3 Classification of the geodesics

The properties of the geodesics are determined by the polynomial $\text {P}$ in Eq. (25) and the function $\varTheta$ in Eq. (26). The characteristics of $\varTheta$ and $\text {P}$ are given by the particle’s constants of motion (energy, angular momenta, Carter constant, $\delta$ parameter) and the metric’s (positive or negative) AdS radius. In this section, features of the function $\varTheta$ and the polynomial $\text {P}$ – and therefore the types of orbits – for various sets of constants of motion are studied. This is done analogously to [23], where geodesic motion of electrically and magnetically charged test particles in the Reissner–Nordström spacetime has been examined.

3.1 The $\theta$ motion

To obtain real values of $\theta$, the requirement $\varTheta \ge 0$ has to be met. From this it follows that $K\ge 0$. The substitution $\xi =\cos \theta$ turns Eq. (21) into

$$\begin{aligned} \left( \frac{{\mathrm{d}} \xi }{{\mathrm{d}} \gamma }\right) ^{2} = \varTheta _\xi \quad \text {with} \quad \varTheta _\xi :=a\xi ^2+b\xi +c\,, \end{aligned}$$

(28)

where $a=-L^2-K$, $b=2LJ$, and $c=K-J^2$. Since $K\ge 0$ holds, it follows $a\le 0$. The zeros of the second degree polynomial $\varTheta _\xi$ correspond to angles that confine the particle’s $\theta$ motion. Note that for vanishing L in Eqs. (21) and (23) the test particle’s motion is planar in the 3-dimensional subspace given by the spherical coordinates $(R,\theta ,\psi )$ as in the Schwarzschild case.

The $\varTheta _\xi$ polynomial’s discriminant is given by $D=b^2-4ac$ and can be expressed as $D=4K\kappa$ with $\kappa =K+L^2-J^2$. $\varTheta _\xi$ describes a downward opened parabola with zeros

$$\begin{aligned} \xi _0=\frac{LJ\pm \sqrt{K\kappa }}{L^2+K} \in [-1,1] \end{aligned}$$

(29)

and maximum at $\big (\frac{LJ}{L^2+K},\frac{K\kappa }{L^2+K}\big )$. A real solution $\theta$ implies real zeros of $\varTheta _\xi$ and thus requires $D\ge 0$. While $|L|\ge |J|$ is sufficient, other cases require an upper limit of |J| given by $J_{\text {max}}=\sqrt{K+L^2}$. For symmetric motion with respect to the equatorial plane L or J have to vanish. Other cases are depending on the sign of $K-J^2$:

• 1. $K<J^2$: The zeros of $\varTheta _\xi$ are either both positive or both negative, which confines the particle’s motion to $\theta \in [0,\pi /2)$ for $LJ>0$ and $\theta \in (\pi /2,\pi ]$ for $LJ<0$.

• 2. $K=J^2$: The zeros of $\varTheta _\xi$ are $\big \lbrace 0,\frac{2LJ}{L^2+K}\big \rbrace$ with $\theta \in [0,\pi /2]$ for $LJ>0$ and $\theta \in [\pi /2,\pi ]$ for $LJ<0$. With the additional condition $|L|=|J|$, the orbit fills an entire hemisphere [see Fig. 1(b) at $L=\pm 4$].

• 3. $K>J^2$: One zero of $\varTheta _\xi$ is positive and one is negative, allowing the particle to cross the equatorial plane and $\theta \in [0,\pi ]$.

Similarly to an effective potential, this behavior can be seen in Fig. 1, where the allowed area of motion with respect to L is shown for different choices of K.

Fig. 1

Allowed $\xi$ motion in dependence of L for $J=4$ and varying K. Physically forbidden areas are marked in gray

In case of a double zero $\xi _0$ of $\varTheta _\xi$, the particle’s motion is confined to a cone of opening angle $\arccos \xi _0$, which simplifies Eqs. (22) and (23). This is possible for $K=0$ or $\kappa =0$ in three cases:

• 1. $K=0,\,\kappa >0$: $\xi _0=J/L$ for $|L|>|J|$.

• 2. $K>0,\,\kappa =0$: $\xi _0=L/J$ for $|L|<|J|$.

• 3. $K=0,\,\kappa =0$: $\xi _0=\text {sign}LJ$ for $|L|=|J|$.

Since the $\theta$ motion is not depending on the particle’s mass parameter $\delta$, all results hold for all particle types.

3.2 The r motion

3.2.1 Possible types of orbits

For a degenerate horizon at $r=1$ the following types of orbits can be found for this spacetime:

• 1. Escape orbits (EO) with range $[r_1,\infty )$ and $1<r_1$.

• 2. Two-world escape orbits (TEO) with range $[r_1,\infty )$ and $r_1<1$.

• 3. Periodic bound orbits (BO) with range $[r_1,r_2]$ and $r_1<r_2<1$ or $1<r_1<r_2$.

• 4. Many-world periodic bound orbits (MBO) with range $[r_1,r_2]$ and $r_1<1<r_2$.

• 5. Terminating orbits (TO) with range $[0,r_2]$ and $r_2<1$ or with range $[0,\infty )$.

3.2.2 Analysis of the radial motion

To obtain real values of r from Eq. (20), the requirement $\text {P}\ge 0$ has to be met. Radial regions of physically allowed motion are separated from forbidden ones by the positive zeros of $\text {P}$, which correspond to the orbits’ turning points. Whenever the polynomial has a non negative double zero, that is,

$$\begin{aligned} \text {P}(r)=0 \quad \text {and} \quad \frac{{\mathrm{d}} \text {P}}{{\mathrm{d}} r}{(r)}=0\,, \end{aligned}$$

(30)

a variation of parameters is expected to change the number of positive zeros. By plotting the zeros of the resultant of the two expressions in Eq. (30), one obtains parameter plots showing the boundaries between regions of 1, 2, 3 or 4 zeros of $\text {P}$. This is shown for parametric L-l, K-E, and L-E diagrams in Fig. 2.

Fig. 2

Parametric L-l, K-E, and L-E diagrams for varying mass parameter $\delta$ and parameters $E = 1.8,\, K = 8$ (a–c), $L = 4,\, l = 4$ (d–f), and $l = 1,\, K = 4$ (g–i), showing regions (1)–(4). This marks the number of positive zeros of the polynomial $\text {P}$ in Eq. (25), i.e., lines corresponding to transitions of negative roots to complex ones are not shown. Associated orbit types can be found in Table 1 and are described in Sect. 3.2.2. In cases (d)–(i) one double zero of $\text {P}$ for $E=0$ and all K or L can be found. Since no regions of different numbers of zeros are separated by these lines (see Fig. 3 for $E=0$), they are omitted

As $\text {P}$ is a polynomial of second degree in E, one can define the two-part effective potential $V_\pm (r)$ as the values of energy that yield $\text {P}=0$, i.e., $\text {P}$ can be rearranged in the form

$$\begin{aligned} \text {P}=f(r)(E-V_+)(E-V_-). \end{aligned}$$

(31)

Some effective potentials are shown in Figs. 3, 4 and 5. Since one can factor out $(r-1)$ in $V_\pm$, $V_+$ and $V_-$ intersect on the horizon at $E=0$, given that $V_\pm$ is real. Additionally, for the requirement that time should always run forward, i.e., ${\mathrm{d}}{t}/{\mathrm{d}}{\gamma }\ge 0$, Eq. (24) is treated in a similar way as Eq. (20) for the effective potential and corresponding regions are shown as well.

Fig. 3

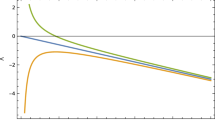
Effective potential $V_\pm$ of the r motion for various sets of parameters. The blue (dark gray) line indicates $V_+$, the green (light gray) one $V_-$. Physically forbidden areas are marked in gray and in the hatched areas it holds ${\mathrm{d}}{t}/{\mathrm{d}}{\gamma }<0$. The horizon at $r=1$ is shown by a vertical dashed line. Some characteristic orbits of type A, B, C, E from Table 1 with 1 to 4 turning points are shown. Points denote the turning points and horizontal dashed lines correspond to the particle’s energy E. Comparing (d) and the L-E diagram in Fig. 2g at $L=20$, orbits of type B and E can be found in regions with 2 and 4 zeros, respectively

Fig. 4

Effective potential $V_\pm$ of the r motion for varying $\delta$ and $K = 0,\, L = 80,\, l = 1$, which allows bound orbits of type D and F (see Table 1) behind the horizon. For a more detailed description see Fig. 3. Additionally, the turnaround energy $E_\text {turn}$ of the $\phi$ motion is shown as a dash-dotted line, which mostly overlaps with the border of the hatched area corresponding to ${\mathrm{d}}{t}/{\mathrm{d}}{\gamma }<0$

Fig. 5

a, b Effective potential $V_\pm$ of the r motion for $\delta =-1$ with parameters chosen to allow for terminating orbits of type $\text {A}_0$ and $\text {D}_0$ (see Table 1). c Effective potential $V_\pm$ of the r motion with parameters chosen to allow for a pointy petal BO of type E. For a more detailed description see Fig. 3. Additionally, the turnaround energy $E_\text {turn}$ of the $\phi$ motion is shown as a dash-dotted line

Since $\text {P}<0$ for $\delta =1$ and $\text {P}>0$ for $\delta =-1$ hold in the limit $r\rightarrow \infty$, orbits of particles of positive mass are always bounded, particles of imaginary mass can exist in unbound orbits for arbitrary energy. More precisely, one finds for particles of non zero mass, i.e., $\delta =\pm 1$, in the limiting case $r\rightarrow \infty$ from $\text {P}=0$

$$\begin{aligned} V_\pm ^\infty =\pm \frac{\sqrt{\delta r}}{|l|}\,. \end{aligned}$$

(32)

Similarly, for massless particles, i.e., $\delta =0$, it follows in the limit $r\rightarrow \infty$

$$\begin{aligned} V_\pm ^\infty =-\frac{L}{2l}\pm \frac{\sqrt{L^2+K}}{2|l|}\,. \end{aligned}$$

(33)

Since here $V_+^\infty >0$ and $V_-^\infty <0$ hold (for $K>0$) and $\text {P}<0$ for $E=0$ in the limit $r\rightarrow \infty$, for every set of parameters a physically forbidden region in the vicinity of $E=0$ can be found. This behavior corresponds to the border of region (2) in Fig. 2e as varying the energy E to region (3)$_+$ allows for an additional unbound orbit.

In special cases, terminating orbits can be found. Due to the smoothness of the polynomial $\text {P}$, the condition $\text {P}(0)\ge 0$ has to be fulfilled, which implies real $V_\pm (0)$, since $\text {P}(0)$ opens downward with respect to E. It follows

$$\begin{aligned} V_\pm (0)=Ll\pm \sqrt{-Kl^2-2K}\,, \end{aligned}$$

(34)

giving $K=0$ and $E=Ll$ as first conditions. To allow for non trivial terminating orbits with non zero range, additionally $\text {P}(r)>0$ has to hold on $r\in (0,\varepsilon )$ with $\varepsilon >0$. This implies that the lowest order non vanishing coefficient of $\text {P}$ must be positive, which is a condition that is always met in case of $\delta =-1$ but never possible in other cases. The influence of the choice of $\delta$ on the effective potential at the singularity around $E=Ll$ is shown in Fig. 4. Here parameters are chosen to allow for bound orbits behind the horizon for all particle masses $\delta$. As regions with ${\mathrm{d}}{t}/{\mathrm{d}}{\gamma }<0$ are shown as well, it can be seen that all depicted bound orbits cross regions where time is running backwards. For a particle of non zero mass this can be avoided by lowering its energy to the bottom of the potential well. A short-range terminating orbit can be found in Fig. 4c at $E=Ll$. Additionally, the two possible types of terminating orbits can be seen in Fig. 5a, b.

With the results of the parametric diagrams and the effective potentials we summarize all combinations of zeros of $\text {P}$ and show their corresponding types of orbits in Table 1. Here the following connection of regions in the parametric diagrams and types of orbits was found:

• 1. Region (1): $\text {P}$ has one non negative zero $r_1<1$, which corresponds to a TEO of type A. For particles of imaginary mass a TO of type $\text {A}_{0}$ is possible for an energy of $E=Ll$ [see, e.g., Fig. 5a].

• 2. Region (2): $\text {P}$ has two positive zeros $r_1<1<r_2$, which corresponds to a MBO of type B.

• 3. Region (3): $\text {P}$ has three non negative zeros $r_i$.

  • (a) Region $\text {(3)}_{+}$: It holds $r_1<1<r_2,r_3$, resulting in a MBO and an EO of type C.

  • (b) Region $\text {(3)}_{-}$: For all zeros it holds $r_i<1$, resulting in a BO and a TEO of type D. Again, for particles of imaginary mass a TO of type $\text {D}_{0}$ is possible for an energy of $E=Ll$ [see, e.g., Fig. 5b].

• 4. Region (4): $\text {P}$ has four positive zeros $r_i$.

  • (a) Region $\text {(4)}_{+}$: It holds $r_1<1<r_2,r_3,r_3$, resulting in a MBO and a BO of type E.

  • (b) Region $\text {(4)}_{-}$: It holds $r_1,r_2,r_3<1<r_4$, resulting in a BO and a MBO of type F.

Table 1 Types of orbits of light and particles in the spacetime of a supersymmetric $\hbox {AdS}_5$ black hole. Thick lines represent the range of the orbits and thick dots indicate their turning points. The vertical double line represents the horizon. The vertical single line corresponds to the singularity, which can only be reached by particles of imaginary mass and $K=0$, resulting in orbits of type $\text {A}_{0}$ and $\text {D}_{0}$. The column $\delta$ distinguishes between particles with imaginary/positive mass ($-1$/1) and light (0)

Note that for every radially allowed orbit an angular momentum J according to Sect. 3.1 can be chosen to allow for $\theta$ motion as well.

3.3 Static orbits

It has been shown in [24] that some axisymmetric rotating spacetimes possess a ring in the equatorial plane, on which stationary particles remain stationary with respect to an asymptotic static observer. As this is possible in higher dimensions as well (see [24] and references therein), we check whether this is the case for the spacetime at hand. Hence, parameters have to be chosen to allow for an extremum of $V_\pm$ at $r_\text {st}$ and a double zero in Eq. (29) at $\cos \theta _\text {st}$. Additionally, the right hand sides of Eqs. (22) and (23) have to vanish. We use $\cos \theta _\text {st}=\frac{LJ}{L^2+K}$ from Eq. (29), under conditions discussed in Sect. 3.1, together with Eq. (23), from which the requirement $K=0$ and $|J|\le |L|$ can be derived. With this, a turnaround energy $E_\text {turn}$ can be defined by solving Eq. (22) for E yielding

$$\begin{aligned} E_\text {turn}(r)=\frac{(r-1)Ll}{2r^2+2r-1}. \end{aligned}$$

(35)

This is also shown in Figs. 4 and 5, since here $K=0$ holds. To obtain a stationary point, $E_\text {turn}$ has to intersect $V_\pm$ in an extremum of $V_\pm$. In this spacetime, we could not find such intersections. However, pointy petal BOs (in front of the horizon), semi BOs (behind the horizon) as well as MBOs, where the particle is periodically at rest, are found at arbitrary intersections of $E_\text {turn}$ and $V_\pm$ for particles of positive mass. In case of a pointy petal BO, an effective r potential and $\phi$ turnaround energy is shown in Fig. 5c.

3.4 Spacelike geodesics and AdS/CFT

Spacelike geodesics are usually not considered in the analysis of geodesic motion, since they represent test particles with imaginary rest mass ($\delta =-1$). In the context of AdS/CFT, however, there are applications for spacelike geodesics. CFT correlators or Feynman propagators describe observables on the asymptotic boundary of an AdS spacetime. Correlation functions of fields in the bulk are related to correlation functions of CFT operators on the boundary. Using the Green function, the correlator of two operators can be written as

$$\begin{aligned} \langle {\mathscr {O}}(t,{\varvec{x}})\,{\mathscr {O}}(t',{\varvec{x}}')\rangle =\int \!\exp [i\varDelta L({\mathscr {P}})]\mathscr {DP}\,. \end{aligned}$$

(36)

Here $L({\mathscr {P}})$ describes the proper length of the path ${\mathscr {P}}$ between the boundary points $(t,{\varvec{x}})$ and $(t,{\varvec{x}}')$. In the case of spacelike trajectories $L({\mathscr {P}})$ is imaginary, so that the whole expression is real. m is the mass of the bulk field, which is related to the conformal dimension $\varDelta =1+\sqrt{1+m^2}$ of the Operator ${\mathscr {O}}$. For large masses, i.e., $\varDelta \approx m$, the WKB approximation can be used to calulate the operator, which is then described by the sum over all spacelike geodesics between the boundary points

$$\begin{aligned} \langle {\mathscr {O}}(t,\mathbf {x})\,{\mathscr {O}}(t',\mathbf {x}')\rangle =\sum _{g}\exp (-\varDelta L_{{g}})\,. \end{aligned}$$

(37)

The real proper length of a geodesic $L_g$ diverges due to contributions near the AdS boundary and has to be renormalized by removing the divergent part in pure AdS. The sum is then dominated by the shortest spacelike geodesic between the boundary points (see, e.g., [9, 25, 26]).

In this formalism we need geodesics that have endpoints on the boundary at $r\rightarrow \infty$. This is the case for escape orbits (EOs) and two-world escape orbits (TEOs) that have a single turning point and reach infinity. For EOs both endpoints of the geodesic are located on a single boundary, since the turning point is outside the horizons. The corresponding two-point correlators can be used to calculate for example the thermalization time [25] or the entanglement entropy [27, 28].

Particles on TEOs cross the horizon and therefore the endpoints are on two disconnected boundaries. TEOs can also be considered as propagators [9, 26]. The boundary correlators can probe the physics behind the horizon. This could be used to study the formation of black holes [9], the black hole singularity [29], or the information paradox [30].

In the spacetime of a supersymmetric $\hbox {AdS}_5$ black hole, geodesics relevant for AdS/CFT exist in the regions (1), (3)$_+$ and (3)$_-$, see Fig. 2 and Table 1. Depending on the parameters of the black hole, we find EOs or TEOs. In region (3)$_+$ EOs exist that return to the same boundary where they started. In region (1) and (3)$_-$, there are TEOs crossing the horizon with endpoints on two disconnected boundaries.

4 Solution of the geodesic equations

In this section we solve the equations of motion (20)–(24) analytically.

4.1 Solution of the $\theta$ equation

Equation (28) can be solved by an elementary function. In case of $a<0$ and $D>0$, this leads to

$$\begin{aligned} \theta (\gamma ){=}\arccos \left( \frac{1}{2a}\left( \sqrt{D}\sin \left( \pm \sqrt{-a} (\gamma {-}\gamma _0){+}\gamma _0^\theta \right) -b\right) \right) \end{aligned}$$

(38)

as a solution of Eq. (21). Here $\gamma _0$ and $\theta _0$ are the initial values of $\gamma$ and $\theta$, respectively, we set $\gamma _0^\theta =\arcsin {\frac{2a\cos \theta _0+b}{\sqrt{D}}}$ and “±” denotes the sign of $\frac{{\mathrm{d}} \theta }{{\mathrm{d}} \gamma }{(\gamma _0)}$.

4.2 Solution of the r equation

By substituting $r=\frac{1}{x}+r_\text {P}$, with $r_\text {P}$ chosen to be a zero of $\text {P}$, one can simplify Eq. (20) to a differential equation of the type $\big (\frac{{\mathrm{d}} x}{{\mathrm{d}} \gamma }\big )^{2}=\text {P}_3^x$ with a polynomial $\text {P}_3^x:=\sum _{i=0}^{3}b_ix^i$ of third order on its right hand side (this step is not necessary for $\delta =0$). The following substitution $x=\frac{1}{b_3}\left( 4y-\frac{b_2}{3}\right)$ transforms this to

$$\begin{aligned} \left( \frac{{\mathrm{d}} y}{{\mathrm{d}} \gamma }\right) ^{2}=4y^3-g_2y-g_3=:\text {P}_3^y, \end{aligned}$$

(39)

with coefficients

$$\begin{aligned} g_2=\frac{b_2^2}{12}-\frac{b_1b_3}{4}, \quad g_3=\frac{b_1b_2b_3}{48}-\frac{b_0b_3^2}{16}-\frac{b_2^3}{216}. \end{aligned}$$

(40)

This elliptic differential equation is solved by the Weierstrass $\wp$ function [31], which leads to

$$\begin{aligned} y(\gamma )=\wp \left( \gamma -\gamma '_0;g_2,g_3\right) \end{aligned}$$

(41)

as a solution of Eq. (39). Here we set $\gamma '_0:=\gamma _0+\int _{y_0}^\infty \frac{{\mathrm{d}}{y}}{\sqrt{\text {P}_3^y}}$ with $y_0=y(x(r_0))$ and the initial value $r_0$ of r. The solution of Eq. (20) is now obtained by

$$\begin{aligned} r(\gamma )=\frac{b_3}{4\wp (\gamma -\gamma '_0;g_2,g_3)-\frac{b_2}{3}}+r_R\,. \end{aligned}$$

(42)

4.3 Solution of the $\phi$ equation

To integrate Eq. (22), we handle its two parts separately and set

$$\begin{aligned} \frac{{\mathrm{d}} \phi }{{\mathrm{d}} \gamma }=:A(r)+B(\theta )\,. \end{aligned}$$

(43)

Again, the substitution $\xi =\cos \theta$ is used, this time upon B. Together with Eq. (28), one gets for the $\theta$ part

$$\begin{aligned} \pm {\mathrm{d}}{\phi _\theta }=\frac{\xi ^2}{\xi ^2-1}\frac{L{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }} -\frac{\xi }{\xi ^2-1}\frac{J{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }}\,. \end{aligned}$$

(44)

Here the “±” indicates the sign of $\frac{{\mathrm{d}} \theta }{{\mathrm{d}} \gamma }{(\gamma _0)}$. Upon the two fractions we apply partial fraction decompositions

$$\begin{aligned} \pm {\mathrm{d}}{\phi _\theta }= \frac{1}{2}\frac{L-J}{\xi -1}\frac{{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }} -\frac{1}{2}\frac{L+J}{\xi +1}\frac{{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }} +L\frac{{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }}. \end{aligned}$$

(45)

The first part can be easily integrated with the substitution $y=\xi -1$, the second part with $y=\xi +1$. The third part is equal to $\mp L{\mathrm{d}}{\gamma }$, as can be seen from Eq. (28). This yields

$$\begin{aligned} \phi _\theta (\gamma )&=\pm \frac{1}{2}\frac{L-J}{\sqrt{-c_1}}\arctan \frac{2c_1+b_1y}{2\sqrt{-c_1\varTheta _{y,1}}}\biggr |_{\xi _0-1}^{\xi (\gamma )-1}\nonumber \\&\quad \mp \frac{1}{2}\frac{L+J}{\sqrt{-c_2}}\arctan \frac{2c_2+b_2y}{2\sqrt{-c_2\varTheta _{y,2}}}\biggr |_{\xi _0+1}^{\xi (\gamma )+1}\nonumber \\&\quad -L(\gamma -\gamma _0) \end{aligned}$$

(46)

$$\begin{aligned}&=:I_1(\gamma )+I_2(\gamma )+I_3(\gamma )\,, \end{aligned}$$

(47)

where $\varTheta _{y,i}:=ay^2+b_iy+c_i$, $i=1,2$ with $b_1=b+2a$, $b_2=b-2a$, $c_1=a+b+c$, and $c_2=a-b+c$. Furthermore, $c_i<0$ was assumed.

Now we integrate the r dependent part A of Eq. (22). We use the two substitutions applied in Sect. 4.2 and recall Eq. (41) to identify $A=A(r(y(\gamma )))$. A partial fraction decomposition on A(y) is performed to get

$$\begin{aligned} {\mathrm{d}}{\phi _r}=\left[ K_0+\frac{K_1}{y(\gamma )-p_1} +\frac{K_2}{y(\gamma )-p_2}\right] {\mathrm{d}}{\gamma }, \end{aligned}$$

(48)

where $K_0,\,K_1$, and $K_2$ are constants of the partial fraction decomposition and $p_1=\frac{(l^2+r_\text {P}+2)b_2-3b_3}{12(l^2+r_\text {P}+2)}$ and $p_2=\frac{(r_\text {P}-1)b_2-3b_3}{12(r_\text {P}-1)}$ are poles of first order. According to [32]¹, the elliptic integrals of third kind $\int _{\nu _0}^{\nu }\frac{{\mathrm{d}}{\nu }}{\wp (\nu )-p}$ can be solved in terms of the Weierstrass $\sigma$ and $\zeta$ functions by using addition theorems. One obtains with $\nu :=\gamma -\gamma _0$

$$\begin{aligned} \begin{aligned} \phi _r(\gamma )&=K_0(\nu -\nu _0) +\sum \limits _{i=1}^{2}\frac{K_i}{\wp '(\nu _{i})} \bigg [2\zeta (\nu _i)(\nu -\nu _0)\\&\quad +\ln \frac{\sigma (\nu -\nu _i)}{\sigma (\nu _0-\nu _i)} -\ln \frac{\sigma (\nu +\nu _i)}{\sigma (\nu _0+\nu _i)}\bigg ]. \end{aligned} \end{aligned}$$

(49)

Here $\nu _i$ is a Weierstrass transformed pole $p_i$, which solves $\wp (\nu _i)=p_i$ for $i=1,2$ in the fundamental parallelogram of $\wp (\nu )$.

The solution of Eq. (43) is given by the sum of this expression, Eq. (46), and the initial value $\phi _0$.

4.4 Solution of the $\psi$ equation

To obtain the $\psi$ motion from Eq. (23), we proceed similarly to the solution of the $\theta$ part of the $\phi$ motion in Sect. 4.3. Again, with the substitution $\xi =\cos \theta$ and partial fraction decompositions, one gets

$$\begin{aligned} \pm {\mathrm{d}}{\psi }=-\frac{1}{2}\frac{L-J}{\xi -1}\frac{{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }} -\frac{1}{2}\frac{L+J }{\xi +1}\frac{{\mathrm{d}}{\xi }}{\sqrt{\varTheta _\xi }}\,. \end{aligned}$$

(50)

Using the definitions of Eq. (47), we find with the initial value $\psi _0$ of $\psi$

$$\begin{aligned} \psi (\gamma )=-I_1(\gamma )+I_2(\gamma )+\psi _0\,. \end{aligned}$$

(51)

4.5 Solution of the t equation

The integral of the right hand side of Eq. (24) can be derived similarly to that of A(r) in Sect. 4.3. Here the partial fraction decomposition leads to

$$\begin{aligned} {\mathrm{d}}{t}=\left[ H_0+\frac{H_1}{y(\gamma )-p_1}+\frac{H_2}{y(\gamma )-p_2} +\frac{H_3}{(y(\gamma )-p_2)^2}\right] {\mathrm{d}}{\gamma } \end{aligned}$$

(52)

with $H_0,\, H_1,\, H_2$, and $H_3$ given by the partial fraction decomposition and $p_1$ and $p_2$ are poles of first and second order, respectively, that are identical to those in Eq. (48). The integral of the first three terms yields an expression of the type obtained in Eq. (49). Again, according to [32],² the elliptic integral of type $\int _{\nu _0}^{\nu }\frac{{\mathrm{d}}{\nu }}{(\wp (\nu )-p)^2}$ can be solved in terms of the Weierstrass $\sigma$ and $\zeta$ functions. One obtains with $\nu :=\gamma -\gamma _0$ and the initial value $t_0$ of t

$$\begin{aligned} \begin{aligned} t(\gamma )&=t_0+H_0(\nu -\nu _0)+\sum \limits _{i=1}^{2}\frac{H_i}{\wp '(\nu _{i})} \bigg [2\zeta (\nu _i)(\nu -\nu _0)\\&\quad +\ln \frac{\sigma (\nu -\nu _i)}{\sigma (\nu _0-\nu _i)} -\ln \frac{\sigma (\nu +\nu _i)}{\sigma (\nu _0+\nu _i)}\bigg ]\\&\quad -\frac{H_3\wp ''(\nu _2)}{(\wp '(\nu _2))^3}\bigg [2\zeta (\nu _2)(\nu -\nu _0)\\&\quad +\ln \frac{\sigma (\nu -\nu _2)}{\sigma (\nu _0-\nu _2)} -\ln \frac{\sigma (\nu +\nu _2)}{\sigma (\nu _0+\nu _2)}\bigg ]\\&\quad -\frac{H_3}{(\wp '(\nu _2))^2}\bigg [2\wp (\nu _2)(\nu -\nu _0) +2[\zeta (\nu )-\zeta (\nu _0)]\\&\quad +\frac{\wp '(\nu )}{\wp (\nu )-\wp (\nu _2)} -\frac{\wp '(\nu _0)}{\wp (\nu _0)-\wp (\nu _2)}\bigg ]\,. \end{aligned} \end{aligned}$$

(53)

Fig. 6

MBO and BO for parameters $K = 4,\, L = 20,\, \delta = 1,\, l = 1,\, J = 0$, and energy $E=0.95$. The projections onto the x-z plane (bottom left) show the turning points of the $\phi$ motion as a dotted line. Projections onto the x-y plane are shown at the bottom right. The spheres and dashed circles show the horizon at $R=1$. The corresponding effective potential of the r motion can be found in Fig. 3d

Fig. 7

MBO and EO for parameters $K = 4,\, L=4,\, \delta = 0,\, l = 1,\, J = 0$, and energy $E = 0.386699$. The projections onto the x-z plane (bottom left) show the turning points of the $\phi$ motion as a dotted line. Projections onto the x-y plane are shown at the bottom right. The spheres and dashed circles show the horizon at $R=1$

Fig. 8

MBO and EO for parameters $K = 12,\, L = 8,\, \delta = 0,\, l = 1,\, J = 4$, and energy $E = 0.6672265$. The trajectory is confined to an area above $\theta =\pi /2$. In b and d the dotted curves denote the turning points of the $\phi$ motion. The spheres and dashed circles show the horizon at $R=1$

Fig. 9

MBO and EO for parameters $K = 0,\, L = 8,\, \delta = 0,\, l = 1,\, J = 4$, and energy $E = 0.343913$. The trajectory lies on a cone with opening angle $\theta <\pi /2$. In b the dotted circle indicates the $\phi$ turning points. The spheres and dashed circles show the horizon at $R=1$

Fig. 10

a, b TEO for parameters $K = 4,\, L = 4,\, \delta = 0,\, l = 1,\, J = 0$, and energy $E = 0.4$. In b the dotted curve denotes the turning points of the $\phi$ motion. c, d TO for parameters $K = 0,\, L = 8,\, \delta = -1,\, l = 1,\, J = 4$, and energy $E = Ll = 8$. The trajectory lies on a cone with opening angle $\theta <\pi /2$. The corresponding effective potential of the r motion can be found in Fig. 5a. The spheres and dashed circles show the horizon at $R=1$

Fig. 11

TO and TEO for parameters $K = 0,\, L = 36.39992,\, \delta = -1,\, l = 0.3,\, J = 4$, and energy $E = Ll= 10.919976$. The trajectory lies on a cone with opening angle $\theta <\pi /2$. The sphere and dashed circle show the horizon at $R=1$. The corresponding effective potential of the r motion is very similar to the one shown in Fig. 5b

5 The orbits

To plot the spatial coordinates $(\phi ,\psi ,\theta ,r)$ of the set of analytical solutions for the particle’s motion in a Cartesian coordinate system, a coordinate transformation has to be chosen. The angular line element ${\mathrm{d}}{\varOmega ^2}=\frac{1}{R^2}\sum _{\mu ,\nu =1}^3g_{\mu \nu }{\mathrm{d}}{x^\mu }{\mathrm{d}}{x^\nu }$ for $x^\mu =(t,\phi ,\psi ,\theta ,R)$ of the metric in Eq. (1) yields in case of $R\rightarrow \infty$

$$\begin{aligned} {\mathrm{d}}{\varOmega ^2}=\frac{1}{4}\left[ {\mathrm{d}}{\theta ^2}+{\mathrm{d}}{\psi ^2}+{\mathrm{d}}{\phi ^2} +2\cos \theta {\mathrm{d}}{\phi } {\mathrm{d}}{\psi }\right] \,. \end{aligned}$$

(54)

On the other hand, the angular line element of flatspace in biazimuthal coordinates $(\varphi _1,\varphi _2,\vartheta ,R)$ is

$$\begin{aligned} {\mathrm{d}}{\varOmega ^2}={\mathrm{d}}{\vartheta ^2}+\sin ^2\vartheta {\mathrm{d}}{\varphi _1^2} +\cos ^2\vartheta {\mathrm{d}}{\varphi _2^2}\,. \end{aligned}$$

(55)

Fig. 12

Pointy petal BO for parameters $K = 0,\, L = 17.1,\, \delta = 1,\, l = 1,\, J = 0$, and energy $E = 0.8686915$. The trajectory lies on a cone with opening angle $\theta =\pi /2$. The sphere and dashed circle show the horizon at $R=1$. The corresponding effective potential and turnaround energy of the r and $\phi$ motion, respectively, can be found in Fig. 5c. The particle periodically stops at the outer turning points

A comparison of Eqs. (54) and (55) suggests the coordinate transformation

$$\begin{aligned} \phi&=\varphi _1+\varphi _2\,,&\psi&=\varphi _2-\varphi _1\,,&\theta&=2\vartheta , \end{aligned}$$

(56)

which, together with the biazimuthal coordinates and $r=R^2$, transforms $(\phi ,\psi ,\theta ,r)$ to (x, y, z, w) by

$$\begin{aligned} x&=\sqrt{r}\sin \frac{\theta }{2}\cos \frac{\phi -\psi }{2}, \end{aligned}$$

(57a)

$$\begin{aligned} y&=\sqrt{r}\sin \frac{\theta }{2}\sin \frac{\phi -\psi }{2},\end{aligned}$$

(57b)

$$\begin{aligned} z&=\sqrt{r}\cos \frac{\theta }{2}\cos \frac{\phi +\psi }{2},\end{aligned}$$

(57c)

$$\begin{aligned} w&=\sqrt{r}\cos \frac{\theta }{2}\sin \frac{\phi +\psi }{2}. \end{aligned}$$

(57d)

Furthermore, we choose a projection in the 3-dimensional Cartesian subspace of the coordinates (x, y, z) by setting $w=0$. This preserves the notion of a horizon on the surface of a sphere with radius $R=1$, but as a consequence we have to set $\psi =-\phi$, so only analytical solutions of $\phi ,\,\theta ,$ and r are used. Another consequence is that the $\theta$ motion on the interval $[0,\pi ]$ is now mapped to the upper hemisphere only, thereby, as the horizon is shown in the following as a complete sphere of radius 1, the lower half sphere is of no physical relevance.

Fig. 13

BO for parameters $K = 0.1,\, L = 80,\, \delta = 1,\, l = 1,\, J = 0$, and energy $E = 81.5082984$. The corresponding effective potential of the r motion is very similar to the one shown in Fig. 4a

The figures above show the particle’s motion for various sets of parameters. The first orbit of a particle of positive mass is of type E and is shown in Fig. 6, its effective potential can be found in Fig. 3d. For similar parameters (L was decreased) a lightlike orbit of type C is shown in Fig. 7. Both of those orbits pass the equatorial plane. An orbit that is confined to one hemisphere has to satisfy $K<J^2$, as was discussed in Sect. 3.1. A lightlike orbit of this kind is shown in Fig. 8 for type C.

In case of $K=0$ and $\kappa >0$, one obtains an orbit confined to a cone of fixed opening angle $\arccos \frac{J}{|L|}$. This is shown in Fig. 9 for type C. A two-world escape orbit of type A can be found in Fig. 10a. This is obtained by increasing the energy slightly above the effective potential’s maximum while the other parameters are unchanged compared to Fig. 7. By the increase in energy, the many-world periodic bound orbit and the escape orbit merged into one two-world escape orbit.

Now we present orbits of particles with imaginary mass that reach the boundary at infinity and therefore are of relevance for AdS/CFT. A terminating orbit of type $\text {A}_0$, with its effective potential depicted in Fig. 5a, can be found in Fig. 10c. In Fig. 11 we show a terminating orbit and a two-world escape orbit of type $\text {D}_0$ of a particle with imaginary mass in an effective potential very similar to the one shown in Fig. 5b.

The pointy petal bound orbit of type E of a particle that is periodically at rest is depicted in Fig. 12, its effective potential in Fig. 5c. Here parameters are chosen by determining the intersection of the effective potential $V_\pm$ and turnaround energy $E_\text {turn}$ while $\theta$ is, for simplicity, chosen to be constant, as discussed in Sect. 3.3.

Finally, a bound orbit behind the horizon for a particle of positive mass (type F) is shown in Fig. 13. This requires small K and large L. Its effective potential is very similar to the one shown in Fig. 4a but its trajectory is not confined to a cone of fixed opening angle $\theta$.

6 Conclusion

In this article the spacetime of a supersymmetric $\hbox {AdS}_5$ black hole was studied by analyzing the geodesics (elliptic) equation of motion and deriving its analytical solutions in terms of the Weierstrass $\wp$, $\sigma$, and $\zeta$ functions. Effective potentials and parametric diagrams were used to classify possible types of orbits, which are characterized by the particle’s energy, angular momenta, Carter constant, and mass parameter as well as the metric’s AdS radius.

We showed that timelike orbits are always bounded and thus do not reach the AdS boundary. For lightlike and spacelike geodesics multiple types of orbits with a boundary at infinity and therefore with relevance for AdS/CFT were found. This, for spacelike geodesics and for a specific energy, includes the possibility of a terminating orbit. Bound orbits behind the horizon (for large angular momentum L) and many-world periodic bound orbits are possible independently of the particle’s mass. However, stable bound orbits outside of the horizon are only possible for particles of positive mass.

Future work might focus on extending the equations of motion to particles with electric and magnetic charge. Additionally, the orbits’ observables, e.g., in case of a bound orbit, its periastron shift or, in case of a lightlike escape orbit, its light deflection or the black hole’s shadow, might be calculated similarly as in [14] by making use of the analytical solutions.