1 Introduction

High-harmonic generation (HHG) has been first observed in gases [1, 2]. Its non-perturbative nature, featuring a plateau of almost constant high-harmonic yield, was subsequently explained by the three-step model [3, 4]: An electron is removed from the atom, propagates under the external field’s influence, and recombines with the atom. The orbital energies of electrons in atoms do not depend on momentum, and the electron’s dispersion relation in the continuum is shaped parabolically. Therefore, electrons in the ground state or free electrons emit no harmonics. Only transitions between bound states or recombination from continuum states back to bound states lead to harmonic emission.

To describe HHG in the bulk of solids, electronic bands replace the orbital energies and the continuum [5]. This opens a whole new field of research [6,7,8,9,10,11,12,13]. Analogous to the HHG process in gases, the transition of electrons between valence and conduction bands causes high harmonics, called interband harmonics. Intraband harmonics, on the other hand, are produced by the movement of electrons in partially filled, non-parabolic bands. Band structures are usually defined for periodic or infinite solid bulk systems. However, every realistic system has boundaries, which may cause completely different HHG spectra compared to the bulk [14,15,16,17,18]. Graphene and hexagonal boron nitride (hBN) are two-dimensional materials that possess fascinating features with promising potential applications [19, 20]. Their hexagonal structure allows for two different edges: zig-zag and armchair. While graphene contains only carbon atoms (all identical), hBN consists of boron and nitrogen atoms. Recently, the interaction of intense-laser light with graphene got into the focus of interest for its prospects to steer electrons at will on ultrafast time scales [21,22,23,24].

In this article, we investigate the harmonic spectra emitted by hexagonal nanoribbons in two different edge configurations, armchair (Sect. 3) and zig-zag (Sect. 4). We performed our calculations using a real-space time-dependent Schrödinger solver (as described in Sect. 2). The results of this publication validate the tight-binding approach in [25].

2 Methods

The nanoribbons’ \(N_\mathrm {ions}\) atomic nuclei were positioned in a hexagonal lattice, as described for the armchair and zig-zag configuration in Sects. 3 and 4. Atomic units are used throughout this paper unless stated otherwise. The distance between neighboring lattice sites was 2.683, the bond length in graphene (1.42Å). An effective Pöschl–Teller potential

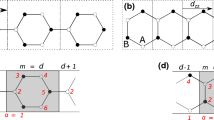
$$\begin{aligned} V(\mathbf {r}) = - \sum _i \frac{V_i}{\cosh ^2(\varepsilon |\mathbf {r} - \mathbf {r}_i|)} \end{aligned}$$
(1)

with ion potentials \(V_i = 3.2 \pm V_\mathrm {os}\) and screening parameter \(\varepsilon = 2\) describe the attractive potentials of the nuclei. For graphene ribbons, all atoms are carbon, therefore the additional on-site potential \(V_\mathrm {os} = 0\). A non-zero on-site potential represents two alternating, different kind of atoms, such as boron and nitrogen in hBN. Figures 1 and 4 show at which lattice sites the ion potentials are increased or decreased by \(V_\mathrm {os}\).

In this work, we did not employ the usual tight-binding approximation commonly made in condensed-matter theory. Instead, we have developed a 2D, real-space, time-dependent Schrödinger solver for the ab initio simulation of the intense-laser interaction with 2D matter. In that way, we can reveal differences and similarities in HHG spectra as compared to corresponding tight-binding studies, e.g., in Ref. [25]. The non-interacting electronic orbitals in our Schrödinger solver are defined on a two-dimensional grid of spacing \(\varDelta x = \varDelta y = 0.2\), which encompasses all lattice sites plus a border of 8 on each side. In contrast to the usual tight-binding description, this allows us to have electron orbitals \(\varphi _i\) (with energies \(E_i\)) that are not only localized at lattice sites but also between them, or free electrons.

The electronic eigenstates of the system were found by imaginary-time propagation of the time-dependent Schrödinger equation

$$\begin{aligned} \mathrm {i} \partial _t \varphi _i(\mathbf {r}, t) = \left[ -\frac{1}{2} \nabla ^2 + V(\mathbf {r}) \right] \varphi _i(\mathbf {r}, t) \end{aligned}$$
(2)

employing the Crank–Nicolson method [26]. Starting from a random initialization, imaginary timesteps \(-0.05\mathrm {i}\) are taken (each step followed by renormalization of the wavefunction) until the ground state is reached and the relative change of the state is smaller than the threshold of \(10^{-18}\) for two consecutive iterations. To find the higher-lying states, the workflow is identical but with an additional (Gram-Schmidt) orthogonalization to all previously found states in each iteration. This procedure gives us all states of interest in the unperturbed system.

Real-time simulations of the interaction of all occupied electronic orbitals with a short laser pulse were performed with a timestep 0.05 using, again, Crank–Nicolson propagation. The pulse was a \(n_\mathrm {cyc} = 4\) cycle \(\sin ^2\)-shaped laser pulse of frequency \(\omega = 0.0075\) (\(\lambda \simeq {6.1}\mathrm{mm}\)) with vector potential

$$\begin{aligned} A(t) = A_0 \sin ^2\left( \frac{\omega t}{2 n_\mathrm {cyc}}\right) \sin \omega t \end{aligned}$$
(3)

for \( 0< t < 2 \pi n_\mathrm {cyc}/\omega \) and zero otherwise. The electronic dipoles were recorded at each time step during the laser pulse and added up according to

$$\begin{aligned} \mathbf {P}(t) = 2 \sum _{i=1}^{N_\mathrm {occupied}} \int \mathbf {r} |\varphi _i(\mathbf {r}, t)|^2 \,\mathrm {d} \mathbf {r}, \end{aligned}$$
(4)

where \(N_\mathrm {occupied} = N_\mathrm {ions} / 2\) is the number of occupied orbitals, each occupied by a spin-up and a spin-down electron. Harmonic spectra were calculated as the absolute square of the Fourier transform of the recorded dipoles, multiplied by a symmetric Hann window [27, 28].

3 Armchair ribbon

First, we investigate a hexagonal nanoribbon in the armchair configuration. A total of 24 lattice sites are arranged in the shape of four hexagons, as shown in Fig.  1. For \(V_\mathrm {os} = 0\), the armchair ribbon is symmetric about the horizontal as well as the vertical axis through the center. The introduction of an on-site potential deepens the blue (square) sites’ potentials while making the orange (circle) ones shallower. This causes a left-right asymmetry, while the top–bottom symmetry is conserved. These (a)symmetries of the system are present for ribbons consisting of both even and odd numbers of hexagons. Calculations for a ribbon of 30 sites arranged in five hexagons are consistent with the results shown here.

Note that the lines drawn in Fig.  1 connect nearest neighbors. In tight-binding calculations (such as in Ref. [25]), hopping takes place along these lines. However, in our simulation based on the time-dependent Schrödinger equation, electronic wavefunctions are not restricted to move along these lines but may propagate in the entire plane.

Fig. 1
figure 1

Armchair ribbon: At the blue (square) lattice sites, the potential depth is increased by the on-site potential, \(V_\mathrm {blue} = V_\mathrm {avg} + V_\mathrm {os}\). The orange (circle) sites correspond to the shallower potentials of depth \(V_\mathrm {orange} = V_\mathrm {avg} - V_\mathrm {os}\). The arrows indicate the polarization directions of the external laser field (along the ribbon) and the harmonics referred to as parallel and perpendicular

Full size image
Fig. 2
figure 2

Orbitals and orbital energies of the armchair ribbon. a Orbitals of the armchair ribbon. (1) Highest occupied orbital without on-site potential (\(V_\mathrm {os} = 0\)). (2) Lowest unoccupied orbital without on-site potential (\(V_\mathrm {os} = 0\)). (3) Highest occupied orbital with on-site potential \(V_\mathrm {os} = 0.4\). (4) Lowest unoccupied orbital with on-site potential \(V_\mathrm {os} = 0.4\). b Orbital energies of the armchair ribbon as a function of on-site potential \(V_\mathrm {os}\). Circles mark the orbital energies of the orbitals shown in (a). The orbitals form three bands: occupied valence band (blue), unoccupied conduction band (orange), and box states (gray). The gray shaded area indicates additional box states lying above those shown explicitly. The arrows mark the bandwidth of the valence band (\(\varDelta E_\mathrm {intra}\)) and the minimum and maximum bandgap between the valence and (first) conduction band (\(\varDelta E_\mathrm {min}\) and \(\varDelta E_\mathrm {max}\))

Full size image

The asymmetry in the potential leads to an asymmetry in the orbitals. Figure 2a shows the highest occupied (1 and 3) and lowest unoccupied (2 and 4) orbitals without (1 and 2) and with (3 and 4) on-site potential. The orbitals without on-site potential are horizontally and vertically symmetric (as is the potential), and there is only a small bandgap between the occupied and unoccupied states. With an on-site potential, the occupied orbitals are localized on the sites with deeper potentials and therefore have a decreased energy. The unoccupied orbitals are localized on the sites with shallower potentials and therefore have increased energy. This leads to a bandgap \(\varDelta E_\mathrm {min}\) between the occupied and unoccupied orbitals, which, for \(V_\mathrm {os} \gtrsim 0.2\), grows linearly with the on-site potential (Fig. 3b). In contrast to tight-binding methods, our approach allows us to calculate an arbitrary number of orbitals of increasing energy. The states above the conduction band describe “free” electrons, which are not localized on the ribbon but still inside the simulation box with reflecting boundary conditions.

Fig. 3
figure 3

Harmonic spectra of the armchair ribbon in parallel direction. a Harmonic spectra without (bold orange line, \(V_\mathrm {os} = 0\)) and with (blue line, \(V_\mathrm {os} = 0.4\)) on-site potential. b Harmonic spectra as a function of harmonic order and on-site potential. The bandwidth \(\varDelta E_\mathrm {intra}\) of the valence band is the upper bound of the intraband harmonics. The minimum (\(\varDelta E_\mathrm {min}\)) and maximum (\(\varDelta E_\mathrm {max}\)) bandgaps limit the energies of the interband harmonics. Transitions to the box states generate harmonics above \(\varDelta E_\mathrm {max}\). Triangles of the corresponding colors indicate the energies of the two spectra shown in (a)

Full size image

The incoming laser field is linearly polarized along the armchair ribbon. All emitted harmonics are linearly polarized in the same direction (parallel harmonics, as indicated in Fig. 1). The armchair ribbon is top–bottom symmetric, regardless of on-site potential. Without a top–bottom asymmetry in the system, the horizontally polarized laser leads to a perfectly horizontal movement of the electrons, which generates only horizontally polarized harmonics. Therefore, the armchair ribbon can not generate perpendicular harmonics. The bandwidths and bandgaps (\(\varDelta E_\mathrm {intra}\), \(\varDelta E_\mathrm {min}\), and \(\varDelta E_\mathrm {max}\)) from Fig. 2b explain the most important features of the harmonic spectra shown in Fig. 3. Intraband harmonics are only present at harmonic energies below the width of the valence band \(\varDelta E_\mathrm {intra}\). Interband harmonics appear between the minimum \(\varDelta E_\mathrm {min}\) and maximum \(\varDelta E_\mathrm {max}\) bandgap between the valence and (first) conduction band. Above the two bands are the box states (marked as gray lines in Fig. 2b), which are not localized on the ribbon, and whose energies are determined by the size of the simulation box. The figure only shows the energies of the four lowest box states (which are pairwise almost degenerate), but many more lie above them, indicated by the gray shaded area. Transitions to these box states cause harmonics above \(\varDelta E_\mathrm {max}\). In an experiment, transitions to higher bands or the continuum would cause harmonics beyond the maximum bandgap. These can not be described in tight-binding approximation with one atomic orbital per site, because then the energy difference between states is bound from above by \(\varDelta E_\mathrm {max}\) (see Ref. [25]).

4 Zig-zag ribbon

Fig. 4
figure 4

Zig-zag ribbon: At the blue (square) lattice sites, the potential depth is increased by the on-site potential, \(V_\mathrm {blue} = V_\mathrm {avg} + V_\mathrm {os}\). The orange (circle) sites correspond to the shallower potentials of depth \(V_\mathrm {orange} = V_\mathrm {avg} - V_\mathrm {os}\). The arrows indicate the polarization directions of the external laser field (along the ribbon) and the harmonics referred to as parallel and perpendicular

Full size image

In the zig-zag configuration, a total of 26 lattice sites are arranged in six hexagons, as shown in Fig. 4. On the orange (circle) sites, the on-site potential decreases the potential depth, while on the blue (square) sites, it deepens the potential. The on-site potential causes a top–bottom asymmetry but no left-right asymmetry. Reference [25] investigates the influence of the ribbon’s length using a computationally less demanding tight-binding approach. Full time-dependent Schrödinger calculation results for a ribbon of 30 sites (seven hexagons) agree with those for 26 sites (six hexagons).

Fig. 5
figure 5

Orbitals and orbital energies of the zig-zag ribbon. a Orbitals of the zig-zag ribbon. (1) Highest occupied orbital without on-site potential (\(V_\mathrm {os} = 0\)). (2) Lowest unoccupied orbital without on-site potential (\(V_\mathrm {os} = 0\)). (3) Highest occupied orbital with on-site potential \(V_\mathrm {os} = 0.4\). (4) Lowest unoccupied orbital with on-site potential \(V_\mathrm {os} = 0.4\). b Orbital energies of the zig-zag ribbon as a function of on-site potential \(V_\mathrm {os}\). Circles mark the orbital energies of the orbitals shown in (a). The orbitals form three bands: occupied valence band (blue), unoccupied conduction band (orange), and box states (gray). The gray shaded area indicates additional box states lying above those shown explicitly. The arrows mark the bandwidth of the valence band (\(\varDelta E_\mathrm {intra}\)) and the minimum and maximum bandgap between the valence and (first) conduction band (\(\varDelta E_\mathrm {min}\) and \(\varDelta E_\mathrm {max}\))

Full size image

As for the armchair ribbon, the asymmetry of the potential leads to decreased energies of states in the valence band, localized at the deeper sites, and increased energies of states in the conduction bands, localized at the shallower sites (see Fig. 5). The minimum bandgap increases almost linearly with the on-site potential; the bandwidths of both bands decrease.

Fig. 6
figure 6

Harmonic spectra of the zig-zag ribbon as a function of on-site potential in a parallel and b perpendicular polarization. The bandwidth \(\varDelta E_\mathrm {intra}\) of the valence band is the upper bound of the intraband harmonics. The minimum (\(\varDelta E_\mathrm {min}\)) and maximum (\(\varDelta E_\mathrm {max}\)) bandgaps limit the energies of the interband harmonics. Transitions to the box states generate harmonics above \(\varDelta E_\mathrm {max}\)

Full size image

The parallelly polarized harmonics (Fig. 6a) are present with and without on-site potential. The bandwidth and bandgaps can explain the cutoffs of both intra- and interband harmonics. Perpendicular harmonics (Fig. 6b) with on-site potential agree with these cutoffs, as well. Without an on-site potential, there is no top–bottom asymmetry, and therefore, almost no harmonics perpendicular to the laser are observed. Transitions to the box states lead to weak harmonic emission above \(\varDelta E_\mathrm {max}\).

5 Conclusion

The introduction of an on-site potential in hexagonal nanoribbons causes lower energies for occupied states and higher energies for unoccupied states. The valence band’s bandwidth decreases, and the minimum and maximum bandgaps between the valence and conduction bands increase. These three energies explain the overall features in harmonic spectra for different on-site potentials. Intraband harmonics are only present at energies below the valence bandwidth. Interband harmonics are present at energies between the minimum and maximum bandgaps. For a laser polarized along the ribbon, the resulting harmonics are polarized in the same direction unless a non-zero on-site potential causes a top–bottom asymmetry, which is only possible in the zig-zag ribbon.

The results of this paper provide valuable verification of simpler tight-binding models [25]. Our approach is not limited to a fixed number of states (grouped in bands), and our results account for transitions to even higher bands or the continuum. However, these transitions are expected to play an important role only in the generation of higher harmonics beyond the cutoff \(\varDelta E_\mathrm {max}\), leading to higher order plateaus with decreasing yield (see, e.g., [29]). On the other hand, tight-binding approaches capture the essential mechanisms underlying high-harmonic generation up to \(\varDelta E_\mathrm {max}\), are computationally much less demanding, and thus can be used to investigate much larger systems.

The datasets generated and analyzed during this study are available at Ref. [30].