Bäcklund transformations and Riemann–Bäcklund method to a (3 + 1)-dimensional generalized breaking soliton equation

Abstract

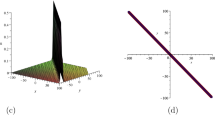
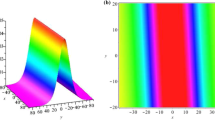
In this paper, the bilinear method is employed to investigate the N-soliton solutions of a (3 + 1)-dimensional generalized breaking soliton equation. Three sets of bilinear Bäcklund transformations are obtained by means of gauge transformation. The Riemann–Bäcklund method is further extended to the (3 + 1)-dimensional nonlinear integrable systems. The quasiperiodic wave solutions of the (3 + 1)-dimensional generalized breaking soliton equation are systematically analyzed. The asymptotic properties of the quasiperiodic solutions are discussed by using a limiting procedure. The one-periodic and two-periodic waves tend to the 1-soliton and 2-soliton under a small amplitude limit, respectively. The dynamical characteristics of the one- and two-periodic waves are summarized by selecting different parameters. Furthermore, we obtain some new types of the quasiperiodic wave solutions of the variable coefficient (3 + 1)-dimensional generalized breaking soliton equation. These solutions present the dynamical behaviors of C-type, anti-C-type and Z-type periodic waves moving on the background of the periodic waves of bell type.

Appendix

Three basic theorems about the theory of Riemann–Bäcklund method are given in “Appendix”. For more details, the readers can see the references [44, 53, 56].

Theorem A

(Periodicity of Riemann theta function (6)) If ${\varvec{e_j}}$ is the jth column of the $N \times N$ identity matrix ${\varvec{I}}$, ${\tau _j}$ is the column of ${\varvec{\tau }}$, and the ${\tau _{jj}}$ is the $\left( {j,j} \right)$ entry of the ${\varvec{\tau }}$, then Riemann theta function $\Theta \left( {{\varvec{\xi }} ,{\varvec{0}} ,{\varvec{0}}|{\varvec{\tau }} } \right)$ possesses the periodicity:

$$\begin{aligned} \begin{array}{l} \Theta \left( {{\varvec{\xi }} + {\varvec{e_j}} + \mathrm{{i}}{\varvec{\tau _j}},{\varvec{0}},{\varvec{0}}|{\varvec{\tau }} } \right) \\ \quad = \exp \left( { - 2\pi \mathrm{{i}}{\xi _j} + \pi {\tau _{jj}}} \right) \Theta \left( {{\varvec{\xi }} ,{\varvec{0}},{\varvec{0}}|{\varvec{\tau }} } \right) .\end{array} \end{aligned}$$

Then, we can conclude that the vectors $\left\{ {{\varvec{e_j}},j = 1,2, \cdots ,N} \right\}$ and $\left\{ {\mathrm{{i}}{\varvec{\tau _j}},j = 1,2, \cdots ,N} \right\}$ can be regarded as periods of the theta function $\Theta \left( {{\varvec{\xi }} ,{\varvec{0}} ,{\varvec{0}}|{\varvec{\tau }} } \right)$ with multipliers 1 and $\exp \left( { - 2\pi \mathrm{{i}}{\xi _j} + \pi {\tau _{jj}}} \right)$, respectively.

Theorem B

For a polynomial operator

$$\begin{aligned} \mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right) \end{aligned}$$

about the operators ${D_x},{D_y},{D_z}$ and ${D_t}$, we have the following formula

$$\begin{aligned} \begin{array}{l} \mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right) \Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon '}},{\varvec{0}}|{\varvec{\tau }} } \right) \Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon }} ,{\varvec{0}}|{\varvec{\tau }} } \right) \\ \quad = \sum \limits _{{\varvec{\mu }}} {C\left( {{\varvec{\varepsilon }} ,{\varvec{\varepsilon '}},{\varvec{\mu }} } \right) } \Theta \left( {2{\varvec{\xi }} ,{\varvec{\varepsilon '}} + {\varvec{\varepsilon }} ,\frac{{\varvec{\mu }} }{2}|2{\varvec{\tau }} } \right) , \end{array} \end{aligned}$$

in which

$$\begin{aligned} \begin{array}{l} C\left( {{\varvec{\varepsilon }} ,{\varvec{\varepsilon '}},{\varvec{\mu }} } \right) \\ \quad = \sum \limits _{{\varvec{n}} \in {Z^N}} {{\mathscr {H}}\left( M \right) } \exp \left[ { - 2\pi \left\langle {{\varvec{\tau }} \left( {{\varvec{n}} - \frac{{\varvec{\mu }} }{2}} \right) ,{\varvec{n}} - \frac{{\varvec{\mu }} }{2}} \right\rangle } \right. \left. {- 2\pi \mathrm{{i}}\left\langle {{\varvec{n}} - \frac{{\varvec{\mu }} }{2},{\varvec{\varepsilon '}} - {\varvec{\varepsilon }} } \right\rangle } \right] , \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} M = \left( {4\pi \mathrm{{i}}\left\langle {n - \dfrac{\mu }{2},{\varvec{\alpha }} } \right\rangle ,4\pi \mathrm{{i}}\left\langle {n - \dfrac{\mu }{2},{\varvec{\beta }} } \right\rangle ,} \right. \left. {4\pi \mathrm{{i}}\left\langle {n - \dfrac{\mu }{2},{\varvec{\gamma }} } \right\rangle ,4\pi \mathrm{{i}}\left\langle {n - \dfrac{\mu }{2},{\varvec{\omega }} } \right\rangle } \right) . \end{array} \end{aligned}$$

If the determining equations of parameters are equal to zero

$$\begin{aligned} C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right) = 0 \end{aligned}$$

for all possible combinations ${\mu _1} = 0,1;\;{\mu _2} = 0,1;\; \cdots$ ${\mu _N} = 0,1$, then $\Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon '}},0|{\varvec{\tau }} } \right)$ and $\Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon }} ,0|{\varvec{\tau }} } \right)$ are N-periodic wave solutions of the bilinear equation

$$\begin{aligned} \mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right) \Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon '}},0|{\varvec{\tau }} } \right) \Theta \left( {{\varvec{\xi }} ,{\varvec{\varepsilon }} ,0|{\varvec{\tau }} } \right) = 0. \end{aligned}$$

Theorem C

$C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right)$ and $\mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right)$ are given in theorem B. To make $C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right) = 0$, one chooses ${\varepsilon _j}^\prime - {\varepsilon _j} = \pm \frac{1}{2},\;j = 1,2, \ldots ,$ N. Then,

• (i) If $\mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right)$ is an even function in the form

  $$\begin{aligned} \mathscr {H}\left( { - {D_x}, - {D_y}, - {D_z}, - {D_t}} \right) = \mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right) , \end{aligned}$$

  then $C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right)$ vanishes automatically for the case when $\sum \nolimits _{j = 1}^N {{\mu _j}}$ is an odd number, i.e.,

  $$\begin{aligned} C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right) {|_{{\varvec{\mu }}} } = 0,\quad \mathrm{{for}}\quad \sum \limits _{j = 1}^N {{\mu _j}} \mathrm{{ = 1}},\quad \,\bmod \,\;\mathrm{{2}}. \end{aligned}$$

• (ii) If $\mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right)$ is an odd function in the form

  $$\begin{aligned} \mathscr {H}\left( { - {D_x}, - {D_y}, - {D_z}, - {D_t}} \right) = -\mathscr {H}\left( {{D_x},{D_y},{D_z},{D_t}} \right) , \end{aligned}$$

  then $C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right)$ vanishes automatically for the case when $\sum \nolimits _{j = 1}^N {{\mu _j}}$ is an even number, i.e.,

  $$\begin{aligned} C\left( {{\varvec{\varepsilon }},{\varvec{\varepsilon '}} ,{\varvec{\mu }} } \right) {|_{{\varvec{\mu }}} } = 0,\quad \mathrm{{for}}\quad \sum \limits _{j = 1}^N {{\mu _j}} = 0,\quad \,\bmod \,\;\mathrm{{2}}. \end{aligned}$$