Isotropic exact solutions in $F(R,Y,\phi )$ gravity via Noether symmetries

Abstract

The present article investigates the existence of Noether and Noether gauge symmetries of flat Friedman–Robertson–Walker universe model with perfect fluid matter ingredients in a generalized scalar field formulation namely $f(R,Y,\phi )$ gravity, where R is the Ricci scalar and Y denotes the curvature invariant term defined by $Y=R_{\alpha \beta }R^{\alpha \beta }$, while $\phi$ represents scalar field. For this purpose, we assume different general cases of generic $f(R,Y,\phi )$ function and explore its possible forms along with field potential $V(\phi )$ by taking constant and variable coupling function of scalar field $\omega (\phi )$. In each case, we find non-trivial symmetry generator and its related first integrals of motion (conserved quantities). It is seen that due to complexity of the resulting system of Lagrange dynamical equations, it is difficult to find exact cosmological solutions except for few simple cases. It is found that in each case, the existence of Noether symmetries leads to power law form of scalar field potential and different new types of generic function. For the acquired exact solutions, we discuss the cosmology generated by these solutions graphically and discuss their physical significance which favors the accelerated expanding eras of cosmic evolution.

1 Introduction

On the basis of significant outcomes of several astrophysical experiments, numerous researchers deduced that the current phase of our cosmos is accelerated expanding since last few decades and this phenomenon is termed as cosmic acceleration. The cosmic microwave background radiation (CMBR), Supernova type Ia (SNIa), X-ray brightness from galaxy erect, large scale constructions surveys, weak lensing and the baryon acoustic oscillation surveys etc. are some interesting examples of such astronomical experiments whose observational data sets illustrate this phenomena of cosmic expansion [1,2,3,4,5,6,7]. The possible motive of this phenomena has been considered as a hidden strange nature of energy which is also seen as a dominating component in the cosmos matter structure and is refereed as dark ingredient or dark energy (DE) [8, 9]. In order to figure out the cryptic nature of this dark leading ingredient, different approaches have been adopted in literature which further resulted into a list of possible candidates, for instance, see [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. By classifying this list of candidates into two major categories on the basis of technique adopted, a possible comparison have also been presented in literature and some candidates have been ruled out due to some downsides. It is argued that the extension of Einstein’s gravitational framework for accommodating DE by the inclusion of extra degrees of freedom is more acceptable on cosmological landscape as compared to modified matter proposals where only the energy-momentum source is modified by adding dark ingredients as extra terms. Some well-known examples of the later approach are cosmological constant, scalar field models like k-essence, quintom, canonical kinetic scalar field term, quintessence, and Chaplygin gas EoS and its different versions. The modified gravitational theories involve many interesting and noteworthy examples like $f(\mathrm {R})$ theory, Gauss-Bonnet gravity, scalar-tensor theories especially Brans-Dicke gravity theory, teleparallel theory and its modifications like $f({\mathcal {T}})$, $f({\mathcal {T}},{\mathcal {T}}_{G})$ and $f({\mathcal {T}},B)$ theories, $f(\mathrm {G})$ gravity, f(R, T) gravitational framework (where the symbols ${\mathcal {T}},~B,~ G$ stand for the torsion scalar, boundary term and Gauss-Bonnet term, respectively while T represents the energy-momentum tensor trace), braneworld scenarios, Kalb-Ramond background etc.. It is argued that the modified gravitational theories yield a successful way to explore various cosmic aspects and have passed all the astrophysical and other necessary solar system tests.

In the context of differential equations and their exact solutions, one of the most intriguing and simple techniques considered by the researchers is the use of Noether and Noether gauge symmetries. The existence of these symmetries can minimize the possible complications in a differential equation and hence yields a systematic and easy way of integration to compute its solution. On physical grounds, one of the other beauties of these symmetries is the existence of conserved quantities via well-known Noether’s theorem which can lead to some new and promising solutions. The well-famed Noteher theorem is stated as any differentiable symmetry of the action for a physical system corresponds to some conservation law [27,28,29,30,31]. In the field of cosmology and theoretical physics, existence of Noether symmetries plays a vital rule in computing specific and significant forms of some unknown generic functions present in the Lagrangian densities of GR and modified gravity theories. On these lines, a lot of work has already been done in literature and researches have obtained numerous interesting cosmological solutions using different gravitational frameworks. In this respect, Hussain et al. [32] used the concept of approximate symmetries of geodesic equations and investigated energy re-scaling for Reissner-$\hbox {Nordstr}\ddot{o}\hbox {m}$ spacetime. Sharif and Waheed [33,34,35] calculated the energy contents of some black holes as well as plane colliding gravitational waves using approximate symmetries. In f(R) gravity, several researchers [36,37,38,39,40,41,42,43] have discussed exact FRW solutions by exploring corresponding Noether symmetries as well as conserved quantities. In scalar-tensor theories, Motavali and Golshani [44] used Noether symmetries to compute the form of coupling function and the scalar field potential by taking FRW universe model. In literature [45,46,47], authors investigated the existence of exact solutions using Noether symmetries for Bianchi I, III, Kantowski-Sachs as well as FRW models in scalar field and Palatini f(R) theories. In generalized Saez-Ballester scalar-tensor theory, Jamil et al. [48] explored the existence of Noether gauge symmetries along with the associated conserved quantities for Bianchi I model by taking different field potentials into account. Motavali et al. [49] computed Noether symmetries and conserved quantities for FRW cosmic model in a gravitational framework involving inverse curvature invariant term. Further, Sharif and Waheed [50] extended their work by calculating Noether and Noether gauge symmetries for FRW and Bianchi type I geometries by taking same Lagrangian density into account. They have also explored the existence of scaling or dilatational symmetries in a general scalar-tensor theory and found some cosmological interesting exact Bianchi type I solutions.

Recently, Bajardi et al. [51] have investigated the existence of Noether symmetries in non-local gravity cosmologies, especially the frameworks involving curvature and Gauss-Bonnet scalar invariants. They determined the specific generic functional present in the Lagrangian and found the exact cosmological solutions. In another paper [52], Kucukakca and Akbarieh have explored the Einstein-aether cosmological model based on the interaction of scalar field and the aether field using spatially flat FRW metric along with standard matter. Sharif and Iqra [53] have explored some cosmologically interesting exact solutions using Noether and Noether gauge symmetries in f(R, T) theory along with perfect fluid matter. The same authors [54] studied the existence of traversable wormhole solutions in the presence of dust and non-dust matter distributions using f(R, T) theory and discussed their physical features. In teleparallel theory and its different extensions, numerous researchers have found the exact solutions by utilizing the technique of Noether and Noether gauge symmetries using FRW and anisotropic spacetimes [55,56,57,58,59]. In another study [60], Sadjadi explored the explicit form of the generic function in f(T) framework by utilizing generalized Noether theorem as well as generalized vector fields as variational symmetries where cold dark matter contents have been taken into account. Capozziello et al. [61] explored the functional form of generic function by requiring the existence of Noether symmetries as well as conserved quantities in the gravitational framework of F(R, T) theory (where R is Ricci scalar and T is torsion) and they also found the corresponding exact solutions.

In the context of f(G, T) gravity, where G represents the Gauss-Bonnet term and T is the energy-momentum tensor trace, Shamir and Ahmad [62, 63] have applied Noether symmetries approach to explore some exact cosmologically viable solutions using both isotropic and anisotropic geometries. Bahamonde and Capozziello [64, 65] have adopted the Noether symmetry approach to study the related dynamical systems and to find cosmological solutions using FRW and static spherically symmetric metrics. In another study, Fazlollahi [66] have discussed the behavior of effective EoS parameter for the obtained cosmology by exploring existence of Noether gauge symmetries in f(R) theory. They have also shown significance of the obtained cosmic scale factor by taking observational data into account. In f(R, G) theory, Bahamonde et al. [67] worked for finding Noether symmetries as well as conserved quantities using static spherically symmetric spacetime and they have also found some interesting exact solutions. Likewise, Shamir and Kanwal [68] studied Noether symmetries analysis for Bianchi type I universe in f(R, G) gravity and they also reconstructed some important cosmological solutions. In another paper [69], Sharif et al. investigated the existence of stable static wormhole structures in Gauss-Bonnet theory by taking isotropic matter as well as different models of f(G) (like quadratic and exponential) into account. In the gravitational framework of $f(R,\phi ,\chi )$ theory, Bahamonde et al. [70] and Shamir [71] found a class of new exact spherically symmetric solutions using Noether’s symmetry approach. Capozziello et al. [72] have adopted Noether point symmetries for classification and integration of dynamical systems coming from Horndeski cosmologies and they have also found exact solutions in different subcases of Horndeski theory. This literature motivated us to further explore symmetries as well as exact solutions in a generalized scalar-tensor theory namely $f(R,Y,\phi )$ gravity and discuss their cosmological significance.

In the present article, our primary objective is to investigate the existence of first Noether symmetries and then full set of Noether gauge symmetries for flat FRW universe geometry in $f(R,Y,\phi )$ gravitational framework. The coming sections of the article will appear in this sequence. Next section will provide a detailed introduction to Noether gauge symmetries and its related concepts. In the same section, we shall introduce the principle structure of general scalar-tensor theory and some basic ingredients assumed for this work. The simple Noether symmetries for FRW model will be explored and presented in Sect. 3. Section 4 shall list full set of Noether gauge symmetries along with corresponding conserved quantities. In respective sections, we shall also discuss some exact solutions mathematically and illustrate their significance graphically. The last segment will summarize the whole article.

2 Basic formulation of $f(R,Y,\phi )$ modified gravity and noether symmetry analysis

In this section, we shall present the basic mathematical structure of $f(R,Y,\phi )$ modified gravity and a brief introduction to Noether symmetries analysis. Particularly, we shall discuss this process for flat FRW spacetime in the presence of perfect fluid matter contents.

The action of $f(R,R_{\alpha \beta }R^{\alpha \beta },\phi )$ gravity [73,74,75,76] involving the scalar field coupling function and the scalar field potential is given by the following equation:

$$\begin{aligned} S_{m}&=\int d^{4}x\sqrt{-g}\Bigg [\frac{1}{\kappa ^2}\left( f\left( R,Y,\phi \right) \right. \nonumber \\&\left. \quad +\omega (\phi )\,\phi _{;\alpha }\,\phi ^{;\alpha }+V(\phi )\right) \Bigg ] +{\mathcal {L}}_m, \end{aligned}$$

(1)

where f is a generic function depending on the quantities Ricci scalar R, the curvature invariant $Y\equiv R_{\alpha \beta }R^{\alpha \beta }$ (where $R_{\alpha \beta }$ is the Ricci tensor) and the scalar field $\phi$. Further, the functions ${\mathcal {L}}_m,~V(\phi )$ and $\omega (\phi )$ are referred as the matter Lagrangian density of ordinary matter, scalar field potential and coupling function of scalar field $\phi$, respectively. Also, here the symbol g stands for the determinant of metric tensor $g_{\mu \nu }$ and $\kappa ^2$ is the gravitational coupling constant.

Varying the action (1) with respect to metric, we have the following set of field equations:

$$\begin{aligned}&f_{R}\,R_{\mu \nu }-\frac{1}{2}\left( f+\omega (\phi )\,\phi _{;\alpha } \,\phi ^{;\alpha }\right) \,g_{\mu \nu }-f_{R;\mu \nu }+g_{\mu \nu }\,\Box f_{R}\nonumber \\&\quad +2f_{Y} R_{\mu }^{\alpha }\,R_{\alpha \nu }-2\,[f_{Y}R^{\alpha }_{(\mu }]_{;\nu )\alpha } +\Box [f_{Y}R_{\mu \nu }]\nonumber \\&\quad +[f_{Y}R_{\alpha \beta }]^{;\alpha \beta }g_{\mu \nu }+\omega (\phi )\,\phi _{;\mu }\, \phi _{;\nu }=\kappa ^2\,T_{\mu \nu }\,, \end{aligned}$$

(2)

$$\begin{aligned}&2\,\omega (\phi )\,\Box \phi +\omega _{\phi }(\phi )\,\phi _{;\alpha }\,\phi ^{;\alpha } -f_{\phi }+V_{\phi }(\phi )=0\,, \end{aligned}$$

(3)

where $\Box =g^{\mu \nu }\nabla _{\mu }\nabla _{\nu }$ and $\kappa ^2\equiv 8 \pi G$.

Symmetry is a point transformation (a transformation which maps one point (x, y) into another $(x^*, y^*)$) under which the form of DE remains invariant. These transformations form a group known as point transformation group. Symmetries are interesting and mathematically significant because of their direct connection with the conservation laws through the Noether theorem. A $n^{th}$-order Lagrangian involving one independent variable and m independent variables given by the form $L(t,q_i,{\dot{q}}_i,\ddot{q}_i,\ldots ,q^{(n)}_i);~i=1,2,3,\ldots m$, can admit a Noether gauge symmetry generator [77]

$$\begin{aligned} X=\tau \partial _t+\eta _i\partial _{q_i} \end{aligned}$$

if there exists a function G called gauge function such that

$$\begin{aligned} {\dot{G}}&={\dot{\tau }}L+\tau \partial _t L\nonumber \\&\quad +\sum _{j=0}^{n}\sum _{i=0}^{m}\left( \eta _i^{(j)} -\sum _{k=1}^{j}\left( {\begin{array}{c}j\\ k\end{array}}\right) q_i^{(j+1-k)}\tau ^{(k)}\right) \partial q_i^{(j)}L. \end{aligned}$$

(4)

The first integral of motion, in this case, takes the following form:

$$\begin{aligned} I= & {} G-\left[ \tau L+\sum _{k=1}^{m}\sum _{i=0}^{n-1}\right. \nonumber \\&\quad \left. \times \,\sum _{j=0}^{n-1-i}(-1)^j(\eta _k-{\dot{q}}_k\tau )^{(i)}\frac{d^j}{dt^j} \left( \frac{\partial L}{\partial q^{(i+j+1)}}\right) \right] . \end{aligned}$$

(5)

In the present work, let us consider the flat FRW geometry given by the line element:

$$\begin{aligned} ds^{2}=dt^{2}-a^{2}(t)\left( dx^{2}+dy^{2}+dz^{2}\right) , \end{aligned}$$

(6)

where a(t) represents the cosmological scale factor. For this model, the Ricci scalar and the curvature invariant term will take the form given by

$$\begin{aligned} R=-6\left( \frac{{\dot{a}}^2}{a^2}+\frac{\ddot{a}}{a}\right) ,~~~~ Y=6\left( \frac{{\dot{a}}^4}{a^4}+\frac{2{\dot{a}}^2\ddot{a}}{a^3}+ \frac{3\ddot{a}^2}{a^2}\right) . \end{aligned}$$

(7)

It is worthwhile to mention here that for FRW model, the field equations (2) have already been calculated in literature and are provided in Appendix. Here we consider that ordinary matter part of the Lagrangian density is defined in terms of perfect fluid energy-momentum tensor and is given by

$$\begin{aligned} T_{{\mu }{\nu }}=({\rho }_m+p_m)u_{\mu }u_{\nu }-p_mg_{{\mu }{\nu }}, \end{aligned}$$

where $\rho _m$ and $p_m$ represent the density and pressure of ordinary matter, respectively. For the construction of point-like Lagrangian, we introduce these two scalar curvature quantities as constraints with the corresponding Lagrange multipliers $\lambda _1$ and $\lambda _2$ as follows

$$\begin{aligned} S= & {} \frac{1}{8\pi G}\int a^3\Bigg [f(R,Y,\phi )+\omega (\phi ){\dot{\phi }}^2+V(\phi )\nonumber \\&+\lambda _1\left( R +6\left( \frac{{\dot{a}}^2}{a^2}+\frac{\ddot{a}}{a}\right) \right) \nonumber \\&+\lambda _2\left( Y-6\left( \frac{{\dot{a}}^4}{a^4} +\frac{2{\dot{a}}^2\ddot{a}}{a^3}\right. \right. \left. \left. +\frac{3\ddot{a}^2}{a^2}\right) \right) \Bigg ] d^4x+{\mathcal {L}}_m. \end{aligned}$$

(8)

The possible integration of the double and higher-order derivative terms lead to some boundary and first-order terms. After neglecting the boundary terms, the point-like Lagrangian will take the form:

$$\begin{aligned}&L=\frac{1}{8\pi G}\left[ a^3f(R,Y,\phi )+a^3Rf_{R}+a^3Yf_Y+a^3\omega (\phi ){\dot{\phi }}^2\right. \nonumber \\&\qquad +a^3V(\phi )-12a{\dot{a}}^2f_R \nonumber \\&\quad -6a^2{\dot{a}}{\dot{R}}f_{RR}-6a^2{\dot{a}}{\dot{Y}}f_{RY}-6a^2{\dot{a}}{\dot{\phi }}f_{R\phi }\nonumber \\&\quad +6a{\dot{a}}^2f_{R}-\frac{6{\dot{a}}^4}{a}f_Y+4{\dot{a}}^3{\dot{R}}f_{RY}\nonumber \\&\quad \left. +4{\dot{a}}^3{\dot{Y}}f_{YY} +4{\dot{a}}^3{\dot{\phi }}f_{Y\phi }-18a\ddot{a}^2f_Y\right] \quad +\rho _0\epsilon a^{-3\epsilon }. \end{aligned}$$

(9)

It is worthwhile to mention here that in the above point-like Lagrangian, second-order term cannot be shifted to first-order via partial integration process and hence is remained present in the point-like Lagrangian. In the construction of point-like Lagrangian, we have assumed ${\mathcal {L}}_m=p_m=\rho _0\epsilon a^{-3(1+\epsilon )}$, where $\epsilon$ represents the EoS parameter of ordinary matter and lies within $0<\epsilon \le 1$. Here clearly, the Lagrangian is dependent on the terms $t,a,R,Y,\phi ,{\dot{a}},{\dot{R}},{\dot{\phi }},{\dot{Y}}$ and $\ddot{a}$. For this configuration, we need to use second-order prolongation of the symmetry generator [77] (this is because of the term $\ddot{a}$) which is given by

$$\begin{aligned} X^{[2]}= & {} \tau \frac{\partial }{\partial t}+\alpha \frac{\partial }{\partial a}+\beta \frac{\partial }{\partial R}+ \gamma \frac{\partial }{\partial Y}+\delta \frac{\partial }{\partial \phi }\nonumber \\&+\alpha ^1\frac{\partial }{\partial {\dot{a}}} +\beta ^1\frac{\partial }{\partial {\dot{R}}}+\gamma ^1\frac{\partial }{\partial {\dot{Y}}}+\delta ^1\frac{\partial }{\partial {\dot{\phi }}} +\alpha ^2\frac{\partial }{\partial \ddot{a}}\nonumber \\&+\beta ^2\frac{\partial }{\partial {\ddot{R}}}+ \gamma ^2\frac{\partial }{\partial {\ddot{Y}}}+\delta ^2\frac{\partial }{\partial \ddot{\phi }} \end{aligned}$$

(10)

and the respective condition for Noether gauge symmetry existence takes the form:

$$\begin{aligned} X^{[2]}L+(D_t\tau )L=D_t G. \end{aligned}$$

(11)

In the second prolongation of generator X, the components $\alpha ,~\beta ,~\gamma$ and $\delta$ stand for without derivative terms while the subscripts 1 and 2, respectively, indicate their first and second-order time rates and are given by

$$\begin{aligned} \alpha ^1= & {} D_t\alpha -{\dot{a}}\tau ,\quad \beta ^1=D_t\beta -{\dot{R}}D_t\tau ,\quad \\ \gamma ^1= & {} D_t\gamma -{\dot{Y}}D_t\tau , \quad \delta ^1=D_t\delta -{\dot{\phi }}D_t\tau ,\\ \alpha ^2= & {} D_{tt}\alpha -2\ddot{a}{\dot{\tau }}-{\dot{a}}\ddot{\tau }, \end{aligned}$$

where the total time derivative operator is defined as

$$\begin{aligned} D_t=\partial _t+{\dot{a}}\partial _a+{\dot{R}}\partial _R+{\dot{Y}}\partial _Y+{\dot{\phi }}\partial _\phi . \end{aligned}$$

(12)

Clearly, our constructed Lagrangian is only dependent on $\ddot{a}$ term so the other components of second-order time rates like $\beta ^2,~\gamma ^2$ and $\delta ^2$ in Eq. (10) are ignored for the present discussion. Using the total time rate given by Eq. (12) twice on the function $\alpha$, we can write the value for $\alpha ^2$ as follows

$$\begin{aligned} \alpha ^2= & {} \alpha _{tt}+2{\dot{a}}\alpha _{ta}+2{\dot{R}}\alpha _{tR}+2{\dot{Y}}\alpha _{tY}\nonumber \\&+2{\dot{\phi }}\alpha _{t\phi }+\ddot{a}\alpha _{,a} +{\dot{a}}^2\alpha _{,aa}+2{\dot{a}}{\dot{R}}\alpha _{aR}+2{\dot{a}}{\dot{Y}}\alpha _{aY}\nonumber \\&+2{\dot{a}}{\dot{\phi }}\alpha _{a\phi }+{\ddot{R}}\alpha _R+{\dot{R}}^2\alpha _{RR}+2{\dot{R}}{\dot{\phi }}\alpha _{R\phi }\nonumber \\&+2{\dot{R}}{\dot{Y}}\alpha _{RY}+{\ddot{Y}}\alpha _{Y} +{\dot{Y}}^2\alpha _{YY}+2{\dot{Y}}{\dot{\phi }}\alpha _{Y\phi }\ddot{\phi }\alpha _{,\phi }+{\dot{\phi }}^2\alpha _{\phi \phi }\nonumber \\&-2\ddot{a}(\tau _t+{\dot{a}}\tau _a+{\dot{R}}\tau _R+{\dot{Y}}\tau _Y+{\dot{\phi }}\tau _{\phi }) -{\dot{a}}[\tau _tt+2{\dot{a}}\tau _{ta}\nonumber \\&+2{\dot{R}}\tau _{tR}+2{\dot{Y}}\tau _{tY}+2{\dot{\phi }}\tau _{t\phi }+\ddot{a}\tau _{,a} \nonumber \\&+{\dot{a}}^2\tau _{,aa}+2{\dot{a}}{\dot{R}}\tau _{aR}\nonumber \\&+2{\dot{a}}{\dot{Y}}\tau _{aY}+2{\dot{a}}{\dot{\phi }}\tau _{a\phi }+{\ddot{R}}\tau _R+{\dot{R}}^2\tau _{RR} \nonumber \\&+2{\dot{R}}{\dot{\phi }}\tau _{R\phi }+2{\dot{R}}{\dot{Y}}\tau _{RY}+{\ddot{Y}}\tau _{Y} \nonumber \\&+{\dot{Y}}^2\tau _{YY}+2{\dot{Y}} {\dot{\phi }}\tau _{Y\phi }+\ddot{\phi }\tau _{,\phi }+{\dot{\phi }}^2\tau _{\phi \phi }].\nonumber \\ \end{aligned}$$

(13)

In the present case, the first integrals of motion can be obtained by the equation

$$\begin{aligned} I=G-\left[ \tau L+\sum _{k=1}^{4}\sum _{i=0}^{1}\sum _{j=0}^{1-i}(-1)^j(\eta _k-{\dot{q}}_k\tau )^{(i)}\frac{d^j}{dt^j} \left( \frac{\partial L}{\partial q^{(i+j+1)}}\right) \right] ,\nonumber \\ \end{aligned}$$

(14)

which further leads to

$$\begin{aligned} G= & {} f-\tau L-(\alpha -{\dot{a}}\tau )\frac{\partial L}{\partial {\dot{a}}}-(\delta -{\dot{\phi }}\tau )\frac{\partial L}{\partial {\dot{\phi }}} \nonumber \\&-(\beta -{\dot{R}}\tau )\frac{\partial L}{\partial {\dot{R}}}-(\gamma -{\dot{Y}}\tau )\frac{\partial L}{\partial {\dot{Y}}}- (\alpha -{\dot{a}}\tau )_{,t}\frac{\partial L}{\partial \ddot{a}}\nonumber \\&+(\alpha -{\dot{a}}\tau )\frac{\partial L}{\partial \ddot{a}}. \end{aligned}$$

Usually, the Euler-Lagrange equations are defined for first-order derivative term of generalized coordinates. In general, for a system involving nth-order derivative of generalized coordinates, i.e., $L(t,q,q_k^{(n)}); k=1,2,3\ldots ,m$, the Euler-Lagrange equations can be written as:

$$\begin{aligned} \sum _{j=0}^{n}(-1)^{j}\frac{d^j}{dt^j}\left( \frac{\partial L}{\partial q_k^{(j)}}\right) =0; ~~~~~ k=1,2,...,m. \end{aligned}$$

In our case, it takes the form

$$\begin{aligned} \sum _{j=0}^{2}(-1)^{j}\frac{d^j}{dt^j}\left( \frac{\partial L}{\partial q_k^{(j)}}\right) =0; ~~~~~ k=1,2,3,4, \end{aligned}$$

which can be simplified as follows

$$\begin{aligned} \frac{\partial L}{\partial q_k}-\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q_k}}\right) +\frac{d^2}{dt^2}\left( \frac{\partial L}{\partial \ddot{q_k}}\right) =0. \end{aligned}$$

By using the configuration space $(t,a,R,Y,\phi )$ and the point-like Lagrangian, the set of four Euler-Lagrange equations turn out to be

$$\begin{aligned}&3a^2f+3a^2Rf_R+3a^2Yf_Y+3a^2\omega {\dot{\phi }}^2+3a^2V+6f_R{\dot{a}}^2\nonumber \\&\quad -\frac{18{\dot{a}}^4}{a^2}f_Y-54f_Y\ddot{a}^2-3\epsilon ^2\rho _0a^{-(1+3\epsilon )}\nonumber \\&\quad + 12af_R\ddot{a}+12a{\dot{f}}_R{\dot{a}}\nonumber \\&\quad +6a^2{\dot{f}}_{RR}{\dot{R}}+6a^2f_{RR}{\ddot{R}}+6a^2f_{RY}{\ddot{Y}}\nonumber \\&\quad +6a^2{\dot{f}}_{RY}{\dot{Y}}+6a^2f_{R\phi }\ddot{\phi } +6a^2{\dot{f}}_{R\phi }{\dot{\phi }}+\frac{72}{a}f_Y{\dot{a}}^2\ddot{a}\nonumber \\&\quad +\frac{24}{a}{\dot{f}}_Y{\dot{a}}^3-24f_{RY}{\dot{a}}\ddot{a}{\dot{R}}\nonumber \\&\quad -12f_{RY}{\dot{a}}^2{\ddot{R}} -12{\dot{f}}_{RY}{\dot{a}}^2{\dot{R}}-12f_{YY}{\dot{a}}^2{\ddot{Y}} \nonumber \\&\quad -12{\dot{f}}_{YY}{\dot{a}}^2{\dot{Y}}-24f_{YY}{\dot{a}}{\dot{Y}}\ddot{a}\nonumber \\&\quad -12f_{Y\phi }{\dot{a}}^2\ddot{\phi } -12{\dot{f}}_{Y\phi }{\dot{a}}^2\ddot{\phi }-12{\dot{f}}_{Y\phi }{\dot{a}}^2{\dot{\phi }}\nonumber \\&\quad -24f_{Y\phi }{\dot{a}}\ddot{a}{\dot{\phi }}-72f_Y{\dot{a}}\dddot{a} \nonumber \\&\quad -72{\dot{f}}_Y{\dot{a}}\ddot{a}-36af_Y\ddddot{a}-72{\dot{a}}\ddot{a}{\dot{f}}_Y-36a\ddot{a}\ddot{f}_Y=0, \end{aligned}$$

(15)

$$\begin{aligned}&2a^3f_R+a^3Rf_{RR}+a^3Yf_{YR}+6af_{RR}{\dot{a}}^2-6a^2f_{RRR}{\dot{a}}{\dot{R}}\nonumber \\&\quad -6a^2f_{RRY}{\dot{a}}{\dot{Y}}-6a^2f_{RR\phi }{\dot{a}}{\dot{\phi }} \nonumber \\&\quad -\frac{6}{a}f_{YR}{\dot{a}}^4+4f_{RRY}{\dot{a}}^3{\dot{R}}\nonumber \\&\quad +4f_{YYR}{\dot{a}}^3{\dot{Y}}+4f_{YR\phi }{\dot{a}}^3{\dot{\phi }}-18af_{YR}\ddot{a}^2 \nonumber \\&\quad +6a^2f_{RR}\ddot{a}+6a^2{\dot{f}}_{RR}{\dot{a}}\nonumber \\&\quad -12f_{RY}{\dot{a}}^2\ddot{a}-4{\dot{f}}_{RY}{\dot{a}}^3=0, \end{aligned}$$

(16)

$$\begin{aligned}&2a^3f_Y+a^3Rf_{RY}+a^3Yf_{YY}+6af_{RY}{\dot{a}}^2-6a^2f_{RRY}{\dot{a}}{\dot{R}}\nonumber \\&\quad -6a^2f_{RYY}{\dot{a}}{\dot{Y}}-6a^2f_{R\phi Y}{\dot{a}}{\dot{\phi }}-\frac{6}{a}f_{YY}{\dot{a}}^4+4f_{RYY}{\dot{a}}^3{\dot{R}}\nonumber \\&\quad +4f_{YYY}{\dot{a}}^3{\dot{Y}}+4f_{YY\phi }{\dot{a}}^3{\dot{\phi }}\nonumber \\&\quad -18af_{YY}\ddot{a}^2 +6a^2f_{RY}\ddot{a}+6a^2{\dot{f}}_{RY}{\dot{a}}\nonumber \\&\quad -4{\dot{f}}_{YY}{\dot{a}}^3-12f_{YY}{\dot{a}}^2\ddot{a}=0, \end{aligned}$$

(17)

$$\begin{aligned}&a^3f_{\phi }+a^3Rf_{R\phi }+a^3Yf_{Y\phi }+a^3\omega _{\phi }{\dot{\phi }}^2 \nonumber \\&\quad +a^3V_{\phi }-6a^2f_{RR\phi }{\dot{a}}{\dot{R}}-6a^2f_{RY\phi }{\dot{a}}{\dot{Y}}\nonumber \\&\quad - 6a^2f_{R\phi \phi }{\dot{a}}{\dot{\phi }}-\frac{6}{a}f_{Y\phi }{\dot{a}}^4\nonumber \\&\quad +4f_{RY\phi }{\dot{a}}^3{\dot{R}}+4f_{YY\phi }{\dot{a}}^3{\dot{Y}}+ 4f_{Y\phi \phi }{\dot{a}}^3{\dot{\phi }} \nonumber \\&\quad -18af_{Y\phi }\ddot{a}^2-2a^3{\dot{\omega }}{\dot{\phi }}-2a^3\omega \ddot{\phi } \nonumber \\&\quad -6a^2\omega {\dot{a}}{\dot{\phi }}+12af_{R\phi }{\dot{a}}^2+6a^2f_{R\phi }\ddot{a}\nonumber \\&\quad +6a^2{\dot{f}}_{R\phi }{\dot{a}}-12f_{Y\phi }{\dot{a}}^2\ddot{a}-4{\dot{f}}_{Y\phi }{\dot{a}}^3=0. \end{aligned}$$

(18)

Also, the Hamiltonian, yielding the total energy of the system, for a Lagrangian based on the first-order derivatives of generalized coordinates is defined by the relation $H=\sum _{i=1}^{m}p^i{\dot{q}}_i-L$. For a more general system involving nth-order derivative of generalized coordinates, the conjugate momenta are defined by [78]

$$\begin{aligned} p^1_k= & {} \frac{\partial L}{\partial {\dot{q}}_k}-\frac{d}{dt}\left( \frac{\partial L}{\partial \ddot{q}_k}\right) +\cdots +(-1)^n\frac{t^{n-1}}{dt^{n-1}}\left( \frac{\partial L}{\partial q^{(n)}_k}\right) ,\\ p^2_k= & {} \frac{\partial L}{\partial \ddot{q}_k}+\cdots +(-1)^{n-2}\frac{d^{n-2}}{dt^{n-2}}\left( \frac{\partial L}{\partial q^{(n)}_k}\right) ,\\&\vdots \\ p^n_k= & {} \frac{\partial L}{\partial q^{(n)}_k}. \end{aligned}$$

Consequently, the Hamiltonian takes the form

$$\begin{aligned} H=p^1_1{\dot{q}}_1+p^2_1\ddot{q}_1+p^1_2{\dot{q}}_2+p^1_3{\dot{q}}_3+p^1_4{\dot{q}}_4-L, \end{aligned}$$

and alternatively, in our present configuration space, it can be written as

$$\begin{aligned} H=p^1_a{\dot{a}}+p^2_a\ddot{a}+p^1_R{\dot{R}}+p^1_Y{\dot{Y}}+p^1_{\phi }{\dot{\phi }}-L. \end{aligned}$$

Using this formalism along with the point-like Lagrangian, the Hamiltonian, in the present case, turns out to be

$$\begin{aligned} H= & {} \frac{1}{8\pi G}\left[ -6a^2f_{RR}{\dot{a}}{\dot{R}}-6a^2f_{RY}{\dot{a}}{\dot{Y}}-6a^2f_{R\phi }{\dot{a}}{\dot{\phi }} \right. \\&-\frac{18}{a}f_Y{\dot{a}}^4+12f_{RY}{\dot{a}}^3{\dot{R}}+12f_{YY}{\dot{a}}^3{\dot{Y}}\\&+12f_{Y\phi }{\dot{a}}^3{\dot{\phi }} -6af_R{\dot{a}}^2\\&- 18af_Y\ddot{a}^2+36f_Y{\dot{a}}^2\ddot{a}+36af_Y{\dot{a}}\dddot{a}\\&\left. +36a{\dot{f}}_Y{\dot{a}}\ddot{a} a^3\omega {\dot{\phi }}^2-a^3f-a^3Rf_R-a^3Yf_Y-a^3V\right] \\&-\rho _0\epsilon a^{-3\epsilon }. \end{aligned}$$

We will firstly develop the set of determining equations for simple Noether symmetries case in which time is not directly involved in point-like Lagrangian and hence we take $\tau$ component of the symmetry generator as zero and the gauge term G also disappears. Consequently, the existence condition (11) will take the form $X^{[2]}L=0$. After inserting the values of $X^{[2]}$ and the point-like Lagrangian, we compare the coefficients of different product derivative terms of a,  R,  Y and $\phi$ on both sides of condition and consequently, we obtain the following system of differential equations:

$$\begin{aligned}&\left( 3a^2f+3a^2Rf_R+3a^2f_{Y}Y+3a^2V-3\epsilon ^2\rho _0a^{-(3\epsilon +1)}\right) \alpha \nonumber \\&\quad +\left( 2a^3f_R+a^3Rf_RR-12af_{RR}+a^3Yf_{YR}\right) \beta \nonumber \\&\quad +(a^3f_Y+a^3Rf_{RY}+a^3Yf_{YY})\gamma \nonumber \\&\quad +(a^3f_{\phi }+a^3Rf_{R\phi }+a^3Yf_{Y\phi }+a^3V_{\phi })\delta =0, \end{aligned}$$

(19)

$$\begin{aligned}&\quad -6f_R\alpha +6af_{RR}\beta -6af_{RY}\gamma -6af_{R\phi }\delta \nonumber \\&\quad -12af_R\alpha _a-6a^2f_{RR}\beta _a-6a^2f_{RY}\gamma _a-6a^2f_{R\phi }\delta _a=0,\nonumber \\&-12a\alpha f_{RR}-6a^2f_{RRR}\beta -6a^2f_{RRY}\gamma -6a^2f_{RR\phi }\delta \nonumber \\&\quad -12af_R\alpha _R-6a^2f_{RR}\alpha _a-6a^2f_{RR}\beta _{R} \end{aligned}$$

(20)

$$\begin{aligned}&\quad -6a^2f_{RY}\gamma _R-6a^2f_{R\phi }\delta _R=0,\nonumber \\&\quad -12af_{RY}\alpha -6a^2\beta f_{RRY}-6a^2f_{RYY}\gamma -6a^2f_{RY\phi }\delta \nonumber \\&\quad -12af_R\alpha _Y-6a^2\alpha _af_{RY}-6a^2f_{RR}\beta _Y \end{aligned}$$

(21)

$$\begin{aligned}&\quad -6a^2\gamma _Yf_{RY}-6a^2f_{R\phi }\delta _Y=0,\nonumber \\&\quad -12af_{R\phi }\alpha -6a^2f_{RR\phi }\beta -6a^2\gamma f_{R\phi Y}\nonumber \\&\quad -6a^2f_{R\phi \phi }\delta -12af_R\alpha _{\phi }-6a^2f_{R\phi }\alpha _a \nonumber \\&\quad -6a^2\beta _{\phi }f_{RR}-6a^2f_{RY}\gamma _{\phi } \end{aligned}$$

(22)

$$\begin{aligned}&\quad -6a^2f_{R\phi }\delta _{\phi }+2a^3\omega \delta _a=0, \end{aligned}$$

(23)

$$\begin{aligned}&\frac{6}{a^2}f_Y\alpha -\frac{6}{a}f_{YR}\beta -\frac{6}{a}f_{YY}\gamma -\frac{6}{a}f_{Y\phi }\delta -\frac{24}{a}f_Y\alpha _a \nonumber \\&\quad +4\beta _af_{RY}+4f_{YY}\gamma _a+4f_{Y\phi }\delta _a=0, \end{aligned}$$

(24)

$$\begin{aligned}&\quad -18f_Y\alpha -18af_{YR}\beta -18a\gamma f_{YY}-18af_{Y\phi }\delta =0, \end{aligned}$$

(25)

$$\begin{aligned}&4f_{RRY}\beta +4\gamma f_{RYY}+4f_{RY\phi }\delta -\frac{24}{a}f_Y\alpha _R \nonumber \\&\quad +12f_{RY}\alpha _a+4\beta _R f_{RY}+4f_{YY}\gamma _R+4f_{Y\phi }\delta _R=0, \end{aligned}$$

(26)

$$\begin{aligned}&4f_{RYY}\beta +4\gamma f_{YYY}+4f_{YY\phi }\delta -\frac{24}{a}f_Y\alpha _Y \nonumber \\&\quad +12f_{YY}\alpha _a+4\beta _Y f_{RY}+4f_{YY}\gamma _Y+4f_{Y\phi }\delta _Y=0, \end{aligned}$$

(27)

$$\begin{aligned}&4f_{RY\phi }\beta +4\gamma f_{YY\phi }+4f_{Y\phi \phi }\delta \nonumber \\&\quad -\frac{24}{a}f_Y\alpha _{\phi } +12f_{Y\phi }\alpha _a+4\beta _{\phi } f_{RY}\nonumber \\&\quad +4f_{YY}\gamma _{\phi }+4f_{Y\phi }\delta _{\phi }=0, \end{aligned}$$

(28)

$$\begin{aligned}&a^3\omega _{\phi }\delta -6a^2\alpha _{\phi }f_{R\phi }+2a^3\omega \delta _{\phi }+3a^2\omega \alpha =0, \end{aligned}$$

(29)

$$\begin{aligned}&\quad -6a^2f_{RR}\alpha _R=0, \quad -6a^2f_{RR}\alpha _{\phi }\nonumber \\&\quad -6a^2f_{R\phi }\alpha _R+2a^3\omega \delta _R=0, \quad -6a^2f_{RY}\alpha _Y=0, \end{aligned}$$

(30)

$$\begin{aligned}&\quad -6a^2f_{RR}\alpha _Y-6a^2f_{RY}\alpha _Ra=0, \quad -6a^2f_{RY}\alpha _{\phi }\nonumber \\&\quad -6a^2f_{R\phi }\alpha _Y+2a^3\omega \delta _Y=0, \quad 12\alpha _Rf_{RY}=0, \end{aligned}$$

(31)

$$\begin{aligned}&12\alpha _{\phi }f_{RY}+12\alpha _Rf_{Y\phi }=0, \quad 12\alpha _{Y}f_{RY}\nonumber \\&\quad +12\alpha _Rf_{YY}=0, \quad -72af_Y\alpha _{Y\phi }=0, \end{aligned}$$

(32)

$$\begin{aligned}&\quad -72af_Y\alpha _Y\alpha _{R\phi }=0, \quad \nonumber \\&\quad -36af_Y\alpha _{YY}=0, \quad 12\alpha _{\phi }f_{YY}+12\alpha _Yf_{Y\phi }=0, \end{aligned}$$

(33)

$$\begin{aligned}&12\alpha _Yf_{YY}=0, \quad 12\alpha _{\phi }f_{Y\phi }=0, \quad \nonumber \\&\quad -36af_Y\alpha _{\phi \phi }=0, \quad -36af_Y\alpha _{aa}=0, \end{aligned}$$

(34)

$$\begin{aligned}&-72af_Y\alpha {aR}=0, \quad -72af_Y\alpha _{aY}=0 \nonumber \\&\quad -72af_Y\alpha _{aR} =0, \quad -36af_Y\alpha _{RR}=0, \quad -72af_Y\alpha _{RY}=0.\nonumber \\ \end{aligned}$$

(35)

In the forth coming subsections, we shall find the solution of this system of determining equations by taking different cases of generic function along with the constant and power law form of $\omega (\phi )$ into account.

2.1 Model independent of Y: $f(R,\phi )$ Model

Here we shall investigate the existence of Noether symmetries when the generic function is independent of curvature invariant Y. The system of determining equations allows one to pick some form of coupling parameter. We shall explore the solutions by assuming two cases of scalar field coupling function $\omega (\phi )$. Firstly, let us consider the case when the coupling function is a constant, i.e., $\omega (\phi )=m$, then the set of determining equations (19)–(35) yield the following solutions

$$\begin{aligned}&\alpha =-\frac{2}{3}aC_3C_1, \quad \delta =C_3(C_1\phi +C_2), \quad \gamma =0, \quad \beta \nonumber \\&\quad =-\frac{C_3C_1\epsilon ^2\rho _0(C_7+C_8a^{-3(1+\epsilon )})}{C_8C_4C_6(C_1\phi +C_2)^2}. \end{aligned}$$

(36)

Also, the function $f(R,\phi )$ and the potential $V(\phi )$ take the form:

$$\begin{aligned} f(R,\phi )= & {} (C_4R+C_5)(C_1\phi +C_2)^2C_6, \quad \nonumber \\ V(\phi )= & {} -\frac{C_7}{C_8}\epsilon ^2\rho _0+(C_1\phi +C_2)^2. \end{aligned}$$

(37)

Consequently, the corresponding set of symmetries can be written as

$$\begin{aligned}&X_1=-\frac{2}{3}a \frac{\partial }{\partial a}+\phi \frac{\partial }{\partial \phi }, \quad \\&X_2=-\epsilon ^2\rho _0\phi ^{-2}\frac{\partial }{\partial R}, \quad \\&X_3=-\epsilon ^2\rho _0\phi ^{-2}a^{-3(1+\epsilon )}\frac{\partial }{\partial R}, \end{aligned}$$

and the first integrals of motion are

$$\begin{aligned}&I_1=-\frac{2}{3}\left( -24a{\dot{a}}f_{,R}-6a^2{\dot{R}}f_{RR}-6a^2{\dot{\phi }}f_{R\phi } \right. \\&\quad \quad \left. +12a{\dot{a}}f_{,R}\right) -(2a^3m{\dot{\phi }}-6a^2{\dot{a}}f_{R\phi })\phi ,\\&I_2=\epsilon ^2\rho _0\phi ^{-2}(-6a^2{\dot{a}}f_{RR}), \\&\quad \quad I_3 = \epsilon ^2\rho _0a^{-3(1+\epsilon )}\phi ^{-2}(-6a^2{\dot{a}}f_{RR}). \end{aligned}$$

Here we have assumed $C_2=0$ and re-labeled other arbitrary constants for simplicity purposes. It can be easily checked that in case of vacuum ($\rho _0=0$) or dust $\epsilon =0$, the symmetry generators $X_2$ and $X_3$ vanish and hence only $X_1$ is left which is a scaling symmetry. Also, quadratic scalar field potential is obtained. On substitution of derivatives of $f(R,\phi )$, these integrals can be simplified as

$$\begin{aligned} I_1= & {} 8aC_1^*\phi ^2{\dot{a}}+8a^2C_1^*{\dot{\phi }}\phi \\&-2a^3m{\dot{\phi }}\phi +12a^2{\dot{a}}C_1^*\phi ^2,\\&\quad I_2=I_2=0; \quad C_1^*=C_4C_1^2C_6 \end{aligned}$$

For finding the values of scale factor and scalar field which are the only unknown quantities left, we can use either the Euler-Lagrange equations or the above defined integrals of motion. In the first case, the solution using Lagrange equations can be written as

$$\begin{aligned} a(t)=c_{10}e^{\frac{\sqrt{1+c_5}t}{\sqrt{6c_4}}}+c_{11}e^{\frac{-\sqrt{1+c_5}t}{\sqrt{6c_4}}}, \end{aligned}$$

(38)

and

$$\begin{aligned} \phi (t)= & {} \frac{-\rho _0\epsilon }{\sqrt{6}c_1}\left[ c_8\int e^{\frac{-1}{6c_4} \int \frac{18c_4{\dot{a}}^2(1+\epsilon )+a^2(1+c_5)+6c_4a\ddot{a}}{a{\dot{a}}}dt}dt\right. \\&\left. -c_7\epsilon \int e^{\frac{-1}{6c_4} \int \frac{18c_4{\dot{a}}^2(1+\epsilon ) +a^2(1+c_5)+6c_4a\ddot{a}}{a{\dot{a}}}dt}dt+c_9\right] \end{aligned}$$

along with $m=c_2=0$. The integration of exponential power is computed as:

$$\begin{aligned}&-\sqrt{6}\sqrt{c_4}\sqrt{1+c_5}\left[ t(5+3\epsilon )-\frac{\sqrt{6}\sqrt{c_4}(1+3\epsilon ) \tanh ^{-1} \left( \frac{c_{10}e^{\frac{\sqrt{2/3(1+c_5)}}{\sqrt{c_4}}}}{c_{11}}\right) }{\sqrt{1+c_5}} \right. \\&\quad \left. -\frac{\sqrt{3/2}\sqrt{c_4}(5+3\epsilon ) \log [c_{11}^2-c_{10}^2e^{\frac{2\sqrt{2/3(1+c_5)}}{\sqrt{c_4}}}]}{\sqrt{1+c_5}}\right] . \end{aligned}$$

By taking some simple values of arbitrary constants $C_i's$ and $\rho _0=1$, the scalar field can be computed as

$$\begin{aligned} \phi (t)= & {} \frac{1}{\sqrt{6}}\left[ 2-\left( \sqrt{3}\left( \sqrt{2}e^{\frac{t}{\sqrt{6}}} \left( 315+4200e^{\sqrt{\frac{2}{3}}t}+22512e^{2\sqrt{\frac{2}{3}}t} \right. \right. \right. \right. \nonumber \\&+39200e^{4\sqrt{\frac{2}{3}}t}+227712e^{5\sqrt{\frac{2}{3}}t}+268800e^{7\sqrt{\frac{2}{3}}t}\nonumber \\&+\left. 80640e^{8\sqrt{\frac{2}{3}}t}+56928e^{\sqrt{6}t}+360192e^{2\sqrt{6}t}\right) \nonumber \\&\left. \left. +315\left( -1+2e^{\sqrt{\frac{2}{3}}t}\right) \left( 1+2e^{\sqrt{\frac{2}{3}}t}\right) ^8 ArcTan\left[ \sqrt{2}e^{\frac{t}{\sqrt{6}}}\right] \right) \right) \nonumber \\&\left. \div \left( 315\left( -1+2e^{\sqrt{\frac{2}{3}}t}\right) \left( 1+2e^{\sqrt{\frac{2}{3}}t}\right) ^8\right) \right] . \end{aligned}$$

(39)

Fig. 1

The left and right graphs indicate the behavior of $f(R,\phi )$ function and scalar field potential for $\omega (\phi )=m$

Fig. 2

The left and right graphs indicate the behavior of expansion factor and scalar field versus time for Noether symmetry case (where $\omega (\phi )=m$)

Fig. 3

The graphs indicate the behavior of ordinary matter density and cosmic volume for Noether symmetry case with $\omega (\phi )=m$

Fig. 4

The left and right graphs indicate the behavior of deceleration parameter and effective EoS parameter, respectively, versus time for Noether symmetry case for $\omega (\phi )=m$

The deceleration parameter, effective EoS parameter, jerk and snap parameters are also defined in Appendix. In this case, the deceleration parameter becomes

$$\begin{aligned} q=-\frac{\left( C_{11}+C_{10}e^{\frac{\sqrt{2/3}\sqrt{1+C_5}t}{\sqrt{C_4}}}\right) ^2}{\left( C_{11}-C_{10}e^{\frac{\sqrt{2/3}\sqrt{1+C_5}t}{\sqrt{C_4}}}\right) ^2} \end{aligned}$$

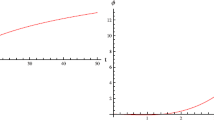
which, clearly, is a negative quantity for any arbitrary choice of free constants. The graphical behavior of evaluated $f(R,\phi )$, $V(\phi )$, scale factor and scalar field is provided in Figs. 1 and 2. It is seen that these functions show positive and increasing behavior versus cosmic time. Further, different cosmic measures like ordinary matter density, cosmic volume, deceleration parameter, effective EoS parameter, and snap as well as jerk parameters are illustrated graphically in Figs. 3, 4 and 5. It is easy to check that all these cosmic measures favor the accelerated expanding nature of cosmos.

Since $I_1$ is the only non-zero first integral of motion which involves both a(t) and $\phi (t)$, therefore in order to find exact solutions, one need to assume some power law ansatz for either scale factor or scalar field and find the other quantity. Here we consider the power law form of $\phi =\phi _0a^{\alpha }$, where $\alpha \ne 0;~~\alpha \in {\mathbb {R}}$. The resulting form of first integral can be written as

$$\begin{aligned} 2C_1^*a^{2\alpha +1}\phi _0^2\left( 4(1+\alpha )-a(6-m\alpha )\right) {\dot{a}}=I_1 \end{aligned}$$

whose solution can be written as

$$\begin{aligned} a(t)=\left( \frac{I_1(t+C_1)}{4C_1^*\phi _0^2}\right) ^{\frac{1}{2(\alpha +1)}} \end{aligned}$$

(40)

and hence the scalar field is given by

$$\begin{aligned} \phi =\phi _0\left( \frac{I_1(t+C_1)}{4C_1^*\phi _0^2}\right) ^{\frac{\alpha }{2(\alpha +1)}}. \end{aligned}$$

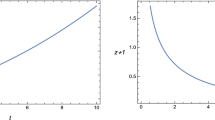
For these solutions, we have imposed some constraints like $\alpha \ne -\frac{3}{2}$ and $\alpha =\frac{6}{m}$. Clearly, the obtained scale factor is in power law form. In this case, the deceleration parameter turns out to be $q=1+2\alpha$ which, consequently, imposes the constraint $\alpha <-\frac{1}{2}$, for having accelerated expanding nature of cosmos. It is interesting to mention here that early matter and radiation dominated epochs can be discussed by fixing $\alpha =-\frac{1}{4}$ and $\alpha =0$, respectively. The graphical behavior of obtained scale factor and effective Eos parameter is provided in Fig. 6. From their graphical illustration, it can be easily checked that these cosmic quantities also refer to accelerated cosmic expansion. Furthermore, the jerk and snap parameters also turn out to be constants given by $r=(1+2\alpha )(3+4\alpha )$ and $s=\frac{0.3333+1.6667\alpha +1.3333\alpha ^2}{1/4+\alpha }$. It can be easily checked that for $\alpha =-1$, the point $(r,s)=(1,0)$ can be recovered and hence the constructed model has a correspondence to $\Lambda \hbox {CDM}$ model ($q=-1$) for this specific value of $\alpha$.

Fig. 5

The graph indicates the behavior of jerk and snap parameters for $\omega (\phi )=m$

Fig. 6

The left and right graphs provide the behavior of scale factor and effective EoS parameter for $\omega (\phi )=m$, respectively

Fig. 7

The left graph provides the behavior $f(R,\phi )$, the right plot shows the behavior of scalar field potential while the down curve corresponds to the behavior of scale factor where $\omega (\phi )=m\phi ^s$

In the second case, when the coupling function is defined in terms of power law form, i.e., $\omega (\phi )=m\phi ^s$, where s and m are any real constants. The resulting solutions are given by

$$\begin{aligned}&\alpha =C_1a, \quad \gamma =0, \quad \beta =\frac{(C_4+C_5a^{-3(1+\epsilon )})d_2\phi ^{-s}}{(-3C_1\phi +C_2C_3(s+2)\phi ^{-\frac{s}{2}})^2}, \nonumber \\&\quad \quad \delta = C_2\left( -\frac{3\phi }{C_2(s+2)}+C_3\phi ^{-\frac{s}{2}}\right) . \end{aligned}$$

(41)

Further, the functions $f(R,\phi )$ and $V(\phi )$ take the form

$$\begin{aligned} f(R,\phi )= & {} \frac{3C_9C_1\epsilon ^2\rho _0}{2d_1}\phi ^s R\left( C_3C_2(s+2)^2\phi ^{-\frac{s}{2}}-3C_1\phi \right) , \nonumber \\ V(\phi )= & {} \frac{-3\epsilon ^2\rho _0C_1C_4\phi \left( C_2^2C_3^2(4+4s+s^2) -18C_1C_2C_3\phi ^{\frac{s}{2}+1}+9C_1^2\phi ^{s+2}\right) }{C_5C_3^2C_2^2 (s+2)^2\left( C_3C_2(s+2)\phi ^{-\frac{s}{2}}-3C_1\phi \right) }.\nonumber \\ \end{aligned}$$

(42)

Here all $C_i 's$ are constants of integration. Here the solution is valid only if one picks $m=s$. For defining the corresponding set of symmetries along with first integrals of motion, let us assume that $d_2=0$ which further leads to $\beta =0$. Consequently, we get

$$\begin{aligned} X_1= & {} a\frac{\partial }{\partial a}-\frac{3\phi }{2(s+2)}\frac{\partial }{\partial \phi }, \quad X_2=-\frac{3\phi }{2(s+2)}\frac{\partial }{\partial \phi }\\&+\phi ^{-s/2}\frac{\partial }{\partial \phi },\\ I_1= & {} 12a^2{\dot{a}}f_{R}+6a^3{\dot{R}}f_{RR}+6a^3{\dot{\phi }}f_{R\phi }\\&+\frac{3\phi }{2(s+2)}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }), \\ I_2= & {} \phi ^{-s/2}(6a^2{\dot{a}}f_{R\phi }-2a^3\omega {\dot{\phi }})\\&+\frac{3\phi }{2(s+2)}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }). \end{aligned}$$

Here both symmetry generators $X_1$ and $X_2$ represent scaling symmetries. Clearly, on substituting the derivatives of $f(R,\phi )$ in the above defined conserved quantities, it can be written as

$$\begin{aligned} I_1-I_2= & {} 12a^2{\dot{a}}\left( C^*C_3C_2(s+2)^2\phi ^{s/2}-3C_1C^*\phi ^{s+1}\right) \\&+6a^3{\dot{\phi }}\left( C^*C_3C_2(s+2)^2\frac{s}{2}\phi ^{s/2-1}-3C_1C^* (s+1)\phi ^s\right) \\&-6a^2{\dot{a}}\phi ^{s/2}\left( C^*C_3C_2(s+2)^2\frac{s}{2}\phi ^{s/2-1}-3C^*C_1(s+1)\phi ^s\right) \\&-2a^3s\phi ^s{\dot{\phi }}; \quad C^*=\frac{3C_9C_1\epsilon ^2\rho _0}{2d_1}. \end{aligned}$$

By picking the same power law choice of scalar field, this equation can be shifted to a differential equation for scale factor and is given by

$$\begin{aligned}&-2a^{2-\alpha }\left( 48-3(41+16\alpha )a^{2\alpha }+(18+29\alpha )a^{4\alpha }\right) \\&\qquad {\dot{a}}=I_1-I_2 \end{aligned}$$

whose solution can be found as

$$ \begin{aligned} a(t)= & {} InverseFunction\left[ \frac{48\#1^{3-\alpha }}{3-\alpha }\right. \\&\quad +\frac{(18+29\alpha )\#1^{3(1+\alpha )}}{3(1+\alpha )}\\&\quad \left. -\frac{3(41+16\alpha )\#1^{3+\alpha }}{3+\alpha } \& \right] \left[ -\frac{t}{2}+C^{'}\right] ; \end{aligned}$$

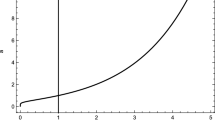
where $C^{'}$ indicates the integration constant. The graphical behavior of generic function, scalar field potential and the evaluated scale factor is provided in Fig. 7. It is easy to check that the scale factor indicates positive as well as increasing behavior versus time and hence corresponds to accelerated expanding cosmos.

2.2 Model independent of $\phi$: f(R, Y) model

In this section, we shall explore the components of generator and the unknown functions by taking the assumption that the generic function is independent of scalar field, i.e., f(R, Y) along with non-zero scalar field potential and coupling function. Here we again consider two cases for coupling function as taken in the last section. For constant coupling function, the solutions to the system of determining equations (19)–(35) are

$$\begin{aligned}&\alpha =0, \quad \delta =\frac{C_1C_2}{a}, \beta =\frac{C_3C_4C_5}{9aC_{10}}\\&\qquad \times \left( (C_{10}R+C_{11})(C_5Y+C_6)^2(C_7\phi +C_8)\right) ,\\&\gamma =\frac{C_3C_4}{9a}(C_7\phi +C_8)\\&\qquad \times \left( C_5Y\left\{ \frac{C_5^2Y^2}{3}+C_5C_6Y+C_6^2\right\} +\frac{C_6^2}{3}\right) . \end{aligned}$$

Also, the scalar field potential and generic function turn out to be as

$$\begin{aligned} V(\phi )= & {} -\frac{1}{3}\frac{mC_{11}}{C_7C_{10}}\left( \frac{C_7\phi ^2}{2}+C_8\phi \right) +C_{14},\quad \\ f(R,Y)= & {} \frac{9}{2}\frac{mC_1C_2(C_{10}R+C_{11})}{(C_5Y+C_6)^2C_3C_4C_5C_7C_{10}}. \end{aligned}$$

In this case, the set of symmetries can be written as

$$\begin{aligned} X_1= & {} \frac{1}{a}\frac{\partial }{\partial \phi }, \quad X_2=\frac{RY^2\phi }{a}\frac{\partial }{\partial R}+\frac{\phi Y^3}{3a}\frac{\partial }{\partial Y}, \quad \\ X_3= & {} \frac{RY^2}{a}\frac{\partial }{\partial R} +\frac{Y^3}{3a}\frac{\partial }{\partial Y}, \quad \\ X_4= & {} \frac{R\phi }{a}\frac{\partial }{\partial R}+\frac{\phi Y}{a}\frac{\partial }{\partial Y}, \quad X_5 = \frac{R}{a}\frac{\partial }{\partial R} +\frac{Y}{a}\frac{\partial }{\partial Y}, \quad \\ X_6= & {} \frac{RY\phi }{a}\frac{\partial }{\partial R}+\frac{\phi Y^2}{2a}\frac{\partial }{\partial Y}, \quad \\ X_7= & {} \frac{RY}{a}\frac{\partial }{\partial R} +\frac{Y^2}{2a}\frac{\partial }{\partial Y}, \quad X_8= \frac{Y^2\phi }{a}\frac{\partial }{\partial R}, \\ X_9= & {} \frac{1}{a}\frac{\partial }{\partial R}, \quad X_{10}=\frac{\phi }{a}\frac{\partial }{\partial R}, \quad \\ X_{11}= & {} \frac{\phi Y}{a}\frac{\partial }{\partial R}, \quad X_{12}=\frac{Y}{a}\frac{\partial }{\partial R}, \quad \\ X_{13}= & {} \frac{\phi }{a}\frac{\partial }{\partial Y}, \quad X_{14}=\frac{1}{a}\frac{\partial }{\partial Y}. \end{aligned}$$

The corresponding set of first integrals of motion can be written as

$$\begin{aligned} I_1= & {} -2a^2\omega (\phi ){\dot{\phi }}, \quad I_2=-\frac{RY^2\phi }{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{\phi Y^3}{3a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_3= & {} -\frac{RY^2}{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{Y^3}{3a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_4= & {} -\frac{R\phi }{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{\phi Y}{a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_5= & {} -\frac{R}{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{Y}{a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_6= & {} -\frac{RY\phi }{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{\phi Y^2}{2a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) ,\\ I_7= & {} -\frac{RY}{a}\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&+\frac{Y^2}{2a}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_8= & {} -\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \frac{Y^2\phi }{a}, \quad \\ I_9= & {} -\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \frac{1}{a}, \\ I_{10}= & {} -\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \frac{\phi }{a}, \quad \\ I_{11}= & {} -\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \frac{Y\phi }{a}, \\ I_{12}= & {} -\left( 6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \frac{Y}{a}, \quad \\ I_{13}= & {} -\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) \frac{\phi }{a}, \quad \\ I_{14}= & {} -\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) \frac{1}{a}. \end{aligned}$$

It can be seen that on substitution of different derivatives of generic function, these integrals can be written as

$$\begin{aligned}&I_1=-2a^2m{\dot{\phi }}, \quad I_2=-\frac{RY^2\phi }{a}\left( 4{\dot{a}}^3(\frac{-2C_{10}C^*C_5}{(C_5Y+C_6)^3})\right) \\&\quad +\frac{\phi Y^3}{3a}\left( 6a^2{\dot{a}}(\frac{-2C_{10}C^*C_5}{(C_5Y+C_6)^3})-4{\dot{a}}^3 \frac{6C_{10}C^*{C_5}^2}{(C_5Y+C_6)^4}\right) , \\&I_7=\frac{I_6I_2}{I_3}, \quad I_4=\frac{I_5I_3}{I_2}, \quad \\&I_9=-\frac{4{\dot{a}}^3}{a}(\frac{-2C_{10}C^*C_5}{(C_5Y+C_6)^3}), \quad I_8=\frac{I_{11}I_{12}}{I_9}, \quad \\&I_{10}=\frac{I_{11}I_9}{I_{12}}; \quad \\&C^*=\frac{9}{2}\frac{mC_1C_2}{C_3C_4C_5C_7C_{10}}. \end{aligned}$$

Clearly, $I_9$ and $I_{13}$ integrals are purely in terms of scale factor and its derivatives (curvature invariant Y) and hence giving rise to a non-linear differential equation which can be solved numerically. This equation is given by

$$\begin{aligned} I_8=\frac{8{\dot{a}}^3}{a}\frac{C^*C_{10}C_5}{(C_5Y+C_6)^3}. \end{aligned}$$

Then, from $I_1$, one can compute the behavior of scalar field numerically by the relation ${\dot{\phi }}=\frac{I_1}{-2a^2m}$. We have solved this relation for scale factor numerically and its behavior is provided in Fig. 8. It is seen that it indicates positive and increasing behavior and hence corresponds to an expanding universe model. As the scalar field evolves inversely to scale factor, thus it can be concluded that the corresponding scalar field will exhibit decreasing behavior versus time. The graphical behavior of generic function and scalar field potential is also provided in Fig. 9.

Fig. 8

The left graph indicates the behavior of f(R, Y) function, the right plot corresponds to scalar field potential behavior while the down curve provides the behavior of scale factor versus time (numerical solution), where $\omega (\phi )=m$

Fig. 9

The left plot provides the graph of f(R, Y) function while right curve refers to scalar field potential graph for $\omega (\phi )=m\phi ^s$

For the power law form of coupling function, the solutions take the form

$$\begin{aligned}&\alpha (a)=0, \quad \delta (a,\phi )=\frac{C_1C_2\phi ^{-\frac{s}{2}}}{a}, \quad \beta (a,R,Y,\phi )\\&\quad =\frac{(C_3R+C_4)(C_5Y+C_6)^2}{aC_3^2(s+2)}\\&\quad \left( C_1C_2m\phi ^{\frac{s}{2}+1}+12d_1(s+2)\right) ,\\&\gamma (a,Y,\phi )=\frac{C_7C_8C_9}{a}(C_5Y+C_6)^2\\&\quad \left( \frac{\phi ^{\frac{s}{2}+1}C_1C_2m}{12d_2(s+2)}+C_{10}\right) . \end{aligned}$$

The scalar field potential and the function f(R, Y) are given by

$$\begin{aligned}&V(\phi )=\frac{-2C_4}{3(s+2)^2C_1C_3C_2}\\&\quad \left( mC_1C_2\phi ^{s+2}+24C_3C_5C_7C_8C_9C_{10} \phi ^{\frac{s}{2}+1}(s+2)\right) \\&\quad +C_{14}, \\&f(R,Y)=\frac{4(C_3R+C_4)}{(C_5Y+C_6)^2}. \end{aligned}$$

The corresponding set of symmetries is given by

$$\begin{aligned} X_1= & {} \frac{\phi ^{-s/2}}{a}\frac{\partial }{\partial \phi }, \quad X_2 = m\phi ^{s/2+1}RY^2\frac{\partial }{\partial R}, \quad \\ X_3= & {} (s+2)RY^2\frac{\partial }{\partial R}, \quad X_4 = m\phi ^{s/2+1}R\frac{\partial }{\partial R}, \quad \\ X_5= & {} (s+2)R\frac{\partial }{\partial R}, X_6 = m\phi ^{s/2+1}RY\frac{\partial }{\partial R}, \quad \\ X_7= & {} (s+2)RY\frac{\partial }{\partial R}, \quad X_8 = Y^2m\phi ^{s/2+1}\frac{\partial }{\partial R}, \quad \\ X_9= & {} (s+2)Y^2\frac{\partial }{\partial R}, \quad X_{10}= m\phi ^{s/2+1}\frac{\partial }{\partial R}, \\ X_{11}= & {} (s+2)\frac{\partial }{\partial R}, \quad X_{12} = m\phi ^{s/2+1}Y\frac{\partial }{\partial R}, \quad \\ X_{13}= & {} (s+2)Y\frac{\partial }{\partial R}, \quad X_{14} = \phi ^{s/2+1}Y^2\frac{\partial }{\partial Y}, \quad \\ X_{15}= & {} \phi ^{s/2+1}\frac{\partial }{\partial Y}, \quad X_{16}= \phi ^{s/2+1}Y \frac{\partial }{\partial Y}, \\ X_{17}= & {} Y^2\frac{\partial }{\partial Y}, \quad X_{18} = \frac{\partial }{\partial Y}, \quad X_{19}= Y\frac{\partial }{\partial Y}. \end{aligned}$$

The corresponding first integrals are:

$$\begin{aligned} I_1= & {} -2a^2\omega (\phi )\phi ^{-s/2}{\dot{\phi }}, \quad \\ I_2= & {} m\phi ^{s/2+1}RY^2\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_3= & {} (s+2)RY^2\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \\ I_4= & {} m\phi ^{s/2+1}R\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_5= & {} (s+2)R\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_6= & {} m\phi ^{s/2+1}RY\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) ,\\ I_7= & {} (s+2)RY\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) \quad \\ I_8= & {} mY^2\phi ^{s/2+1}\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_9= & {} (s+2)Y^2\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \\ I_{10}= & {} m\phi ^{s/2+1}\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_{11}= & {} (s+2)\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) ,\quad \\ I_{12}= & {} m\phi ^{s/2+1}Y\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \\ I_{13}= & {} (s+2)Y\left( 6a^2{\dot{a}}f_{RR}-4{\dot{a}}^3f_{RY}\right) , \quad \\ I_{14}= & {} \phi ^{s/2+1}Y^2\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) ,\quad \\ I_{15}= & {} \phi ^{s/2+1}\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_{16}= & {} \phi ^{s/2+1}Y\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \quad \\ I_{17}= & {} Y^2\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \quad \\ I_{18}= & {} \left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) , \\ I_{19}= & {} Y\left( 6a^2{\dot{a}}f_{RY}-4{\dot{a}}^3f_{YY}\right) . \end{aligned}$$

Here, on substitution of generic function’s derivatives, these integrals can be simplified. But similar to the previous case of constant coupling function, the analytical solution is not possible, only numerical solution can be obtained. The plots of Fig. 9 indicate the behavior of computed generic function and scalar field potential which provide positive and increasing behavior versus cosmic time.

2.3 Model independent of R: $f(\phi ,Y)$ model

In this section, we shall investigate the components of symmetry generator and the unknown functions by taking the generic function independent of Ricci scalar, i.e., $f(Y,\phi )$. For constant scalar field coupling, the solution of determining equations (19)–(35) is given by

$$\begin{aligned}&\alpha =\beta =0, \quad \delta =mC_1, \gamma =2mC_1\phi +2C_3, \quad \\&f(Y,\phi )=C_2Y+mC_1\phi ^2+2C_3\phi , \\&V(\phi )=-\frac{2C_2}{C_1}(mC_1\phi ^2+2C_3\phi )\\&-(mC_1\phi ^2+2C_3\phi )+C_4. \end{aligned}$$

Here it is worthwhile to mention here that this solution exists only for $m=1$. In this case, the symmetries along with first integrals of motion can be written as

$$\begin{aligned} X_1= & {} 2m\phi \frac{\partial }{\partial Y}+m\frac{\partial }{\partial \phi }, \quad X_2=2\frac{\partial }{\partial Y}, \\ I_1= & {} -\left( 2a^3m^2{\dot{\phi }}+4{\dot{a}}^3mf_{Y\phi }\right) -8m\phi {\dot{a}}^3f_{YY},\\ I_2= & {} -8{\dot{a}}^3f_{YY}. \end{aligned}$$

On replacing the values of derivatives, it can be checked that only $I_1$ is non-zero and is given by $I_1=-2a^3m^2{\dot{\phi }}$. It can be solved for scale factor if one pick the power law form of scalar field $\phi =\phi _0a^{\alpha }$ and consequently, we obtain

$$\begin{aligned} a(t)= & {} \root 3 \of {\left( \frac{3}{\phi _0\alpha }t+C_1^{'}\right) }, \quad \nonumber \\ \phi (t)= & {} \phi _0\left( \frac{3}{\phi _0\alpha }t+C^{'}\right) ^{\alpha /3}. \end{aligned}$$

(43)

Here $C_1^{'}$ is a constant of integration. The graphical behavior of constructed generic function and scalar field potential is provided in Fig. 10 which exhibit smooth, positive and increasing behavior. Clearly, the scale factor is in power law form and its graph is provided in left panel of Fig. 11. In this case, the deceleration parameter is find to be $q=2$ representing Zel’dovich universe model (stiff matter). The evolution of effective EoS parameter is shown in right panel of Fig. 11 which clearly approaches the $\Lambda \hbox {CDM}$ epoch. It is significant to mention that though the background solution exhibits the stiff matter but the contributions from higher curvature invariant and scalar field results in $\Lambda \hbox {CDM}$ epoch.

For the second case when the coupling function is taken in terms of power law form, then the resulting solutions take the form

$$\begin{aligned}&\alpha =\beta =0, \quad \delta =C_6\phi ^{-\frac{s}{2}}, \quad \nonumber \\&\quad \gamma =e^{C_2ms\frac{\phi ^2}{2}+C_3\frac{\phi }{4}+C_5},\quad \nonumber \\&\quad f(Y,\phi )=C_1Y+e^{C_2ms\frac{\phi ^2}{2}+C_3\frac{\phi }{4}+C_5}, \nonumber \\&V(\phi )=\int \left( -\frac{e^{C_2ms\frac{\phi ^2}{2}+C_3\frac{\phi }{4}+C_5}}{4C_6}(8C_1\phi ^{\frac{s}{2}}+4ms\phi C_6+C_3C_6)\right) d\phi .\nonumber \\ \end{aligned}$$

(44)

The corresponding symmetries and first integrals are:

$$\begin{aligned} X_1= & {} \phi ^{-s/2}\frac{\partial }{\partial \phi }, \quad X_2=\frac{\partial }{\partial Y}, \quad \\ X_3= & {} \frac{ms\phi ^2}{2}\frac{\partial }{\partial Y}, \quad X_4=\frac{\phi }{4}\frac{\partial }{\partial Y}, \\ I_1= & {} -\phi ^{-s/2}\left( 2a^3\omega (\phi ){\dot{\phi }}+4{\dot{a}}^3f_{Y\phi }\right) , \quad \\ I_2= & {} -\left( 4{\dot{a}}^3f_{YY}\right) , \quad I_3=-\frac{ms\phi ^2}{2}\left( 4{\dot{a}}^3f_{YY}\right) , \quad \\ I_4= & {} -\frac{\phi }{4}\left( 4{\dot{a}}^3f_{YY}\right) . \end{aligned}$$

Here the symmetry generators $X_1$ and $X_2$ are scaling symmetries. In this case, only $I_1$ is non-zero integral which can be solved for scale factor by assuming the same power law from of scalar field. The corresponding solutions are given by

$$\begin{aligned} a(t)= & {} \left( \frac{s\alpha +6}{2\alpha \phi _0^{s/2+1}}t+C_2^{'}\right) ^{\frac{2}{s\alpha +6}}, \quad \\ \phi (t)= & {} \phi _0\left( \frac{s\alpha +6}{2\alpha \phi _0^{s/2+1}}t+C_2^{'}\right) ^{\frac{2\alpha }{s\alpha +6}}. \end{aligned}$$

Fig. 10

The left and right graphs indicate the behavior of $f(Y,\phi )$ function and scalar field potential for $\omega (\phi )=m$

Fig. 11

The left and right graphs provide the behavior of scale factor and effective EoS parameter for $\omega (\phi )=m$

Fig. 12

The left graph indicate the behavior $f(Y,\phi )$ function while right plot shows the behavior of scalar field potential for $\omega (\phi )=m\phi ^s$

Fig. 13

The left curve corresponds to plot of scale factor while right curve refers to effective EoS parameter versus time for $\omega (\phi )=m\phi ^s$

The graphical behavior of obtained generic function, scalar field potential, scale factor and corresponding EoS parameter for power law scalar field coupling is provided in Figs. 12 and 13. It is easy to verify that for accelerated expanding cosmic model, deceleration parameter imposes the constraint on free parameters as $q=-\frac{1}{2}(6+s\alpha )(-1+\frac{2}{6+s\alpha })<0$ which further leads to the condition $s<-\frac{4}{\alpha }$ or $\alpha <-\frac{4}{s}$. The scalar field potential and obtained generic function exhibit positive smooth behavior. It can also be seen that scale factor, being a power law function, provides positive and increasing behavior with time. Using the constraint $s<-\frac{4}{\alpha }$, we plot effective EoS parameter and show its behavior in right plot of Fig. 13. It clearly exhibits $\Lambda \hbox {CDM}$ model. Thus it can be concluded that the cosmology generated in both cases favor the cosmic expansion. Further we calculate the expressions of jerk and snap parameters which are also constant values given by $r=\frac{1}{2}(4+s\alpha )(5+s\alpha )$ and $s=\frac{6+3s\alpha +0.3333s^2\alpha ^2}{3+s\alpha }$. It can be easily verified that for $\alpha =-\frac{6}{s}$, the point $(r,s)=(1,0)$ can be recovered and hence our constructed model can corresponds to $\Lambda \hbox {CDM}$ model for this specific choice of $\alpha$. It is worthy to mention here that for describing early cosmic epochs, one needs to impose the condition $\alpha >-\frac{4}{s}$.

2.4 General $f(R,\phi ,Y)$ model

Here we shall study the existence of Noether symmetries for the generic function depending on all three variables namely R,  Y and $\phi$. For the first case, we consider the constant coupling function, the resulting set of solutions is given by

$$\begin{aligned}&\alpha =0, \quad \delta (a)=\frac{C_1C_2}{a}, \quad \gamma (a,R,\phi )\nonumber \\&\quad =\beta (a,R,\phi )=-\frac{2(C_9R+C_{10}) (m\phi -3C_3C_5C_6)C_2C_1}{aC_9(m\phi ^2-6C_5(C_6\phi +C_7)C_3)}.\nonumber \\ \end{aligned}$$

(45)

Also, the scalar field potential and the function f take the following form

$$\begin{aligned}&V(\phi )=\frac{\left( 2C_3C_{10}-C_9C_{11}\right) \left( 3C_3C_5C_6\phi -\frac{m\phi ^2}{2}\right) }{3C_3C_9}+C_{12}, \nonumber \\&f(R,Y,\phi )=(C_3R+C_4)\left( C_7+C_6\phi -\frac{m\phi ^2}{6C_3C_5}\right) C_5.\nonumber \\F \end{aligned}$$

(46)

In this case, we assume arbitrary integration constants $C_6=C_7=0$ for simplicity purposes, which yields

$$\begin{aligned}&\alpha =0, \quad \delta (a)=\frac{C_1C_2}{a}, \quad \gamma (a,R,\phi )=\beta (a,R,\phi )\\&\quad =-\frac{2(C_9R+C_{10})m\phi C_2C_1}{aC_9m\phi ^2}, \\&V(\phi )=\frac{\left( 2C_3C_{10}-C_9C_{4}\right) \left( -\frac{m\phi ^2}{2}\right) }{3C_3C_9}+C_{12}, \quad \\&\quad f(R,Y,\phi )=(C_3R+C_4)\left( -\frac{m\phi ^2}{6C_3C_5}\right) C_5. \end{aligned}$$

Consequently, we get the symmetries and first integrals of motion as follows

$$\begin{aligned} X_1= & {} -\frac{2R}{a\phi }\left( \frac{\partial }{\partial R}+\frac{\partial }{\partial Y}\right) \\&\quad +\frac{1}{a}\frac{\partial }{\partial \phi }, \quad \\ X_2= & {} -\frac{2}{a\phi }\left( \frac{\partial }{\partial R}+\frac{\partial }{\partial Y}\right) , \\ I_1= & {} -\frac{1}{a}\left( 2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }\right) \\&\quad +\frac{2R}{a\phi } \left( -6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \\&\quad +\frac{2R}{a\phi }(4{\dot{a}}^3f_{YY}), \\ I_2= & {} \frac{2}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY})\\&\quad +\frac{2}{a\phi }(4{\dot{a}}^3f_{YY}). \end{aligned}$$

Here the solutions turn out to be independent of Y. On substituting the derivatives, it is seen that $I_2=0$, while $I_1=-2a^m{\dot{\phi }}-2a{\dot{a}}m\phi$ which further leads to $\phi (t)=\frac{C_3^{'}}{a(t)}$. This indicates that the scalar field behaves oppositely to scale factor, i.e., for an expanding universe, the scalar field decreases versus time.

For the second case when the coupling function is given by the power law, the system of determining equations yields

$$\begin{aligned}&\alpha =0, \quad \delta (a,\phi )=\frac{C_1C_2\phi ^{-\frac{s}{2}}}{a}, \quad \\&\quad \beta (a,R,Y,\phi )\\&\quad =\frac{(C_9R+C_{10})(C_5Y+C_6)^2(C_7+C_8\phi ^{\frac{s}{2}+1})C_3C_4C_5}{9aC_9},\\&\gamma (a,\phi ,Y)=\frac{C_3C_4}{a} \left[ (C_7+C_8\phi ^{\frac{s}{2}+1})\right. \\&\quad \left. \left( \frac{C_5Y}{9} \left( \frac{C_5^2}{3}+C_5C_6Y+C_6^2\right) \right) +\frac{C_6^2}{27}\right] . \end{aligned}$$

Consequently, the scalar field potential and the generic function are given by

$$\begin{aligned}&V(\phi )=-\frac{2mC_{10}}{3C_9C_8}\left( \frac{2C_7\phi ^{\frac{s}{2}+1}+C_8\phi ^{s+2}}{(s+2)^2}\right) +C_{15},\\&f(R,Y,\phi )=\frac{9(C_9R+C_{10})m\phi ^{\frac{s}{2}+1}C_1C_2}{(s+2)(C_5Y+C_6)^2C_3C_4C_5C_8C_9}. \end{aligned}$$

In this case, the set of symmetries can be written as

$$\begin{aligned} X_1= & {} \frac{\phi ^{-s}}{2}\frac{\partial }{\partial \phi }, \quad X_2=\frac{RY^2}{a}\frac{\partial }{\partial R}+\frac{Y}{3a}\frac{\partial }{\partial Y}, \quad \\ X_3= & {} \frac{R}{a}\frac{\partial }{\partial R}+\frac{Y}{a}\frac{\partial }{\partial Y}, \quad \\ X_4= & {} \frac{RY}{a}\frac{\partial }{\partial R} +\frac{Y^2}{2a}\frac{\partial }{\partial Y}, \\ X_5= & {} \frac{Y^2}{a}\frac{\partial }{\partial R}+\frac{Y}{3a}\phi ^{s/2+1}, \quad \\ X_6= & {} \frac{\phi ^{s/2+1}}{a}\frac{\partial }{\partial R}+\frac{Y\phi ^{s/2+1}}{a}\frac{\partial }{\partial Y}, \quad \\ X_7= & {} \frac{Y\phi ^{s/2+1}}{a}\frac{\partial }{\partial R}, \quad X_8=\frac{Y^2}{a}, \\ X_9= & {} \frac{1}{a}\frac{\partial }{\partial R}, \quad X_{10}=\frac{Y}{a}\frac{\partial }{\partial R}, \quad \\ X_{11}= & {} \frac{\phi ^{s/2+1}Y^2}{a}\frac{\partial }{\partial R}, \quad X_{12}=\frac{\phi ^{s/2+1}}{a}\frac{\partial }{\partial R}, \quad \\ X_{13}= & {} \frac{Y\phi ^{s/2+1}}{a}\frac{\partial }{\partial R}, \\ X_{14}= & {} \frac{Y^2\phi ^{s/2+1}}{a}\frac{\partial }{\partial Y}. \end{aligned}$$

Also, the first integrals of motion take the form:

$$\begin{aligned} I_1= & {} -\frac{\phi ^{-s}}{2}\left( 2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }\right) , \quad \\ I_2= & {} -\frac{RY^2}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) \\&\quad -\frac{Y}{3a}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) ,\\ I_3= & {} -\frac{R}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) \\&\quad -\frac{Y}{a}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) , \\ I_4= & {} -\frac{RY}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) \\&\quad -\frac{Y^2}{2a}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) , \\ I_5= & {} -\frac{Y^2}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) \\&\quad -\frac{Y}{3a}\phi ^{s/2+1}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) ,\\ I_6= & {} -\frac{\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) \\&\quad -\frac{Y\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) ,\\ I_7= & {} -\frac{Y\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \quad \\ I_8= & {} -\frac{Y^2}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \quad \\ I_9= & {} -\frac{1}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \\ I_{10}= & {} -\frac{Y}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \quad \\ I_{11}= & {} -\frac{Y^2\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \quad \\ I_{12}= & {} -\frac{\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) ,\\ I_{13}= & {} -\frac{Y\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{RY}-6a^2{\dot{a}}f_{RR}\right) , \quad \\ I_{14}= & {} -\frac{Y^2\phi ^{s/2+1}}{a}\left( 4{\dot{a}}^3f_{YY}-6a^2{\dot{a}}f_{RY}\right) . \end{aligned}$$

Here the first integrals can be simplified by substituting the values of derivatives but the resulting equations are quite complicated which can not be solved analytically.

3 Noether gauge symmetries for Friedman universe model

In this section, we shall investigate the existence of Noether gauge symmetries for Friedman universe model with perfect fluid matter contents. For this purpose, we consider the full symmetry generator (10) along with the point-like Lagrangian (9) in Eq.(11), we get the following system of determining equations for Noether gauge symmetries. These equations are obtained after collecting the coefficients of different derivative product terms of a,  R,  Y and $\phi$ and then setting them equal to zero.

$$\begin{aligned}&3a^2\tau f+3a^2\tau Rf_{R}+3a^2\tau Yf_{Y}+3a^2\tau V\nonumber \\&\qquad -3\epsilon ^2\rho _0a^{-(3\epsilon +1)}\tau -12af_{R}\alpha _t\nonumber \\&\quad -6a^2f_{RR}\beta _t-6a^2f_{RY}\gamma _t-6a^2f_{R\phi }\delta _t+\tau _a(a^3f\nonumber \\&\quad +a^3Rf_R+a^3Yf_Y+a^3V)+\rho _0\epsilon a^{-3\epsilon }\tau _a=G_a, \end{aligned}$$

(47)

$$\begin{aligned}&2a^3\tau f_R+a^3R\tau f_{RR}+a^3Y\tau f_{YR}-6a^2f_{RR}\alpha _{t}\nonumber \\&\quad +\tau _{R}(a^3f+a^3Rf_{R}+a^3Yf_{Y}+a^3V)\nonumber \\&\quad +\rho _0\epsilon a^{-3\epsilon }\tau _R=G_R, \end{aligned}$$

(48)

$$\begin{aligned}&2a^3\tau f_Y+a^3R\tau f_{RY}+a^3Y\tau f_{YY}\nonumber \\&\quad -6a^2f_{RY}\alpha _{t}+\tau _{Y}(a^3f+a^3Rf_{R}+a^3Yf_{Y}+a^3V) \nonumber \\&\quad +\rho _0\epsilon a^{-3\epsilon }\tau _Y=G_Y, \end{aligned}$$

(49)

$$\begin{aligned}&2a^3\tau f_{\phi }+a^3R\tau f_{R\phi }+a^3Y\tau f_{Y\phi }+a^3V_{\phi }\tau \nonumber \\&\quad -6a^2f_{R\phi }\alpha _{t} +2a^3\omega \delta _t\nonumber \\&\quad +\tau _{\phi }(a^3f+a^3Rf_{R}+a^3Yf_{Y}+a^3V) \end{aligned}$$

(50)

$$\begin{aligned}&+\rho _0\epsilon a^{-3\epsilon }\tau _{\phi }=G_{\phi }, \end{aligned}$$

(51)

$$\begin{aligned}&3a^2\omega -6a^2\tau f_{R\phi \phi }\nonumber \\&\quad +6a^2f_{R\phi }\tau _{\phi }-a^3\omega \tau _a=0 \end{aligned}$$

(52)

$$\begin{aligned}&a^3\frac{d\omega }{d\phi }-a^3\omega \tau _{\phi }=0,\nonumber \\&\quad -6\tau f_{R}-\frac{24}{a}f_Y\alpha _t+6a\tau _af_R\nonumber \\&\quad +4f_{RY}\beta _t+4f_{YY}\gamma _t+4f_{Y\phi }\delta _t=0, \end{aligned}$$

(53)

$$\begin{aligned}&-18a\tau f_{RR}+12f_{RY}\alpha _t+6af_R\tau _R+6a^2f_{RR}\tau _a=0, \end{aligned}$$

(54)

$$\begin{aligned}&\quad -18a\tau f_{R\phi }+12\alpha _tf_{Y\phi }+6af_R\tau _{\phi }+6a^2f_{R\phi }\tau _a=0, \end{aligned}$$

(55)

$$\begin{aligned}&\quad -6a\tau f_{RY}+12f_{YY}\alpha _t+6af_R\tau _Y+6a^2f_{RY}\tau _a=0, \end{aligned}$$

(56)

$$\begin{aligned}&3\alpha a^2 f+3a^2R\alpha f_{R}+3a^2Yf_Y\alpha +3a^2V\alpha \nonumber \\&\quad -3\epsilon ^2\rho _0\alpha a^{-(3\epsilon +1)}+a^3f_R\beta +a^3f_{RR}R\beta +a^3Yf_{RY}\beta \nonumber \\&\quad +(a^3f_Y+a^3Rf_{RY}+a^3Yf_{Y}+a^3Yf_{YY})\gamma \nonumber \\&\quad +(a^3f_{\phi }+a^3Rf_{R\phi }+a^3Yf_{Y\phi })\delta \nonumber \\&\quad +a^3V_{\phi }\delta +\tau _t(a^3f+a^3Rf_R+a^3Yf_Y)\nonumber \\&\quad +\rho _0\epsilon a^{-3\epsilon }\tau _t=G_t, \end{aligned}$$

(57)

$$\begin{aligned}&3a^2\omega \alpha +a^3\delta \omega _{\phi }-6a^2f_{R\phi }\alpha _{\phi }\nonumber \\&\quad +2a^3\omega \delta _{\phi }-a^3\omega \tau _t=0,\end{aligned}$$

(58)

$$\begin{aligned}&\quad -6\alpha f_R-12af_{R}\alpha _{a}-6af_{RR}\beta -6a^2f_{RR}\beta _a\nonumber \\&\quad -6af_{RY}\gamma -6a^2f_{RY}\gamma _a-6af_{R\phi }\delta - 6a^2f_{R\phi }\delta _a\nonumber \\&\quad -18af_R\tau _t=0, \end{aligned}$$

(59)

$$\begin{aligned}&\quad -12a\alpha f_{RR}-6a^2f_{RR}\alpha _a-6a^2f_{RRR}\beta -6a^2f_{RR}\beta _R\nonumber \\&\quad -6a^2f_{RYY}\gamma -6a^2f_{RY}\gamma _R-6a^2\delta f_{R\phi \phi } -6a^2f_{R\phi }\delta _R \nonumber \\&\quad -12a\alpha _Rf_R+6a^2f_{RR}\tau _t=0, \end{aligned}$$

(60)

$$\begin{aligned}&\quad -12a\alpha f_{RY}-6a^2\alpha _af_{RY}-6a^2f_{RRY}\beta -6a^2f_{RR}\beta _Y\nonumber \\&\quad -6a^2f_{RYY}\gamma -6a^2f_{RY}\gamma _Y-6a^2f_{RY\phi }\delta -6a^2f_{R\phi }\delta _Y \nonumber \\&\quad -12af_{R}\alpha _Y+6a^2f_{RY}\tau _t=0, \end{aligned}$$

(61)

$$\begin{aligned}&\quad -12a\alpha f_{R\phi }-6a^2f_{R\phi }\alpha _a-12a\alpha _{\phi }f_R\nonumber \\&\quad -6a^2f_{RR\phi }\beta -6a^2f_{RR}\beta _{\phi } \nonumber \\&\quad -6a^2f_{RY\phi }\gamma -6a^2f_{RY}\gamma _{\phi }-6a^2f_{R\phi \phi }\delta +2a^3\omega \delta _a \nonumber \\&\quad -6a^2f_{R\phi }\delta _{\phi }+6a^2f_{R\phi }\tau _t=0, \end{aligned}$$

(62)

$$\begin{aligned}&\frac{6}{a^2}\alpha f_Y-\frac{24}{a}f_Y\alpha _a-\frac{6}{a}\beta f_{RY}+4f_{RY}\beta _a\nonumber \\&\quad -\frac{6}{a}f_{YY}\gamma + 4f_{YY}\gamma _a-\frac{6}{a}f_{Y\phi }\delta +4f_{Y\phi }\delta _a+\frac{18}{a}f_Y\tau _t=0, \nonumber \\ \end{aligned}$$

(63)

$$\begin{aligned}&\quad -18f_Y\alpha -18af_{RY}\beta -18af_{YY}\gamma -18af_{Y\phi }\delta \nonumber \\&\quad -18af_{Y}\tau _t-36af_Y\alpha _a+72af_Y\tau _t=0, \end{aligned}$$

(64)

$$\begin{aligned}&4f_{RRY}\beta +4f_{RY}\beta _R+4f_{RYY}\gamma +4f_{YY}\gamma _R\nonumber \\&\quad +4\delta f_{RY\phi }+4f_{Y\phi }\delta _R+12f_{RY}\alpha _a \nonumber \\&\quad -\frac{24}{a}f_Y\alpha _R-12f_{RY}\tau _t=0, \end{aligned}$$

(65)

$$\begin{aligned}&4f_{RYY}\beta +4f_{RY}\beta _Y+4f_{YYY}\gamma +4f_{YY}\gamma _Y+4\delta f_{YY\phi }\nonumber \\&\quad +4f_{Y\phi }\delta _Y+12f_{YY}\alpha _a \nonumber \\&\quad -\frac{24}{a}f_Y\alpha _Y-12f_{YY}\tau _t=0, \end{aligned}$$

(66)

$$\begin{aligned}&4f_{RY\phi }\beta +4f_{RY}\beta _{\phi }+4f_{YY\phi }\gamma +4f_{YY}\gamma _{\phi }+4\delta f_{Y\phi \phi }\nonumber \\&\quad +4f_{Y\phi }\delta _{\phi } +12f_{Y\phi }\alpha _a-\frac{24}{a}f_Y\alpha _{\phi }-12f_{Y\phi }\tau _t=0, \end{aligned}$$

(67)

$$\begin{aligned}&\quad -6a^2f_{RR}\alpha _R=0, \quad 6a^2(f_{RY}\alpha _R+f_{RR}\alpha _Y)=0, \quad \nonumber \\&\quad 6a^2f_{R\phi }\alpha _R+6a^2f_{RR}\alpha _{\phi }-2a^3\omega \delta _R=0, \end{aligned}$$

(68)

$$\begin{aligned}&6a^2f_{RR}\tau =0, \quad 6a^2f_{RR}\tau +72af_Y\alpha _{tR}=0, \nonumber \\&\quad -6a^2\tau f_{RRR}+6a^2f_{RR}\tau _R=0, \end{aligned}$$

(69)

$$\begin{aligned}&-12a^2\tau f_{RR\phi }+6a^2f_{RR}\tau _{\phi }+6a^2f_{R\phi }\tau _R=0, \quad \nonumber \\&\quad -12a\tau f_{RY}=0, \quad -6a^2\tau f_{RY}=0, \end{aligned}$$

(70)

$$\begin{aligned}&-12a^2\tau f_{RRY}+6a^2f_{RR}\tau _{Y}+6a^2f_{RY}\tau _R=0, \quad \nonumber \\&\quad -6a^2\tau f_{RY}-72af_Y\alpha _{ty}=0, \end{aligned}$$

(71)

$$\begin{aligned}&-12af_R\tau -72af_Y\alpha _{at}+36af_Y\tau _{tt}=0, \quad 3a^2\omega \tau =0,\nonumber \\ \end{aligned}$$

(72)

$$\begin{aligned}&-12a^2\tau f_{RY\phi }+6a^2f_{RY}\tau _{\phi }+6a^2f_{R\phi }\tau _Y=0, \quad \nonumber \\&\quad -6a^2\tau f_{RYY}+6a^2f_{RY}\tau _Y=0, \end{aligned}$$

(73)

$$\begin{aligned}&-6a^2\tau f_{R\phi }-72af_Y\alpha _{t\phi }=0, \quad -6a^2\tau f_{R\phi }=0, \quad \nonumber \\&\quad -\frac{24}{a}f_Y\tau +36af_Y\tau _{aa}=0, \end{aligned}$$

(74)

$$\begin{aligned}&\frac{6}{a^2}f_Y\tau +\frac{18}{a}f_Y\tau _a=0, \quad \nonumber \\&\quad -\frac{6}{a}\tau f_{YR}+\frac{18}{a}f_Y\tau _R-12f_{RY}\tau _a=0, \quad -\frac{6}{a}\tau f_{Y\phi }\nonumber \\&\quad +\frac{18}{a}f_Y\tau _{\phi }-12f_{Y\phi }\tau _a=0, \end{aligned}$$

(75)

$$\begin{aligned}&-\frac{6}{a}\tau f_{YY}+\frac{18}{a}f_Y\tau _Y-12f_{YY}\tau _a=0 \quad \nonumber \\&\quad -18a\tau f_{YY}+54af_Y\tau _Y=0, \quad \nonumber \\&\quad -18a\tau f_{Y\phi }+54af_Y\tau _{\phi }=0, \end{aligned}$$

(76)

$$\begin{aligned}&-18a\tau f_{YR}+54af_Y\tau _R=0, \quad -36a\tau f_Y=0, \quad \nonumber \\&\quad -18\tau f_Y-18af_Y\tau _a=0, \quad 4\tau f_{Y\phi \phi }-12f_{Y\phi }\tau _{\phi }=0, \end{aligned}$$

(77)

$$\begin{aligned}&4f_{Y\phi }\tau =0, \quad f_{RY}\tau =0, \quad 12\tau f_{Y\phi }\nonumber \\&\quad +72af_Y\tau _{a\phi }=0, \quad 12\tau f_{RY}+72af_Y\tau _{a\phi }=0, \end{aligned}$$

(78)

$$\begin{aligned}&4\tau f_{RYY}-12f_{RY}\tau _{R}=0, \quad 8\tau f_{RY\phi }\nonumber \\&\quad -12f_{RY}\tau _{\phi }-12f_{Y\phi }\tau _R=0, \quad 4f_{YY}\tau =0, \end{aligned}$$

(79)

$$\begin{aligned}&8\tau f_{RYY}-12f_{RY}\tau _{Y}-12f_{YY}\tau _R=0, \quad 8\tau f_{YY\phi }\nonumber \\&\quad -12f_{YY}\tau _{\phi }-12f_{Y\phi }\tau _{\phi }=0, \end{aligned}$$

(80)

$$\begin{aligned}&12f_{YY}\tau +72af_{Y}\tau _{aY}=0, \quad 4\tau f_{YYY}\nonumber \\&\quad -12f_{YY}\tau _{YY}=0, \quad f_{RY}\alpha _R=0, \quad f_{Y\phi }\alpha _{\phi }=0, \quad \nonumber \\&\quad f_{RY}\alpha _Y=0, \end{aligned}$$

(81)

$$\begin{aligned}&f_{YY}\alpha _R+f_{RY}\alpha _Y=0, \quad f_{Y\phi }\alpha _R+f_{RY}\alpha _{\phi }=0, \quad \nonumber \\&\quad f_{Y\phi }\alpha _Y+f_{YY}\alpha _{\phi }=0, \quad f_{YY}\alpha _{Y}=0, \end{aligned}$$

(82)

$$\begin{aligned}&-6a^2f_{R\phi }\alpha _Y-6a^2f_{RY}\alpha _{\phi }+2a^2\omega \delta _Y=0, \quad \nonumber \\&\quad a^3\omega \tau _R=0, \quad a^3\omega \tau _Y=0, \quad 36af_Y\alpha _{\phi }=0, \end{aligned}$$

(83)

$$\begin{aligned}&-36af_{Y}\alpha _{tt}=0, \quad -36af_Y\alpha _{aa}+72af_Y\tau _{ta}=0. \end{aligned}$$

(84)

For solving this system of equations, we consider some specific cases as we discussed in the last section.

3.1 Model independent of curvature invariant: $f(R,\phi )$

Here we shall explore the solutions of determining equations (47)–(84) for full Noether gauge symmetry generator. In the present case, its solution can be written as

$$\begin{aligned}&\alpha (a)=0, \quad \gamma =0, \quad \beta (t,a,R,\phi )\nonumber \\&\quad =\frac{(b_9R+b_7)b_{10}}{2a(b_7\phi +b_8)} \left( e^{(\frac{t+b_4}{b_3})^2}+1\right) \sqrt{-\frac{b_2}{e^{(\frac{t+b_4}{b_3})^2}}},\nonumber \\&\delta (t,a)=-\frac{b_1\left( e^{(\frac{t+b_4}{b_3})^2}+1\right) \sqrt{-\frac{b_2}{e^{(\frac{t+b_4}{b_3})^2}}}}{4ab_7},\nonumber \\&\quad f(R,\phi )=(b_5R+b_6)(b_7\phi +b_8), \nonumber \\&V(\phi )=-\frac{3b_7b_5\phi }{b_3}-b_7b_6\phi +2b_5b_7b_9\phi +b_{10}, \quad \nonumber \\&\quad G(t,a)=\frac{3}{4}\frac{\left[ -b_2\left( e^{(\frac{t+b_4}{b_3})^2}+1\right) a^2b_1\right] }{b_3e^{(\frac{t+b_4}{b_3})^2}\sqrt{-\frac{b_2}{e^{(\frac{t+b_4}{b_3})^2}}}}. \end{aligned}$$

(85)

Here the coupling parameter $\omega$ is also turned out to be zero. The corresponding set of symmetries along with the first integrals of motion can be written as

$$\begin{aligned}&X_1=\frac{2R}{a\phi }\frac{\partial }{\partial R}, \quad X_2=\frac{2}{a\phi }\frac{\partial }{\partial R}, \quad \nonumber \\&X_3=\frac{t^2R}{a\phi }\frac{\partial }{\partial R}, \quad X_4=\frac{t^2}{a\phi }\frac{\partial }{\partial R}, \nonumber \\&X_5=\frac{tR}{a\phi }\frac{\partial }{\partial R}, \quad X_6=\frac{t}{a\phi }\frac{\partial }{\partial R}, \quad \nonumber \\&X_7=\frac{t^3R}{a\phi }\frac{\partial }{\partial R}, \quad X_8=\frac{t^3}{a\phi }\frac{\partial }{\partial R}, \nonumber \\&X_9=\frac{1}{a}\frac{\partial }{\partial \phi }, \quad X_{10}=\frac{t^2}{a}\frac{\partial }{\partial \phi }, \quad \nonumber \\&X_{11}=\frac{t}{a}\frac{\partial }{\partial \phi }, \quad X_{12}=\frac{t^3}{a}\frac{\partial }{\partial \phi } \end{aligned}$$

(86)

and

$$\begin{aligned}&I_1=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{2R}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}), \quad \nonumber \\&I_2=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{2}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}), \nonumber \\&I_3=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^2R}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}),\quad \nonumber \\&I_4=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^2}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}),\nonumber \\&I_5=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{tR}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}),\quad \nonumber \\&I_6=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}), \nonumber \\&I_7=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^3R}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}), \quad \nonumber \\&I_8=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^3}{a\phi }(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}), \nonumber \\&I_9=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{1}{a}(2\omega a^3{\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }),\quad \nonumber \\&I_{10}=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^2}{a}(2\omega a^3{\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }),\nonumber \\&I_{11}=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t}{a}(2\omega a^3{\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }),\quad \nonumber \\&I_{12}=(c_{13}+c_{14}t^4)\frac{a^2}{12}-\frac{t^3}{a}(2\omega a^3{\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }).\nonumber \\ \end{aligned}$$

(87)

Here we have assumed that the arbitrary constants satisfy the conditions: $b_4=0,~ b_8=0$ and $b_2<0$. It is interesting to mention here that the symmetry corresponding to energy conservation can not be recovered in this case.

In case of Noether gauge symmetry, when the function is independent of curvature invariant term, i.e., $f(R,\phi )$, the set of dynamical Lagrange equations result into the following set of equations:

$$\begin{aligned}&a^3f_{\phi }+a^3Rf_{R\phi }+a^3V_{\phi }-6a^2{\dot{a}}{\dot{R}}f_{RR\phi }\\&\quad -6a^2{\dot{a}}{\dot{\phi }}f_{R\phi \phi }+12a{\dot{a}}^2f_{R\phi }\\&\quad +6a^2\ddot{a}f_{R\phi }+6a^2{\dot{a}}{\dot{R}}f_{RR\phi }+6a^2{\dot{a}}{\dot{\phi }}f_{R\phi \phi }=0,\\&3a^2(f+Rf_R+V)+6{\dot{a}}^2f_R-3\epsilon ^2\rho _0a^{-(1+3\epsilon )}\\&\quad +12a\ddot{a}f_R+12a{\dot{a}}{\dot{R}}f_{RR}+12a{\dot{a}}{\dot{\phi }}f_{R\phi }\\&\quad +6a^2\ddot{\phi }f_{R\phi }+6a^2{\dot{\phi }}{\dot{R}}f_{RR\phi } +6a^2{\dot{\phi }}^2f_{R\phi \phi }=0, \\&6a^2{\dot{a}}{\dot{R}}f_{RR}+6a^2{\dot{a}}{\dot{\phi }}f_{R\phi }\\&\quad +6a{\dot{a}}^2f_R+\rho _0\epsilon a^{-3\epsilon }+a^3(f+Rf_R+V)=0, \end{aligned}$$

Since the form of generic function coming from the existence of Noether gauge symmetry is given by $f(R,\phi )=(b_5R+b_6)(b_7\phi +b_8)$, therefore the above equations reduce to the following forms:

$$\begin{aligned}&a^2(f_{\phi }+Rf_{R\phi }+V_{\phi })+6(2{\dot{a}}^2f_{R}+a\ddot{a})f_{R\phi }=0,\\&a^2(f+Rf_R+V)+2{\dot{a}}^2f_R-\epsilon ^2\rho _0a^{-1-3\epsilon }\\&\quad +2a\ddot{a}f_R+2a{\dot{a}}{\dot{\phi }}f_{R\phi }+6a^2\ddot{\phi }f_{R\phi }=0. \end{aligned}$$

Solving the above equations for scale factor, we obtain

$$\begin{aligned} a(t)=k_1e^{\frac{(\sqrt{2b_7b_3-3})t}{\sqrt{6b_3}}}+k_2e^{-\frac{(\sqrt{2b_7b_3-3})t}{\sqrt{6b_3}}} \end{aligned}$$

Likewise, the scalar field take the following form:

$$\begin{aligned}&\phi (t)=e^{\frac{ut}{3}}(e^{\frac{-2ut}{3}}-1)(k_3+\int {zdt}); \quad \\&u=\sqrt{\frac{6}{b_3}(2b_7b_3-3)}, \end{aligned}$$

where

$$\begin{aligned} \int {zdt}= & {} \frac{b_5b_7}{k_2^3}u\sqrt{\frac{b_3}{6}}(Ae^{s_1t-s_2t+s_3t}(s_1-s_2+s_3)^{-1}\\&-2Ae^{s_1t-s_2t+\frac{s_3}{3}t} (s_1-s_2+\frac{s_3}{3})^{-1}\\&-2Ae^{s_1t-s_2t-\frac{s_3t}{3}}(s_1-s_2-\frac{s_3}{3})^{-1}\\&+ Ae^{s_1t-s_2t+\frac{5s_3}{3}}(s_1-s_2+\frac{5s_3}{3})^{-1}\\&+Ae^{s_1t-s_2t-s_3}(s_1-s_2-s_3)^{-1}\\&+Ae^{s_1t-s_2t-\frac{5s_3}{3}t}(s_1-s_2-\frac{5s_3}{3})^{-1}\\&+\epsilon \rho _0k_2\frac{\sqrt{6}}{u}\left\{ 6b_3e^{\frac{ut}{6\sqrt{6}}}+12b_3e^{-\frac{ut}{6\sqrt{6}}} \right. \\&+4b_3e^{-\frac{ut}{2\sqrt{6}}}+2b_3e^{\frac{ut}{2\sqrt{6}}}\\&\left. \left. -\frac{6}{5}b_3e^{-\frac{5ut}{6\sqrt{6}}}-\frac{6}{7}b_3e^{-\frac{7ut}{6\sqrt{6}}}\right\} \right) , \end{aligned}$$

where we have introduced $s_1=\frac{12}{ub_3},~s_2=\frac{8b_9}{u}$ and $s_3=u$, and $A=49k_2^3b_5b_8-32k_2^3b_9b_5b_3b_8+8k_2^3b_3b_5b_8+8k_2^3b_3b_{10}$. The graphical behavior of the calculated generic function and scalar field potential is provided in Fig. 14. It is seen that the scalar field potential is positive and increasing function. The graphical behavior of expansion factor, scalar field and cosmic volume is provided in Fig. 15 which indicates that all these functions exhibit positive and increasing behavior versus time. Figure 16 provides the positive but decreasing trend of matter density versus time. Furthermore, it can be seen that deceleration and effective EoS parameters exhibit negative behavior versus time. So, it can be concluded that all these cosmic measures collectively support the accelerated expanding nature of cosmos.

Fig. 14

The left and right graphs provide the behavior of function $f(R,\phi )$ and scalar field potential for Noether gauge symmetry, ($f(R,\phi )$ case)

Fig. 15

The left, right and down graphs indicate the behavior of expansion radius, scalar field and cosmic volume, respectively, for Noether gauge symmetry ($f(R,\phi )$ case)

Fig. 16

The left, right and down plots refer to the behavior of ordinary matter density, deceleration and effective EoS parameters, respectively, for Noether gauge symmetry ($f(R,\phi )$ case)

Next, by replacing the values of derivatives of generic function, the first integrals can be simplified. It easy to check that $I_1=(c_{13}+c_{14}t^4)\frac{a^2}{12}$ and $I_1=I_i; ~i=2,3,\ldots ,8$. Likewise, $I_9,\ldots , I_{12}$ results into similar equations for scale factor (as $\omega =0$). Thus these integrals will provide only the forms of scale factor while scalar field remains as unknown quantity. By re-arranging $I_1$, we can get the form of scale factor as $a(t)=\sqrt{\frac{12I_1}{c_{13}+c_{14}t^4}}$. Clearly, scale factor is in power law form and hence indicates positive increasing behavior for specific choices of free parameters. Likewise, other quantities also exhibit cosmological viable behavior and hence can correspond to cosmic expansion. Others integrals can provide slightly different forms of scale factor exhibiting a similar behavior.

3.2 Model independent of scalar field: f(R, Y)

Here we shall investigate the solutions of determining equations for the model independent of scalar field. However, in this case, the scalar field potential and coupling will be non-zero. The obtained solutions are given by

$$\begin{aligned}&\alpha (a)=0, \quad \delta (t,a)=-\frac{C_1C_3C_2}{aC_{10}}d_1\left( \frac{1}{2}C_7t^2\right. \nonumber \\&\left. +C_8\right) +C_{12}C_7t, \quad \nonumber \\&\beta (t,a,R,Y)=-\frac{(\frac{1}{2}C_7t^2+C_8)d_1}{a^3Ye^{C_1(R+Y)}}, \nonumber \\&\gamma (t,a,R,Y)=\frac{(\frac{1}{2}C_7t^2+C_8)C_9C_4C_6C_{11}}{a^3Ye^{C_1(R+Y)}}, \nonumber \\&V(\phi )=C_5\phi +C_6, \quad \nonumber \\&f(R,Y)=C_2C_3e^{C_1(R+Y)},\quad \nonumber \\&G(t,a)=\frac{C_7t^2}{2}+C_8. \end{aligned}$$

(88)

Further, the set of symmetries and first integrals of motion can be written as

$$\begin{aligned}&X_1=\frac{t^2}{a}\partial _\phi , \quad X_2=\frac{1}{a}\partial _\phi , \quad X_3=t\partial _\phi , \quad \nonumber \\&X_4=-\frac{t^2}{a^3Y}\partial _R+\frac{t^2}{a^3Y}\partial _Y, \quad X_5=-\frac{1}{a^3Y}\partial _R+\frac{1}{a^3Y}\partial _Y,\nonumber \\&X_6=-\frac{t^2(R+Y)}{a^3Y}\partial _R+\frac{t^2(R+Y)}{a^3Y}\partial _Y, \quad \nonumber \\&X_7=\frac{R+Y}{-a^3Y}\partial _R+\frac{R+Y}{a^3Y}\partial _Y \end{aligned}$$

(89)

and

$$\begin{aligned}&I_1=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) -\frac{t^2}{a}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }), \quad \nonumber \\&I_2=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) -\frac{1}{a}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }), \nonumber \\&I_3=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) -t(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }),\nonumber \\&I_4=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) +\frac{t^2}{a^3Y}(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY})\nonumber \\&\quad -\frac{t^2}{a^3Y}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}), \nonumber \\&I_5=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) +\frac{1}{a^3Y}(-6a^2{\dot{a}}f_{RR}\nonumber \\&\quad +4{\dot{a}}^3f_{RY})-\frac{1}{a^3Y}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}),\nonumber \\&I_6=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) +\frac{t^2(R+Y)}{a^3Y}(-6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY})\nonumber \\&\quad -\frac{t^2(R+Y)}{a^3Y}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}), \nonumber \\&I_7=\left( \frac{C_7}{14}t^2+\frac{C_8}{7}\right) \nonumber \\&\quad +\frac{R+Y}{-a^3Y}\left( -6a^2{\dot{a}}f_{RR}+4{\dot{a}}^3f_{RY}\right) \nonumber \\&\quad -\frac{R+Y}{a^3Y}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}). \end{aligned}$$

(90)

Fig. 17

The left and right graphs provide the behavior of generic function and scalar field potential for Noether gauge symmetry

By replacing the values of derivatives in these integrals, it can be easily seen that the resulting equations are quite complicated and hence analytical solution for scale factor and scalar field is not possible. The graphical behavior of generic function and scalar field potential is provided in Fig. 17. Both these functions exhibit positive and increasing behavior.

3.3 Model independent of Ricci Scalar: $f(\phi ,Y)$

In this section, we shall explore the solutions of the determining equations for the case when the generic function is independent of Ricci scalar. The corresponding solutions can be written as

$$\begin{aligned}&\alpha =\beta =0, \quad \delta (a)=\frac{2C_{10}C_{11}C_{12}C_{13}C_4^2C_9}{C_7}a^{-3}, \quad \nonumber \\&\gamma (a,Y)=\frac{C_9C_{10}C_{11}C_{12}C_{13}(Y^2C_4^2-2)}{a^3(1+Y)}, \nonumber \\&V(\phi )=-\frac{C_1C_7C_3\phi }{2C_4^2C_9C_{10}C_{11}C_{12}C_{13}}(C_8C_6e^{C_7\phi })+C_{15}, \quad \nonumber \\&f(Y,\phi )=\left( -\frac{1}{2}e^{\sqrt{2}C_4\tanh ^{-1}(\frac{YC_4}{\sqrt{2}})+C_5}\right) e^{C_7\phi }C_8, \nonumber \\&G(t,a)=(C_1t+C_2)C_3. \end{aligned}$$

(91)

In this case, the set of symmetries and first integral of motion are given by

$$\begin{aligned} X_1= & {} \frac{1}{a^3}\frac{\partial }{\partial \phi }, X_2 =\frac{Y^2}{a^3(1+Y)}\frac{\partial }{\partial Y}, \quad \nonumber \\ X_3= & {} -\frac{1}{a^3(1+Y)}\frac{\partial }{\partial Y}, \nonumber \\ I_1= & {} \frac{1}{3}(C_4t+C_5)-\frac{1}{a^3}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi }+4{\dot{a}}^3f_{Y\phi }), \quad \nonumber \\ I_2= & {} \frac{1}{3}(C_4t+C_5)-\frac{Y^2}{a^3(1+Y)}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}),\nonumber \\ I_3= & {} \frac{1}{3}(C_4t+C_5)+\frac{1}{a^3(1+Y)}(-6a^2{\dot{a}}f_{RY}+4{\dot{a}}^3f_{YY}).\nonumber \\ \end{aligned}$$

(92)

Fig. 18

The left and right graphs provide the behavior of generic function and scalar field potential for Noether gauge symmetry

Similar to the previous case, here the analytical solutions are also not possible. The graphical behavior of generic function along with scalar field potential is provided in Fig. 18.

3.4 General model $f(R,Y,\phi )$

Here we shall find the existence of Noether gauge symmetries through system of determining equations for general function $f(R,Y,\phi )$ depending on all three variables. In this case, the system yields the following solutions:

$$\begin{aligned}&\alpha =\gamma =0, \quad \delta (a)=\frac{C_8C_9}{a^3}, \quad \nonumber \\&\beta (a,\phi )=-\frac{C_6C_8C_9e^{C_3\phi }}{a^3(C_5+C_6e^{C_3\phi })},\nonumber \\&V(\phi )=K_1\phi +C_2, \quad \nonumber \\&f(R,Y,\phi )=C_1\ln (Y)(C_5+C_6e^{C_3\phi })e^{C_3R}C_4, \quad \nonumber \\&G(t,a)=C_6t+C_7. \end{aligned}$$

(93)

The corresponding set of symmetries and first integral of motion are given by

$$\begin{aligned} X= & {} \frac{1}{a^3}\left( \frac{\partial }{\partial \phi }-\frac{\partial }{\partial R}\right) , \quad \\ I= & {} (C_6t+C_7)-\frac{1}{a^3}(2a^3\omega {\dot{\phi }}-6a^2{\dot{a}}f_{R\phi } -6a^2{\dot{a}}f_{RR}\\&+4{\dot{a}}^3f_{RY}). \end{aligned}$$

Here we have assumed that $C_5=0$, for the sake of simplicity. Here the resulting first integral also leads to a complicated differential equation in terms of scale factor and scalar field which can not be solved for these functions analytically.

4 Summary

Noether and Noether gauge symmetries are considered as one of the most powerful techniques for determining exact solutions of a complicated dynamical system of differential equations. In Lagrangian of modified gravity theories, there are some generic functions present whose exact and significant forms always pose a challenge for researchers. The search for a cosmologically viable form of these generic functions fascinated the researchers to use the technique of Noether and Noether gauge symmetries and obtain some interesting new forms. The present paper will provide a significant contribution in this respect. In the present work, we have investigated the existence of Noether and Noether gauge symmetries of flat FRW model using perfect fluid matter contents in a generalized framework of $f(R,Y,\phi )$ theory, where Y represents curvature invariant $R_{\alpha \beta }R^{\alpha \beta }$. Generally, a fourth-order theory of gravity is obtained by adding higher-order curvature invariant terms namely $R_{\alpha \beta }R^{\alpha \beta }$ and $R_{\alpha \beta \gamma \delta }R^{\alpha \beta \gamma \delta }$ in the standard Einstein Hilbert action [79, 80]. However, it is now established that the term $R_{\alpha \beta \gamma \delta }R^{\alpha \beta \gamma \delta }$ can be ignored by using the Gauss-Bonnet theorem [81]. This theory is different from other available modifications of GR in the sense that these theories involve only Ricci scalar, along with either scalar field, potential as well as its kinetic term or higher-order derivatives of scalar field are added like Horndeski theory. In the present work, we have considered the framework involving higher-order curvature invariant term (which is the basic and distinct feature) along with scalar field kinetic term and it’s potential. This theory is recently proposed and found to be very interesting and successful in discussing some cosmic issues. This theory can be reduced to $f(R,\phi )$ gravity if $Y=0$ and also, by taking its specific form $f(R,\phi )=R\phi$, simple BD theory can be recovered. In some sense, one can conclude that this theory is the extension of generalized Brans-Dicke theory with the inclusion of higher-order curvature invariant. Up to our knowledge, this is first work on the subject within this extended gravity.

In this work, we have first evaluated simple Noether symmetries and then explored full Noether gauge symmetries and evaluated the corresponding conserved quantities. It is interesting to mention here that the present work is quite general in the sense that second-order prolongation of symmetry generator have applied as the Lagrangian involves second-order derivative term even after applying partial integration. Up to our knowledge, no such work is available in literature where the second-order prolongation have been considered for obtaining symmetries and exact cosmological solutions. We have further formulated the second-order Euler-Lagrange equations and the corresponding Hamiltonian. It have been seen that the resulting equations are quite complicated and hence difficult to solve. By imposing the condition for Noether and Noether gauge symmetries existence, we have found the corresponding system of determining equations. Since, these are quite long systems whose solutions are difficult to find, therefore we have assumed some specific cases of generic function $f(R,Y,\phi )$ along with constant and power law coupling of scalar field. In graphical analysis, we have considered simple values of integration constants and other free parameters (like 0 or 1). The results can be summarized as follows:

• For simple Noether symmetry case, we have obtained symmetries, conserved quantities and corresponding exact solutions using first integrals and Euler-Lagrange equations. It has been observed that the exact solutions can be obtained only for some simple cases. For $f(R,\phi )$ case, we have obtained exact solutions using dynamical equations. The scale factor and scalar field both turned out to be in exponential form. In order to discuss cosmology generated by these solutions, we have explored different cosmic measures like cosmic volume, ordinary matter density, deceleration and effective EoS parameters as well as snap and jerk parameters graphically. It is seen that scale factor, scalar field and cosmic volume exhibited positive and increasing behavior versus time. Moreover, deceleration parameter along with effective EoS showed negative behavior (particularly, it corresponds to phantom phase) and hence supported to the accelerated expanding nature of our cosmos. The graphs of ordinary matter density showed positive but decreasing behavior indicating a less dense universe in later cosmic epochs. From the plot of snap and jerk parameters, it can be seen that the curve is passing through a point $(s,r)=(0,1)$ which is indicating that the obtained exact model has a correspondence with standard $\Lambda \hbox {CDM}$ cosmic model. By using the first integrals, we have also found analytical form of scale factor using power law choice of scalar field. From the graphical behavior of scale factor and cosmic volume, it can be concluded that these measures support to phenomenon of cosmic acceleration. The same conclusion can be drawn from the plot of effective EoS parameter which exhibited negative behavior (particularly, refers to quintessence or phantom phases). For the power law choice of coupling parameter, the obtained scale factor also showed positive and increasing behavior and hence similar conclusions can be drawn in this case;

• For F(R, Y) case, we have found and listed non-trivial symmetries along with conserved quantities. It is seen that only numerical solutions can be obtained in this case as the Euler-Lagrange equations and first integrals resulted in quite complicated differential equations in terms of scale factor. For the constant coupling case, we have solved this differential equation (first integral) numerically and it is seen that obtained scale factor also indicated positive increasing behavior versus time. For the $F(\phi ,Y)$ case, we have found exact solutions using power law form of scalar field for both constant and power law scalar field coupling. It is seen that graphical behavior of scale factor and effective EoS parameter refers to expanding cosmic nature. It is worthwhile to mention here that these solutions exhibit the $\Lambda \hbox {CDM}$ era. We have also discussed possible constraint on free parameters using deceleration parameter $q<0$. Also, the values for which the obtained model can show correspondence with $\Lambda \hbox {CDM}$ model have also been provided using snap and jerk parameters;

• It has been argued that quadratic term $R^2$ or its higher-order give rise to strong gravity [82,83,84] and predict an over production of scalarons in the very early universe. Also, the inclusion of $R^{-1}$ term in GR action results in the field equations which naturally produce the observed cosmological acceleration [85, 86]. In the present work, obtained $f(R,\phi ), ~f(R,Y),~ f(Y,\phi )$ and $f(R,Y,\phi )$ generic functions are either in some type of polynomial (involving negative or positive powers of R. Y or $\phi$), or in exponential or natural logarithm form. It is argued that quadratic potential $V\sim \phi ^2$ is widely used in the discussion of chaotic inflationary models [49, 87]. It would be worthwhile to mention here that in majority of the discussed cases of present work, the scalar field potential turned out to be quadratic in nature. Further, in some cases, it have been seen that by constraining the value of parameter $\alpha$, the early radiation and matter dominated eras of cosmos can be discussed. In these cases, the deceleration parameter is turned as a positive quantity and therefore, in these cases, early cosmic epochs can be explained. For example, it has been pointed out that in $f(Y,\phi )$ case, the deceleration parameter is found to be $q=2$ representing Zel’dovich universe model (stiff matter);

• For general $F(R,Y,\phi )$ case, we have listed the non-trivial symmetries and conserved quantities but the exact solutions are not possible due to the complexity of resulting dynamical equations and first integrals.

• In Noether gauge symmetry case, the same cases of generic functions have been taken into account. It is seen that in each case, both $\tau$ and scalar field coupling $\omega$ turned out to be zero and consequently, energy conservation law can not be recovered in these cases. For $F(R,\phi )$ function, we have found the non-trivial symmetries, non-zero gauge function and first integrals of motion. In this case, exact solutions are also obtained using Euler-Lagrange equations and first integrals. From the graphical behavior of these solutions, it is seen that expansion factor, cosmic volume and scalar field indicate positive and increasing behavior which is in accordance with the expanding cosmic nature. Also, the negative behavior of deceleration parameter and effective EoS (provided phantom cosmic epoch) also affirmed the accelerated cosmic expansion in this case. For other cases, we have evaluated the non-trivial symmetries and corresponding conserved quantities only as the exact solutions were not possible to be found due to complicated system of differential equations.

There are many works available in literature on the subject using Lagrangians involving either curvature invariants or higher-order derivatives of scalar field. Like, Motavali et al. [49] and Sharif and Waheed [50] explored the existence of Noether gauge symmetries using FRW spacetime by considering the curvature correction term $\frac{\mu _0}{R}$ or induced gravity. These cases can be considered as sub cases of our work where one can fix $f(R,\phi )=\phi (R-\frac{\mu _0}{R})$ or $f(R,\phi )=\phi ^2R$ and $Y=0$. They have investigated the cosmology generated by the exact solutions obtained by scaling/dilatational symmetries and interpolation method (numerical approach). In literature [88, 89], Noether symmetry analysis have been applied to some general frameworks involving higher-order curvature corrections namely $\Box R$ (without scalar field) or F(R, G) generic function, where some anstaz were taken into account like $F(R,G)=f_0R^n+g_0G^m$ and $F(R,G)=f_0R^nG^m$, with n and m as real numbers. Similarly, Frasat [71] investigated the existence of Noether symmetries for flat FRW model in $f(R,\phi ,\chi )$ theory (where $\phi$ and $\chi$ denote the scalar field and its kinetic term, respectively) and found the scale factors by taking different ansatz for $f(R,\phi ,\chi )$ function and discussed it graphically which indicated expanding behavior versus cosmic time but no further graphical illustration of other important cosmological measures like effective EoS parameter, deceleration parameter, statefinders etc. was provided. Likewise, Massaeli et al. [90] found exact solutions by taking ceratin assumptions in Horndeski theory and explored the possible constraints on free parameters using effective EoS parameter only which turned out as a constant quantity in each case. In [72], Capozziello et. al. discussed the Noteher symmetries for flat FRW model using Horndeski theory but their primary objective was just to provide classification of solutions and hence no cosmological discussion was provided. In the present work, we have solved the system of determining equations in a general way without assuming any ansatz for generic function $f(R,Y,\phi )$ or field potential $V(\phi )$. In fact, we proposed their forms by solving system of determining equations where we have considered two cases of scalar field coupling parameter $\omega (\phi )$ and full phase space $\{t, a, \phi , R, Y\}$. So, our work not only specifies the new forms of generic function and scalar field potential but also further provides the exact solutions for the obtained Lagrangian forms. It would be worthwhile to check the existence of non-trivial symmetries and possibility of exact solutions for Bianchi type models in this non-minimally coupled curvature and scalar field theory.

Appendix

$$\begin{aligned} q= & {} -\frac{a\ddot{a}}{{\dot{a}}^2}, r = q+2q^2-\frac{{\dot{q}}}{H}, \quad s=\frac{r-1}{3(q-1/2)}, \quad \\ \rho _{eff}= & {} \frac{1}{f_R}(\rho _m+\rho _d) \quad p_{eff}=\frac{1}{f_R}(p_m+p_d),\\ \rho _d= & {} \frac{1}{\kappa ^2}\left( \frac{1}{2}(Rf_R-f)-\frac{1}{2}\omega (\phi ){\dot{\phi }}^2-3H{\dot{f}}_{R}\right. \\&\quad -6H(2{\dot{H}}-3H^2){\dot{f}}_Y -f_Y(\dddot{H}+4H{\ddot{H}}\\&\quad \left. +6{\dot{H}}H^2-2H^4)-\frac{V(\phi )}{2}\right) ,\\ p_d= & {} \frac{1}{\kappa ^2}\left( \frac{1}{2}(f-Rf_R)\right. \\&\quad -\frac{1}{2}\omega (\phi ){\dot{\phi }}^2-\ddot{f}_R+2H{\dot{f}}_{R} +4H({\dot{H}}+3H^2){\dot{f}}_Y\\&\quad +f_Y(4\dddot{H}+20H{\ddot{H}}+10{\dot{H}}H^2+16{\dot{H}}^2-18H^4)\\&\quad \left. +\frac{V(\phi )}{2}\right) . \end{aligned}$$