1 Introduction

Intriguing and exciting at the same time. The dark side of the Universe, today constitutes one of the greatest challenges to be clarified for both theoretical and experimental physics. Undetectable by existing astronomical instruments, it is estimated within the background of the cosmological \(\varLambda \)CDM model, that the so-called dark matter (DM) represents the \(27\%\) of the total mass of our Universe [1, 2]. The first hint about the existence of this mysterious component comes from the rotational curve of spiral galaxies [3,4,5]. Among the possible alternatives to explain the main constituent and origin of dark matter, Neutralino has been proposed as the main candidate. This particle belongs to the lightest supersymmetric particles group [6,7,8]. Regarding the study of compact structures, such neutron stars and white dwarfs, in [9] was proposed a model consisting of DM, represented by standard model (SM) fermion gauge singlets based on a background composed by dark energy (DE), as predicted by pseudo complex general relativity. On the other hand, the mass–radius ratio for different DM profiles was investigated in [10] and the influences by spin polarized self-interacting DM have been explored by using a polytropic equation of state to build the structure of neutron stars [11, 12]. In further studies [13, 14], the gravitational effects of condensed DM on compact configurations were analyzed, as well as the existence of DM core inside neutron star [15].

In a more widely context, since the pioneering work by Bowers and Liang [16], the understanding of how this type of structureFootnote 1 works has been extensively explored. Furthermore, the usage of matter distributions with anisotropic content, has been strongly incorporated in the study of relativistic objects [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Besides, since the work carried out by Lake and Delgaty [38] proved, that only 9 of the 127 solutions known until 1998 (in spherical and isotropic coordinates and described by a perfect fluid \(p _{r}=p_{t}\)) were admissible from the physical point of view, there was a growing interest that lasts until today to further elucidate new aspects that local anisotropies introduce into a stellar interior [39,40,41,42,43,44,45,46,47,48,49] (and references contained therein). The inclusion of an anisotropic behaviour into the matter distribution driven collapsed structures such as neutron or quark stars, entails an intriguing and interesting features, for example: i) allows to build more compact structures, ii) the hydrostatic balance is enhanced by the introduction of a new term, that helps to counteract the gravitational collapse onto a point singularity (only if the anisotropy factor \(\varDelta \equiv p_{t}-p_{r}\) is positive defined everywhere), iii) the stability is also improved and iv) the gravitational surface red-shift \(z_{s}\) reaches greater values than its isotropic counterpart. Nevertheless, some questions arise, for example: how is the process to include local anisotropies into the stellar matter distribution? The physical admissibility of the resulting toy model depends on this mechanism? The resulting numerical data matches the experimental data? In principle the simplest way to introduce anisotropies into the stellar matter, is by the imposition of an energy–momentum tensor with different stresses in the principal directions of the fluid sphere ı.e, \(p_{r}\ne p_{t}\), or include an electromagnetic field, to name a few possibilities.

Incidentally, the gravitational decoupling (GD) by means of minimal geometric deformation (MGD), introduced in [50, 51] in the framework of general relativity (GR), results to be a natural manner to induce such modifications. In principle this methodology was employed in the context of Randall–Sundrum brane-world [52,53,54,55,56,57,58,59,60,61,62,63,64,65] and then spread to investigate new classes of black holes solutions, by deforming the well-known Schwarzschild space–time [54, 55]. The earlier applications of this approach were mainly developed on the stage of the brane-world [56,57,58,59,60,61,62,63,64,65], black hole acoustic [66] and GUP Hawking fermions [67]. After that, this scheme was translated into the GR arena to extent isotropic fluid distributions satisfying Einstein field equations, to an anisotropic domains [50, 51]. As we shall review in the next section, this methodology contains two main ingredients: i) two sources \({\bar{T}}_{\mu \nu }\) and \(\theta _{\mu \nu }\), which only interact gravitationally and ii) a minimal geometric deformation introduced in the \(g^{rr}\) component of the metric, which allows to decouple the system into two set of equations, one for each source. It is worth mentioning that in many applications of the GD, \({\bar{T}}_{\mu \nu }\) is the source of a well known isotropic interior solution, so the effect of \(\theta _{\mu \nu }\) is to introduce a local anisotropy behaviour in the system and consequently, it is said that GD leads to an extension of isotropic solutions to anisotropic scenarios. In this case, either the geometric deformation and the components of \(\theta _{\mu \nu }\) field remain unknown and the main goal is to provide suitable extra constraints which allow to find them. In this regard, a wide range of possibilities have been proposed, among which are: i) the so-called mimic constraint procedure [51, 66,67,68,69,70,71,72], ii) the imposition of an adequate decoupling function f(r) meeting all the physical and mathematical requirements [73, 74] or iii) some anisotropy mechanism [75, 76].

Depending on the mechanism considered to close the \(\theta \)-sector the magnitude and sign of the dimensionless coupling constant \(\alpha \) is determined in order to preserve a well defined anisotropy factor \(\varDelta \) throughout the stellar medium.

Given the versatility of GD by MGD, its application to deal with a variety of situations has grown considerably during the last 2 years [77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102], what is more the inverse problem and the extended case were developed in [103, 104], respectively. Despite the great versatility that GD through MGD has, there are some open question about the origin of the \(\theta _{\mu \nu }\) source. In this respect was argued in [77, 104] the possibility of interpreting the new field \(\theta _{\mu \nu }\) as dark matter, what is more in [96] were explored the contributions of this new sector in the well-known CDM and \(\varLambda \)CDM cosmological models. Based on this good antecedents, the main motivation of the present work, is to investigate the existence of dark stars within the framework of GR by using GD technology. In this concern, we have considered that the temporal component of the \(\theta \)-sector is mimicking the isothermal dark matter profile. Then the decoupler function f(r) carries the dark matter contribution into the deformed space–time and also into the remaining components of the energy–momentum tensor. Since, the isothermal dark matter profile is a monotonous decreasing function of the radial coordinate r, by choosing suitable parameters matching the observational data, the resulting toy model is admissible from the physical and mathematical point of view. To support all the analysis we have performed an exhaustive graphical study by using real observational data. Specifically, we have taken the mass and radius corresponding to the strange star candidates Her X-1 [105], SMC X-1 and LMC X-4 [106], where the seed space–time supporting this analysis is described by the well-known Tolman IV solution [107]. Besides, to provide a more realistic scenario, we have studied the impact of MGD on the total mass and compactness factor of the mentioned compact structures.

The article is organized as follows: Sect. 2 introduces the gravitational decoupling by means of minimal geometric deformation approach. Section 3 presents the model and all its properties. Section 4 deals with the junction conditions and Sect. 5 provides a detailed physical and mathematical analysis of the salient toy model. In Sect. 6 the hydrostatic balance and stability of the system are studied throughout the relativistic adiabatic index and pressure waves velocities criteria. Sections 7 and 8 studied the incident of MGD on some astrophysical properties of the structure and the generating function of the present model is obtained, respectively. Finally, Sect. 9 concludes the work.

Throughout the work, relativistic geometrized units \(c=G=1\) and the mostly negative signature \(\{+,-,-,-\}\) are employed.

2 Gravitational decoupling: a MGD approach

In this section we revisited the gravitational decoupling method by means of minimal geometric deformation (MGD). As was explained in Sect. 1, gravitational decoupling is separating one source from another by means of some mechanism that preserves geometrical properties of the original problem, where once the sources are separated, the respective conservation law for each committed entity is also satisfied. The fact that both sources are separately conserved, means that the interaction between them is of gravitational nature. The question is how to decouple the sources fulfilling the previous premises. To understand in detail the problem under study, consider a matter distribution, which represents a perfect or isotropic fluid described by the following energy–momentum tensor

$$\begin{aligned} {\bar{T}}_{\mu \nu }=\left( {\bar{\rho }}+{\bar{p}}\right) \chi _{\mu }\chi _{\nu }-{\bar{p}}g_{\mu \nu }, \end{aligned}$$
(1)

where \({\bar{\rho }}\) and \({\bar{p}}\) denote the isotropic density and pressure, respectively (throughout the text we shall employ barred quantities to refer the isotropic material content). Now, we extend the source given by Eq. (1) by adding the following source \(\theta _{\mu \nu }\) coupled via a dimensionless constant parameter \(\alpha \). Therefore one gets

$$\begin{aligned} {\bar{T}}_{\mu \nu }\rightarrow T_{\mu \nu }={\bar{T}}_{\mu \nu }+\alpha \theta _{\mu \nu }. \end{aligned}$$
(2)

This extra piece, introduces new ingredients which in principle are beyond GR. As it is well known GR covers a wide range of studies, including cosmological problems, solar system, black holes, neutron stars, or exotic structures such as wormholes. Regarding the study of neutron stars (including quark stars), it is common to assume that these compact objects possess spherical symmetry and are static. In mathematical language this means that they are represented by the next line element

$$\begin{aligned} ds^{2}=e^{\nu }dt^{2}-e^{\lambda }dr^{2}-r^{2}d\varOmega ^{2}, \end{aligned}$$
(3)

where in order to ensure the staticity of the above space–time one requires \(\nu =\nu (r)\) and \(\lambda =\lambda (r)\). Besides, in considering these ingredients the time-like 4-velocity has the following form \(\chi ^{\mu }=e^{-\nu /2}\delta ^{\mu }_{t}\). Now, suppose that a compact structure representing a neutron or quark star is described by Eqs. (1) and (3). Then, due to the isotropy of the matter content and the spherical symmetry of the space–time: \({\bar{p}}_{r}={\bar{p}}_{\phi }={\bar{p}}_{\varphi }={\bar{p}}\). On the other hand, if one considers (2) instead of (1), the new sector could introduce a different behaviour ı.e, \({p}_{r}\ne {p}_{\phi }={p}_{\varphi }\). So, an anisotropic behaviour arises into the system. The nature of this anisotropic conduct of the fluid distribution, strongly depends on the nature of the \(\theta _{\mu \nu }\) field. In this regard, \(\theta _{\mu \nu }\) could be a scalar, vector or tensor field, even more this could be seen as a dark field ı.e, dark matter o dark energy [77, 96, 104].

To decouple \({\bar{T}}_{\mu \nu }\) and \(\theta _{\mu \nu }\), it is convenient to see how these sources are linked with the geometry of the space–time. So, this relation is obtained by taking variation of the action

$$\begin{aligned} S=S_{E-H}+S_{\text {matter}} \end{aligned}$$
(4)

with respect to \(g^{\mu \nu }\). The Einstein–Hilbert (E–H) action is given by

$$\begin{aligned} S_{E-H}=\frac{1}{16\pi }\int \sqrt{-g}Rd^{4}x, \end{aligned}$$
(5)

where \(g\equiv det(g_{\mu \nu })\) is the determinant of the metric tensor \(g_{\mu \nu }\), R the Ricci’s scalar. The matter sector \(S_{\text {matter}}\) is described by

$$\begin{aligned} S_{\text {matter}}=\int \sqrt{-g}{\fancyscript{L}}_{\text {matter}}d^{4}x, \end{aligned}$$
(6)

being \({\fancyscript{L}}_{\text {matter}}\) the Lagrangian-density matter. In principle, this Lagrangian-density could contain different fields describing different kind of matter distributions. So, let us write \({\fancyscript{L}}_{\text {matter}}\) as

$$\begin{aligned} {\fancyscript{L}}_{\text {matter}}={\fancyscript{L}}_{{\bar{M}}}+\alpha {\fancyscript{L}}_{X}. \end{aligned}$$
(7)

The information on the isotropic fluid is encoded in the Lagrangian-density \({\fancyscript{L}}_{{\bar{M}}}\), while \({\fancyscript{L}}_{X}\) encipher the new matter fields. These new contributions can be seen as corrections to GR [104]. From the variational principle one gets the following field equations describing the gravitational–matter interaction

$$\begin{aligned} \frac{\delta S}{\delta g^{\mu \nu }}=0 \Rightarrow G_{\mu \nu }\equiv R_{\mu \nu }-\frac{R}{2}g_{\mu \nu }=-8\pi T_{\mu \nu }, \end{aligned}$$
(8)

where \(G_{\mu \nu }\) is the Einstein’s tensor and as before

$$\begin{aligned} T_{\mu \nu }=\underbrace{-2\frac{\delta {\fancyscript{L}}_{{\bar{M}}}}{\delta g^{\mu \nu }}+g_{\mu \nu }{\fancyscript{L}}_{{\bar{M}}}}_{{\bar{T}}_{\mu \nu }}+\alpha \underbrace{\left( -2\frac{\delta {\fancyscript{L}}_{X}}{\delta g^{\mu \nu }}+g_{\mu \nu }{\fancyscript{L}}_{X}\right) }_{\theta _{\mu \nu }}. \end{aligned}$$
(9)

An important consequence derived from contracted Bianchi’s identities together with Eq. (8) is

$$\begin{aligned} \nabla _{\mu }G^{\mu \nu }=0 \Rightarrow \nabla _{\mu }T^{\mu \nu }=0. \end{aligned}$$
(10)

So, covariant conservation of the stress–energy tensor is ensured. Taking into account Eq. (2) one has

$$\begin{aligned} \nabla _{\mu }T^{\mu \nu }=0\rightarrow \nabla _{\mu }{\bar{T}}^{\mu \nu }+\alpha \nabla _{\mu }\theta ^{\mu \nu }=0. \end{aligned}$$
(11)

Then, the equality is satisfied if both \(\nabla _{\mu }{\bar{T}}^{\mu \nu }\) and \(\nabla _{\mu }\theta ^{\mu \nu }\) are zero on the equations of motion, once the geometry and the material content have been specified. Next, Eqs. (1), (2), (3) and (8) reproduce the following set of equations

$$\begin{aligned}&{\mathrm{-e}^{-\lambda }}\left( {\frac{\lambda ^{{\prime }}}{r}}-\frac{1}{r^2}\right) -\frac{1}{r^2}=-\left( {\bar{\rho }}+\alpha \theta ^{t}_{t}\right) , \end{aligned}$$
(12)
$$\begin{aligned}&{\mathrm{e}^{-\lambda }} \left( {\frac{\nu ^{{\prime }}}{r}}+\frac{1}{r^2}\right) -\frac{1}{r^2}=-\left( -{\bar{p}}+\alpha \theta ^{r}_{r}\right) ,\end{aligned}$$
(13)
$$\begin{aligned}&\frac{\mathrm{e}^{-\lambda }}{4} \left( 2 \nu ^{{\prime \prime }}+\nu ^{\prime 2}+2{\frac{\nu ^{{\prime }}-\lambda ^{{\prime }}}{r}}-\nu ^{\prime }\lambda ^{\prime } \right) =-\left( -{\bar{p}}+\alpha \theta ^{\varphi }_{\varphi }\right) ,\nonumber \\ \end{aligned}$$
(14)

along with the following conservation equation

$$\begin{aligned} \begin{aligned}&-\frac{d{\bar{p}}}{dr}-\alpha \left[ \frac{\nu ^{\prime }}{2}\left( \theta ^{t}_{t}-\theta ^{r}_{r}\right) -\frac{d \theta ^{r}_{r}}{dr}+\frac{2}{r}\,(\theta ^{\varphi }_{\varphi }-\theta ^{r}_{r})\right] \\&\quad -\frac{\nu ^\prime }{2} ({\bar{\rho }}+{\bar{p}})=0. \end{aligned} \end{aligned}$$
(15)

At this point one can identify the effective amounts as follows

$$\begin{aligned} T^{t}_{t}= & {} {\bar{\rho }}+\alpha \theta ^{t}_{t}\equiv {\rho }, \end{aligned}$$
(16)
$$\begin{aligned} T^{r}_{r}= & {} {\bar{p}}-\alpha \theta ^{r}_{r}\equiv {p}_{r}, \end{aligned}$$
(17)
$$\begin{aligned} T^{\varphi }_{\varphi }= & {} {\bar{p}}-\alpha \theta ^{\varphi }_{\varphi }\equiv {p}_{t}. \end{aligned}$$
(18)

At this stage it is clear how the matter and geometry are involved. A simple and versatile mechanism to separate the sources is to deform the radial metric potential (or equivalently the mass function) as follows

$$\begin{aligned} e^{-\lambda (r)}\mapsto e^{-\lambda (r)}=\mu (r)+\alpha f(r). \end{aligned}$$
(19)

This linear map known as minimal geometric deformation (MGD) entails intriguing consequences. The MGD process means that only one metric potential is disturbed leaving the other one unaltered (in this case the temporal one). So, we summarize the main features of this minimal deformation process as follows

  • From Eq. (12) it is clear that the density depends only on the radial metric potential. So, the map (19) is the only possibility (as we will see soon) to separate \({\bar{T}}_{\mu \nu }\) and \(\theta _{\mu \nu }\). In this regard, performing only deformations on the temporal component is not feasible, unless the extended case be employed [104].

  • To preserve the spherical symmetry, the deformation or decoupler function f(r) is a purely radial function.

  • From the mathematical point of view, the behaviour of the decoupler function f(r) is controlled by the seed metric potential \(\mu (r)\), since \(\mu (r)\) is a monotonously increasing function in the interval [0, R] it does not matter if f(r) is positive (negative) or increasing (decreasing) function, what is really important is that its behaviour must be overcome by \(\mu (r)\), in order to preserve a well behaved stellar interior. Besides, f(r) must be null at \(r=0\) (the center of the object).

  • As \(\mu (r)\) is intimately related with mass the function m(r), the map (19) modifies the usual gravitational mass definition by introducing an extra piece. Hence,

    $$\begin{aligned} m(r)=\frac{r}{2}\left[ 1-\mu (r)-\alpha f(r)\right] , \end{aligned}$$
    (20)

    this can be accommodated as

    $$\begin{aligned} m(r)=m_{0}(r)-\alpha \frac{r}{2}f(r). \end{aligned}$$
    (21)

    Moreover, other associated quantities such as the compactness factor (mass–radius ratio) and gravitational surface red-shift \(z_{s}\) are disturbed by MGD. For example the mass–radius ratio takes the following form

    $$\begin{aligned} 2u(R)=2u_{0}(R)-\alpha f(R), \end{aligned}$$
    (22)

    where \(u_{0}=M_{0}/R\) is the seed compactness factor. It is clear that if \(\alpha <0\) and \(f(R)>0\) (or vice-versa) the mass of the system grows up, then gravitational decoupling by MGD allows an extra packing of mass [108].

Next, using (19) into the set of Eqs. (12)–(14) we arrive to

$$\begin{aligned} 8\pi {\bar{\rho }}= & {} \frac{1}{r^{2}}-\frac{\mu }{r^{2}}-\frac{\mu ^{\prime }}{r}\end{aligned}$$
(23)
$$\begin{aligned} 8\pi {\bar{p}}= & {} -\frac{1}{r^{2}}+\mu \left( \frac{1}{r^{2}}+\frac{\nu ^{\prime }}{r}\right) \end{aligned}$$
(24)
$$\begin{aligned} 8\pi {\bar{p}}= & {} \frac{\mu }{4}\left( 2\nu ^{\prime \prime }+\nu ^{\prime 2}+2\frac{\nu ^{\prime }}{r}\right) +\frac{\mu ^{\prime }}{4}\left( \nu ^{\prime }+\frac{2}{r}\right) , \end{aligned}$$
(25)

along with the conservation equation

$$\begin{aligned} {\bar{p}}^{\prime }+\frac{\nu ^{\prime }}{2}\left( {\bar{\rho }} +{\bar{p}}\right) =0, \end{aligned}$$
(26)

for the isotropic sector. Similarly, we have the following equations for the \(\theta \)-sector

$$\begin{aligned} 8\pi \theta ^{t}_{t}= & {} -\frac{f}{r^{2}}-\frac{f^{\prime }}{r} \end{aligned}$$
(27)
$$\begin{aligned} 8\pi \theta ^{r}_{r}= & {} -f\left( \frac{1}{r^{2}}+\frac{\nu ^{\prime }}{r}\right) \end{aligned}$$
(28)
$$\begin{aligned} 8\pi \theta ^{\varphi }_{\varphi }= & {} -\frac{f}{4}\left( 2\nu ^{\prime \prime }+\nu ^{\prime 2}+2\frac{\nu ^{\prime }}{r}\right) -\frac{f^{\prime }}{4}\left( \nu ^{\prime }+\frac{2}{r}\right) . \end{aligned}$$
(29)

The corresponding conservation equation \(\nabla ^{\nu }\theta _{\mu \nu }=0\) yields to

$$\begin{aligned} \left( \theta ^{r}_{r}\right) ^{\prime }-\frac{\nu ^{\prime }}{2}\left( \theta ^{t}_{t}-\theta ^{r}_{r}\right) -\frac{2}{r}\left( \theta ^{\varphi }_{\varphi }-\theta ^{r}_{r}\right) =0. \end{aligned}$$
(30)

The above expression (30) is a linear combination of the Eqs. (27)–(29). At this point some comments are in order. First, Eqs. (27)–(29) correspond to the so-called quasi Einstein field equations, in the sense that there is a missing factor \(\frac{1}{r^{2}}\). Second, it is clear that the interaction between the two sources is completely gravitational, since both are independently conserved as shown Eqs. (26) and (30). At this stage it is clear that the isotropic seed solution becomes anisotropic if and only if \(\theta ^{r}_{r}\ne \theta ^{\varphi }_{\varphi }\), being the measure of this anisotropic behavior

$$\begin{aligned} \varDelta (r;\alpha )\equiv \alpha \left( \theta ^{r}_{r}-\theta ^{\varphi }_{\varphi }\right) . \end{aligned}$$
(31)

It must be taken into account that a physically admissible model must meet \(\varDelta (r)>0\) for all \(r\in [0,R]\).

On the other hand, it should be noted that the seed system of equations (23)–(25) is already determined by the seed space–time. However, the set (27)–(29) is not closed. This new sector contains four unknown, namely \(\{\theta ^{t}_{t},\theta ^{r}_{r},\theta ^{\varphi }_{\varphi },f\}\) and three equations. Therefore, it is inevitable to prescribe information by hand. Nevertheless, this information must be physically consistent and relevant. In this regard, several procedures have been employed to close the \(\theta \)-sector, yielding in most cases to a well behaved interior solution. Among all the proposals the usual ones are: i) the so-called mimic constraint scheme [51, 68,69,70,71,72], ii) the imposition of a suitable decoupler function f(r) [73, 74, 90, 97] and iii) by using a regularity condition on the decoupler sector induced by the well-known Consenza–Herrera–Esculpi–Witten anisotropy condition [75, 76]. In this opportunity, the \(\theta \)-sector is closed in a different way. As pointed out in [104] and explored in the cosmological scenario [96], the unknown origin of the \(\theta _{\mu \nu }\) source, can be justified by assuming that this field is one of the dark components present in our Universe. Specifically, the \(\theta \)-source can be seen as dark matter. So, taking advantage of this situation, we have assumed that the temporal component of the \(\theta _{\mu \nu }\) field corresponds to a dark matter density profile. Concretely, we have placed \(\theta ^{t}_{t}=\rho _{PI}\) (for further details see next section), where \(\rho _{PI}\) means Pseudo Isothermal (PI) density profile, commonly used to model galactic dark matter halos in the context of modified gravity, such as Modified Newtonian Dynamics (MOND).

3 The model

In this section the model representing compact structures with dark matter component is presented. We start by revisiting the seed space–time used in this work, then in the next subsections, the dark matter sector and its thermodynamic and geometric description are provided as well as the salient modified space–time solution.

3.1 Revisiting in short: Tolman IV solution

As was pointed out above, the main point here is to extent spherically symmetric and static isotropic fluid spheres satisfying Einstein’s field equations, to an anisotropic domains by including some elements beyond GR. In this opportunity we have selected as a seed space–time, the well-known Tolman IV solution [107]. This toy model has been used to represent real astrophysical objects such as neutron and quark stars, driven by a perfect fluid matter distribution. This model is described by the following metric potentials

$$\begin{aligned} e^{\nu (r)}=B^{2}\left( 1+\frac{r^{2}}{A^{2}}\right) \quad \text{ and }\quad \mu (r)=\frac{\left( 1-\frac{r^{2}}{C^{2}}\right) \left( 1+\frac{r^{2}}{A^{2}}\right) }{1+2\frac{r^{2}}{A^{2}}},\nonumber \\ \end{aligned}$$
(32)

and thermodynamic variables

$$\begin{aligned} {\bar{\rho }}(r)= & {} \frac{3A^{4}+3A^{2}C^{2}+7A^{2}r^{2}+2C^{2}r^{2}+6r^{4}}{8\pi \left( A^{2}+2r^{2}\right) ^{2}C^{2}}, \end{aligned}$$
(33)
$$\begin{aligned} {\bar{p}}(r)= & {} \frac{C^{2}-A^{2}-3r^{2}}{8\pi \left( A^{2}+2r^{2}\right) C^{2}}. \end{aligned}$$
(34)

This solution satisfies Eqs. (20)–(22) ı.e, pure Einstein’s field equations (\(\alpha =0\)). It is worth mentioning that this model has been extended previously within the framework of MGD grasp [51], although by using a different approach to obtain the new sector. Specifically, the mimic constrain procedure.

3.2 Pseudo isothermal density profile

To close the \(\theta \)-sector, we have employed the PI dark matter density profile given by

$$\begin{aligned} \rho _{PI}=\frac{a}{1+\left( \frac{r}{b}\right) ^{2}}, \end{aligned}$$
(35)

where in studies related with dark matter halos and galaxies rotation curves [109, 110] the parameter a with units of \(\text {length}^{-2}\) denotes the finite central density and b with units of length represents the core radius. In our case these parameters will be taken as free parameters. The main motivation to use (35) concerns in the fact that \(\rho _{PI}\) is completely regular and monotonously decreasing function with increasing r within the interval [0, R] (see below for further details). So, equating Eqs. (27) and (35) one arrives at the following decoupler function

$$\begin{aligned} f(r)=\frac{8\pi ab^{2}}{r}\left[ b\text {Arctan}\left( \frac{r}{b}\right) -r\right] +\frac{D}{r}. \end{aligned}$$
(36)

In considering the map (19), the deformation function f(r) is conditioned by the seed metric potential \(\mu (r)\). So, in order to describe a well posed stellar interior from (36) we have the following restrictions: i) \(D=0\) to avoid singularities at the center of the structure and ii) since arc-tangent is smooth within the interval [0, R] we can expand in a series around to \(r=0\) to eliminate the singular behaviour. So, one gets

$$\begin{aligned} \text {Arctan}\left( \frac{r}{b}\right) \approx \frac{r}{b}-\frac{r^{3}}{3b^{3}}+\frac{r^{5}}{5b^{5}}+\text {O}(r^{7}). \end{aligned}$$
(37)

Then (36) becomes

$$\begin{aligned} f(r)= -\frac{8}{3}\pi ar^{2}+\frac{8}{5}\frac{\pi a}{b^{2}}r^{4}. \end{aligned}$$
(38)

Therefore, taking into account (35) and inserting (38) into Eqs. (28)–(29) the full \(\theta \)-sector is given by

$$\begin{aligned} \theta ^{t}_{t}= & {} \frac{a}{1+\left( \frac{r}{b}\right) ^{2}}, \end{aligned}$$
(39)
$$\begin{aligned} \theta ^{r}_{r}= & {} \frac{a\left( A^{2}+3r^{2}\right) \left( 5b^{2}-3r^{2}\right) }{15b^{2}\left( A^{2}+r^{2}\right) }, \end{aligned}$$
(40)
$$\begin{aligned} \theta ^{\varphi }_{\varphi }= & {} \frac{a\left( -15r^{6}-24A^{2}r^{4}-6A^{4}r^{2}+15b^{2}r^{4}+25A^{2}b^{2}r^{2}+5A^{4}b^{2}\right) }{15b^{2}\left( A^{2}+r^{2}\right) ^{2}},\nonumber \\ \end{aligned}$$
(41)

and from (31) the anisotropy factor reads

$$\begin{aligned} \varDelta (r;\alpha )=\alpha \frac{\left[ 3A^{4}+6r^{4}+A^{2}\left( 12r^{2}-5b^{2}\right) \right] }{15b^{2}\left( A^{2}+r^{2}\right) ^{2}}ar^{2}. \end{aligned}$$
(42)

Now, the minimally deformed Tolman IV space–time is expressed by

$$\begin{aligned} \begin{aligned} ds^{2}=B^{2}\left( 1+\frac{r^{2}}{A^{2}}\right) dt^{2}-\Bigg [\frac{\left( 1-\frac{r^{2}}{C^{2}}\right) \left( 1+\frac{r^{2}}{A^{2}}\right) }{1+2\frac{r^{2}}{A^{2}}}&\\ +8\alpha \pi ar^{2}\left( \frac{r^{2}}{5b^{2}}-\frac{1}{3}\right) \Bigg ]^{-1}dr^{2}-r^{2}d\varOmega ^{2}, \end{aligned} \end{aligned}$$
(43)

and its full thermodynamic description can be obtaining by putting together the expressions (16)–(18) along with (33)–(34) and (39)–(41). The principal physical and mathematical properties of the salient model will be analysed in the next sections.

Table 1 The numerical values of constant parameters A, B and C for a fixed a and different values of b and \(\alpha =0.25\)
Full size table
Fig. 1
figure 1

Upper row: the metric potentials trend (left panel) and the density (right panel) versus the dimensionless radial coordinate r/R. Lower row: the path of the radial and tangential pressures (left panel) and anisotropy factor (right panel) against the dimensionless radial variable r/R. These plots were constructed for different values mentioned in Tables 1 and 3 with \(\alpha =2.5\). It should be noted that, as we are working in relativistic geometrized units, the vertical axis has units of [km\(^{-2}]\) for density, pressures and anisotropy factor plots, while in the metric potential plot the vertical axis is dimensionless

Full size image

4 Israel–Darmois matching conditions

To be consistent, the toy model given by Eq. (43) must be joining in a smoothly way with the outer space–time. As this toy model is representing finite compact structures with a defined and confined matter distribution, it is necessary to imposed a limit at the boundary \(\varSigma :r=R\) of the object. In this concern, as our model does not contain neither electric charge and cosmological constant contributions, the exterior manifold \(\fancyscript{M^{+}}\) is well described by the vacuum Schwarzschild solution

$$\begin{aligned} ds^{2}=\left( 1-2\frac{M_{\text {Sch}}}{r}\right) dt^{2}-\left( 1-2\frac{M_{\text {Sch}}}{r}\right) ^{-1}dr^{2}-r^{2}d\varOmega ^{2}.\nonumber \\ \end{aligned}$$
(44)

The junction condition process allows to determine in a consistent way the full set of arbitrary parameters that characterize the model, in this case \(\{A,B,C\}\). To perform the matching conditions we shall employ the so-called Israel–Darmois (ID) [111, 112] grasp. So, the ID matching conditions invoke the continuity of the temporal \(g_{tt}\) and radial \(g_{rr}\) metric potentials (first fundamental form), across the boundary \(\varSigma \) of the structure between the inner manifold \(\fancyscript{M^{-}}\) (43) and the outer space–time \(\fancyscript{M^{+}}\) (44). Explicitly it reads

$$\begin{aligned} g^{-}_{tt}\bigg |_{r=R}=g^{+}_{tt}\bigg |_{r=R} \quad \text{ and } \quad g^{-}_{rr}\bigg |_{r=R}=g^{+}_{rr}\bigg |_{r=R}. \end{aligned}$$
(45)

For the present situation we have

$$\begin{aligned}&B^{2}\left( 1+\frac{R^{2}}{A^{2}}\right) =1-2\frac{M}{R}, \end{aligned}$$
(46)
$$\begin{aligned}&\frac{\left( 1-\frac{R^{2}}{C^{2}}\right) \left( 1+\frac{R^{2}}{A^{2}}\right) }{1+2\frac{R^{2}}{A^{2}}}\nonumber \\&\quad +8\alpha \pi aR^{2}\left( \frac{R^{2}}{5b^{2}}-\frac{1}{3}\right) =1-2\frac{M}{R}, \end{aligned}$$
(47)

where the Schwarzschild mass \(M_{\text {Sch}}\) coincides at \(\varSigma \) with the total mass M contained by the fluid sphere. On the other hand, the inner \(g^{-}_{\mu \nu }\) and outer \(g^{+}_{\mu \nu }\) metric tensors induce on \(\varSigma \) an intrinsic geometry described by a symmetric tensor \(K_{ij}\) (the extrinsic curvature tensor). The continuity of the radial component \(K_{rr}\) across \(r=R\) (second fundamental form), assures a vanishing radial pressure

$$\begin{aligned} p_{r}(R)={\bar{p}}(R)-\alpha \theta ^{r}_{r}(R)=0. \end{aligned}$$
(48)

This condition determines the size of the compact structure and confines the matter distribution within a finite region: \(0\le r\le R\). The continuity of the angular components \(K_{\phi \phi }\) and \(K_{\varphi \varphi }\) fix the total mass inside the star

$$\begin{aligned} \left[ K^{-}_{\phi \phi }-K^{+}_{\phi \phi }\right] \bigg |_{\varSigma }=\left[ K^{-}_{\varphi \varphi }-K^{+}_{\varphi \varphi }\right] \bigg |_{\varSigma }=0\nonumber \\ \Rightarrow m(R)=M. \end{aligned}$$
(49)

It should be noted that, in principle the outer manifold could be altered by the \(\theta \)-source. In that case the exterior space–time is no longer vacuum, then Schwarzschild solution is not valid to join the inner geometry at the surface with the outer manifold. Nevertheless, in the simplest case, the \(\theta _{\mu \nu }\) contributions to the exterior space–time can be suppressed [51]. Therefore, one ends with a stellar interior embedded into a vacuum space–time which geometry is given by the Schwarzschild solution. In table 1 are exhibited the numerical values by the space parameter \(\{A,B,C\}\). These values were obtained by fixing \(\alpha =0.25\), \(a=0.0004 [\text {km}^{-2}]\) and different choices of b.

5 Physical and mathematical study

In this section we analyze in details the physical and mathematical properties of the main salient variables that characterize the model. To do this, we shall follow the usual analysis presented in [29, 33]. So, the first point is to analyze the inner geometry. In the present case the stellar interior is well described by the following metric potentials

$$\begin{aligned} e^{\nu (r)}= & {} B^{2}\left( 1+\frac{r^{2}}{A^{2}}\right) , \end{aligned}$$
(50)
$$\begin{aligned} e^{\lambda (r)}= & {} \left[ \frac{\left( 1-\frac{r^{2}}{C^{2}}\right) \left( 1+\frac{r^{2}}{A^{2}}\right) }{1+2\frac{r^{2}}{A^{2}}} +8\alpha \pi ar^{2}\left( \frac{r^{2}}{5b^{2}}-\frac{1}{3}\right) \right] ^{-1}.\nonumber \\ \end{aligned}$$
(51)

From the space–time represented by Eqs. (50) and (51), can be highlighted the following characteristics

  • Both, \(e^{\nu }\) and \(e^{\lambda }\) are completely regular at all points within the stellar interior. Specifically, for all \(r\in [0,R]\).

  • At \(r=0\) (the center of the star), (50) leads to \(e^{\nu (0)}=B^{2}\) and (51) to \(e^{\lambda (0)}=1\). These conditions say that the minimum value for each metric potential, is attained at center of the structure. Besides, this minimum is positive, then from \(r=0\) to \(r=R\) the metric potentials are strictly and monotonous increasing functions from the center towards the boundary.

  • Regarding the previous comment, this is exactly the appropriate behavior that \(e^{\lambda }\) must have, since it is connected with the mass function m(r) and density \(\rho (r)\) of the fluid distribution.

As can be seen from the upper left panel in Fig. 1, the mentioned information about the behaviour of the metric potentials \(e^{\nu }\) and \(e^{\lambda }\) is corroborated. This plot was built by using the numerical data listed in Tables 1 and 3 . It is remarkable to note that the metric potential \(e^{\lambda }\) corresponding to most massive star (blue curve), takes greater values in comparison with the other compact structures. This is so because as was mentioned the radial metric potential is involved with the mass of the configuration.

Connected with the geometry of the space–time, we have the thermodynamic variables \(\{\rho ,p_{r},p_{t}\}\) defining the energy–momentum tensor associated with the anisotropic matter distribution. To represent an anisotropic content, filling the interior of a compact object, these variables must satisfy some requirements. First, they must have their maximum values attained at the center of the structure. This implies that all these physical quantities, are monotonous decreasing functions with increasing radial coordinate r throughout the stellar interior. Second, they must be positive defined for all \(r\in [0,R]\), in order to avert non-physical behaviour of the material content. Additionally, it is required for the radial and tangential pressures: \(p_{t}>p_{r} \Rightarrow \varDelta >0\). This condition assures a healthy stellar interior, what is more a positive anisotropy factor in principle enhances the stability and hydrostatic equilibrium of the structure (see below for further details). Furthermore, a peremptory condition to be satisfied by the radial pressure is \(p_{r}(R)=0\), determining the size of the object. However, the above constraint does not need to be satisfied by tangential pressure.

Therefore, to satisfy the above criteria, it is important to analyze the restrictions that the parameters \(\{A,B,C,a,b,\alpha \}\) should obey. So, evaluating the density \(\rho \) and the radial pressure \(p_{r}\) (due to the spherical symmetry one has \(p_{t}(0)=p_{r}(0)\)) at the center, one obtains the following conditions

$$\begin{aligned} p_{r}(0)> & {} 0 \Rightarrow a<\frac{3}{8\pi \alpha }\left( \frac{1}{A^{2}}-\frac{1}{C^{2}}\right) , \end{aligned}$$
(52)
$$\begin{aligned} \frac{p_{r}(0)}{\rho (0)}\le & {} 1\Rightarrow a\ge -\frac{3\left( 2A^{2}+C^{2}\right) }{16\pi A^{2}C^{2}\alpha }, \end{aligned}$$
(53)
$$\begin{aligned} \rho (0)> & {} 0\Rightarrow a>-\frac{3\left( A^{2}+C^{2}\right) }{8\pi A^{2}C^{2}\alpha }. \end{aligned}$$
(54)

Moreover, as \(\rho \) must be a monotonous decreasing function for all \(r\in [0,R]\), then we have

$$\begin{aligned} \frac{d\rho }{dr}=\frac{d{\bar{\rho }}}{dr}+\alpha \frac{d\theta ^{t}_{t}}{dr}<0, \end{aligned}$$
(55)

but the seed density \({\bar{\rho }}\) is already decreasing within the interval \(0\le r\le R\). Therefore, to ensure (55) we need to analyze the behaviour of the \(\theta ^{t}_{t}\) component and the sign of \(\alpha \) parameter. In this concern, we mention the following possibilities (some of them)

  • \(\alpha >0\) & \(\theta ^{t}_{t}\) positive and decreasing: in this case the left hand side of (55) is satisfied.

  • \(\alpha <0\) & \(\theta ^{t}_{t}\) positive and increasing: in this case the term \(\alpha \theta ^{t}_{t}\) in (55) becomes negative and decreasing, then, it must be less than \({\bar{\rho }}\) in magnitude, to preserve a positive defined and decreasing density \(\rho \).

  • \(\alpha >0\) & \(\theta ^{t}_{t}\) positive and increasing: this case is similar to the previous one.

The same criteria applies for \(\theta ^{r}_{r}\) and \(\theta ^{\varphi }_{\varphi }\). So, in this particular case \(\theta ^{t}_{t}\) given by (39), will be decreasing and positive defined iff \(a>0\). This yields from (52) to \(C>A\), what is more the equality in (53) is discarded. Furthermore, \(\alpha \) should be strictly positive, hence (55) is satisfied. Despite \(\alpha \) could take negative values, this situation is ruled out by Eq. (42). This is so because \(\alpha \) is an overall factor and \(3A^{4}+6r^{4}+12A^{2}r^{2}>5A^{2}b^{2}\) in order to guarantee \(\varDelta (r)>0\) everywhere.

Table 2 The numerical values for central and surface density, central pressure, critical adiabatic index and central adiabatic index for different values listed in Table 1 and \(\alpha =0.25\)
Full size table
Fig. 2
figure 2

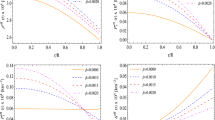
Left panel: the path of the strong energy condition versus the dimensionless quantity r/R. Middle panel: the behaviour of the dominant energy condition against the dimensionless coordinate r/R. Right panel: the sound speed velocities of the pressure waves versus r/R. These plots were built for different values mentioned in Tables 1 and 3 with \(\alpha =2.5\). It should be noted that, as we are working in relativistic geometrized units, the vertical axis has units of [km\(^{-2}]\) for SEC and DEC, while for the sound speeds plot the vertical axis is dimensionless

Full size image

As it is depicted in Fig. 1, the density \(\rho \) (upper right panel), radial \(p_{r}\) and tangential \(p_{t}\) pressures (lower left panel) are in complete agreement with the mentioned requirements. Besides, the most massive object (LMC X-4) has a denser core and reaches high central pressure with respect to the other compact structures ı.e, Her X-1 and SMC X-1. In considering the anisotropy factor \(\varDelta \), from the expression (42) and the lower right panel in Fig. 1 one can see that this quantity is null at \(r=0\) and reaches its maximum value at \(r=R\). This fact allows to build more compact structures [26]. Table 2 collects the central density \(\rho (0)\), surface density \(\rho (R)\) and central pressure \(p_{r}(0)\). As can be seen, the order of magnitude of these quantities are within the range of previous studies that suggest that a central density beyond the nuclear density saturation (\(\sim 2.4\times 10^{14}[\text {g}/\text {cm}^{3}]\)) corresponds to compact configurations made of strange quark matter [113].

However, the matter distribution must meet some additional restrictions that confirm its viability to describe a stellar interior. Those are: i) positive and well behaved energy–momentum tensor and ii) preservation of causality condition. Of course, both requirements are related. Regarding the first one, a well defined energy–momentum tensor should meet the following inequalities [114]:

  1. 1.

    (NEC): \(\rho \ge 0\),

  2. 2.

    (WEC): \(\rho +p_{t}\ge 0\), \(\rho +p_{r}\ge 0\),

  3. 3.

    (SEC): \(\rho +2p_{t}+p_{r}\ge 0\),

  4. 4.

    (DEC): \(\rho -|p_{r}|\ge 0\), \(\rho -|p_{t}|\ge 0\).

These conditions are known as energy conditions. The null energy condition (NEC) says that the observed density must be positive defined everywhere, the weak energy condition (WEC) means that the matter distribution can not travel faster than the speed of light neither in the radial or tangential directions (for further details see below). The strong (SEC) and dominant (DEC) energy conditions imply the NEC and WEC. So, if SEC an DEC are satisfied, the energy–momentum tensor describing the matter distribution driven the stellar interior is well defined. From Fig. 2 (left and middle panels) it is clear that SEC and DEC are satisfied at all points, thus the stellar interior is threading by a well defined and positive energy–momentum tensor. On the other hand, the pressure waves of the matter distribution must respect the so-called causality condition. When the fluid distribution contains anisotropies, causality condition dictates

$$\begin{aligned} 0\le v^{2}_{r}=\frac{dp_{r}}{d\rho }\le 1 \quad \text{ and } \quad 0\le v^{2}_{t}=\frac{dp_{t}}{d\rho }\le 1. \end{aligned}$$
(56)

The above inequalities tell to us that any signal cannot exceed the speed of light \(c=1\). From the right panel in Fig. 2, causality condition is preserved along the principal directions of the fluid sphere.

6 Hydrostatic balance and stability

In the simplest scenario ı.e, a perfect fluid matter distribution. The hydrostatic balance of the system is subject to the gravitational and hydrostatic gradients. Nevertheless, when new ingredients are added to the material content, they contribute to the equilibrium mechanism. In this opportunity the configuration is under the action of gravitational \(F_{g}\), hydrostatic \(F_{h}\) and anisotropy \(F_{a}\) gradients. If the structure is in equilibrium, the mentioned gradients must satisfy

$$\begin{aligned} F_{h}+F_{a}+F_{g}=0, \end{aligned}$$
(57)

or in terms of the main physical variables

$$\begin{aligned} \begin{aligned}&-\frac{d{\bar{p}}}{dr}-\alpha \left[ \frac{\nu ^{\prime }}{2}\left( \theta ^{t}_{t}-\theta ^{r}_{r}\right) -\frac{d \theta ^{r}_{r}}{dr}+\frac{2}{r}\,(\theta ^{\varphi }_{\varphi }-\theta ^{r}_{r})\right]&\\&\quad -\frac{\nu ^\prime }{2} ({\bar{\rho }}+{\bar{p}})=0. \end{aligned} \end{aligned}$$
(58)

Equation (58) is just the conservation equation (15). As this point some comments are in order. First, if \(\alpha =0\) one recovers the usual Tolman–Oppenheimer–Volkoff equation [107, 118] driven the hydrostatic balance of compact isotropic fluid spheres. Second, despite that in the \(\theta \)-system (27)–(29) there is a missing term \(1/r^{2}\), the \(\theta _{\mu \nu }\) contribution to Eq. (58) coincides with relativistic hydrostatic balance equation when the matter distribution contains anisotropies. In this respect, one can identify inside the bracket, that the first term is just the gravitational gradient, the second one the hydrostatic gradient and the third one the anisotropic gradient. In general, one can combine the first term in (58) with the second term within the bracket and form an effective hydrostatic gradient, the same with the last term and the first one in the bracket, constitute the gravitational gradient. Finally, the third term in the bracket constitutes the main ingredient of gravitational decoupling by MGD ı.e, extent an isotropic fluid to anisotropic domains. In this case, this new piece incorporates a positive anisotropy factor \(\varDelta \), then the associated anisotropy gradient \(F_{a}\) is repulsive in nature. This repulsive gradient helps to counteract the gravitational one. Besides, the presence of this anisotropic repulsive gradient, avoids the gravitational collapse of the structure onto a point singularity. In Fig. 3 is shown the balance of the system for all cases. As it is appreciated, the system is in hydrostatic equilibrium under the mentioned gradients.

On the other hand, it remains to be determined whether the hydrostatic equilibrium is stable or unstable. Among all the possibilities at hand to check stability against the presence of local anisotropies (at least from the theoretical point of view), we shall employ two of the most common. Those are: i) the relativistic adiabatic index \(\Gamma \) and ii) the criterion based on the velocities of the fluid pressure waves (also known as Abreu et al. criterion [34]).

Fig. 3
figure 3

The trend of the hydrostatic \(F_{h}\), gravitational \(F_{g}\) and anisotropic \(F_{a}\) gradients for each strange star candidate. These plots were built for different values mentioned in Tables 1 and 3 with \(\alpha =2.5\). It should be noted that, as we are working in relativistic geometrized units, the vertical axis has units of [km\(^{-3}]\) for all panels

Full size image
Fig. 4
figure 4

Left panel: the relativistic adiabatic index path against the dimensionless radial coordinate r/R. Middle panel: the different of the squared sound velocities versus the dimensionless radial coordinate r/R. Right panel: Abreu’s stability factor versus r/R. These plots were built for different values mentioned in Tables 1 and 3 with \(\alpha =2.5\). It should be noted that, as we are working in relativistic geometrized units, the vertical axis is dimensionless for all panels

Full size image

To understand how the relativistic adiabatic index works, it is necessary to compare with its Newtonian counterpart. In this concern, in the Newtonian scenario and considering an isotropic fluid distribution, the stability condition is \(\Gamma >4/3\) [17, 23]. Nevertheless, in the relativistic scenario with local anisotropies, the situation is quite different. Local anisotropies within the matter distribution introduce drastic changes on the stability condition [24, 25]. Under this situation the stability condition shifts

$$\begin{aligned} \Gamma >\frac{4}{3}+\left[ \frac{1}{3}\kappa \frac{\rho _{0}p_{r0}}{|p^{\prime }_{r0}|}r+\frac{4}{3}\frac{\left( p_{t0}-p_{r0}\right) }{|p^{\prime }_{r0}|r}\right] _{max} \end{aligned}$$
(59)

representing \(\rho _{0}\), \(p_{r0}\) and \(p_{t0}\) the initial density, radial and tangential pressure when the matter distribution is in static equilibrium. The terms enclosed in the bracket, are representing the relativistic corrections and the contributions coming from the local anisotropies. Although in principle local anisotropies into the stellar interior can be seen as a stabilizer mechanism, Chandrasekhar pointed out [115, 116] that relativistic corrections to the adiabatic index \(\Gamma \) could introduce some instabilities within the matter distribution. To overcome this issue in [117] was proposed a new condition on the relativistic adiabatic index \(\Gamma \). In general, the restriction is based on the critical relativistic adiabatic index \(\Gamma _{\text {crit}}\). The value of this critical quantity, depends on the amplitude of the Lagrangian displacement from equilibrium and the compactness factor \(u\equiv M/R\). The amplitude of the Lagrangian displacement is controlled by the parameter \(\xi \), so taking a particular form of this parameter, the critical relativistic adiabatic index is given by

$$\begin{aligned} \Gamma _{\text {crit}}=\frac{4}{3}+\frac{19}{21}u, \end{aligned}$$
(60)

being the stability condition \(\Gamma \ge \Gamma _{\text {crit}}\), where \(\Gamma \) is computed from [22]

$$\begin{aligned} \Gamma =\frac{\rho +p_{r}}{p_{r}}\frac{dp_{r}}{d\rho }. \end{aligned}$$
(61)

From the left panel of Fig. 4 it is appreciated that in all cases the relativistic adiabatic index \(\Gamma \) is greater than 4/3. Commonly, it is assumed that when \(\Gamma >4/3\) at \(r=0\) the system is stable under this criterion. Nevertheless, as was discussed earlier, an accurate analysis dictates \(\Gamma \ge \Gamma _{\text {crit}}\) at \(r=0\). In Table 2 on the fifth and sixth columns are displayed the corresponding values for \(\Gamma \) and \(\Gamma _{\text {crit}}\) for each considered compact structure. As can be seen, for LMC X-4 the above constraint is not satisfied, then under this criterion this compact star representing by the space–time (43) is not stable.

On the other hand, we have also checked the stability of the compact object by using the sound speed criteria. Abreu and his collaborators [34] determined a way to check the presence of stable/unstable regions within the stellar interior, when local anisotropies are there. Varying the anisotropy factor \(\varDelta \) with respect to the density \(\rho \), one gets

$$\begin{aligned} \frac{\delta {\varDelta }}{\delta {\rho }}\sim \frac{\delta \left( {p}_{t}-{p}_{r}\right) }{\delta {\rho }} \sim \frac{\delta {p}_{t}}{\delta {\rho }}-\frac{\delta {p}_{r}}{\delta {\rho }}\sim v^{2}_{t}-v^{2}_r. \end{aligned}$$
(62)

As both \(v^{2}_{r}\) and \(v^{2}_{t}\) are constrained by causality condition \(0\le v^{2}_{r}\le 1\) and \(0\le v^{2}_{t}\le 1\), this implies \(0\le |v^{2}_{t}-v^{2}_{r}|\le 1\). This can be re-expressed as follows

$$\begin{aligned} \begin{aligned} -1\le v^{2}_{t}-v^{2}_{r}\le 1&\\ = \left\{ \begin{array}{ll} -1\le v^{2}_{t}-v^{2}_{r}\le 0~~ &{} \mathrm {Potentially\ stable\ } \\ 0< v^{2}_{t}-v^{2}_{r}\le 1 ~~ &{} \mathrm {Potentially\ unstable} \end{array} \right\} . \end{aligned} \end{aligned}$$
(63)

Therefore, the compact structure will be stable under radial perturbations induced by local anisotropies, if the subliminal radial \(v^{2}_{r}\) sound speed of the pressure waves dominates everywhere the subliminal sound velocity of the pressure waves in the transverse direction \(v^{2}_{t}\). For the present model it is corroborated from the right panel in Fig. 2, where \(v^{2}_{r}>v^{2}_{t}\), what is more from Fig. 4 (middle and right panels), the difference of the square pressure waves velocities lies between − 1 and 0 and the absolute value of this quantity between 0 and 1. Then all the regions inside the compact configuration are stable under this criteria.

Table 3 The numerical values for the total mass and compactness factor considering the MGD contribution for parameters mentioned in table 1 and \(\alpha =0.25\)
Full size table

7 Macro physical parameters: some implications induced by MGD

As was discussed in Sect. 2, GD by MGD translates the matter distribution beyond to the perfect fluid behaviour. Furthermore, this mechanism modifies the geometry and the gravitational mass function, in such a way that the original symmetry of the seed space–time is preserved. Remembering that for any spherically symmetric configuration the mass function is obtained by

$$\begin{aligned} m(r)=4\pi \int ^{r}_{0}\rho (x)x^{2}dx=4\pi \int ^{r}_{0}\left[ {\bar{\rho }}(x)+\alpha \theta ^{t}_{t}(x)\right] x^{2}dx,\nonumber \\ \end{aligned}$$
(64)

or equivalently

$$\begin{aligned} m(r)=\frac{r}{2}\left[ 1-e^{-\lambda (r)}\right] =\frac{r}{2}\left[ 1-\mu (r)-\alpha f(r)\right] . \end{aligned}$$
(65)

Then, the total mass is refereed at \(r=R\) and given by

$$\begin{aligned} m(R)=M=\frac{R}{2}\left[ 1-\mu (R)\right] -\alpha \frac{R}{2}f(R), \end{aligned}$$
(66)

where the first term in the r.h.s of (66) is just the total gravitational mass definition within the context of GR. Then (66) can written as

$$\begin{aligned} M=M_{0}-\alpha \frac{R}{2}f(R), \end{aligned}$$
(67)

being \(M_{0}\) the GR mass. Now from (67) the compactness factor u reads

$$\begin{aligned} 2u=2u_{0}-\alpha f(R). \end{aligned}$$
(68)

At this stage some comments are pertinent

  • It is clear that the total original mass \(M_{0}\) increases if the second term in the right member of (67) is positive. The same occurs with the compactness parameter \(u_{0}\) in (68). So, an extra packing of mass is possible within the context of GD by MGD [108]. In this regard, the extra packing of mass has been already studied by considering that the matter field is affected by the Kalb–Ramond field [119]. However, the main different between this approach and the present one is that the outer space–time is affected by Kalb–Ramond field, indistinct with what happens in GD by MGD, where the \(\theta _{\mu \nu }\) contributions can be suppressed [51]. Then the outer manifold still is described by a vacuum space–time.

  • In considering the modified compactness factor u. It can be appreciated that GR+MGD allows more compact structures than in the pure GR picture. As it is well-known, in the case of isotropic fluid distributions u respects the Buchdahl limit [120] ı.e, \(u\le \frac{4}{9}\). However, in this situation this upper limit could be overcome, being the new upper bound the black hole one \(u=1/2\). Moreover, the compactness factor acquires a lower bound [108]. Of course all these things depend on the choice made on \(\alpha \) and \(u_{0}\).

  • The fact that the compactness is shifted by an amount \(\alpha f(R)\), implies that the surface gravitational red-shift \(z_{s}\) is modified. Indeed, \(z_{s}\) now reads

    $$\begin{aligned} z_{s}=\left[ 1-2u_{0}+\alpha f(R)\right] ^{-1/2}-1. \end{aligned}$$
    (69)

    Of course, from the astrophysical point of view this is a very interesting consequence.

On the other hand, we want to clarify how junction conditions work after (67). So, in previous studies [51, 68,69,70,71,72,73,74, 90, 95, 97] concerning stellar interiors, to close the matching condition set of equation, the mass M and R radius of the object were set taking some real observational data, like in this work. Mathematically this is correct, but in that way the MGD contributions are hidden. Then it is not clear at all, how this technology incises on the total mass and compactness factor. What is more, the masses of these real objects were obtained within the framework of GR without considering any extra field or modification, neither on the material sector or gravitational sector. The right step is to assume that this real data correspond only to \(M_{0}\). Respect to the radius R, it can be considered as the original one, if one wants to study the extra packing of mass, otherwise it should be obtained for example, from the second fundamental form (48), where are present the \(\theta \)-sector contributions. Nevertheless, unless the problem be solved numerically, it is unavoidable to fix by hand some constant parameters to match the observational reports. In the present case the total mass is obtained by using Eqs. (38) and (67) as follows

$$\begin{aligned} M=M_{0}+4\pi \alpha a R^{3}\left[ \frac{1}{3}-\frac{R^{2}}{5b^{2}}\right] , \end{aligned}$$
(70)

where b should satisfy the following constraint

$$\begin{aligned} b>\sqrt{\frac{3}{5}}R. \end{aligned}$$
(71)

As can be seen from (70) \(\alpha \) and a should have the same sign to preserve in conjunction with (71) \(M>M_{0}>0\). Remembering the previous discussion both \(\alpha \) and a must be positive defined quantities. In Tables 3 and 4 are presented the numerical values of the total mass, compactness factor and surface gravitational red-shift for each strange star candidate in both scenarios: pure GR and GR+MGD. Moreover, the trend of these observables is illustrated in the Fig. 5. All this information fits the GR results, however the GD by means of MGD offers interesting modifications on the main salient features of the model when the matter distribution goes beyond the perfect fluid situation.

Table 4 The numerical data of surface gravitational red-shift
Full size table
Fig. 5
figure 5

Left panel: the mass function trend against the dimensionless radial coordinate r/R. Middle panel: the compactness factor versus the dimensionless radial coordinate r/R. Right panel: the gravitational surface red-shift versus r/R. These plots were built for different values mentioned in Table 1 with \(\alpha =2.5\). It should be noted that, as we are working in relativistic geometrized units, the vertical axis is dimensionless for all panels

Full size image

8 The generating function

It has been demonstrated that all spherically symmetric and static isotropic solutions of the Einstein’s field equations, can be generated by choosing a single monotone function subject to the boundary conditions [121]. In a broader context Herrera et al. [122] extended the previous work to include a more realistic and complete component ı.e, local anisotropies into the matter distribution. They concluded that all spherically symmetric static anisotropic solutions of the Einstein’s field equations can be generated from two generating functions \(\zeta (r)\) and \(\varPi (r)\). The generator \(\zeta (r)\) linked with the metric potential \(e^{\nu }\) and other with the negative of pressure anisotropy \(\varDelta (r)\). These generators are defined via

$$\begin{aligned} e^{2\nu (r)}= & {} \text {Exp}\left[ \int \left( 2\zeta (r)-\frac{2}{r}\right) dr\right] , \end{aligned}$$
(72)
$$\begin{aligned} \varPi (r)= & {} p_{r}(r)-p_{t}(r)=-\varDelta (r). \end{aligned}$$
(73)

So, from (72) solving for the generator \(\zeta (r)\) one gets

$$\begin{aligned} \zeta (r)=\nu ^{\prime }(r)+\frac{1}{r}, \end{aligned}$$
(74)

where by virtue of (50) one gets

$$\begin{aligned} \zeta (r)=\frac{2r}{A^{2}+r^{2}}+\frac{1}{r}, \end{aligned}$$
(75)

and the second generator expressed by (73) is given by

$$\begin{aligned} \varPi (r)=\alpha \frac{\left[ 3A^{4}+6r^{4}+A^{2}\left( 12r^{2}-5b^{2}\right) \right] }{15b^{2}\left( A^{2}+r^{2}\right) ^{2}}ar^{2}, \end{aligned}$$
(76)

where Eq. (42) was employed. As can be seen, the second generator (73) is naturally induced by MGD. Besides, if \(\alpha =0\), then the results reporting in [121] are recovered.

9 Conclusions and remarks

In this work, it is provided an analytic anisotropic fluid sphere, whose space–time is represented by the minimally deformed Tolman IV isotropic solution. To introduce the anisotropic behaviour into the matter distribution, we have employed gravitational decoupling via minimal geometric deformation approach. Where the temporal component of the extra source \(\theta _{\mu \nu }\) is mimicking the isothermal dark matter density profile. This allows to close the \(\theta \)-system of equations, to obtain the decoupler function f(r). To check the feasibility of the resulting thermodynamic variables (33)–(34) and (39)–(41) along with the minimally deformed inner geometry (43) describing the stellar interior, we have performed an exhaustive physical, mathematical and graphical analysis. The trend of the most important physical quantities is depicted in Figs. 1, 2, 3 and 4. As it is observed, these plots corroborate the physical viability of this toy model to describe realistic collapsed configurations such as neutron or quark stars. This first conclusion, is supported by Tables 1, 2 and 3, where the obtained numerical data for the central density, surface density, central pressure, mass and compactness factor matches the reported experimental data for this kind of structures. It is worth mentioning that real observational data corresponding to the strange star candidates Her X-1, SMC X-1 and LCM X-4 was employed to determine the arbitrary constant parameters \(\{A,B,C\}\) that characterize the model.

As gravitational decoupling by means of minimal geometric deformation scheme translates isotropic fluid distributions to anisotropic domains, we have analyzed the impact that these local anisotropies introduce on the hydrostatic balance and stability of the system. Furthermore, we have studied the influences on the total mass, compactness factor and surface gravitational red-shift. In considering the hydrostatic equilibrium and stability mechanism, the MGD grasp introduces a new gradient that helps to counteract the gravitational action. Specifically, this corresponds to the anisotropic gradient. To check the reliability of the hydrostatic balance, that is, to verify if it is stable or unstable, stability mechanisms are an indispensable tool in this task. In this occasion, the criteria of the relativistic adiabatic index and the subliminal sound speeds of the pressure waves have been used. It is found that the system is completely stable under the analysis of these criteria, except in one case corresponding to the strange star candidate LMC X-4 where the central adiabatic index is less (in a small amount) than the critical value.

To close the work, it is important to highlight the influence that MGD has on the total mass M and compactness factor \(u=M/R\) of the salient model. In this regard, both quantities are increased, modifying related quantities such as the surface gravitational red-shift \(z_{s}\). These modifications are important from the physical and astrophysical point of view. This is so because when an isotropic matter distribution is extended to an anisotropic scenario by MGD grasp, it is possible the extra packing of mass. Then, objects become more massive and dense. The affection on the mentioned quantities alter the surface gravitational red-shift. This observable plays a relevant role from the astrophysical point of view, since by measuring it many properties can be elucidated when celestial bodies are observed.