1 Introduction

Bañados, Silk and West (BSW) [1] demonstrated some years ago that two particles colliding near the degenerate horizon of an extreme Kerr black hole could create a large center of mass (CM) energy if one of the particles has a critical angular momentum; thus, extreme Kerr black holes can act as natural particle accelerators. Nowadays, this process is known as the BSW mechanism, which was found for the first time by Piran, Shaham and Katz in 1975 [2,3,4]. Then, based on the infinite acceleration being able to occur not only for extremal black holes but also for non-extremal ones [5], it was shown that an infinite energy in the CM frame of colliding particles is a universal property of rotating black holes as long as the angular momentum of one of the colliding particles approaches the critical value [6]. The requirement that the black hole be rotating seems to be an essential ingredient in obtaining ultra-high CM energy; however, it was shown that the similar effect exists for non-rotating charged black holes [7]. Moreover, the extension of the BSW mechanism to non-extremal backgrounds shows that particles cannot collide with arbitrarily high energies at the outer horizon and that ultra-energetic collisions can only occur near the Cauchy horizon of a Kerr black hole with any spin parameter [8]. The non-extremal Kerr-de Sitter black holes could also act as particle accelerators with arbitrarily high CM energy if one of the colliding particles has the critical angular momentum [9].

The BSW mechanism has been studied for different black hole geometries; for instance, rotating charged cylindrical black holes were studied in Ref. [10] and an extreme rotating black holes in Horava–Lifshitz gravity in Ref. [11]. However, the fundamental parameter of Horava–Lifshitz gravity avoids an infinite value of the CM energy being obtained. Higher-dimensional rotating black holes have been studied in Refs. [12,13,14] and lower-dimensional black holes in Refs. [15,16,17,18,19]. The collision of two neutral particles on the vicinity of the extremal Kerr black hole horizon considered as a complete vacuum spacetime in its own right was studied in [20]. Particle collision in the strong gravitational field of a rotating black hole in a Randall–Sundrum brane with a nonvanishing cosmological constant was studied in [21]. The particle collisions near the cosmological horizon of non-extremal Reissner–Nordstrom de Sitter black holes were studied in Ref. [22], charged dilatonic black holes in Ref. [23], non-rotating and rotating regular black holes in Refs. [24,25,26,27], and extremal modified Hayward and Bardeen rotating black holes in Ref. [28]. On the other hand, charged particles in general stationary charged black holes was considered in Ref. [29], and on string black holes in Ref. [30]. The collisions of spinning particles on rotating black holes in Refs. [31, 32], and on Schwarzschild black holes was considered in Ref. [33]; however, the unavoidable appearance of superluminal motion and the change of trajectories from timelike to spacelike can be avoided as the energy in the CM frame can grow unbounded provided that one of the particles is not exactly critical but slightly deviates from the critical trajectory [34]. On the other hand, the formation of black holes through the BSW mechanism was investigated in [35].

The aim of this work is to consider the special class of well-known three-dimensional warped anti-de Sitter black holes solutions [36,37,38,39] and to study, via the BSW mechanism, the possibility of obtaining unbounded energy in the CM frame of two colliding particles and to analyze the effect of the warped parameter that controls the stretching deformation on this. It is worth noting that warped \(\hbox {AdS}_{3}\) black holes can be viewed as discrete quotients of warped \(\hbox {AdS}_{3}\) spacetime just like the BTZ black holes as discrete quotients of the \(\hbox {AdS}_{3}\). Also, when the warped parameter \(\nu =1\), the metric reduces to the metric of a BTZ black hole in a rotating frame. An important feature of these black holes is that the Killing vector \(\partial _{t}\) is spacelike everywhere in spacetime and consequently its ergoregion extends to infinity. Also, it is known that two particles in the ergosphere lead to infinity growth of the energy of the CM frame, provided the angular momentum of one of the two particles has a large negative angular momentum and a fixed energy at infinity for the Kerr black holes [5], which was subsequently proven to be a universal property of the ergosphere [40].

It worth mentioning that the collision of two particles near the horizon of a BTZ black hole was studied in Refs. [16,17,18]. In Refs. [16, 17] the authors found that the particle with the critical angular momentum could exist inside the outer horizon of the BTZ black hole regardless of the particle energy with the BSW process being possible on the inner horizon for the non-extremal BTZ black hole. Also, the BSW process could also happen for the extremal BTZ black hole, where the particle with the critical angular momentum could only exist on the degenerate horizon. On the other hand, in Ref. [18], the authors studied the collision of two particles on an event horizon and outside of the BTZ black hole, and they showed that although in principle the CM energy of two ingoing particles can be arbitrarily large on an event horizon, if either of the two particles has a critical angular momentum and the other has a non-critical angular momentum, the critical particles never reach the event horizon. However, the motion of a particle with a subcritical angular momentum is allowed near an extremal rotating BTZ black hole and that a CM energy for a tail-on collision at a point can be arbitrarily large in a critical angular momentum limit.

On the other hand, the warped \(\hbox {AdS}_{3}\) space has non-AdS asymptotics and is not a solution of pure three-dimensional gravity, and it appears as a submanifold, at fixed polar coordinate, of the near horizon extreme Kerr black hole [41, 42]. So, it is interesting to study if the BSW effect, which was first noted for the extreme Kerr black holes, also occurs in the warped \(\hbox {AdS}_3\) black hole in analogy with the extremal Kerr geometry. In fact, we will show that the BSW effect is possible on the outer horizon in the extremal warped \(\hbox {AdS}_3\) black hole, and the particle with critical angular momentum can reach the degenerate horizon when a condition on its energy is fulfilled, which resembles to what occurs in the extremal Kerr-AdS black hole; however, in the extremal Kerr-AdS black hole two conditions must be fulfilled [9]; besides, this effect is also possible on the inner horizon for the non-extremal warped \(\hbox {AdS}_3\) black hole. In addition, we describe the kinds of orbits in this background for timelike and null geodesics by analyzing the effective potential. It is worth mentioning that the study of null geodesics in backgrounds with and without horizon are very important in studies about reconstruction of scalar field in the bulk from data defined on the boundary. It is known that for an asymptotically AdS spacetime, the reconstruction of a scalar field in the bulk from data defined on the boundary fails if there exist null geodesic originating in the bulk that do not reach the boundary [43,44,45], which is analogous to what occurs in flat spacetime, where a necessary condition for a continuous bulk reconstruction of a field from data defined on a boundary is that every null geodesic originating in the bulk intersects the boundary [46]. We will show that, similar to the BTZ black hole, not all the outgoing null geodesics outside the warped \(\hbox {AdS}_{3}\) black hole can reach infinity. On the other hand, the warped \(\hbox {AdS}_3\)/CFT\(_2\) correspondence was proposed in [38], the asymptotical symmetry group analysis was studied in [47,48,49,50], and some studies of quasinormal modes and real-time correlators were carried out in [51, 52].

The manuscript is organized as follows: In Sect. 2 we give a brief review of the three-dimensional warped AdS black hole. Then, we study the particle’s motion in the three-dimensional warped black hole background in Sect. 3. In Sect. 4 we obtain the CM energy of two colliding particles, and in Sect. 5 we study the radial motion of a particle with critical angular momentum and we investigate the possibility that the black hole acts as a particle accelerator. Finally, our conclusions are in Sect. 6.

2 Three-dimensional warped AdS black holes

The models of gravity in three spacetime dimensions and their modifications have attracted remarkable interest in the last decade. One of them is topologically massive gravity (TMG), which modifies the theory of general relativity (GR) by adding a Chern–Simons gravitational term [53,54,55] to the Hilbert-Einstein action. The action is described by

$$\begin{aligned} I= & {} \frac{1}{16 \pi G}\int _M d^3x\sqrt{-g}\left( R+\frac{2}{l^2}\right) \nonumber \\&+\,\frac{l}{96\pi G \nu }\int _M d^3x\sqrt{-g}\epsilon ^{\lambda \mu \nu }\Gamma ^r_{\lambda \sigma }\left( \partial _{\mu }\Gamma ^\sigma _{r\nu }+\frac{2}{3}\Gamma ^\sigma _{\mu \tau }\Gamma ^\tau _{\nu r}\right) ,\nonumber \\ \end{aligned}$$
(1)

where \(\epsilon ^{\tau \sigma \mu }=1/\sqrt{-g}\) is the Levi–Civita tensor and \(\nu \) is a dimensionless coupling constant, which is related to the graviton mass \(\mu \) by \(\nu =\mu l/3\). This model, in contrast to GR in three spacetime dimensions, has a propagating degree of freedom which corresponds to a massive graviton. Also, the possibility of constructing a chiral theory of gravity at a special point in the space of parameters [56] are some of its important characteristics. Accordingly, it was conjectured that a consistent quantum theory of the so-called chiral gravity can be defined at \(\mu l=1\) or \(\nu =1/3\) [57]. However, for non-chiral values of \(\mu l\), it has been shown that there are other two warped \(\hbox {AdS}_{3}\) vacuum solutions for every value of \(\mu l \ne 3 \) [38]. The warped \(\hbox {AdS}_{3}\) geometry corresponds to a one parameter-stretched deformation of \(\hbox {AdS}_3\). Further aspects of TMG can be found in [58,59,60,61,62,63,64] and references therein.

The metric describing the spacelike stretched black holes [36,37,38,39] in ADM form is given by

$$\begin{aligned} ds^2= & {} -N^2(r)dt^2+\ell ^2 R^2(r) \left( d\phi + N_{\phi } (r) dt \right) ^2\nonumber \\&+\,\frac{\ell ^4 dr^2}{4 R^2 (r) N^2 (r)}, \end{aligned}$$
(2)

where the metric functions are

$$\begin{aligned} R^2(r)= & {} \frac{r}{4}\left( 3 (\nu ^2-1)r+(\nu ^2+3)(r_++r_-)\nonumber \right. \\&\left. -\,4 \nu \sqrt{r_+ r_- (\nu ^2+3)}\right) , \end{aligned}$$
(3)
$$\begin{aligned} N^2 (r)= & {} \frac{\ell ^2 (\nu ^2+3)(r-r_+)(r-r_-)}{4 R^2}, \end{aligned}$$
(4)
$$\begin{aligned} N_{\phi } (r)= & {} \frac{2 \nu r-\sqrt{r_+ r_- (\nu ^2+3)}}{2 R^2}, \end{aligned}$$
(5)

with \(\nu ^{2} \ge 1\) being the parameter that controls the stretching deformation, and \(r_{+}\) and \(r_{-}\) being the outer and inner horizon, respectively. For \(\nu = 1\) the metric reduces to the metric of BTZ black holes in a rotating frame. An important feature of these black holes is that the Killing vector \(\partial _{t}\) is spacelike everywhere in the spacetime and consequently its ergoregion extends to infinity; therefore, observers cannot follow the orbits of \(\partial _{t}\) in the exterior region. Also, the energy of a particle can have negative energy in the exterior region. It is worth noting that the warped \(\hbox {AdS}_{3}\) space also arises in other contexts, for instance see [41, 65,66,67,68,69,70,71,72,73,74].

3 Motion of particles in the three-dimensional warped AdS black hole background

The equations of the geodesics can be derived from the Lagrangian of a test particle, which is given by [75]

$$\begin{aligned} \mathcal {L}=\frac{1}{2}\left( g_{\mu \nu }\frac{dx^\mu }{d\tau }\frac{dx^\nu }{d\tau } \right) . \end{aligned}$$
(6)

So, for the three-dimensional warped AdS black hole (2), the Lagrangian reads

$$\begin{aligned} 2\mathcal {L}= & {} \left( -N^2(r)+\ell ^2 R^2(r) N_{\phi }^2 (r)\right) \dot{t}^2+2 \ell ^2 R^2(r) N_{\phi }(r)\dot{t}\dot{\phi }\nonumber \\&+\, \frac{\ell ^4}{4 R^2 (r) N^2 (r)}\dot{r}^2+ \ell ^2 R^2(r)\dot{\phi }^2, \end{aligned}$$
(7)

where \(\dot{q}=dq/d\tau \), and \(\tau \) is an affine parameter along the geodesic that we choose as the proper time. Since the Lagrangian (7) is independent of the cyclic coordinates (\(t,\phi \)), their conjugate momenta (\(\Pi _t, \Pi _{\phi }\)) are conserved. The equations of motion are obtained from \( \dot{\Pi }_{q} - \frac{\partial \mathcal {L}}{\partial q} = 0\), where \(\Pi _{q} = \partial \mathcal {L}/\partial \dot{q}\) are the conjugate momenta to the coordinate q, and are given by

$$\begin{aligned} \Pi _{t}= & {} \left( -N^2(r)+\ell ^2 R^2(r) N_{\phi }^2 (r)\right) \dot{t}\nonumber \\&+\, \ell ^2 R^2(r) N_{\phi }(r)\dot{\phi }\equiv -E, \end{aligned}$$
(8)
$$\begin{aligned} \Pi _{r}= & {} \frac{\ell ^4}{4 R^2 (r) N^2 (r)}\dot{r}, \end{aligned}$$
(9)
$$\begin{aligned} \Pi _{\phi }= & {} \ell ^2 R^2(r) N_{\phi }(r)\dot{t} +\ell ^2 R^2(r)\dot{\phi }\equiv L, \end{aligned}$$
(10)

where E and L are dimensionless integration constants associated with each of them. The Hamiltonian is given by

$$\begin{aligned} \mathcal {H}= & {} \Pi _{t} \dot{t} + \Pi _{\phi }\dot{\phi }+\Pi _{r}\dot{r} -\mathcal {L}, \end{aligned}$$
(11)
$$\begin{aligned} 2\mathcal {H}= & {} -\,E\, \dot{t} + L\,\dot{\phi }+\frac{\ell ^4}{4 R^2 (r) N^2 (r)}\dot{r}^2\equiv -m^2. \end{aligned}$$
(12)

By normalization, we shall consider that \(m^2 = 1\) for massive particles (\(m^2 = 0\) for photons). We solve the above equation for \(\dot{r}^2\) in order to obtain the radial equation, \(\dot{t}\), and \(\dot{\phi }\), which allows us to characterize the possible movements of the test particles without an explicit solution of the equations of motion, which yields

$$\begin{aligned}&\dot{t}= \frac{E+LN_{\phi }}{N^2}, \end{aligned}$$
(13)
$$\begin{aligned}&\dot{\phi }= -\,\frac{ E N_{\phi }}{N^2}+L\left( \frac{1}{\ell ^2 R^2}-\frac{N_{\phi }^2}{N^2} \right) , \end{aligned}$$
(14)
$$\begin{aligned}&\dot{r}^{2}= \frac{4 N^2 R^2 }{\ell ^4} \left( \frac{1}{N^2} (E+L N_{\phi })^2-\frac{L^2}{\ell ^2 R^2}-m^2 \right) , \end{aligned}$$
(15)

where the above equations represent all nonzero 3-velocity components \(u=(\dot{t},\dot{r},\dot{\phi })\) for the geodesic motion that will be used in the next section to obtain the CM energy of two colliding particles falling freely from rest with the same rest mass \(m_{0}\) in the warped \(\hbox {AdS}_{3}\) black hole background. We will assume \(\dot{t}>0\) for all \(r>r_+\) so that the motion is forward in time outside the horizon. So, the following condition must be fulfilled

$$\begin{aligned} E+LN_{\phi }>0, \quad \text {for all}\,\, r>r_+. \end{aligned}$$
(16)

Now, in order to see if a particle can reach the event horizon, we will analyze the effective potential of the three-dimensional warped AdS black hole by using the equation of motion of the particle in the radial direction given by

$$\begin{aligned} \dot{r}^{2}+V=0, \end{aligned}$$
(17)

where V is the effective potential of the particle in the radial direction. Hence by comparing Eq. (15) with Eq. (17), we obtain:

$$\begin{aligned} V(r)= & {} -\frac{4}{\ell ^{4}}R^{2}(r)\left( \left( E+LN_{\phi }(r)\right) ^{2}\nonumber \right. \\&\left. -\,N^{2}(r)\left( m^2+\frac{L^{2}}{\ell ^{2}R^{2}(r)}\right) \right) . \end{aligned}$$
(18)

The motion of the particle is allowed in regions where \(V(r)\le 0\), and it is prohibited in regions where \(V(r)>0\). It is clear that the particle can exist on the event horizon \(r=r_{+}\) because \(N^{2}(r_{+})=0\), and then the effective potential is negative. On the other hand, when \(r \rightarrow \infty \) it is easy to show that the effective potential is given by

$$\begin{aligned} V(r \rightarrow \infty ) \approx \frac{((\nu ^{2}+3) m^2 \ell ^2-3 E^{2}(\nu ^{2}-1))r^{2}}{\ell ^{4}}. \end{aligned}$$
(19)

This expression shows that the existence of massive particles at infinity depends on the warped parameter \(\nu \) and on its energy E. Therefore, massive particles can exist at infinity when the following condition is fulfilled, with \(\nu \ne 1\):

$$\begin{aligned} E^2>\frac{(\nu ^2+3) \ell ^2}{3(\nu ^2-1)}. \end{aligned}$$
(20)
Fig. 1
figure 1

The behavior of the effective potential V(r) for massless particles as a function of r for different values of \(\nu \) with \(E=l=1\), \(r_-=1\), \(r_+=2\) and \(\nu =1,2,2.5,3\). \(L=-\,1\) (left figure) and \(L=1\) (right figure)

Full size image
Fig. 2
figure 2

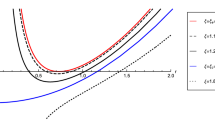
The behavior of the effective potential V(r) for massive particles as a function of r for different values of \(\nu \) with \(E=l=1\), \(L=-\,1\), \(r_-=1\), \(r_+=2\) and \(\nu =1,2,2.5,3\). Left figure shows the behavior of the effective potential between \(r=0\) and \(r=3\), while the right figure shows the behavior of the effective potential between \(r=0\) and \(r=100\)

Full size image

Note that the effective potential (18) is a parabola, and it can be written as\(V(r)=ar^2+br+c\), where

$$\begin{aligned} a= & {} \frac{-3E^2(\nu ^2-1)+m^2 \ell ^2 (\nu ^2+3)}{\ell ^4},\end{aligned}$$
(21)
$$\begin{aligned} b= & {} \frac{E^2 \left( 4 \nu \sqrt{r_+ r_- (\nu ^2+3)}-(\nu ^2+3) (r_+ + r_-)- (\nu ^2+3) (r_+ + r_-) m^2 \ell ^2-8 \nu E L \right) }{\ell ^4},\end{aligned}$$
(22)
$$\begin{aligned} c= & {} \frac{-4 L^2 + (\nu ^2+ 3) r_+ r_- m^2 \ell ^2 +4 E L \sqrt{ r_+ r_- (\nu ^2 +3)}}{\ell ^4}. \end{aligned}$$
(23)

In the case\(\nu =1\) (BTZ black hole in a rotating frame), a simplifies to \(a=4 m^2 / \ell ^2\); thus, for \(m=0\), the effective potential is a straight line. In this case there are trapped null geodesics and the condition for the existence of these null geodesics outside the event horizon that cannot reach spatial infinity can be obtained by studying the effective potential, which yields

$$\begin{aligned} E ( \sqrt{r_+ r_-}-r_+)< L< E \sqrt{r_+ r_- }-\frac{E (r_++r_-)}{2}. \end{aligned}$$
(24)

Otherwise, the outgoing null geodesics can reach infinity (see Fig. 1), which could have holographic implications in the studies of bulk reconstruction, see for instance [43,44,45,46]. However, for \(\nu \ne 1\) and massless particles (\(m=0\)), a reduces to \(a=-3 E^2 (\nu ^2-1) / \ell ^4 <0\). So, the effective potential is a convex parabola, and thus there are massless particles that can reach infinity (see Fig. 1). However, there are also, trapped null geodesics, in fact, by studying the behavior of the potential V(r) with \(\nu > 1\), yields the condition for the existence of null geodesics outside the event horizon that cannot reach spatial infinite, the condition can be written as

$$\begin{aligned}&\frac{1}{2} E \left( -2 r_+ \nu + \sqrt{r_+ r_- (\nu ^2+3)}\right)< L \nonumber \\&\quad < \frac{1}{4} \left( - \sqrt{3 E^2 (r_+- r_-)^2 (\nu ^2-1)}\nonumber \right. \\&\left. \qquad +\,2 E \left( - (r_++r_-)\nu + \sqrt{r_+ r_- (\nu ^2+3)}\right) \right) , \end{aligned}$$
(25)

which reduces to (24) when \(\nu =1\). Additionally, in contrast to the BTZ black hole, there are unstable circular orbits, this occurs when the effective potential has a unique real root \(r_0\) bigger than \(r_+\). A unique real root exists when the following condition is satisfied

$$\begin{aligned} L= & {} \frac{1}{4} \left( - \sqrt{3 E^2 (r_+- r_-)^2 (\nu ^2-1)}\nonumber \right. \\&\left. +\,2 E \left( - (r_++r_-)\nu + \sqrt{r_+ r_- (\nu ^2+3)}\right) \right) . \end{aligned}$$
(26)

On the other hand, for massive particles (\(m=1\)), the effective potential is a concave parabola (\(a>0\)) for \(\nu =1\) (see Fig. 2). So, massive particles cannot reach infinity. However, for \(\nu \ne 1\) and \(m=1\), \(a=\left( -3E^2(\nu ^2-1)+\ell ^2 (\nu ^2+3) \right) / \ell ^4\), and when \(E^2< \frac{(\nu ^2+3) \ell ^2}{3 (\nu ^2-1)}\) the parabola is concave (\(a>0\)). So, the massive particles cannot reach infinity in this case, whereas for \(E^2> \frac{(\nu ^2+3) \ell ^2}{3 (\nu ^2-1)}\), the parabola is convex (\(a<0\)) and there are massive particles that can reach spatial infinity, which is different to the BTZ black hole (see Fig. 2).

4 The CM energy of two colliding particles

In this section we calculate the CM energy of two colliding particles in the warped \(\hbox {AdS}_{3}\) black hole. To achieve this, we must derive the 2+1 dimensional 3-velocity components to obtain the CM energy of the colliding particles. We consider that the particles have the same rest mass \(m_0\), energies \(E_1\) and \(E_2\) and angular momentum \(L_1\) and \(L_2\), respectively. From the relation \(E_{CM}=\sqrt{2} m_0 \sqrt{1-g_{\mu \nu }u_1^{\mu }u_2^{\nu }}\), where \(u_1\) and \(u_2\) denotes the 3-velocities of the particles, we obtain

$$\begin{aligned} \frac{E_{CM}^2}{2 m_0^{2}}= \frac{R^2 N^2 (R^2 -L_1 L_2 / \ell ^2 )+(K_1 K_2-H_1 H_2)}{(R^2)^2 N^2}, \end{aligned}$$
(27)

where

$$\begin{aligned} K_i= & {} E_i R^2+ L_i R^2 N_{\phi }, \nonumber \\ H_i= & {} \sqrt{(E_i R^2+ L_i R^2 N_{\phi })^2-R^2 N^2 (R^2+L_i^2 /\ell ^2)}, \end{aligned}$$
(28)

with \(i=1,2\). Also, when the particles arrive to the horizon \(r=r_{+}\), \(N^2(r_+) \rightarrow 0\), \(H_1 \rightarrow \sqrt{K_1^2}\) and \(H_2 \rightarrow \sqrt{K_2^2}\), the CM energy (27) at the horizon yields:

$$\begin{aligned} \frac{E_{CM}^2}{2 m_0^{2}}(r \rightarrow r_{+})=\frac{1}{(R^2)^2 N^2} \left( K_1 K_2 -\sqrt{K_1^2} \sqrt{K_2^2}\right) . \end{aligned}$$
(29)

Note that \(K_1K_2<0\) the \(E_{CM}^{2}\) on the horizon will be a negative infinity therefore the energy center of mass will be imaginary and then it is not a physical solution. In fact, we can set \(K_1<0\) and \(K_2>0\) without loss of generality; however, \(K_1<0\) outside the event horizon is in contradiction with condition (16). However, when \(K_1K_2 \ge 0\), the numerator of this expression will be zero and the value of \(E_{CM}\) will be undetermined. Now, in order to find the limiting value of the CM energy at the horizon we use the L’Hopital rule, obtaining

$$\begin{aligned} \frac{E_{CM}^2}{2 m_0}=\frac{ R^2(r_+) (K_1(r_+)+K_2(r_+))^2 +\frac{1}{\ell ^2}(K_1(r_+) L_2-K_2(r_+)L_1)^2}{2 R^2(r_+) K_1(r_+) K_2(r_+)}. \end{aligned}$$
(30)

Note that the numerator of the above expression is finite at the horizon and when \(K_i(r_+)=0\) the CM energy of two colliding particles on the horizon could be arbitrarily high, \(E_{CM} \big | _{K_i=0} \rightarrow \infty \). So, from \(K_i(r_+)=0\) we obtain that the critical angular momentum is given by:

$$\begin{aligned} L_{ci}= & {} \frac{E_i r_+ \left( 3r_-+\nu ^2 r_-+4\nu ^2 r_+-4 \nu \sqrt{r_+ r_- (3+\nu ^2)} \right) }{2 \left( -2 \nu r_++\sqrt{r_+ r_- (3+\nu ^2)} \right) }, \nonumber \\&i=1,2. \end{aligned}$$
(31)

On the other hand, when \(K_1(r_+)\) and \(K_2(r_+)\) are both zero, then \(E_{CM}\) is finite at the horizon. In this case \(H_1(r_+)=H_2(r_+)=0\) and

$$\begin{aligned} \frac{E_{CM}^2}{2 m_0}=1-\frac{L_1 L_2}{ \ell ^2 R^2(r_+)}. \end{aligned}$$
(32)

Therefore, in order to obtain an infinite CM energy only one of the colliding particles should have the critical angular momentum, making the BSW process possible. In Fig. 3, we show the behavior of \(E_{CM}\) versus \(L_{1}\) with the other parameters fixed. We observe that there is a critical value of angular momentum for the particle 1 at which the CM energy blows up. Note that in order to get positive \(E_{CM}\) the asymptotic value of critical angular momentum has to be reached from the right. Additionally, in Fig. 4, we have plotted \(L_{c}\) in terms of warped parameters \(\nu \) for different values of energy E. Notice that when the energy of particle 1 and the warped parameter increases, the critical angular momentum \(L_{c}\) decreases. By a similar analysis, it is possible to evaluate the \(E_{CM}\) on the inner horizon, finding that this is also infinity as long as one of the two particles has the following critical angular momentum:

$$\begin{aligned} L_{ci}= & {} \frac{E_i r_- \left( 3r_++\nu ^2 r_+ +4\nu ^2 r_- -4\nu \sqrt{r_-r_+(3+\nu ^2)}\right) }{2 \left( -2 \nu r_-+\sqrt{r_-r_+(3+\nu ^2)}\right) }, \nonumber \\&i=1,2. \end{aligned}$$
(33)
Fig. 3
figure 3

The behavior of the CM energy \(E_{CM}^2(r_+)\) at the horizon as a function of \(L_1\) with \(\nu =2.5\), \(E_1=E_2=1\), \(L_2=-1\) \(r_-=1\), \(r_+=2\) and \(l=1\)

Full size image
Fig. 4
figure 4

The behavior of \(L_{c}\) as a function of \(\nu \) for different values of the energy \(E=1,2,4,8\) with \(r_-=1\) and \(r_+=2\)

Full size image

5 Radial motion of the particle with critical angular momentum

In this section, we will study the radial motion of the particle with critical angular momentum and energy E. As we have mentioned, the particle reaches the event horizon of the black holes if the square of the radial component of the 3-velocity \(\dot{r}^{2}\) in Eq. (15) is positive or V is negative in the neighborhood of the black hole horizon. We will denote the explicit form of \(\dot{r}^{2}\) with critical angular momentum as \(R^{c}(r)\), which is given by

$$\begin{aligned} R^{c}=\frac{(r-r_{+})\left( -m^{2}l^{2}(r-r_{-})(3+\nu ^{2})+E^{2}(3r(-1+\nu ^{2})+r_{-}(3+\nu ^{2})-4r_{+}\nu ^{2})\right) }{l^{4}}, \end{aligned}$$
(34)

and it vanishes on the event horizon. Also, for some values of the parameters, \(R^c\) can be positive, which implies that particles with critical angular momentum can exist outside the event horizon; as we shall see, however they cannot reach the event horizon unless \(r_+=r_-\). Particles with critical angular momentum can reach the event horizon if

$$\begin{aligned} \frac{dR^{c}}{dr}\Big |_{r=r_{+}}>0, \end{aligned}$$
(35)

which yields

$$\begin{aligned} \frac{dR^{c}}{dr}\Big |_{r=r_{+}}=-\frac{(E^{2}+l^{2}m^{2})(r_{+}-r_{-})(\nu ^{2}+3)}{l^{4}}<0. \end{aligned}$$
(36)

Therefore, if particles with critical angular momentum exist outside the black hole such particles cannot reach the event horizon. In Fig. 5 we plot the behavior of \(R^c\) as a function of r for the three-dimensional warped black hole. Notice that if \(\frac{d^{2}R^{c}}{dr^{2}}=\frac{-2\left( m^{2}l^{2}(3+\nu ^{2}\right) -3E^{2}(\nu ^{2}-1))}{l^{4}}>0\), \(R^c(r)\) has a zero also at \(r_0=\frac{(\nu ^2+3) \ell ^2 r_-+ (3 r_-+(r_- -4 r_+)\nu ^2) E^2 }{(\nu ^2+3)\ell ^2 -3 E^2 ( \nu ^2-1)}\) which is greater than \(r_+\), and particles with critical angular momentum can exist outside the event horizon at \(r>r_0 >r_+\), see Fig. 5.

Fig. 5
figure 5

The behavior of \(R^c(r)\) as a function of r with \(r_- = 1\), \(r_+=2\), \(\nu =1\, (L_c=-0.586)\), \(\nu =1.5\, (L_c=-1.380)\), \(\nu =\sqrt{3}\, (L_c=-1.732)\), \(\nu =2.5\, (L_c=-2.894)\), \(E=1\) and \(l=1\)

Full size image

On the other hand, we notice that the particle with the critical angular momentum can exist inside the event horizon \(r_{+}\). This can be shown by replacing the critical angular momentum Eq. (33) in the square of the radial component of the 3-velocity Eq. (15), obtaining the analog of Eq. (34), whose derivative evaluated on the internal horizon \(r_-\) is positive \(\frac{dR^{c}}{dr}\vert _{r=r_-}>0\); therefore, the particle with critical angular momentum can reach the inner horizon and the center of mass energy can be arbitrarily high, with the BSW process being possible on the inner horizon.

On the other hand, in the extremal case \(r_{+}=r_{-}\) we obtain

$$\begin{aligned} R^{c}=-\frac{(r-r_{+})^{2}\left( m^{2}l^{2}(3+\nu ^{2})-3E^{2}(\nu ^{2}-1)\right) }{l^{4}}, \end{aligned}$$
(37)

and

$$\begin{aligned} \frac{dR^{c}}{dr}=-\frac{2(r-r_{+})\left( m^{2}l^{2}(3+\nu ^{2})-3E^{2}(\nu ^{2}-1)\right) }{l^{4}}. \end{aligned}$$
(38)

Then, clearly Eqs. (37) and (38) are zero on the event horizon, then it is necessary to calculate \(\frac{d^{2}R^{c}}{dr^{2}}\vert _{r=r_{+}}\):

$$\begin{aligned} \frac{d^{2}R^{c}}{dr^{2}}\Big |_{r=r_{+}}=\frac{-2\left( m^{2}l^{2}(3+\nu ^{2}\right) -3E^{2}(\nu ^{2}-1))}{l^{4}}. \end{aligned}$$
(39)

If \(\frac{d^{2}R^{c}}{dr^{2}}\Big |_{r=r_{+}}>0\), the particle with critical angular momentum will reach the degenerate horizon. Our case it is fulfilled if:

$$\begin{aligned} E^2> \frac{(\nu ^2+3) \ell ^2}{3 (\nu ^2 - 1 )}, \end{aligned}$$
(40)

which is the same expression given in Eq. (20). In Fig. 6 we plot the behavior of the \(R^c\) as a function of r for the three-dimensional extremal warped AdS black hole. Notice that the particle with critical angular momentum can reach the degenerate horizon if the condition (40) is satisfied, and thus the BSW process is possible. This result is similar to that found in [9] for Kerr-AdS black holes. Notice that for \(\nu =1\) the particle with critical angular momentum cannot exist outside the event horizon; however, it can exist on the degenerate horizon, that corresponds to the behavior observed for the extremal BTZ black hole [17].

Fig. 6
figure 6

The behavior of \(R^c(r)\) as a function of r for the extremal warped \(\hbox {AdS}_3\) black hole for different values of the warped parameter \(\nu =1, \nu =1.5\, (L_c=-0.709),\, \nu =\sqrt{3}\, (L_c=-1.015), \nu =2.5\, (L_c=-1.959)\), \(E=1\) and \(l=1\)

Full size image

6 Final remarks

In this paper we considered two colliding particles in the vicinity of the horizon of a three-dimensional warped AdS black hole, and we analyzed the energy in the CM frame of the colliding particles in order to investigate the possibility that the three-dimensional warped AdS black hole can act as a particle accelerator. We found for the warped \(\hbox {AdS}_3\) black hole that despite the particle with critical angular momentum being able to exist for certain values of the conserved energy outside the black hole, it will never reach the event horizon; therefore, the black hole cannot act as a particle accelerator with arbitrarily high CM energy on the event horizon. However, the particle with the critical angular momentum could also exist inside the outer horizon of the warped \(\hbox {AdS}_3\) black hole, with the BSW process being possible on the inner horizon. Also, we showed that the critical angular momentum decreases when the parameter that controls the stretching deformation increases. At \(\nu =1\), the non-extremal warped \(\hbox {AdS}_{3}\) black hole solution is given by the BTZ black hole in the rotating frame, and we showed that there are trapped null geodesics, when the condition \(E ( \sqrt{r_+ r_-}-r_+)< L< E \sqrt{r_+ r_- }-\frac{E (r_++r_-)}{2}\), is satisfied. That corresponds to the behavior observed for the BTZ black hole [76]. Otherwise, the outgoing null geodesics can reach infinity. However, for \(\nu \ne 1\) there are massless particles that can reach infinity, as well as, there are trapped null geodesics when the condition \(\frac{1}{2} E \left( -2 r_+ \nu + \sqrt{r_+ r_- (\nu ^2+3)}\right)< L < \frac{1}{4} \big (- \sqrt{3 E^2 (r_+- r_-)^2 (\nu ^2-1)}+2 E \big ( - (r_++r_-)\nu + \sqrt{r_+ r_- (\nu ^2+3)}\big ) \big )\) is satisfied. Also, we found that in contrast to the BTZ black hole, there are unstable circular orbits. On the other hand, massive particles cannot reach infinity for \(\nu =1\). However, for \(\nu \ne 1\), when \(E^2< \frac{(\nu ^2+3) \ell ^2}{3 (\nu ^2-1)}\) the massive particles cannot reach infinity. Otherwise, there are massive particles that can reach spatial infinity, which is different to the BTZ black hole.

On the other hand, for the extremal warped \(\hbox {AdS}_{3}\) black holes, we found that the particle with critical angular momentum could exist outside the event horizon and reach a high CM energy on the event horizon as long as its conserved energy fulfills the condition \(E^{2}>\frac{(\nu ^{2}+3)l^{2}}{3(\nu ^{2}-1)}\), with the BSW process being possible. At \(\nu =1\) the particle with critical angular momentum cannot exist outside the event horizon; however it can exist on the degenerate horizon, that corresponds to the behavior for the extremal BTZ black hole. It would be interesting to explore the possible holographic implications of the results found here.