Refractive index in generalized superconductors with Born–Infeld electrodynamics

Abstract

We investigate, in the probe limit, the negative refraction in the generalized superconductors with the Born–Infeld electrodynamics. We observe that the system has a negative Depine–Lakhtakia index in the superconducting phase at small frequencies and the greater the Born–Infeld corrections the larger the range of frequencies or the range of temperatures for which the negative refraction occurs. Furthermore, we find that the tunable Born–Infeld parameter can be used to improve the propagation of light in the holographic setup. Our analysis indicates that the Born–Infeld electrodynamics plays an important role in determining the optical properties of the boundary theory.

1 Introduction

As one of the most significant developments in the theoretical physics over the last decade, the anti-de Sitter/conformal field theories (AdS/CFT) correspondence [1,2,3,4], which provides an astonishing duality between the gravity in the d-dimensional spacetime and the gauge field theory living on its ($d-1$)-dimensional boundary, has been employed to study the strong coupled systems in condensed matter physics which are intractable by the traditional approaches [5]. In particular, such a strong/weak duality might give some insights into the pairing mechanism in the high $T_{c}$ superconductors [6]. It was first suggested by Gubser [7] that the spontaneous U(1) symmetry breaking by bulk black holes can be used to construct gravitational duals of the transition from a normal state to a superconducting state in the boundary theory, which exhibit characteristic behaviors of superconductors [8]. Along this line, there have been a lot of works studying various gravity models with the property of the so-called holographic superconductor, for reviews, see Refs. [9,10,11,12] and references therein.

On the other hand, the refractive index, which reflects the propagation property of light in an electromagnetic medium, is one of the most important electromagnetic properties of a medium. In 1968, Veselago first considered the case of a medium which has both negative dielectric permittivity and negative magnetic permeability at a given frequency and proposed in theory that the refraction index might be negative [13]. Around 2000, this exotic electromagnetic phenomenon – negative refraction, which implies that the energy flux of the electromagnetic wave flows in the opposite direction with respect to the phase velocity, was experimentally realized in a new class of artificial media commonly called “metamaterials” [14, 15]. Since then, the study on the negative refraction has attracted intensive interest and a large number of the negative refractive index materials have been introduced [16]. Interestingly, recent studies show that in the radio, microwave and low-terahertz frequency ranges the superconductors can behave as metamaterials and exhibit negative refraction [17]. Using the AdS/CFT correspondence, Gao and Zhang investigated the optical properties in the s-wave superconductors and found that the negative refraction does not appear in these holographic models in the probe limit [18]. However, in the fully backreacted spacetime, Amariti et al. showed that the negative refraction is allowed in the superconducting phase [19]. Extending the investigation to the generalized holographic superconductors in which the spontaneous breaking of a global U(1) symmetry occurs via the Stückelberg mechanism [20, 21], Mahapatra et al. observed that a negative Depine–Lakhtakia index may appear at low frequencies in the theory dual to the R-charged black hole, which indicates that the system exhibits negative refraction even in the probe limit [22]. Other investigations based on the refractive index in the holographic dual models can be found, for example, in Refs. [23,24,25,26,27,28,29,30,31,32].

The aforementioned works on the refractive index in the holographic superconductor models are based on the usual Maxwell electrodynamics. Considering the Maxwell theory as only a special case of or a leading order approximation to nonlinear electrodynamics, we may extend the investigation to the nonlinear electrodynamics which essentially implies higher derivative corrections of the gauge field [33]. As a first attempt to investigate how the nonlinear electrodynamics affects the properties of the holographic dual model, Jing and Chen introduced the holographic superconductors in the Born–Infeld electrodynamics and observed that the nonlinear Born–Infeld corrections make it harder for the scalar condensation to form [34]. Later the holographic dual models with the Power-Maxwell electrodynamics [35], the Maxwell field strength corrections [36], the logarithmic form of nonlinear electrodynamics [37] and the exponential form of nonlinear electrodynamics [38] were realized and some interesting properties were disclosed. Considering the increasing interest in the study of the holographic dual models with the nonlinear electrodynamics [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66], in this paper, we are going to examine the influence of the Born–Infeld electrodynamics on the optical properties of the generalized holographic superconductors in the probe limit. We will show that the Born–Infeld corrections affect not only the range of frequencies or the range of temperatures for which negative refraction occurs but also the dissipation in the system, and this is helpful for us to understand the influences of the 1 / N (N is the color quantum number) or $1/\lambda$ ($\lambda$ is the ’t Hooft coupling) corrections on the holographic superconductor models and their optical properties.

The structure of this work is as follows. In Sect. 2 we will construct the generalized holographic superconductors with the Born–Infeld electrodynamics in the probe limit and analyze the effect of the Born–Infeld electrodynamics on the condensate of the system. In Sect. 3 we will consider the effect of the Born–Infeld electrodynamics on the negative refraction in generalized superconductors. We will summarize our results in the last section.

2 Generalized holographic superconductors with Born–Infeld electrodynamics

In order to construct the generalized holographic superconductors with the Born–Infeld electrodynamics in the probe limit, we consider a four-dimensional planar Schwarzschild-AdS black hole background

$$\begin{aligned} ds^2=-f\left( r\right) dt^2+\frac{1}{f\left( r\right) }dr^2+r^2\left( dx^2+dy^2\right) , \end{aligned}$$

(1)

with

$$\begin{aligned} f(r)=r^2\left( 1-\frac{r_{h}^{3}}{r^{3}}\right) , \end{aligned}$$

(2)

where $r_{h}$ is the radius of the event horizon. The Hawking temperature of the black hole, which will be interpreted as the temperature of the CFT, is determined by $T=3r_{h}/4\pi$. We then introduce the Born–Infeld electrodynamics and a charged scalar field coupled via a generalized Lagrangian

$$\begin{aligned} S= & {} \int d^{4}x\sqrt{-g}\left[ \frac{1}{b}\left( 1-\sqrt{1+\frac{b F^2}{2}}\right) -\frac{(\partial _{\mu }\Psi )^2}{2}\right. \nonumber \\&\left. -\frac{m^2\Psi ^2}{2}-|\text {G}(\Psi )|(\partial \alpha -A)^2\right] , \end{aligned}$$

(3)

where both the charged scalar field $\Psi$ and the phase $\alpha$ are real, and the local U(1) gauge symmetry in this theory is given by $A_{\mu }\rightarrow A_{\mu }+\partial _{\mu }\lambda$ together with $\alpha \rightarrow \alpha +\lambda$. When the Born–Infeld parameter $b\rightarrow 0$, the model (3) reduces to the generalized holographic superconductors with the usual Maxwell electrodynamics investigated in [20,21,22].

Fig. 1

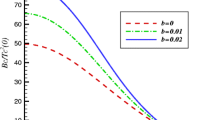
The condensate as a function of the chemical potential with the fixed coefficient $\xi =0.2$ (left) and $\xi =0.5$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel from left to right correspond to increasing Born–Infeld parameter, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively. For concreteness, we have set the mass of the scalar field $m^{2}=-2$

Using the gauge symmetry to fix the phase $\alpha =0$ and taking the ansatz $\Psi =\Psi (r)$, $A=\Phi (r)dt$, we can get the equations of motion

$$\begin{aligned}&\Psi ''+\biggl (\frac{2}{r}+\frac{f'}{f}\biggr )\Psi '-\frac{m^2}{f}\Psi +\frac{\Phi ^2}{f^{2}}\frac{d\text {G}(\Psi )}{d\Psi }=0, \end{aligned}$$

(4)

$$\begin{aligned}&\Phi ''+\frac{2}{r}(1-b\Phi '^2)\Phi '-\frac{2\text {G}(\Psi )}{f}(1-b\Phi '^2)^{3/2}\Phi =0, \end{aligned}$$

(5)

where a prime denotes the derivative with respect to r. Imposing the appropriate boundary conditions, we can solve Eqs. (4) and (5) numerically by doing integration from the horizon out to the infinity [6]. At the horizon $r=r_{h}$, we require the regularity conditions

$$\begin{aligned} \Phi (r_{h})=0,~~~~\Psi '(r_{h})=\frac{m^2\Psi (r_{h})}{f'(r_{h})}. \end{aligned}$$

(6)

At infinity $r\rightarrow \infty$, we have asymptotic behaviors

$$\begin{aligned} \Phi =\mu -\frac{\rho }{r},~~~~\Psi =\frac{\Psi _{-}}{r^{\Delta _{-}}} + \frac{\Psi _{+}}{r^{\Delta _{+}}}, \end{aligned}$$

(7)

with $\Delta _\pm =(3\pm \sqrt{9+4m^2})/2$. According to the AdS/CFT correspondence, $\mu$ and $\rho$ are interpreted as the chemical potential and the charge density in the dual field theory, respectively. Note that, provided $\Delta _{-}$ is larger than the unitarity bound, both $\Psi _{-}$ and $\Psi _{+}$ can be normalizable and be used to define operators on the dual field theory, $\Psi _{-}=\langle O_{-}\rangle$, $\Psi _{+}=\langle O_{+}\rangle$, respectively [6]. In this work, we impose the boundary condition $\Psi _{-}=0$ since we concentrate on the condensate for the operator $\langle O_{+}\rangle$. Considering that the choices of the scalar field mass will not qualitatively modify our results, we will set $m^2=-2$ for concreteness. Thus, the scalar condensate is now described by the operator $\langle O_{2}\rangle =\Psi _{2}$.

We will investigate the effect of the Born–Infeld electrodynamics on the condensate of the system. For simplicity, we consider a particular form of $\text {G}(\Psi )$, i.e.,

$$\begin{aligned} \text {G}(\Psi )=\Psi ^{2}+\xi \Psi ^{8}, \end{aligned}$$

(8)

with the model parameter $\xi$ introduced in Ref. [22]. We solve the equations of motion numerically, and plot in Fig. 1 the condensate around the critical region for chosen values of $\xi$ and various Born–Infeld parameters. In the case of $\xi =0$ or small $\xi$, for example $\xi =0.2$, the transition is of the second order and the condensate approaches zero as $\langle O_{2}\rangle \sim (\mu -\mu _{c})^{1/2}$ for all values of b considered here. However, the story is different if we increase the model parameter $\xi$. Focusing on the case of $\xi =0.5$ in Fig. 1, as an example, we observe that $\langle O_{2}\rangle$ becomes multivalued near the critical point and the first-order phase transition appears. This behavior keeps for all values of b except for $b=0.00$ and increasing b makes the behavior more distinct, which supports the findings in Ref. [39] and indicates that the greater the Born–Infeld corrections the easier it is for the first-order phase transition to emerge. Thus, we find that not only the model parameter $\xi$ but also the Born–Infeld parameter b can manipulate the order of the phase transition. The Born–Infeld electrodynamics provides richer physics in terms of the phase transition. On the other hand, we can see clearly from Fig. 1 that the critical chemical potential $\mu _{c}$ increases with the increase of the Born–Infeld parameter for a fixed model parameter $\xi$, which indicates that large Born–Infeld electrodynamics corrections hinder the formation of the condensation. This agrees well with the findings in the first holographic superconductor model with the Born–Infeld electrodynamics introduced in [34].

3 Negative refraction in generalized superconductors with Born–Infeld electrodynamics

In the preceding section we have constructed the generalized holographic superconductors with the Born–Infeld electrodynamics. Now we are in a position to discuss the optical properties of these holographic systems and reveal the effect of the Born–Infeld electrodynamics on the negative refraction in generalized superconductors. Just as the standard assumption in the usual Maxwell electrodynamics [23, 26], we will assume that the boundary theory is weakly coupled to a dynamical electromagnetic field since the Born–Infeld electrodynamics is a correction to the usual Maxwell electrodynamics and calculate the refractive index of the system perturbatively.

3.1 Holographic setup

Using the linear response theory (for more details see Ref. [23]), we can find that the electric permittivity and the effective magnetic permeability for isotropic media are determined by the frequency dependent transverse current correlators as follows

$$\begin{aligned}&\epsilon \left( \omega \right) = 1+\frac{4\pi }{\omega ^{2}} C_{em}^{2}G_{T}^{0}\left( \omega \right) , \nonumber \\&\mu \left( \omega \right) = \frac{1}{1- 4\pi C_{em}^{2}G_{T}^{2}\left( \omega \right) }, \end{aligned}$$

(9)

where $C_{em}$ is the electromagnetic coupling which will be set to unity when performing numerical calculations, and $G_{T}^{0}\left( \omega \right)$ and $G_{T}^{2}\left( \omega \right)$ are the expansion coefficients of the retarded correlators [67] in the spatial momentum k, i.e.,

$$\begin{aligned} G_{T}\left( \omega ,k \right) =G_{T}^{0}\left( \omega \right) +k^{2} G_{T}^{2}\left( \omega \right) + \cdots . \end{aligned}$$

(10)

So the refractive index can be given by

$$\begin{aligned} n^{2}(\omega )=\epsilon (\omega )\mu \left( \omega \right) . \end{aligned}$$

(11)

Generally, the existence of a negative refractive index can be predicted by using the Depine–Lakhtakia (DL) index $n_{DL}$ expressed as [68]

$$\begin{aligned} n _{DL}= Re[\epsilon (\omega )]|\mu (\omega )| +Re[\mu (\omega )]| \epsilon (\omega )|, \end{aligned}$$

(12)

where the negativity of the DL index indicates that the phase velocity in the medium is opposite to the direction of the energy flow, i.e., the system has negative refractive index.

Let us now move on to the strategy to calculate these quantities in our holographic superconducting system with the Born–Infeld electrodynamics. Considering the gauge field perturbation

$$\begin{aligned} \delta A_{x}= A_{x}(r) e^{-i \omega t + iky}, \end{aligned}$$

(13)

we obtain the equation of motion for $A_{x}(r)$ as

$$\begin{aligned}&A_{x}''+\biggl (\frac{f'}{f}+\frac{b\Phi '\Phi ''}{1-b\Phi '^2}\biggr )A_{x}'\nonumber \\&\quad +\biggl [\frac{\omega ^{2}}{f^{2}}-\frac{k^{2}}{r^{2}f}-\frac{2 \sqrt{1-b\Phi '^2}\text {G}(\Psi )}{f}\biggr ]A_{x}=0. \end{aligned}$$

(14)

We can numerically solve this equation with the appropriate boundary conditions, i.e., the ingoing wave boundary condition at the event horizon

$$\begin{aligned} A_{x}\propto f^{-\frac{i\omega }{3r_{h}}}, \end{aligned}$$

(15)

and the asymptotic behavior at the asymptotic AdS boundary

$$\begin{aligned} A_{x} = A_{x}^{(0)} + \frac{A_{x}^{(1)}}{r} +\cdots . \end{aligned}$$

(16)

Thus, according to the AdS/CFT correspondence, the retarded correlator has the form [69]

$$\begin{aligned} G_{T}\left( \omega ,k \right) =\frac{A_{x}^{(1)}}{A_{x}^{(0)}}. \end{aligned}$$

(17)

In order to calculate $G_{T}^{0}(\omega )$ and $G_{T}^{2}(\omega )$, we will expand $A_x(r)$ in powers of k just as in Eq. (10) for $G_{T}\left( \omega ,k \right)$

$$\begin{aligned} A_{x}(r)=A_{x0}(r)+k^{2}A_{x2}(r)+\cdots , \end{aligned}$$

(18)

which leads to the equations of motion

$$\begin{aligned}&A_{x0}''+\biggl (\frac{f'}{f}+\frac{b\Phi '\Phi ''}{1-b\Phi '^2}\biggr )A_{x0}'\nonumber \\&\quad + \biggl [\frac{\omega ^{2}}{f^{2}}-\frac{2 \sqrt{1-b\Phi '^2}\text {G}(\Psi )}{f}\biggr ]A_{x0}=0, \end{aligned}$$

(19)

$$\begin{aligned}&A_{x2}''+\biggl (\frac{f'}{f}+\frac{b\Phi '\Phi ''}{1-b\Phi '^2}\biggr )A_{x2}'\nonumber \\&\quad +\biggl [\frac{\omega ^{2}}{f^{2}}-\frac{2 \sqrt{1-b\Phi '^2}\text {G}(\Psi )}{f}\biggr ]A_{x2}-\frac{A_{x0}}{r^{2}f}=0. \end{aligned}$$

(20)

With the asymptotic forms of $A_{x0}$ and $A_{x2}$ found from Eqs. (19) and (20), i.e.,

$$\begin{aligned} A_{x0} = A_{x0}^{(0)} + \frac{A_{x0}^{(1)}}{r} +\cdots , ~~~~~A_{x2} = A_{x2}^{(0)} + \frac{A_{x2}^{(1)}}{r} +\cdots , \end{aligned}$$

(21)

we get

$$\begin{aligned} G_{T}^0 (\omega )=\frac{A_{x0}^{(1)}}{A_{x0}^{(0)}}, \ \ \ \ G_{T}^2 (\omega )=\frac{A_{x0}^{(1)}}{A_{x0}^{(0)}} \biggl [\frac{A_{x2}^{(1)}}{A_{x0}^{(1)}} - \frac{A_{x2}^{(0)}}{A_{x0}^{(0)}} \biggr ]. \end{aligned}$$

(22)

Substituting Eq. (22) into Eqs. (9) and (12), we can obtain $\epsilon \left( \omega \right)$, $\mu \left( \omega \right)$ and $n _{DL}$ in terms of $A_{x0}^{(0)}$, $A_{x0}^{(1)}$, $A_{x2}^{(0)}$ and $A_{x2}^{(1)}$.

3.2 Numerical results and discussion

Using the shooting method, we can solve the equations of motion (19) and (20) numerically and then examine the effect of the Born–Infeld electrodynamics on the negative refraction. For concreteness, we will set $\xi =0.2$ for the fixed mass of the scalar field $m^{2}=-2$. It should be noted that other choices of the model parameter $\xi$ will not qualitatively modify our results. On the other hand, we will investigate our system below the critical temperature, i.e., $T<T_{c}$ since we concentrate on the superconducting phase.

Fig. 2

The permittivity $\epsilon$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel from top to bottom correspond to increasing Born–Infeld parameter, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively

Fig. 3

The permeability $\mu$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel correspond to the Born–Infeld parameter $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively

In Figs. 2 and 3 , we plot the permittivity $\epsilon$ and permeability $\mu$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively. Regardless of the fixed temperature and Born–Infeld parameter, we observe that, for the permittivity, Re$(\epsilon )$ is negative at low frequencies and Im$(\epsilon )$ is always positive and has a pole at the zero frequency, but for the permeability, Re$(\mu )$ is always positive and Im$(\mu )$ is negative. Obviously, Re$(\epsilon )$ and Re$(\mu )$ are not simultaneously negative, which may be a signal of the negative refraction [23]. However, just as pointed out in [19, 22, 29], Im$(\mu )<0$ could imply some problem in the $\epsilon -\mu$ approach, although we have defined an effective magnetic permeability that is not an observable. We will not comment on this further since this delicate issue is beyond the scope and the purpose of our work.

Fig. 4

The Depine–Lakhtakia index $n_{DL}$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel from top to bottom correspond to increasing Born–Infeld parameter, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively

Our main purpose here is to calculate the DL index $n_{DL}$ and its dependence on the Born–Infeld parameter b. In Fig. 4, we present $n_{DL}$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively. From this Figure, we can see the emergence of the negative DL index, below a certain value of $\omega /T$ except in the case of $b=0$ with $T=0.86T_{c}$. Fixing the temperature of the system, we find that the value of $\omega /T$, below which the negative $n_{DL}$ appears, increases as the Born–Infeld parameter increases, which indicates that the geater the Born–Infeld corrections, the larger the range of frequencies for which negative refraction occurs. On the other hand, we note that the negative $n_{DL}$ appears in the case of the Born–Infeld parameter $b=0$ at the temperature $T=0.81T_{c}$ and disappears at $T=0.86T_{c}$, but the negative $n_{DL}$ always appears in the case of the Born–Infeld parameter $b=0.05$ ($b=0.10$ or $b=0.15$) at the temperatures $T=0.81T_{c}$ and $T=0.86T_{c}$, which shows that greater Born–Infeld corrections also make the range of temperatures larger for which negative refraction occurs. Interestingly, the Born–Infeld electrodynamics can play an important role in determining the appearance of negative refraction.

Fig. 5

$|\frac{G^{2}_{T}(\omega )}{G^{0}_{T}(\omega )}n^{2}|\omega ^{2}$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel from top to bottom correspond to increasing Born–Infeld parameter, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively

In order to ensure the validity of the expansion used in Eq. (10), we require a constraint

$$\begin{aligned} \left| \frac{k^{2}G^{2}_{T}(\omega )}{G^{0}_{T}(\omega )}\right| =\left| \frac{G^{2}_{T}(\omega )}{G^{0}_{T}(\omega )}n^{2}\right| \omega ^{2}\ll 1. \end{aligned}$$

(23)

Thus, our $\epsilon -\mu$ analysis is valid only for the frequencies for which this constraint is not violated. The behaviors of $|\frac{G^{2}_{T}(\omega )}{G^{0}_{T}(\omega )}n^{2}|\omega ^{2}$ as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b are given in Fig. 5, which shows that, within the plotted frequency range, the constraint (23) is marginally satisfied in the frequency region where $n_{DL}$ is negative for all values of b considered here. Of course, Eq. (23) is not very strictly satisfied and the caveat may be related to the appearance of a negative imaginary part of the magnetic permeability, just as pointed out in [22, 29]. Though Markel proposed that Im$(\mu )$ (the loss term in the permeability) can in fact be negative for diamagnetic materials [70], it is worthwhile to have a better understanding of this point in our holographic approach. Interestingly, the inclusion of the backreaction can make Im$(\mu )$ positive [19, 29, 31]. We will leave this subject for future research.

Fig. 6

The ratio Re(n) / Im(n) as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b. The four lines in each panel from top to bottom correspond to increasing Born–Infeld parameter, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively

Finally, we consider the ratio Re(n) / Im(n) and discuss the dissipation effects in our system. In Fig. 6, we plot the ratio Re(n) / Im(n) as a function of $\omega /T$ with the fixed temperatures $T=0.81T_{c}$ (left) and $T=0.86T_{c}$ (right) for different values of the Born–Infeld parameter b, i.e., $b=0.00$ (red), 0.05 (blue), 0.10 (green) and 0.15 (black), respectively. For the fixed temperature, we observe that the ratio decreases with increasing values of b for the fixed $\omega /T$, and the magnitude of Re(n) / Im(n) is small within the negative refraction frequency range, which implies large dissipation in the system. However, we can use the Born–Infeld corrections to reduce the dissipation since the negative refraction frequency range depends on the Born–Infeld parameter b. For example, the ratio Re(n) / Im(n) is about 0.10 when $\omega /T=2.0$ with $b=0.00$ but is about 0.13 when $\omega /T=2.6$ with $b=0.05$ for the case of $T=0.81T_{c}$. Obviously, the Born–Infeld electrodynamics can be used to improve the propagation in the holographic setup.

4 Conclusions

We have constructed the generalized superconductors with the Born–Infeld electrodynamics and studied their negative refraction in the probe limit, which may help us to understand the influences of the 1 / N or $1/\lambda$ corrections on the holographic superconductor models and their optical properties. Varying the Born–Infeld parameter as well as the temperature, we calculated in details the electric permittivity, the effective magnetic permeability, the refractive index, and the Depine–Lakhtakia (DL) index of our system and observed the existence of negative refraction in the superconducting phase at small frequencies. Interestingly, we found that the greater the Born–Infeld corrections the larger the range of frequencies or the range of temperatures for which a negative DL index occurs, which indicates that the Born–Infeld electrodynamics facilitates the appearance of negative refraction. Furthermore, we analyzed the dissipation effects in our system and found that the tunable Born–Infeld parameter can be used to improve the propagation in the holographic setup. Thus, we concluded that the Born–Infeld electrodynamics can play an important role in determining the optical properties of the boundary theory. The extension of this work to the fully backreacted spacetime would be interesting since the backreaction provides richer physics in the generalized holographic superconductors and significantly affects their optical properties [29, 31]. We will leave this for future study.