1 Introduction

In 2013, the BESIII Collaboration studied the process \(e^+e^- \rightarrow \pi ^+\pi ^-J/\psi \) at a center-of-mass energy of 4.260 GeV using a \(525\, \mathrm{pb}^{-1}\) data sample collected with the BESIII detector, and observed a structure \(Z_c(3900)\) in the \(\pi ^\pm J/\psi \) mass spectrum [1]. Then the structure \(Z_c(3900)\) was confirmed by the Belle and CLEO Collaborations [2, 3]. Also in 2013, the BESIII Collaboration studied the process \(e^+e^- \rightarrow \pi D \bar{D}^*\), and observed a distinct charged structure \(Z_c(3885)\) in the \((D \bar{D}^*)^{\pm }\) mass spectrum [4]. The angular distribution of the \(\pi Z_c(3885)\) system favors a \(J^P=1^+\) assignment [4]. Furthermore, the BESIII Collaboration measured the ratio \( R_{exp}\) [4],

$$\begin{aligned} R_{exp}= & {} \frac{\Gamma (Z_c(3885)\rightarrow D\bar{D}^*)}{\Gamma (Z_c(3900)\rightarrow J/\psi \pi )} =6.2 \pm 1.1 \pm 2.7 . \end{aligned}$$
(1)

In 2015, the BESIII Collaboration observed the neutral parter \(Z_c^0(3900)\) with a significance of \(10.4\, \sigma \) in the process \(e^+e^- \rightarrow \pi ^0\pi ^0J/\psi \) [5]. Recently, the BESIII Collaboration determined the spin and parity of the \(Z_c^\pm (3900)\) state to be \(J^P = 1^+\) with a statistical significance larger than \(7\sigma \) over other quantum numbers in a partial wave analysis of the process \(e^+e^- \rightarrow \pi ^+\pi ^-J/\psi \) [6].

Now we list out the mass and width from different measurements.

$$\begin{aligned} Z_c^\pm (3900) : M&= 3899.0\pm 3.6\pm 4.9 \text{ MeV } , \nonumber \\ \Gamma&= 46\pm 10\pm 20 \text{ MeV } , \quad \mathrm{BESIII} \ [1] ,\nonumber \\ Z_c^\pm (3900) : M&= 3894.5\pm 6.6\pm 4.5 \text{ MeV } , \nonumber \\ \Gamma&= 63\pm 24 \pm 26 \text{ MeV } , \quad \mathrm{Belle} \ [2] , \nonumber \\ Z_c^\pm (3900) : M&= 3886 \pm 4 \pm 2 \text{ MeV } , \nonumber \\ \Gamma&=37 \pm 4 \pm 8 \text{ MeV } , \quad \mathrm{CLEO}\ [3] , \nonumber \\ Z_c^\pm (3885) : M&= 3883.9 \pm 1.5 \pm 4.2 \text{ MeV } , \nonumber \\ \Gamma&= 24.8 \pm 3.3 \pm 11.0 \text{ MeV } , \quad \mathrm{BESIII} \ [4] ,\nonumber \\ Z_c^0(3900) : M&= 3894.8 \pm 2.3 \pm 3.2 \text{ MeV } , \nonumber \\ \Gamma&= 29.6 \pm 8.2 \pm 8.2 \text{ MeV } , \quad \mathrm{BESIII} \ [5] . \end{aligned}$$
(2)

The values of the mass are consistent with each other from different measurements, while the values of the width differ from each other greatly. The \(Z_c(3900)\) and \(Z_c(3885)\) may be the same particle according to the mass, spin and parity.

Faccini et al. tentatively assign the \(Z_c(3900)\) to be the negative charge conjunction partner of the X(3872) [7]. There have been several possible assignments, such as tetraquark state [8,9,10,11,12,13], molecular state [14,15,16,17,18,19,20], hadro-charmonium [21], rescattering effect [22,23,24].

In Ref. [12], we study the masses and pole residues of the \(J^{PC}=1^{+\pm }\) hidden charm tetraquark states with the QCD sum rules by calculating the contributions of the vacuum condensates up to dimension-10 in a consistent way in the operator product expansion, and explore the energy scale dependence in details for the first time. The predicted masses \(M_{X}=3.87^{+0.09}_{-0.09}\,\mathrm{GeV}\) and \(M_{Z}=3.91^{+0.11}_{-0.09}\,\mathrm{GeV}\) support assigning the X(3872) and \(Z_c(3900)\) to be the \(1^{++}\) and \(1^{+-}\) diquark–antidiquark type tetraquark states, respectively.

In Ref. [20], we study the axialvector hidden charm and hidden bottom molecular states with the QCD sum rules by calculating the vacuum condensates up to dimension-10 in the operator product expansion, and explore the energy scale dependence of the QCD sum rules for the heavy molecular states in details. The numerical results support assigning the \(X(3872), Z_c(3900), Z_b(10610)\) to be the color singlet-singlet type molecular states with \(J^{PC}=1^{++}, 1^{+-}, 1^{+-}\), respectively.

We can reproduce the experimental value of the mass of the \(Z_c(3900)\) based on the QCD sum rules both in the scenario of tetraquark states and in the scenario of molecule states [12, 20]. Additional theoretical works on the width are still needed to identify the \(Z_c(3900)\).

In Ref. [13], Dias et al identify the \(Z_c^\pm (3900)\) as the charged partner of the X(3872) state, and study the two-body strong decays \(Z_c^+(3900)\rightarrow J/\psi \pi ^+, \eta _c\rho ^+, D^+ \bar{D}^{*0}, D^0 \bar{D}^{*+}\) with the QCD sum rules by evaluating the three-point correlation functions and take into account only the connected Feynman diagrams, and they obtain the width \(\Gamma _{Z_c}=63.0 \pm 18.1\,\mathrm{MeV}\).

In Ref. [25], Agaev et al study the two-body strong decays \(Z_c^+(3900)\rightarrow J/\psi \pi ^+, \eta _c\rho ^+\) with the light-cone QCD sum rules by taking into account both the connected and disconnected Feynman diagrams, and obtain the width \(\Gamma _{Z_c}=\Gamma (Z_c^+(3900)\rightarrow J/\psi \pi ^+)+\Gamma (Z_c^+(3900)\rightarrow \eta _c\rho ^+)=65.7 \pm 10.6\,\mathrm{MeV}\).

It is interesting to know that the connected Feynman diagrams alone or the connected plus disconnected Feynman diagrams lead to the same result [13, 25]. As far as the X(5568) is concerned, if we take the scenario of tetraquark states, the width can also be reproduced based on the connected Feynman diagrams alone [26] or the connected plus disconnected Feynman diagrams [27, 28]. We should prove that the contributions of the disconnected Feynman diagrams can be neglected safely.

In this article, we assign the \(Z_c(3900)\) to be the diquark–antidiquark type tetraquark state with \(J^{PC}=1^{+-}\), study the hadronic coupling constants \(G_{Z_cJ/\psi \pi }, G_{Z_c\eta _c\rho }, G_{Z_cD \bar{D}^{*}}\) with the three-point QCD sum rules by including both the connected and disconnected Feynman diagrams, special attentions are paid to the hadronic spectral densities of the three-point correlation functions, then calculate the partial decay widths of the strong decays \(Z_c^+(3900)\rightarrow J/\psi \pi ^+, \eta _c\rho ^+, D^+ \bar{D}^{*0}, D^0 \bar{D}^{*+}\), and diagnose the nature of the \(Z_c^\pm (3900)\) based on the width and the ratio \(R_{exp}=6.2 \pm 1.1 \pm 2.7\), if the \(Z_c(3900)\) and \(Z_c(3885)\) are the same particle with the diquark–antidiquark type structure.

The article is arranged as follows: we derive the QCD sum rules for the hadronic coupling constants \(G_{Z_cJ/\psi \pi }, G_{Z_c\eta _c\rho }, G_{Z_cD \bar{D}^{*}}\) in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusion.

2 The width of the \(Z_c(3900)\) as an axialvector tetraquark state

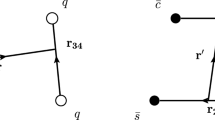
We study the two-body strong decays \(Z_c^+(3900)\rightarrow J/\psi \pi ^+, \eta _c\rho ^+, D^+ \bar{D}^{*0}, \bar{D}^0 D^{*+}\) with the following three-point correlation functions \(\Pi _{\mu \nu }^{1}(p,q), \Pi _{\mu \nu }^{2}(p,q)\) and \(\Pi _{\mu \nu }^{3}(p,q)\), respectively,

$$\begin{aligned} \Pi _{\mu \nu }^{1}(p,q)= & {} i^2\int d^4xd^4y e^{ipx}e^{iqy} \langle 0|T \{J_\mu ^{J/\psi }(x)J_5^{\pi }(y)J_{\nu }(0) \}|0\rangle , \end{aligned}$$
(3)
$$\begin{aligned} \Pi _{\mu \nu }^{2}(p,q)= & {} i^2\int d^4xd^4y e^{ipx}e^{iqy} \langle 0|T \{J_5^{\eta _c}(x)J_\mu ^{\rho }(y)J_{\nu }(0)\}|0\rangle , \end{aligned}$$
(4)
$$\begin{aligned} \Pi _{\mu \nu }^{3}(p,q)= & {} i^2\int d^4xd^4y e^{ipx}e^{iqy} \langle 0|T\{J_\mu ^{D^*}(x)J_5^{D}(y)J_{\nu }(0) \}|0\rangle , \end{aligned}$$
(5)

where the currents

$$\begin{aligned} J_\mu ^{J/\psi }(x)= & {} \bar{c}(x)\gamma _\mu c(x) ,\nonumber \\ J_5^{\pi }(y)= & {} \bar{u}(y)i\gamma _5 d(y) , \end{aligned}$$
(6)
$$\begin{aligned} J_5^{\eta _c}(x)= & {} \bar{c}(x)i\gamma _5 c(x) ,\nonumber \\ J_\mu ^{\rho }(y)= & {} \bar{u}(y)\gamma _\mu d(y) , \end{aligned}$$
(7)
$$\begin{aligned} J_\mu ^{D^*}(x)= & {} \bar{u}(x)\gamma _\mu c(x) ,\nonumber \\ J_5^{D}(y)= & {} \bar{c}(y)i\gamma _5 d(y) , \end{aligned}$$
(8)
$$\begin{aligned} J_\nu (0)= & {} \frac{\varepsilon ^{ijk}\varepsilon ^{imn}}{\sqrt{2}} \{c^n(0)C\gamma _\nu u^m(0) \bar{c}^k(0)\gamma _5 C \bar{d}^j(0) \nonumber \\&-c^n(0)C\gamma _5 u^m(0)\bar{c}^k(0)\gamma _\nu C \bar{d}^j(0) \} , \end{aligned}$$
(9)

interpolate the mesons \(J/\psi , \pi , \eta _c, \rho , D^*, D\) and \(Z_c(3900)\), respectively.

We insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators into the three-point correlation functions \(\Pi _{\mu \nu }^{1}(p,q), \Pi _{\mu \nu }^{2}(p,q)\) and \(\Pi _{\mu \nu }^{3}(p,q)\) [29,30,31], and isolate the ground state contributions to obtain the following results,

$$\begin{aligned} \Pi _{\mu \nu }^{1}(p,q)= & {} \frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d} \nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\pi }^2-q^2)}\nonumber \\&\times \, \left( -g_{\mu \alpha }+\frac{p_{\mu }p_{\alpha }}{p^2} \right) \left( -g_{\nu }{}^{\alpha }+\frac{p^{\prime }_{\nu }p^{\prime \alpha }}{p^{\prime 2}} \right) +\cdots \nonumber \\= & {} \left\{ \frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d} \right. \nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\pi }^2-q^2)} \nonumber \\&+\, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)} \int _{s^0_\pi }^\infty dt\frac{\rho _{Z_c\pi ^\prime }(p^{\prime 2},p^2,t)}{t-q^2}\nonumber \\&+ \,\frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\pi }^2-q^2)} \int _{s^0_{J/\psi }}^\infty dt\frac{\rho _{Z_c \psi ^\prime }(p^{\prime 2},t,q^2)}{t-p^2}\nonumber \\&+\,\frac{-i}{(M_{J/\psi }^2-p^{2})(M_{\pi }^2-q^2)} \nonumber \\&\times \,\left. \int _{s^0_{Z_c}}^\infty dt \frac{\rho _{Z_c^\prime J/\psi }(t,p^2,q^2)+\rho _{Z_c^\prime \pi }(t,p^2,q^2)}{t-p^{\prime 2}}+\cdots \right\} \nonumber \\&\times \, (g_{\mu \nu }+\cdots ) +\cdots \nonumber \\= & {} \Pi _1(p^{\prime 2},p^2,q^2)\,g_{\mu \nu }+\cdots , \end{aligned}$$
(10)
$$\begin{aligned} \Pi _{\mu \nu }^{2}(p,q)= & {} \frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c}\nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)(M_{\rho }^2-q^2)}\nonumber \\&\times \, \left( -g_{\mu \alpha }+\frac{q_{\mu }q_{\alpha }}{q^2} \right) \left( -g_{\nu }{}^{\alpha }+\frac{p^{\prime }_{\nu }p^{\prime \alpha }}{p^{\prime 2}} \right) +\cdots \nonumber \\= & {} \left\{ \frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c}\right. \nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)(M_{\rho }^2-q^2)}\nonumber \\&+\, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)}\int _{s^0_\rho }^\infty dt \frac{\rho _{Z_c\rho ^\prime }(p^{\prime 2},p^2,t)}{t-q^2} \nonumber \\&+\, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\rho }^2-q^2)} \int _{s^0_{\eta _c}}^\infty dt\frac{\rho _{Z_c\eta _c^\prime } (p^{\prime 2},t,q^2)}{t-p^2}\nonumber \\&+\, \frac{-i}{(M_{\eta _c}^2-p^{2})(M_{\rho }^2-q^2)} \int _{s^0_{Z_c}}^\infty dt\nonumber \\&\times \, \left. \frac{\rho _{Z_c^\prime \eta _c} (t,p^2,q^2)+\rho _{Z_c^\prime \rho }(t,p^2,q^2)}{t-p^{\prime 2}}+\cdots \right\} \nonumber \\&\times \, \left( g_{\mu \nu }+\cdots \right) +\cdots \nonumber \\= & {} \Pi _2(p^{\prime 2},p^2,q^2)\,g_{\mu \nu }+\cdots , \end{aligned}$$
(11)
$$\begin{aligned} \Pi _{\mu \nu }^{3}(p,q)= & {} \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_c D\bar{D}^*}}{m_c}\nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)(M_{D}^2-q^2)}\nonumber \\&\times \, \left( -g_{\mu \alpha }+\frac{p_{\mu }p_{\alpha }}{p^2} \right) \left( -g_{\nu }{}^{\alpha }+\frac{p^{\prime }_{\nu }p^{\prime \alpha }}{p^{\prime 2}} \right) +\cdots \nonumber \\= & {} \left\{ \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_cD\bar{D}^*}}{m_c}\right. \nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)(M_{D}^2-q^2)} \ \nonumber \\&+ \,\frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)} \int _{s^0_D}^\infty dt\frac{\rho _{Z_cD^\prime }(p^{\prime 2},p^2,t)}{t-q^2}\nonumber \\&+ \,\frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D}^2-q^2)} \int _{s^0_{D^*}}^\infty dt\frac{\rho _{Z_c D^{*\prime }}(p^{\prime 2},t,q^2)}{t-p^2}\nonumber \\&+ \,\frac{-i}{(M_{D^*}^2-p^{2})(M_{D}^2-q^2)} \int _{s^0_{Z_c}}^\infty dt\nonumber \\&\times \, \left. \frac{\rho _{Z_c^\prime D^*}(t,p^2,q^2)+\rho _{Z_c^\prime D}(t,p^2,q^2)}{t-p^{\prime 2}}+\cdots \right\} \nonumber \\&\times \, \left( g_{\mu \nu }+\cdots \right) +\cdots \nonumber \\= & {} \Pi _3(p^{\prime 2},p^2,q^2)\,g_{\mu \nu }+\cdots , \end{aligned}$$
(12)

where \(p^\prime =p+q\), the \(f_{J/\psi }, f_{\pi }, f_{\eta _c}, f_{\rho }, f_{D^*}, f_{D}\) and \(\lambda _{Z_c}\) are the decay constants of the mesons \(J/\psi , \pi , \eta _c, \rho , D^*, D\) and \(Z_c(3900)\), respectively, the \(G_{Z_cJ/\psi \pi }, G_{Z_c\eta _c\rho }\) and \(G_{Z_c D\bar{D}^*}\) are the hadronic coupling constants, which are defined by

$$\begin{aligned} \langle 0|J_{\mu }^{J/\psi }(0)|J/\psi (p)\rangle= & {} f_{J/\psi }M_{J/\psi }\,\xi _\mu , \nonumber \\ \langle 0|J_{5}^{\pi }(0)|\pi (q)\rangle= & {} \frac{f_{\pi }M_{\pi }^2}{m_u+m_d} , \end{aligned}$$
(13)
$$\begin{aligned} \langle 0|J_{5}^{\eta _c}(0)|\eta _c(p)\rangle= & {} \frac{f_{\eta _c}M_{\eta _c}^2}{2m_c} , \nonumber \\ \langle 0|J_{\mu }^{\rho }(0)|\rho (q)\rangle= & {} f_{\rho }M_{\rho }\,\varepsilon _\mu , \nonumber \\ \langle 0|J_{\mu }^{D^*}(0)|D^*(p)\rangle= & {} f_{D^*}M_{D^*}\,\varsigma _\mu , \nonumber \\ \langle 0|J_{5}^{D}(0)|D(q)\rangle= & {} \frac{f_{D}M_{D}^2}{m_c} , \end{aligned}$$
(14)
$$\begin{aligned} \langle Z_c(p^\prime )|J_\nu (0)|0\rangle= & {} \lambda _{Z_c}\,\zeta _\nu ^* \end{aligned}$$
(15)
$$\begin{aligned} \langle J/\psi (p)\pi (q)|Z_c(p^{\prime })\rangle= & {} \xi ^*(p)\cdot \zeta (p^{\prime })\, G_{Z_cJ/\psi \pi } , \nonumber \\ \langle \eta _c(p)\rho (q)|Z_c(p^{\prime })\rangle= & {} \varepsilon ^*(q)\cdot \zeta (p^{\prime }) G_{Z_c\eta _c\rho } , \nonumber \\ \langle D^*(p)D(q)|Z_c(p^{\prime })\rangle= & {} \varsigma ^*(p)\cdot \zeta (p^{\prime })\, G_{Z_c D\bar{D}^*} , \end{aligned}$$
(16)

the \(\xi , \varepsilon , \varsigma \) and \(\zeta \) are polarization vectors of the \(J/\psi \), \(\rho , D^*\) and \(Z_c(3900)\), respectively. The \(s^0_{\pi }, s^0_{J/\psi }, s^0_{Z_c}, s^0_{\eta _c}, s^0_{\rho }, s^0_{D^*}\) and \(s^0_{D}\) are the continuum threshold parameters. The 12 unknown functions \( \rho _{Z_c\pi ^\prime }(p^{\prime 2},p^2,t)\), \(\rho _{Z_c\psi ^\prime }(p^{\prime 2},t,q^2)\), \(\rho _{Z_c^\prime \pi }(t,p^2,q^2)\), \(\rho _{Z_c^\prime J/\psi }(t,p^2,q^2)\), \( \rho _{Z_c\rho ^\prime }(p^{\prime 2},p^2,t)\), \(\rho _{Z_c\eta _c^\prime }(p^{\prime 2},t,q^2)\), \( \rho _{Z_c^\prime \rho }(t,p^2,q^2)\), \( \rho _{Z_c^\prime \eta _c}(t,p^2,q^2)\), \( \rho _{Z_c D^{*\prime }}(p^{\prime 2}, t, q^2)\), \(\rho _{Z_cD^\prime }(p^{\prime 2}, p^2, t)\), \( \rho _{Z_c^\prime D^*}(t,p^2,q^2)\), \( \rho _{Z_c^\prime D}(t,p^2,q^2)\) have complex dependence on the transitions between the ground states and the high resonances or the continuum states.

In this article, we choose the tensor \(g_{\mu \nu }\) to study the hadronic coupling constants \(G_{Z_cJ/\psi \pi }, G_{Z_c\eta _c\rho }\) and \(G_{Z_c D^* D}\) to avoid the contaminations from the corresponding scalar and pseudoscalar mesons, as the following current-meson couplings are non-vanishing,

$$\begin{aligned} \langle 0|J_{\mu }^{J/\psi }(0)|\chi _{c0}(p)\rangle= & {} f_{\chi _{c0}}p_\mu , \nonumber \\ \langle 0|J_{\mu }^{\rho }(0)|a_0(q)\rangle= & {} f_{a_0}q_\mu , \nonumber \\ \langle 0|J_{\mu }^{D^*}(0)|D_0^*(p)\rangle= & {} f_{D^*_0}p_\mu , \nonumber \\ \langle Z_{c0}(p^\prime )|J_\nu (0)|0\rangle= & {} -i\,\lambda _{Z_{c0}}\,p^\prime _\nu , \end{aligned}$$
(17)

where the \(f_{\chi _{c0}}, f_{a_0}, f_{D^*_0}, \lambda _{Z_{c0}}\) are the decay constants of the \(\chi _{c0}(3414), a_0(980), D_0^*(2400)\) and \(Z_{c}(J^P=0^-)\), respectively. The terms proportional to \(p_\mu p^\prime _\nu \) in the \(\Pi _{\mu \nu }^1(p,q)\) and \(\Pi _{\mu \nu }^3(p,q)\) and the terms proportional to \(q_\mu p^\prime _\nu \) in the \(\Pi _{\mu \nu }^2(p,q)\) have contaminations from the hadronic coupling constants \(G_{Z_c \chi _{c0}\pi }, G_{Z_c D^*_0 D}\) and \(G_{Z_c\eta _c a_0}\), respectively.

We introduce the notations \(C_{Z_c\pi ^\prime }\), \( C_{Z_c\psi ^\prime }\), \( C_{Z_c^\prime \pi }\), \( C_{Z_c^\prime J/\psi }\), \( C_{Z_c\rho ^\prime }\), \( C_{Z_c\eta _c^\prime }\), \( C_{Z_c^\prime \rho }\), \( C_{Z_c^\prime \eta _c}\), \( C_{Z_cD^{*\prime }}\), \( C_{Z_cD^\prime }\), \( C_{Z_c^\prime D^*}\) and \(C_{Z_c^\prime D}\) to parameterize the net effects,

$$\begin{aligned} C_{Z_c\pi ^\prime }= & {} \int _{s^0_\pi }^\infty dt\frac{ \rho _{Z_c\pi ^\prime }(p^{\prime 2},p^2,t)}{t-q^2} ,\nonumber \\ C_{Z_c\psi ^\prime }= & {} \int _{s^0_{J/\psi }}^\infty dt\frac{\rho _{Z_c\psi ^\prime }(p^{\prime 2},t,q^2)}{t-p^2} ,\nonumber \\ C_{Z_c^\prime \pi }= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime \pi }(t,p^2,q^2)}{t-p^{\prime 2}} ,\nonumber \\ C_{Z_c^\prime J/\psi }= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime J/\psi }(t,p^2,q^2)}{t-p^{\prime 2}} , \end{aligned}$$
(18)
$$\begin{aligned} C_{Z_c\rho ^\prime }= & {} \int _{s^0_{\rho }}^\infty dt \frac{\rho _{Z_c\rho ^\prime }(p^{\prime 2},p^2,t)}{t-q^2} ,\nonumber \\ C_{Z_c\eta _c^\prime }= & {} \int _{s^0_{\eta _c}}^\infty dt \frac{ \rho _{Z_c\eta _c^\prime }(p^{\prime 2},t,q^2)}{t-p^2} , \nonumber \\ C_{Z_c^\prime \rho }= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime \rho }(t,p^2,q^2)}{t-p^{\prime 2}} ,\nonumber \\ C_{Z_c^\prime \eta _c}= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime \eta _c}(t,p^2,q^2)}{t-p^{\prime 2}} , \end{aligned}$$
(19)
$$\begin{aligned} C_{Z_cD^{*\prime }}= & {} \int _{s^0_{D^*}}^\infty dt \frac{\rho _{Z_c D^{*\prime }}(p^{\prime 2},t,q^2)}{t-p^2} ,\nonumber \\ C_{Z_cD^\prime }= & {} \int _{s^0_{D}}^\infty dt \frac{ \rho _{Z_cD^\prime }(p^{\prime 2},p^2,t)}{t-q^2} , \nonumber \\ C_{Z_c^\prime D^*}= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime D^*}(t,p^2,q^2)}{t-p^{\prime 2}} ,\nonumber \\ C_{Z_c^\prime D}= & {} \int _{s^0_{Z_c}}^\infty dt\frac{ \rho _{Z_c^\prime D}(t,p^2,q^2)}{t-p^{\prime 2}} . \end{aligned}$$
(20)

Then the correlation functions on the phenomenological side can be written as

$$\begin{aligned} \Pi _1(p^{\prime 2},p^2,q^2)= & {} \frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d}\nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\pi }^2-q^2)}\nonumber \\&+ \frac{-i C_{Z_c\pi ^\prime }}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)}\nonumber \\&+ \frac{-i C_{Z_c\psi ^\prime }}{(M_{Z_c}^2-p^{\prime 2})(M_{\pi }^2-q^2)} \nonumber \\&+ \frac{-i C_{Z_c^\prime J/\psi }-i C_{Z_c^\prime \pi }}{(M_{J/\psi }^2-p^{2})(M_{\pi }^2-q^2)} +\cdots , \end{aligned}$$
(21)
$$\begin{aligned} \Pi _2(p^{\prime 2},p^2,q^2)= & {} \frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c}\nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)(M_{\rho }^2-q^2)}\nonumber \\&+ \frac{-i C_{Z_c\rho ^\prime }}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)}\nonumber \\&+\frac{-i C_{Z_c\eta _c^\prime }}{(M_{Z_c}^2-p^{\prime 2})(M_{\rho }^2-q^2)} \nonumber \\&+ \frac{-i C_{Z_c^\prime \eta _c}-i C_{Z_c^\prime \rho }}{(M_{\eta _c}^2-p^{2})(M_{\rho }^2-q^2)} +\cdots , \end{aligned}$$
(22)
$$\begin{aligned} \Pi _3(p^{\prime 2},p^2,q^2)= & {} \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_cD\bar{D}^*}}{m_c}\nonumber \\&\times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)(M_{D}^2-q^2)} \nonumber \\&+ \frac{-iC_{Z_cD^\prime }}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)}\nonumber \\&+ \frac{-i C_{Z_c D^{*\prime }}}{(M_{Z_c}^2-p^{\prime 2})(M_{D}^2-q^2)} \nonumber \\&+ \frac{-i C_{Z_c^\prime D^* }-i C_{Z_c^\prime D }}{(M_{D^*}^2-p^{2})(M_{D}^2-q^2)} +\cdots . \end{aligned}$$
(23)

In numerical calculations, we smear the dependencies of the \(C_{Z_c\pi ^\prime }\), \( C_{Z_c\psi ^\prime }\), \( C_{Z_c^\prime \pi }\), \( C_{Z_c^\prime J/\psi }\), \( C_{Z_c\rho ^\prime }\), \( C_{Z_c\eta _c^\prime }\), \( C_{Z_c^\prime \rho }\), \( C_{Z_c^\prime \eta _c}\), \( C_{Z_cD^{*\prime }}\), \( C_{Z_cD^\prime }\), \( C_{Z_c^\prime D^*}\) and \(C_{Z_c^\prime D}\) on the momentums \(p^{\prime 2}\), \( p^2, q^2\), and take them as free parameters, and choose the suitable values to eliminate the contaminations from the high resonances and continuum states to obtain the stable QCD sum rules with the variations of the Borel parameters.

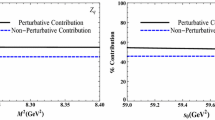
We carry out the operator product expansion up to the vacuum condensates of dimension 5 and neglect the tiny contributions of the gluon condensate. On the QCD side, the correlation functions \(\Pi _{1}(p^{\prime 2},p^2,q^2)\) and \(\Pi _{2}(p^{\prime 2},p^2,q^2)\) can be written as

$$\begin{aligned} \Pi _1(p^{\prime 2},p^2,q^2)= & {} \frac{i}{32\sqrt{2}\pi ^4} \int _{4m_c^2}^{\infty } ds \frac{1}{s-p^2} \int _{0}^{\infty } du\nonumber \\&\times \, \frac{1}{u-q^2}\, u \left( s+2m_c^2 \right) \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&+\frac{i m_c\langle \bar{q} q\rangle }{4\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds\nonumber \\&\times \, \frac{1}{s-p^2} \frac{p^{\prime 2}-s-q^2}{q^2}\, \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&+\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{16\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds \frac{1}{s-p^2}\nonumber \\&\times \, \frac{p^{\prime 2}-s-q^2}{q^4}\, \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&+\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \frac{\partial }{\partial m_A^2}\int _{(m_A+m_c)^2}^{\infty } ds \frac{1}{s-p^2} \nonumber \\&\times \, \frac{p^{\prime 2}-s-q^2}{q^2}\, \frac{\sqrt{\lambda (s,m_A^2,m_c^2)}}{s}\mid _{m_A \rightarrow m_c} \nonumber \\&-\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{16\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds \nonumber \\&\times \, \frac{1}{s-p^2} \frac{p^{\prime 2}-s-q^2}{q^4}\, \sqrt{1-\frac{4m_c^2}{s}} , \end{aligned}$$
(24)
$$\begin{aligned} \Pi _2(p^{\prime 2},p^2,q^2)= & {} -\frac{i}{32\sqrt{2}\pi ^4} \int _{4m_c^2}^{\infty } ds \frac{1}{s-p^2} \int _{0}^{\infty } du\nonumber \\&\times \, \frac{1}{u-q^2}\, u s \, \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&-\frac{i m_c\langle \bar{q} q\rangle }{4\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds \frac{1}{s-p^2}\nonumber \\&\quad \quad \frac{p^{\prime 2}-s-q^2}{q^2}\, \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&-\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{16\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds \frac{1}{s-p^2}\nonumber \\&\times \, \frac{p^{\prime 2}-s-q^2}{q^4}\, \sqrt{1-\frac{4m_c^2}{s}} \nonumber \\&+\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \frac{\partial }{\partial m_A^2}\int _{(m_A+m_c)^2}^{\infty } ds \frac{1}{s-p^2} \nonumber \\&\times \, \frac{p^{\prime 2}-s-q^2}{q^2}\, \frac{\sqrt{\lambda (s,m_A^2,m_c^2)}}{s}\mid _{m_A \rightarrow m_c} \nonumber \\&-\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \int _{4m_c^2}^{\infty } ds \nonumber \\&\times \, \frac{1}{s-p^2} \frac{p^{\prime 2}-s-q^2}{q^4}\, \sqrt{1-\frac{4m_c^2}{s}} , \end{aligned}$$
(25)

where the last two terms originate from the Feynman diagrams where a quark pair \(\bar{q}q\) absorbs a gluon emitted from other quark line. The term

$$\begin{aligned}&+\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \frac{\partial }{\partial m_A^2}\int _{(m_A+m_c)^2}^{\infty } ds\nonumber \\&\quad \frac{1}{s-p^2} \frac{p^{\prime 2}-s-q^2}{q^2}\, \frac{\sqrt{\lambda (s,m_A^2,m_c^2)}}{s}\mid _{m_A \rightarrow m_c} , \end{aligned}$$
(26)

in above equations comes from the connected Feynman diagrams, if we set \(p^{\prime 2}=p^2\), then it reduces to

$$\begin{aligned}&-\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \frac{\partial }{\partial m_A^2}\int _{(m_A+m_c)^2}^{\infty } ds\nonumber \\&\quad \times \, \frac{1}{s-p^2} \frac{\sqrt{\lambda (s,m_A^2,m_c^2)}}{s}\mid _{m_A \rightarrow m_c} \nonumber \\&-\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{48\sqrt{2}\pi ^2} \frac{\partial }{\partial m_A^2}\int _{(m_A+m_c)^2}^{\infty } ds\nonumber \\&\quad \times \, \frac{1}{q^2} \, \frac{\sqrt{\lambda (s,m_A^2,m_c^2)}}{s}\mid _{m_A \rightarrow m_c} . \end{aligned}$$
(27)

It has no contribution after performing the double Borel transformation with respect to the variables \(P^2=-p^2\) and \(Q^2=-q^2\). It is more reasonable to performing the Borel transformation than taking the limit \(q^2 \rightarrow 0\), as we carry out the operator product expansion at the large spacelike region \(Q^2=-q^2 \rightarrow \infty \). So the connected Feynman diagrams have no contributions in the correlation functions \(\Pi _{1/2}(p^{\prime 2},p^2,q^2)\), which are in contrary to Refs. [13, 26], where only the connected Feynman diagrams have contributions and the limit \(Q^2 \rightarrow 0\) is taken.

For the correlation function \(\Pi _3(p^{\prime 2},p^2,q^2)\), only the connected Feynman diagrams have contributions, we can set \(p^{\prime 2}=4p^2\) according to the relation \(M_{Z_c(3900)}\approx 2M_{D^*}\), the complex expression of the correlation function \(\Pi _3(p^{\prime 2},p^2,q^2)\) can be reduced to a more simple form,

$$\begin{aligned} \Pi _3(4p^{2},p^2,q^2)= & {} \frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{\infty } ds \nonumber \\&\times \, \frac{1}{s-p^2}\frac{1}{q^2-m_c^2}\left( \frac{9}{2}-\frac{10m_c^2}{s}+\frac{3m_c^4}{2s^2}\right) \nonumber \\&+\frac{i m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2} \frac{1}{p^2-m_c^2}\int _{m_c^2}^{\infty } du \nonumber \\&\times \,\frac{1}{u-q^2} \left( \frac{9}{2}-\frac{8m_c^2}{u}+\frac{15m_c^4}{2u^2}\right) . \end{aligned}$$
(28)

In the limit \(M_{\pi }^2 \rightarrow 0, M^2_{\rho }\rightarrow 0, M_{D}^2 \rightarrow 0\) and \(m_c^2\rightarrow 0\), we maybe expect to choose \(Q^2=-q^2\) off-shell, and match the terms proportional to \(\frac{1}{Q^2}\) in the limit \(Q^2 \rightarrow 0\) on the hadron side with the ones on the QCD side to obtain QCD sum rules for the momentum dependent hadronic coupling constants \(G_{Z_cJ/\psi \pi }(Q^2), G_{Z_c\eta _c\rho }(Q^2), G_{Z_cD \bar{D}^{*}}(Q^2)\), then extract the values to the mass-shell \(Q^2=-M_{\pi }^2, -M_{\rho }^2\) or \(-M_{D}^2\) to obtain the physical values [13]. However, the approximations \(M^2_{\rho }\rightarrow 0, M_{D}^2 \rightarrow 0\) and \(m_c^2\rightarrow 0\) are rather crude, and we carry out the operator product expansion at the large space-like region \(Q^2=-q^2 \rightarrow \infty \). We prefer taking the imaginary parts of the correlation functions \(\Pi _{1/2/3}(p^{\prime 2},p^2,q^2)\) with respect to \(q^2+i\epsilon \) through dispersion relation and obtain the physical hadronic spectral densities, then take the Borel transform with respect to the \(Q^2\) to obtain the QCD sum rules for the physical hadronic coupling constants.

We have to be cautious in matching the QCD side with the hadron side of the correlation functions \(\Pi _{1/2/3}(p^{\prime 2},p^2,q^2)\), as there appears the variable \(p^{\prime 2}=(p+q)^2\). We rewrite the correlation functions \(\Pi ^H_{1/2/3}(p^{\prime 2},p^2,q^2)\) on the hadron side into the following form through dispersion relation,

$$\begin{aligned} \Pi _1^{H}(p^{\prime 2},p^2,q^2)= & {} \int _{(M_{J/\psi }+M_{\pi })^2}^{s_{Z_c}^0}ds^\prime \int _{4m_c^2}^{s^0_{J/\psi }}ds \int _0^{u^0_{\pi }}du\nonumber \\&\times \, \frac{\rho _1^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(29)
$$\begin{aligned} \Pi ^H_2(p^{\prime 2},p^2,q^2)= & {} \int _{(M_{\eta _c}+M_{\rho })^2}^{s_{Z_c}^0}ds^\prime \int _{4m_c^2}^{s^0_{\eta _c}}ds \int _0^{u^0_{\rho }}du\nonumber \\&\times \, \frac{\rho _2^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(30)
$$\begin{aligned} \Pi ^H_3(p^{\prime 2},p^2,q^2)= & {} \int _{(M_{D^*}+M_{D})^2}^{s^0_{Z_c}}ds^\prime \int _{m_c^2}^{s^0_{D^*}}ds \int _{m_c^2}^{u^0_D}du\nonumber \\&\times \, \frac{\rho _3^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(31)

where the \(\rho _{1/2/3}^H(s^\prime ,s,u)\) are the hadronic spectral densities,

$$\begin{aligned}&\rho _{1/2/3}^H(s^\prime ,s,u)={\lim _{\epsilon _3\rightarrow 0}} {\lim _{\epsilon _2\rightarrow 0}} {\lim _{\epsilon _1\rightarrow 0}} \nonumber \\&\quad \times \, \frac{ \mathrm{Im}_{s^\prime }\, \mathrm{Im}_{s}\,\mathrm{Im}_{u}\,\Pi ^H_{1/2/3}(s^\prime +i\epsilon _3,s+i\epsilon _2,u+i\epsilon _1) }{\pi ^3} ,\nonumber \\ \end{aligned}$$
(32)

we add the superscript H to denote the hadron side. However, on the QCD side, the QCD spectral densities \(\rho _{QCD}^{1/2/3}(s^\prime ,s,u)\) do not exist,

$$\begin{aligned}&\rho _{QCD}^{1/2/3}(s^\prime ,s,u)={\lim _{\epsilon _3\rightarrow 0}} {\lim _{\epsilon _2\rightarrow 0}} {\lim _{\epsilon _1\rightarrow 0}} \nonumber \\&\quad \times \, \frac{ \mathrm{Im}_{s^\prime }\, \mathrm{Im}_{s}\,\mathrm{Im}_{u}\,\Pi ^{QCD}_{1/2/3}(s^\prime +i\epsilon _3,s+i\epsilon _2,u+i\epsilon _1) }{\pi ^3} =0,\nonumber \\ \end{aligned}$$
(33)

because

$$\begin{aligned} {\lim _{\epsilon _3\rightarrow 0}} \frac{ \mathrm{Im}_{s^\prime }\,\Pi ^{QCD}_{1/2/3}(s^\prime +i\epsilon _3,p^2,q^2) }{\pi }= & {} 0 , \end{aligned}$$
(34)

we add the superscript QCD to denote the QCD side.

On the QCD side, the correlation functions \(\Pi ^{QCD}_{1/2/3}(p^{\prime 2},p^2,q^2)\) can be written into the following form through dispersion relation,

$$\begin{aligned} \Pi ^{QCD}_1(p^{\prime 2},p^2,q^2)= & {} \int _{4m_c^2}^{s^0_{J/\psi }}ds \int _0^{u^0_{\pi }}du\nonumber \\&\times \, \frac{\rho ^{QCD}_1(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(35)
$$\begin{aligned} \Pi ^{QCD}_2(p^{\prime 2},p^2,q^2)= & {} \int _{4m_c^2}^{s^0_{\eta _c}}ds \int _0^{u^0_{\rho }}du\nonumber \\&\times \, \frac{\rho _2^{QCD}(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(36)
$$\begin{aligned} \Pi ^{QCD}_3(p^{\prime 2},p^2,q^2)= & {} \int _{m_c^2}^{s^0_{D^*}}ds \int _{m_c^2}^{u^0_D}du \nonumber \\&\times \, \frac{\rho _3^{QCD}(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)}+\cdots , \end{aligned}$$
(37)

where the \(\rho _{1/2/3}^{QCD}(p^{\prime 2},s,u)\) are the QCD spectral densities,

$$\begin{aligned}&\rho _{1/2/3}^{QCD}(p^{\prime 2},s,u)= {\lim _{\epsilon _2\rightarrow 0}} {\lim _{\epsilon _1\rightarrow 0}} \nonumber \\&\quad \times \, \frac{ \mathrm{Im}_{s}\,\mathrm{Im}_{u}\,\Pi _{1/2/3}^{QCD}(p^{\prime 2},s+i\epsilon _2,u+i\epsilon _1) }{\pi ^2} , \end{aligned}$$
(38)

We math the hadron side of the correlation functions with the QCD side of the correlation functions,

$$\begin{aligned}&\int _{4m_c^2}^{s^0_{J/\psi }}ds \int _0^{u^0_{\pi }}du \frac{\rho ^{QCD}_1(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)} \nonumber \\&\quad =\int _{(M_{J/\psi }+M_{\pi })^2}^{\infty }ds^\prime \int _{4m_c^2}^{s^0_{J/\psi }}ds \int _0^{u^0_{\pi }}du\nonumber \\&\qquad \times \, \frac{\rho _1^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)} \nonumber \\&\quad = \frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d}\nonumber \\&\qquad \times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{J/\psi }^2-p^2)(M_{\pi }^2-q^2)}\nonumber \\&\qquad + \frac{-i C_{Z_c^\prime J/\psi }-i C_{Z_c^\prime \pi }}{(M_{J/\psi }^2-p^{2})(M_{\pi }^2-q^2)} , \end{aligned}$$
(39)
$$\begin{aligned}&\int _{4m_c^2}^{s^0_{\eta _c}}ds \int _0^{u^0_{\rho }}du \frac{\rho _2^{QCD}(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)} \nonumber \\&\quad = \int _{(M_{\eta _c}+M_{\rho })^2}^{\infty }ds^\prime \int _{4m_c^2}^{s^0_{\eta _c}}ds \int _0^{u^0_{\rho }}du\nonumber \\&\qquad \times \, \frac{\rho _2^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)}\nonumber \\&\quad = \frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c}\nonumber \\&\qquad \times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{\eta _c}^2-p^2)(M_{\rho }^2-q^2)}\nonumber \\&\qquad + \frac{-i C_{Z_c^\prime \eta _c}-i C_{Z_c^\prime \rho }}{(M_{\eta _c}^2-p^{2})(M_{\rho }^2-q^2)} , \end{aligned}$$
(40)
$$\begin{aligned}&\int _{m_c^2}^{s^0_{D^*}}ds \int _{m_c^2}^{u^0_D}du \frac{\rho _3^{QCD}(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)} \nonumber \\&\quad = \int _{(M_{D^*}+M_{D})^2}^{\infty }ds^\prime \int _{m_c^2}^{s^0_{D^*}}ds \int _{m_c^2}^{u^0_D}du\nonumber \\&\qquad \times \, \frac{\rho _3^H(s^\prime ,s,u)}{(s^\prime -p^{\prime 2})(s-p^2)(u-q^2)} \nonumber \\&\quad = \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_cD\bar{D}^*}}{m_c}\nonumber \\&\qquad \times \, \frac{-i}{(M_{Z_c}^2-p^{\prime 2})(M_{D^*}^2-p^2)(M_{D}^2-q^2)} \nonumber \\&\qquad + \frac{-i C_{Z_c^\prime D^* }-i C_{Z_c^\prime D }}{(M_{D^*}^2-p^{2})(M_{D}^2-q^2)} , \end{aligned}$$
(41)

where the integrals over \(ds^\prime \) are carried out firstly to obtain the solid duality,

$$\begin{aligned}&\int _{\Delta _s^2}^{s^0} ds \int _{\Delta _u^2}^{u^0} du \frac{\rho _{QCD}(p^{\prime 2},s,u)}{(s-p^2)(u-q^2)}=\int _{\Delta _s^2}^{s^0}ds\nonumber \\&\quad \times \,\int _{\Delta _u^2}^{u^0} du \frac{1}{(s-p^2)(u-q^2)} \left[ \int _{\Delta ^2}^{\infty } ds^\prime \frac{\rho _{H}(p^{\prime 2},s,u)}{s^\prime -p^{\prime 2}}\right] , \nonumber \\ \end{aligned}$$
(42)

the \(\Delta _s^2\) and \(\Delta _u^2\) denote the thresholds \(4m_c^2, m_c^2, 0\), the \(\Delta ^2\) denotes the thresholds \((M_{J/\psi }+M_{\pi })^2, (M_{\eta _c}+M_{\rho })^2\) and \((M_{D^*}+M_{D})^2\). No approximation is needed, the continuum threshold parameter \(s^0_{Z_c}\) in the \(s^\prime \) channel is also not needed. The present routine can be applied to study other hadronic couplings directly.

Then we set \(p^{\prime 2}=p^2\) and \(p^{\prime 2}=4p^2\) in the correlation functions \(\Pi _{1/2}(p^{\prime 2},p^2,q^2)\) and \(\Pi _{3}(p^{\prime 2},p^2,q^2)\), respectively, and perform the double Borel transformations with respect to the variables \(P^2=-p^2\) and \(Q^2=-q^2\), respectively to obtain the following QCD sum rules,

$$\begin{aligned}&\frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d}\frac{1}{M_{Z_c}^2-M_{J/\psi }^2} \nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{J/\psi }^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \exp \left( -\frac{M_{\pi }^2}{T_2^2} \right) \nonumber \\&\qquad +\left[ C_{Z_c^\prime J/\psi }+C_{Z_c^\prime \pi }\right] \exp \left( -\frac{M_{J/\psi }^2}{T^2} -\frac{M_{\pi }^2}{T_2^2} \right) \nonumber \\&\quad =-\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{J/\psi }} ds \int _{0}^{u^0_{\pi }} du u\nonumber \\&\qquad \times \, \left( s+2m_c^2\right) \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} -\frac{u}{T_2^2} \right) , \end{aligned}$$
(43)
$$\begin{aligned}&\frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c } \frac{1}{M_{Z_c}^2-M_{\eta _c}^2}\nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{\eta _c}^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \exp \left( -\frac{M_{\rho }^2}{T_2^2} \right) \nonumber \\&\quad +\left[ C_{Z_c^\prime \eta _c}+C_{Z_c^\prime \rho }\right] \exp \left( -\frac{M_{\eta _c}^2}{T^2} -\frac{M_{\rho }^2}{T_2^2} \right) \nonumber \\&\quad =\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{\eta _c}} ds \int _{0}^{u^0_{\rho }} du us\nonumber \\&\qquad \times \,\sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} -\frac{u}{T_2^2} \right) \nonumber \\&\qquad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{12\sqrt{2}\pi ^2} \int _{4m_c^2}^{s^0_{\eta _c}} ds \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} \right) , \end{aligned}$$
(44)
$$\begin{aligned}&\qquad \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_c D\bar{D}^*}}{4m_c } \frac{1}{\widetilde{M}_{Z_c}^2-M_{D^*}^2}\nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{D^*}^2}{T^2} \right) -\exp \left( -\frac{\widetilde{M}_{Z_c}^2}{T^2} \right) \right] \exp \left( -\frac{M_{D}^2}{T_2^2} \right) \nonumber \\&\qquad +\left[ C_{Z_c^\prime D^*}+C_{Z_c^\prime D}\right] \exp \left( -\frac{M_{D^*}^2}{T^2} -\frac{M_{D}^2}{T_2^2} \right) \nonumber \\&\quad =\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{s^0_{D^*}} ds \left( \frac{9}{2}-\frac{10m_c^2}{s}+\frac{3m_c^4}{2s^2}\right) \nonumber \\&\qquad \times \, \exp \left( -\frac{s}{T^2} -\frac{m_c^2}{T_2^2} \right) +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{u^0_{D}} du \nonumber \\&\qquad \times \, \left( \frac{9}{2}-\frac{8m_c^2}{u}+\frac{15m_c^4}{2u^2}\right) \exp \left( -\frac{m_c^2}{T^2} -\frac{u}{T_2^2} \right) , \end{aligned}$$
(45)

where the \(s^0_{J/\psi }, u^0_{\pi }\), \(s^0_{\eta _c}, u^0_{\rho }, s^0_{D^*}\) and \(u^0_{D}\) are the continuum threshold parameters, the \(T^2\) and \(T^2_2\) are the Borel parameters.

In the three QCD sum rules, the terms depend on \(T^2_2\) can be factorized out explicitly,

$$\begin{aligned}&\frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d}\frac{1}{M_{Z_c}^2-M_{J/\psi }^2} \nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{J/\psi }^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime J/\psi }+C_{Z_c^\prime \pi }\right] \exp \left( -\frac{M_{J/\psi }^2}{T^2} \right) \nonumber \\&\quad =-\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{J/\psi }} ds \int _{0}^{u^0_{\pi }} du u\left( s+2m_c^2\right) \sqrt{1-\frac{4m_c^2}{s}}\nonumber \\&\qquad \times \, \exp \left( -\frac{s}{T^2} -\frac{u-M_{\pi }^2}{T_2^2} \right) , \end{aligned}$$
(46)
$$\begin{aligned}&\frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c } \frac{1}{M_{Z_c}^2-M_{\eta _c}^2}\nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{\eta _c}^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime \eta _c}+C_{Z_c^\prime \rho }\right] \exp \left( -\frac{M_{\eta _c}^2}{T^2} \right) \nonumber \\&\quad =\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{\eta _c}} ds \int _{0}^{u^0_{\rho }} du us\nonumber \\&\qquad \times \, \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} -\frac{u-M_{\rho }^2}{T_2^2} \right) \nonumber \\&\qquad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{12\sqrt{2}\pi ^2} \int _{4m_c^2}^{s^0_{\eta _c}} ds \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2}+\frac{M_{\rho }^2}{T_2^2} \right) ,\end{aligned}$$
(47)
$$\begin{aligned}&\frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_c D\bar{D}^*}}{4m_c } \frac{1}{\widetilde{M}_{Z_c}^2-M_{D^*}^2}\nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{D^*}^2}{T^2} \right) -\exp \left( -\frac{\widetilde{M}_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime D^*}+C_{Z_c^\prime D}\right] \exp \left( -\frac{M_{D^*}^2}{T^2} \right) \nonumber \\&\quad =\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{s^0_{D^*}} ds \left( \frac{9}{2}-\frac{10m_c^2}{s}+\frac{3m_c^4}{2s^2}\right) \nonumber \\&\qquad \times \, \exp \left( -\frac{s}{T^2} -\frac{m_c^2-M_{D}^2}{T_2^2} \right) +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{u^0_{D}} du \nonumber \\&\qquad \times \, \left( \frac{9}{2}-\frac{8m_c^2}{u}+\frac{15m_c^4}{2u^2}\right) \exp \left( -\frac{m_c^2}{T^2} -\frac{u-M_{D}^2}{T_2^2} \right) , \nonumber \\ \end{aligned}$$
(48)

the dependence on the Borel parameter \(T^2_2\) is trivial, \(\exp \left( -\frac{u-M_{\pi }^2}{T_2^2} \right) ,\quad \exp \left( -\frac{u-M_{\rho }^2}{T_2^2} \right) ,\quad \exp \left( -\frac{u-M_{D}^2}{T_2^2} \right) , \exp \left( -\frac{m_c^2-M_{D}^2}{T_2^2} \right) \), which differ from the QCD sum rules for the three-meson hadronic coupling constants greatly [32]. It is difficult to obtain \(T_2^2\) independent regions in the present three QCD sum rules, as no other terms to stabilize the QCD sum rules. We can take the local limit \(T^2_2\rightarrow \infty \), which is so called local-duality limit (the local QCD sum rules are reproduced from the original QCD sum rules in infinite Borel parameter limit) [33,34,35], then \(\exp \left( -\frac{u}{T_2^2} \right) =\exp \left( -\frac{m_c^2}{T_2^2} \right) =\exp \left( -\frac{M_\pi ^2}{T_2^2} \right) =\exp \left( -\frac{M_\rho ^2}{T_2^2} \right) =\exp \left( -\frac{M_D^2}{T_2^2} \right) =1\), the three QCD sum rules are greatly simplified.

Now we write down the simplified QCD sum rules explicitly,

$$\begin{aligned}&\frac{f_{\pi }M_{\pi }^2f_{J/\psi }M_{J/\psi }\lambda _{Z_c}G_{Z_cJ/\psi \pi }}{m_u+m_d}\frac{1}{M_{Z_c}^2-M_{J/\psi }^2} \nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{J/\psi }^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime J/\psi }+C_{Z_c^\prime \pi }\right] \exp \left( -\frac{M_{J/\psi }^2}{T^2} \right) \nonumber \\&\quad =-\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{J/\psi }} ds \int _{0}^{u^0_{\pi }} du u\left( s+2m_c^2\right) \nonumber \\&\qquad \times \, \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} \right) , \end{aligned}$$
(49)
$$\begin{aligned}&\frac{f_{\eta _c}M_{\eta _c}^2f_{\rho }M_{\rho }\lambda _{Z_c}G_{Z_c\eta _c \rho }}{2m_c } \frac{1}{M_{Z_c}^2-M_{\eta _c}^2}\nonumber \\&\qquad \times \, \left[ \exp \left( -\frac{M_{\eta _c}^2}{T^2} \right) -\exp \left( -\frac{M_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime \eta _c}+C_{Z_c^\prime \rho }\right] \exp \left( -\frac{M_{\eta _c}^2}{T^2} \right) \nonumber \\&\quad =\frac{1}{32\sqrt{2}\pi ^4}\int _{4m_c^2}^{s^0_{\eta _c}} ds \int _{0}^{u^0_{\rho }} du us\sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} \right) \nonumber \\&\qquad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{12\sqrt{2}\pi ^2} \int _{4m_c^2}^{s^0_{\eta _c}} ds \sqrt{1-\frac{4m_c^2}{s}}\exp \left( -\frac{s}{T^2} \right) ,\end{aligned}$$
(50)
$$\begin{aligned}&\qquad \frac{f_{D}M_{D}^2f_{D^*}M_{D^*}\lambda _{Z_c}G_{Z_c D\bar{D}^*}}{4m_c } \frac{1}{\widetilde{M}_{Z_c}^2-M_{D^*}^2}\nonumber \\&\qquad \times \,\left[ \exp \left( -\frac{M_{D^*}^2}{T^2} \right) -\exp \left( -\frac{\widetilde{M}_{Z_c}^2}{T^2} \right) \right] \nonumber \\&\qquad +\left[ C_{Z_c^\prime D^*}+C_{Z_c^\prime D}\right] \exp \left( -\frac{M_{D^*}^2}{T^2} \right) \nonumber \\&\quad =\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{s^0_{D^*}} ds \left( \frac{9}{2}-\frac{10m_c^2}{s}+\frac{3m_c^4}{2s^2}\right) \exp \left( -\frac{s}{T^2} \right) \nonumber \\&\qquad +\frac{m_c\langle \bar{q}g_s\sigma Gq\rangle }{96\sqrt{2}\pi ^2}\int _{m_c^2}^{u^0_{D}} du \left( \frac{9}{2}-\frac{8m_c^2}{u}+\frac{15m_c^4}{2u^2}\right) \exp \left( -\frac{m_c^2}{T^2} \right) ,\nonumber \\ \end{aligned}$$
(51)

where \(\widetilde{M}_{Z_c}^2=\frac{M_{Z_c}^2}{4}\).

Fig. 1
figure 1

The hadronic coupling constants \(G_{Z_cJ/\psi \pi }\) (I), \(G_{Z_c\eta _c\rho }\) (II) and \(G_{Z_cD \bar{D}^{*}}\) (III) with variations of the Borel parameter \(T^2\)

Full size image

3 Numerical results and discussions

The input parameters on the QCD side are taken to be the standard values \(\langle \bar{q}q \rangle =-(0.24\,\pm \,0.01\, \mathrm{GeV})^3, \langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle , m_0^2=(0.8 \pm 0.1)\,\mathrm{GeV}^2\) at the energy scale \(\mu =1\, \mathrm{GeV}\) [29,30,31, 36], \(m_{c}(m_c)=(1.28\pm 0.03)\,\mathrm{GeV}\) from the Particle Data Group [37]. Furthermore, we set \(m_u=m_d=0\) due to the small current quark masses. We take into account the energy-scale dependence of the input parameters from the renormalization group equation,

$$\begin{aligned} \langle \bar{q}g_s \sigma Gq \rangle (\mu )= & {} \langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{25}}, \nonumber \\ m_c(\mu )= & {} m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}} ,\nonumber \\ \alpha _s(\mu )= & {} \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} \right. \nonumber \\&\left. +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] , \end{aligned}$$
(52)

where \(t=\log \frac{\mu ^2}{\Lambda ^2}, b_0=\frac{33-2n_f}{12\pi }, b_1=\frac{153-19n_f}{24\pi ^2}, b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}, \Lambda =210, 292\) and \(332\,\mathrm{MeV}\) for the flavors \(n_f=5, 4\) and 3, respectively [37], and evolve all the input parameters to the optimal energy scale \(\mu =1.4\,\mathrm{GeV}\) to extract hadronic coupling constants [12, 38].

The hadronic parameters are taken as \(M_{\pi }=0.13957\,\mathrm{GeV}, M_{\rho }=0.77526\,\mathrm{GeV}, M_{J/\psi }=3.0969\,\mathrm{GeV}, M_{\eta _c}=2.9834\mathrm{GeV}\) [37], \(f_{\pi }=0.130\,\mathrm{GeV}, f_{\rho }=0.215\,\mathrm{GeV}, \sqrt{s^0_{\pi }}=0.85\,\mathrm{GeV}, \sqrt{s^0_{\rho }}=1.3\,\mathrm{GeV}\) [36], \(M_{D}=1.87\,\mathrm{GeV}, f_{D}=208\,\mathrm{MeV}, u^0_{D}=6.2\,\mathrm{GeV}^2, M_{D^*}=2.01\,\mathrm{GeV}, f_{D^*}=263\,\mathrm{MeV}, s^0_{D^*}=6.4\,\mathrm{GeV}^2\) [39, 40], \(f_{J/\psi }=0.418\,\mathrm{GeV}, f_{\eta _c}=0.387 \,\mathrm{GeV}\) [41], \(\sqrt{s^0_{J/\psi }}=3.6\,\mathrm{GeV}, \sqrt{s^0_{\eta _c}}=3.5\,\mathrm{GeV}, M_{Z_c}=3.899\,\mathrm{GeV}, \lambda _{Z_c}=2.1\times \, 10^{-2}\,\mathrm{GeV}^5\) [12, 38], \(f_{\pi }M^2_{\pi }/(m_u+m_d)=-2\langle \bar{q}q\rangle /f_{\pi }\) from the Gell–Mann–Oakes–Renner relation.

In the scenario of tetraquark states, the QCD sum rules indicate that the \(Z_c(3900)\) and Z(4430) can be tentatively assigned to be the ground state and the first radial excited state of the axialvector tetraquark states, respectively [42], the coupling of the current \(J_\nu (0)\) to the excited state Z(4430) is rather large, so the unknown parameters cannot be neglected. The unknown parameters are fitted to be \( C_{Z_c^\prime J/\psi }+C_{Z_c^\prime \pi }=0.001\,\mathrm{GeV}^8, C_{Z_c^\prime \eta _c}+C_{Z_c^\prime \rho }=0.0046\,\mathrm{GeV}^8 \) and \(C_{Z_c^\prime D^*}+C_{Z_c^\prime D}=0.00013\,\mathrm{GeV}^8 \) to obtain platforms in the Borel windows \(T^2=(1.9-2.6)\,\mathrm{GeV}^2, (1.9-2.5)\,\mathrm{GeV}^2\) and \((1.5-2.1)\,\mathrm{GeV}^2\) for the hadronic coupling constants \(G_{Z_cJ/\psi \pi }, G_{Z_c\eta _c\rho }, G_{Z_cD \bar{D}^{*}}\), respectively.

Then it is easy to obtain the values of the hadronic coupling constants,

$$\begin{aligned} |G_{Z_cJ/\psi \pi }|= & {} 3.63\pm 0.70\,\mathrm{GeV} , \nonumber \\ G_{Z_c\eta _c\rho }= & {} 4.38\pm 1.86\,\mathrm{GeV} , \nonumber \\ |G_{Z_cD\bar{D}^*}|= & {} 0.62\pm 0.09\,\mathrm{GeV} , \end{aligned}$$
(53)

which are shown explicitly in Fig. 1

We choose the masses \(M_{\pi }=0.13957\,\mathrm{GeV}, M_{\rho }=0.77526\,\mathrm{GeV}, M_{J/\psi }=3.0969\,\mathrm{GeV}, M_{\eta _c}=2.9834\,\mathrm{GeV}, M_{D^+}=1.8695 \,\mathrm{GeV}, M_{D^{*0}}=2.00685\,\mathrm{GeV}\), \(M_{D^0}=1.86484 \,\mathrm{GeV}, M_{D^{*+}}=2.01026\,\mathrm{GeV}\) [37], \(M_{Z_c}=3.899\,\mathrm{GeV}\) [1], and obtain the partial decay widths,

$$\begin{aligned} \Gamma (Z_c^+(3900)\rightarrow J/\psi \pi ^+)= & {} 25.8\pm 9.6\,\mathrm{MeV} ,\nonumber \\ \Gamma (Z_c^+(3900)\rightarrow \eta _c\rho ^+)= & {} 27.9\pm 20.1 \,\mathrm{MeV} , \nonumber \\ \Gamma (Z_c^+(3900)\rightarrow D^+ \bar{D}^{*0})= & {} 0.22\pm 0.07\,\mathrm{MeV} ,\nonumber \\ \Gamma (Z_c^+(3900)\rightarrow \bar{D}^0 D^{*+})= & {} 0.23\pm 0.07\,\mathrm{MeV} , \end{aligned}$$
(54)

and the total width,

$$\begin{aligned} \Gamma _{Z_c}= & {} 54.2\pm 29.8\,\mathrm{MeV} , \end{aligned}$$
(55)

which is consistent with the experimental data considering the uncertainties [1,2,3, 5]. If we take the central values of the hadronic coupling constants \(|G_{Z_cJ/\psi \pi }| =3.63\,\mathrm{GeV}, G_{Z_c\eta _c\rho }=4.38\,\mathrm{GeV}\), \(|G_{Z_cD\bar{D}^*}|=0.62\,\mathrm{GeV}\), we can obtain the total width \(\Gamma _{Z_c(3900)}=48.9\,\mathrm{MeV}\), which happens to coincide with the central value of the experimental dada \(\Gamma = 46\pm 10\pm 20 \text{ MeV }\) from the BESIII Collaboration [1], while the predicted ratio

$$\begin{aligned} R= & {} \frac{\Gamma (Z_c(3900)\rightarrow D\bar{D}^*)}{\Gamma (Z_c(3900)\rightarrow J/\psi \pi )}=0.02\ll R_{exp} \nonumber \\= & {} \frac{\Gamma (Z_c(3885)\rightarrow D\bar{D}^*)}{\Gamma (Z_c(3900)\rightarrow J/\psi \pi )}=6.2 \pm 1.1 \pm 2.7 , \end{aligned}$$
(56)

from the BESIII Collaboration [4]. It is difficult to assign the \(Z_c(3900)\) and \(Z_c(3885)\) to be the same diquark–antidiquark type axialvector tetraquark state. We can assign the \(Z_c(3900)\) to be the diquark–antidiquark type axialvector tetraquark state, and assign the \(Z_c^+(3885)\) to be the molecular state \(D^+\bar{D}^{*0}+D^{*+}\bar{D}^0\) according to the predicted mass \(3.89\pm 0.09\,\mathrm{GeV}\) from the QCD sum rules [20]. If the \(Z_c(3885)\) is the \(D^+\bar{D}^{*0}+D^{*+}\bar{D}^0\) molecular state, the decays to \(D^+\bar{D}^{*0}\) and \(D^{*+}\bar{D}^0\) take place through its component directly, it is easy to account for the large ratio \(R_{exp}\).

Now we compare the present work with the work in Ref. [13] in details. In the two works, the same currents are chosen except for the currents to interpolate the \(\pi \) meson, the operator product expansion is carried out at the large space-like regions \(P^2=-p^2\rightarrow \infty \) and \(Q^2=-q^2\rightarrow \infty \). In the present work, we take into account both the connected and disconnected Feynman diagrams, and obtain the solid quark–hadron duality by getting the physical spectral densities through dispersion relation, then perform double Borel transforms with respect to the variables \(P^2\) and \(Q^2\) to obtain the QCD sum rules for the physical hadronic coupling constants directly. We pay special attention to the hadron spectral spectral densities, and present detailed discussions and subtract the continuum contaminations in a solid foundation. In Ref. [13], Dias et al take into account only the connected Feynman diagrams, and obtain the quark–hadron duality by taking the limit \(Q^2 \rightarrow 0\), \(M_{\pi }^2 \rightarrow 0, M^2_{\rho }\rightarrow 0, M_{D}^2 \rightarrow 0\) and \(m_c^2\rightarrow 0\) and choosing special tensor structures, then perform single Borel transform with respect to the variable \(P^2\) to obtain the QCD sum rules for the momentum dependent hadronic coupling constants. They subtract the continuum contaminations by hand, then parameterize the momentum dependent hadronic coupling constants by some exponential functions with arbitrariness to extract the values to the mass-shell \(Q^2=-M_{\pi }^2, -M_{\rho }^2\) or \(-M_{D}^2\) to obtain the physical hadronic coupling constants. Although the values of the width of the \(Z_c(3900)\) obtained in the present work and in Ref. [13] are both compatible with the experimental data, the present predictions have much less theoretical uncertainties.

4 Conclusion

In this article, we tentatively assign the \(Z_c^\pm (3900)\) to be the diquark–antidiquark type axialvector tetraquark state, study the hadronic coupling constants \(G_{Z_cJ/\psi \pi }\), \(G_{Z_c\eta _c\rho }\), \(G_{Z_cD \bar{D}^{*}}\) with the QCD sum rules in details. We introduce the three-point correlation functions, and carry out the operator product expansion up to the vacuum condensates of dimension-5, and neglect the tiny contributions of the gluon condensate. In calculations, we take into account both the connected and disconnected Feynman diagrams, as the connected Feynman diagrams alone cannot do the work. Special attentions are paid to matching the hadron side of the correlation functions with the QCD side of the correlation functions to obtain solid duality, the routine can be applied to study other hadronic couplings directly. We study the two-body strong decays \(Z_c^+(3900)\rightarrow J/\psi \pi ^+, \eta _c\rho ^+, D^+ \bar{D}^{*0}, \bar{D}^0 D^{*+}\) and obtain the total width of the \(Z_c^\pm (3900)\), which is consistent with the experimental data. The numerical results support assigning the \(Z_c^\pm (3900)\) to be the diquark–antidiquark type axialvector tetraquark state, and assigning the \(Z_c^\pm (3885)\) to be the meson–meson type axialvector molecular state.