1 Introduction

After many observational astronomical consequences coming from Supernovae Type Ia, BICEP, and cosmic microwave background radiation [1,2,3], it has been affirmed that our cosmos is in an accelerated expanding phase. Dark energy (DE) is thought to be a reliable source behind this enigmatic behavior of the universe. The modified gravity theories are believed to belong to the mathematical tools to deal with its nature. These theories are explored by modifying the Einstein–Hilbert (EH) action and they have been extensively applied to the study of the nature of DE, which may address accelerating cosmic expansion [4,5,6,7].

Nojiri and Odintsov [8, 9] introduced some modified gravitational models for the complete description of early- and late-time evolutionary universe eras. The simplest generalization of GR includes the f(R) gravity in which R is the Ricci scalar. Harko et al. [10] modified this theory by invoking corrections coming from the trace of the energy-momentum tensor (T) in the EH action. This theory is known as f(R, T) gravity theory. The motivation of this theory stems from the fact that the influences introduced by quantum effects or a dark non-ideal relativistic matter environment are being invoked in this analysis.

Houndjo [11] obtained some observationally consistent f(R, T) models that could assist well enough in analyzing the behavior of matter dominated universe epochs. Baffou et al. [12] used a perturbation scheme to investigate the viability of a few cosmic models by taking de Sitter and power law formulations. Bamba et al. [13] checked the role of the dark source terms coming from the modified gravity models on the dynamics of the accelerating and expanding universe. Durrer and Maartens [14] presented some results to the credibility of GR in terms of f(R) gravity. Gravitational stabilities of relativistic compact structures were examined in f(R) gravity by [15,16,17]. Yousaf et al. examined the rate of the gravitational implosion with the help of various modified gravity models for the planar [18,19,20], spherical [21,22,23,24,25,26,27,28] as well as cylindrical [29,30,31] relativistic objects. Moraes et al. [32] calculated the modified hydrostatic expression for investigating the dynamical features of some strange and neutron stars with the help of the \(f(R,T)=R+2\lambda T\) model.

Herrera et al. [33, 34] discussed the gravitational implosion of the cylindrical as well as spherical collapse via some specific boundary conditions. Tewari et al. [35] investigated the spherical anisotropic collapse and presented a new class of relativistic models that could be helpful to understand various dynamical features of stellar models. Sharif and Bhatti [36] examined the role of the adiabatic index as well as the physical parameters on the onset of the gravitational collapse of axially symmetric self-gravitating systems. Sharif and Yousaf [37, 38] considered the problem of the dynamical instability of celestial bodies in modified gravity and found the role of f(R, T) and f(R) in the subsequent phases of collapsing systems. Recently, Yousaf et al. [39, 40] joined the interior non-static anisotropic cylindrical system with the exterior Einstein–Rosen bridge and investigated the impact of the modified corrections on the onset of dynamical instability.

The inhomogeneous state is found to be the predecessor in the process of gravitational collapse for the initially homogeneous stellar structures. It is pertinent to mention that some dynamical properties of self-gravitating systems can be understood by investigating the behavior of pressure anisotropy, tidal forces, inhomogeneous energy density (IED), etc.. There has been extensive work related to check the cause of an IED over the surface of regular compact objects. Penrose and Hawking [41] were among the pioneers exploring this. They found the Weyl tensor as a key entity in the emergence of the IED in the evolution of spherically symmetric objects. Herrera et al. [42] calculated some factors responsible for creating an IED over the anisotropic stellar spheres and inferred that pressure anisotropy may lead to developing a naked singularity (NS) for the system. Virbhadra et al. [43,44,45] provided a mathematical platform under which one can differentiate between the formation of NS and black holes.

Herrera et al. [46] described the gravitational arrow of time for the dissipative compact systems by making a relation between the Weyl invariant, the pressure anisotropy and the IED. Herrera et al. [47] examined the influences of the IED on the expressions of shear and expansion evolutions in the presence of an electromagnetic field. Yousaf et al. [48] covered this problem for spherical radiating geometries in the modified gravitational theory and concluded that a special combination of a f(R, T) gravity model could significantly interfere in the appearance of an IED. Bhatti et al. [49, 50] looked into the reasons behind the maintenance of the IED against the gravitational collapse of relativistic interiors in modified gravity. Herrera et al. [51] and Herrera [52] considered the case of a non-comoving coordinate system and checked the reasons for the start up of the spherical collapse by evaluating transport equations. Yousaf et al. [53] modified these results by invoking Palatini f(R) corrections. Recently, Herrera [54] illustrated the answer to the question why observations of tilted congruences show a dissipative process in stellar interiors which seem to be isentropic for non-tilted observers.

This paper is a continuation of previous work presented by Herrera et al. [47] in order to check the role of the \(f(R,T)=R+\lambda R^2T^2\) cosmic model in the formulations of structure scalars, shear and expansion evolution equations. The paper is outlined as follows. In the next section some essentials, required to understand the f(R, T) gravity as well as the spherical distribution of radiating fluids, are described. In Sect. 3, we shall compute a modified form of structure scalars in the realm of \(R+\lambda R^2T^2\) corrections. We shall also examine the role of shear and expansion evolution equations in this gravity. Section 4 demonstrates the role of scalar parameters in the emergence of the IED of the dust relativistic cloud in today values of R and T. A brief description as well as the conclusion are reported in the last section.

2 Radiating sphere and f(R, T) gravity

In the f(R, T) gravity the EH action can be written [10]

$$\begin{aligned} A=\int \mathrm{d}^4x[f(R,T)+L_M]\sqrt{-g}, \end{aligned}$$
(1)

where g,  T are the traces of the metric and usual energy-momentum tensors respectively, while \(L_\mathrm{M}\) is the Lagrangian matter. In the following calculations we shall use relativistic units, with \(8{\pi }G=c=1\). After considering \(L_\mathrm{M}=\mu \) (where \(\mu \) is the fluid energy density) and applying variations in the above modified action with \(g_{\alpha \beta }\), the field equations can be written

$$\begin{aligned} {G}_{\lambda \nu }={{T}_{\lambda \nu }}^{\text {eff}}, \end{aligned}$$
(2)

where

$$\begin{aligned} {{T}_{\lambda \nu }}^{\text {eff}}&=\Bigg [-\mu g_{\lambda \nu }f_T(R,T)+T^{(m)}_{\lambda \nu }(1+f_T(R,T))\nonumber \\&\quad +\left( f_R(R,T)-\frac{f(R,T)}{R}\right) \left. \frac{R}{2}\right. \nonumber \\&\quad +\,\left( {\nabla }_\lambda {\nabla }_ \nu +g_{\lambda \nu }{\Box }\right) f_R(R,T)\Bigg ]\frac{1}{f_R(R,T)}. \end{aligned}$$

In Eq. (2), \({G}_{\alpha \beta }\) is the Einstein tensor, while \({{T}_{\lambda \nu }}^{\text {eff}}\) is widely known as the effective form of the energy-momentum tensor. However, \(\nabla _\alpha \), \(\Box \), \(f_T(R,T)\) and \(f_R(R,T)\) stand for the covariant derivative, \(\nabla _\alpha \nabla ^\alpha \), and partial derivatives with respect to R and T, respectively. One can find a visualized and detailed illustration of the field equations (2) in Refs. [10] and [48].

Let us consider an irrotational diagonal non-static form of spherically symmetric metric

$$\begin{aligned} \mathrm{d}s^2=H^2(t,r)\mathrm{d}r^{2}-A^2(t,r)\mathrm{d}t^{2}+C^2(\mathrm{d}\theta ^{2} +\sin ^2\theta {\mathrm{d}\phi ^2}), \end{aligned}$$
(3)

in which A,  B and C depend on t and r. It is assumed that the above geometry is being coupled with a radiating shear locally anisotropic fluid represented by

$$\begin{aligned} T_{\lambda \nu }= & {} {\mu }V_\lambda V_\nu +P_{\bot }h_{\lambda \nu }+\Pi \chi _\lambda \chi _\nu -2{\eta }{\sigma }_{\lambda \nu }\nonumber \\&+\,{\varepsilon }l_\lambda l_\nu +q(\chi _\nu V_\lambda +\chi _\lambda V_\nu ), \end{aligned}$$
(4)

where \(\varepsilon \) is the radiation density, \(q_{\beta }\) is the heat flux, \(\Pi \equiv P_\mathrm{r}-P_{\perp }\), \(h_{\alpha \beta },~\sigma _{\alpha \beta }\) are the projection and shear tensor, \(P_\bot ,~P_\mathrm{r}\) are the tangential and radial pressure elements, \(\mu \) is the energy density and \(\eta \) is the coefficient of the shear viscosity. The projection tensor is defined as \(h_{\alpha \beta }=g_{\alpha \beta }+V_{\alpha }V_{\beta }\), while \(\chi ^\beta \) and \(l^\beta \) are the radial and null four-vectors, respectively. Under a comoving coordinate system, the definitions of these vectors are found to be \(V^{\nu }=\frac{1}{A}\delta ^{\nu }_{0},~ \chi ^{\nu }=\frac{1}{C}\delta ^{\nu }_{1},~ l^\nu =\frac{1}{A}\delta ^{\nu }_{0}+\frac{1}{B}\delta ^{\nu }_{1},~ q^\nu =q(t,r)\chi ^{\nu }\). In order to maintain the comoving coordinate frame, these obey the relations

$$\begin{aligned} \chi ^{\nu }\chi _{\nu }= & {} 1,\quad V^{\nu }V_{\nu }=-1, \quad \chi ^{\nu }V_{\nu }=0,\\ l^\nu V_\nu= & {} -1, \quad V^\nu q_\nu =0, \quad l^\nu l_\nu =0. \end{aligned}$$

With reference to Eq. (3), the shear tensor and the scalar corresponding to the expansion tensor are

$$\begin{aligned} \sigma A=\left( \frac{\dot{H}}{H} -\frac{\dot{C}}{C}\right) ,\quad \Theta A=\left( \frac{\dot{H}}{H}+\frac{2\dot{C}}{C}\right) , \end{aligned}$$

where an overdot means \(\frac{\partial }{\partial t}\).

In order to have an observationally consistent gravitational theory, an appropriate f(R, T) gravity model is needed. In this perspective, we take the following combinations of a f(R, T) model [55]:

$$\begin{aligned} f(R,T)=f_1(R)+f_2(R)f_3(T). \end{aligned}$$
(5)

This form of the model description states a minimal background of matter and geometry coupling, thereby indicating higher-order corrections in the well-known f(R) theory. Realistic f(R, T) models can be achieved by picking any Ricci scalar function from [56] along with any linear form of the function of T. In this context we shall take \(f(R,T)=R+\lambda R^2T^2\), where \(\lambda \ll 1\). The dynamics proposed by Einstein can be found by setting \(\lambda =0\) in the above model. The f(R, T) field equations for Eqs. (3)–(5) are

$$\begin{aligned} G_{00}&=\frac{A^2}{1+2R\lambda T^2}\left[ {\mu }+{\varepsilon }+2T\lambda R^2 -\frac{\lambda }{2}T^2R^2+\frac{\varphi _{00}}{A^2} \right] , \end{aligned}$$
(6)
$$\begin{aligned} G_{01}&=\frac{AH}{1+2R\lambda T^2}\left[ -\frac{(1+2T\lambda R^2)}{1+2R\lambda T^2}(q+{\varepsilon }) +\frac{\varphi _{01}}{AH}\right] , \end{aligned}$$
(7)
$$\begin{aligned} G_{11}&=\frac{H^2}{1+2R\lambda T^2}\Bigg [\mu 2T\lambda R^2+(1+2T\lambda R^2)\nonumber \\&\quad \times (P_r+\varepsilon -\frac{4}{3}\eta {\sigma }) +\frac{\lambda }{2}T^2R^2+\frac{\varphi _{11}}{H^2}\Bigg ], \end{aligned}$$
(8)
$$\begin{aligned} G_{22}&=\frac{C^2}{1+2R\lambda T^2}\Bigg [(1+2T\lambda R^2)({P_{\bot }}\nonumber \\&\quad +\frac{2}{3}\eta {\sigma })+\mu 2T\lambda R^2 +\frac{\lambda }{2}T^2R^2+\frac{\varphi _{22}}{C^2}\Bigg ], \end{aligned}$$
(9)

where

$$\begin{aligned} \psi _{00}&=2\partial _{tt}f_R+\partial _tf_R\left( -2\frac{\dot{A}}{A}+\frac{\dot{H}}{H} +2\frac{\dot{C}}{C}\right) \nonumber \\&\quad +\frac{\partial _rf_R}{H^2}\left( -2AA'+A^2\frac{H'}{H} -2A^2\frac{C'}{C}\right) ,\\ \psi _{11}&=-\frac{H^2}{A^2}\partial _{tt}f_R +\frac{\partial _tf_R}{A^2}\left( -2H^2\frac{\dot{C}}{C}+H^2\frac{\dot{A}}{A}-2H\dot{H} \right) \\&\quad +\partial _{rr}f_R+\left( \frac{A'}{A}+2\frac{C'}{C} -2\frac{H'}{H}\right) \partial _rf_R,\\ \psi _{01}&=-\frac{A'}{A}\partial _tf_R+\partial _t\partial _rf_R -\frac{\dot{H}}{H}\partial _rf_R,\\ \psi _{22}&=-C^2\frac{\partial _{tt}f_R}{A^2}+\frac{C^2}{A^2}\left( \frac{\dot{A}}{A}-3\frac{\dot{C}}{C}-\frac{\dot{H}}{H}\right) \partial _tf_R\\&\quad +\frac{C^2}{H^2}\partial _rf_R\left( \frac{A'}{A}+\frac{C'}{C} -\frac{H'}{H}\right) , \end{aligned}$$

while the \(G_{\gamma \delta }\) are mentioned in [47]. Here, the prime indicates \(\frac{\partial }{\partial r}\). The relativistic fluid 4-velocity, U can be given by

$$\begin{aligned} U=D_{T}C=\frac{\dot{C}}{A}. \end{aligned}$$
(10)

The spherical mass function via the Misner–Sharp formulations can be recast in the form [57]

$$\begin{aligned} m(t,r)=\frac{C}{2}\left( 1+\frac{\dot{C}^2}{A^2} -\frac{C'^2}{H^2}\right) . \end{aligned}$$
(11)

The temporal and radial derivatives of the above equation after using Eqs. (6)–(8) and (10) are found as follows:

$$\begin{aligned} D_T{m}=&\frac{-1}{2(1+2R\lambda T^2)}\left[ U\left\{ (1+2T\lambda R^2)(\bar{P}_r-\frac{4}{3}\eta \sigma )\right. \right. \nonumber \\&\left. +2T\lambda R^2\mu -\frac{\lambda }{2}R^2T^2+\frac{\varphi _{11}}{H^2}\right\} \nonumber \\&\left. +E \left\{ \frac{(1+2T\lambda R^2)}{1+2R\lambda T^2}\bar{q}-\frac{\varphi _{01}}{AH}\right\} \right] , \end{aligned}$$
(12)
$$\begin{aligned} D_Cm=&\frac{C^2}{2(1+2R\lambda T^2)}\left[ \bar{\mu }+2T\lambda R^2-\frac{\lambda }{2}R^2T^2 +\frac{\varphi _{00}}{A^2}\right. \nonumber \\&\left. -\frac{U}{E}\left\{ \frac{\varphi _{01}}{AH}-\frac{(1+2T\lambda R^2)}{1+2R\lambda T^2}\bar{q}\right\} \right] , \end{aligned}$$
(13)

where the over-bar notation describes \(\bar{X}=\varepsilon +X,\) while \(D_{T}=\frac{1}{A} \frac{\partial }{\partial t}\). The second equation from the above set of equations leads to

$$\begin{aligned} m=&\frac{1}{2}\int ^C_{0}\frac{C^2}{1+2R\lambda T^2}\left[ \bar{\mu }+2T\lambda R^2-\frac{\lambda }{2}R^2T^2\right. \nonumber \\&\left. +\frac{\varphi _{00}}{A^2}-\frac{U}{E}\left\{ \frac{\varphi _{01}}{AH}-\frac{(1+2T\lambda R^2)}{1+2R\lambda T^2}\bar{q}\right\} \right] \mathrm{d}C, \end{aligned}$$
(14)

where \(E\equiv \frac{C'}{H}\), whose value can be written through the mass function as

$$\begin{aligned} E\equiv \frac{C'}{H}=\left[ 1+U^{2}-\frac{2m(t,r)}{C}\right] ^{1/2}. \end{aligned}$$
(15)

Equations (12)–(15) yield

$$\begin{aligned} \frac{3m}{C^3}=&\frac{3\kappa }{2C^3}\int ^r_{0}\left[ \bar{\mu }+2T\lambda R^2 -\frac{\lambda }{2}R^2T^2 +\frac{\varphi _{00}}{A^2}\right. \nonumber \\&\left. +\frac{U}{E}\left\{ \frac{(1+2T\lambda R^2)}{1+2R\lambda T^2}\bar{q}-\frac{\varphi _{01}}{AH}\right\} C^2C'\right] \mathrm{d}r, \end{aligned}$$
(16)

which connects various structural variable elements, like the energy density, the mass function etc., with f(R, T) extra curvature terms. It is well known that in the spherical case the Weyl tensor can be decomposed into two different tensors, i.e., the magnetic \(H_{\alpha \beta }\) part and the electric \(E_{\alpha \beta }\) part. These two are defined, respectively, as

$$\begin{aligned} H_{\alpha \beta }= & {} \frac{1}{2}\epsilon _{\alpha \gamma \eta \delta }C^{\eta \delta }_{~~\beta {\rho }}V^\gamma V^{\rho }=\tilde{C}_{\alpha \gamma \beta \delta }V^{\gamma }V^\delta ,\nonumber \\ E_{\alpha \beta }= & {} C_{\alpha \phi \beta \varphi }V^{\phi }V^{\varphi }, \end{aligned}$$

where \(\epsilon _{\lambda \mu \nu \omega }\equiv \sqrt{-g}\eta _{\lambda \mu \nu \omega }\) with \(\eta _{\lambda \mu \nu \omega }\) as a Levi-Civita symbol. The electric component of the Weyl tensor can be expressed through the fluid’s four-vectors by

$$\begin{aligned} E_{\lambda \nu }=\left[ \chi _{\lambda }\chi _{\nu }-\frac{g_{\lambda \nu }}{3} -\frac{1}{3}V_\lambda V_\nu \right] \mathcal {E}, \end{aligned}$$

in which \(\mathcal {E}\) represents the scalar corresponding to the Weyl tensor. The value of \(\mathcal {E}\) through spherical geometric variables is found by

$$\begin{aligned} \mathcal {E}= & {} -\frac{1}{2C^{2}}+\left[ -\frac{\ddot{B}}{B}+ \left( \frac{\dot{C}}{C}+\frac{\dot{A}}{A}\right) \left( \frac{\dot{B}}{B}-\frac{\dot{C}}{C}\right) +\frac{\ddot{C}}{C}\right] \frac{1}{2A^{2}}\nonumber \\&-\left[ -\left( \frac{A'}{A}-\frac{C'}{C}\right) \left( \frac{C'}{C}+\frac{B'}{B}\right) +\frac{C''}{C}-\frac{A''}{A}\right] \frac{1}{2B^{2}}.\nonumber \\ \end{aligned}$$
(17)

Another way of writing \(\mathcal {E}\) with the inclusion of f(R, T) extra curvature terms is

$$\begin{aligned} \mathcal {E}&=\frac{1}{2(1+2R\lambda T^2)}\left[ \bar{\mu }+2R^2\lambda T -(1+2R^2\lambda T)(\bar{\Pi }-2\eta \sigma )\right. \nonumber \\&\quad -\left. \frac{\lambda }{2}T^2R^2 +\frac{\varphi _{00}}{A^2}-\frac{\varphi _{11}}{B^2} +\frac{\varphi _{22}}{C^2}\right] \nonumber \\&\quad -\frac{3}{2C^3} \int ^r_{0}\frac{C^2}{1+2R\lambda T^2} \left[ \bar{\mu }+2R^2\lambda T-\frac{\lambda }{2}T^2R^2\right. \nonumber \\&\quad \left. +\frac{\varphi _{00}}{A^2}+\frac{U}{E}\left\{ \frac{(1+2R^2\lambda T)}{1+2R\lambda T^2}\bar{q} -\frac{\varphi _{01}}{AH}\right\} C^2C'\right] \mathrm{d}r,\nonumber \\ \end{aligned}$$
(18)

where the bar over \(\Pi \) indicates \(\bar{\Pi }=\bar{P}_\mathrm{r}-P_\perp \).

3 Modified scalar variables and f(R, T) gravity

Here, we shall compute structure scalars corresponding to radiating spherical bodies in \(R+\lambda R^2T^2\) gravity. In this background, we will use two well-known tensors, i.e., \(X_{\alpha \beta }\) and \(Y_{\alpha \beta }\). These tensors were proposed by Bel [58] and Herrera et al. [46, 47] after the orthogonal splitting of the Riemann curvature tensor. These are

$$\begin{aligned} X_{\alpha \beta }= & {} ~^{*}R^{*}_{\alpha \gamma \beta \delta }V^{\gamma }V^{\delta }= \frac{1}{2}\eta ^{\varepsilon \rho }_{~~\alpha \gamma }R^{*}_{\epsilon \rho \beta \delta }V^{\gamma }V^{\delta },\quad Y_{\alpha \beta }\nonumber \\= & {} R_{\alpha \gamma \beta \delta }V^{\gamma }V^{\delta }, \end{aligned}$$
(19)

where stars on the right, left and both sides of the tensor describe the operation related to the right, left and double dual of that term, respectively. These tensors with the help of the four-vector \(V_{\alpha }\) and the projection tensor, \(h_{\alpha \beta }\), can be written

$$\begin{aligned} X_{\alpha \beta }&=\frac{1}{3}X_{T}h_{\alpha \beta } +X_{TF}\left( \chi _{\alpha }\chi _{\beta }-\frac{1}{3}h_{\alpha \beta } \right) , \end{aligned}$$
(20)
$$\begin{aligned} Y_{\alpha \beta }&=\frac{1}{3}Y_{T}h_{\alpha \beta }+Y_{TF}\left( \chi _{\alpha }\chi _{\beta } -\frac{1}{3}h_{\alpha \beta }\right) , \end{aligned}$$
(21)

here \(X_T\) and \(Y_T\) indicate trace parts of the tensors \(X_{\alpha \beta }\) and \(Y_{\alpha \beta }\), respectively, while \(X_{TF}\) and \(Y_{TF}\) stand for the trace-free components of the tensors \(X_{\alpha \beta }\) and \(Y_{\alpha \beta }\), respectively (for details, see [59,60,61,62,63,64,65,66,67]). Using Eqs. (6)–(10), (20) and (21), we obtain

$$\begin{aligned} X_{T}&=\frac{1}{1+2R\lambda T^2}\left\{ \bar{\mu }+2R^2\lambda T +\frac{{\varphi }_{00}}{A^2}+\frac{\lambda }{2}R^2T^2\right\} , \end{aligned}$$
(22)
$$\begin{aligned} X_{TF}&=-\mathcal {E}-\frac{1}{2(1+2R\lambda T^2)} \left\{ (2R^2\lambda T+1)(-2{\sigma }{\eta }+\bar{\Pi })\right. \nonumber \\&\quad -\left. \frac{{\varphi }_{22}}{C^2}+\frac{{\varphi }_{11}}{H^2}\right\} , \end{aligned}$$
(23)
$$\begin{aligned} Y_{T}&=\frac{1}{2(1+2R\lambda T^2)}\left\{ 6\mu R^2\lambda T+\bar{\mu }+2R^2\lambda T\right. \nonumber \\&\quad \left. +3(1+2R^2\lambda T)\bar{P_r}-2\bar{\Pi }(2R^2\lambda T+1)\right. \nonumber \\&\quad \left. +\frac{{\varphi }_{00}}{A^2}+\frac{{\varphi }_{11}}{H^2}+\frac{2{\varphi }_{22}}{C^2}++2{\lambda }T^2R^2\right\} , \end{aligned}$$
(24)
$$\begin{aligned} Y_{TF}&=\mathcal {E}-\frac{1}{2(1+2R\lambda T^2)} \left\{ (\bar{\Pi }-2{\eta }{\sigma })(2R^2\lambda T+1)\right. \nonumber \\&\quad -\left. \frac{{\varphi }_{22}}{C^2}+\frac{{\varphi }_{11}}{H^2}\right\} . \end{aligned}$$
(25)

The value of \(Y_{TF}\) follows from Eqs. (18) and (25) as

$$\begin{aligned} Y_{TF}&=\frac{1}{2(1+2R\lambda T^2)}\left( \bar{\mu }+2R^2\lambda T\right. \nonumber \\&\quad \left. -2(1+2R^2\lambda T)(\bar{\Pi }-4{\eta }{\sigma })+\frac{\lambda }{2}T^2R^2\right. \nonumber \\&\left. +\frac{{\varphi }_{00}}{A^2}-\frac{2{\varphi }_{11}}{H^2} +\frac{2{\varphi }_{22}}{C^2}\right) -\frac{3}{2C^3} \int ^r_{0}\frac{C^2}{1+2R\lambda T^2} \left[ \bar{\mu }+2R^2\lambda T\right. \nonumber \\&\left. -\frac{\lambda }{2}T^2R^2+\frac{{\varphi }_{00}}{A^2}+\frac{U}{E} \left\{ \frac{(1+2R^2\lambda T)}{1+2R\lambda T^2}\bar{q} -\frac{{\varphi }_{01}}{AH}\right\} C^2C'\right] \mathrm{d}r. \end{aligned}$$
(26)

One can define a few particular fluid and dark source terms with dagger variables as

$$\begin{aligned} \mu ^{\dag }&\equiv \bar{\mu }+2R^2\lambda T+\frac{{\varphi }_{00}}{A^2}, \quad P^{\dag }_{\mathrm{r}}\equiv \bar{P_\mathrm{r}}+\frac{{\varphi }_{11}}{H^2}-\frac{4}{3}{\eta }{\sigma },\\ P^{\dag }_{\bot }&\equiv P_{\bot }+\frac{{\varphi }_{22}}{C^2}+\frac{2}{3}{\eta }\sigma ,\\ \Pi ^{\dag }&\equiv P^{\dag }_{\mathrm{r}}-P^{\dag }_{\bot }=\Pi -2{\eta }{\sigma } -\frac{\varphi _{22}}{C^2}+\frac{\varphi _{11}}{H^2}. \end{aligned}$$

In this context, it follows from Eqs. (22)–(25) that

$$\begin{aligned} X_{TF}=&\frac{3\kappa }{2C^3} \int ^r_{0}\left[ \frac{1}{\{1+2R\lambda T^2\}}\left\{ \mu ^{\dag } -\frac{\lambda }{2}T^2R^2 +\left( \hat{q}-\frac{\varphi _q}{AB}\right) \frac{U}{E}\right\} \right. \nonumber \\&\left. \times C^2C'\right] \mathrm{d}r-\frac{1}{2\{1+2R\lambda T^2\}}\left[ \mu ^{\dag }-\frac{\lambda }{2}T^2R^2\right] , \end{aligned}$$
(27)
$$\begin{aligned} Y_{TF}=&\frac{1}{2(1+2R\lambda T^2)}\Bigg [\mu ^{\dag }-\frac{\lambda }{2}T^2R^2- 2(1+2R^2\lambda T)\Pi ^{\dag }\nonumber \\&\quad +4R^2\lambda T\times \left( \frac{{\varphi }_{11}}{H^2} -\frac{{\varphi }_{22}}{C^2}\right) \Bigg ]-\frac{3}{2C^3}\int ^r_{0}\left[ \frac{1}{\{1+2R\lambda T^2\}}\right. \nonumber \\&\quad \left. \times \left\{ \mu ^{\dag }-\frac{\lambda }{2}T^2R^2+\left( \hat{q}-\frac{\varphi _q}{AH}\right) \frac{U}{E}\right\} C^2C'\right] \mathrm{d}r, \end{aligned}$$
(28)
$$\begin{aligned} Y_{T}&=\frac{1}{2(1+2R\lambda T^2)}\Bigg [(1+6R^2\lambda T)\mu ^{\dag } -6\varepsilon R^2\lambda T\nonumber \\&\quad +\left. 3(1+2R^2\lambda T)P_r^{\dag }-2(1+2R^2\lambda T)\Pi ^{\dag } -2R^2\lambda T \right. \nonumber \\&\quad \times \left( \frac{\varphi _{11}}{H^2}+3 \frac{\varphi _{00}}{A^2}\right) +2(2+2R^2\lambda T)\frac{\varphi _{22}}{C^2}-2{\lambda }T^2R^2\Bigg ], \end{aligned}$$
(29)
$$\begin{aligned} X_{T}&=\frac{1}{(1+2R\lambda T^2)}\left[ \mu ^{\dag }-\frac{\lambda }{2}T^2R^2\right] . \end{aligned}$$
(30)

The GR structure scalars [47] can be retrieved by taking \(f(R,T)=R\) in the above equations. These quantities have utmost relevance in the study of some important dynamical features of self-gravitating objects, for instance the IED and the quantity of matter content. In order to understand the role of f(R, T) terms on the shear and expansion evolution of radiating relativistic interiors we compute the Raychaudhuri equations. These relations were also evaluated independently by Landau [68]. With the help of the f(R, T) structure scalars the following can be written:

$$\begin{aligned} -(Y_{T})=\frac{{\Theta }^{2}}{3}+\frac{2}{3}{\sigma }^{ \alpha \beta }{\sigma }_{\alpha \beta }+V^{\alpha }\Theta _{;\alpha } -a^\alpha _{~;\alpha }, \end{aligned}$$
(31)

describing the importance of one of the f(R, T) scalar functions in the modeling of the expansion scalar evolution equation. In a similar fashion we calculate the shear evolution equation:

$$\begin{aligned} Y_{TF}=a^{2}+\chi ^{\alpha }a_{;\alpha }-\frac{aC'}{BC} -\frac{2}{3}{\Theta }\sigma -V^\alpha \sigma _{;\alpha }-\frac{1}{3}\sigma ^{2}. \end{aligned}$$
(32)

It is pertinent to mention that this equation has been expressed successfully via the f(R, T) structure scalar, \(Y_{TF}\). Using field equations and Eq. (27), the differential equation can be written

$$\begin{aligned} \left[ X_{TF}+\frac{\kappa \mu ^{\dag }}{2(1+2R\lambda T^2)}\right] '= & {} -X_{TF}\frac{3C'}{C}\nonumber \\&+\frac{\kappa (\Theta -\sigma )}{2(1+2R\lambda T^2)} \left( {q}B-\frac{\varphi _q}{A}\right) .\nonumber \\ \end{aligned}$$
(33)

By solving the equation for \(X_{TF}\) it is seen that it is \(X_{TF}\) that is controlling the IED of the spherical dissipative celestial bodies.

Fig. 1
figure 1

Plot of the dynamical variable \(\tilde{Y}_{T}\) for the strange star candidate 4U 1820-30

Full size image
Fig. 2
figure 2

Behavior of the dynamical variable \(\tilde{X}_T\) for the strange star candidate 4U 1820-30

Full size image
Fig. 3
figure 3

Role of the dark dynamical variable \(\tilde{X}_{TF}\) on the evolution of the strange star candidate 4U 1820-30

Full size image
Fig. 4
figure 4

Plot for the dark dynamical variable \(\tilde{Y}_{TF}\) on the evolution of the strange star candidate 4U 1820-30

Full size image

4 Evolution equations with constant R and T

In this section we shall investigate the influences of the \(R+\lambda R^2T^2\) corrections on the formulations of the shear, the expansion and the Weyl evolution equation for a relativistic dust cloud with constant curvature quantities. In order to represents constant values of R and T we shall use the tilde over the corresponding mathematical quantities. In this framework the spherical mass function in the presence of \(\bar{R}+\lambda \tilde{R}^2\tilde{T}^2\) corrections is found to be

$$\begin{aligned} m&=\frac{1}{2\{1+2R\lambda T^2\}} \int ^r_{0}(\mu +2T\lambda R^2) C^2C'\mathrm{d}r\nonumber \\&\quad -\frac{{\lambda }R^2T^2}{2\{1+2R\lambda T^2\}}\int ^r_{0} C^2C'\mathrm{d}r, \end{aligned}$$
(34)

while the Weyl scalar turns out to be

$$\begin{aligned} \mathcal {E}&=\frac{1}{2C^3\{1+2R\lambda T^2\}} \int ^r_{0}\mu 'C^3\mathrm{d}r-\frac{{\lambda }R^2T^2}{4\{1+2R\lambda T^2\}}. \end{aligned}$$
(35)

The widely known equation relating the spherical mass with the radiating structural parameters can be recast:

$$\begin{aligned} \frac{3m}{C^3}&=\frac{1}{2\{1+2R\lambda T^2\}} \left[ \mu +2T\lambda R^2-\frac{1}{C^3}\int ^r_{0}\mu 'C^3\mathrm{d}r\right] \nonumber \\&\quad +\frac{{\lambda }R^2T^2}{2\{1+2R\lambda T^2\}}. \end{aligned}$$
(36)

The f(R, T) structure scalars with \(\bar{R}+\lambda \tilde{R}^2\tilde{T}^2\) corrections boil down to be

$$\begin{aligned} \tilde{X}_{T}&=\frac{1}{\{1+2R\lambda T^2\}}\left[ {\mu }+2T\lambda R^2 -\frac{\lambda }{2}R^2T^2\right] , \end{aligned}$$
(37)
$$\begin{aligned} \tilde{Y}_{TF}&=-\tilde{X}_{TF}=\mathcal {E}, \end{aligned}$$
(38)
$$\begin{aligned} \tilde{Y}_{T}&=\frac{1}{2\{1+2R\lambda T^2\}}\left[ {\mu }+2T\lambda R^2+6\mu T\lambda R^2 -2{\lambda }R^2T^2\right] . \end{aligned}$$
(39)

These equations indicate that \(X_T,~Y_T\) and \(Y_{TF},~X_{TF}\) are the controlling effects induced by the fluid energy density and the tidal forces caused by the the Weyl scalar, respectively in an environment of f(R, T) extra degrees of freedom. An equation describing the evolution of inhomogeneity factors in the emergence of the IED for dust fluid is

$$\begin{aligned}&\left[ \frac{\mu }{2\{1+2R\lambda T^2\}} -\frac{{\lambda }T^2R^2}{4\{1+2R\lambda T^2\}}+\tilde{X}_{TF}\right] ' =-\frac{3}{C}\tilde{X}_{TF}C'.\nonumber \\ \end{aligned}$$
(40)

This equation involves the \(\tilde{X}_{TF}\), which was pointed out to be the inhomogeneity factor in the context of GR. It is seen from the above equation that \(\mu =\mu (t)\) if and only if \(\tilde{X}_{TF}=0=\lambda \). This shows that, even in \(\tilde{R}+\lambda \tilde{R}^2 \tilde{T}^2\) gravity, \(\tilde{X}_{TF}\) is an IED factor. In the famework of non-interacting particles evolving with a constant R and T the shear and the expansion evolution equations turn out to be

$$\begin{aligned}&V^\alpha \Theta _{;\alpha }+\frac{2}{3}\sigma ^2 +\frac{\Theta ^2}{3} -a^\alpha _{;\alpha }\nonumber \\&\quad =\frac{1}{\{1+2R\lambda T^2\}}\left[ {\mu }+2T\lambda R^2-\frac{\lambda }{2}T^2R^2\right] =-\tilde{Y}_T, \end{aligned}$$
(41)
$$\begin{aligned}&V^{\alpha }\sigma _{;\alpha }+\frac{\sigma ^{2}}{3}+\frac{2}{3}\sigma \Theta =-\mathcal {E}=-\tilde{Y}_{TF}. \end{aligned}$$
(42)

These equations have been expressed with the help of \(\tilde{Y}_{TF}\) and \(\tilde{Y}_T\). It is worthy to notice that one can use these set of equations to check the structure formation of compact objects under expansion-free scenario [69,70,71,72].

The study of compact objects is among the most burning issues of our mysterious dark universe in which stars came into being during the dying phenomenon of relativistic massive stars. Such celestial bodies have the size of a big city and in general contain at least 40% more mass than the solar mass. Due to this fact their core density exceeds the density of an atomic nucleus. This shows in particular that compact stars could be treated as test particles in the study of some physical features beyond the nuclear density.

Rossi X-ray timing explorer gathered information based on satellite observations about the structure of a neutron star, named 4U1820-30. They found the mass of this star to be \(2.25M_{\odot }\) containing a high amount of exotic matter. We now apply our results of dynamical dark variables to the observational values of this compact star. As our f(R, T) field equations are non-linear in nature we suppose that our star consists of non-interacting particles. We suppose also that our geometry is demarcated with the three-dimensional boundary surface. The interior is given by (3), while the exterior vacuum geometry is given by

$$\begin{aligned} \mathrm{d}s^2_+=-Z^2\mathrm{d}\nu ^2+Z^{-1}\mathrm{d}\rho ^2 +\rho ^2(\mathrm{d}\theta ^2+\sin ^2{\theta }\mathrm{d}\phi ^2), \end{aligned}$$
(43)

where \(Z=\left( 1-\frac{2M}{\rho }\right) \) with M and \(\nu \) are the total matter content and the retarded time, respectively. We use the Darmois junction conditions [73] to make continuous connections between Eqs. (3) and (43) over the hypersurface. These conditions, after some manipulations, lead to

$$\begin{aligned} A\mathrm{d}t&\overset{\Sigma }{=}\mathrm{d}\nu \left( 1-2\frac{M}{\rho }\right) ,\quad C\overset{\Sigma }{=}\rho (\nu ), \end{aligned}$$
(44)
$$\begin{aligned} M&\overset{\Sigma }{=}m(t,r). \end{aligned}$$
(45)

These constraints should be fulfilled by both manifolds in order to remove jumps over the boundary.

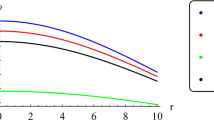
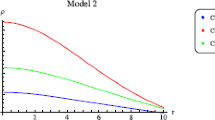
It is well known from the literature that the dynamical variable, \(Y_T\), plays the same role as that of the Tolman mass density in the evolutionary phases of those relativistic systems which are in the state of equilibrium or quasi-equilibrium. Figures 1 and 2 state the evolution of the \(\tilde{Y_T}\) and \(\tilde{X_T}\) variables with the increase of r and T, respectively. Other very important dark scalar functions are the \(\tilde{X_{TF}}\) and the \(\tilde{Y_{TF}}\). These two variables have opposite behavior on the dynamical phases of our relativistic 4U 1820-30 star candidate. The modified structure scalar \(\tilde{X_{TF}}\) controls the appearance of inhomogeneities on the initially regular compact object. It can be observed from Fig. 3 that the inhomogeneity of the compact star keeps on decreasing by increasing the radial coordinate of the spherical self-gravitating object. The totally reverse behavior of \(Y_{TF}\) can be observed from Fig. 4.

5 Conclusions

This paper is dedicated to exploring the effects of the extra curvature ingredients of the f(R, T) gravity theory on the dynamical variables of a compact spherical star. The matter contents in the stellar interior is considered to be imperfect due to anisotropic stresses, shear viscosity and dissipative terms. A particular form of the f(R, T) function, i.e. \(f(R,T)=f_1(R)+f_2(R)f_3(T)\), is utilized to explore the modified field equations. The Misner–Sharp mass function is generalized by including the higher curvature ingredients of the f(R, T) theory. We have split the Weyl tensor, which describes the distortion in the shapes of celestial objects due to tidal forces, in an electric part and in a magnetic part. The magnetic part vanishes due to the symmetry of the spherical star and all the tidal effects are due to its electric component.

A correspondence between the scalar component associated with the Weyl tensor with matter variables has been established under the influence of the extra curvature ingredients of f(R, T) theory. In a similar way the electric part of Riemann tensor is extracted and its second dual tensor formulated. These two tensors are furthers divided into their constituent scalar parts, named structure scalars. These scalar parts are written in terms of matter variables with the help of modified field equations and the Weyl scalar. The effects of higher-order terms are also found in the formation of the dynamical equations obtained in Eqs. (27)–(30). These structural dynamical equations have enough significance to discuss the evolution of self-gravitating compact objects. We have also explored the Raychaudhuri equations for the shear and expansion scalar which are related with some of the structure scalars. Further, a differential equation is formulated by adopting the procedure developed by Ellis which is of significance in the discussion of the inhomogeneous density distribution in the universe. One can find that the irregularities in the matter density can be controlled via one of the scalar variable. We also have explored the dark dynamical variables under the condition of the constant Ricci invariant and the trace of the stress energy tensor. These dark dynamical variables are effected by the tidal effects due to the electric part of the Weyl tensor. Further, the evolution equations for the shear and the expansion are formulated in this background and linked with the structure scalars. All our results are consistent with those already obtained in the literature.