1 Introduction

In the Standard Model of particle physics (SM), muons decay through the purely leptonic weak interaction: the tree level process is \({\upmu } \rightarrow \mathrm {e} {\upnu }{\bar{\nu }}\) (Michel decay). This decay has been carefully studied since the discovery of the muon and still provides one of the most useful tools for studying the weak interactions. Radiative muon decay, \({\upmu } \rightarrow \mathrm {e} {\upnu }\bar{{\upnu }}{\upgamma }\) (RMD), is the first order QED correction to Michel decay with the additional emission of one inner bremsstrahlung photon.

The importance of studying RMD is twofold: on one hand, it provides a tool for investigating weak interactions since it is sensitive to some of parameters appearing in the most general formula of muon decay; this approach is followed in e.g. [1, 2]. On the other hand, it constitutes important sources of background for experiments searching for rare muon decays, not allowed in the minimal SM, such as \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\). RMD events form a time-correlated background for the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search when the two neutrinos carry away so little momentum that the RMD event falls within the signal window for \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) events, determined by the experimental resolutions. Moreover, high energy \(\gamma \)-rays from RMD events constitute the dominant accidental background for experiments operating at high muon stopping rates, by random time-overlapping with high energy positrons from Michel decays. Finally, the identification of the time-correlated peak due to RMD events allows a calibration of the positron–photon relative timing as well as a measure of the associated resolution and provides a strong internal consistency check for the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) analysis.

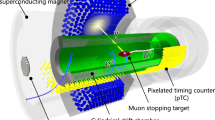
2 MEG experiment

The MEG experiment has been searching for the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) decay since 2008 [3, 4] at Paul Scherrer Institut in Switzerland [5] reaching the most stringent upper limit up to date on the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) branching ratio based on the data sample collected in 2009–2011 [6]. The experiment is briefly described below; a full description is available in [7].

In this paper, we use a cylindrical coordinate system \((r,\phi ,z)\) with origin at the centre of MEG and the z-axis being parallel to the incoming muon beam. Where used, the polar angle \(\theta \) is defined with respect to the z-axis.

A high intensity positive muon beam is brought to rest in a 205 \(\mathrm {\upmu m}\) thick slanted plastic target, placed at the centre of the experimental set-up. MEG uses surface muons, originating from pion decays at rest, at the surface of the production target. Hence, they are fully polarized at their origin. The depolarization mechanisms along the beam-line and in the stopping target have been estimated in detail and are small and under control. The residual muon polarization at the decay point along the beam axis is measured to be [8]

$$\begin{aligned} P_{\mu ^{+}} = -0.85 \pm 0.03 ~ \mathrm {(stat.)} ~ ^{+ 0.04}_{-0.05} ~ \mathrm {(sys.)} \end{aligned}$$
(1)

from the angular distribution of decay positrons, in agreement with expectations.

The muon decay products are detected by a liquid xenon (LXe) photon detector and a positron spectrometer with a gradient magnetic field generated by the superconducting magnet COBRA. The LXe detector consists of 900 \(\ell \) LXe and 846 photomultiplier tubes and measures energy, interaction time and position of the photon. Its geometrical acceptance is \(\theta _{\upgamma }\in (70^{\circ },110^{\circ })\) and \(\phi _{\upgamma }\in (-60^{\circ },60^{\circ })\) covering \(\sim \)11 % of the total solid angle. The opposite angular region is covered by the spectrometer consisting of a set of 16 drift chambers, radially aligned, for the measurement of the positron momentum, complemented by a timing counter (TC), composed of two scintillator arrays, for the measurement of the positron timing. The MEG detector and the trigger are optimized to search for \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) events. Therefore, there is only a limited energy and angular window to detect RMD events.

The time (\(t_\mathrm {e}\)) and vertex of the positron at the target are obtained by extrapolating the time measurement at the TC back along the track trajectory. The photon time (\(t_{{\upgamma }}\)) is calculated by connecting the photon interaction position in the LXe volume to the positron vertex on the target and extrapolating the time measurement at the LXe detector back to the target.

The kinematics of the events is described by five observables: the photon and positron energies (\(E_{{\upgamma }}\), \(E_\mathrm {e}\)), their relative directions (\(\theta _{{\mathrm{e}\upgamma }}\), \(\phi _{{\mathrm{e}\upgamma }}\)),Footnote 1 and the emission time (\(t_{{\mathrm{e}\upgamma }}= t_{{\upgamma }}- t_\mathrm {e}\)).

A dedicated trigger system allows an efficient pre-selection of \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) candidate events (the MEG trigger), with an almost zero dead-time [9, 10]. Background is efficiently suppressed by an on-line requirement of a positron and a photon close to their kinematic limit moving in opposite direction in time coincidence. In parallel to the main trigger, several other triggers are activated in a physics run. In this analysis, we select RMD events from the MEG trigger data while other trigger data are used for the calibration of the detectors and the normalization.

Fig. 1
figure 1

Photon energy spectra with different trigger thresholds (top). The solid (open) circles correspond to the normal (lower) threshold. The dot-dashed line is the MC simulation spectrum smeared with the detector response; the calculated spectrum is used to correct for the trigger effect in the lower threshold distribution. The bottom plot shows the ratio of the normal threshold spectrum to the lower threshold one

Full size image

Several kinds of dedicated runs are frequently taken at different intervals to calibrate and monitor the detectors. Among them a run to calibrate the LXe detector with high energy photons close to the signal region is especially important. In this run, neutral pions are produced through the charge-exchange reaction \(\pi ^{-} \mathrm {p} \rightarrow \pi ^{0} \mathrm {n}\), by using a negative pion beam brought to rest in a liquid-hydrogen target. The photons from neutral pion decay \(\pi ^0\rightarrow \gamma \gamma \) are used to calibrate the LXe detector. A counter formed by nine NaI(Tl) crystalsFootnote 2 is placed on the opposite side of the LXe detector to tag one of the \(\gamma \)-rays, yielding an almost monochromatic source of 55 and 83 MeV photons. The photon energy, timing and position resolutions as well as the energy scale are measured in this run.

The photon energy is limited by the trigger threshold, \(E_{{\upgamma }}\gtrsim 40~\mathrm {MeV}\). A pre-scaled trigger with a lowered \(E_{{\upgamma }}\) threshold (by \(\sim \)4 MeV) is enabled during the normal physics run. This allows a relative measurement of the energy-dependent efficiency curve of the LXe detector (Fig. 1), while the absolute photon detection efficiency is evaluated via MC simulation [7]. The position dependence of the detection efficiency is investigated and the average value is calculated by taking into account the observed event distribution. This evaluation is cross-checked by measuring the probability of detecting one of the two photons from a neutral pion decay in the LXe detector under the condition that the other photon is detected by the NaI(Tl) counter. The measurement and the MC simulation agree to within 2 %; the spread is considered as an estimate of the systematic uncertainty, resulting in the detection efficiency \(\epsilon _\gamma =0.63\pm 0.02\) at the plateau.

The LXe detector also exhibits good linearity; the non-linearity of the energy scale is found to be \(<\)0.1 %, estimated from the 55 and 83 MeV photons from the pion decays as well as from the \(17.7~\mathrm {MeV}\) peak position of the \(^7\mathrm {Li}(\mathrm {p},\gamma )^8\mathrm {Be}\) reaction induced by using a Cockcroft–Walton proton accelerator [11]. The uncertainty of the energy scale around the signal region is evaluated to be 0.3 % from combining several kinds of calibration data.

The spectrometer preferentially selects high energy positrons, with \(E_\mathrm {e}\gtrsim 45~\mathrm {MeV}\). The Michel positron spectrum is used as a calibration tool for the spectrometer by comparing the measured one with the precisely known theoretical one, including the first order radiative corrections [12]. The resolution and the energy-dependent efficiency are simultaneously extracted by fitting the theoretical Michel spectrum folded with the detector response to the measured spectrum, as shown in Fig. 2. The absolute positron detection efficiency is not needed because of the normalization scheme adopted (described in Sect. 5.1).

Fig. 2
figure 2

Michel positron spectrum (top). The dots are data and the red-solid line is the best-fit function. The blue-dotted line shows the detector resolution and the dot-dashed line shows the theoretical Michel spectrum, folded with the detector resolution. The bottom plot shows the energy dependence of the acceptance extracted from the fit and normalized to 1 at 52.8 MeV

Full size image

As reported in [4], the resolutions for positrons and photons with energies close to the kinematic limit \(m_{\mu }/2\) are \(\sigma (E_\mathrm {e}) \sim 330~\mathrm {keV}\), \(\sigma (E_{{\upgamma }}) \sim 1.0~\mathrm {MeV}\), \(\sigma (\theta _{{\mathrm{e}\upgamma }}) \sim 17~\mathrm {mrad}\), \(\sigma (\phi _{{\mathrm{e}\upgamma }}) \sim 14~\mathrm {mrad}\), \(\sigma (t_{{\mathrm{e}\upgamma }}) \sim 130~\mathrm {ps}\).

Although measurements of RMD have already been obtained by other experiments [13], the MEG data provides the unprecedented opportunity of measuring RMD from polarized muons at the kinematic edge.

3 Distribution of radiative muon decay

The RMD differential branching ratio was calculated by several authors [14–17]. In the framework of the \(V-A\) theory of weak interactions, it reads as [18]

$$\begin{aligned} d\mathcal{B}({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upnu }\bar{{\upnu }}{\upgamma })&= \frac{\alpha }{64\pi ^3} \beta \, dx \,\frac{dy}{y}\, d\Omega _\mathrm {e} \,d\Omega _{\gamma } \,\big [ F(x,y,d) \nonumber \\&\quad - \beta {\varvec{P}_{\mu ^{+}}} \cdot {\hat{\varvec{p}}}_\mathrm {e} G(x,y,d) \nonumber \\&\quad - {\varvec{P}_{\mu ^{+}}} \cdot {\hat{\varvec{p}}}_\gamma H(x,y,d) \big ], \end{aligned}$$
(2)

where \(x=2E_\mathrm {e}/m_\mu \), \(y=2E_{{\upgamma }}/m_\mu \), \({\hat{\varvec{p}}}_k\) is the unit vector of the particle k (positron or photon) momentum in the muon rest frame, \({\varvec{P}_{\mu ^{+}}}\) is the muon polarization vector, and \(d = 1 - \beta {\hat{\varvec{p}}}_e \cdot {\hat{\varvec{p}}}_\gamma \). Detailed descriptions of the functions F, G and H are given in [18]. A few authors calculated the higher order corrections for some special cases [19–21] and only recently a full next-to-leading order (NLO) calculation became available [22]. In this paper only the lowest-order general calculation is used.

The relative angle distribution shows an asymmetric shape in \(\theta _{{\mathrm{e}\upgamma }}\), while the distribution in \(\phi _{{\mathrm{e}\upgamma }}\) remains symmetric. The \(\theta _{{\mathrm{e}\upgamma }}\) distributions for polarized muons with \(P_{\mu ^{+}}=-0.85\) for four different values of \(\theta _\mathrm {e}\) are shown in Fig. 3 after integration over \(\phi _{{\mathrm{e}\upgamma }}\) and the positron and photon energies. The relative-angle range kinematically allowedFootnote 3 for RMD is so restricted by the energy selection imposed on the positron and photon that it is fully covered by the MEG detector and trigger. However, the distribution is somewhat distorted due to the energy-dependent variation of the trigger efficiency over the angular range, as explained below.

Fig. 3
figure 3

Differential branching ratio of RMD for \(P_{\mu ^{+}}=-0.85\) as a function of \(\theta _{\mathrm {e}\gamma }\) for four different values of positron polar angle \(\theta _\mathrm {e}\). These distributions are obtained by the numerical integration of Eq. (2) over \(E_\mathrm {e}>45\), \(E_{{\upgamma }}>40\) MeV, and \(\phi _{{\mathrm{e}\upgamma }}\)

Full size image

The directional match efficiency of the trigger is evaluated via MC simulation and the distribution of the accidental background. Because the spectrometer response introduces a correlation in the distribution of the positron emission angle and momentum, the relative angle distribution, after the directional match selection induced by the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) trigger, is asymmetric and dependent on the positron energy. Therefore, the directional match efficiency is calculated for different values of \(E_\mathrm {e}\), as shown in Fig. 4. The spread between calculations and measurements is considered as an estimate of the systematic uncertainty.

Fig. 4
figure 4

Efficiencies of the trigger directional match selection versus relative angles. The bands around the curves show the uncertainties (\(1\sigma \))

Full size image

4 Measurement of radiative muon decay

The data sample used in this analysis corresponds to \(\sim \)1.8\(\times 10^{14}\) positive muon decays in the target, collected in 2009–2010.Footnote 4 We used events reconstructed in the analysis window defined as \(45<E_\mathrm {e}<53\) MeV, \(40<E_{{\upgamma }}<53~\mathrm {MeV}\), \(|\phi _{{\mathrm{e}\upgamma }}|<0.3\) rad and \(|\theta _{{\mathrm{e}\upgamma }}|<0.3\) rad. The event reconstruction and event selection as well as the data sample for this study are identical to those for the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search in [4]. A complete description of the MEG analysis procedure is given in [3, 4, 7].

Fig. 5
figure 5

Distributions of \(t_{e\gamma }\) in a 2009 data and b 2010 data. The best-fit functions of the sum of the RMD and the accidental-background PDFs (red solid) and those of the accidental-background only (dashed) are superimposed

Full size image
Fig. 6
figure 6

Projected distributions of RMD events in a \(E_\mathrm {e}\), b \(E_{{\upgamma }}\) and c \(\theta _{\mathrm {e}\gamma }\). The solid circles are measurements obtained from the 2009 and 2010 data sets, the histograms show the expectations assuming \(P_{\mu ^{+}} = -0.85\) and the normalization based on Michel positron events. The bands show the systematic uncertainties in the calculation of the expectations. The bottom plots show the ratio of the measurements to the expectations. In c the expected distribution calculated assuming \(P_{\mu ^{+}} = 0\) (magenta dashed line) is also superimposed for comparison

Full size image

The main background to the RMD signal comes from the accidental coincidence of positrons and photons originating from different muon decays. Because the two particles are uncorrelated, the accidental background events are distributed randomly with respect to \(t_{{\mathrm{e}\upgamma }}\). On the other hand, the positron and the photon from a RMD are emitted simultaneously; therefore, the presence of RMD events is signalled by a peak around zero in the \(t_{{\mathrm{e}\upgamma }}\) distribution and it is well described by a sum of two Gaussian functions.Footnote 5

To measure the number of RMD events (\(N^{\mathrm {e}\nu \bar{\nu }\gamma }\)), we fitted a probability density function (PDF), given by the sum of the RMD PDF and the accidental background PDF (a uniform distribution), to the \(t_{\mathrm {e}\gamma }\) distribution (Fig. 5). We separately analysed 2009 and 2010 data because of the different time resolutions: the electronics were improved in the time measurement of 2010. To measure the distribution of RMD in terms of energy and angle, the fits were repeated for data-sets divided into bins. Figure 6 shows the experimental distributions of RMD events in \(E_\mathrm {e}\), \(E_{{\upgamma }}\) and \(\theta _{{\mathrm{e}\upgamma }}\).

5 Results

5.1 Branching ratio measurement

Since the total branching ratio for RMD is infrared divergent, a well defined measure of the branching ratio requires a region of the phase space which includes a lower limit on the photon energy. Here we measure the branching ratio for the largest phase space allowed by our detector set-up, namely for \(E_\mathrm {e}>45\) and \(E_{{\upgamma }}>40~\mathrm {MeV}\).

To convert the number of measured RMD events into the branching ratio, it is normalized to the number of Michel positrons counted simultaneously. This is accomplished by a pre-scaled unbiased Michel positron trigger:

$$\begin{aligned} N_\mu = \frac{N^{\mathrm {e}\nu \bar{\nu }}}{f^{\mathrm {e}\nu \bar{\nu }}_{E_\mathrm {e}}}\times \frac{p^{\mathrm {e}\nu \bar{\nu }}}{\epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {trg}}} \times \frac{1}{\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {e}}\rangle }, \end{aligned}$$
(3)

where \(N^{\mathrm {e}\nu \bar{\nu }}\) is the number of detected Michel positrons, \(f^{\mathrm {e}\nu \bar{\nu }}_{E_\mathrm {e}}\) is the fraction of Michel spectrum in the corresponding energy range, and \(p^{\mathrm {e}\nu \bar{\nu }}=10^7\) is the pre-scaling factor of the Michel positron trigger corrected by \(\epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {trg}}=0.88\pm 0.01\) to account for the dead time of the trigger scaler. The positron detection efficiency is \(E_\mathrm {e}\) dependent, \(\epsilon _\mathrm {e}(E_\mathrm {e}\)), as described in Sect. 2, and \(\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {e}}\rangle \) is the weighted average efficiency over the corresponding range of the Michel spectrum.

The branching ratio is calculated as follows,

$$\begin{aligned} \mathcal {B}({\upmu } \rightarrow \mathrm {e} {\upnu }\bar{{\upnu }}{\upgamma })&= \frac{N^{\mathrm {e}\nu \bar{\nu }\gamma }}{N_\mu \times \langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }\rangle }\nonumber \\&= N^{\mathrm {e}\nu \bar{\nu }\gamma }\times \Biggl ( \frac{f^{\mathrm {e}\nu \bar{\nu }}_{E_\mathrm {e}}}{N^{\mathrm {e}\nu \bar{\nu }}} \times \frac{\epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {trg}}}{p^{\mathrm {e}\nu \bar{\nu }}} \Biggr ) \times \frac{\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }}_{\mathrm {e}}\rangle }{\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\mathrm {e}}\rangle }\nonumber \\&\quad \times \frac{1}{\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\gamma }\rangle } \times \frac{1}{\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\mathrm {trg}}\rangle }, \end{aligned}$$
(4)

where \(\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\mathrm {e}}\rangle \), \(\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\gamma }\rangle \), and \(\langle \epsilon ^{\mathrm {e}\nu \bar{\nu }\gamma }_{\mathrm {trg}}\rangle \) are the weighted average efficiencies for the positron detection, the photon detection, and the trigger directional match, respectively, over the RMD spectrum. The positron detection efficiencies for the two channels appear in ratio and thus the branching-ratio measurement is insensitive to the absolute value of the positron detection efficiency and independent of the instantaneous beam rate.

The total number of RMD events \(N^{\mathrm {e}\nu \bar{\nu }\gamma } =12\,920\pm 299\) corresponds to

$$\begin{aligned} \mathcal {B}({\upmu } \rightarrow \mathrm {e} {\upnu }\bar{{\upnu }}{\upgamma }) = (6.03\pm 0.14\pm 0.53)\times 10^{-8} \nonumber \\ \mathrm {for} \quad (E_\mathrm {e}>45, E_{{\upgamma }}>40~\mathrm {MeV}), \end{aligned}$$
(5)

where the first uncertainty is statistical and the second one is systematic. This result is in good agreement with the SM value calculated by a numerical integration of the theoretical formula (2), \(\mathcal {B}^{\mathrm {SM}}({\upmu } \rightarrow \mathrm {e} {\upnu }\bar{{\upnu }}{\upgamma }) = 6.15\times 10^{-8}\) (this estimation does not include the contributions from radiative corrections, see Sect. 6.2).

The overall detection efficiency of RMD events in this region is \(\sim \)0.1 %. This low efficiency is due to the small geometrical acceptance (\(\sim \)10 %) and the detector and trigger optimization for the detection of \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) events.

The systematic uncertainties are summarised in Table 1. The largest contribution comes from the energy dependence of the positron detection efficiency. This is due to the correlation between the acceptance curve and the response function, which are simultaneously extracted in the Michel spectrum fit, and to the dependence of the positron energy threshold and spectral shape on the positron azimuthal emission angle induced by the directional match of the trigger. This dependence affects the determination of the normalization factor based on Michel decays, since for events involving isolated positrons the directional match is clearly not imposed; thus, acceptance factors are different between RMD and Michel events and do not cancel out perfectly.

Table 1 Summary of relative uncertainties in the branching ratio measurement
Full size table

5.2 Spectral analysis

We also performed a \(\chi ^2\)-fit to the measured spectrum with the polarization and the normalization as floating parameters in order to study the spectral shape in the three-dimensional space \((E_\mathrm {e},E_{{\upgamma }},\theta _{{\mathrm{e}\upgamma }})\). The data sample was divided into \(2\times 2\times 6\) bins in \((E_\mathrm {e},E_{{\upgamma }},\theta _{{\mathrm{e}\upgamma }})\) respectively (24 bins in total). The expected number of events for the bin i was calculated as follows: \(N^\mathrm {cal}_i(P_{\mu ^{+}},\alpha ) = \mathcal{B}_i(P_{\mu ^{+}})\cdot \epsilon _i ^{\mathrm {e}\nu \bar{\nu }\gamma }\cdot \alpha N_{\mu }\), where the partial branching ratio \(\mathcal{B}_i(P_{\mu ^{+}})\) is given by the SM value, that depends on the muon polarization \(P_{\mu ^{+}}\) according to Eq. (2); \(\epsilon _i^{\mathrm {e}\nu \bar{\nu }\gamma }\) is the efficiency for RMD events in this bin; and \(\alpha \) is a normalization scale parameter, relative to the normalization based on the Michel positron measurement. Since the systematic uncertainties introduce correlations among the bins, we built a covariance matrix V. The covariance matrix for each source of systematic uncertainty was evaluated by calculating the deviation of \(N^\mathrm {cal}_i\) when the corresponding parameter was varied by one standard deviation. The total covariance matrix including the statistical uncertainty is the sum of the covariance matrices for individual uncertainty sources, except for those related to the absolute scale, that is, the uncertainties in the Michel positron counting and the absolute trigger and photon efficiencies. The \(\chi ^2\) is defined as:

$$\begin{aligned} \chi ^2(P_{\mu ^{+}},\alpha ) = \sum _{i,j=1}^{24}(N^{\mathrm {meas}}_i - N^{\mathrm {cal}}_i)(V_{ij})^{-1}(N^{\mathrm {meas}}_j - N^{\mathrm {cal}}_j).\nonumber \\ \end{aligned}$$
(6)

The \(\chi ^2\) values for \(P_{\mu ^{+}}=-0.85\) and for the best-fit value are \(\chi ^2(P_{\mu ^{+}}=-0.85)/\mathrm {DOF} = 12.8 /23=0.557\) and \(\chi ^2_\mathrm {min} / \mathrm {DOF} = 11.9/22 = 0.541\), respectively, where the scale parameter \(\alpha \) is at the best-fit value for each case. These results show consistency of the experimental spectral shape with the SM-based predictions. The distribution of measured RMD events and the calculated ones, both for predicted parameters and for the best-fit ones, are shown in Fig. 7.

The best-fit values are \((P_{\mu ^{+}}, \alpha ) = (-0.70 \pm 0.16,0.95\pm 0.04)\). When \(\alpha \) is fixed to 1, \(P_{\mu ^{+}} = -0.71 \pm 0.15\). These results are consistent with Eq. (1) within one standard deviation. The scale parameter \(\alpha \) is weakly sensitive to the polarization, and the result changes negligibly when \(P_{\mu ^{+}}\) is fixed to \(-0.85\). The result confirms the Michel normalization.

Fig. 7
figure 7

Distribution of RMD events in the 24 bins used in the fit. The dots show the data and the solid lines show the expected distribution with \(P_{\mu ^{+}}=-0.85\) normalized by the Michel positron measurement. The bands show the systematic uncertainty (square root of the diagonal elements of the covariance matrix). The red-dashed histograms show the best-fit distribution

Full size image

6 Discussions

6.1 Impact on \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search

The measurement of RMD is a powerful internal cross-check of the experiment. This analysis uses the same data sample, calibrations, reconstruction and event selections as that of the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search in [4]. Therefore, the agreement in the branching ratio and the distribution between the measurements and the SM predictions provides additional confidence in the reliability of the search for \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\).

A more practical purpose of analysing RMD is to estimate the number of RMD events in the fit region of the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search. We extrapolate the number of RMD events measured in the low-\(E_{{\upgamma }}\) region (\(40<E_\gamma <48~\mathrm {MeV}\)) to the fit region (\(48<E_\gamma <58~\mathrm {MeV}\)) by using the ratio of the partial branching ratios and the ratio of the efficiencies. This estimate is directly implemented in the likelihood of the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search as a constraint on the number of RMD events [4, 6].

Another application of the RMD analysis is the use of RMD events as an alternative normalization channel. The advantage of using RMD is its closer resemblance to \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) decay compared to that of Michel decay, since not only a positron but also a photon from a muon decay is measured. The Michel positron approach provides normalization with 5 % uncertaintyFootnote 6 while the RMD approach has an uncertainty of 6 %. The systematic uncertainties of those two approaches are independent, so that the combination leads to 4 % uncertainty in the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) normalization [6].

6.2 RMD measurements and the future

With the experimental precision of the RMD measurement at the level of \(\sim \)9 %, radiative corrections to RMD are not negligible any more, as reported in [21], especially at the kinematic edge of its phase space where the higher order contribution could be as large as O(10 %). Only recently a full NLO calculation of RMD became available [22] in addition to higher-order calculations for special cases [19–21].

In the next stage of \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search experiments, such as the MEG upgrade (MEG II) [24] and also in the future search for \({\upmu }^{+} \rightarrow \mathrm {e}^{+}\mathrm {e}^-\mathrm {e}^{+}\) [25], detectors with higher resolutions are planned in order to reach the desired sensitivities. They will require refined control and precise measurements of all types of background.Footnote 7 These measurements as well as tests of the structure of weak interactions using RMD events require precise theoretical predictions as achieved with the recent fullNLOcalculationwhich has a theoretical errorwell below 1.0 %

7 Conclusion

We performed the first study of radiative decay of polarized muons, \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upnu }\bar{{\upnu }}{\upgamma }\). We measured the branching ratio, \(\mathcal {B} = (6.03\pm 0.14\mathrm {(stat.)}\pm 0.53\mathrm {(sys.)})\times 10^{-8}\) for \(E_\mathrm {e}>45\) MeV and \(E_{{\upgamma }}>40\) MeV, and various distributions in a large sub-sample of muon decays collected by the MEG experiment. Our measurement of RMD is the most precise in the kinematic region relevant to the \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) search and is consistent with the SM expectations. The agreement with the SM strongly validates the experiment and demonstrates the capability of detecting very rare decays such as \({\upmu }^{+} \rightarrow \mathrm {e}^{+} {\upgamma }\) in MEG.