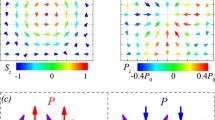
Using stereographic projection approach, we develop a theory for calculation of dynamic susceptibility tensor of Skyrmion crystals (SkX), formed in thin ferromagnetic films with Dzyaloshinskii–Moriya interaction and in the external magnetic field. Staying whenever possible within analytical framework, we employ the model ansatz for static SkX configuration and discuss small fluctuations around it. The obtained formulas are numerically analyzed in the important case of uniform susceptibility, accessible in magnetic resonance experiments. We show that, in addition to three characteristic magnetic resonance frequencies discussed earlier both theoretically and experimentally, one should also expect several resonances of smaller amplitude at somewhat higher frequencies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
Magnetic skyrmions are topologically protected particle-like configurations of local magnetization, appearing particularly in noncentrosymmetric magnets [1] with Dzyaloshinskii–Moriya interaction (DMI). Skyrmions are studied as perspective building blocks for novel computer memory devices [2], programmable logic devices [3], or even artificial neural network devices [4]. It was observed that skyrmions are usually arranged into regular lattices both in bulk compounds [5] and thin films [6–9]. Skyrmion lattices, named also skyrmion crystals (SkX), attract the attention of researchers because of their applications to magnonics [10].
One skyrmion can largely be considered as a small magnetic bubble, whose motion can be described by Thiele equation [11]. But even a single skyrmion is a complex structure, which has its own dynamics that cannot be described in terms of skyrmion’s displacement only. There are also deformations of the skyrmion’s form, such as dilatation, elliptical distortions, triangular distortions, etc. [12, 13].
It was shown that the energy band structure of SkX should possess a Goldstone mode [14], associated with the displacement of skyrmions’ centers. Besides this mode there are many other branches of different symmetry [10, 15, 16], associated with, e.g., elliptical deformation, clockwise (CW) rotation, counterclockwise (CCW) rotation and breathing mode (Br) of skyrmions.
One can observe and explore SkX excitations by several methods, among them inelastic neutron scattering [17], optical inverse-Faraday effect [18], magnetic resonance (MR) technique. In the latter technique it was shown [19] that CW and CCW modes are observed when oscillating component of magnetic field is directed in the plane of SkX and the breathing mode is observed for the field perpendicular to the plane, in accordance with the earlier prediction by means of numerical simulations [15].
It was also demonstrated that other (octupole and sextupole) modes can manifest themselves in MR experiments in bulk SkX systems with strong cubic magnetocrystalline anisotropy, which hybridizes these modes with Br and CCW excitations [20, 21].
In this study we discuss the MR response of SkX formed in thin films with DMI and in presence of magnetic field at low temperatures. We find that beyond the lowest-energy CW, CCW and Br modes, there are also higher-energy modes of the same symmetry. Therefore, they should also be visible in MR response experiment, although with a much smaller the magnitude of the corresponding signals.
MODEL
We consider a thin film of Heisenberg ferromagnet with Dzyaloshinskii–Moriya interaction an in uniform magnetic field, B, perpendicular to the film. The energy density is given by
with C and D are exchange and DMI constants, respectively. This is perhaps the minimal model where the SkX exists (apart from centrosymmetric frustrated magnets (see [22, 23]). We ignore here the dipole-dipole interaction, which in the long-wave limit and in the planar case can be replaced, with a good accuracy, by the easy-plane anisotropy term. It is known, that if the anisotropy is smaller than the magnetic field magnitude, then the phase diagram is largely unchanged [24, 25], so we omit anisotropy terms for simplicity.
We take the low temperature limit, when the local magnetization is saturated to its maximum value \({\mathbf{S}} = S{\mathbf{n}}\), and \({\text{|}}{\mathbf{n}}{\text{|}} = 1\). It is convenient to measure length in units of \(l = C{\text{/}}D\), and energy density in units of \(C{{S}^{2}}{{l}^{{ - 2}}} = {{S}^{2}}{{D}^{2}}{\text{/}}C\). Then the energy density (1) becomes dependent only on the dimensionless field \(b = BC{\text{/}}S{{D}^{2}}\). It turns out that in a range \(0.25 < b < 0.8\) the static configuration for \({\mathbf{n}}\) corresponds to SkX, extensively discussed in the literature [12, 26–28].
We first discuss a general formalism for the calculation of susceptibility, valid for any topologically non-trivial spin configuration, and subsequently apply this formalism for the special case of SkX [29]. In the stereographic projection method, we represent the unit vector \({\mathbf{n}}\) along the local magnetization as
where \(f = f(z,\bar {z})\) is a function of a complex variable \(z = x + iy\) and a conjugate one \(\bar {z} = x - iy\); \(x,y\) are spatial coordinates. The expression for \(\mathcal{E}\) acquires highly nonlinear form in terms of \(f,\bar {f}\), presented elsewhere [29].
We consider the dynamics of the local magnetization in Lagrangian formalism, \(\mathcal{L} = \mathcal{T} - \mathcal{E}\), with the kinetic term given by
here φ and θ define the magnetization direction \({\mathbf{n}} = (\cos \varphi \sin \theta ,\sin \varphi \sin \theta ,\cos \theta )\). This leads to the Landau–Lifshitz equation, \({\mathbf{\dot {S}}} = - {{\gamma }_{0}}{\kern 1pt} {\mathbf{S}} \times {\mathbf{H}},\) with \({{\gamma }_{0}}\) is a gyromagnetic ratio, and \({\mathbf{H}} = \delta E{\text{/}}\delta {\mathbf{S}}\) is an effective magnetic field.
Absorbing the factor \(S{\text{/}}{{\gamma }_{0}}\) into the time redefinition, the kinetic term may be written in terms of the complex function f as
We study the dynamics of local magnetization by considering small fluctuations of the stereographic function, \(f({\mathbf{r}},t)\), around the static field, \({{f}_{0}}({\mathbf{r}})\), providing the minimum of total energy, \(\int d{\mathbf{r}}{\kern 1pt} \mathcal{E}\), and write
with ψ is time-dependent function and α is a small parameter of the theory, clarified below. We then consider the expansion \(\mathcal{L} = {{\mathcal{L}}_{0}} + \alpha {{\mathcal{L}}_{1}} + {{\alpha }^{2}}{{\mathcal{L}}_{2}} + \ldots \).
NORMAL MODES
For properly chosen function \({{f}_{0}}\) the first order terms are absent, \({{\mathcal{L}}_{1}} = 0\), and the second order terms are
with the Hamiltonian operator \(\hat {\mathcal{H}}\) of the form
with \(\nabla = {{{\mathbf{e}}}_{x}}{{\partial }_{x}} + {{{\mathbf{e}}}_{y}}{{\partial }_{y}}\). Here U, V and \({\mathbf{A}} = {{{\mathbf{e}}}_{x}}{{A}_{x}} + {{{\mathbf{e}}}_{y}}{{A}_{y}}\) are rather cumbersome functions of \({{f}_{0}}({\mathbf{r}})\) and its gradients, see [29].
The Lagrangian (6) results in the Euler-Lagrange equation
and the energies of normal modes, \({{\epsilon }_{n}}\), are found from
with \({{\sigma }_{3}}\) the third Pauli matrix. The solutions to Eq. (9) are discussed at length in [29]. They form the complete orthonormal basis, with \(\int {{d}^{2}}{\mathbf{r}}{\kern 1pt} \left( {{\text{|}}{{u}_{n}}{{{\text{|}}}^{2}} - \;{\text{|}}{{v}_{n}}{{{\text{|}}}^{2}}} \right) = 1\), which allows to expand every function ψ (together with its conjugate, \(\bar {\psi }\)) as
where \({{c}_{n}}\) and \(c_{n}^{\dag }\) are mutually complex-conjugated numbers, which become boson creation and annihilation operators upon the second quantization procedure. The Hamiltonian then takes the familiar form, \(\sum\nolimits_n {{\epsilon }_{n}}(c_{n}^{\dag }{{c}_{n}} + 1{\text{/}}2)\).
MAGNETIZATION EXPANSION
The expansion in \(\alpha \) of local magnetization is given by:
with \(S_{i}^{{(0)}} = S{{n}_{i}}\) defined by (2) with \(f = {{f}_{0}}\), and
is a complex r-dependent vector with the following property: three vectors ReF, ImF, and n form the orthonormal basis.
Substituting (10) into (11) we write to the lowest order in α
Using canonical commutation relations, \([{{c}_{n}},c_{m}^{\dag }] = {{\delta }_{{nm}}}\), and the completeness of the basis \(({{u}_{n}},{{v}_{n}})\), one can check that taking the value \(\alpha = 1{\text{/}}\sqrt {2S} \) we obtain the relation
which is expected in the linear spin-wave theory.
SUSCEPTIBILITY
Our aim is to calculate the dynamic susceptibility tensor, \({{\chi }_{{ij}}}({\mathbf{k}},\omega ) = \int dt{\kern 1pt} {{e}^{{i\omega t}}}{{\chi }_{{ij}}}({\mathbf{k}},t)\), which is the Fourier transform of the spin retarded Green’s function
Using the above formulas, we can write
The amplitude of the spin wave with the energy \({{\epsilon }_{n}}\) and the wave-vector k is given by
As a result, we obtain the general expression
We should note here that index n of the mode \({{\epsilon }_{n}}\) assumes both the wave-vector k and the number of the magnon band, see [29]. In the important case of \({\mathbf{k}} = 0\), relevant to MR experiments and discussed below, the above formula is somewhat simplified.
For the uniform susceptibility, we set \({\mathbf{k}} = 0\) and denote \(A_{n}^{j}(0) \equiv {{A}_{{j,n}}}\). Generally, we expect that the tensor \({{\chi }_{{ij}}}\) contains symmetric and antisymmetric part, and the only chosen direction in our problem, Eq. (1), is normal to the plane, \(\hat {h} = (0,0,1)\). We can then write:
SUSCEPTIBILITY OF SkX
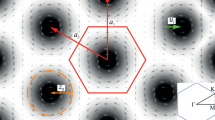
Let us introduce our ansatz for the SkX, that was thoroughly discussed elsewhere [27–29]. We found that the stereographic function of SkX can be well approximated by a sum of stereographic functions of individual skyrmions:
where \({{{\mathbf{a}}}_{1}} = (0,a)\), \({{{\mathbf{a}}}_{2}} = ( - \sqrt 3 a{\text{/}}2,a{\text{/}}2)\), and a is a cell parameter of SkX. The stereographic function \({{f}_{1}}\) of individual skyrmions has a simple pole at the skyrmion’s center and decreases at the infinity, and we write it in the form:
where real-valued \({{z}_{0}}\) is associated with skyrmion size, and κ is a profile function, that can be found numerically [27]. We notice that a good approximation for κ is the Gaussian profile with a width dependent on b. In the absence of B and D our ansatz (20) with \(\kappa \equiv 1\) becomes the exact description of a multiskyrmion configuration [30]. For SkX configuration at non-zero B and D the optimal parameters a and \({{z}_{0}}\) are obtained from the minimization of the energy density (1), see [27, 28].
Using the ansatz (20) for the static SkX configuration \({{f}_{0}}\), we calculate the magnon wave functions corresponding to \({\mathbf{k}} = 0\) in (9), for 36 lowest energies, \({{\epsilon }_{n}} > 0\). The above formulas (12) and (17) are combined for calculation of susceptibility components, Eq. (19).
The results of this calculation can be summarized as follows.
(i) Only some of the normal modes of the spectrum are visible, thanks to selection rules, provided by the matrix elements \({{A}_{{j,n}}}\) in (19). Specifically, the symmetry of the corresponding magnon wave function at the center of skyrmions, \(\psi \sim {{z}^{m}}\), defines this visibility. The modes with magnetic quantum numbers \(m = 0,2\) show up in \({{\chi }_{ \bot }}\) and the modes with \(m = 1\) define \({{\chi }_{\parallel }}\). The lowest-energy modes with \(m = 0,1,2\) were dubbed “counterclockwise” (CCW), “breathing” (Br) and “clockwise” (CW), respectively, thanks to their dynamic pattern discussed elsewhere [15, 29].
(ii) In case of CCW and CW modes the antisymmetric part of susceptibility, \({{\chi }_{{as}}}\), is equal in absolute value to its diagonal part, \({{\chi }_{ \bot }}\), with the residues \({\kern 1pt} {\text{Im}}{\kern 1pt} ({{A}_{{1,n}}}{{\bar {A}}_{{2,n}}}) = - {\text{|}}{{A}_{{1,n}}}{{{\text{|}}}^{2}}\) and \({\kern 1pt} {\text{Im}}{\kern 1pt} ({{A}_{{1,n}}}{{\bar {A}}_{{2,n}}}) = {\text{|}}{{A}_{{1,n}}}{{{\text{|}}}^{2}}\), respectively.
(iii) In contrast to previous studies, we observe several modes with increasing energies for each m, which can in principle be observed experimentally. Generally, the increase in \({{\epsilon }_{n}}\) is accompanied by the decrease in the weight of the corresponding resonance, i.e., the residue \({\text{|}}{{A}_{{j,n}}}{{{\text{|}}}^{2}}\) in (19). We graphically represent the position of the MR lines and their weight in Fig. 1.
(Color online) Imaginary part of (a) transverse, \({{\chi }_{ \bot }}\), and (b) longitudinal, \({{\chi }_{\parallel }}\), components of a susceptibility (19) as a function of magnetic field b. The area of each circle is proportional to the weight, \({\text{|}}{{A}_{{j,n}}}{{{\text{|}}}^{2}}\), of each delta-function. Three well known lowest resonances: breathing (Br), clockwise (CW) and counterclockwise (CCW) are clearly visible, together with higher energy modes of smaller intensity.
(iv) It is seen in this figure that the most intense lines correspond to lowest frequencies, which have a tendency to decrease with the external magnetic field, b. Labeling CW (CCW) in Fig. 1a is done according to sign of \({{\chi }_{{as}}}\), as explained above.
(v) The intensity of the lines, \({\text{|}}{{A}_{{j,n}}}{{{\text{|}}}^{2}}\), in (19) are plotted separately in Fig. 2 as a function of applied field. We see that at higher fields, \(b \simeq 0.75\), close to the melting point of SkX, the intensities of secondary CW2 and Br2 modes become comparable to the intensity of the main CW mode. This prediction would be interesting to check experimentally.
(Color online) Spectral weight of eight resonances depicted in Fig. 1 as a function of magnetic field b.
Summarizing, we present the theory of the dynamic susceptibility of skyrmion crystal in the framework of stereographic projection approach. The obtained formulas are quite general and do not assume a specific type of skyrmion ordering. Applying our theory to hexagonal lattice of Bloch-type skyrmions we show the existence of several resonant frequencies, of which only three lowest ones were previously discussed in the literature.
REFERENCES
N. Bogdanov and D. A. Yablonskii, Sov. Phys. JETP 68, 101 (1989).
H. Vakili, J.-W. Xu, W. Zhou, M. N. Sakib, M. G. Morshed, T. Hartnett, Y. Quessab, K. Litzius, C. T. Ma, S. Ganguly, M. R. Stan, P. V. Balachandran, G. S. D. Beach, S. J. Poon, A. D. Kent, and A. W. Ghosh, J. Appl. Phys. 130, 070908 (2021).
Z. Yan, Y. Liu, Y. Guang, K. Yue, J. Feng, R. Lake, G. Yu, and X. Han, Phys. Rev. Appl. 15, 064004 (2021).
S. Li, W. Kang, X. Zhang, T. Nie, Y. Zhou, K. L. Wang, and W. Zhao, Mater. Horiz. 8, 854 (2021).
S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii, and P. Böni, Science (Washington, DC, U. S.) 323, 915 (2009).
X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui, and Y. Tokura, Nat. Mater. 10, 106 (2010).
X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa, and Y. Tokura, Nature (London, U.K.) 465, 901 (2010).
A. Tonomura, X. Yu, K. Yanagisawa, T. Matsuda, Y. Onose, N. Kanazawa, H. S. Park, and Y. Tokura, Nano Lett. 12, 1673 (2012).
P. Huang, T. Schönenberger, M. Cantoni, L. Heinen, A. Magrez, A. Rosch, F. Carbone, and H. M. Rønnow, Nat. Nanotechnol. 15, 761 (2020).
M. Garst, J. Waizner, and D. Grundler, J. Phys. D: A-ppl. Phys. 50, 293002 (2017).
A. A. Thiele, Phys. Rev. Lett. 30, 230 (1973).
C. Schütte and M. Garst, Phys. Rev. B 90, 094423 (2014).
S.-Z. Lin, C. D. Batista, and A. Saxena, Phys. Rev. B 89, 024415 (2014).
O. Petrova and O. Tchernyshyov, Phys. Rev. B 84, 214433 (2011).
M. Mochizuki, Phys. Rev. Lett. 108, 017601 (2012).
S. A. Díaz, T. Hirosawa, J. Klinovaja, and D. Loss, Phys. Rev. Res. 2, 013231 (2020)
T. Weber, D. M. Fobes, J. Waizner, et al., Science (Washington, DC, U. S.) 375, 1025 (2022).
N. Ogawa, S. Seki, and Y. Tokura, Sci. Rep. 5, 1 (2015).
Y. Onose, Y. Okamura, S. Seki, S. Ishiwata, and Y. Tokura, Phys. Rev. Lett. 109, 037603 (2012).
R. Takagi, M. Garst, J. Sahliger, C. H. Back, Y. Tokura, and S. Seki, Phys. Rev. B 104, 144410 (2021).
A. Aqeel, J. Sahliger, T. Taniguchi, S. Mändl, D. Mettus, H. Berger, A. Bauer, M. Garst, C. Pfleiderer, and C. H. Back, Phys. Rev. Lett. 126, 017202 (2021).
O. I. Utesov, Phys. Rev. B 103, 064414 (2021).
O. I. Utesov, Phys. Rev. B 105, 054435 (2022).
S.-Z. Lin, A. Saxena, and C. D. Batista, Phys. Rev. B 91, 224407 (2015).
U. Güngördü, R. Nepal, O. A. Tretiakov, K. Belashchenko, and A. A. Kovalev, Phys. Rev. B 93, 064428 (2016).
J. H. Han, J. Zang, Z. Yang, J.-H. Park, and N. Nagaosa, Phys. Rev. B 82, 094429 (2010).
V. E. Timofeev, A. O. Sorokin, and D. N. Aristov, JETP Lett. 109, 207 (2019).
V. E. Timofeev, A. O. Sorokin, and D. N. Aristov, Phys. Rev. B 103, 094402 (2021).
V. E. Timofeev and D. N. Aristov, Phys. Rev. B 105, 024422 (2022).
A. A. Belavin and A. M. Polyakov, JETP Lett. 22, 245 (1975).
Funding
The work was supported by the Russian Science Foundation, project no. 22-22-20034, and by the St. Petersburg Science Foundation, project no. 33/2022.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflicts of interest.
Rights and permissions
Open Access. This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Timofeev, V.E., Aristov, D.N. Dynamic Susceptibility of Skyrmion Crystal. Jetp Lett. 117, 676–680 (2023). https://doi.org/10.1134/S002136402260327X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S002136402260327X