Magnetic Skyrmions and Phase Transitions in Antiferromagnetic/Ferroelectric Bilayers

We study in this paper the ground state and the properties of a skyrmions in magnetoelectric films, namely antiferromagnetic/ferroelectric superlattices in a support by steepest descent method and extensive Monte Carlo simulation. The ground state and ordering of the frustrated both classical Heisenberg and Ising models on the simple cubic lattice with a magnetoelectric coupling are studied under magnetic field.

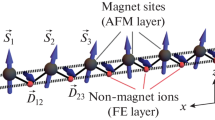
Topological spin textures, which are also known as nanoscale spin vortices, have been investigated as potential information carriers in spintronics and computing devices due to their topology-related properties and extremely small sizes [1–3]. The skyrmion spin texture is named after physicist Tony Skyrme who constructed a topological configuration of a 4d-vector field in 3 + 1 spacetime [4]. The skyrmion-like objects in spin space have attracted much attention in the condensed matter physics community: skyrmions were considered in the framework of the quantum Hall effect [5–7] and, very recently, were experimentally created in the magnetic multilayers [8–10] and bulk magnetic materials [11–14]. In condensed matter, the first skyrmion lattice has been predicted to exist in rotating superfluid ³He, see [15]. Later, they were experimentally observed in rotating cryostat, see [16]. Skyrmion dynamics was used for the observation of the analog of chiral anomaly in condensed matter systems [17, 18]. Exemplary topological spin vortices include skyrmions and vortex-like magnetic nanodots that usually form under the influence of frustration and external magnetic field in noncentrosymmetric nanofilms or at the interfaces in heterostructures and bilayers [19–21]. Kurumaji et al. [22] observed the emergence of a Bloch-type skyrmion lattice phase in the frustrated centrosymmetric triangular-lattice magnetic material Gd₂PdSi₃. The magnetic frustration causes the formation of skyrmions [23] and helps stabilize the skyrmion phase, which was detected by experimental measurements in a magnetic field. The skyrmion lattice configuration can be stabilized by competing interactions in magnetic films with triangular symmetry. The physical properties of skyrmion crystal in frustrated magnetic films remain largely unexplored. In the case of interfacial Dzyaloshinskii–Moriya interaction which takes place in ultrathin heterostructures [12, 13, 24], formation of magnetic skyrmions is possible and they remain stable even at room temperatures. This hints at the potential use of magnetoelectric bilayers and superlattices in nanoelectronic devices. At present, several techniques have been proposed for producing stable skyrmions in non-chiral magnetic films and bilayers [25, 26]. In [27], it was established that vortex-like inhomogeneities can be formed on columnar defects of a certain type in magnetic films. The heterostructures of ferromagnet and ferroelectric insulator that host magnetic skyrmions and vortices may provide an important building block for the next generation of spintronics devices [28–30]. For example, the micromagnetic skyrmion transistor could be used in the skyrmionic-electronic storages. In [31], we investigated the effects of Dzyaloshinskii–Moriya magneto-ferroelectric interaction in unfrustrated ferromagnetic/ferroelectric superlattice. We showed that in the absence of external magnetic field, the ground state spin configuration is periodically non-collinear. In [32], we have investigated the ordering of the frustrated classical Heisenberg model on the triangular lattice with an incommensurate spiral structures in the presence of magnetic field. It is worth emphasizing that we have also shown that frustration gives rise to a perfect skyrmion lattice at the magnetoelectric interface in an external magnetic field. Let us describe our model and present the ground-state spin structure with varying magnetoelectric interaction and strength of external magnetic field. The antiferromagnetic/ferroelectric bilayer that we study here is composed of antiferromagnetic and ferroelectric l-ayers where the spins and polarization are located on a simple cubic lattice. The discrete Hamiltonian of our system is given by the combination of five terms such as

$$\begin{gathered} {{H}_{m}} = - \sum\limits_{i,j} J_{{ij}}^{m}{{{\mathbf{S}}}_{i}} \cdot {{{\mathbf{S}}}_{j}} - \sum\limits_{i,k} J_{{ik}}^{{2m}}{{{\mathbf{S}}}_{i}} \cdot {{{\mathbf{S}}}_{k}} - \sum\limits_i {\mathbf{H}} \cdot {{{\mathbf{S}}}_{i}} \\ - \;\sum\limits_{i,j} J_{{ij}}^{f}{{{\mathbf{P}}}_{i}} \cdot {{{\mathbf{P}}}_{j}} - \sum\limits_{i,j,k} J_{{i,j}}^{{mf}}{{e}_{{i,j}}}{{{\mathbf{P}}}_{{\mathbf{k}}}} \cdot \left[ {{{{\mathbf{S}}}_{{\mathbf{i}}}} \times {{{\mathbf{S}}}_{{\mathbf{j}}}}} \right], \\ \end{gathered} $$

(1)

where ${{{\mathbf{S}}}_{i}}$ is the spin of the ith lattice site, H is the magnetic field applied along the z axis, $J_{{ij}}^{m} < 0$ is the nearest neighbor (NN) antiferromagnetic interaction between two spins ${{{\mathbf{S}}}_{i}}$ and ${{{\mathbf{S}}}_{j}}$, $J_{{ik}}^{{2m}} < 0$ is the next-nearest neighbor (NNN) interaction, ${{{\mathbf{P}}}_{i}}$ is the polarization at the ith lattice site, and $J_{{ij}}^{f} > 0$ is the ferroelectric exchange interaction parameter between polarizations at nearest neighbor sites i and j. The novel part in the Hamiltonian is the last coupling term between spins and polarizations, which is the magnetoelectric interaction at the interface between antiferromagnetic and ferroelectric layers. We note that the vector of polarization is limited to the direction perpendicular to the plane of the layer. For this reason, the energy of the magnetoelectric interaction is minimal if spins in the antiferromagnetic layer lie in the xy plane (${{S}^{z}} = 0$). The antiferromagnetic exchange interaction between the spins competes with the magnetoelectric coupling ${{{\mathbf{P}}}_{{\mathbf{k}}}} \cdot \left[ {{{{\mathbf{S}}}_{{\mathbf{i}}}} \times {{{\mathbf{S}}}_{{\mathbf{j}}}}} \right]$ between two layers. Numerical calculations show that depending on the ratio of the amplitudes of competing interactions on the surface, interesting configurations of the ground state are possible, some of which are stable in a wide range of external fields and temperatures. When the frustration is taken into consideration, it is more convenient to use the numerical steepest descent method to obtain the real ground state spin configuration. In this method, the energy of each spin is minimized by aligning it parallel to the local field acting on it from its neighbors. This is done as follows. We generate a random initial spin configuration; then, we take one spin and calculate the interaction field from its nearest and next nearest neighbors. Then align this spin in the direction of resulting field, and take another spin and repeat the procedure until all spins are considered. This operation is repeated until the total energy converges to a minimum. We perform thousands of calculations with various initial configurations and examine the time-dependent energy. When all of them converge to the same value up to the fifth digit, we conclude that the final energy is not sensitive to the initial spin configuration. As the energy at low temperature tends to the ground state energy, we check the found configuration with Monte Carlo simulations. This shows that the steepest descent method yields the true ground state. We consider the bilayer with a linear size $N \times N \times L$. We select $N = 40$ and $L = {{L}_{m}} + {{L}_{f}}$ = 2 using the periodic boundary conditions in the plane of each layer. Exchange interaction parameters for nearest neighbor sites are taken as ${{J}^{m}} = - 1$, ${{J}^{f}} = 1$. Ground state configurations for small values of interface coupling ${{J}^{{mf}}} \in ( - 0.5,0)$ have antiferromagnetic and non-collinear domains. Finally, a periodic structure of the ground state spin configuration is stabilized. Some interesting and representative ground state configurations of the magnetic interface layer are shown in Figs. 1, 2. We can see the formation of skyrmions of various diameters at the interface in the antiferromagnetic layer. This can be observed in the range ${{J}^{{mf}}} \in ( - 1.05, - 0.5)$, ${{J}^{{2m}}} \in ( - 0.4, - 0.25)$. Figure 1 shows an example with ${{J}^{{mf}}} = - 1.35$ where we observe the beginning of emergence of many skyrmions at the interface.

Fig. 1.

(Color online) Structure of the ground state spin configuration of the antiferromagnetic layer for $H = 0$ with ${{J}^{m}} = - 1,{{J}^{f}} = 1$, ${{J}^{{2m}}} = - 0.3$, and ${{J}^{{mf}}} = - 1.35$.

Fig. 2.

(Color online) Structure of the ground state spin configuration of the antiferromagnetic layer for $H = 1.25$ with ${{J}^{m}} = - 1,\;{{J}^{f}} = 1$, ${{J}^{{2m}}} = - 0.3$, and ${{J}^{{mf}}} = - 1.25$.

The results of numerical calculations of the spin ground state configuration lead us to the conclusion that skyrmions and magnetic vortices in frustrated ${{J}^{{2m}}} \in ( - 0.4,\; - {\kern 1pt} 0.25)$ antiferromagnetic/ferroelectric bilayers with a simple cubic lattice can be created in the region of interface coupling ${{J}^{{mf}}} \in ( - 1.35,\; - {\kern 1pt} 0.5)$ in the absence of magnetic field (Fig. 1b). When an external magnetic field perpendicular to the plane of bilayer is present, an interesting effect can be observed in the range of values of the magnetoelectric interaction ${{J}^{{mf}}} \in ( - 1.35,\; - {\kern 1pt} 0.95)$ and the next nearest neighbor exchange interaction ${{J}^{{2m}}} \in ( - 0.4,\; - {\kern 1pt} 0.25)$, in particular, in the range of external magnetic field strength $H \in (0.1,\;0.5)$ the skyrmions disappear, however with further increase in the field strength to the values comparable to the magnetoelectric interaction parameter, we see the new formation of an ordered skyrmion lattice (see Fig. 2).

This structure of the ground state spin configuration is identical for ${{J}^{{2m}}} = - 0.4$, with the same parameter set ${{J}^{m}} = - 1$, ${{J}^{f}} = 1$, ${{J}^{{mf}}} \in ( - 1.55, - 1.15)$, and $H = 1.25$. With a slight increase in the magnetoelectric coupling, the stability of the skyrmions with respect to the applied magnetic field increases. To simulate the behavior of various physical quantities depending on temperature T and size of system we have used the Metropolis algorithm on an $N \times N \times 2$ cubic lattice. To perform the Monte-Carlo simulation, we choose a ground state configurations of the spin and polarization vectors that we obtained by steepest descent method. The observable physical quantities of interest are the averages of order parameter of the magnetic (${{P}_{m}}$) layer, energy and heat capacity of bilayer. The order parameter of the antiferromagnetic layer is calculated as the projection of an actual ${{{\mathbf{S}}}_{i}}(T,t)$ at a given T on its ground state value at $T = 0$ averaged over multiple simulation steps. It is defined as

$${{P}_{m}} = \frac{1}{{{{N}^{2}}({{t}_{a}} - {{t}_{0}})}}\sum\limits_{i \in n} \left| {\sum\limits_{t = {{t}_{0}}}^{{{t}_{a}}} {{{\mathbf{S}}}_{i}}(T,t) \cdot {\mathbf{S}}_{i}^{0}(T = 0)} \right|,$$

where ${{{\mathbf{S}}}_{i}}(T,t)$ is the ith spin at the time t and temperature T, ${{{\mathbf{S}}}_{i}}(T = 0)$ is its ground state at $T = 0$, and $\langle ...\rangle$ is the thermal average. In Fig. 3, we plot the dependence of order parameter of the antiferromagnetic layer versus temperature and their heat capacity for ${{J}^{{mf}}} = - 1.25$, $H = 1.25$, ${{J}^{m}} = - 1.0$, ${{J}^{f}} = 1.0$, ${{J}^{{2m}}} =$ –0.3 at which we observed a crystal of skyrmions in frustrated antiferromagnetic layer.

Fig. 3.

(Color online) Heat capacity of the antiferromagnetic layer versus temperature and order parameter (inset) for the set of parameters: magnetoelectric interaction ${{J}^{{mf}}} = - 1.25$, $H = 1.25$, ${{J}^{m}} = - 1.0$, ${{J}^{f}} = - 1.0$, and ${{J}^{{2m}}} = - 0.3$.

The above figures show that the order parameter of the antiferromagnetic layer and heat capacity does not have any metastability at low T, because we have performed MC simulations from the correct initial spin configuration corresponding to the interface interaction parameter used for simulations. Note that the antiferromagnetic layer undergoes two second-order transitions, one is associated with the destruction of the skyrmion structure and the other is the transition from the ordered phase to the disordered phase, respectively, at temperatures ${{T}_{{sc}}}$ = 0.52 and ${{T}_{{od}}}$ = 0.67. Note that the skyrmion transition occurs at a lower temperature than magnetic transition. This is very important point because if the skyrmions are stable at finite temperatures, then it will be possible to use the skyrmion properties in different applications. As turns out, the skyrmion phase is stable up to temperatures comparable to the temperatures of transitions from the antiferromagnetic phase to the paramagnetic phase.