Skip to main content
SpringerLink
Log in

Using Chaotic Attractors to Simulate the Wave Effect on the Ship

  • Published:
Gyroscopy and Navigation Aims and scope Submit manuscript

Abstract

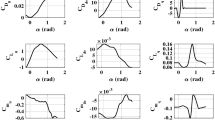
The paper features the simulation of wave forces and moments acting on the ship for synthesizing the motion control algorithms. The available approaches to describing the wave forces and moments are shown so have some weak points. An alternative approach to wave simulation is proposed, based on chaotic oscillations generated in the dynamical systems of chaotic attractor type. The wave spectral characteristics are analyzed, and criteria to define the major frequency range of the signal spectrum are proposed. It is proposed to compare the major frequency range, signal variance, and distribution characteristics of the simulated process and the wave of the preset frequency and average height under comparison. The known Arneodo and Chen attractors are considered, their spectral properties are studied, and phase patterns are constructed. It is proposed to use an attractor phase coordinate as a magnitude modeling the wave. The vehicle mathematical model is supplemented with the attractor equations, and the process becomes quasistochastic due to the attractor features. The adequacy of the proposed wave model is estimated using the estimates of spectra and distributions. The ship rolling has been simulated using the described approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.

Similar content being viewed by others

REFERENCES

  1. Veter i volny v okeanakh i moryakh (Wind and Waves in Oceans and Seas), A Reference book, Leningrad: Transport, 1974.

  2. Kinsman, B., Wind Waves: Their Generation and Propagation on the Ocean Surface, 1965.

  3. Proceedings of the 23rd International Towing Tank Conference, ITTC’02, Venice, Italy, September 8–14, 2002, vol. I and II.

  4. Borodai, I.K. and Netsvetaev, Yu.A., Morekhodnost’ sudov (Navigability of Ships), Leningrad: Sudostroenie, 1982.

  5. Fossen, Th., Handbook of Marine Craft Hydrodynamics and Motion Control, John Wiley & Sons, 2011.

    Book  Google Scholar 

  6. Peretz, T. and Blanke, M., Ship roll motion control, Proceedings of the 8th IFAC Conference on Control Applications in Marine Systems, 2010.

  7. Lukomskii, Yu.A. and Chugunov, V.S., Sistemy upravleniya morskimi podvizhnymi ob’’ektami (Control Systems of Marine Vehicles), Leningrad: Sudostroenie, 1988.

  8. Ambrosovskii, V.M. and Rumyantsev, S.N., Modelirovanie morskogo volneniya, deistvuyushchego na sudno (Modeling the sea waves acting on the ship), deposited manuscript N ДP3490 dated 6.10.93., St. Petersburg: CSRI Rumb.

  9. Ambrosovskii, V.M. and Ambrosovskaya, E.B., Matematicheskie modeli dvizheniya perednego khoda MPO dlya otladochnykh stendov (Mathematical models of the forward motion of marine vehicle for test beds), deposited manuscript VINITI dated 14.06.2018 (N62-B2018).

  10. Pelevin, A.E., Prediction of ship deck inclination angle, Gyroscopy and Navigation, 2017, vol. 8, no. 2, pp. 165−171.

    Article  Google Scholar 

  11. Dmitriev, S. P. and, Pelevin, A. E., Zadachi upravleniya i navigatsii pri stabilizatsii sudna na traektorii (Control and Navigation Problems in Ship Track-Keeping), St. Petersburg: CSRI Elektropribor, 2002.

    Google Scholar 

  12. Ispolov, Yu.G., Numerical solution of Cauchi problem for finite-dimensional mathematical models of mechanical systems, Mekhanika i protsessy upravleniya. Trudy SPbGTU, 1993, no. 446, pp. 35–41.

  13. Sinai, Ya.G., Finite-dimensional randomness, Russian Mathematical Surveys, 1991, vol. 46, no. 3, pp. 177–190.

    Article  MathSciNet  Google Scholar 

  14. Moon, F.C., Chaotic Vibrations, John Wiley and Sons, 1990.

    Google Scholar 

  15. Kuznetsov, N.V., Theory of hidden oscillations and stability of control systems, Journal of Computer and Systems Sciences International, 2020, vol. 59, no. 5, pp. 647–668.

    Article  MathSciNet  Google Scholar 

  16. Andrievskii, B.R. and Fradkov, A.L., Elementy matematicheskogo modelirovaniya v MATLAB 5 i Scilab (Elements of Mathematical Modeling in MATLAB 5 and Scilab), St. Petersburg: Nauka, 2001.

  17. Koszalka, I., Baltic sea waves analysis by using chaos theory tools, Computer Systems Engineering, 2006.

  18. Recommended Practice DNV-RP-C205, Environmental Conditions and Environmental Loads, April 2014.

  19. Ambrosovskaya, E.B., Kalimov, D.V., and Popo-va, I.E., Estimating the frequency range of the wave affecting the ship by experimental data, Proceedings of the Anniversary International Scientific to Practical Conference “Transport Rossii: Problemy i perspektivy” (Transport of Russia: Problems and Perspectives), 2020, pp. 94–99.

  20. Lucas, S.K., Sander, E., and Taalman, L., Modeling dynamical systems for 3D printing, Notices of the American Mathematical Society, 2020, vol. 67, no.11, 1692–1705.

    Article  MathSciNet  Google Scholar 

  21. https://habr.com/ru/post/480660/

  22. Chen, G. and Ueta, T., Yet another chaotic attractor, International Journal of Bifurcation and Chaos, 1999, vol. 9, no. 7, pp. 1465–1466.

    Article  MathSciNet  Google Scholar 

  23. Arneodo, A., Coullet, P., and Tresser, C., Possible new strange attractors with spiral structure, Communications in Mathematical Physics, 1981, vol. 79, no. 4.

  24. Ahmed, I., Mu, C., Zhang, F., A new chaotic attractor with quadratic exponential nonlinear term from Chen’s Attractor, International Journal of Analysis and Applications, 2014, vol. 5, no. 1, pp. 27–32.

    MATH  Google Scholar 

  25. Podgorski, K., Rychlik, I., and Machado, U., Exact distributions for apparent waves in irregular seas, Ocean Engineering, 2000, vol. 27, pp. 979-1016, .https://doi.org/10.1016/S0029-8018(99)00030-X

    Article  Google Scholar 

  26. Leonov, G.A. and Kuznetsov, N.V., On differences and similarities in the analysis of Lorenz, Chen, and Lu systems, Applied Mathematics and Computation, 2015, vol. 256, pp. 334–343.

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. St. Petersburg State Electrotechnical University LETI, St. Petersburg, Russia

    E. B. Ambrosovskaya & A. G. Shpektorov

  2. Navis, St. Petersburg, Russia

    E. B. Ambrosovskaya

  3. Sitroniks KT, St. Petersburg, Russia

    A. G. Shpektorov

Authors
  1. E. B. Ambrosovskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. G. Shpektorov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to E. B. Ambrosovskaya or A. G. Shpektorov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ambrosovskaya, E.B., Shpektorov, A.G. Using Chaotic Attractors to Simulate the Wave Effect on the Ship. Gyroscopy Navig. 13, 110–119 (2022). https://doi.org/10.1134/S207510872202002X

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S207510872202002X

Keywords:

Search

Navigation