Skip to main content
SpringerLink
Log in

Nonlinear Dynamics of a Roller Bicycle

  • Published:
Regular and Chaotic Dynamics Aims and scope Submit manuscript

Abstract

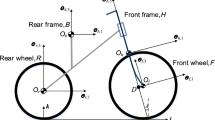
In this paper we consider the dynamics of a roller bicycle on a horizontal plane. For this bicycle we derive a nonlinear system of equations of motion in a form that allows us to take into account the symmetry of the system in a natural form. We analyze in detail the stability of straight-line motion depending on the parameters of the bicycle. We find numerical evidence that, in addition to stable straight-line motion, the roller bicycle can exhibit other, more complex, trajectories for which the bicycle does not fall.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. Since \({\rm Re}\lambda<0\) for stable equilibrium points, it follows that \(|({\rm Re}\lambda)_{\max}|\) is minimal.

References

  1. Borisov, A. V., Jalnine, A. Yu., Kuznetsov, S. P., Sataev, I. R., and Sedova, J. V., Dynamical Phenomena Occurring due to Phase Volume Compression in Nonholonomic Model of the Rattleback, Regul. Chaotic Dyn., 2012, vol. 17, no. 6, pp. 512–532.

    Article  MathSciNet  Google Scholar 

  2. Borisov, A. V., Kilin, A. A., and Mamaev, I. S., A Parabolic Chaplygin Pendulum and a Paul Trap: Nonintegrability, Stability, and Boundedness, Regul. Chaotic Dyn., 2019, vol. 24, no. 3, pp. 329–352.

    Article  MathSciNet  Google Scholar 

  3. Borisov, A. V. and Mamaev, I. S., Strange Attractors in Rattleback Dynamics, Physics-Uspekhi, 2003, vol. 46, no. 4, pp. 393–403; see also: Uspekhi Fiz. Nauk, 2003, vol. 173, no. 4, pp. 407-418.

    Article  Google Scholar 

  4. Borisov, A. V. and Mamaev, I. S., Symmetries and Reduction in Nonholonomic Mechanics, Regul. Chaotic Dyn., 2015, vol. 20, no. 5, pp. 553–604.

    Article  MathSciNet  Google Scholar 

  5. Borisov, A. V., Mamaev, I. S., and Bizyaev, I. A., Dynamical Systems with Non-Integrable Constraints: Vaconomic Mechanics, Sub-Riemannian Geometry, and Non-Holonomic Mechanics, Russian Math. Surveys, 2017, vol. 72, no. 5, pp. 783–840; see also: Uspekhi Mat. Nauk, 2017, vol. 72, no. 5(437), pp. 3-62.

    Article  MathSciNet  Google Scholar 

  6. Dikarev, E. D., Dikareva, S. B., and Fufaev, N. A., Effect of Inclination of Steering Axis and of Stagger of the Front Wheel on Stability of Motion of a Bicycle, Mech. Solids, 1981, vol. 16, no. 1, pp. 60–63; see also: Izv. Akad. Nauk SSSR. Mekh. Tverd. Tela, 1981, no. 1, pp. 69-73.

    MathSciNet  Google Scholar 

  7. Gonchenko, S., Gonchenko, A., Kazakov, A., and Samylina, E., On Discrete Lorenz-Like Attractors, Chaos, 2021, vol. 31, no. 2, Art. 023117, 20 pp.

    Article  MathSciNet  Google Scholar 

  8. Gonchenko, S., Karatetskaia, E., Kazakov, A., and Kruglov, V., Conjoined Lorenz Twins: A New Pseudohyperbolic Attractor in Three-Dimensional Maps and Flows, Chaos, 2022, vol. 32, no. 12, Paper No 121107, 13 pp.

    Article  MathSciNet  Google Scholar 

  9. Gonchenko, S. V., Kazakov, A. O., and Turaev, D. V., Wild Pseudohyperbolic Attractor in a Four-Dimensional Lorenz System, Nonlinearity, 2021, vol. 34, no. 4, pp. 2018–2047.

    Article  MathSciNet  Google Scholar 

  10. Gonchenko, S. V., Ovsyannikov, I. I., Simó, C., and Turaev, D., Three-Dimensional Hénon-Like Maps and Wild Lorenz-Like Attractors, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2005, vol. 15, no. 11, pp. 3493–3508.

    Article  MathSciNet  Google Scholar 

  11. Gonchenko, A. S. and Samylina, E. A., On the Region of Existence of a Discrete Lorenz Attractor in the Nonholonomic Model of a Celtic Stone, Radiophys. Quantum El., 2019, vol. 62, no. 5, pp. 369–384; see also: Izv. Vyssh. Uchebn. Zaved. Radiofizika, 2019, vol. 62, no. 5, pp. 412-428.

    Article  Google Scholar 

  12. Hamel, G., Die Lagrange-Eulerschen Gleichungen der Mechanik, Z. Math. u. Phys., 1904, vol. 50, pp. 1–57.

    Google Scholar 

  13. Hamel, G., Theoretische Mechanik: Eine einheitliche Einführung in die gesamte Mechanik, Grundlehren Math. Wiss., vol. 57, Berlin: Springer, 1978.

    Google Scholar 

  14. Hand, R. S., Comparisons and Stability Analysis of Linearized Equations of Motion for a Basic Bicycle Model, Master’s Thesis, Ithaca,N.Y., Cornell Univ., 1988, 200 pp.

  15. Hénon, M., On the Numerical Computation of Poincaré Maps, Phys. D, 1982, vol. 5, no. 2–3, pp. 412–414.

    Article  MathSciNet  Google Scholar 

  16. Kazakov, A. O., Murillo, A., Vieiro, A., and Zaichikov, K., Numerical Study of Discrete Lorenz-Like Attractors, Regul. Chaotic Dyn., 2024, vol. 29, no. 1, pp. 78–99.

    Article  MathSciNet  Google Scholar 

  17. Kirillov, O. N., Locating the Sets of Exceptional Points in Dissipative Systems and the Self-Stability of Bicycles, Entropy (Basel), 2018, vol. 20, no. 7, pp. 502–517.

    Article  Google Scholar 

  18. Kooijman, J. D. G., Meijaard, J. P., Papadopoulos, J. M., Ruina, A., and Schwab, A. L., A Bicycle Can Be Self-Stable without Gyroscopic or Caster Effects, Science, 2011, vol. 332, no. 6027, pp. 339–342.

    Article  MathSciNet  Google Scholar 

  19. Kooijman, J. D. G., Meijaard, J. P., Papadopoulos, J. M., Ruina, A., and Schwab, A. L., Supporting Online Text Material (SOM Chapters 1–11) for “A Bicycle Can Be Self-Stable without Gyroscopic or Caster Effects”, [Science, 2011, vol. 332, no. 6027, pp. 339-342], http://bicycle.tudelft.nl/stablebicycle/ (2011).

  20. Kozlov, V. V. and Kolesnikov, N. N., On Theorems of Dynamics, J. Appl. Math. Mech., 1978, vol. 42, no. 1, pp. 26–31; see also: Prikl. Mat. Mekh., 1978, vol. 42, no. 1, pp. 28-33.

    Article  MathSciNet  Google Scholar 

  21. Kuptsov, P. V. and Kuznetsov, S. P., Lyapunov Analysis of Strange Pseudohyperbolic Attractors: Angles between Tangent Subspaces, Local Volume Expansion and Contraction, Regul. Chaotic Dyn., 2018, vol. 23, no. 7–8, pp. 908–932.

    Article  MathSciNet  Google Scholar 

  22. Kuznetsov, Yu. A., Meijer, H. G. E., and van Veen, L., The Fold-Flip Bifurcation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2004, vol. 14, no. 7, pp. 2253–2282.

    Article  MathSciNet  Google Scholar 

  23. Meijaard, J. P., Papadopoulos, J. M., Ruina, A., and Schwab, A. L., Linearized Dynamics Equations for the Balance and Steer of a Bicycle: A Benchmark and Review, Proc. R. Soc. A Math. Phys. Eng. Sci., 2007, vol. 463, no. 2084, pp. 1955–1982.

    MathSciNet  Google Scholar 

  24. Ricci, F. and Frosali, G., A Symbolic Method for the Analysis of a Nonlinear Two-Mass-Skate Model, https://arxiv.org/abs/1611.07796 (2016).

  25. Schwab, A. L., Meijaard, J. P., and Papadopoulos, J. M., A Multibody Dynamics Benchmark on the Equations of Motion of an Uncontrolled Bicycle, in Proc. of the 5th EUROMECH Nonlinear Dynamics Conf. (ENOC’2005, Eindhoven University of Technology, The Netherlands, Aug 2005), D. H. van Campen, M. D. Lazurko, W. P. J. M. van den Oever (Eds.), Eindhoven: Eindhoven Univ. of Technology , pp. 511–521.

    Google Scholar 

  26. Shilnikov, L. P., Shilnikov, A. L., Turaev, D., and Chua, L. O., Methods of Qualitative Theory in Nonlinear Dynamics: Part 1, World Sci. Ser. Nonlinear Sci. Ser. A Monogr. Treatises, vol. 4, River Edge, N.J.: World Sci., 1998.

    Google Scholar 

  27. Shil’nikov, A. L., Shil’nikov, L. P., and Turaev, D. V., Normal Forms and Lorenz Attractors, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 1993, vol. 3, no. 5, pp. 1123–1139.

    Article  MathSciNet  Google Scholar 

  28. Wiggins, S., Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed., Texts Appl.Math., vol. 2, New York: Springer, 2003.

    Google Scholar 

  29. Xiong, J., Jia, Y.-B., and Liu, C., Symmetry and Relative Equilibria of a Bicycle System, Russian J. Nonlinear Dyn., 2021, vol. 17, no. 4, pp. 391–411.

    MathSciNet  Google Scholar 

  30. Xiong, J., Wang, N., and Liu, C., Stability Analysis for the Whipple Bicycle Dynamics, Multibody Syst. Dyn., 2020, vol. 48, no. 3, pp. 311–335.

    Article  MathSciNet  Google Scholar 

Download references

ACKNOWLEDGMENTS

The authors extend their gratitude to Alexey O. Kazakov for fruitful discussions.

Funding

The work of I. A. Bizyaev (Sections 2 and 4) was supported by the Russian Science Foundation (No. 21-71-10039). The work of I. S. Mamaev (Sections 3 and 5) was carried out within the framework of the state assignment of the Ministry of Science and Higher Education of Russia (FZZN-2020-0011).

Author information

Authors and Affiliations

  1. Ural Mathematical Center, Udmurt State University, ul. Universitetskaya 1, 426034, Izhevsk, Russia

    Ivan A. Bizyaev

  2. Kalashnikov Izhevsk State Technical University, ul. Studencheskaya 7, 426069, Izhevsk, Russia

    Ivan S. Mamaev

Authors
  1. Ivan A. Bizyaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ivan S. Mamaev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Ivan A. Bizyaev or Ivan S. Mamaev.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

PUBLISHER’S NOTE

Pleiades Publishing remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

MSC2010

37J60, 34A34

APPENDIX. EXPLICIT FORM OF THE MATRIX $${\bf\tilde{I}}$$ AND OF THE VECTOR $$\boldsymbol{\Phi}$$

In order to explicitly write the terms appearing in Eqs. (2.13), we define the vectors introduced above: the normal vector and the unit vector directed along the translational velocity of the contact point of the handlebar

$$\boldsymbol{\gamma}=\left(-\sin\theta,\dfrac{b_{3}}{k}\cos\theta,\dfrac{b_{2}}{k}\cos\theta\right),\quad\boldsymbol{l}=\left(-\sin\varphi,\cos\varphi,0\right).$$
With this notation, the expression for the matrix \({\bf\tilde{I}}\) can be represented as
$$\begin{gathered}\displaystyle{\bf\tilde{I}}=\left[\begin{array}[]{ccc}\displaystyle\frac{\Delta_{2}}{b_{2}b_{3}}-\mu_{2}-2jl_{1}&\displaystyle\Delta_{3}\frac{b_{2}l_{1}^{2}\gamma_{1}}{k^{2}\gamma_{3}}&\displaystyle b_{2}\mu_{3}l_{1}+\frac{\Delta_{5}l_{1}}{b_{2}\gamma_{2}}(\boldsymbol{l},\boldsymbol{\gamma})+b_{2}(I_{11}-I_{22})\frac{\gamma_{1}l_{1}^{2}l_{2}}{k^{2}\gamma_{3}}\\ *&I_{33}&-\Delta_{3}l_{2}\\ *&*&\Delta_{1}+I_{11}l_{1}^{2}+I_{22}l_{2}^{2}\\ \end{array}\right],\\ \displaystyle j=\mu_{1}\frac{l_{1}}{2}-\frac{\Delta_{2}\gamma_{1}l_{2}}{k^{2}\gamma_{3}}-\frac{\Delta_{5}\gamma_{1}l_{2}}{k^{2}\gamma_{2}\gamma_{3}}(\boldsymbol{l},\boldsymbol{\gamma})+b_{2}^{2}\frac{(I_{11}-I_{22})l_{1}^{2}-\Delta_{4}}{2k^{4}\gamma_{3}^{2}}\gamma_{1}^{2}l_{1},\end{gathered}$$
(A.1)
where \(*\) denotes the elements \({\bf\tilde{I}}\), which can be easily restored from the symmetry of the matrix with respect to the principal diagonal.

The components of the vector \(\boldsymbol{\Phi}\) which appears in Eqs. (2.13) have the following form:

$$\displaystyle\Phi_{1}=Z_{vv}^{(1)}v^{2}+\left[\frac{\Delta_{5}}{b_{3}}+\frac{\Delta_{3}b_{2}l_{1}l_{2}\gamma_{1}}{k^{2}\gamma_{3}}\right]\omega_{\varphi}^{2}$$
$$\displaystyle\quad+\left[2\frac{\Delta_{5}l_{2}}{b_{3}}(\boldsymbol{l},\boldsymbol{\gamma})+\frac{b_{2}l_{1}\gamma_{1}}{k^{2}}\big{(}I_{33}+(I_{11}-I_{22})(l_{2}^{2}-l_{1}^{2})\big{)}\right]\frac{\omega_{\varphi}\omega_{2}}{\gamma_{3}}+Z_{v\omega_{\varphi}}^{(1)}v\omega_{\varphi}+Z_{v\omega_{2}}^{(1)}v\omega_{2}$$
$$\displaystyle\quad+\left[\frac{l_{1}\gamma_{1}}{k^{2}}(\Delta_{1}b_{3}-k^{2}b_{2}\mu_{3})+\frac{\Delta_{5}}{b_{3}\gamma_{3}}\big{(}l_{1}^{2}\gamma_{3}^{2}+l_{2}\gamma_{2}(\boldsymbol{l},\boldsymbol{\gamma})\big{)}+\frac{l_{1}\gamma_{1}}{k^{2}}(I_{11}l_{2}^{2}b_{3}+I_{22}l_{1}^{2}b_{3}-\Delta_{3}b_{2}l_{2})\right]\frac{\omega_{2}^{2}}{\gamma_{3}},$$
$$\displaystyle Z_{vv}^{(1)}=\frac{l_{1}}{k^{4}b_{3}\gamma_{3}^{2}}\Big{[}\Delta_{2}\big{(}b_{3}^{2}l_{1}l_{2}-k^{2}(l_{1}^{2}-l_{2}^{2})\gamma_{1}\gamma_{2}\big{)}+\frac{\Delta_{5}}{\gamma_{3}}\big{(}b_{2}b_{3}l_{1}l_{2}(l_{2}\gamma_{2}+2l_{1}\gamma_{1}^{3})-k^{2}\gamma_{1}\gamma_{3}\big{(}l_{1}\gamma_{1}(l_{1}^{2}-2l_{2}^{2})-l_{2}^{3}\gamma_{2}\big{)}\big{)}\Big{]}$$
$$\displaystyle{}\quad-\mu_{1}\frac{l_{1}^{2}l_{2}}{b_{2}}+\frac{\Delta_{4}b_{2}l_{1}^{2}\gamma_{1}}{k^{6}\gamma_{3}^{3}}\left(b_{2}b_{3}l_{1}+k^{2}l_{2}\gamma_{1}\gamma_{3}\right)-\frac{\left(I_{11}-I_{22}\right)b_{2}}{k^{4}\gamma_{3}^{3}}l_{1}^{4}\gamma_{1}\Big{[}2l_{2}\gamma_{1}\gamma_{3}+\frac{b_{2}b_{3}}{k^{2}}l_{1}\Big{]},$$
$$\displaystyle Z_{v\omega_{\varphi}}^{(1)}=\frac{\Delta_{2}\gamma_{1}}{k^{2}\gamma_{3}}\left(l_{2}^{2}-l_{1}^{2}\right)-\mu_{1}l_{1}l_{2}+\frac{\Delta_{4}b_{2}^{2}}{k^{4}\gamma_{3}^{2}}l_{1}l_{2}\gamma_{1}^{2}-\frac{3\left(I_{11}-I_{22}\right)b_{2}^{2}}{k^{4}\gamma_{3}^{2}}l_{1}^{3}l_{2}\gamma_{1}^{2}$$
$$\displaystyle\quad+\frac{\Delta_{5}b_{2}\gamma_{1}}{k^{2}b_{3}\gamma_{3}^{2}}\big{(}l_{2}\gamma_{2}(l_{2}^{2}-3l_{1}^{2})+2l_{1}\gamma_{1}(l_{2}^{2}-l_{1}^{2})\big{)},$$
$$\displaystyle Z_{v\omega_{2}}^{(1)}=\frac{\Delta_{2}}{k^{2}b_{2}b_{3}\gamma_{3}^{2}}\big{(}b_{2}b_{3}l_{2}(l_{1}+l_{2}\gamma_{1}\gamma_{2})-l_{1}^{2}\gamma_{1}\gamma_{3}(k^{2}+b_{3}^{2})\big{)}+\mu_{1}\frac{l_{1}}{\gamma_{3}}\left(l_{1}\gamma_{1}-l_{2}\gamma_{2}\right)+\frac{\Delta_{3}b_{2}^{2}l_{1}^{3}\gamma_{1}^{2}}{k^{4}\gamma_{3}^{2}}$$
$$\displaystyle\quad{}-\frac{\Delta_{4}b_{2}^{2}l_{1}\gamma_{1}}{k^{4}\gamma_{3}^{3}}\big{(}l_{1}(\gamma_{1}^{2}-2)-l_{2}\gamma_{1}\gamma_{2}\big{)}+\mu_{3}\frac{b_{2}^{2}l_{1}^{2}\gamma_{1}\gamma_{2}}{k^{2}\gamma_{3}^{2}}+(I_{11}-I_{22})\frac{b_{2}^{2}l_{1}^{3}\gamma_{1}}{k^{4}\gamma_{3}^{3}}\big{(}l_{1}(\gamma_{1}^{2}-2)-2l_{2}\gamma_{1}\gamma_{2}\big{)}$$
$$\displaystyle\quad{}-\frac{\Delta_{5}b_{2}}{k^{2}b_{3}\gamma_{3}^{3}}\big{(}(\boldsymbol{l},\boldsymbol{\gamma})(2l_{1}l_{2}-(l_{1}^{2}-l_{2}^{2})\gamma_{1}\gamma_{2})+2l_{1}^{2}l_{2}\gamma_{1}\gamma_{3}^{2}\big{)}+\mu_{2}\frac{l_{1}}{\gamma_{3}}(\boldsymbol{l},\boldsymbol{\gamma}),$$
$$\displaystyle\Phi_{2}=\left[\frac{b_{2}b_{3}\Delta_{3}}{k^{2}\gamma_{3}}l_{1}+2\Delta_{3}l_{2}\gamma_{1}+\Delta_{5}\frac{\gamma_{1}}{\gamma_{2}}(\boldsymbol{l},\boldsymbol{\gamma})+b_{2}^{2}\frac{I_{11}-I_{22}}{k^{2}\gamma_{3}}l_{1}l_{2}\gamma_{1}^{2}\right]\frac{l_{1}^{2}v^{2}}{k^{2}\gamma_{3}}+\left[\Delta_{3}b_{3}\frac{l_{1}l_{2}\gamma_{1}}{k^{2}\gamma_{2}}-\frac{\Delta_{5}}{b_{3}}\right]v\omega_{\varphi}$$
$$\displaystyle{}\quad+\left[\frac{\Delta_{3}b_{2}l_{1}}{\gamma_{3}k^{2}}\big{(}l_{1}(2-\gamma_{1}^{2})+2l_{2}\gamma_{1}\gamma_{2}\big{)}+\frac{b_{2}l_{1}\gamma_{1}}{k^{2}}(I_{11}-I_{22})(l_{1}^{2}-l_{2}^{2})-\frac{\Delta_{5}l_{2}}{b_{3}\gamma_{3}}(\boldsymbol{l},\boldsymbol{\gamma})\right]\frac{v\omega_{2}}{\gamma_{3}}$$
$$\displaystyle\quad+\left[\Delta_{3}\frac{l_{1}\gamma_{2}}{\gamma_{3}}-(I_{11}-I_{22})l_{1}l_{2}\right]\omega_{y}^{2},$$
$$\displaystyle\Phi_{3}=Z^{(3)}_{vv}v^{2}+Z^{(3)}_{v\omega_{2}}v\omega_{2}+Z^{(3)}_{v\omega_{\varphi}}v\omega_{\varphi}+\Delta_{3}l_{1}\omega_{\varphi}^{2}+2(I_{11}-I_{22})l_{1}l_{2}\omega_{2}\omega_{\varphi}+\frac{b_{3}}{b_{2}}(I_{11}-I_{22})l_{1}l_{2}\omega_{2}^{2},$$
$$\displaystyle Z^{(3)}_{vv}=\frac{l_{1}^{2}}{k^{2}\gamma_{3}^{2}}\left[\Delta_{5}\gamma_{1}(\boldsymbol{l},\boldsymbol{\gamma})-\Delta_{3}\frac{b_{2}^{2}l_{1}\gamma_{1}^{2}}{k^{2}}+(I_{11}-I_{22})l_{2}\Big{(}\frac{b_{2}b_{3}}{k^{2}}l_{1}+2l_{2}\gamma_{1}\gamma_{3}\Big{)}\right]-\frac{l_{1}}{\gamma_{3}}\big{(}\mu_{1}l_{1}\gamma_{1}+\mu_{2}(\boldsymbol{l},\boldsymbol{\gamma}))$$
$$\displaystyle{}\quad+\frac{l_{1}}{k^{2}\gamma_{3}}\left[\Delta_{2}\frac{l_{1}\gamma_{1}}{b_{2}b_{3}}(k^{2}+b_{3}^{2})-\Delta_{4}l_{1}\gamma_{1}-\mu_{3}(b_{2}b_{3}l_{1}\gamma_{1}-k^{2}l_{2}\gamma_{3})\right],$$
$$\displaystyle Z^{(3)}_{v\omega_{\varphi}}=b_{2}\mu_{3}l_{2}-\frac{\Delta_{5}l_{1}}{b_{3}\gamma_{3}}\left(l_{1}\gamma_{2}-l_{2}\gamma_{1}\right)-b_{2}\frac{l_{1}\gamma_{1}}{k^{2}\gamma_{3}}\left(\left(I_{11}-I_{22}\right)\left(l_{1}^{2}-2l_{2}^{2}\right)+I_{33}\right),$$
$$\displaystyle Z^{(3)}_{v\omega_{2}}=\mu_{3}\frac{b_{2}}{\gamma_{3}}(\boldsymbol{l},\boldsymbol{\gamma})+\frac{\Delta_{5}l_{1}\gamma_{1}}{b_{3}\gamma_{3}^{2}}(\boldsymbol{l},\boldsymbol{\gamma})-\frac{l_{1}\gamma_{1}}{k^{2}\gamma_{3}}\left(\Delta_{1}b_{3}-\Delta_{3}b_{2}l_{2}\right)+b_{2}\frac{(I_{11}-I_{22})l_{2}l_{1}^{2}}{k^{2}\gamma_{3}^{2}}(2-\gamma_{1}^{2})$$
$$\displaystyle-b_{3}\frac{l_{1}\gamma_{1}}{k^{2}\gamma_{3}}\big{(}I_{11}(l_{1}^{2}-l_{2}^{2})+2I_{22}l_{2}^{2}\big{)}.$$

We see that, when \(\theta=\pm\pi/2\), the components of the matrix \({\bf\tilde{I}}\) and the vector \(\boldsymbol{\Phi}\) have a singularity.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bizyaev, I.A., Mamaev, I.S. Nonlinear Dynamics of a Roller Bicycle. Regul. Chaot. Dyn. (2024). https://doi.org/10.1134/S1560354724530017

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1134/S1560354724530017

Keywords

Search

Navigation