Comparative Analysis of the Parameters of the Normal and Abnormal DC Glow Discharges

Abstract

A comparative numerical study of the parameters of normal and abnormal direct current glow discharges between two flat disk electrodes with a radius of 3 cm in a 1-cm-high electric discharge gap is performed. A two-dimensional axisymmetric drift-diffusion model of the glow discharge is used for the numerical simulation, including equations for the transfer of electrons and molecular nitrogen ions, and the Poisson equation for finding the electric potential in the discharge gap taking into account the regions of the space charge and the positive column. Abnormal discharges are obtained when the radius of the cathode decreases. A numerical procedure is proposed for smoothing local maxima of the electric field strength near the boundaries of the abnormal glow discharge cathode, which ensures the stability of the solution and the weak effect on the calculated data. The numerical simulation results of the electrodynamic structure of normal and abnormal glow discharges are presented.

1 INTRODUCTION

The normal direct current glow discharge has attracted the attention of researchers for more than 100 years. The classical scheme of such a discharge is shown in Fig. 1. Its typical parameters: electromotive force of the power supply ε ~ 200–1000 V and electric currents through the discharge gap I ~ 0.1–10 mA.

Fig. 1.

Calculation scheme for normal and abnormal glow discharges.

On the one hand, a normal glow discharge is an example of the simplest plasma formation, quite easily implemented in physical laboratories [1], on the other hand, this discharge is a typical object of the self-organization of a localized plasma structure, which exists owing to the competition between dissipation and the appearance of charged particles in an external electric field. Figure 1 shows that the normal discharge has finite transverse dimensions in the radial direction. When the voltage drop between the electrodes V_d increase, the radius of such a column increases, and when V_d decreases, the radius decreases. It is important that the discharge burning between the electrodes, together with the external electrical circuit, which includes a source of electromotive force ε and ohmic resistance ${{R}_{0}}$, is an example of a self-regulating system with a positive feedback. When the voltage on the electrodes increases, the intensity of ionization processes increases and, as a result, the current through the discharge gap increases. But this leads to a decrease in the voltage drop across the electrodes. When the voltage on the electrodes decreases, the intensity of ionization processes decreases and, thus, a plasma structure is formed, in which a balance is maintained between losses and reproduction of charges.

The main feature of a normal glow discharge is that with a change in the radial dimensions of such a column owing to a variation in the voltage drop across the electrodes, the current density near the symmetry axis changes slightly. This phenomenon is called law of normal current density or Gel law [2]. Of course, this regularity exists only within certain limits of the glow discharge. parameters In [3, 4] (see also the extensive bibliography therein), it was shown that the experimentally measured parameters of a normal glow discharge in its axial regions, namely, the voltage drop across the cathode layer V_n, the current density on the symmetry axis  j_n, the thickness of the cathode layer d_n, are predicted by the one-dimensional Engel–Steenbeck theory [5] with good accuracy

$${{V}_{n}} = \frac{{3B}}{A}\ln \left( {1 + \frac{1}{\gamma }} \right),\;{\text{V,}}$$

$$\frac{{{{j}_{n}}}}{{{{p}^{2}}}} = 5.92 \times {{10}^{{ - 14}}}\frac{{A{{B}^{2}}\left( {{{\mu }_{i}}p} \right)\left( {1 + \gamma } \right)}}{{\ln \left( {1 + 1{\text{/}}\gamma } \right)}},\;{\text{A/(c}}{{{\text{m}}}^{{\text{2}}}}\;{\text{Torr),}}$$

$${{d}_{n}}p = 3.78\frac{{\ln \left( {1 + 1{\text{/}}\gamma } \right)}}{A},\;{\text{cm}}\;{\text{Torr,}}$$

where А, В are approximation coefficients in the formula for the first Townsend coefficient, which determines the efficiency of the impact ionization of molecules by electrons (see formula (9) below), γ is the coefficient of secondary electron emission at the interaction of ions with the cathode surface, ${{\mu }_{i}}$ is the ion mobility in a glow discharge, р is pressure. In later works [6–8], where the normal glow discharge was studied in the two-dimensional geometry using mathematical simulation, it was shown that the calculated data obtained using the drift-diffusion model are close to the results of the Engel–Steenbeck theory.

Another feature of a normal glow discharge is its surprisingly complex longitudinal structure. At least seven sections of the longitudinal structure of a normal glow discharge are identified, each of which provides the conditions for its existence. The physical processes in each of the regions (with increasing distance from the cathode): Aston dark space, cathode glow, cathode dark space, negative glow, Faraday dark space, positive column, and anode dark space were analyzed in [4, 6].

The main elements of the structure of a normal glow discharge have been studied quite well using the so-called drift-diffusion model [7, 8], the detailed derivation of equations of which is given in [6]. This model well describes the so-called local processes of ionization, recombination and diffusion in a glow discharge, which is sufficient for simulating its main integral characteristics: the radial dimensions of the current column, the dimensions of the cathode and anode regions of the space charge, where there is an increased density of ions and electrons, respectively, density current at the cathode and anode, total current through the discharge gap and voltage drop between the electrodes.

There are two other classes of computational-theoretical models that are used, but noticeably less, to study the structure of DC glow discharges. These are the so-called ambipolar model and nonlocal kinetic models. The ambipolar model [6] assumes the absence of space charge regions, i.e., in fact, only the positive column of the glow discharge is considered. Using kinetic models, nonlocal kinetic processes are studied, first of all, the region of the electron beam in the immediate vicinity of the cathode, and the region of the Faraday dark space [9].

The ambipolar model has found its application in problems of applied physics of gas discharges. Its main drawback is associated with the need for a special formulation of the boundary conditions near the cathode and anode, where the specified model is not applicable because are space charge regions. However, due to its simplicity and high computational efficiency, the ambipolar model is quite often used in plasma aerodynamics problems [6, 10, 11], where it was possible to obtain a good description of experimental data [12, 13] with its help.

As already noted, the drift-diffusion model makes it possible to describe the space charge regions near the cathode and anode. However, the use of this model in conjunction with the equations describing the motion of a partially ionized gas encounters two obstacles. The first obstacle is the high complexity of solving the problem with a space charge. The second obstacle is that the glow discharge in plasma aerodynamics burns in an anomalous regime due to the finite size of the electrodes. The gas flow often “blows off” the cathode and anode spots to the boundaries of the electrodes. It was established that high electric fields arise at the boundaries of the electrodes, leading to a breakdown of the gas, and during the numerical simulation, to the instability of the resulting solution.

In this work, we study changes in the structure of a normal glow discharge during its gradual transition to an abnormal discharge due to an artificial decrease in the radius of the cathode surrounded by a dielectric surface. For these purposes, the drift-diffusion model of the discharge in the axisymmetric formulation is used. The design scheme is shown in Fig. 1. First, the problem of finding the parameters of a normal glow discharge is solved for given parameters of the external electric circuit and the geometry of the electric discharge gap, which is characterized by the electrode radius R = 3 cm and the distance between the electrodes H = 1.0 cm. In the calculations, the gas pressure was set constant p = 5 Torr, the gas temperature was 300 K. A series of subsequent calculations was carried out for a gradually decreasing radius of the cathode, R_c = 1.0, 0.6, 0.4 and 0.2 cm (the rest of the cathode surface was assumed to be dielectric), which led to the transition of a normal glow discharge into an abnormal one.

For each of the calculated options, the electrodynamic structure of the discharge and, in particular, the electric field voltage and the density of charged particles near the boundary of the cathode were studied. An additional series of calculations was performed using the procedure for numerical smoothing of the electric field strength near the cathode boundary, which imitates technological methods for smoothing the electrode boundaries in experiments.

2 MATHEMATICAL STATEMENT OF THE PROBLEM

The system of equations for the computational drift-diffusion model of a glow discharge is formulated as follows [6, 14]:

$$\frac{\partial {{n}_{e}}}{\partial t}+\text{div}{\kern 1pt} {{\mathbf{\Gamma }}_{e}}=\alpha \left( E\text{/}p \right)p\left| {{\mathbf{\Gamma }}_{e}} \right|-\beta {{n}_{i}}{{n}_{e}}={{\dot{\omega }}_{i}},$$

(1)

$$\frac{\partial {{n}_{i}}}{\partial t}+\text{div}{\kern 1pt} {{\mathbf{\Gamma }}_{i}}=\alpha \left( E\text{/}p \right)p\left| {{\mathbf{\Gamma }}_{i}} \right|-\beta {{n}_{i}}{{n}_{e}}={{\dot{\omega }}_{i}},$$

(2)

$${\text{div}}\left( {{\text{grad}}{\kern 1pt} \varphi } \right) = 4\pi e\left( {{{n}_{e}} - {{n}_{i}}} \right),$$

(3)

where ${{\mathbf{\Gamma }}_{e}}=-{{D}_{e}}\text{grad}{{n}_{e}}-{{n}_{e}}{{\mu }_{e}}\mathbf{E}$; ${{{\mathbf{\Gamma }}}_{i}} = - {{D}_{i}}{\text{grad}}{{n}_{i}}$ + n_iμ_iE; ${\mathbf{j}} = e\left( {{{{\mathbf{\Gamma }}}_{i}} - {{{\mathbf{\Gamma }}}_{e}}} \right)$; ${\mathbf{E}} = - {\text{grad}}{\kern 1pt} \varphi$; ${{n}_{e}},{{n}_{i}}$ is the density of electrons and ions in 1 cm³; e is the charge of electron, E and φ are the electric field strength vector and its potential; ${{{\mathbf{\Gamma }}}_{e}},\;{{{\mathbf{\Gamma }}}_{i}}$ are electron and ion flux density vectors; ${{D}_{e}},\,{{D}_{i}}$ are diffusion coefficients of electrons and ions; ${{\mu }_{e}},\,{{\mu }_{i}}$ are mobilities of electrons and ions; $\alpha = \alpha \left( {E{\text{/}}p} \right)$ is the coefficient of impact ionization of molecules by electrons (the first Townsend coefficient), $E = \left| {\mathbf{E}} \right|$; β is the ion–electron recombination coefficient. The total volumetric rate of the electron production in the right-hand side of Eqs. (1) and (2)${{\dot {\omega }}_{i}}$ is determined by the difference between the ionization and recombination rates.

When solving the system of equations of the drift-diffusion model, an orthogonal cylindrical coordinate system is used. The boundary conditions for Eqs. (1)−(3) have the form

$$x = 0,\quad {{\Gamma }_{{e,x}}} = \gamma {{\Gamma }_{{i,x}}},\quad \frac{{\partial {{n}_{i}}}}{{\partial x}} = 0,\quad \varphi = 0;$$

(4)

$$x = H,\quad \frac{{\partial {{n}_{e}}}}{{\partial x}} = 0,\quad {{n}_{i}} = 0,\quad \varphi = {{V}_{{\text{d}}}};$$

(5)

$$r = 0,\quad \frac{{\partial {{n}_{e}}}}{{\partial r}} = \frac{{\partial {{n}_{i}}}}{{\partial r}} = \frac{{\partial \varphi }}{{\partial r}} = 0;$$

(6)

$$r = R,\quad {{n}_{e}} = {{n}_{i}} = 0,\quad \frac{{\partial \varphi }}{{\partial r}} = 0.$$

(7)

Here, V_d is the voltage drop across the discharge gap, ${{\Gamma }_{{e,x}}},\,\,{{\Gamma }_{{i,x}}}$ are electron and ion flux density projections onto the x axis; $R,\;H$ are coordinates of the boundary of the computational domain in r and x directions. The boundary conditions on the electrodes for charged particles are approximate. The admissibility of their use was discussed in [8], where it was shown by numerical experiments that the complication of the boundary conditions does not significantly affect the calculation results in a wide range of glow discharge parameters, while increasing the risk of numerical instabilities. In the boundary conditions Eq. (5), there is still an undetermined voltage drop across the discharge gap V_d, which includes the components of the voltage drop on the cathode and anode layers, and on the positive column. To determine it, it is necessary to involve the conditions in the external circuit (see Fig. 1). Under the conditions of steady-state burning of a glow discharge, it is possible to write the obvious relation

$$\frac{{\varepsilon - {{V}_{{\text{d}}}}}}{{e{{R}_{0}}}} = 2\pi \int\limits_0^R {{{\Gamma }_{e}}\left( {r,x = 0} \right)r{\kern 1pt} {\text{d}}{\kern 1pt} r} ,$$

(8)

which postulates the equality of the sum of voltage drops across the resistance ${{R}_{0}}$ and discharge gap to the electromotive force ε.

The computational model is derived to study the structure of a glow discharge in molecular nitrogen at pressures $p = 1{-} 20$ Torr, therefore, the following values of the coefficients included in the mathematical formulation of the problem were set:

$$\begin{gathered} {{\mu }_{e}}p = 4.4 \times {{10}^{5}}, \\ {{\mu }_{i}}p = 1.45 \times {{10}^{3}}\;({\text{Torr}}\;{\text{c}}{{{\text{m}}}^{2}}){\text{/}}({\text{V}}\;{\text{s}}), \\ \end{gathered} $$

$$\beta = 2 \times {{10}^{{ - 7}}}\;{\text{c}}{{{\text{m}}}^{{\text{3}}}}{\text{/s,}}$$

(9)

$$\frac{\alpha }{p} = A\exp \left( { - \frac{B}{{E{\text{/}}p}}} \right)~\;{{({\text{cm}}\;{\text{Torr}})}^{{ - 1}}},$$

where $A = 12$ (cm Torr)⁻¹, $B = 342$ V/(cm Torr).

The empirical formula Eq. (9) for the first Townsend coefficient is recommended in [3] for the following range of field strength-to-pressure ratios:

$$100 < E{\text{/}}p < 600\;{\text{V/(cm}}\;{\text{Torr)}}.$$

The diffusion coefficients were determined from the Einstein relations

$${{D}_{e}} = {{\mu }_{e}}{{T}_{e}},\quad {{D}_{i}} = {{\mu }_{i}}{{T}_{i}},$$

where ${{T}_{e}},\;{{T}_{i}}$ is the temperature of electrons and ions, eV, respectively.

It is necessary to make general remarks regarding the choice of the given semi-empirical electrophysical parameters. The main thing is that in order to estimate the eligibility of using the presented numerical values and approximations, one should take into account the objective function of the constructed calculation model, which belongs to the class of heuristic models based on a number of semi-empirical functions. The mobility coefficients of electrons and ions, and the recombination coefficient, were chosen in accordance with the recommendations [3, 4] for molecular nitrogen for similar conditions in the discharge. Temperatures of electrons and ions were considered constant, ${{T}_{e}}$ = 1 eV and ${{T}_{i}}$ = 0.026 eV. The effect of possible variations of the electron temperature in the range of ${{T}_{e}}$ = 1–10 eV was studied, and the selection of an empirical dependence for the characteristic electron temperature in a glow discharge of the type under consideration, was performed in [5, 16, 17]. No fundamental effect on the calculated parameters of the normal glow discharge was noted.

At the same time, a noticeable effect of the used approximation of the ionization coefficient on the integral characteristics of the discharge (total current through the discharge, voltage drop across the gas-discharge gap) was established in the calculations. Therefore, when tending to achieve numerical closeness of the calculated and experimental data, the choice of this approximation should be treated very carefully. The same applies to the choice of the coefficient of secondary ion–electron emission ($\gamma \sim 0.01{-} 0.1$). In general, the calculation results using the proposed numerical model are in good agreement with the Engel–Steenbeck theory for the parameters of a normal glow discharge and with our own experimental data [1, 5, 8].

Details of the numerical solution of the equations of the drift-diffusion model of a glow discharge are given in [6].

3 NUMERICAL SIMULATION RESULTS

The initial data in all calculation options were the same: р = 5 Torr, ε = 1000 V, ${{R}_{0}}$ = 300 kΩ. Figure 2 shows the electrodynamic structure of a normal glow discharge in an electric discharge gap of height H = 1 cm and radius R = 3 cm. The distributions of ion and electron densities (Fig. 2a) clearly show the main structural elements of the discharge: a cathode layer with an increased ion density and a positive column, a region of almost quasi-neutral plasma. Here and below, the densities of charged particles are referred to the quantity ${{n}_{0}}$ = 10⁹ cm^–3. The anode layer, in which the ion density tends to zero, is located in the immediate vicinity of the anode. This is the region of the negative space charge.

Fig. 2.

Distributions of the density of ions (N_i, left) and electrons (N_e, right) (a), normal (${{E}_{x}}$, left) and radial (${{E}_{r}}$, right) electric field components (b), electric potential (${\text{Fi}} = \varphi$, left) and ionization rate (${\text{RateIon}} = {{\dot {\omega }}_{i}}{\text{/}}\Omega$, right) (c) in the normal glow discharge.

Figure 2b shows distributions of the axial and radial components of the electric field strength referred to the $\varepsilon {\text{/}}H$ value, and Fig. 2c (left) shows the distribution of the electric potential. In the cathode layer, i.e., in the region of positive space charge, there is a sharp increase in the electric potential.

We note that the distribution of the electric potential shown in Fig. 2c (left) clearly indicates a potential well in which there is a current layer of a normal glow discharge. The comparison of data in Figs. 2c (left) and 2b (right) explains the local maximum of the radial component of the electric field strength at the upper right-hand boundary of the cathode layer. Here, the electric potential decreases in the radial direction. We emphasize this fact and it will be shown below that the situation changes to the opposite one in the abnormal discharge.

Figure 2c (right) shows the distribution of the ionization rate in a normal glow discharge, referred to the quantity $\Omega = {{n}_{0}}{{\mu }_{e}}\varepsilon {\text{/}}H$. It can be seen that gas ionization also occurs in the anode layer and, to a much lesser extent, in the positive column. It was shown in [15] that the current column in the normal glow discharge is largely due to the competition between ionization and diffusion processes in the radial direction. The visible boundary of the current column in Fig. 2a (right) approximately corresponds to the electron current line, to the right of which diffusion makes the loss of electrons irreplaceable, and to the left, ionization and drift allow electrons to close the electrical circuit.

Figure 3 shows the distribution of the electron and ion density along the symmetry axis of the discharge. In these figures, the regions of the cathode and anode layers are clearly visible, where ion and electron density reaches ${{n}_{i}}$ = 24 × 10⁹ cm^–3 and ${{n}_{e}}$ = 3 × 10⁹ cm^–3, respectively. In the positive column, the density of charged particles is ${{n}_{e}} \approx {{n}_{i}}\sim 6 \times {{10}^{9}}$ cm^–3.

Fig. 3.

Distributions of densities of ions (N_i) and electrons (N_e) along the symmetry axis of the normal glow discharge.

Figure 4 shows the distribution of the absolute value of the electric field strength along the symmetry axis of the discharge and electric potential. The highest electric field strength is observed in the cathode layer. A much lower increase in the electric field strength is observed in the anode layer. However, this increase is sufficient for a noticeable increase in the ionization rate in this layer. It is also noteworthy that the electric field strength is Е_х ~ 40 V/cm in the quasi-neutral positive column, which is sufficient to make up for the loss of electrons by diffusion caused by impact ionization and the motion of electrons along the field between the cathode and anode.

Fig. 4.

Distribution of the electric potential (${\text{Fi}} = \varphi$) and absolute value of the axial component of the electric field (|E_x|) along the symmetry axis of the normal glow discharge in the gas-discharge gap.

Figure 5 shows radial distributions of current densities on the cathode and anode in normal and abnormal glow discharges, which differ quite significantly. For a normal glow discharge (curves 1), the current density on the cathode (dotted line) is approximately four times lower than the current density on the anode. We note that the current density at the cathode is a conservative quantity with respect to changes in the parameters of a normal glow discharge. The current density on the anode can change noticeably [6, 8].

Fig. 5.

Distribution of the current density on the anode (solid lines) and cathode (dotted lines) along the electrode radius in the gas-discharge gap: 1—normal discharge, 2, 3—abnormal discharge at R_c = 0.6 and 0.2 cm, respectively.

The following figures present the results on the structure of an abnormal glow discharge. The matrix of calculation results is constructed as follows. Calculations are performed for successively decreasing cathode radii R_с = 1.0, 0.6, 0.4 and 0.2 cm. The radius of the anode remained the same, R_с = 3 cm. Figures 6а and 7а show calculation results for the density of charged particles, Figs. 6b and 7b those of components of the electric field strength, and Figs. 6c and 7c those of the electric potential and ionization rates for two radii of cathode R_с = 0.6 and 0.2 cm.

Fig. 6.

Distributions of densities of ions (N_i, left) and electrons (N_e, right) (a), normal (${{E}_{x}}$, left) and radial (${{E}_{r}}$, right) electric field components (b), electric potential (${\text{Fi}} = \varphi$, left) and ionization rate (${\text{RateIon}} = {{\dot {\omega }}_{i}}{\text{/}}\Omega$, right) (c) in the abnormal glow discharge. The radius of the cathode section is R_c = 0.6 cm.

Fig. 7.

Distributions of the density of ions (N_i, left) and electrons (N_e, right) (a), normal (${{E}_{x}}$, left) and radial (${{E}_{r}}$, right) electric field components (b), electric potential (${\text{Fi}} = \varphi$, left) and ionization rate (${\text{RateIon}} = {{\dot {\omega }}_{i}}{\text{/}}\Omega$, right) (c) in the abnormal glow discharge. The radius of the cathode section is R_c = 0.2 cm.

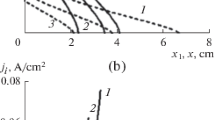
As already noted, a feature of abnormal glow discharges is an increased electric field strength near the boundaries of the electrodes. This is illustrated in Fig. 8a, where the distributions of the axial components of the absolute value of the electric field strength along the radius of the cathode section of the discharge are shown for different sizes of cathode. The local strength maxima correspond to the boundaries of the cathode sections. The same figure shows the distribution of the electric potential on the cathode section of the glow discharge. It is obvious that φ = 0 on the cathode. Because of the boundary conditions used, $\varphi \ne 0$ on the dielectric surface.

Fig. 8.

Distributions of the axial component of the electric field strength (dashed curves) and electric potential along the cathode surface without smoothing (a) and with smoothing of the electric field near the cathode surface (b); 1–4: abnormal glow discharge at R_c = 0.2, 0.4, 0.6 and 1.0 cm; 5– normal glow discharge (b).

In the abnormal glow discharge with a cathode radius R_c = 0.6 cm, the current density at the cathode and anode dropped by two and four times, respectively (Fig. 5). In this case, the current density on the cathode becomes more uniform along the radius. In the abnormal glow discharge with a cathode radius R_c = 0.2 cm, the current density on the cathode sharply increases. This is due to the strong localization of the cathode spot when it is necessary to maintain the current almost at the same level.

We also note features in the distributions of the electric potential and the radial component of the electric field strength for an abnormal glow discharge, which were discussed above. Figures 9b, 9c shows that the potential increases in the radial direction, and does not decrease, as it does in a normal glow discharge. As a consequence, the radial component of the electric field strength is directed towards the center. However, this does not fundamentally change the discharge characteristics.

Fig. 9.

Distributions of the densities of ions (N_i, left) and electrons (N_e, right) (a), normal (${{E}_{x}}$, left) and radial (${{E}_{r}}$, right) electric field components (b), electric potential (${\text{Fi}} = \varphi$, left) and ionization rate (${\text{RateIon}} = {{\dot {\omega }}_{i}}{\text{/}}\Omega$, right) (c) in the abnormal glow discharge. The radius of the cathode section R_c = 0.2 cm. The smoothing procedure is used.

It has already been discussed that the observed jumps in the electric field strength lead to a sharp increase in the ionization rate in the corresponding zones. The physical analogue of this effect is the improvement of conditions for the electrical breakdown of the gas. The numerical simulation procedure for obtaining a solution becomes much more complicated. The study of the structure of an abnormal glow discharge has not only a purely scientific motivation, but also the need to build computational models for problems of plasma aerodynamics. Therefore, we used the procedure for smoothing the electric field strength near the boundaries of the electrodes, which is physically analogous to rounding the electrode boundaries in a physical experiment.

The smoothing procedure was as follows. If smoothing was not used, then the following boundary conditions were set for the electric potential on the cathode section:

$$\begin{gathered} {{r}_{i}} \leqslant {{R}_{{\text{c}}}}{\kern 1pt} :\quad \varphi = 0, \hfill \\ {{r}_{i}} > {{R}_{{\text{c}}}}{\kern 1pt} :\quad \frac{{\partial \varphi }}{{\partial x}} = 0, \hfill \\ \end{gathered} $$

which had the following expression in the finite difference form:

$$\begin{gathered} {{r}_{i}} \leqslant {{R}_{{\text{c}}}}{\kern 1pt} :\quad {{\alpha }_{i}} = 0,\quad {{\beta }_{i}} = 0, \\ {{r}_{i}} > {{R}_{{\text{c}}}}{\kern 1pt} :\quad \,{{\alpha }_{i}} = 1,\quad {{\beta }_{i}} = 0. \\ \end{gathered} $$

(10)

It is assumed here that the boundary condition on the cathode surface at the points ${{r}_{i}}$ is given in the following form:

$${{\varphi }_{{i,1}}} = {{\alpha }_{i}}{{\varphi }_{{i,2}}} + {{\beta }_{i}},$$

(11)

where ${{\varphi }_{{i,1}}}$ is the potential on the surface, and ${{\varphi }_{{i,2}}}$ is the potential in the layer of the finite-difference grid closest to the surface.

When using the smoothing procedure, the following formulas were applied:

$$\begin{gathered} {{r}_{i}} < {{R}_{\delta }}{\kern 1pt} :\quad {{\alpha }_{i}} = 0,\quad {{\beta }_{i}} = 0, \hfill \\ {{r}_{i}} \geqslant {{R}_{\delta }}{\kern 1pt} :\quad {{\alpha }_{i}} = 1 - \exp \left[ { - \frac{{{{{({{r}_{i}} - {{R}_{\delta }})}}^{4}}}}{{{{\delta }^{4}}}}} \right], \hfill \\ {{r}_{i}} > {{R}_{{\text{c}}}}{\kern 1pt} :\quad {{\alpha }_{i}} = 1,\quad {{\beta }_{i}} = 0, \hfill \\ \end{gathered} $$

(12)

where ${{R}_{\delta }} = {{R}_{{\text{c}}}} - \delta$, δ = 0.25 or 0.05 cm. In relationships (10)–(12) ${{\alpha }_{i}},\,\,\,{{\beta }_{i}}$ are approximating coefficients of boundary conditions of the first and second kind.

Figure 9 shows the calculation results of the electrodynamic structure of the discharge when using the procedure for smoothing the axial component of the electric field strength near the cathode with a radius R_c = 0.2 cm.

The comparison of the given data with smoothing and without smoothing (Fig. 8) shows that smoothing has little effect on the distribution of all functions except, of course, for the electric field strength in the immediate vicinity of the cathode boundary. We attract attention to the fact that from a mathematical point of view, this smoothing procedure specifies a smooth transition from the boundary condition of the first kind for the electric potential to the boundary condition of the second kind in some boundary region of the cathode.

Figure 10 shows the distributions of the electric potential along the symmetry axis of the current column for different radii of the cathode, obtained without and with the smoothing procedure. Attention is drawn to the closeness of these distributions, except for the parameters of the abnormal glow discharge at R_c = 0.2 cm. This is not surprising, since the discharge structure already changes quite significantly at very small cathode radii (Fig. 9). A further decrease in the cathode radius aggravates the combustion regime even stronger.

Fig. 10.

Distribution of the electric potential (Fi = φ) along the symmetry axis of the normal and abnormal glow discharge without smoothing (a) and with smoothing of the electric potential distribution near the cathode (b).

Figures 11 and 12 show axial distributions of the density of electrons and ions, which also confirm the conclusions that, up to certain limits of the decrease in the radius of the cathode, the parameters of the abnormal glow discharge change insignificantly, but at the smallest radius of the cathode, a new combustion regime practically sets in, which is characterized by a sharp increase in the electric potential in the cathode layer and, consequently, the ionization rates.

Fig. 11.

Distribution of electron densities along the symmetry axis of the normal and abnormal glow discharge without smoothing (a) and with smoothing of the electric potential distribution near the cathode.

Fig. 12.

Distribution of the ion densities along the symmetry axis of the normal and abnormal glow discharges without smoothing (a) and with smoothing (b) of the electric potential distribution near the cathode.

All distributions indicate a weak effect of the smoothing procedure on the main discharge characteristics. Figure 8 shows the axial distributions of the absolute value of the axial component of the electric field and potential along the surface of the cathode section for different electrode radii. It is clearly seen here that the smoothing procedure used very effectively cuts off local jumps in the electric field strength near the cathode boundary, while changing the average values on the cathode surface not very strongly.

All distributions indicate a weak effect of the smoothing procedure on the main discharge characteristics, while changing the average values on the cathode surface not very strongly.

To complete the analysis of the abnormal discharge, Table 1 shows its integral characteristics, such as the voltage across the electric discharge gap and the total current through the discharge channel, which also confirm the above conclusions. The structure of normal and abnormal glow discharges was calculated at the increased interelectrode distance, Н = 2 cm. We note a regular increase in the voltage drop across the discharge gap, which is necessary to maintain the discharge burning in a larger volume and a slight decrease in the total current through the discharge, associated with increased losses due to radial diffusion. The conclusions about the admissibility of using the proposed smoothing procedure for an abnormal discharge remain valid.

Table 1. Integral characteristics of normal and abnormal glow discharges with the discharge chamber radius R = 3 cm

4 CONCLUSIONS

A comparative numerical study of the parameters of normal and anomalous direct current glow discharges between two flat disk electrodes with a radius of 3 cm in a 1 cm high electric discharge gap has been performed. Abnormal discharges were obtained by decreasing the radius of the cathode, while the rest of the cathode surface was filled with a dielectric.

For numerical simulation, a drift-diffusion model of a glow discharge was used together with an equation for an external electrical circuit, including an ohmic resistance and a DC glow discharge power supply. Taking into account the external electric circuit provided positive feedback with respect to the determination of the voltage drop across the electrodes after calculating the total electric current through the discharge gap.

It is shown that local maxima of the electric field strength arise in an anomalous direct current glow discharge near the cathode boundaries, which lead to breakdown phenomena (avalanche gas ionization) and instability of the numerical solution of the equations of the drift-diffusion model.

In order to expand the range of initial data for which a steady-state solution is obtained, a procedure for smoothing the electric field strength at the cathode boundaries is proposed, the physical analogue of which can be rounding the electrode boundaries in a real experiment. It is shown that the stability of numerical simulation results of the discharge to the application of the smoothing procedure is high and this procedure has no strong effect on the calculated electrodynamic parameters.

In the numerical simulation of abnormal glow discharges, conditions are established under which the parameters of the abnormal discharge and the normal discharge start to differ strongly.