The Fundamental Scale of QCD

Abstract

There are several scales in the QCD as the theory of strong interaction: the vacuum gluonic condensate (as the divergence of the dilatation current), the nucleon mass as the basic mass scale in our universe, which is connected to the string tension $\sigma$, and the perturbative QCD scale $\Lambda_{\mathrm{QCD}}$, which defines the scale of the renormalized perturbative expansions. In this paper we connect all these scales to the vacuum condensate, using the field correlator method, where the string tension is expressed in terms of nonlocal field correlators, which are connected to the local condensates, while the perturbative $\Lambda_{V}$ is connected to $\sigma$ in the framework of the Background Perturbation Theory (BPT). We also demonstrate how the IR singularities and IR renormalons disappear in BPT making the resulting theory internally consistent.

Appendices

Appendix

THE QCD VECTOR COUPLING $\alpha_{V}(r)$

The spin-average masses of all mesons are described by the universal static potential $V(r)$, taken in the linear $+$ gluon-exchange (GE) form,

$$V\left(r\right)=\sigma r-\frac{4}{3}\frac{\alpha\left(r\right)}{r}.$$

(A.1)

Here the vector coupling $\alpha_{V}(r)$ in the coordinate space is defined via the vector coupling in the momentum space $\alpha_{V}(Q^{2})$ as

$$\alpha_{V}\left(r\right)=\frac{2}{\pi}\int\limits_{0}^{\infty}dQ\frac{\sin\left({Qr}\right)}{Q}\alpha_{V}\left({Q^{2}}\right),$$

(A.2)

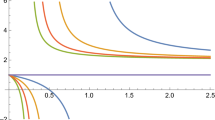
where the integration goes over three regions: small momenta $Q\lesssim 1.5$ GeV, where $\alpha_{V}\left({Q^{2}}\right)$ is defined by $\Lambda_{V}(n_{f}=3)$; second interval, $1.5\text{ GeV}\leqslant Q\leqslant m_{b}(m_{b}\cong 4.20$ GeV is the $b$-quark current mass), where the coupling is defined by $\Lambda_{V}(n_{f}=4)$, and the region of large momenta, $q\geqslant m_{b}$, where $\Lambda_{V}(n_{f}=5)$ has to be used. This vector coupling in the coordinate spaces will be called the compound $\alpha_{V}^{c}(r)$. It can be compared with $\alpha_{V}(r,n_{f}=3)$, calculated via $\alpha_{V}(Q,n_{f}=3)$, defined by the QCD constant $\Lambda_{V}(n_{f}=3)$ over the whole region of the integration. The calculations show that the compound coupling $\alpha_{V}^{c}(r)$ coincides with precision accuracy with $\alpha_{V}(r,n_{f}=3)$ at all distances with exception of very small $r\lesssim 0.1$ fm, where the compound coupling is a bit smaller and this difference has to be taken into account only for the bottomonium ground state $\Upsilon(1S)$. Here in calculations we use the IR regulator $M_{B}=1.15$ GeV.

The vector constants $\Lambda_{V}(n_{f})$ are expressed via $\Lambda_{\overline{MS}}(n_{f})$ as $\Lambda_{V}(n_{f})=\Lambda_{\overline{MS}}\left({n_{f}}\right)\exp\left({\dfrac{a_{1}}{2\beta_{0}}}\right)$ [17] and hence $\Lambda_{V}(n_{f}=3)=1.4753\Lambda_{\overline{MS}}(n_{f}=3)$. The value $\Lambda_{\overline{MS}}\left({n_{f}=3}\right)=332(19)$ MeV, is now well established in lattice QCD [19]. It gives

$$\Lambda_{V}(n_{f}=3)=492(28)\text{ MeV}.$$

(A.3)

Very close value, $\Lambda_{\overline{MS}}\left({n_{f}=3}\right)=339(10)$ MeV, was also found in the analysis of experimental data in [18].

Now we can define the characteristic scales $r_{i}$, ($r_{0},r_{1},r_{2}$) of the static potential (the forth) and compare them with the lattice results [19, 20].

Firstly, with the use of (A.2) we calculate the two-loop coupling $\alpha_{V}(r,n_{f}=3)$ and the constants $C_{i}$, defined at three points $r_{i}$, $i=0$, 1, 2,

$$C_{i}=r_{i}^{2}\frac{\partial V(r)}{\partial r};\quad C_{0}=1.65,$$

(A.4)

$$C_{1}=1.0,\quad C_{2}=0.50.$$

In the coupling $\alpha_{V}(r,n_{f}=3)$ we use $M_{B}=1.15$ GeV and obtain

$$r_{0}=2.319\text{ GeV}^{-1}=0.459\text{ fm};$$

(A.5)

$$r_{1}=1.530\text{ GeV}^{-1}=0.303\text{ fm};$$

$$r_{2}=0.70\text{ GeV}^{-1}=0.139\text{ fm},$$

for which the following $\alpha_{V}(r_{i})$ and the derivatives $\alpha^{\prime}_{V}(r_{i})$ are calculated,

$$\alpha(r_{2})=0.4479,\quad\alpha^{\prime}_{V}(r_{2})=0.1967;$$

(A.6)

$$\alpha_{V}(r_{1})=0.49715,\quad\alpha^{\prime}_{V}(r_{1})=0.1363;$$

$$\alpha_{V}(r_{0})=0.5954,\quad\alpha^{\prime}_{V}(r_{0})=0.0840.$$

Now we give also $\alpha(\lambda_{0})$ at the important point $\lambda_{0}=1.0$ GeV${}^{-1}=0.20$ fm,

$$\alpha(0.20\text{ fm})=0.497,$$

(A.7)

which is close to $\alpha_{V}(r=0.20\text{ fm})=0.567$, derived in (17). Notice that the calculated $r_{0}$ and $r_{1}=0.303$ fm are in good agreement with the lattice result, $r_{1}=0.3106$ fm in [41]. Also in our calculations the ratio

$$\frac{r_{1}}{r_{2}}=2.186,$$

(A.8)

is in good agreement with the same ratio, defined in the lattice calculations, $\dfrac{r_{1}}{r_{2}}=2.198(9)$ [41].