Unsteady Bending of an Orthotropic Cantilever Timoshenko Beam with Allowance for Diffusion Flux Relaxation

Abstract

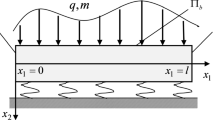
The problem of unsteady bending of an elastic diffusion orthotropic cantilever Timoshenko beam under loading applied to its free end is considered. The model takes into account that the velocity of propagation of diffusion perturbations is finite due to diffusion flux relaxation. The elastic diffusion processes are described by a coupled system of equations for the Timoshenko beam with allowance for diffusion. A solution of the problem is sought by the method of equivalent boundary conditions. For this purpose, an auxiliary problem is considered, whose solution is obtained by applying the Laplace integral transform in time and trigonometric Fourier series expansions in space. Next, relations connecting the right-hand sides of the boundary conditions of the original and auxiliary problems are constructed. These relations represent a system of Volterra integral equations of the first kind. The system is solved numerically by applying quadrature rules. For an orthotropic beam made of a three-component material, the interaction of unsteady mechanical and diffusion fields is numerically analyzed. Finally, the main conclusions concerning the coupling effect of the fields on the stress-strain state and mass transfer in the beam are given.

APPENDIX

1. The coefficients ${{k}_{{1n}}}\left( s \right)$ and the right-hand sides ${{F}_{{1kln}}}$ of system (8) are given by

$${{k}_{{1n}}}\left( s \right) = {{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} + {{s}^{2}},\quad {{k}_{{2n}}}\left( s \right) = \lambda _{n}^{2} + {{s}^{2}} + a{{C}_{{66}}}{{k}^{2}},\quad {{k}_{{q + 2,n}}}\left( s \right) = \sum\limits_{k = 0}^K \frac{{\tau _{q}^{k}}}{{k!}}{{s}^{{k + 1}}} + D_{1}^{{\left( q \right)}}\lambda _{n}^{2},$$

$$\begin{gathered} {{F}_{{1kln}}} = 2{{C}_{{66}}}{{k}^{2}}{{\lambda }_{n}}{{\delta }_{{1k}}}{{\delta }_{{1l}}} + 2{{C}_{{66}}}{{k}^{2}}{{\left( { - 1} \right)}^{{n + 1}}}{{\delta }_{{1k}}}{{\delta }_{{2l}}}, \\ {{F}_{{2kln}}} = - 2a{{C}_{{66}}}{{k}^{2}}{{\delta }_{{1k}}}{{\delta }_{{1l}}} - 2{{\delta }_{{2k}}}{{\delta }_{{1l}}} + 2{{\left( { - 1} \right)}^{{n + 1}}}{{\lambda }_{n}}{{\delta }_{{2k}}}{{\delta }_{{2l}}}, \\ {{F}_{{q + 2,kln}}} = 2\Lambda _{{11}}^{{\left( q \right)}}{{\lambda }_{n}}{{\delta }_{{2k}}}{{\delta }_{{1l}}} - 2\Lambda _{{11}}^{{\left( q \right)}}{{\left( { - 1} \right)}^{{n + 1}}}\lambda _{n}^{2}{{\delta }_{{2k}}}{{\delta }_{{2l}}} \\ \end{gathered} $$

(25)

$$\, + 2{{\left( { - 1} \right)}^{{n + 1}}}{{\delta }_{{q + 2,k}}}{{\delta }_{{2l}}} + 2{{\lambda }_{n}}\left( {D_{1}^{{\left( q \right)}}{{\delta }_{{q + 2,k}}}{{\delta }_{{1l}}} - \Lambda _{{11}}^{{\left( q \right)}}\sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}{{\delta }_{{j + 2,k}}}{{\delta }_{{1l}}}} \right).$$

2. The polynomials ${{P}_{n}}\left( s \right)$, ${{Q}_{{qn}}}\left( s \right)$, and ${{P}_{{jkln}}}\left( s \right)$ for solutions (10) are given by

$$\begin{array}{*{20}{c}} {{{P}_{n}}\left( s \right) = \left[ {{{k}_{{1n}}}\left( s \right){{k}_{{2n}}}\left( s \right) - C_{{66}}^{2}{{k}^{4}}\lambda _{n}^{2}a} \right]{{\Pi }_{n}}\left( s \right) - \lambda _{n}^{4}{{k}_{{1n}}}\left( s \right)\sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}{{\Pi }_{{jn}}}\left( s \right),} \\ {{{Q}_{{qn}}}\left( s \right) = {{k}_{{q + 2,n}}}\left( s \right){{P}_{n}}\left( s \right),\quad {{\Pi }_{n}}\left( s \right) = \prod\limits_{j = 1}^N \,{{k}_{{j + 2,n}}}\left( s \right),\quad {{\Pi }_{{jn}}}\left( s \right) = \prod\limits_{k = 1,k \ne j}^N {\kern 1pt} {{k}_{{k + 2,n}}}\left( s \right);} \end{array}$$

(26)

$$\begin{array}{*{20}{c}} {{{P}_{{111n}}}\left( s \right) = 2{{C}_{{66}}}{{k}^{2}}{{\lambda }_{n}}\left[ {S_{n}^{{\left( 2 \right)}}\left( s \right) - a{{C}_{{66}}}{{k}^{2}}{{\Pi }_{n}}\left( s \right)} \right],} \\ {{{P}_{{121n}}}\left( s \right) = - 2{{C}_{{66}}}{{k}^{2}}{{\lambda }_{n}}S_{n}^{{\left( 1 \right)}}\left( s \right),\quad {{P}_{{1,q + 2,1n}}}\left( s \right) = 2{{C}_{{66}}}{{k}^{2}}\alpha _{1}^{{\left( q \right)}}\lambda _{n}^{3}{{S}_{{qn}}}\left( s \right),} \end{array}$$

(27)

$$\begin{array}{*{20}{c}} {{{P}_{{211n}}}\left( s \right) = 2{{C}_{{66}}}{{k}^{2}}a{{\Pi }_{n}}\left( s \right)\left[ {{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} - {{k}_{{1n}}}\left( s \right)} \right],} \\ {{{P}_{{221n}}}\left( s \right) = - 2{{k}_{{1n}}}\left( s \right)S_{n}^{{\left( 1 \right)}}\left( s \right),\quad {{P}_{{2,q + 2,1n}}}\left( s \right) = 2\lambda _{n}^{2}\alpha _{1}^{{\left( q \right)}}{{k}_{{1n}}}\left( s \right){{S}_{{qn}}}\left( s \right),} \end{array}$$

$$\begin{array}{*{20}{c}} {{{P}_{{q + 2,11n}}}\left( s \right) = 2{{C}_{{66}}}{{k}^{2}}\Lambda _{{11}}^{{\left( q \right)}}\lambda _{n}^{3}a\left[ {{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2} - {{k}_{{1n}}}\left( s \right)} \right]{{\Pi }_{{qn}}}\left( s \right),} \\ {{{P}_{{q + 2,21n}}}\left( s \right) = - 2\Lambda _{{11}}^{{\left( q \right)}}{{k}_{{1n}}}\left( s \right)\lambda _{n}^{3}S_{n}^{{\left( 1 \right)}}\left( s \right),\quad {{P}_{{q + 2,p + 2,1n}}}\left( s \right) = 2\lambda _{n}^{4}{{k}_{{1n}}}\left( s \right)\alpha _{1}^{{\left( p \right)}}\Lambda _{{11}}^{{\left( q \right)}}{{S}_{{qn}}}\left( s \right),} \end{array}$$

$$\begin{array}{*{20}{c}} {{{P}_{{112n}}}\left( s \right) = 2{{C}_{{66}}}{{k}^{2}}{{{\left( { - 1} \right)}}^{{n + 1}}}S_{n}^{{\left( 2 \right)}}\left( s \right),\quad {{P}_{{122n}}}\left( s \right) = 2{{{\left( { - 1} \right)}}^{{n + 1}}}{{C}_{{66}}}{{k}^{2}}\lambda _{n}^{2}S_{n}^{{\left( 1 \right)}}\left( s \right),} \\ {{{P}_{{1,q + 2,2n}}}\left( s \right) = 2{{{\left( { - 1} \right)}}^{{n + 1}}}{{C}_{{66}}}\alpha _{1}^{{\left( q \right)}}{{k}^{2}}\lambda _{n}^{2}{{\Pi }_{{qn}}}\left( s \right),} \end{array}$$

$$\begin{array}{*{20}{c}} {{{P}_{{212n}}}\left( s \right) = 2{{{\left( { - 1} \right)}}^{{n + 1}}}{{a}^{2}}C_{{66}}^{2}{{k}^{4}}{{\lambda }_{n}}{{\Pi }_{n}}\left( s \right),\quad {{P}_{{222n}}}\left( s \right) = 2{{{\left( { - 1} \right)}}^{{n + 1}}}{{\lambda }_{n}}{{k}_{{1n}}}\left( s \right)S_{n}^{{\left( 1 \right)}}\left( s \right),} \\ {{{P}_{{2,q + 2,2n}}}\left( s \right) = 2{{{\left( { - 1} \right)}}^{{n + 1}}}\alpha _{1}^{{\left( q \right)}}{{\lambda }_{n}}{{k}_{{1n}}}\left( s \right){{\Pi }_{{qn}}}\left( s \right),} \end{array}$$

$$\begin{gathered} {{P}_{{q + 2,12n}}}\left( s \right) = 2{{\left( { - 1} \right)}^{{n + 1}}}{{a}^{2}}C_{{66}}^{2}{{k}^{4}}\Lambda _{{11}}^{{\left( q \right)}}\lambda _{n}^{4}{{\Pi }_{n}}\left( s \right),\quad {{P}_{{q + 2,22n}}}\left( s \right) = 2{{\left( { - 1} \right)}^{{n + 1}}}\Lambda _{{11}}^{{\left( q \right)}}\lambda _{n}^{4}{{k}_{{1n}}}\left( s \right)S_{n}^{{\left( 1 \right)}}\left( s \right), \\ {{P}_{{q + 2,p + 2,2n}}}\left( s \right) = 2{{\left( { - 1} \right)}^{{n + 1}}}\alpha _{1}^{{\left( p \right)}}\Lambda _{{11}}^{{\left( q \right)}}\lambda _{n}^{4}{{k}_{{1n}}}\left( s \right){{\Pi }_{{pn}}}\left( s \right), \\ \end{gathered} $$

$$\begin{array}{*{20}{c}} {S_{n}^{{\left( 1 \right)}}\left( s \right) = {{\Pi }_{n}}\left( s \right) - \lambda _{n}^{2}{\kern 1pt} \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}{{\Pi }_{{jn}}}\left( s \right),\quad {{S}_{{qn}}}\left( s \right) = {{\Pi }_{{qn}}}\left( s \right)D_{1}^{{\left( q \right)}} - \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}{{\Pi }_{{jn}}}\left( s \right),} \\ {S_{n}^{{\left( 2 \right)}}\left( s \right) = {{k}_{{2n}}}\left( s \right){{\Pi }_{n}}\left( s \right) - \lambda _{n}^{4}{\kern 1pt} \sum\limits_{j = 1}^N \,\alpha _{1}^{{\left( j \right)}}\Lambda _{{11}}^{{\left( j \right)}}{{\Pi }_{{jn}}}\left( s \right).} \end{array}$$