Skip to main content
SpringerLink
Log in

Well-posedness of difference schemes for semilinear parabolic equations with weak solutions

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

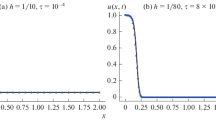
The well-posedness of difference schemes approximating initial-boundary value problem for parabolic equations with a nonlinear power-type source is studied. Simple sufficient conditions on the input data are obtained under which the weak solutions of the differential and difference problems are globally stable for all 0 ⩽ t ⩽ +∞. It is shown that, if the condition fails, the solution can blow up (become infinite) in a finite time. A lower bound for the blow-up time is established. In all the cases, the method of energy inequalities is used as based on the application of the Chaplygin comparison theorem, Bihari-type inequalities, and their difference analogues. A numerical experiment is used to illustrate the theoretical results and verify two-sided blow-up time estimates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. I. Pohozaev, “On the Blow-up of Solutions to Nonlinear Initial-Boundary Value Problems,” Tr. Mat. Inst. im. V.A. Steklova Ross. Akad. Nauk 260, 213–226 (2008) [Proc. Steklov Inst. Math. 260, 204–217 (2008)].

    MathSciNet  Google Scholar 

  2. A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov, and A. P. Mikhailov, Blow-up in Quasilinear Parabolic Equations (Nauka, Moscow, 1987; Walter de Gruyter, Dordrecht, 1995).

    Google Scholar 

  3. E. I. Galakhov, “On the Instantaneous Blow-Up of Solutions of Some Quasilinear Evolution Problems,” Differ. Uravn. 46, 326–335 (2010) [Differ. Equations 46, 329–338 (2010)].

    Google Scholar 

  4. E. Mitidieri and S. I. Pohozaev, “A priori Estimates and Blow-up of Solutions to Partial Differential Equations and Inequalities,” Tr. Mat. Inst. im. V.A. Steklova Ross. Akad. Nauk 234, 3–383 (2001) [Proc. Steklov Inst. Math. 234, 1–362 (2001)].

    Google Scholar 

  5. H. Fujita, On the Blowing up of Solutions to the Cauchy Problem for u t = Δu + u 1 + α, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 13, 109–124 (1966).

    MATH  Google Scholar 

  6. M. Fila, “Blow-Up of Solutions of Semilinear Parabolic Equations,” Spec. Lect. Tohoku Univ., May, 9–12 (2006).

  7. A. G. Sveshnikov, A. B. Al’shin, M. O. Korpusov, and Yu. D. Pletner, Linear and Nonlinear Equations of Sobolev Type (Fizmatlit, Moscow, 2007) [in Russian].

    MATH  Google Scholar 

  8. A. Friedman, “Remarks on Nonlinear Parabolic Equations,” Proc. Symp. Appl. Am. Math. Soc. 13, 2–23 (1965).

    Google Scholar 

  9. S. Kaplan, “On the Growth of Solutions of Quasilinear Parabolic Equations,” Commun. Pure Appl. Math. 16, 305–330 (1963).

    Article  MATH  Google Scholar 

  10. H. Brezis and T. Cazenave, “A Nonlinear Heat Equation with Singular Initial Data,” J. Anal. Math. 68, 277–304 (1996).

    Article  MATH  MathSciNet  Google Scholar 

  11. I. Bihari, “A Generalization of a Lemma of Bellman and Its Application to Uniqueness Problems of Differential Equation,” Acta Math. Acad. Sci. Hungar. 7, 81–94 (1956).

    Article  MATH  MathSciNet  Google Scholar 

  12. M. Pinto, “Integral Inequalities of Bihari-Type and Applications,” Funkcialaj Ekvacioj 33, 387–403 (1990).

    MATH  MathSciNet  Google Scholar 

  13. V. B. Demidovich, “On a Stability Condition for Difference Equations,” Differ. Uravn. 5, 1247–1255 (1969).

    MATH  Google Scholar 

  14. P. Matus, “Stability of Difference Schemes for Nonlinear Time-Dependent Problems,” Comput. Methods Appl. Math. 3, 313–329 (2003).

    MATH  MathSciNet  Google Scholar 

  15. H. A. Levine, “Some Nonexistence and Instability Theorems for Solutions of Formally Parabolic Equations of the Form Pu t = −Au + F(u),” Arch. Ration. Mech. Anal. 51, 371–386 (1973).

    Article  MATH  Google Scholar 

  16. O. A. Ladyzhenskaya, V. A. Solonnikov, and N. N. Ural’tseva, Linear and Quasilinear Equations of Parabolic Type (Nauka, Moscow, 1967; Am. Math. Soc., Providence, R.I., 1968).

    MATH  Google Scholar 

  17. S. A. Chaplygin, “New Method for Approximate Integration of Differential Equations,” Selected Papers: Fluid Dynamics and Mathematics (Nauka, Moscow, 1976), pp. 307–362.

    Google Scholar 

  18. P. N. Vabishchevich, “Two-Level Finite Difference Scheme of Improved Accuracy Order for Time-Dependent Problems of Mathematical Physic,” Zh. Vychisl. Mat. Mat. Fiz. 50, 118–130 (2010) [Comput. Math. Math. Phys. 50, 112–123 (2010)].

    MathSciNet  Google Scholar 

  19. A. A. Samarskii, The Theory of Difference Schemes (Nauka, Moscow, 1977; Marcel Dekker, New York, 2001).

    Google Scholar 

  20. A. A. Samarskii, P. P. Matus, and P. N. Vabishchevich, Difference Schemes with Operator Factors (Kluwer, Boston, 2002).

    MATH  Google Scholar 

  21. R. E. Mickens, “Nonstandard Finite Difference Schemes for Differential Equations,” J. Differ. Equations Appl. 8, 823–847 (2002).

    Article  MATH  MathSciNet  Google Scholar 

  22. Y. Zhou, Application of Discrete Functional Analysis to the Finite Difference Methods (International Acad., Beijing, 1990).

    Google Scholar 

  23. S. I. Pohozaev, “On a priori Estimates and Gradient Catastrophes of Smooth Solutions to Hyperbolic Systems of Conservation Laws,” Tr. Mat. Inst. im. V.A. Steklova Ross. Akad. Nauk 243, 257–288 (2003) [Proc. Steklov Inst. Math. 243, 247–277 (2003)].

    MathSciNet  Google Scholar 

  24. P. Matus, V. Irkhin, and M. Lapinska-Chrzczonowicz, “Exact Difference Schemes for Time-Dependent Problems,” Comput. Methods Appl. Math. 5, 422–448 (2005).

    MATH  MathSciNet  Google Scholar 

  25. B. S. Jovanovič and P. P. Matus, “Coefficient Stability of Second-Order Operator-Differential Equations,” Differ. Uravn. 38, 1371–1377 (2002) [Differ. Equations 38, 1460–1466 (2002)].

    Google Scholar 

  26. P. Matus and A. Kolodynska, “Nonlinear Stability of the Difference Schemes for Equations of Isotropic Gas Dynamics,” Comput. Methods Appl. Math. 8, 155–170 (2008).

    MATH  MathSciNet  Google Scholar 

  27. P. Matus and S. Lemeshevsky, “Stability and Monotonicity of Difference Schemes for Nonlinear Scalar Conservation Laws and Multidimensional Quasi-Linear Parabolic Equations,” Comput. Methods Appl. Math. 9, 253–280 (2009).

    MATH  MathSciNet  Google Scholar 

  28. P. P. Matus and M. M. Chuiko, “Investigation of the Stability and Convergence of Difference Schemes for a Polytropic Gas with Subsonic Flows,” Differ. Uravn. 45, 1053–1064 (2009) [Differ. Equations 45, 1074–1085 (2009)].

    MathSciNet  Google Scholar 

  29. P. P. Matus, G. L. Marcinkiewicz, and M. M. Chuiko, “Stability of Difference Schemes in Terms of Riemann Invariants for a Polytropic Gas,” Zh. Vychisl. Mat. Mat. Fiz. 50, 1078–1091 (2010) [Comput. Math. Math. Phys. 50, 1024–1037 (2010)].

    Google Scholar 

  30. A. A. Samarskii, R. D. Lazarov, and V. L. Makarov, Difference Schemes for Differential Equations with Weak Solutions (Vysshaya Shkola, Moscow, 1987) [in Russian].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, National Academy of Sciences of Belarus, ul. Surganova 11, Minsk, 220072, Belarus

    P. P. Matus

  2. John Paul II Catholic University of Lublin, Al. Raclawickie 14, 20-950, Lublin, Poland

    P. P. Matus

Authors
  1. P. P. Matus
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. P. Matus.

Additional information

Dedicated to Academician A.A. Dorodnicyn on the Occasion of the Centenary of His Birth

Original Russian Text © P.P. Matus, 2010, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2010, Vol. 50, No. 12, pp. 2155–2175.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Matus, P.P. Well-posedness of difference schemes for semilinear parabolic equations with weak solutions. Comput. Math. and Math. Phys. 50, 2044–2063 (2010). https://doi.org/10.1134/S0965542510120079

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542510120079

Keywords

Search

Navigation