Skip to main content
SpringerLink
Log in

Possibility to Describe the Alternating and Nonmonotonic Time Dependence of Poisson’s Ratio during Creep Using a Nonlinear Maxwell-Type Viscoelastoplasticity Model

  • DEFORMATION AND FRACTURE MECHANICS
  • Published:
Russian Metallurgy (Metally) Aims and scope

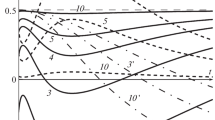
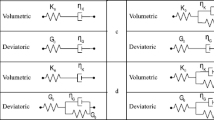Abstract—A physically nonlinear constitutive equation with four arbitrary material functions for isotropic rheonomic materials is studied to determine the rheological effects simulated by it and the spheres of influence of the material functions. The properties of the volumetric, axial, and lateral creep curves generated by this equation and the dependence of the lateral strain coefficient (Poisson’s ratio) on the material functions, time, and stress during creep are analytically investigated. A general exact estimate of the upper and lower bounds of the Poisson’s ratio and criteria of its negativeness, increase, decrease, and constancy are obtained. The Poisson’s ratio of the model is proved not to be a nonmonotonic function of time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.

Similar content being viewed by others

REFERENCES

  1. S. B. Aibinder, E. L. Tyunina, and K. I. Tsirule, Properties of Polymers in Various States of Stress (Khimiya, Moscow, 1981).

    Google Scholar 

  2. A. Ya. Gol’dman, Volumetric Deformation of Plastics (Mashinostroenie, Leningrad, 1984).

    Google Scholar 

  3. R. S. Lakes, Viscoelastic Materials (Cambridge Univ. Press, Cambridge, 2009).

    Book  Google Scholar 

  4. N. W. Tschoegl, W. G. Knauss, and I. Emri, “Poisson’s ratio in linear viscoelasticity–a critical review,” Mech. Time-Dependent Mater. 6 (1), 3–51 (2002).

  5. E. V. Lomakin, “Mechanics of media with the properties dependent on the state of stress,” Fizich. Mezomekh. 10 (5), 41–52 (2007).

  6. D. J. O’Brien, N. R. Sottos, and S. R. White, “Cure-dependent viscoelastic Poisson’s ratio of epoxy,” Exp. Mech. 47, 237–249 (2007).

    Article  Google Scholar 

  7. D. Tscharnuter, M. Jerabek, Z. Major, and R. W. Lang, “Time-dependent Poisson’s ratio of polypropylene compounds for various strain histories,” Mech. Time-Dependent Mater. 15 (1), 15–28 (2011).

    Article  Google Scholar 

  8. V. D. Brekhova, “Poisson’s ratio of some polycrystalline polymers during compression at a constant load,” Mech. Polym., No. 4, 43–46 (1965).

  9. I. Ya. Dzene and A. V. Putans, “Poisson’s ratio during one-dimensional creep of polyethylene,” Mech. Polym., No. 5, 947–949 (1967).

  10. A. S. Savinykh, G. V. Garkushin, S. V. Razorenov, and G. I. Kanel’, “Longitudinal and volumetric compressibility of sodium–lime glass at pressures up to 10 GPa,” 77 (3), 38–42 (2007).

  11. M. E. Kozhevnikova, “Cahnge in the plasticity zone boundary and Poisson’s ratio as a function of plastic softening,” Fizich. Mezomekh. 15 (6), 59–66 (2012).

  12. S. Ozupek and E. B. Becker, “Constitutive equations for solid propellants,” J. Eng. Mater. Techn. 119 (2), 125–132 (1997).

  13. H. Shekhar and A. D. Sahasrabudhe, “Longitudinal strain dependent variation of Poisson’s ratio for HTPB based solidrocket propellants in uniaxial tensile testing,” Propellants Explos. Pyrotechn. 36 (6), 558–563 (2011). https://doi.org/10.1002/preP.200900079

    Article  CAS  Google Scholar 

  14. H. R. Cui, G. J. Tang, and Z. B. Shen, “Study on viscoelastic Poisson’s ratio of solid propellants using digital image correlation method,” Propellants Explos. Pyrotechn. 41 (5), 835–843 (2016).

    Article  CAS  Google Scholar 

  15. I. Ya. Dzene, A. F. Kregers, and U. K. Vilks, “Deformation during creep and repeated creep of polymers during uniaxial tension. Part 1.” Mech. Polym., No. 3, 399–405 (1974).

  16. R. Lakes, “Foam structure with a negative Poisson’s ratio,” Science 235, 1038–1040 (1987).

    Article  CAS  Google Scholar 

  17. E. A. Friis, R. S. Lakes, and J. B. Park, “Negative Poisson’s ratio of polymeric and metallic materials,” J. Mater. Sci. 23, 4406–4414 (1988).

  18. Al. Al. Berlin, L. Rotenburg, and R. Basert, “Deformation of disordered polymer and nonpolymer bodies,” Vysokomol. Soedin., Ser. B 34 (7), 6–32 (1992).

  19. G. W. Milton, “Composite materials with Poisson’s ratios close to –1,” J. Mechan. Phys. Solids 40, 1105–1137 (1992).

    Article  Google Scholar 

  20. R. S. Lakes and K. Elms, “Indentability of conventional and negative Poisson’s ratio foams,” J. Comp. Mater. 27, 1193–1202 (1993).

    Article  Google Scholar 

  21. B. D. Caddock and K. E. Evans, “Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses,” Biomater. 16, 1109–1115 (1995).

    Article  CAS  Google Scholar 

  22. N. Chan and K. E. Evans, “Indentation resilience of conventional and auxetic foams,” J. Cell. Plastics 34, 231–260 (1998).

    Article  Google Scholar 

  23. K. L. Alderson, A. Fitzgerald, and K. E. Evans, “The strain dependent indentation resilience of auxetic microporous polyethylene,” J. Mater. Sci. 35, 4039–4047 (2000).

  24. D. A. Konek, K. V. Voitskhovski, Yu. M. Pleskachevskii, and S. V. Shil’ko, “Negative Poisson’s ratio materials (review),” Mech. Komposit. Mater. Konstr. 10 (1), 35–69 (2004).

  25. A. L. Greer, R. S. Lakes, T. Rouxel, and G. N. Greaves, “Poisson’s ratio and modern materials,” Nature Mater. 10 (11), 823–837 (2011).

    Article  CAS  Google Scholar 

  26. A. C. Fischer-Cripps, Nanoindentation (Springer, New York, 2002).

    Book  Google Scholar 

  27. Yu. I. Golovin, Nanoindentation and Its Possibilities (Mashinostroenie, Moscow, 2009).

    Google Scholar 

  28. A. V. Kokhklov, “Long-term strength curves of a nonlinear Maxwell-type viscoelastoplastic model and the rule of summation of damage during steplike loading,” Vestn. Samar. Tekhn. Univ., Ser. Fiz.-Mat. Nauki, 20 (3), 524–543 (2016). https://doi.org/10.1448/vsgtu1512

  29. A. V. Kokhklov, “Nonlinear Maxwell-type viscoelastoplastic model: properties of a family of relaxation curves and limitations on material functions,” Vestn. MGTU, Ser. Estestv. Nauki, No. 6, 31–55 (2017).https://doi.org/10.18698/1812-3368-2017-6-31-55

    Article  Google Scholar 

  30. A. V. Kokhklov, “Nonlinear Maxwell-type viscoelastoplastic model: simulation of the effect of temperature on deformation, relaxation, and creep curves” Vestn. Samar. Tekhn. Univ., Ser. Fiz.-Mat. Nauki, 21 (1), 160–179 (2017). https://doi.org/10.1448/vsgtu1524

  31. A. V. Kokhklov, “Nonlinear Maxwell-type viscoelastoplastic model: plastic deformation accumulation rate during cyclic loading,” Deform. Razrushenie Mater., No. 7, 7–19 (2017).

  32. A. V. Kokhklov, “Identification of a nonlinear Maxwell-type viscoelastoplastic model using creep curves with at initial stage of loading. Part. 2. Techniques,” Deform. Razrushenie Mater., No. 10, 2–9 (2017).

  33. A. V. Kokhklov, “Identification of a nonlinear Maxwell-type viscoelastoplastic model using loading curves at constant rates,” Deform. Razrushenie Mater., No. 4, 2–10 (2018).

  34. A. V. Kokhklov, “Properties of loading and unloading diagrams generated by a nonlinear Maxwell-type constitutive relation for rheonomic materials,” Vestn. Samar. Tekhn. Univ., Ser. Fiz.-Mat. Nauki, 22 (2), 293–324 (2016). https://doi.org/10.1448/vsgtu1573

  35. Yu. N. Rabotnov, Creep of Structural Members (Nauka, Moscow, 1966).

    Google Scholar 

  36. J. Betten, Creep Mechanics (Springer, Berlin, 2008).

    Google Scholar 

  37. J. S. Bergstrom, Mechanics of Solid Polymers. Theory and Computational Modeling (Elsevier, William Andrew, 2015).

  38. A. M. Lokoshchenko, Creep and Long-Term Strength of Metals (Fizmatlit, Moscow, 2016).

    Google Scholar 

  39. K. A. Padmanabhan, R. A., Vasin, and F. U. Enikeev, Superplastic Flow: Phenomenology and Mechanics (Springer, Berlin, 2001).

    Book  Google Scholar 

  40. V. M. Segal, I. J. Beyerlein, C. N. Tome, V. N. Chuvil’deev, and V. I. Kopylov, Fundamentals and Engineering of Severe Plastic Deformation (Nova Science Publ. Inc., New York, 2010).

    Google Scholar 

Download references

Funding

This work was supported by the Russian Foundation for Basic Research, project no. 17-08-01146_a.

Author information

Authors and Affiliations

  1. Institute of Mechanics, Moscow State University, 119992, Moscow, Russia

    A. V. Khokhlov

Authors
  1. A. V. Khokhlov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. V. Khokhlov.

Additional information

Translated by K. Shakhlevich

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khokhlov, A.V. Possibility to Describe the Alternating and Nonmonotonic Time Dependence of Poisson’s Ratio during Creep Using a Nonlinear Maxwell-Type Viscoelastoplasticity Model. Russ. Metall. 2019, 956–963 (2019). https://doi.org/10.1134/S0036029519100136

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0036029519100136

Keywords:

Search

Navigation