Bremsstrahlung at the Nonresonant Inelastic Scattering of a Photon by an Atomic Ion

The analytical structure, absolute value, and angular anisotropy of the double differential cross section for bremsstrahlung at the nonresonant inelastic scattering of an X-ray photon by a multicharged helium-like atomic ion have been theoretically predicted.

1 INTRODUCTION

Beginning from works by Sommerfeld [1] and Bethe and Heitler [2] to date, the fundamental microcosm effect of bremsstrahlung at the scattering of a free electron in the electric field of an atom (atomic nucleus) is studied within quantum theory (see, e.g., monographs [3, 4] and reviews [5, 6]). In addition to this effect, bremsstrahlung effects induced by the free electron scattering of a photon by an atom (atomic nucleus) are of fundamental interest (e.g., for the physics of laboratory [7] and astrophysical [8] plasma). In this case, the bremsstrahlung probability amplitudes {e.g., the emission of a photon by a continuous spectrum electron (Fig. 1b) [4–6] and the polarization of the atom (atomic nucleus) by the continuous spectrum electron with the subsequent emission of a photon (Fig. 1d) [3]} appear as substructures of the total scattering probability amplitudes. The first such study was performed in our works [9, 10] for the single resonant inelastic scattering [11–13] of a photon by a multielectron atom. In this work, we carry out the first theoretical study of the bremsstrahlung effect induced by single nonresonant inelastic scattering of a photon by a multicharged atomic ion [14–16]. Such studies are necessary, in particular, for the interpretation of background (continuum) structure of X-ray emission spectra of multicharged atomic ions of the hot plasma. For our study, a helium-like silicon atomic ion Si¹²⁺ (the charge number of the nucleus of the ion is Z = 14 and the configuration and term of the ground state are $[0] = 1{{s}^{2}}{{[}^{1}}{{S}_{0}}]$) was chosen because the ground state of the Si¹²⁺ ion is spherically symmetric and this ion is assumingly available in the gas phase for highly precise experiments. In particular, such an experiment can combine the generation of multicharged ions and their capture in a “trap” with the subsequent scattering of radiation of an X-ray free electron laser (XFEL; see, e.g., [17] and review [18]).

Fig. 1.

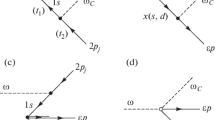
Probability amplitudes of the nonresonant inelastic scattering of the photon by the helium-like silicon atomic ion Si¹²⁺ in the Feynman diagram representation: (a) nonresonant Compton scattering, (b) bremsstrahlung, (c) “time-reverse” scattering, and (d) polarization bremsstrahlung. The right and left arrows mark the electron and vacancy, respectively. The double line indicates a state obtained in the Hartree–Fock field of the 1s vacancy. The wavy line marks the electrostatic interaction. The filled (empty) circle is the interaction vertex in the radiative (contact) transition operator and ω (ω_C) is the incident (scattered) photon. The time direction is from left to right $({{t}_{1}} < {{t}_{2}} < {{t}_{3}})$.

2 THEORY

We consider processes of the nonresonant inelastic scattering of the photon by electrons of the helium-like atomic ion:

$$\omega + [0]{\text{ }} \to 1s\varepsilon l{{(}^{1}}{{L}_{J}}) + {{\omega }_{{\text{C}}}},$$

(1)

$$\omega + [0] \to 1sxp{{(}^{1}}{{P}_{1}}) \to \left\{ {\begin{array}{*{20}{c}} {{{K}_{s}}} \\ {{{K}_{d}}} \end{array}} \right\} + {{\omega }_{{\text{C}}}},$$

(2)

$${{K}_{s}} = 1s\varepsilon s{{(}^{1}}{{S}_{0}}),\quad {{K}_{d}} = 1s\varepsilon d{{(}^{1}}{{D}_{2}}).$$

(3)

Here and below, the atomic system of units is used $(\hbar = e = {{m}_{e}} = 1)$, $l \geqslant 0$, $J = L$, ω (ω_C) is the energy of the incident (scattered) photon, x ϵ [0, ∞) (ε = ω – I_1s – ω_C) is the energy of the continuous-spectrum electron of the intermediate (final) scattering state, and I_1s is the ionization threshold energy of the 1s² shell. Process (1) is nonresonant Compton scattering (Fig. 1a) described by the contact interaction operator

$$\hat {Q} = \frac{1}{{2{{c}^{2}}}}\sum\limits_{n = 1}^N ({{\hat {A}}_{n}} \cdot {{\hat {A}}_{n}}).$$

(4)

Process (2) corresponds to stimulated bremsstrahlung (Fig. 1b) described by the radiative transition operator

$$\hat {R} = - \frac{1}{c}\sum\limits_{n = 1}^N ({{\hat {p}}_{n}} \cdot {{\hat {A}}_{n}}),$$

(5)

where ${{\hat {A}}_{n}}$ is the electromagnetic field operator in the secondary quantization representation, ${{\hat {p}}_{n}}$ is the momentum operator of the nth electron of the ion, c is the speed of light in vacuum, and N is the number of electrons in the ion. In this work, scattering probability amplitudes are constructed in the Tamm–Dancoff approximation [19] with the limit on the number of “particles” (photons, electrons, and vacancies) by limiting Feynman diagrams with the maximum value N₀ = 2. In particular, the probability amplitude of polarization bremsstrahlung (Fig. 1d) with N₀ = 5 is omitted. The probability amplitude of spontaneous production of particles before the absorption of the incident photon (Fig. 1c with N₀ = 4) is neglected in the Tamm–Dancoff approximation. It is noteworthy that the analytical justification of the Tamm–Dancoff approximation and limits of its applicability is an open problem (see, e.g., [20] and references therein). However, the inclusion of the Feynman diagrams only with N₀ ≤ 2 in the Tamm–Dancoff approximation corresponds in our case to quantum mechanical perturbation theory. The truncation of, e.g., Feynman diagrams in Fig. 1d is mathematically justified by a higher order of smallness of this diagram compared to the diagram in Fig. 1b. It can certainly be assumed that the inclusion of the resonant production of the virtual electron and vacancy at the time ${{t}_{2}} < {{t}_{3}}$ (Fig. 1d) will allow the description of the physically significant effect of resonant polarization bremsstrahlung.

Let us determine the analytical structures of the double differential scattering cross sections through channels (1) and (2) using the methods of algebra of creation (annihilation) operators for photons, the theory of irreducible tensor operators, the theory of nonorthogonal orbitals (see, e.g., [20] and references therein), and the approximation of zero natural decay width of the 1s vacancy. Beyond the dipole approximation for the $\hat {Q}$ operator, the cross section for nonresonant Compton scattering (CS; Figs. 1a and 2b) is given by the expression [15]

$$\frac{{{{d}^{2}}{{\sigma }_{{{\text{CS}}}}}}}{{d{{\omega }_{{\text{C}}}}d{{\Omega }_{{\text{C}}}}}} \equiv \sigma _{{{\text{CS}}}}^{{(2)}} = r_{0}^{2}\frac{{{{\omega }_{{\text{C}}}}}}{\omega }\eta \mu C.$$

(6)

Fig. 2.

(Color online) Double differential cross section for the nonresonant inelastic scattering of the photon by the Si¹²⁺ ion for the $\bot$ experimental scheme: (a) bremsstrahlung cross section $({{\rho }^{ \bot }} = 1)$ and (b) nonresonant Compton scattering cross section $({{\mu }^{ \bot }} = 1)$. The scattering angle is θ = 90° and ℏω (ℏω_C) is the energy of the incident (scattered) photon.

Here, Ω_C is the solid emission angle of the scattered photon, r₀ is the classical electron radius, η = 〈1s₀|1s₊〉²/27.21, and

$$C = \sum\limits_{l = 0}^\infty (4l + 2){{\langle 1{{s}_{0}}{\text{|}}{{\hat {j}}_{l}}(qr){\text{|}}\varepsilon {{l}_{ + }}\rangle }^{2}}.$$

(7)

Here, ${{\hat {j}}_{l}}$ is the lth order spherical Bessel function of the first kind; q = |k – k_C|, where k (k_C) is the wave vector of the incident (scattered) photon; and subscripts 0 and + correspond to the radial parts of the wavefunctions of electrons obtained by solving the Hartree–Fock equations for the initial ([0]) and final $([1{{s}_{ + }}])$ states of the ion, respectively. The calculation shows that the l = 1 term makes the dominant contribution to the sum in Eq. (7) for the Si¹²⁺ ion, whereas the contribution from terms with l ≠ 1 is negligibly small. As a result, the quantum interference of channels (1) and (2) is absent. The axisymmetric (with respect to the vector k) parameter μ in Eq. (6) determines, along with the parameter q in the Bessel function ${{\hat {j}}_{l}}$, the angular anisotropy of nonresonant Compton scattering. This parameter is specified in application to three schemes of the proposed experiment. In the first scheme, the polarization vectors of photons are perpendicular to the plane of scattering $(\mathbf{e},{\mathbf{e}_{{\text{C}}}} \bot P)$. In the second scheme, the polarization vectors of photons are parallel to the plane of scattering (e, e_C || P). In the third scheme, unpolarized (NP) photons are used. Here, P is the plane of scattering determined by the vectors k and k_C. As a result,

$${{\mu }^{ \bot }} = 1,$$

(8)

$${{\mu }^{\parallel }} = {{\cos }^{2}}\theta ,$$

(9)

$${{\mu }_{{{\text{NP}}}}} = \frac{1}{2}({{\mu }^{ \bot }} + {{\mu }^{\parallel }}),$$

(10)

where θ is the scattering angle, i.e., the angle between the vectors k and k_C. In the dipole approximation for the $\hat {R}$ operator, the bremsstrahlung cross section (BS; Figs. 1b and 2a) is specified by the formula

$$\sigma _{{{\text{BS}}}}^{{(2)}} = r_{0}^{2}\frac{{{{\omega }_{{\text{C}}}}}}{\omega }\eta \rho B,$$

(11)

where

$$B = \frac{4}{5}\varepsilon {{\left( {1 - \frac{\omega }{{{{\omega }_{{\text{C}}}}}}} \right)}^{2}}{{\langle 1{{s}_{0}}{\text{|}}\hat {r}{\text{|}}\varepsilon {{p}_{ + }}\rangle }^{2}}$$

(12)

and the parameter ρ determines the angular anisotropy of bremsstrahlung and has the form

$${{\rho }^{ \bot }} = 1,$$

(13)

$${{\rho }^{\parallel }} = \frac{1}{3}(1 + 2{{\cos }^{2}}{\kern 1pt} \theta ),$$

(14)

$${{\rho }_{{{\text{NP}}}}} = \frac{1}{2}({{\rho }^{ \bot }} + {{\rho }^{\parallel }}).$$

(15)

The singular single-electron bremsstrahlung probability amplitude was obtained in the form of velocity in the plane wave approximation for radial parts of the wavefunctions of continuous-spectrum electrons: ${\text{|}}x\rangle \cong {{\left( {\frac{2}{{{{\pi }^{2}}x}}} \right)}^{{1/4}}}\sin (r\sqrt {2x} )$ and, as a result,

$$(x - \varepsilon )\langle x{{p}_{ + }}{\text{|}}\hat {r}{\text{|}}\varepsilon {{(s,d)}_{ + }}\rangle \cong i\sqrt {2x} \delta (x - \varepsilon ),$$

(16)

where δ is the Dirac delta function. The analytical structure of the cross section given by Eq. (11) qualitatively reproduces the following known results. First, in the approximation of zero natural decay width of the 1s vacancy, the “infrared divergence” of the bremsstrahlung cross section appears at zero energy of the scattered photon [11, 12]:

$$\mathop {\lim }\limits_{{{\omega }_{{\text{C}}}} \to 0} \sigma _{{{\text{BS}}}}^{{(2)}} = \infty .$$

(17)

Second, at zero energy of the continuous-spectrum electron in the final state (Fig. 2a; the ω_C = ω – I_1s straight line on the (ω, ω_C) plane),

$$\mathop {\lim }\limits_{\varepsilon \to 0} \sigma _{{{\text{BS}}}}^{{(2)}} = 0.$$

(18)

This equality corresponds to the Born approximation for the differential cross section for bremsstrahlung by the nonrelativistic electron in the Coulomb field of the nucleus [21, 22]:

$$\frac{{d\sigma }}{{d{{\omega }_{{\text{C}}}}}} \sim \ln \left( {\frac{{{{v}_{1}} + {{v}_{2}}}}{{{{v}_{2}} - {{v}_{1}}}}} \right) \to 0$$

(19)

at ${{v}_{2}} \to 0$, where ${{v}_{1}}({{v}_{2}})$ is the velocity of the incident (scattered) electron. As expected, the cross section given by Eq. (11) satisfies not only Eqs. (17) and (18) but also the asymptotic condition: the single-electron transition probability amplitude in the limit $\omega \to \infty$ is $\langle 1{{s}_{0}}{\text{|}}r{\text{|}}\varepsilon {{p}_{ + }}\rangle \sim {{\omega }^{{ - 7/4}}}$ and, as a result,

$$\mathop {\lim }\limits_{\omega \to \infty } \sigma _{{{\text{BS}}}}^{{(2)}} = 0.$$

(20)

3 RESULTS AND DISCUSSION

The results of the calculation are presented in Figs. 2 and 3. The value I_1s = 2437.650 eV [23] was accepted for the ionization energy threshold of the 1s² shell of the Si¹²⁺ ion. The energy of the incident photon ω was considered in the range of 4.5–15.0 keV, where the criterion of applicability of the dipole approximation for the $\hat {R}$ operator ${{\lambda }_{\omega }}{\text{/}}\langle {{r}_{{1s}}}\rangle \gg 1$ for the calculation of the bremsstrahlung cross section is satisfied, e.g., at the wavelength of the incident photon ${{\lambda }_{\omega }} = 1.852{\kern 1pt}$ Å ($\omega = 6.70{\kern 1pt}$ keV; the energy of the $K\alpha$ emission line of Fe²⁴⁺ [24]) and the average radius $\langle {{r}_{{1s}}}\rangle = 0.058$ Å of the 1s shell of the Si¹²⁺ ion.

Fig. 3.

(Color online) Indicatrix of bremsstrahlung for the Si¹²⁺ ion with the polar radius $\sigma _{{{\text{BS}}}}^{{(2)}}$ and the polar angle θ at the energies ℏω = 6.70 keV and ℏω_C = 2.88 keV of the incident and scattered photons, respectively, in the (green solid line) $\bot$, (blue dash-dotted line) ||, and (red dotted line) unpolarized-photon experimental schemes.

The results in Fig. 2a demonstrate that the bremsstrahlung cross section tends to infrared divergence (17) and to the satisfaction of the asymptotic condi-tion (20) and that it makes the leading contribution to the total scattering cross section in the near superthreshold region (${{I}_{{1s}}} < \omega < 15{\kern 1pt}$ keV). The cross section for nonresonant Compton scattering becomes leading at $\omega \geqslant 15{\kern 1pt}$ keV (Fig. 2b). However, we note that the cross section for nonresonant Compton scattering in the || scheme of the experiment vanishes at the scattering angle θ = 90° (${{\mu }^{\parallel }} = 0 \Rightarrow \sigma _{{CS}}^{{(2)}} = 0$) and the total scattering cross section is determined only by bremsstrahlung (ρ^|| = 1/3). The results in Fig. 3 demonstrate angular anisotropy (predominant scattering in the directions θ = 0° and 180°) of bremsstrahlung in the || scheme of the experiment and the experiment with unpolarized photons. This result qualitatively reproduces the result obtained in [10] for resonant inelastic scattering of the photon by the multielectron atom. It is noteworthy that the ${{K}_{s}}$ and ${{K}_{d}}$ scattering states in Eq. (3) make comparable contributions to the total scattering cross section. If the ${{K}_{d}}$ state is di-sregarded, the bremsstrahlung cross section in the || scheme of the experiment vanishes at the scattering angle θ = 90°.

4 CONCLUSIONS

The double differential cross section for the nonresonant inelastic scattering of an X-ray photon by a multicharged helium-like atomic ion has been theoretically studied. We have established (i) the leading role of bremsstrahlung in the near superthreshold scattering region and (ii) the pronounced angular anisotropy of bremsstrahlung in the corresponding schemes of the expected experiment. The results are predictive. Their possible generalization, e.g., to other multicharged ions and multielectron atoms, inclusion of next orders of the Tamm–Dancoff approximation, and allowance for a nonzero spectral width resolution of the XFEL experiment (${{\Gamma }_{{{\text{beam}}}}} \cong 0.15{-} 0.50$ eV [25]) will be studied in the future.