Skip to main content
SpringerLink
Log in

Computing hyperbolic choreographies

  • Published:
Regular and Chaotic Dynamics Aims and scope Submit manuscript

Abstract

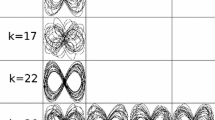
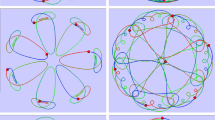
An algorithm is presented for numerical computation of choreographies in spaces of constant negative curvature in a hyperbolic cotangent potential, extending the ideas given in a companion paper [14] for computing choreographies in the plane in a Newtonian potential and on a sphere in a cotangent potential. Following an idea of Diacu, Pérez-Chavela and Reyes Victoria [9], we apply stereographic projection and study the problem in the Poincaré disk. Using approximation by trigonometric polynomials and optimization methods with exact gradient and exact Hessian matrix, we find new choreographies, hyperbolic analogues of the ones presented in [14]. The algorithm proceeds in two phases: first BFGS quasi-Newton iteration to get close to a solution, then Newton iteration for high accuracy.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Borisov, A.V. and Mamaev, I.S., The Restricted Two-Body Problem in Constant Curvature Spaces, Celestial Mech. Dynam. Astronom., 2006, vol. 96, no. 1, pp. 1–17.

    Article  MathSciNet  MATH  Google Scholar 

  2. Borisov, A.V. and Mamaev, I.S., Relations between Integrable Systems in Plane and Curved Spaces, Celestial Mech. Dynam. Astronom., 2007, vol. 99, no. 4, pp. 253–260.

    Article  MathSciNet  MATH  Google Scholar 

  3. Borisov, A.V., Mamaev, I.S., and Kilin, A.A., Two-Body Problem on a Sphere: Reduction, Stochasticity, Periodic Orbits, Regul. Chaotic Dyn., 2004, vol. 9, no. 3, pp. 265–279.

    Article  MathSciNet  MATH  Google Scholar 

  4. Cariñena, J.F., Rañada, M.F., and Santander, M., Central Potentials on Spaces of Constant Curvature: The Kepler Problem on the Two-Dimensional Sphere S 2 and the Hyperbolic Plane H 2, J. Math. Phys., 2005, vol. 46, no. 5, 052702, 25 pp.

    Article  MathSciNet  MATH  Google Scholar 

  5. Chernoivan, V.A. and Mamaev, I.S., The Restricted Two-Body Problem and the Kepler Problem in the Constant Curvature Spaces, Regul. Chaotic Dyn., 1999, vol. 4, no. 2, pp. 112–124.

    Article  MathSciNet  MATH  Google Scholar 

  6. Diacu, F., Relative Equilibria of the Curved N-Body Problem, Atlantis Studies in Dynamical Systems, vol. 1, Paris: Atlantis, 2012.

    Book  Google Scholar 

  7. Diacu, F., Martínez, R., Pérez-Chavala, E., and Simó, C., On the Stability of Tetrahedral Relative Equilibria in the Positively Curved 4-Body Problem, Phys. D, 2013, vol. 256/257, pp. 21–35.

    Article  MathSciNet  MATH  Google Scholar 

  8. Diacu, F. and Pérez-Chavala, E., Homographic Solutions of the Curved 3-Body Problem, J. Differential Equations, 2011, vol. 250, no. 1, pp. 340–366.

    Article  MathSciNet  MATH  Google Scholar 

  9. Diacu, F., Pérez-Chavala, E., and Reyes Victoria, J.G., An Intrinsic Approach in the Curved n-Body Problem: The Negative Curvature Case, J. Differential Equations, 2012, vol. 252, no. 8, pp. 4529–4562.

    Article  MathSciNet  MATH  Google Scholar 

  10. Diacu, F., Pérez-Chavala, E., and Santoprete, M., The n-Body Problem in Spaces of Constant Curvature: Part 1. Relative Equilibria, J. Nonlinear Sci., 2012, vol. 22, no. 2, pp. 247–266.

    Article  MathSciNet  MATH  Google Scholar 

  11. Diacu, F., Pérez-Chavala, E., and Santoprete, M., The n-Body Problem in Spaces of Constant Curvature: Part 2. Singularities, J. Nonlinear Sci., 2012, vol. 22, no. 2, pp. 267–275.

    Article  MathSciNet  MATH  Google Scholar 

  12. Chebfun Guide, T.A. Driscoll, N. Hale, and L.N. Trefethen (Eds.), Oxford: Pafnuty, 2014; see also: www.chebfun.org

  13. Kilin, A.A., Libration Points in Spaces S 2 and L 2, Regul. Chaotic Dyn., 1999, vol. 4, no. 1, pp. 91–103.

    Article  MathSciNet  MATH  Google Scholar 

  14. Montanelli, H. and Gushterov, N.I., Computing Planar and Spherical Choreographies, SIAM J. Appl. Dyn. Syst., 2016, vol. 15, no. 1, pp. 235–256.

    Article  MathSciNet  MATH  Google Scholar 

  15. Newton, P.K., The N-Vortex Problem: Analytical Techniques, Appl. Math. Sci., vol. 145, New York: Springer, 2001.

    Google Scholar 

  16. Pérez-Chavela, E. and Reyes Victoria, J.G., An Intrinsic Approach in the Curved n-Body Problem: The Positive Curvature Case, Trans. Amer. Math. Soc., 2012, vol. 364, no. 7, pp. 3805–3827.

    Article  MathSciNet  MATH  Google Scholar 

  17. Shchepetilov, A.V., Calculus and Mechanics on Two-Point Homogeneous Riemannian Spaces, Lect. Notes Phys., vol. 707, Berlin: Springer, 2006.

    Google Scholar 

  18. Simó, C., New Families of Solutions in N-Body Problems, in Proc. of the 3rd European Congress of Mathematics (Barcelona, 2000): Vol. 1, Progr. Math., vol. 201, Basel: Birkhäuser, 2001, pp. 101–115.

    Google Scholar 

  19. Trefethen, L.N. and Weideman, J.A.C., The Exponentially Convergent Trapezoidal Rule, SIAM Rev., 2014, vol. 56, no. 3, pp. 385–458.

    Article  MathSciNet  MATH  Google Scholar 

  20. Wright, G.B., Javed, M., Montanelli, H., and Trefethen, L.N., Extension of Chebfun to Periodic Functions, SIAM J. Sci. Comput., 2015, vol. 37, no. 5, C554–C573.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Oxford University Mathematical Institute, Oxford, OX2 6GG, UK

    Hadrien Montanelli

Authors
  1. Hadrien Montanelli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hadrien Montanelli.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Montanelli, H. Computing hyperbolic choreographies. Regul. Chaot. Dyn. 21, 522–530 (2016). https://doi.org/10.1134/S1560354716050038

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1560354716050038

Keywords

MSC2010 numbers

Search

Navigation