Abstract
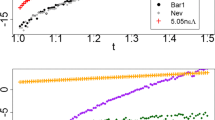
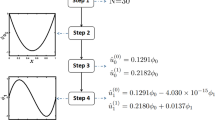
The Seidel method for solving a system of linear algebraic equations and an estimate of its convergence rate are considered. It is proposed to change the order of equations. It is shown that the method described in Faddeevs’ book Computational Methods of Linear Algebra can deteriorate the convergence rate estimate rather than improve it. An algorithm for establishing the optimal order of equations is proposed, and its validity is proved. It is shown that the computational complexity of the reordering is 2n 2 additions and (12)n 2 divisions. Numerical results for random matrices of order 100 are presented that confirm the proposed improvement.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
D. K. Faddeev and V. N. Faddeeva, Computational Methods of Linear Algebra (Lan’, St. Petersburg, 2002; Freeman, San Francisco, 1963).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © A.N. Borzykh, 2017, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2017, Vol. 57, No. 1, pp. 3–8.
Rights and permissions
About this article
Cite this article
Borzykh, A.N. Improving an estimate of the convergence rate of the seidel method by selecting the optimal order of equations in the system of linear algebraic equations. Comput. Math. and Math. Phys. 57, 1–6 (2017). https://doi.org/10.1134/S0965542517010055
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0965542517010055