Abstract
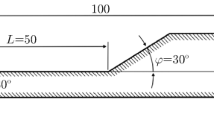
A theory of unsteady separation in inviscid supersonic flow around a convex corner is developed. Within the framework of the hypothesis suggested the mechanism of separationless-to-separated flow transition is explained and the forces leading to flow separation are determined as functions of the angle θ and the oncoming flow velocity. The values of the angle θ k at which the flow is separated from the corner vertex and the stall angle θ s determining the separated flow direction obtained previously in experiments and by numerical simulation are confirmed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M.J. Lighthill, “The Diffraction of a Blast. 1,” Proc. Roy. Soc., London. Ser. A, 198, No. 1055, 454 (1949).
R. Hillier, “Computation of Shock Wave Diffraction at a Ninety Degrees Convex Edge,” Shock Waves, 1. No. 2, 89 (1991).
R.Ya. Tugazakov, “Investigation of the Problem of the Decay of an Arbitrary Two-Dimensional Discontinuity,” Fluid Dynamics 24, 296 (1989).
D.M. Jones, P.M. Martin, and C.K. Thornhill, “A Note on the Pseudostationary Flow behind a Strong Shock Diffracted or Reflected at a Corner,” Proc. Roy. Soc. London., Ser. A, 209, No. 1097, 238 (1951).
T.V. Bazhenova and L.G. Gvozdeva, Unsteady Interactions of Shock Waves [in Russian], Nauka, Moscow (1977).
T.V. Bazhenova, S.B. Bazarov, O.V. Bulat, V.V. Golub, and A.M. Schul'meister, “Experimental and Numerical Study of Shock Wave Attenuation at the Outlet of Two-Dimensional and Axisymmetric Ducts,” Fluid Dynamics 28, 590 (1993).
G.A. Tarnavskii, V.N. Khonichev, and V.I. Yakovlev, “Shock Wave Diffraction at a Right Angle and at a Plane Channel Exit,” Izv. Sib. Otd. Akad. Nauk SSSR. Ser. Tekhn. Nauk, Issue 2, No. 8, 56 (1974).
J.A. Ekaterinaris, “Compressible Studies on Dynamic Stall,” AIAA Paper, No. 0024 (1989).
L.E. Ericson and H.H. King, “Rapid Prediction of High-AlphaUnsteadyAerodynamics of Slender-WingAircraft,” J. Aircraft, 29, 85 (1992).
N.E. Kochin, “On the Theory of Discontinuities in Fluids,” in: N.E. Kochin, Selected Works. Vol. 2 [in Russian], Moscow & Leningrad (1949), p. 5.
L.D. Landau and E.M. Lifshitz, Fluid Dynamics, Pergamon, London (1959).
G.G. Chernyi, Gas Dynamics [in Russian], Nauka, Moscow (1988).
R.Ya. Tugazakov and A.S. Fonarev, “Initial Stage of the Collision of BlastWaves,” Fluid Dynamics 6, 755 (1971).
R.Ya. Tugazakov, “Study of Gasdynamic Discontinuity Shedding from a Plate Edge within the Framework of the Euler Equations,” Uch. Zap. TsAGI, 18, No. 1, 9 (1987).
Additional information
Original Russian Text © R.Ya. Tugazakov, 2007, published in Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, 2007, Vol. 42, No. 3, pp. 169–179.
Rights and permissions
About this article
Cite this article
Tugazakov, R.Y. Theory of unsteady separation in supersonic flow around a convex corner. Fluid Dyn 42, 485–494 (2007). https://doi.org/10.1134/S0015462807030167
Received:
Issue Date:
DOI: https://doi.org/10.1134/S0015462807030167