Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T20:46:32.730Z Has data issue: false hasContentIssue false
  • English
  • Français

The essential skeleton of a product of degenerations

Part of: Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  13 June 2019

Morgan V. Brown  and
Enrica Mazzon
Morgan V. Brown
Affiliation:
Department of Mathematics, University of Miami, 1365 Memorial Drive, Ungar 515, Coral Gables, FL 33146, USA email mvbrown@math.miami.edu
Enrica Mazzon
Affiliation:
Department of Mathematics, Imperial College London, 180 Queen’s Gate, London SW7 2AZ, UK email e.mazzon15@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the problem of how the dual complex of the special fiber of a strict normal crossings degeneration 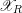$\mathscr{X}_{R}$ changes under products. We view the dual complex as a skeleton inside the Berkovich space associated to 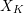$X_{K}$. Using the Kato fan, we define a skeleton 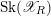$\text{Sk}(\mathscr{X}_{R})$ when the model 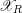$\mathscr{X}_{R}$ is log-regular. We show that if 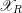$\mathscr{X}_{R}$ and 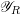$\mathscr{Y}_{R}$ are log-smooth, and at least one is semistable, then 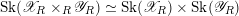$\text{Sk}(\mathscr{X}_{R}\times _{R}\mathscr{Y}_{R})\simeq \text{Sk}(\mathscr{X}_{R})\times \text{Sk}(\mathscr{Y}_{R})$. The essential skeleton 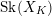$\text{Sk}(X_{K})$, defined by Mustaţă and Nicaise, is a birational invariant of 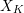$X_{K}$ and is independent of the choice of 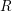$R$-model. We extend their definition to pairs, and show that if both 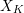$X_{K}$ and 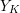$Y_{K}$ admit semistable models, 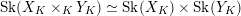$\text{Sk}(X_{K}\times _{K}Y_{K})\simeq \text{Sk}(X_{K})\times \text{Sk}(Y_{K})$. As an application, we compute the homeomorphism type of the dual complex of some degenerations of hyper-Kähler varieties. We consider both the case of the Hilbert scheme of a semistable degeneration of K3 surfaces, and the generalized Kummer construction applied to a semistable degeneration of abelian surfaces. In both cases we find that the dual complex of the 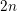$2n$-dimensional degeneration is homeomorphic to a point, $n$-simplex, or 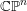$\mathbb{C}\mathbb{P}^{n}$, depending on the type of the degeneration.

Keywords

Berkovich spacesdual complexKato fan

MSC classification

Primary: 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 7 , July 2019 , pp. 1259 - 1300
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramovich, D., Chen, Q., Marcus, S., Ulirsch, M. and Wise, J., Skeletons and fans of logarithmic structures , in Nonarchimedean and tropical geometry, Simons Symposia, eds Baker, M. and Payne, S. (Springer, Cham, 2016).Google Scholar
Alexeev, V., Moduli spaces M g, n(W) for surfaces , in Higher-dimensional complex varieties (Trento, 1994) (de Gruyter, Berlin, 1996), 1–22.Google Scholar
Beauville, A., Variétés Kähleriennes dont la première classe de Chern est nulle , J. Differential Geom. 18 (1983), 755–782.10.4310/jdg/1214438181Google Scholar
Berkovich, V. G., Spectral theory and analytic geometry over non-Archimedean fields, Mathematical Surveys and Monographs, vol. 33 (American Mathematical Society, Providence, RI, 1990).Google Scholar
Berkovich, V. G., The automorphism group of the Drinfeld half-plane , C. R. Acad. Sci. Paris Sér. I Math. 321 (1995), 1127–1132.Google Scholar
Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type , J. Amer. Math. Soc. 23 (2010), 405–468.10.1090/S0894-0347-09-00649-3Google Scholar
Bouchiba, S. and Kabbaj, S., Tensor products of Cohen-Macaulay rings: solution to a problem of Grothendieck , J. Algebra 252 (2002), 65–73.10.1016/S0021-8693(02)00019-4Google Scholar
Bultot, E., Motivic integration and logarithmic geometry, Preprint (2015), arXiv:1505.05688 [math.AG].Google Scholar
de Fernex, T., Kollár, J. and Xu, C., The dual complex of singularities , in Higher dimensional algebraic geometry, in honour of Professor Yujiro Kawamata’s 60th birthday, Advanced Studies in Pure Mathematics, vol. 74 (Mathematical Society of Japan, 2017), 103–130.10.2969/aspm/07410103Google Scholar
Fogarty, J., Algebraic families on an algebraic surface , Amer. J. Math. 90 (1968), 511–521.10.2307/2373541Google Scholar
Friedman, R. and Morrison, D. R., The birational geometry of degenerations: an overview , in The birational geometry of degenerations, Progress in Mathematics, vol. 29 (Birkhäuser, Boston, MA, 1983), 1–32.Google Scholar
Fulton, W., Introduction to toric varieties, The William H. Roever Lectures in Geometry, vol. 131 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
Gabber, O. and Ramero, L., Foundations for almost ring theory – release 6.95, Preprint (2004), arXiv:math/0409584.10.1007/b10047Google Scholar
Gubler, W., Rabinoff, J. and Werner, A., Skeletons and tropicalizations , Adv. Math. 294 (2016), 150–215.10.1016/j.aim.2016.02.022Google Scholar
Gulbrandsen, M. G., Halle, L. H. and Hulek, K., A relative Hilbert-Mumford criterion , Manuscripta Math. 148 (2015), 283–301.10.1007/s00229-015-0744-8Google Scholar
Gulbrandsen, M. G., Halle, L. H. and Hulek, K., A GIT construction of degenerations of Hilbert schemes of points, Doc. Math., to appear. Preprint (2016), arXiv:1604.00215 [math.AG].Google Scholar
Gulbrandsen, M. G., Halle, L. H., Hulek, K. and Zhang, Z., The geometry of degenerations of Hilbert schemes of points, Preprint (2018), arXiv:1802.00622 [math.AG].Google Scholar
Hacon, C. D., McKernan, J. and Xu, C., Boundedness of varieties of log general type , in Algebraic geometry: Salt Lake City 2015, Proceedings of Symposia in Pure Mathematics, vol. 97 (American Mathematical Society, Providence, RI, 2018), 309–348.10.1090/pspum/097.1/01677Google Scholar
Halle, L. H. and Nicaise, J., Motivic zeta functions of degenerating Calabi-Yau varieties , Math. Ann. 370 (2017), 1277–1320.10.1007/s00208-017-1578-3Google Scholar
Harris, J. and Morrison, I., Moduli of curves, Graduate Texts in Mathematics, vol. 187 (Springer, New York, 1998).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).10.1007/978-1-4757-3849-0Google Scholar
Hatcher, A., Algebraic topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Hwang, J.-M., Base manifolds for fibrations of projective irreducible symplectic manifolds , Invent. Math. 174 (2008), 625–644.10.1007/s00222-008-0143-9Google Scholar
Kato, K., Logarithmic structures of Fontaine-Illusie , in Algebraic analysis, geometry, and number theory (Baltimore, MD, 1988) (Johns Hopkins University Press, Baltimore, MD, 1989), 191–224.Google Scholar
Kato, K., Toric singularities , Amer. J. Math. 116 (1994), 1073–1099.10.2307/2374941Google Scholar
Kempf, G., Knudsen, F. F., Mumford, D. and Saint-Donat, B., Toroidal embeddings. I (Springer, Berlin, 1973).10.1007/BFb0070318Google Scholar
Kollár, J., Laza, R., Saccà, G. and Voisin, C., Remarks on degenerations of hyper-Kähler manifolds, Ann. Inst. Fourier, to appear. Preprint (2017), arXiv:1704.02731 [math.AG].10.5802/aif.3228Google Scholar
Kollár, J. and Mori, S., Birational geometry of algebraic varieties (Cambridge University Press, Cambridge, 2008).Google Scholar
Kollár, J., Nicaise, J. and Xu, C., Semi-stable extensions over 1-dimensional bases , Acta Math. Sin. (Engl. Ser.) (2017).Google Scholar
Kollár, J. and Shepherd-Barron, N. I., Threefolds and deformations of surface singularities , Invent. Math. 91 (1988), 299–338.10.1007/BF01389370Google Scholar
Kollár, J. and Xu, C., The dual complex of Calabi–Yau pairs , Invent. Math. 205 (2016), 527–557.10.1007/s00222-015-0640-6Google Scholar
Kontsevich, M. and Soibelman, Y., Homological mirror symmetry and torus fibrations , in Symplectic geometry and mirror symmetry (Seoul, 2000) (World Scientific, River Edge, NJ, 2001), 203–263.10.1142/9789812799821_0007Google Scholar
Kontsevich, M. and Soibelman, Y., Affine structures and non-Archimedean analytic spaces , in The unity of mathematics: in honor of the ninetieth birthday of I.M. Gelfand, eds Etingof, P., Retakh, V. and Singer, I. M. (Birkhäuser, Boston, MA, 2006), 321–385.Google Scholar
Kulikov, V. S., Degenerations of K3 surfaces and Enriques surfaces , Math. USSR-Izv. 11 (1977), 957–989.10.1070/IM1977v011n05ABEH001753Google Scholar
Li, J., Stable morphisms to singular schemes and relative stable morphisms , J. Differential Geom. 57 (2001), 509–578.10.4310/jdg/1090348132Google Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Vol. 6 (Oxford University Press, Oxford, 2002); translated from the French by Reinie Erné.Google Scholar
Looijenga, E., Root systems and elliptic curves , Invent. Math. 38 (1976/77), 17–32.10.1007/BF01390167Google Scholar
Morton, H. R., Symmetric products of the circle , Proc. Cambridge Philos. Soc. 63 (1967), 349–352.10.1017/S0305004100041256Google Scholar
Mustaţă, M. and Nicaise, J., Weight functions on non-Archimedean analytic spaces and the Kontsevich–Soibelman skeleton , Algebr. Geom. 2 (2015), 365–404.10.14231/AG-2015-016Google Scholar
Nicaise, J. and Xu, C., The essential skeleton of a degeneration of algebraic varieties , Amer. J. Math. 138 (2016), 1645–1667.10.1353/ajm.2016.0049Google Scholar
Nizioł, W., Toric singularities: log-blow-ups and global resolutions , J. Algebraic Geom. 15 (2006), 1–29.10.1090/S1056-3911-05-00409-1Google Scholar
Nowak, K. J., Flat morphisms between regular varieties , Univ. Iagel. Acta Math. 35 (1997), 243–246.Google Scholar
O’Grady, K. G., Desingularized moduli spaces of sheaves on a K3 , J. Reine Angew. Math. 512 (1999), 49–117.Google Scholar
O’Grady, K. G., A new six-dimensional irreducible symplectic variety , J. Algebraic Geom. 12 (2003), 435–505.10.1090/S1056-3911-03-00323-0Google Scholar
Persson, U. and Pinkham, H., Degeneration of surfaces with trivial canonical bundle , Ann. of Math. (2) 113 (1981), 45–66.10.2307/1971133Google Scholar
Saito, T., Log smooth extension of a family of curves and semi-stable reduction , J. Algebraic Geom. 13 (2004), 287–321.10.1090/S1056-3911-03-00338-2Google Scholar
Strominger, A., Yau, S.-T. and Zaslow, E., Mirror symmetry is T-duality , Nuclear Phys. B 479 (1996), 243–259.10.1016/0550-3213(96)00434-8Google Scholar
Temkin, M., Metrization of differential pluriforms on Berkovich analytic spaces , in Nonarchimedean and tropical geometry, Simons Symposia, eds Baker, M. and Payne, S. (Springer, Cham, 2016), 195–285.10.1007/978-3-319-30945-3_8Google Scholar
Thuillier, A., Géométrie toroïdale et géométrie analytique non archimédienne. Application au type d’homotopie de certains schémas formels , Manuscripta Math. 123 (2007), 381–451.10.1007/s00229-007-0094-2Google Scholar
Ulirsch, M., Functorial tropicalization of logarithmic schemes: the case of constant coefficients , Proc. Lond. Math. Soc. 114 (2017), 1081–1113.10.1112/plms.12031Google Scholar
Ulirsch, M., Non-Archimedean geometry of Artin fans , Adv. Math. 345 (2019), 346–381.10.1016/j.aim.2019.01.008Google Scholar
Vidal, I., Monodromie locale et fonctions zeta des log schémas , in Geometric aspects of Dwork theory. Vols I, II, eds Adolphson, A., Baldassarri, F., Berthelot, P., Katz, N. and Loeser, F. (Walter de Gruyter, Berlin, 2004), 983–1038.Google Scholar