Search
Close
Search
Advanced Search
Search Menu

Abstract

We have developed a universal approach to compute accurately the brightness of eclipsing binary systems during the transit of a planet in front of the stellar disc. This approach is uniform for all values of the system parameters and applicable to most limb-darkening laws used in astrophysics. In the cases of the linear and quadratic limb-darkening laws, we obtained analytical expressions for the light curve and its derivatives in terms of elementary functions, elliptic integrals and a piecewise-defined function of one variable. In the cases of the logarithmic and square-root laws of limb darkening, the flux and its derivatives were expressed in terms of integrals which can be efficiently computed using the Gaussian quadrature formula, taking into account singularities of the integrand.

methods: analytical, methods: numerical, eclipses, binaries: eclipsing

1 INTRODUCTION

Recently several authors have developed algorithms for the calculation of transit light curves (see e.g. Mandel & Agol 2002; Pal 2008; 2012). However, the problem of the calculation of the light curves is still relevant, because the existing algorithms are not applicable to all values of the system parameters for some limb-darkening laws. Besides, they do not allow sufficiently accurate calculations of the light curves for some limb-darkening laws. In addition, calculations of derivatives of the light curve as a function of system parameters are important, because they can be used to solve the inverse problem of interpretation of the light curve.

The paper Mandel & Agol (2002) contains an analytical expression of the light curve by elliptic integrals, for the cases of the linear and quadratic limb-darkening laws. In doing so, 13 variants of relations between the parameters are considered. For other limb-darkening laws (law of square root and its power) only an approximate method of light-curve calculation at the radius of the planet more than 10 times smaller than the radius of the star is being used. In this case, the accuracy is 2 per cent of the depth of the eclipse. In the paper Pal (2012), directly, there is only an expression of the light curve in the linear and quadratic limb-darkening laws, and the derivatives of the light curve are calculated by difference methods which is less favourable in terms of the time and accuracy of the computation. (This work contains no direct analytical expressions for the derivatives.) In addition, none of the above works considered the logarithmic law of darkening, which is most preferred for early-type stars (Klinglesmith & Sobieski 1970; Van Hamme 1993).

The approach presented in this paper allows us to calculate a light curve and with almost machine accuracy for any values of the parameters (including near singularities). Binary system parameters are the radii of the components and the distance between the centres of the components in the projection on the picture plane. In general, the algorithm is uniform for all values of the system parameters, which significantly facilitates its implementation. We obtained analytical expressions for the transit light curve of the eclipsing binary system and for its derivatives in the cases of the linear and quadratic limb-darkening laws. These quantities are expressed in terms of a piecewise-defined function of one variable and incomplete elliptic integrals, which can be computed with methods proposed by Carlson (1995). In the cases of the logarithmic limb-darkening law and the square-root limb-darkening law, the light function is expressed through integrals that can be efficiently computed using the Gaussian quadrature formula. In this respect, the computation time of the light curve is not much more than the computation time by analytical expressions.

2 MODEL DESCRIPTION

We considered the model of the eclipse of a spherically symmetric star with a thin atmosphere by another spherical opaque component (the other spherical star or a spherical planet).

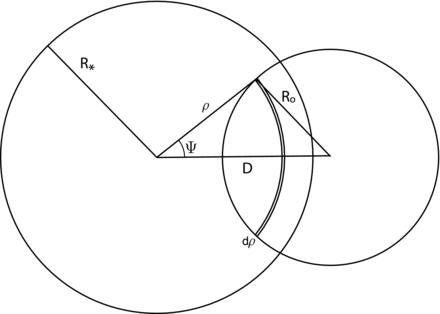
Fig. 1 shows the geometry of the stellar disc in an eclipse.

Figure 1.
A model of the eclipsing binary system. The projection is on the picture plane. Here the smaller component is a star or an exoplanet. The geometry of stellar discs in an eclipse. Here R* is the radius of the eclipsed star, Ro is the radius of the eclipsing component, $\displaystyle {D}$ is the distance between the centres of the discs of the components, and ρ and Ψ are, respectively, the polar radius and the polar angle of a point on the disc of the eclipsed star. The origin is located at the centre of the eclipsed star and the polar angle is measured counterclockwise from the radius vector connecting centres of the star and the transiting component.
Open in new tabDownload slide

A model of the eclipsing binary system. The projection is on the picture plane. Here the smaller component is a star or an exoplanet. The geometry of stellar discs in an eclipse. Here R* is the radius of the eclipsed star, Ro is the radius of the eclipsing component, |$\displaystyle {D}$| is the distance between the centres of the discs of the components, and ρ and Ψ are, respectively, the polar radius and the polar angle of a point on the disc of the eclipsed star. The origin is located at the centre of the eclipsed star and the polar angle is measured counterclockwise from the radius vector connecting centres of the star and the transiting component.

The brightness at the point of the disc of the eclipsed star with polar coordinate ρ is given by
\begin{equation*} J(\rho ) = J(0)I\left(\frac{\rho }{{R}_{{*}}}\right). \end{equation*}
Here J(0) is the brightness at the centre of this stellar disc,
\begin{eqnarray} I(r)&=& (1 - f(\mu (r))) ,\nonumber \\ \mu (r)&=& \sqrt{1-r^2}\,,\nonumber \\ f(\mu )&=& \sum \limits _k \Lambda _k f_k(\mu ), \end{eqnarray}
(1)
where the functions fk are such that fk(1) = 0, defined by the law of limb darkening in question, and Λk are the coefficients of limb-darkening.

In this paper, we consider the following frequently used limb-darkening laws:

  • Linear limb-darkening law, for which f(μ)s = Λlfl(μ) = Λl(1 − μ)

  • Square law of limb darkening, which is characterized by the presence of the term Λqfq(μ) = Λq(1 − μ)2 in the expression for f

  • Logarithmic limb-darkening law, which is characterized by the presence of the term ΛLfL(μ) = − ΛLμln μ in the expression for f

  • Square-root limb-darkening law, which is characterized by the presence of the term |$\Lambda _Q f_Q (\mu ) ={} \Lambda _{Q} (1 - \sqrt{\mu })$| in the expression for f. |$\sqrt{\mu ^l}$| where l is a positive integer.

Corresponding results can be easily extended to the case when the expression for the brightness contains a term.

3 GENERAL INTEGRAL FORMULA FOR THE FLUX

The decrease of the flux of the binary system due to the eclipse is
\begin{equation} L^{F}- L(\displaystyle {D},{R}_{{*}},{R}_{{o}}) = \Delta \! L(\displaystyle {D},{R}_{{*}},{R}_{{o}}) = \int\!\!\!\!\int \limits _{\displaystyle {S}(\displaystyle {D})} J\left(|\boldsymbol {R}|\right){\rm d}\boldsymbol {R} , \end{equation}
(2)
where LF is the unobscured flux of the binary system, L is the obscured flux of the binary system, i.e. the light-curve value, |$S(\displaystyle {D})$| is the area of overlapping discs and |$\boldsymbol {R}$| is the radius vector of the point on the stellar disc.
To calculate the integral (2), we introduce the following functions:
\begin{equation} \mathop {\mathcal {A}}\nolimits x \equiv \left\lbrace \begin{array}{@{}l@{\quad }l@{}}\pi , & x < -1 \\ \arccos x, & -1 \le x \le 1 \\ 0, & x > 1 \; \end{array}\right. \end{equation}
(3)
and
\begin{equation} \mathop {\mathcal {Q}}\nolimits x \equiv \left\lbrace \begin{array}{@{}l@{\quad }l@{}}\sqrt{x}, & \quad x \ge 0 \\ 0, & \quad x < 0. \end{array}\right. \end{equation}
(4)
Then,
\begin{equation} \frac{{\rm d} \mathop {\mathcal {A}}\nolimits x}{{\rm d}\,x} = -\mathop {{Q}}\nolimits \left( \displaystyle {\frac{1}{1-x^2}} \right). \end{equation}
(5)
The relation (5) is obtained naturally by noting that |$\mathop {\mathcal {A}}\nolimits z = \mathop {\mathrm{Re}}\arccos z$|⁠, |$\mathop {\mathcal {Q}}\nolimits x = \mathop {\mathrm{Re}}\sqrt{z}$| for a complex number z with |$\mathop {\mathrm{Im}}z = 0$| and for the functions of the complex argument |$\arccos$| and |$\sqrt{\cdot }$| that are analytic continuations of the inverse cosine and square root of a real argument. The analyticity region is such that |$-\pi < \arg z \le \pi$| for each z.
In the polar coordinate system, the region of the integration |$S(\displaystyle {D})$| is given by
\begin{equation} S(\displaystyle {D}) = \left\lbrace \begin{array}{l} \rho < {R}_{{*}}\\ -\pi < \varphi \le \pi \\ \frac{\rho ^2 + \displaystyle {D}^2-{R}_{{o}}^2}{2 \rho \displaystyle {D}} \le \cos \varphi \,. \end{array} \right. \end{equation}
(6)
In the case of integration (2) with respect to the coordinate φ, for the values of ρ, which satisfy |${ \left|\frac{\rho ^2 + {D}^2-{R}_{{o}}^2}{2 \rho {D}}\right|} \le 1$|⁠, the variable φ takes the values such that
\begin{equation*} \frac{\rho ^2 + \displaystyle {D}^2-{R}_{{o}}^2}{2 \rho \displaystyle {D}} \le \cos \varphi \Leftrightarrow |\varphi | \le \arccos \ \left(\frac{\rho ^2 + \displaystyle {D}^2-{R}_{{o}}^2}{2 \rho \displaystyle {D}}\right). \end{equation*}
Hence, the integration over φ is from |$ {-\arccos \ \left(\frac{\rho ^2 + {D}^2-{R}_{{o}}^2}{2 \rho {D}}\right)}$| to |${\arccos \ \left(\frac{\rho ^2 + {D}^2-{R}_{{o}}^2}{2 \rho {D}}\right)}$|⁠.
For the values of ρ for which |$ { \frac{\rho ^2 + {D}^2-{R}_{{o}}^2}{2 \rho {D}}} < -1,$| the inequality
\begin{equation*} \frac{\rho ^2 + \displaystyle {D}^2-{R}_{{o}}^2}{2 \rho \displaystyle {D}} < \cos \varphi \end{equation*}
holds for every value of φ. In this case, the integration with respect to φ runs from − π to π.

For the values of ρ, for which |$ { \frac{\rho ^2 + {D}^2-{R}_{{o}}^2}{2 \rho {D}}} > 1$|⁠, the last inequality (6) is not satisfied for any values of φ. Formally, at these values of ρ both integration limits by φ are set equal to zero.

Next, using the notation (3) and introducing the function
\begin{equation*} \Psi (\displaystyle {D},x,y)\equiv \mathop {\mathcal {A}}\nolimits \left(\frac{x^2+\displaystyle {D}^2-y^2}{2\, x \, \displaystyle {D}}\right), \end{equation*}
the integral in (2) can be rewritten as
\begin{eqnarray} \Delta \! L(\displaystyle {D},{R}_{{*}},{R}_{{o}}) &=& \int _0^{{R}_{{*}}} \rho {\rm d}\rho \int _{-\displaystyle {\Psi (\displaystyle {D},\rho ,{R}_{{o}})}}^{\displaystyle {\Psi (\displaystyle {D},\rho ,{R}_{{o}})}} {\rm d} \varphi J\left(\rho \right) \nonumber\\ &=& 2 J(0) \int _0^{{R}_{{*}}} \rho \, \Psi (\displaystyle {D},\rho ,{R}_{{o}})\, I\left(\frac{\rho }{{R}_{{*}}}\right) \mathrm{d}\rho \nonumber\\ &=& J(0) {R}_{{*}}^2 \Delta \! L\left(\frac{\displaystyle {D}}{{R}_{{*}}},1,\frac{{R}_{{o}}}{{R}_{{*}}}\right) = J(0) {R}_{{*}}^2 \Delta \! \mathcal{L}(\delta ,r),\nonumber\\ \end{eqnarray}
(7)
where |$r=\frac{{R}_{{o}}}{{R}_{{*}}}$|⁠, |$\delta =\frac{\displaystyle {\displaystyle {D}}}{{R}_{{*}}}$| and
\begin{eqnarray} \Delta \! \mathcal{L}(\delta ,r) &=& 2\int _0^{1} \rho \, \Psi (\delta ,\rho , r)\, I(\rho ) {\rm d}\rho \nonumber\\ &=& \int _0^{1} \, \Psi (\delta ,\sqrt{\rho }, r)\, I(\sqrt{\rho }) {\rm d}\rho. \end{eqnarray}
(8)
Note that |$\Delta \! \mathcal{L}(\delta ,r)$| is the value of the decrease of the flux of the binary system when the radius and brightness at the centre of the eclipsed star equals unity, the radius of the second (eclipsing) component equals r and the distance between the centres of discs equals δ. In view of (1) we can express the decrease of the flux as a linear combination with limb-darkening coefficients:
\begin{eqnarray} \Delta \! \mathcal{L}(\delta ,r) &=& \Delta \! \mathcal{L}_{{0}}(\delta ,r) + \Lambda _l \Delta \! \mathcal{L}_l(\delta ,r) \nonumber\\ &&+ \Lambda _q \Delta \! \mathcal{L}_q(\delta ,r) + \Lambda _L \Delta \! \mathcal{L}_L(\delta ,r) + \Lambda _Q \Delta \! \mathcal{L}_Q(\delta ,r). \end{eqnarray}
(9)
The unobscured flux Lf of the star is
\begin{equation*} L^{f} = J(0) R^2 \mathcal{L}^{f}, \end{equation*}
where R is the radius of the star and
\begin{eqnarray} \mathcal{L}^{f} &=& \pi\int _0^{1} I(\sqrt{\rho }) {\rm d}\rho \nonumber\\ & =& \mathcal{L}^{f}_0 + \Lambda _l \mathcal{L}^{f}_l + \Lambda _q \mathcal{L}^{f}_q + \Lambda _L \mathcal{L}^{f}_L + \Lambda _Q \mathcal{L}^{f}_Q. \end{eqnarray}
(10)
When both components of the binary system are stars, the unobscured flux LF of the binary system is the sum of Lf for each star. For a binary star and planet, LF equals Lf for the star.
Let g be a function such that g(ρ) is a separate linear term in the expression for |$I(\sqrt{\rho })$| [given by equation (1)]. g(−1) is one of its primitives: |$g(\rho )={\frac{{\rm d}g^{(-1)}\!(\rho )}{{\rm d}\rho }}$|⁠. We consider the integral of the general form, which is a contribution to |$\Delta \! \mathcal{L}(\delta ,r)$| caused by the term g(ρ) in the expression for |$I(\sqrt{\rho })$|⁠:
\begin{equation} \Delta \! \mathcal{L}_g (\delta , r) = \int _0^{1} \, \Psi (\delta ,\sqrt{\rho }, r)\, g(\rho ) {\rm d}\rho . \end{equation}
(11)
We note that for δ > 0, r > 0
\begin{equation*} \lim \limits _{\rho \rightarrow 0} \Psi (\delta ,\sqrt{\rho },r) = \pi \Theta (r-\delta ), \end{equation*}
where
\begin{equation*} \Theta (t) \equiv \left\lbrace \begin{array}{@{}l@{\quad }l@{}}1, & \quad t > 0 \\ \frac{1}{2}, & \quad t = 0 \\ 0, & \quad t < 0. \end{array}\right. \end{equation*}
Using integration by parts, we obtain
\begin{eqnarray} \Delta \! \mathcal{L}_g (\delta , r) &=& \Psi (\delta ,1, r)g^{(-1)}\!(1) - \pi \Theta (r-\delta )g^{(-1)}\!(0) \nonumber \\ && - \int _0^{1} \frac{(\delta ^2-r^2-\rho )g^{(-1)}\!(\rho )}{2 \rho } \nonumber\\ && \times \mathop {\mathcal {Q}}\nolimits \left(\frac{1}{\left(\rho -\left(\delta -r\right)^2\right) \left(\left(\delta +r\right)^2-\rho \right)}\right){\rm d}\rho, \end{eqnarray}
(12)
where (5) is used for differentiating Ψ.
For a non-negative r and δ the integrand in (12) is non-zero only if (δ − r)2 < ρ < (δ + r)2. Therefore, the integral in (12) is zero if |δ − r| ≥ 1, and if |δ − r| < 1, integration can be performed over the interval ((δ − r)2, min ((δ + r)2, 1)). In this interval |$\arccos \left({\frac{\delta ^2+ r^2-\rho }{2 \, \delta \, r}} \right)$| is a monotone function of ρ, so we can perform the change of variable in integration in the following way:
\begin{equation} x={}\arccos \left(\displaystyle {\frac{\delta ^2+ r^2-\rho }{2 \, \delta \, r}}\right). \end{equation}
(13)
Then,
\begin{equation} \rho = \delta ^2 + r^2 - 2 r \delta \cos x. \end{equation}
(14)
Integration with respect to x will be performed over the interval
\begin{equation*} \left(0,\arccos \left(\frac{\delta ^2+ r^2-\min \left((\delta + r)^2, 1\right)}{2 \, \delta \, r}\right) \right). \end{equation*}
Taking into account the fact that
\begin{eqnarray*} &&{\frac{\rm d}{{\rm d} \rho }\arccos \left(\frac{\delta ^2+ r^2-\rho }{2 \, \delta \, r}\right) = \frac{1}{\sqrt{\left(\rho -\left(\delta - r\right)^2\right) \left(\left(\delta + r\right)^2-\rho \right)}}\,} \end{eqnarray*}
and
\begin{eqnarray*} \arccos \left(\frac{\delta ^2+ r^2-\min \left((\delta + r)^2, 1\right)}{2 \, \delta \, r}\right) &=& \mathop {\mathcal {A}}\nolimits \left(\frac{\delta ^2+ r^2- 1}{2 \, \delta \, r}\right)\nonumber\\ &=& \Psi (\delta , r, 1), \end{eqnarray*}
we obtain
\begin{eqnarray} \Delta \! \mathcal{L}_g (\delta , r) &=& \Psi (\delta ,1, r)g^{(-1)}\!(1) - \pi \Theta (r-\delta )g^{(-1)}\!(0) + \!\int _0^{\displaystyle {\Psi }(\delta , r, 1)}\nonumber \\ && \times\, \frac{(r^2 - r \delta \cos x))g^{(-1)} (\delta ^2 + r^2 - 2 r \delta \cos x)}{\delta ^2 + r^2 - 2 r \delta \cos x}{\rm d}x. \nonumber\\ \end{eqnarray}
(15)

Expression (15) is obtained assuming |δ − r| < 1. If |δ − r| ≥ 1, then the value of Ψ(δ, r, 1) = 0 and the integral in (15) vanishes. As noted above, when |δ − r| ≥ 1, the integral in (12) is zero because the integrand vanishes. Thus, the expression (15) is valid for all positive values of |$\delta \text{ and } r$|⁠.

By differentiating the integrand in (11) with respect to δ and r, we similarly find an expression for the corresponding partial derivative |$\Delta \! \mathcal{L}_g$|⁠:
\begin{eqnarray} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_g(\delta ,r)}}{\mathrm{\partial} {\delta }}= -2 r \int _0^{\displaystyle {\Psi }(\delta , r, 1)} \cos x\, g(\delta ^2 + r^2 - 2 r \delta \cos x){\rm d}x, \nonumber\\ \end{eqnarray}
(16)
\begin{equation} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_g(\delta ,r)}}{\mathrm{\partial} {r}}= 2 r \int _0^{\displaystyle {\Psi }(\delta , r, 1)} g(\delta ^2 + r^2 - 2 r \delta \cos x)\mathrm{d}x. \end{equation}
(17)
The contribution to the |$\mathcal{L}^{f}$| caused by the term g(ρ) in the expression for |$I(\sqrt{\rho })$| is
\begin{equation} \mathcal{L}^{f}_g = \pi (g^{(-1)}\!(1) - g^{(-1)}\!(0)). \end{equation}
(18)

4 INDIVIDUAL LAWS OF LIMB DARKENING

The expression for the decrease of flux due to the eclipse of the stellar disc with uniform brightness (with zero coefficients of limb darkening) can be obtained if we substitute in equations (15), (16) and (17) g(x) = 1, g−1(x) = x. Then,
\begin{eqnarray} \mathcal{L}^{f}_0 &=& \pi,\nonumber \\ \Delta \! \mathcal{L}_{{0}}(\delta , r) &=& \Psi (\delta , 1, r) +\Psi (\delta , r, 1) r^2 -\frac{1}{2} Q\left(\delta , r\right), \end{eqnarray}
(19)
\begin{equation} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{0}}(\delta , r)}}{\mathrm{\partial} {\delta }}=-\frac{Q(\delta , r)}{\delta }\, \end{equation}
(20)
and
\begin{equation} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{0}}(\delta , r)}}{\mathrm{\partial} {r}}=2\Psi (\delta , r, 1) r. \end{equation}
(21)
Here
\begin{equation*} Q\left(\delta , r\right)\equiv \mathop {\mathcal {Q}}\nolimits \left( \left( 1-\left(\delta - r\right)^2\right) \left(\left(\delta + r\right)^2- 1 \right) \right). \end{equation*}
(i) Putting |$g(x)=\mu (\sqrt{x})=\sqrt{1-x}$| and |$g^{(-1)}\!(x) ={} -\frac{2}{3}(1-x)^{\frac{3}{2}}$|⁠, we get
\begin{equation*} \mathcal{L}^{f}_1 = \frac{2 \pi }{3}, \end{equation*}
\begin{eqnarray} \boldsymbol {\Delta L}_{{1}}(\delta , r) &=& \frac{2 \pi }{3}\Theta ( r-\delta ) \nonumber \\ && + \mathop {\mathcal {Q}}\nolimits \left(\frac{1}{ 1-( r-\delta )^2} \right) \left[ \frac{2 (\delta + r)}{3 (\delta - r)} \hat{\Pi } \right. \nonumber\\ && - \left. \frac{2}{9}\! \left(3 (\delta ^2- r^2)+ ( 1-( r-\delta )^2)(( r+\delta )^2- 1)\right)\! \hat{F} \right]\nonumber\\ &&+\frac{2}{9} \mathop {\mathcal {Q}}\nolimits \left( 1-( r-\delta )^2 \right) (7 r^2 + \delta ^2 - 4) \hat{E}. \end{eqnarray}
(22)
Here
\begin{equation*} \hat{\Pi } \equiv \Pi \left(-\frac{4 \delta r}{( r-\delta )^2}; \frac{\Psi (\delta , r, 1)}{2} \left| \frac{4 \delta r}{ 1-( r-\delta )^2}\right. \right), \end{equation*}
\begin{equation*} \hat{F} \equiv F\left(\frac{\Psi (\delta , r, 1)}{2} \left| \frac{4 \delta r}{ 1-( r-\delta )^2}\right. \right), \end{equation*}
\begin{equation*} \hat{E} \equiv E\left(\frac{\Psi (\delta , r, 1)}{2} \left| \frac{4 \delta r}{ 1-( r-\delta )^2}\right. \right), \end{equation*}
where F, E and Π are incomplete elliptic integrals of the first, second and third kind:
\begin{equation*} F(\phi \,|m) \equiv \int ^\phi _0 \frac{{\rm d}\theta }{\sqrt{1 - m \sin ^2(\theta )}}, \end{equation*}
\begin{equation*} E(\phi \,|m) \equiv \int ^\phi _0 \sqrt{1 - m \sin ^2(\theta )}, \end{equation*}
\begin{equation*} \Pi (n;\phi \,|m) \equiv \int ^\phi _0 \frac{{\rm d}\theta }{(1 - n \sin ^2(\theta ))\sqrt{1 - m \sin ^2(\theta )}}. \end{equation*}
The efficient algorithms for their calculations were suggested by Carlson (1995). When |δ − r| → 0 or |δ − r| → 1, the limit of the term containing the factor |$\hat{\Pi }$| in (22) is equal to zero. Note that a similar expression was obtained by Pal (2012) for the integral (primitive) of the appropriately chosen vector field along the limb of the eclipsed component. However, application of this expression for the calculation of the flux of the system requires further account of its singularities. Expressions (22) and (19) give a direct algorithm for calculating the brightness, and the possible singularities are taken into account automatically by piecewise smooth functions of one variable |$\mathop {\mathcal {A}}\nolimits$| and |$\mathop {\mathcal {Q}}\nolimits$|
\begin{eqnarray} &&{\frac{\mathrm{\partial} {\boldsymbol {\Delta L}_{{1}}(\delta , r)}}{\mathrm{\partial} {\delta }} } \nonumber\\ && \quad= -2 r \int _0^{\displaystyle {\Psi }(\delta ,r,1)} \cos (x) \sqrt{1-(\delta -r)^2-4\,\delta r \sin ^2\left(\frac{x}{2} \right) }\;{\rm d}x \nonumber \\ && \quad= - \frac{2}{3 \delta } \mathop {\mathcal {Q}}\limits \left(1-( r-\delta )^2 \right) \left[\left((r + \delta )^2 - 1 \right) \hat{F} \right.\nonumber\\ && \qquad+ \left(1 - \delta ^2 - r^2 \right) \hat{E} ], \end{eqnarray}
(23)
\begin{eqnarray} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{1}}(\delta , r)}}{\mathrm{\partial} {r}}&=& 2 r \int _0^{\displaystyle {\Psi }(\delta ,r,1)} \, \sqrt{1-(\delta -r)^2-4\,\delta r \sin ^2\left(\frac{x}{2} \right) }\;{\rm d}x \nonumber \\ &=& 4 r \mathop {\mathcal {Q}}\nolimits \left(1-( r-\delta )^2 \right) \hat{E}. \end{eqnarray}
(24)
For the term with linear limb-darkening coefficients in (9)
\begin{equation} \Delta \! \mathcal{L}_l(\delta , r)= \Delta \! \mathcal{L}_{{1}}(\delta , r) - \Delta \! \mathcal{L}_{{0}}(\delta , r), \end{equation}
(25)
\begin{equation*} \mathcal{L}^{f}_l = \mathcal{L}^{f}_1 - \mathcal{L}^{f}_0 = - \frac{\pi }{3}. \end{equation*}
(ii) Assuming g(x) = x and g( − 1)(x) = x2/2 we get
|$\mathcal{L}^{f}_2 = \frac{\pi }{2},$|
\begin{eqnarray} \Delta \! \mathcal{L}_{{2}}(\delta , r) &=& \frac{ 1}{2} \Psi (\delta , 1, r) + \frac{ r^2}{2} \left(2 \delta ^2+ r^2 \right) \Psi (\delta , r, 1) \nonumber\\ && - \frac{1}{8}\left(\delta ^2 + 5 r^2 + 1 \right) Q\left(\delta , r\right). \end{eqnarray}
(26)
The partial derivatives of |$\Delta \! \mathcal{L}_{{2}}$| are as follows:
\begin{equation} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{2}}(\delta , r)}}{\mathrm{\partial} {\delta }}= 2 \delta r^2 \Psi (\delta , r, 1) -\frac{\delta ^2 + r^2 + 1 }{2 \delta }\, Q(\delta , r), \end{equation}
(27)
\begin{equation} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{2}}(\delta , r)}}{\mathrm{\partial} { r}}= 2 r \left(\delta ^2 + r^2 \right) \Psi (\delta , r, 1) - 2 r Q(\delta , r) , \end{equation}
(28)
\begin{equation} \Delta \! \mathcal{L}_q(\delta , r)={} 2 \Delta \! \mathcal{L}_{{1}}(\delta , r) - \Delta \! \mathcal{L}_{{0}}(\delta , r) - \Delta \! \mathcal{L}_{{2}}(\delta , r), \end{equation}
(29)
\begin{equation*} \mathcal{L}^{f}_q = 2 \mathcal{L}^{f}_1 - \mathcal{L}^{f}_0 - \mathcal{L}^{f}_2 = \frac{\pi }{6}. \end{equation*}
Further, we note that
\begin{equation*} \frac{\Psi (\delta , r, 1)}{2} = \frac{\pi }{2} - \mathop {\mathcal {A}}\nolimits \mathop {\mathcal {Q}}\nolimits \left( \frac{1 - (\delta - r)^2}{4 \delta r} \right). \end{equation*}
(iii) Assuming |$g(x)= \sqrt{1-x}\ln (1-x)$| and g( − 1)(x) = (1 − x)3/2(4/9 − 2/3ln (1 − x)), we obtain for the logarithmic limb-darkening law
\begin{equation*} \mathcal{L}^{f}_L = - \frac{4}{9} \pi, \end{equation*}
\begin{eqnarray} \Delta \! \mathcal{L}_L(\delta , r) &=& \Delta \! \mathcal{L}_{{1}}(\delta , r) \left(\ln (4 \delta r) - \frac{2}{3}\right) \nonumber\\ && - \frac{2 \pi }{3} \ln (4 \delta r) \Theta (r - \delta ) \nonumber\\ && - \frac{8}{3}\sqrt{\delta r}\left[r^2 {\mathop {{P}}\nolimits }^L_1\left(\frac{(\delta - r)^2}{4 \delta r}, \frac{1 - (\delta - r)^2}{4 \delta r}\right) \right. \nonumber\\ && - \left. \delta r {\mathop {{P}}\nolimits }^L_2\left(\frac{(\delta - r)^2}{4 \delta r}, \frac{1 - (\delta - r)^2}{4 \delta r}\right) \right], \end{eqnarray}
(30)
where
\begin{eqnarray} {\mathop {{P}}\nolimits }^L_1 (n, k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \frac{\left( k - \sin ^2 x \right)^{\frac{3}{2}} \ln \left( k - \sin ^2 x \right)}{n + \sin ^2 x}\;{\rm d}x ,\nonumber\\ \end{eqnarray}
(31)
\begin{eqnarray} {\mathop {{P}}\nolimits }^L_2 (n, k) \!=\! \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\limits (\mathop {\mathcal {Q}}\nolimits k) } \!\cos 2 x \frac{\left( k - \sin ^2 x \right)^{\frac{3}{2}} \ln \left( k - \sin ^2 x \right)}{n + \sin ^2 x}\;{\rm d}x.\nonumber\\ \end{eqnarray}
(32)
The partial derivatives of |$\Delta \! \mathcal{L}_L$| are as follows:
\begin{eqnarray} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_L(\delta , r)}}{\mathrm{\partial} {\delta }}= \ln (4 \delta r) \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{1}}(\delta , r)}}{\mathrm{\partial} {\delta }} - 8 r \sqrt{r \delta } {\mathop {{P}}\nolimits }^L_{\delta }\left(\frac{1 - (\delta - r)^2}{4 \delta r}\right),\nonumber\\ \end{eqnarray}
(33)
\begin{eqnarray} {\mathop {{P}}\nolimits }^L_{\delta } (k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \cos 2 x \sqrt{k - \sin ^2 x} \ln \left( k - \sin ^2 x \right)\;{\rm d}x,\nonumber\\ \end{eqnarray}
(34)
\begin{eqnarray} \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_L(\delta , r)}}{\mathrm{\partial} {r}}= \ln (4 \delta r) \frac{\mathrm{\partial} {\Delta \! \mathcal{L}_{{1}}(\delta , r)}}{\mathrm{\partial} {r}} + 8 r \sqrt{r \delta } {\mathop {{P}}\nolimits }^L_{r}\left(\frac{1 - (\delta - r)^2}{4 \delta r}\right),\nonumber\\ \end{eqnarray}
(35)
\begin{eqnarray} {\mathop {{P}}\nolimits }^L_{r} (k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \sqrt{k - \sin ^2 x} \ln \left( k - \sin ^2 x \right){\rm d}x. \end{eqnarray}
(36)
(iv) Assuming |$g(x)= \root 4 \of {1-x}$| and |$g^{(-1)}\!(x) ={} - \displaystyle {\frac{4}{5}} (1-x)^{5/4}$|⁠, we obtain the following expression for the case of the square-root limb-darkening law:
\begin{equation*} \mathcal{L}^{f}_3 = \frac{4 \pi }{5}, \end{equation*}
\begin{eqnarray} \boldsymbol {\Delta L}_{3}(\delta , r) &=& \frac{4 \pi }{5}\Theta (r-\delta ) \nonumber \\ &&- \frac{8}{5}\root 4 \of {4 \delta r} \left[r^2 {\mathop {{P}}\nolimits }^Q_1\left(\frac{(\delta - r)^2}{4 \delta r},\frac{1 - (\delta - r)^2}{4 \delta r}\right) \right. \nonumber\\ && - \left. \delta r {\mathop {{P}}\nolimits }^Q_2\left(\frac{(\delta - r)^2}{4 \delta r}, \frac{1 - (\delta - r)^2}{4 \delta r}\right) \right], \end{eqnarray}
(37)
where
\begin{equation} {\mathop {{P}}\nolimits }^Q_1 (n, k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \frac{\left(k - \sin ^2 x \right)^{\frac{5}{4}}}{n + \sin ^2 x}\;{\rm d}x, \end{equation}
(38)
\begin{equation} {\mathop {{P}}\nolimits }^Q_2 (n, k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \cos 2 x \frac{\left( k - \sin ^2 x \right)^{\frac{5}{4}}}{n + \sin ^2 x}\;{\rm d}x. \end{equation}
(39)
The partial derivatives of |$\Delta \! \mathcal{L}_Q$| are as follows:
\begin{eqnarray} \frac{\mathrm{\partial} {\boldsymbol {\Delta L}_3(\delta , r)}}{\mathrm{\partial} {\delta }}= -4 r \root 4 \of {4 r \delta } {\mathop {{P}}\nolimits }^Q_{\delta }\left(\frac{1 - (\delta - r)^2}{4 \delta r}\right), \end{eqnarray}
(40)
where
\begin{equation} {\mathop {{P}}\nolimits }^Q_{\delta } (k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \cos 2 x \left(k^2 - \sin ^2 x \right)^{\frac{1}{4}}\!{\rm d}x, \end{equation}
(41)
and
\begin{eqnarray} \frac{\mathrm{\partial} {\boldsymbol {\Delta L}_3(\delta , r)}}{\mathrm{\partial} {r}}= 4 r \root 4 \of {4 r \delta } {\mathop {{P}}\nolimits }^Q_{r}\left(\frac{1 - (\delta - r)^2}{4 \delta r}\right), \end{eqnarray}
(42)
where
\begin{equation} {\mathop {{P}}\nolimits }^Q_{r} (k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \left(k - \sin ^2 x \right)^{\frac{1}{4}} {\rm d}x. \end{equation}
(43)
For the term with square-root limb-darkening coefficients in (9):
\begin{equation} \Delta \! \mathcal{L}_Q(\delta , r)= \Delta \! \mathcal{L}_3 (\delta , r) - \Delta \! \mathcal{L}_{{0}}(\delta , r), \end{equation}
(44)
\begin{equation*} \mathcal{L}^{f}_Q = \mathcal{L}^{f}_3 - \mathcal{L}^{f}_0 = -\frac{\pi }{5} . \end{equation*}

It is easy to generalize the formulas obtained for the square root to the case of the limb-darkening law which contain the brightness term |$\sqrt{\mu ^{l}}$| in expression of brightness, where l is an odd positive number. It's enough just to put in (15), (16) and (17) |$g(x)= \root 4 \of {(1-x)^l}$| and |$g^{(-1)}\!(x) ={} - {\frac{4}{4+l}}(1-x)^{1+l/4}$|⁠. For an even l of non-multiple of 4, the light curve and its derivative can be expressed by elliptical integrals similarly to the formulae (22)–(24). If l is divisible by 4, the light curve and its derivative can be expressed by elementary functions similarly to the formulae (26)–(28) obtained for quadratic limb darkening.

5 NUMERICAL CALCULATION OF INTEGRALS

Thus, the calculation of the brightness for the logarithmic and square-root limb-darkening law is reduced to the calculation of the integrals |${\mathop {{P}}\nolimits }^L_{1}$|⁠, |${\mathop {{P}}\nolimits }^L_{2}$|⁠, |${\mathop {{P}}\nolimits }^L_r$||${\mathop {{P}}\nolimits }^L_{\delta }$|⁠, |${\mathop {{P}}\nolimits }^L_r$|⁠, |${\mathop {{P}}\nolimits }^L_{1}$|⁠, |${\mathop {{P}}\nolimits }^Q_{2}$|⁠, |${\mathop {{P}}\nolimits }^Q_r$||${\mathop {{P}}\nolimits }^Q_{\delta }$|⁠, |${\mathop {{P}}\nolimits }^Q_r$| (depending on parameters). These integrals can be represented in a general form as
\begin{equation} \tilde{{\mathop {{P}}\nolimits }}(n, k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k) } \frac{V(k, x) K\left(k - \sin ^2 x \right)}{n + \sin ^2 x}\;{\rm d}x, \end{equation}
(45)
for |${\mathop {{P}}\nolimits }^L_{1}$|⁠, |${\mathop {{P}}\nolimits }^L_{2}$|⁠, |${\mathop {{P}}\nolimits }^Q_{1}$|⁠, |${\mathop {{P}}\nolimits }^Q_{2}$|⁠, or
\begin{equation} \bar{{\mathop {{P}}\nolimits }}(k) = \int _0^{\displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k)} V(k, x) K\left(k - \sin ^2 x \right)\;{\rm d}x, \end{equation}
(46)
for |${\mathop {{P}}\nolimits }^L_r$||${\mathop {{P}}\nolimits }^L_{\delta }$|⁠, |${\mathop {{P}}\nolimits }^L_r$|⁠, |${\mathop {{P}}\nolimits }^Q_r$||${\mathop {{P}}\nolimits }^Q_{\delta }$|⁠, |${\mathop {{P}}\nolimits }^Q_r$|⁠. Here |$V(k, x) ={}\sum \limits _{i=1}^s u_i(k)v_i(x),$| where vi(x) are some trigonometric polynomials, n > 0, k > 0. We denote the maximum degree of these trigonometric polynomials by τ. |$K (y) ={} \sqrt{y} \ln y$| or |$K (y) ={} \root 4 \of {y^{\gamma }}$|⁠, respectively, has a logarithmic or fractional power singularity at t = 0. In the case of calculating |${\mathop {{P}}\nolimits }^Q_r$||${\mathop {{P}}\nolimits }^Q_{\delta }$|⁠, |${\mathop {{P}}\nolimits }^Q_r$|⁠, we put γ = 1. For the limb darkening of the general form, which is characterized by the presence of the term |$\sqrt{\mu ^l}$| in the expression for brightness (odd l), it is enough to put γ = l mod 4.
By applying the Gaussian quadrature formula, we can find the numerical value of the integrals with high precision, producing a relatively small number of elementary computations (the amount of computation of the integrand is proportional to the required number of significant digits). However, at the same time, an integrable function must satisfy certain conditions. In particular, this can be achieved if the higher derivatives of the integrand (or its non-singular component) are uniformly bounded on the section of integration. To reduce the computation of the integrals (45) and (46) to the computation of the integrals that satisfy the above conditions, we divide the interval of integration |$(0, {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k))$| into a sequence X0 > X1 > ⋅⋅⋅ > XM, such that |$X_0 ={} \displaystyle {\frac{\pi }{2}} - \mathop {\mathcal {A}}\nolimits (\mathop {\mathcal {Q}}\nolimits k)),\, X_M ={} 0$|⁠,
\begin{equation} \frac{k - \sin ^2 X_{i+1}}{k - \sin ^2 X_{i}} \le 2 \,\, \text{for} \,\, i \ge 1 \,\, \text{and} \,\, k \ne 1 , \end{equation}
(47)
\begin{equation} X_{i} - X_{i+1} \le \frac{1}{\max \lbrace \tau , 2 \rbrace } \,\, \text{for all} \,\, i < M \,\, \text{and} \,\, k . \end{equation}
(48)
In the case of equation (45), we also require the following inequality:
\begin{equation} \frac{n + \cos X_{i}}{n + \cos X_{i+1}} \le 2 \,\, \text{for all} \,\, i < M \,\, \text{and} \,\, k . \end{equation}
(49)
If k > 1, the inequality from (47) also holds for i = 0. If k < 1, then
\begin{equation} \frac{k-\sin ^2 X_1}{(X_0 - X_1) \sin (2 X_0)} \le \frac{3}{2} \,\, \text{and} \,\, X_1 \ge X_0 / 2. \end{equation}
(50)
(47)–(50) can be used as recurrent relations, allowing us to construct the sequence Xi.
Thus,
\begin{equation*} \tilde{{\mathop {{P}}\nolimits }} (n, k)=\sum \limits _{i=0}^{M-1} \tilde{{\mathop {{P}}\nolimits }}_{i} (n, k), \end{equation*}
\begin{equation*} \bar{{\mathop {{P}}\nolimits }} (k)=\sum \limits _{i=0}^{M-1} \bar{{\mathop {{P}}\nolimits }}_{i} (k), \end{equation*}
where
\begin{equation} \tilde{{\mathop {{P}}\nolimits }}_{i} (n, k) = \int _{X_{i+1}}^{X_i} \frac{V(k, x) K\left(k - \sin ^2 x \right)}{n + \sin ^2 x}\;{\rm d}x\, \end{equation}
(51)
and
\begin{equation} \bar{{\mathop {{P}}\nolimits }}_{i}(k) = \int _{X_{i+1}}^{X_i} V(k, x) K\left(k - \sin ^2 x \right)\;{\rm d}x. \end{equation}
(52)
For fixed values of n and k the last two integrals can be represented in the following form:
\begin{equation*} {\mathop {{P}}\nolimits }_i = \int _{X_{i+1}}^{X_i} U(x) K\left(k - \sin ^2 x \right)\;{\rm d}x, \end{equation*}
where |$U(x) ={} {\frac{V(k, x)}{n + \sin ^2 x}}$| for (51) and U(x) = V(k, x) for (52).
By linear substitution of the variable of integration
\begin{equation*} x(t) = X_{i+1}+ t (X_{i}-X_{i+1}) \end{equation*}
in (53), we turn to the integration from zero to unity:
\begin{equation} {\mathop {{P}}\nolimits }_i = (X_{i}-X_{i+1}) \int _{0}^{1} U(x(t)) K\left[k - \sin ^2(x(t)) \right]\;{\rm d}t. \end{equation}
(53)
In this form, |${\mathop {{P}}\nolimits }_i$| can be computed by applying the Gaussian quadrature formula:
\begin{equation} \int _0^1 h(t) \omega (t) {\rm d}t \approx \sum \limits _{l=1}^N w_l h(t_l). \end{equation}
(54)
Here ω(t) > 0 ∀t ∈ (0, 1), nodes ti are the roots of the polynomial HN(t), where {Hi} is the system of orthogonal polynomials with weight ω in the interval (0, 1):
\begin{equation*} \int _0^1 H_l(t) H_j(t) \omega (t) {\rm d}t = 0 \, \text{for } l \ne j. \end{equation*}
wl can be found as the solution of the system of N linear algebraic equations, which can be obtained if we put h(t) ≡ 1, h(t) ≡ t, …, h(t) ≡ tN in (54) and replace the approximate equality with exact equality.

N can be adjusted so as to ensure the required accuracy of the calculation of |${\mathop {{P}}\nolimits }_{0i} (n, k)$| and |${\mathop {{P}}\nolimits }_{di} (k)$| and can be the same for all values of i, n, k. N is of the same order of magnitude as the number of significant digits in the result, and this allows us to calculate the integral with the required accuracy in a reasonable time. So, after the calculation of the roots of polynomials xl and weights wl (this may take a while), we can reuse them for computing |${\mathop {{P}}\nolimits }_{0i} (n, k), {\mathop {{P}}\nolimits }_{di} (k)$| for all i, n, k.

In the case of i > 0 or of k > 1 we put in (54): ω(t) = 1∀t ∈ (0, 1), h(t) = (Xi − Xi + 1)U(x(t))K(k − sin 2x(t)). Then,
\begin{equation*} {\mathop {{P}}\nolimits }_i \approx \sum \limits _{l=1}^N w_l h(t_l). \end{equation*}
Note that in this case Hi(t) ≡ Pi(2t − 1), where Pi are Legendre polynomials.
In the case of i > 0, k < 1 and the logarithmic limb-darkening law (⁠|$K (y) ={} \sqrt{y} \ln y$|⁠), we represent the integrand from (53) in the form
\begin{eqnarray*} &&{U(x(t)) \sqrt{1-t} \sqrt{\frac{k - \sin ^2(x(t))}{1-t}}} \\ && &&{\times \left[ \ln \left(\frac{k - \sin ^2(x(t))}{1-t}\right) + \ln (1-t) \right].} \end{eqnarray*}
Next, we put in (54): |$\omega (t) = \sqrt{1-t} \forall t \in (0, 1)$|⁠,
\begin{equation*} h(t)= U(x(t)) \sqrt{\frac{k - \sin ^2(x(t))}{1-t}} \ln \left(\frac{k - \sin ^2(x(t))}{1-t}\right). \end{equation*}
Note that here |$H_i(t) \equiv P^{(\frac{1}{2},0)}_i(2 t - 1),$| where |$P^{(\frac{1}{2},0)}_i$| are Jacobi polynomials. Let |$S_1 ={} \sum \limits _{l=1}^N w_l h(t_l)$|⁠.
Next, we put in (54): |$\omega (t) ={} {-\sqrt{1-t}\ln (1-t) \forall t \in (0, 1)}$|⁠,
\begin{equation*} h(t)= -U(x(t)) \sqrt{\frac{k - \sin ^2(x(t))}{1-t}}. \end{equation*}
The polynomials corresponding to this value of ω can be obtained through the standard procedure of orthogonalization. Let |$S_2 ={} \sum \limits _{l=1}^N w_l h(t_l)$|⁠. Then, |${\mathop {{P}}\nolimits }_0 \approx {(S_1 + S_2)(X_{0}-X_{1})}$|⁠.
In the case of i > 0, k = 1 and the logarithmic limb-darkening law (⁠|$K (y) ={} \sqrt{y} \ln y$|⁠), we represent the integrand from (53) in the form
\begin{equation*} 2 U(x(t)) \cos (x(t)) \left[\ln \left(\frac{\cos (x(t))}{1-t}\right) + \ln (1-t) \right] . \end{equation*}
Next, we put in (54): ω(t) = 1∀t ∈ (0, 1),
\begin{equation*} h(t)= 2 U(x(t)) \cos (x(t)) \ln \left(\frac{\cos (x(t))}{1-t}\right). \end{equation*}
Let |$S_1 ={} \sum \limits _{l=1}^N w_l h(t_l)$|⁠.
Next, we put in (54): ω(t) = − ln (1 − t)∀t ∈ (0, 1),
\begin{equation*} h(t)= -2U(x(t)) \cos (x(t). \end{equation*}
Let |${S_2 = \sum \limits _{l=1}^N w_l h(t_l)}$|⁠. Then, |${\mathop {{P}}\nolimits }_0 \approx {}{(S_1 + S_2)(X_{0}-X_{1})}$|⁠.
In the case of i > 0, k < 1 and the square-root limb-darkening law (⁠|$K (y) ={} \root 4 \of {y^{\gamma }}$|⁠), we put in (54): |$\omega (t) ={} (1-t)^{\frac{\gamma }{4}} \forall t \in (0, 1)$|⁠,
\begin{equation*} h(t)= U(x(t)) \left(\frac{k - \sin ^2 x(t)}{1-t}\right)^{\frac{\gamma }{4}}. \end{equation*}
Note that here |$H_i(t) \equiv {}P^{(\frac{\gamma }{4},0)}_i(2 t - 1),$| where |$P^{(\frac{\gamma }{4},0)}_i$| are Jacobi polynomials. Then, |${\mathop {{P}}\nolimits }_0 \approx {}{(X_{0}-X_{1}) \sum \limits _{l=1}^N w_l h(t_l)}$|⁠.
In the case of i > 0, k = 1 and the square-root limb-darkening law, we put in (54): |$\omega (t) = \sqrt{1-t} \, \forall t \in {}(0, 1)$|⁠,
\begin{equation*} h(t)= U(x(t)) \left(\frac{\cos (x(t))}{1-t}\right)^{\frac{\gamma }{2}}. \end{equation*}
Then, |${\mathop {{P}}\nolimits }_0 \approx {}{(X_{0}-X_{1}) \sum \limits _{l=1}^N w_l h(t_l)}$|⁠.

Calculations show that in all cases of the applications of the Gauss quadrature accuracy of 19 significant decimal digits (corresponding to 80-bit machine numbers) can be achieved by choosing N to be 14. Value sets of points ti and weights wi corresponding to each of the considered forms of the function ω can be downloaded from the Internet, along with other materials (see the Conclusion section).

6 CONCLUSION

We have derived the expression for the calculation of the eclipsing binary flux and its derivatives. We considered the linear limb-darkening law, the quadratic limb-darkening law, the logarithmic limb-darkening law and the square-root limb-darkening law. In general, the decrease of the flux is given by the expression (9). In (19)–(21), |$\boldsymbol {\Delta L}_0$| corresponds to uniform brightness and its derivatives; it is expressed in terms of easily computed piecewise-defined functions of one variable |$\mathop {\mathcal {A}}\nolimits \,\,$|(equation 3) and |$\mathop {\mathcal {Q}}\nolimits \,\,$| (equation 4). |$\boldsymbol {\Delta L}_l$| corresponds to the linear limb-darkening law, given as a linear combination of |$\boldsymbol {\Delta L}_0$| and |$\boldsymbol {\Delta L}_1$| (equation 44), where |$\boldsymbol {\Delta L}_1$| with its derivatives are expressed in terms of incomplete elliptic integrals in equations (22)–(24). |$\boldsymbol {\Delta L}_q$| corresponds to the quadratic limb-darkening law, given as a linear combination of |$\Delta \! \mathcal{L}_0$|⁠, |$\Delta \! \mathcal{L}_1$| and |$\Delta \! \mathcal{L}_1$| (equation 29), where |$\Delta \! \mathcal{L}_2$| with its derivatives are given in equations (26)–(28). |$\Delta \! \mathcal{L}_L$| corresponds to the logarithmic limb-darkening law and |$\Delta \! \mathcal{L}_Q$| corresponds to the square-root limb-darkening law expressed by two- and one-parametric integrals. Further, we described how these integrals can be found numerically by multiple applications of the Gaussian quadrature formula. It is important that the nodes for this formula can be found once and reused for the calculations for different values of parameters. Also, the general integral form (15)–(17) of the flux component allows us to extend this approach to other limb-darkening laws.

The algorithm described above was tested by Abubekerov, Gostev & Cherepashchuk (2010, 2011) and Gostev (2011) for the interpretation of the high-precision polychrome light curves of the binary system with exoplanets HD 209458 (Brown et al. 2001), HD 189733 (Pont et al. 2007) and monochrome light curves of Kepler-5b, Kepler-6b and Kepler-7b (Dunham et al. 2010; Koch et al. 2010; Latham et al. 2010).

The algorithm is implemented in ANSI c in the form of the functions for the computation of the individual component |$\Delta \! \mathcal{L}(\delta ,r)$| and its derivatives. This implementation is available from http://lnfm1.sai.msu.ru/~ngostev/algorithm.html

We thank Professor Anatoly Cherepashchuk for some helpful suggestions and useful comments that improved the presentation of the paper. This work was supported by the President of Russian Federation grant MK-893.2012.2 and RFBR grant 12-02-31466.

REFERENCES

Abubekerov
M. K.
, 
Gostev
N. Yu.
, 
Cherepashchuk
A. M.
. , 
Astron. Rep.
, 
2010
, vol. 
54
 pg. 
1105
 
Crossref
Search ADS
 
Abubekerov
M. K.
, 
Gostev
N. Yu.
, 
Cherepashchuk
A. M.
. , 
Astron. Rep.
, 
2011
, vol. 
55
 pg. 
1051
 
Crossref
Search ADS
 
Brown
T. M.
, 
Charbonneau
D.
, 
Gilliland
R. L.
, 
Noyes
R. W.
, 
Burrows
A.
. , 
ApJ
, 
2001
, vol. 
552
 pg. 
699
 
Crossref
Search ADS
 
Carlson
B. C.
. , 
Numer. Algorithms
, 
1995
, vol. 
10
 pg. 
13
 
Crossref
Search ADS
 
Dunham
E. W.
, et al. , 
ApJ
, 
2010
, vol. 
713
 pg. 
L136
 
Crossref
Search ADS
 
Gostev
N. Yu.
. , 
Astron. Rep.
, 
2011
, vol. 
55
 pg. 
649
 
Crossref
Search ADS
 
Klinglesmith
D. A.
, 
Sobieski
S.
. , 
AJ
, 
1970
, vol. 
75
 pg. 
175
 
Crossref
Search ADS
 
Koch
D. G.
, et al. , 
ApJ
, 
2010
, vol. 
713
 pg. 
131
 
Crossref
Search ADS
 
Latham
D. W.
, et al. , 
ApJ
, 
2010
, vol. 
713
 pg. 
L140
 
Crossref
Search ADS
 
Mandel
K.
, 
Agol
E.
. , 
ApJ
, 
2002
, vol. 
580
 pg. 
L171
 
Crossref
Search ADS
 
Pal
A.
. , 
MNRAS
, 
2008
, vol. 
390
 pg. 
281
 
Crossref
Search ADS
 
Pal
A.
. , 
MNRAS
, 
2012
, vol. 
420
 pg. 
1630
 
Crossref
Search ADS
 
Pont
F.
, et al. , 
A&A
, 
2007
, vol. 
476
 pg. 
1347
 
Crossref
Search ADS
 
Van Hamme
W.
. , 
AJ
, 
1993
, vol. 
106
 pg. 
2096
 
Crossref
Search ADS
 

SUPPORTING INFORMATION

Additional Supporting Information may be found in the online version of this article:

The algorithm for calculating the light curve (Supplementary Data).

Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

© 2013 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides
  • Supplementary data

    • Supplementary data

    Supplementary Data - zip file