Search
Close
Search
Advanced Search
Search Menu

Abstract

The timing errors for individual planetary transits using the photometric transit timing technique (TTVp) are derived for light curves contaminated with either white additive noise, realistic stellar noise or filtered stellar noise. For the case of white noise, the timing errors are derived analytically, while timing errors for realistic and filtered noise are numerically derived using solar data from the Solar and Heliospheric Observatory satellite. These results are then used to explore the conjecture that moons of transiting planets become easier to detect using the TTVp method the farther their planet is from the star. Using transit duration as a proxy for planet–star distance, it is found that in the case of realistic stellar noise, an increase in star–planet distance/transit duration does not necessarily lead to an increase in moon detectability.

techniques: photometric, Sun: general, planets and satellites: detection

1 INTRODUCTION

The possibility of detecting planets around other stars by measuring the dip in the host star's intensity as the planet transits across its disc was first suggested by Struve (1952). With the advent of wide field CCD surveys and the launch of the CoRoT and Kepler satellites, this planet detection method has come of age with over 280 transiting planets known.1 Not only does the transit technique allow for planetary detection, it also allows for the measurement of observables which allow tests of theories of planet formation and structure. For example, measurements of the orbital orientation relative to the star's spin axis (e.g. Queloz et al. 2000; Narita et al. 2007; Triaud et al. 2010) facilitate tests of theories of planetary migration (e.g. Fabrycky & Tremaine 2007), and detection or non-detection of moons, using e.g. the methods proposed by Sartoretti & Schneider (1999), can be compared with mass limits predicted from planet formation models (e.g. Wada, Kokubo & Makino 2006; Sasaki, Stewart & Ida 2010).

In order for this scientifically valuable data to be obtained, the planetary nature of transiting planet candidates must be confirmed. For bright, slowly rotating stars this could involve measurement of planetary mass through detection of the radial velocity signal (e.g. Marcy & Butler 1992), while for dimmer stars this could involve using transit timing variations in multiplanet systems (e.g. Holman & Murray 2005) or additional photometric effects such as beaming, elipsoidal and rotation effects (Faigler & Mazeh 2011). In addition, as systems capable of mimicking all the photometric and timing effects corresponding to a physically realistic moon system are likely to be rare, and as moon formation is predicted to be a common outcome of planet formation (e.g. Elser et al. 2011), another possible avenue for planetary followup would be the detection of a moon or a system of moons of a given candidate planet.

Four techniques have been proposed for detecting moons of transiting planets using transit light curves: direct detection, transit duration variation (TDV), barycentric transit timing (TTVb) and photometric transit timing (TTVp). Direct detection involves searching the light curve for the additional dip due to the transit of the moon (Sartoretti & Schneider 1999). Using this method, a limit of 1.2 and 0.8 Earth radii has been placed on the radii of moons orbiting HD 209458 b (Brown et al. 2001) and HD 189733 b (Pont et al. 2007), respectively. In addition, a modified version of the direct detection method was also proposed by Simon et al. (2012). In their version, the dips due to a moon are not detected in individual transits, but detected by statistically investigating the variance in a stack of light curves. The remaining three methods involve measuring a time which is sensitive to motion of the planet about the planet–moon barycentre. The TDV method uses transit to transit variation of the planetary transit duration to measure any perturbation in the velocity of the transiting planet (Kipping 2009). The TTVb technique involves searching for a periodicity, not in the duration, but in the mid-time of consecutive planetary transits due to possible motion of the planet about the planet–moon barycentre (Sartoretti & Schneider 1999). Using this technique, Brown et al. (2001), Gillon et al. (2006) and Kipping & Bakos (2011) placed upper limits on the masses of moons orbiting HD 209458, OGLE-TR-113 b and TrES-2 of 3 Earth masses, 7 Earth masses and 1.15 Earth masses, respectively. Unfortunately, other physical systems can also cause periodicities in transit timing e.g. the presence of an additional planet (Miralda-Escudé 2002; Agol et al. 2005; Steffen & Agol 2005). The TTVp method also uses the timing of transits to search for moons, but in this case, the time used is not the mid-point of the transit but τ, the first moment of the photon deficit caused by the planet–moon pair. From Szabó et al. (2006), τ is defined as
\begin{eqnarray} \tau = \frac{\sum _{i}\left(t_i \alpha (t_i)\right)}{\sum _{i} \alpha (t_i)}, \end{eqnarray}
(1)
where α(ti) is the photometric deficit at time ti and where the summation index i is defined only for regions of the light curve corresponding to times during which either or both the planet and moon are in transit. As the position (or even existence) of the moon is not known prior to detection, this assumption cannot be used in constructing physically attainable detection thresholds. Consequently, here we choose to evaluate the sum over a window of known size Tobs centred on the planetary transit instead (see Fig. 1).
Figure 1.
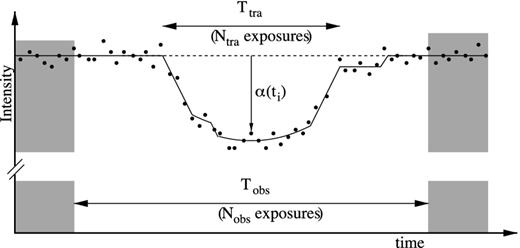
An example transit showing measured intensities (dots) and theoretical intensity (line). The quantity α(ti) is shown for one of the exposures and the region which is outside the window that is counted in the sum is shaded grey.
Open in new tabDownload slide

An example transit showing measured intensities (dots) and theoretical intensity (line). The quantity α(ti) is shown for one of the exposures and the region which is outside the window that is counted in the sum is shaded grey.

The detectability of moons using the TTVp technique is determined by the size of the timing perturbations they produce relative to the error in the measured value of τ due to photometric noise. In the investigation of Szabó et al. (2006) into moon detectability using this technique, a number of simplifying assumptions were made, including assuming that the noise in the light curve was white, that is, the noise is Gaussian and uncorrelated. Unfortunately not all photometric noise sources relevant to transit surveys are white.

Intrinsic photometric variability of most Sun-like stars is known to be a red noise process (e.g. Lockwood et al. 2007), that is, the noise is characterized by a sloping spectral energy distribution with extra power in the low frequencies or the ‘red’ end of the spectrum. Due to this excess of long wavelength components, consecutive data points in a light curve dominated by the intrinsic variability of the host star are correlated. It has long been known that red photometric noise due to stellar variability is a limiting factor in transit surveys (e.g. Borucki, Scargle & Hudson 1985). Consequently, it is of interest to determine the effect of this type of noise on the error in τ, and thus moon detectability. Also, as an increasing number of algorithms developed for transit detection use a pre-whitening filter, it is also of interest to determine the effect of filtering on the error in τ.

Finally, in addition to being a method proposed to search for moons and follow up planets, Oshagh et al. (2012) have used this method to try and detect additional planet-mass bodies in the LHS 6343 system by looking for dynamically induced timing perturbations in the transits of the brown dwarf LHS 6343 C across the M star LHS 6343 A. The methods presented here could also be applied to this system.

With these aims in mind, in Section 2 a framework for calculating the noise in τ due to photometric variability is developed. In Sections 3, 4 and 5, this framework is then used to determine the noise in τ as a function of observing duration and exposure time for the cases of white noise, realistic stellar noise and filtered stellar noise, respectively. In Section 6, the results from Sections 3, 4 and 5 are used to investigate the relationship between moon detectability and increasing transit duration for this technique.

2 THEORETICAL GROUNDWORK

Before investigating the effect of white, realistic stellar and filtered stellar noise on the error in τ, an equation relating this error to physical parameters of the system needs to be derived. To begin we write τ as
\begin{eqnarray} \tau = t_0 + jT_{\rm p} + \Delta \tau + \epsilon _j, \end{eqnarray}
(2)
where j is the transit number with the first transit corresponding to j = 0, t0 is the mid-point of the first transit if there were no moon, Tp is the orbital period of the planet–moon pair about the star, Δτ is the perturbation in τ due to the moon and ϵj is the error in τ due to the photometric noise. This expression will later in the proof be compared with equation (1), the definition of τ, to produce expressions for ϵj as a function of α(ti), the photometric deficit, and in particular the contributions to α(ti) arising from photometric noise. Consequently, to proceed, α(ti), must be divided into components.
To do this, consider a noisy light curve, such as the one shown in Fig. 1. Assuming that the transit depth is small compared to the total luminosity of the star, the noise in the light curve can be considered to be additive. We begin by writing the photometric deficit as
\begin{eqnarray} \alpha (t_i) = \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i) + \alpha _{\rm n}(t_i), \end{eqnarray}
(3)
where αp(ti) is the absolute photon deficit due to the transit of the planet at time ti, αm(ti) is the absolute photon deficit due to the transit of the moon at time ti and αn(ti) is the absolute photometric deficit due to the photometric noise at time ti, where, we assume that this noise has zero mean. Substituting equation (3) into equation (1) gives
\begin{eqnarray} \tau = \frac{\sum _{i}\left(t_i \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i) + \alpha _{\rm n}(t_i)\right)\right)}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i) + \alpha _{\rm n}(t_i)}. \end{eqnarray}
(4)
As αn(ti) is present in both the numerator and the denominator, the numerator and denominator are correlated, and thus we cannot investigate these two terms in isolation, and then combine the results.
To see how this correlation manifests practically, we consider an example. First, we write ti = ti − tmid, p + tmid, p, where tmid, p is the mid-time of the window used to calculate the sum, so that
\begin{eqnarray} \tau = t_{\rm {mid,p}} + \frac{\sum _i (t_i - t_{\rm {mid,p}}) (\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i) + \alpha _{\rm n}(t_i))}{\sum _i \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i) + \alpha _{\rm n}(t_i)}. \end{eqnarray}
(5)
Now, consider the case where one value of αn, lets say αn(tk), is large (and positive) and where tk > tmid, p (i.e a data point near the egress of the transit). As (tk − tmid, p) is positive, αn(tk) acts to make both the denominator and numerator of the fraction more positive. These two effects partially cancel, thus, the error in τ resulting from the effect of αn(tk) will be small. Conversely, for the case where αn(tk) is still large and positive, but where tk < tmid, p (i.e a data point near the ingress of the transit) this is no longer the case. As (tk − tmid, p) is now negative αn(tk) now acts to make the numerator more negative but make the denominator more positive. Consequently, for this case the error in τ resulting from the effect of αn(tk) will be amplified. For the case where αn(tk) is large and negative, these effects are reversed.
To remove this correlation, equation (4) needs to be expanded. In particular, our aim is to express τ in the form τ = τtrue + ∑iβiαn(ti), where τtrue is the value of τ that would be derived in the absence of photometric noise and βi are weights. The end goal of writing τ in this form is to exploit the statistical properties of the distribution of αn to determine the form of the probability distribution of ϵj. Assuming that the combined effect of both planet and moon is detectable for each transit, that is, ∑iαn(ti) ≪ ∑i[αp(ti) + αm(ti)], a binomial expansion of equation (4) gives
\begin{eqnarray} \tau &=& \frac{\sum _{i}t_i \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)\right)}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)} +\frac{1}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)}\nonumber\\ && \times \sum _{i}\left[t_i - \frac{\sum _{j} t_j\left(\alpha _{\rm p}(t_j) + \alpha _{\rm m}(t_j)\right)}{\sum _{j} \alpha _{\rm p}(t_j) + \alpha _{\rm m}(t_j)}\right] \alpha _{\rm n}(t_i), \end{eqnarray}
(6)
where we have neglected terms of the order of [∑iαn(ti)]2/[∑i[αp(ti) + αm(ti)]]2.
Comparing this expression to equation (2), it can be seen that as the first term does not contain αn, it cannot contribute to ϵj, and must contribute entirely to t0 + jTp + Δτ. As the second term is a sum of random variables with zero mean, it has zero mean, and must contribute entirely to ϵj. Consequently,
\begin{eqnarray} \Delta \tau = - t_0 - jT_{\rm p} + \frac{\sum _{i}t_i \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)\right)}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)} \end{eqnarray}
(7)
and
\begin{eqnarray} \epsilon _{j} &=& \frac{1}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)}\nonumber\\ && \times \sum _{i}\left[t_i - \frac{\sum _{j} t_j\left(\alpha _{\rm p}(t_j) + \alpha _{\rm m}(t_j)\right)}{\sum _{j} \alpha _{\rm p}(t_j) + \alpha _{\rm m}(t_j)}\right] \alpha _{\rm n}(t_i), \end{eqnarray}
(8)
at this level of approximation.
Substituting equation (7) into equation (8), and defining the area of the dips in the light curve caused by the planet and moon to be Ap = ∑iαp(ti) and Am = ∑iαm(ti), gives
\begin{eqnarray} \epsilon _{j} = \frac{1}{A_{\rm p} + A_{\rm m}} \sum _{i}\left[t_i - t_0 - jT_{\rm p} - \Delta \tau \right] \alpha _{\rm n}(t_i). \end{eqnarray}
(9)
For this work it would be convenient to investigate the timing noise in isolation from the timing perturbation due to the moon, represented by Δτ in the equation above and Δtp in Section 3.2. We can do this by noting that the relative size of the ti + t0 + jTp term is much larger than the Δτ term for the case of equation (9), as well as the Δtp term for the case of equation (23). In particular, the maximum duration of a planetary transit for a planet on a circular orbit of radius 1 au about a Sun-like star is ∼13 h. In comparison, the maximum Δτ and Δtp values produced for the case of Earth–Moon analogues on 1 au orbits are 15 min and 16 s, respectively, while for the case of Jupiter–Ganymede analogues on similar 1 au orbits are 55 and 2.8 s, respectively. As the observing duration, Tobs, must be equal to or greater than the transit duration, Ttra, equation (9) is dominated by large values of ti − t0 − jTp, and consequently, the Δτ term can be neglected. In addition as Δτ is of the same order of magnitude as Δtp, neglecting Δτ here requires that Δtp is also neglected in equation (23). Neglecting Δτ gives
\begin{eqnarray} \epsilon _{j} = \frac{1}{A_{\rm p} + A_{\rm m}} \sum _{i}\left[t_i - t_0 - jT_{\rm p}\right] \alpha _{\rm n}(t_i). \end{eqnarray}
(10)
This is the governing equation for ϵj and will be used to investigate the case of white noise.
For the case of red and filtered noise, we use out-of-transit light curves to yield a sample of ϵj values which could consequently be used to estimate the distribution of ϵj. To begin, we define τ* as
\begin{eqnarray} \tau ^* = \frac{\sum _{i} t_i L(t_i) }{\sum _{i} L(t_i)}, \end{eqnarray}
(11)
where L(ti) = L0 + αn(ti) and L0 is the mean luminosity of the target star. Physically, L(ti) corresponds to an out-of-transit light curve which has been reflected across the line L(ti) = L0. Our aim is to transform τ*, a quantity that can be directly calculated from an out-of-transit light curve to ϵj.
To begin, note that equation (11) is equivalent to equation (4) for the case where αp(ti) + αm(ti) = L0. Applying the same procedure used to derive equations (7) and (10) from equation (4), we have from equation (11)
\begin{eqnarray} \Delta \tau ^* &= 0, \end{eqnarray}
(12)
\begin{eqnarray} \epsilon _j^* &= \displaystyle\frac{1}{N_{\rm obs} L_0} \sum _{i}\left[t_i - t_0 - jT_{\rm p}\right] \alpha _{\rm n}(t_i), \end{eqnarray}
(13)
where Nobs is the total number of exposures. Comparing equation (10) and equation (13), we have
\begin{eqnarray} \epsilon _j = \frac{N_{\rm obs} L_0}{A_{\rm p} + A_{\rm m}} \epsilon _j^*. \end{eqnarray}
(14)
In addition, substituting equations (12) and (13) into equation (2), noting that, in this case, t0 + jTp is equal to tmid, the mid-time of the section of out-of-transit light curve used in the summation, gives
\begin{eqnarray} \epsilon _j^*= \tau ^* - t_{\rm mid}. \end{eqnarray}
(15)

Equations (11), (14) and (15) provide a simple method for determining a sequence of ϵj values for a transit with a given Ap + Am, using out-of-transit light curves. This formulation will be used to analyse the cases of realistic and filtered stellar noise.

3 WHITE NOISE: ANALYTIC DERIVATION

3.1 Introduction to white noise

White noise is a type of additive noise which occurs in many physical processes such as photon counting. It is known as white, as the Fourier transform of white noise contains the same power at all frequencies.

In order for a sequence of discrete numbers x = {x1, x2, …xj, …, xn} to describe white noise, two conditions must be satisfied. First, each of the xj must be drawn from a Gaussian distribution, that is, they are described by the probability density function
\begin{eqnarray} P(x_j) = \frac{1}{\sigma \sqrt{2 \pi }} {\rm e}^{-\frac{(x_j - \mu )^2}{2\sigma ^2}}, \end{eqnarray}
(16)
where μ and σ are the mean and the standard deviation, respectively. Secondly, the individual values of x must be uncorrelated, that is, the probability distribution for any xj is unaffected by the values of any of the xk, where k ≠ j.
Uncorrelated, normally distributed random variables, such as those used to produce white noise, have a number of useful properties (see e.g. Kokoska & Zwillinger 2000, p. 100). In particular, if X1 and X2 are uncorrelated normally distributed random variables with mean μ1 and μ2 and standard deviation σ1 and σ2, then a linear combination of these variables, aX1 + bX2, is also normally distributed with mean μ1 + 2 and standard deviation σ1 + 2, given by
\begin{eqnarray} \mu _{1+2} &= a\mu _1 + b\mu _2, \end{eqnarray}
(17)
\begin{eqnarray} \sigma _{1+2} &= \sqrt{a^2\sigma _1^2 + b^2\sigma _2^2}. \end{eqnarray}
(18)

3.2 Derivation of ϵj

For the case where the photometric noise is white, from the definition of white noise, we have that the αn(ti) are normally distributed and uncorrelated. Restating the definition of ϵj given by equation (9),
\begin{equation*} \epsilon _j = \frac{1}{A_{\rm p} + A_{\rm m}}\sum _i\left[t_i - (jT_{\rm p} + t_0) \right]\alpha _{\rm n}(t_i), \end{equation*}
it can be seen that as ϵj is a weighted sum of a set of normally distributed random variables, αn, it too is normally distributed. In addition, recalling that we have defined αn to have mean 0 and writing the standard deviation of αn as σL we can use equations (17) and (18) to determine μϵ and σϵ, the mean and standard deviation of the distribution of ϵj, respectively. Applying equations (17) and (18) to equation (9), we have that
\begin{eqnarray} \mu _\epsilon = 0 \end{eqnarray}
(19)
and
\begin{eqnarray} \sigma _\epsilon = \frac{\sigma _L}{A_{\rm p} + A_{\rm m}}\sqrt{\sum _i(t_i - (jT_{\rm p} + t_0))^2}. \end{eqnarray}
(20)
In order to evaluate equation (20), we need to write ti in terms of physical variables such as the tmid, the mid-point of the window, Δt, the exposure length and Nobs, the number of exposures used to calculate τ. Using these variables, ti can be written as
\begin{eqnarray} t_i = t_{\rm mid} + \left(i - \frac{N_{\rm obs}}{2}\right)\Delta t. \end{eqnarray}
(21)
Noting that the window over which the transit is examined is centred on the planetary transit, we have that the centre of the jth transit will occur at
\begin{eqnarray} t_{\rm mid} = jT_{\rm p} + t_0 + \Delta t_{\rm p}, \end{eqnarray}
(22)
where Δtp is the unknown time delay in the centre of the planetary transit due to the motion of the planet about the planet–moon barycentre. Consequently, ti is given by
\begin{eqnarray} t_i = jT_{\rm p} + t_0 + \Delta t_{\rm p} + \left(i - \frac{N_{\rm obs}}{2}\right)\Delta t. \end{eqnarray}
(23)

This expression can be simplified by considering the relative sizes of the terms. Recalling from Section 2 that both Δτ and Δtp are much smaller than ti − (jTp + t0), and following the procedure used to simplify equation (9), we can also neglect the Δtp term from equation (23).

Performing this simplification, and writing out ti and the sum limits in full, we have
\begin{eqnarray} \sigma _\epsilon = \frac{\sigma _L}{A_{\rm p} + A_{\rm m}}\sqrt{\sum _{i = 0}^{N_{\rm obs}-1} \left(i - \frac{N_{\rm obs}}{2}\right)^2\Delta t ^2 }. \end{eqnarray}
(24)
Expanding the terms under the square root and using the identities
\begin{eqnarray} \displaystyle\sum _{i = 0}^{n} i &= \displaystyle\frac{n(n+1)}{2} \end{eqnarray}
(25)
\begin{eqnarray} \sum _{i = 0}^{n} i^2 &= \displaystyle\frac{n(n+1)(2n + 1)}{6}, \end{eqnarray}
(26)
equation (24) becomes
\begin{eqnarray} \sigma _\epsilon = \frac{\sigma _L}{A_{\rm p} + A_{\rm m}} \sqrt{\Delta t^2\frac{N_{\rm obs}^3}{12} + \Delta t^2\frac{N_{\rm obs}}{6} }. \end{eqnarray}
(27)
As the first term under the square root is approximately N2obs times greater than the second term, where Nobs, the number of exposures, is a large number, the second term can be neglected, giving
\begin{eqnarray} \sigma _\epsilon = \sigma _L \frac{N_{\rm obs} \Delta t}{A_{\rm p} + A_{\rm m}} \sqrt{\frac{N_{\rm obs}}{12}}. \end{eqnarray}
(28)
Rearranging equation (28), using the expression Nobs = Ntra(Tobs/Ttra), gives
\begin{eqnarray} \sigma _\epsilon &=& 47.9\,{\rm s} \left[\left(\frac{\sigma _L/L_0}{3.95 \times 10^{-4}}\right)\left(\frac{\Delta t}{1\, {\rm min}}\right)^{1/2}\right] \nonumber\\ && \times \left[\frac{100(A_{\rm p} + A_{\rm m})}{N_{{\rm tra}} L_0} \right]^{-1} \left[\left(\frac{T_{\rm obs}}{24\, {\rm h}}\right)^{3/2} \left(\frac{T_{\rm tra}}{13 \,{\rm h}}\right)^{-1}\right], \end{eqnarray}
(29)
where we note that the comparison system is a Jupiter-like planet orbiting a 12th magnitude Sun-like star at 1 au, monitored by a space telescope with the capacities of Kepler.2

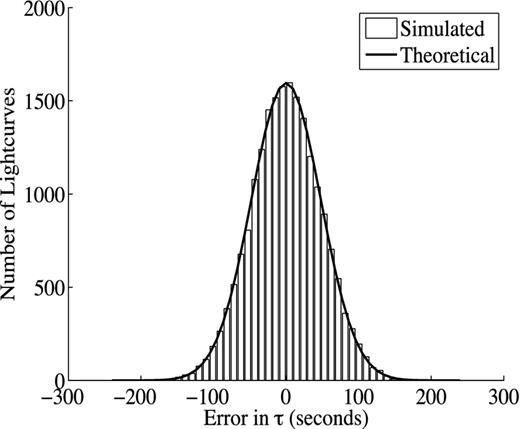
To check this formula, a Monte Carlo simulation was run. A mock transit light curve was constructed using three straight line segments corresponding to the ingress, flat bottom and egress. To this, Gaussian noise with a known standard deviation was added to produce a sequence of model transit light curves. For each light curve, the ϵj value, that is, the difference between the centre of the transit and the value of τ, was calculated. The histogram of the errors of these model light curves and the theoretical prediction are both shown in Fig. 2. As can be seen the agreement is very strong.

Figure 2.
Comparison between a Monte Carlo simulation (white bar) and theoretical prediction (black line) for the distribution of ϵj values for a noisy transit.
Open in new tabDownload slide

Comparison between a Monte Carlo simulation (white bar) and theoretical prediction (black line) for the distribution of ϵj values for a noisy transit.

3.3 Relationship between moon detectability and exposure time

Szabó et al. (2006) found that a decrease in exposure time leads to an increase in moon detectability. From equation (2), we see that there are two candidate causes for a relationship between exposure time and moon detectability using the TTVp. First, that the calculated value of τ may depend on the timing and duration of the exposures, and second, that the exposure time alters the characteristic size of σϵ, thus modifying moon detectability. It turns out that for transit parameters corresponding to the planetary systems of interest, the timing and duration of exposures does not significantly alter the calculated value of τ (see Appendix A). Consequently, we can investigate the relationship between moon detectability and exposure time by investigating the relationship between σϵ and exposure time using equation (29).

To begin, consider the first term in square brackets in equation (29). This term describes both the dependence of σϵ on the relative photometric accuracy (σL/L0) and the exposure time (Δt). Unsurprisingly, the smaller the relative photometric error, the smaller the value of σϵ and consequently, the smaller the error in τ. However, while the relative photometric noise can be altered without changing the exposure time, for example, by moving to a larger telescope or by upgrading the instrumentation, changing the exposure time can alter the photometric noise depending on its source. For the case of shot noise, error due to small number statistics, the total error is proportional to the square root of the total number of photons collected for that star (i.e. |$\sigma _L \propto \sqrt{\Delta t}$|⁠) while the total intensity is proportional to the total number of photons (i.e. L0 ∝ Δt), so the relative photometric error is proportional to |$\sqrt{\Delta t}/\Delta t = (\Delta t)^{-1/2}$|⁠.3 For the case of read noise, error resulting from the process of measuring the number of photons collected at the end of an exposure, the total error does not depend on the exposure time. Consequently, the relative photometric error is proportional to (Δt)−1. So, for a star with white photometric noise that is dominated by shot noise, σϵ is independent of exposure time, while for a star dominated by read noise, σϵ should decrease with increasing exposure time.4

4 RED NOISE: OBSERVATIONAL DERIVATION

4.1 Introduction to red noise

Red noise is additive noise which contains a surplus of power at the lower (or ‘redder’) frequencies. While in signal processing, red noise refers to Brownian noise or random walk noise and has spectral density proportional to f−2, where f is the frequency, in astrophysics, the term is colloquially used to describe any noise process which produces an excess of low frequencies.

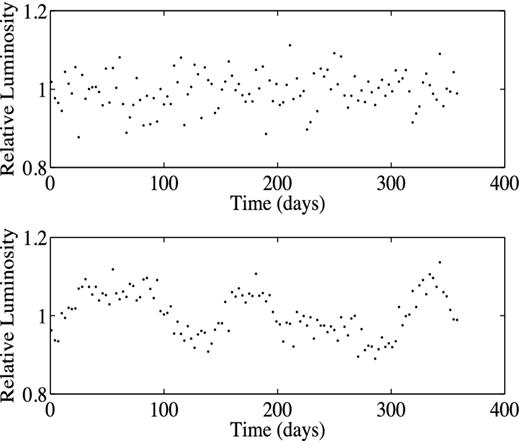
The fact that stars in general (e.g. Dorren & Guinan 1982; Radick et al. 1982) and the Sun in particular (e.g. Willson et al. 1981) have a red noise component in their light curves has long been known. Due to this excess of long wavelength components, consecutive data points in a light curve dominated by the intrinsic variability of the host star are correlated, that is, there are long-term trends in the data (see Fig. 3). Consequently, the statistical methods used in the previous section no longer apply. As mentioned in Section 2, for the case of realistic photometric noise, the distribution and behaviour of ϵj are calculated numerically, in particular, using solar photometric light curves.

Figure 3.
Comparison between white noise (top panel) and red noise (bottom panel).
Open in new tabDownload slide

Comparison between white noise (top panel) and red noise (bottom panel).

4.2 Discussion of suitability of solar photometric data for calculating ϵj

In order to determine the effect of intrinsic stellar photometric variability on ϵj using equation (14), a suitable sample light curve which is dominated by realistic photometric stellar variability corresponding to a typical star is required. This data series should optimally have a number of properties. First, it needs to be long enough such that a statistically valid estimate of ϵj can be constructed. Secondly, the data must have high signal-to-noise ratio to ensure that the majority of recorded photometric noise is inherent to the star, and not resulting from instrumental or statistical effects. Thirdly, the data need to be high cadence, such that the effect of long and short exposure times on ϵj can be investigated. Finally, this data must be easily available and easy to manipulate. Fortunately, photometric measurements of the Sun meet all these requirements.

Over 12 yr of high-quality solar data are available as a result of the Solar and Heliospheric Observatory (SoHO). This satellite is positioned at the L1 point between the Earth and the Sun, which allows it uninterrupted access to the Sun's behaviour. For this work, it is the measurements of Total Solar Irradience, the total intensity of the solar face, that are important. This measurement is made within the VIRGO (Variability of solar IRradiance and Gravity Oscillations) module (Fröhlich et al. 1995), by comparing the output of the photometers PMO6V (PMO6-type radiometer on VIRGO, indicated by a V) and DIARAD (DIfferential Absolute RADiometer) (Fröhlich et al. 1997). These data were kindly made available by the SoHO team and can be freely downloaded from the SoHO archive.5

While high-quality solar data may be freely available, whether it should be used depends on whether the photometric behaviour of the Sun is representative of the photometric behaviour of Sun-like stars, in particular, the stars to be targeted by CoRoT and Kepler. Indeed, it has been found that the Sun shows two to three times less variation on the decadal time-scale compared to similar stars (Lockwood, Skiff & Radick 1997; Radick et al. 1998; Lockwood et al. 2007). In addition, these findings are in agreement with the preliminary findings from the CoRoT (e.g. Aigrain et al. 2009) and Kepler (e.g. Basri et al. 2010; McQuillan, Aigrain & Roberts 2012) satellites. While this discrepancy may seem discouraging, it needs to be viewed in the context of two other findings: the effect of star orientation with respect to the observer, and the results of studies of extra-solar planet host stars. First, it has been suggested that the low observed value of solar photometric noise is due to our privileged observing position, that is, in the plane of the Sun's equator. The maximum predicted magnitude of this effect ranges from an increase in photometric variability of 6 (Schatten 1993) to 1.3 (Knaack et al. 2001) times that observed in the equatorial plane as the viewing angle is altered. Fortunately, it has been observed for both non-transiting (Le Bouquin et al. 2009) and transiting planets that there is a preference for the orbital angular momentum vector of the planet and the spin axis of the host star to be aligned. For the case of transiting planets there is a population of hot Jupiters with orbits that are not aligned with the stellar equator (e.g. Triaud et al. 2010); however, Triaud (2011) finds that the degree of orbital misalignment is related to the age of the star, and in particular is reduced for older systems, possibly as a result of tidal interactions between the planet and the star. Consequently, as the planets of interest transit, the equator of the target star is likely to be preferentially aligned with the line of sight. Secondly, while the survey conducted by Lockwood et al. (2007) into the photometric variability of Sun-like stars is the most temporally complete, it is not the only survey. In particular, the survey of Henry et al. (2000) has looked at the photometric variability of extra-solar planet host stars detected by the radial velocity technique. Within this subset, the Sun appears typical. Unfortunately, as only relatively magnetically inactive stars are chosen as targets for radial velocity searches, and long-term photometric variability increases with increasing magnetic activity (e.g Radick et al. 1998), this set of stars is statistically biased. Consequently, the study of Henry et al. (2000) cannot be used to argue that the Sun's photometric stability is representative of most stars. However, while not all planetary hosts will display the same photometric stability as the Sun e.g. CoRoT-2b (Alonso et al. 2008), this study does indicate that there is a substantial subset of planetary host stars which will. As this is a first investigation into the effect of realistic stellar photometric noise on the TTVp technique, and solar photometric noise is relatively representative of stellar photometric noise, solar data were used as a test bed for this analysis. However, we note that the procedure described here could be applied to the photometry of other stars.

4.3 Derivation of ϵj

For the case of the Sun, equation (10) becomes
\begin{eqnarray} \epsilon _{j} = \frac{N_{\rm obs}L_o}{A_{\rm p} + A_{\rm m}} \epsilon _{\odot }, \end{eqnarray}
(30)
where ϵ⊙ is given by equation (15). By evaluating ϵ⊙ for enough segments of solar light curve, an observed distribution for ϵ⊙, and correspondingly ϵj, can be constructed.

As, in this case, the distribution of ϵ⊙ will be numerically determined, a finite number of values of the independent variables, in this case the exposure time Δt and the observing duration Tobs, need to be selected. It was decided to use observing durations of 0.5, 1, 2, 4, 8, 12, 24 and 36 h to cover the most extreme systems likely to be encountered. For comparison, GJ 436 b, a planet with a relatively short transit duration, takes just over 1 h to transit its host, while the Earth would take up to 13 h to transit the central chord of the Sun. In addition, it was also decided to investigate exposure times representative of those used by the satellites CoRoT and Kepler. For the case of CoRoT, a 16 min exposure time is used for its catalogue of approximately 12 000 targets, but it is also capable of a 32 s readout for a subset of 1000 highlighted sources (Quentin et al. 2006). For the case of Kepler, a 30 min exposure time is used for its set of approximately 150 000 sources, but it is also capable of 1 min exposures for a subset of 512 highlighted sources (Borucki et al. 2008). So, ideally, it would be useful to compare the distribution of ϵj for the case of ‘short’ exposures (32 s or 1 min) and ‘long’ exposures (16 or 30 min).

As the two photometers on the VIRGO module, PMO6V and DIARAD have exposure times of 1 and 3 min, respectively, it was decided to use these individual exposures as the ‘short’ exposures, and artificially construct the long exposures, by dividing the data into 30 min segments and then co-adding all exposures within each segment. To investigate the suitability of the data from the two photometers for this analysis, the number of valid data segments for each pair of possible exposure time and observing duration was determined for each photometer (see Table 1). As a result of the dearth of contiguous sequences of data within the PMO6V data set, it was decided to use the DIARAD data, and consequently to use 3 min as the ‘short’ exposure time.

Table 1

Number of complete lengths of data of a given duration, Tobs, for each of the four possible data sets.

DIARADDIARADPMOV6VPMOV6V
Tobs3 min30 min1 min30 min
30 min163 039–132 185–
1 h78 97176 95663 80261 681
2 h37 20836 24429 73629 604
4 h16 50316 11312 65712 153
8 h6471631840773679
12 h34383365475462
16 h20802038238228
24 h8248057371
36 h3173075453
DIARADDIARADPMOV6VPMOV6V
Tobs3 min30 min1 min30 min
30 min163 039–132 185–
1 h78 97176 95663 80261 681
2 h37 20836 24429 73629 604
4 h16 50316 11312 65712 153
8 h6471631840773679
12 h34383365475462
16 h20802038238228
24 h8248057371
36 h3173075453
Open in new tab
Table 1

Number of complete lengths of data of a given duration, Tobs, for each of the four possible data sets.

DIARADDIARADPMOV6VPMOV6V
Tobs3 min30 min1 min30 min
30 min163 039–132 185–
1 h78 97176 95663 80261 681
2 h37 20836 24429 73629 604
4 h16 50316 11312 65712 153
8 h6471631840773679
12 h34383365475462
16 h20802038238228
24 h8248057371
36 h3173075453
DIARADDIARADPMOV6VPMOV6V
Tobs3 min30 min1 min30 min
30 min163 039–132 185–
1 h78 97176 95663 80261 681
2 h37 20836 24429 73629 604
4 h16 50316 11312 65712 153
8 h6471631840773679
12 h34383365475462
16 h20802038238228
24 h8248057371
36 h3173075453
Open in new tab

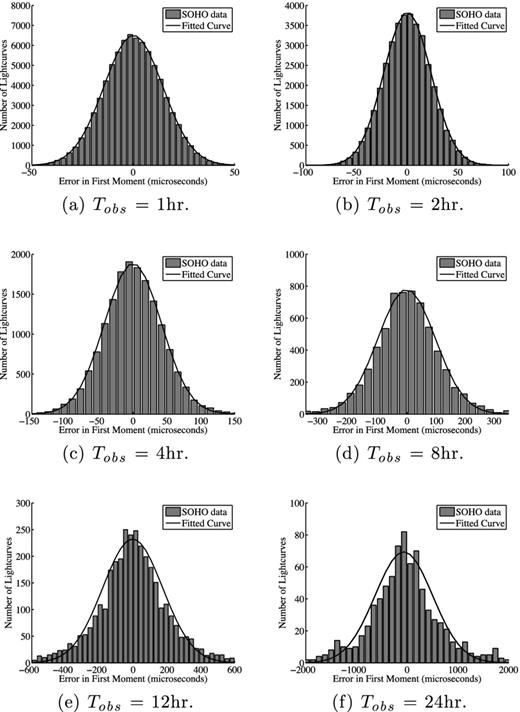
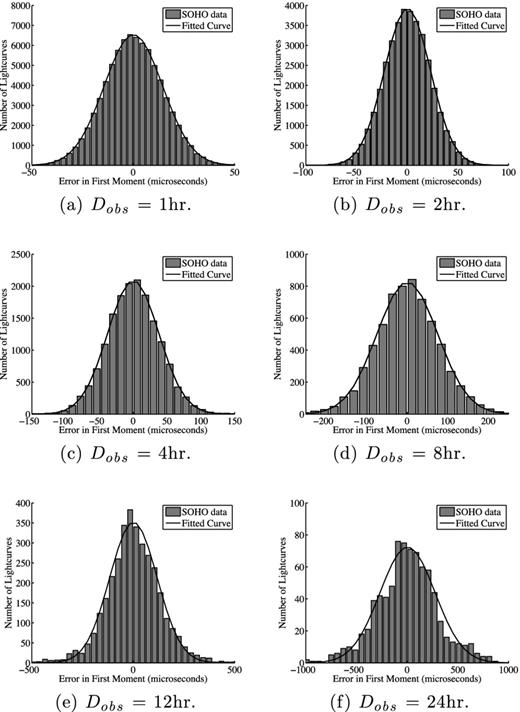
The distribution of ϵ⊙ was calculated for each pair of exposure time and observation duration as follows. The raw level 1.8 irradience data from SoHO were converted to level 2 data using the tables given on the SoHO website.6 These data then needed to be analysed. For the case of 3 min exposures, this involved dividing the sequence into sequences of valid data of length Tobs. For the case of 30 min exposures, the data were first pre-processed by dividing it into sets of 10 contiguous exposures and treating each of these lengths as a single exposure. This was done by co-adding the exposures for the case where all the exposures were valid, or by recording an invalid intensity for the case where they were not. These pre-processed data were then divided into lengths of valid data of length Tobs. ϵ⊙, the difference between the central time and first moment of each of these lengths, was then calculated using equations (11) and (15), and the values binned to produce a frequency histogram (see Fig. 4). As all the distributions were approximately normal and had zero mean, they could be fully described by their standard deviation. The values of σ⊙, the standard deviation of ϵ⊙, along with their associated observing duration and exposure time are presented in Table 2.

Figure 4.
The observationally determined distribution of ϵ⊙ (grey bar) for the case of realistic solar photometric noise for six different length observing windows. For observing windows less than 12 h long, the distribution of ϵ⊙ is very nearly a normal distribution (black line). Note the different scales.
Open in new tabDownload slide

The observationally determined distribution of ϵ⊙ (grey bar) for the case of realistic solar photometric noise for six different length observing windows. For observing windows less than 12 h long, the distribution of ϵ⊙ is very nearly a normal distribution (black line). Note the different scales.

Table 2

The size of σ⊙ for the case of realistic stellar noise, as a function of length of observation window, Tobs, and exposure time Δt. The value in parentheses is the error in the last significant figure.

TobsΔt = 3 minΔt = 30 min
30 min9.49(1) × 10−3 s–
1 h1.4507(2) × 10−2 s1.248(1) × 10−2 s
2 h2.3201(7) × 10−2 s2.232(1) × 10−2 s
4 h4.178(4) × 10−2 s4.160(4) × 10−2 s
8 h9.863(3) × 10−2 s9.77(2) × 10−2 s
12 h1.78(1) × 10−1 s1.760(4) × 10−1 s
16 h2.85(1) × 10−1 s2.86(1) × 10−1 s
24 h5.6(1) × 10−1 s5.7(1) × 10−1 s
36 h1.15(4) s1.14(3) s
TobsΔt = 3 minΔt = 30 min
30 min9.49(1) × 10−3 s–
1 h1.4507(2) × 10−2 s1.248(1) × 10−2 s
2 h2.3201(7) × 10−2 s2.232(1) × 10−2 s
4 h4.178(4) × 10−2 s4.160(4) × 10−2 s
8 h9.863(3) × 10−2 s9.77(2) × 10−2 s
12 h1.78(1) × 10−1 s1.760(4) × 10−1 s
16 h2.85(1) × 10−1 s2.86(1) × 10−1 s
24 h5.6(1) × 10−1 s5.7(1) × 10−1 s
36 h1.15(4) s1.14(3) s
Open in new tab
Table 2

The size of σ⊙ for the case of realistic stellar noise, as a function of length of observation window, Tobs, and exposure time Δt. The value in parentheses is the error in the last significant figure.

TobsΔt = 3 minΔt = 30 min
30 min9.49(1) × 10−3 s–
1 h1.4507(2) × 10−2 s1.248(1) × 10−2 s
2 h2.3201(7) × 10−2 s2.232(1) × 10−2 s
4 h4.178(4) × 10−2 s4.160(4) × 10−2 s
8 h9.863(3) × 10−2 s9.77(2) × 10−2 s
12 h1.78(1) × 10−1 s1.760(4) × 10−1 s
16 h2.85(1) × 10−1 s2.86(1) × 10−1 s
24 h5.6(1) × 10−1 s5.7(1) × 10−1 s
36 h1.15(4) s1.14(3) s
TobsΔt = 3 minΔt = 30 min
30 min9.49(1) × 10−3 s–
1 h1.4507(2) × 10−2 s1.248(1) × 10−2 s
2 h2.3201(7) × 10−2 s2.232(1) × 10−2 s
4 h4.178(4) × 10−2 s4.160(4) × 10−2 s
8 h9.863(3) × 10−2 s9.77(2) × 10−2 s
12 h1.78(1) × 10−1 s1.760(4) × 10−1 s
16 h2.85(1) × 10−1 s2.86(1) × 10−1 s
24 h5.6(1) × 10−1 s5.7(1) × 10−1 s
36 h1.15(4) s1.14(3) s
Open in new tab

As can be seen in Table 2, the values of σ⊙ for both exposure times, for Tobs greater than 4 h agree to within a few per cent. As the vast majority of realistic values of Tobs are likely to be greater than 4 h, these two data sets are effectively equal. As can be seen from Fig. 5, the values of ϵj calculated for the cases of realistic solar noise and white noise of the same power7 are in close agreement with those calculated for the case of noise for short transit durations, but diverge for longer transit durations. This divergence is the result of the longer transit durations ‘letting in’ more of the lower frequency components of the noise. Disturbingly, in the investigation by Szabó et al. (2006), they found that the most easily detectable moons are around planets far from their host, with correspondingly long transit durations.

Figure 5.
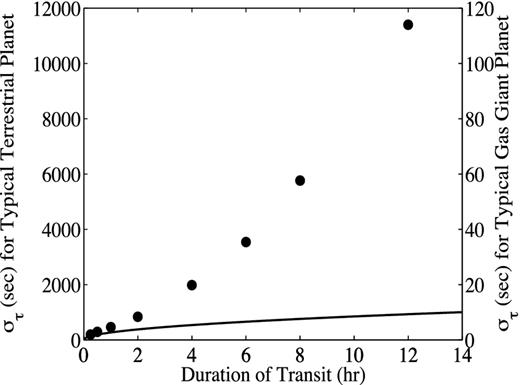
Comparison between measured errors, ϵj using solar light curves (dots) and theoretically predicted ϵj using white noise with the same power as the noise in the solar light curves (thick line). As the results for 3 and 30 min exposures are so similar, only the data for three minute exposures are shown. These relations are shown for the case of the transit of a gas giant (Ap/L0Ntra = 10− 2) and a terrestrial planet (Ap/L0Ntra = 10− 4), assuming Tobs ≈ 2Ttra.
Open in new tabDownload slide

Comparison between measured errors, ϵj using solar light curves (dots) and theoretically predicted ϵj using white noise with the same power as the noise in the solar light curves (thick line). As the results for 3 and 30 min exposures are so similar, only the data for three minute exposures are shown. These relations are shown for the case of the transit of a gas giant (Ap/L0Ntra = 10− 2) and a terrestrial planet (Ap/L0Ntra = 10− 4), assuming Tobs ≈ 2Ttra.

Performing a quadratic fit to this data, the following formula for the standard deviation, σ⊙ is obtained
\begin{eqnarray} \sigma _{\odot } &=& 5.32 \times 10^{-3}{\rm \,s} + 6.48 \times 10^{-3} {\rm \,s h}^{-1} T_{\rm obs} +\, 6.96 \nonumber\\ &&\times 10^{-4} {\rm \,s h}^{-2} T_{\rm obs}^2. \end{eqnarray}
(31)
Substituting this into equation (30) and rearranging using the expression Nobs = Ntra(Tobs/Ttra) gives
\begin{eqnarray} \sigma _\epsilon &=& 103.7\,{\rm s} \left[\frac{L_{0}N_{{\rm tra}}}{100(A_{\rm p} + A_{\rm m})}\right] \left[\frac{T_{\rm tra}}{13\, {\rm h}}\right]^{-1} \nonumber\\ &&\times \bigg[0.010 \left(\frac{T_{\rm obs}}{24 \,{\rm h}}\right) + 0.277 \left(\frac{T_{\rm obs}}{24 \,{\rm h}}\right)^2 +\, 0.714 \left(\frac{T_{\rm obs}}{24 {\rm \,h}}\right)^3\bigg],\nonumber\\ \end{eqnarray}
(32)
where we note that the comparison system is a Jupiter-like planet orbiting a Sun-like star at 1 au and the noise budget is dominated by solar-like photometric noise.

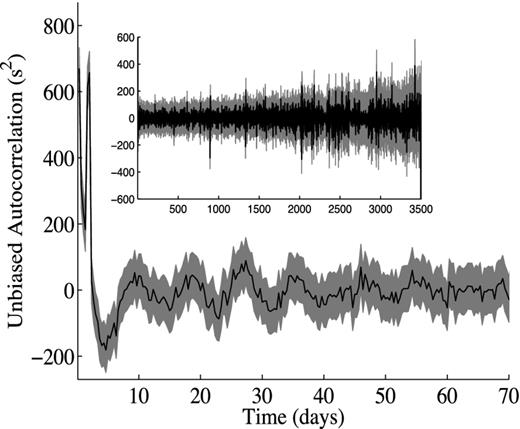
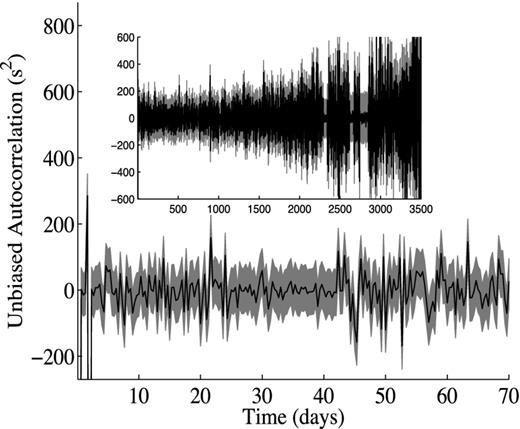
In addition to determining the distribution of ϵj, it is also important to determine whether or not consecutive values of ϵj are correlated. Consequently, the auto-correlation8 of the sequence of ϵj values was computed (see Fig. 6). Physically, we would expect that there would be some correlation on time-scales comparable with the rotational period of the Sun (≈25 d) as the gradient of the luminosity is also correlated over those time-scales. As can be seen from Fig. 6, ϵj is effectively uncorrelated for all transiting planets with orbital periods above 40 d. Assuming a host planet with a Jupiter-like Q-value of 105, we have from Barnes & O'Brien (2002) that the shortest interval between transits, given that the planet has a Ganymede-sized moon is approximately one month. For the case where the Q-value is much higher, 1012–1013, for example, as a result of dependence of the Q-value on the orbital period of the moon, the minimum planetary orbital period, i.e. the minimum time between transits, for giant planets with large dynamically stable moons reduces to a couple of days (Cassidy et al. 2009). Consequently, for the case where the host planet has a Q-value of 105, ϵj is uncorrelated and for the case where the Q-value is higher and the planet orbital period shorter, ϵj may be correlated.

Figure 6.
Normalized autocorrelation function of ϵj (black line) calculated using realistic stellar noise for the case where the observing window is 8 h. For reference, the one sigma error bars (grey) are also shown. As short period planets are more likely to be discovered by the transit technique than longer period planets as a result of the higher transit probabilities of short period planets, the inner section of the autocorrelation function is shown in the main plot. For completeness, the full autocorrelation function is shown in the inset.
Open in new tabDownload slide

Normalized autocorrelation function of ϵj (black line) calculated using realistic stellar noise for the case where the observing window is 8 h. For reference, the one sigma error bars (grey) are also shown. As short period planets are more likely to be discovered by the transit technique than longer period planets as a result of the higher transit probabilities of short period planets, the inner section of the autocorrelation function is shown in the main plot. For completeness, the full autocorrelation function is shown in the inset.

Now that the case of raw realistic stellar noise has been investigated, the analysis can be refined by ‘filtering’ the data to remove long-term trends. In the case to be investigated these trends are due to the advection of active regions across the solar surface.

5 FILTERED NOISE: OBSERVATIONAL DERIVATION

5.1 Introduction to filtered noise

As the presence of red noise in light curves significantly alters the detection probability of transiting planets (e.g. Borucki et al. 1985; Pont, Zucker & Queloz 2006), a range of methods for reducing the effect of this type of noise have been investigated. These include methods where the physical processes believed to be underlying the red noise are modelled (Lanza et al. 2003), methods where the red noise is pre-processed with a whitening filter before transit detection (e.g. Carpano, Aigrain & Favata 2003; Guis & Barge 2005; Moutou et al. 2005, team 3) and methods where the filtering is performed in combination with a transit finding algorithm (e.g. Jenkins 2002).

As, for this investigation, moon searches will be conducted on a star by star basis, it was decided to use a method which modelled the physical processes appropriate to each star. Consequently, the method selected was the three-spot model method of Lanza et al. (2003) as, it was developed using SoHO data, it was designed to be adapted to model photometric variation for any Sun-like star (Lanza, Rodonò & Pagano 2004), and it has been used to model variability in real stellar data, specifically, the CoRoT targets CoRoT-2 (Lanza et al. 2009b) and CoRoT-4 (Lanza et al. 2009a).9 To provide a reality check, the results for this filtering technique were compared with those calculated using the a simple high-pass filter, such as the one investigated by Carpano et al. (2003).

5.2 Description of the three-spot model

One source of long-term photometric variability of the Sun is rotational modulation of the active regions, that is, regions on the Sun's surface where the magnetic field strengths are high. Active regions are complex structures comprising of clusters of magnetic phenomenon such as darker sunspots and brighter faculae. While there is a lognormal distribution of active region sizes (Bogdan et al. 1988), Lanza et al. (2003) determined that the long-term photometric variation of the Sun could be effectively modelled by only accounting for three distinct active regions on the face of the Sun in any given 14 d window.

To perform the fitting required to implement this ‘three-spot model’, the extent to which the substructure of the active regions needs to be modelled must be determined. In particular, the issues of active region composition, evolution and distribution across the solar surface need to be explored. While the ratio between the area of faculae and sunspots changes as a function of active region size and position in the solar cycle (Chapman, Cookson & Dobias 1997), Lanza et al. (2003) assumed a constant ratio of sunspot area to facular area of 1:10. Consequently, this assumption was also used for this work. Not only are active regions composed of complex structures, these structures evolve over time. Fortunately, the time-scale for active region evolution is longer than that for solar rotation. Consequently, the solar intensity data can be divided into blocks, such that it can be assumed that the position and size of an active region does not change within the block. Lanza et al. (2003) found that a good compromise between modelling the effect of solar rotation and minimizing active region evolution was 14 d.10 Consequently, for this work, data were divided into 14 d segments, each consisting of 6720 data points. In addition, as active regions are generally much smaller than the radius of the Sun, the entire active region can be modelled as having the same μ value, where the μ value is given by the cosine of the angle between the surface normal and the direction of the line of sight at that position on the solar surface. Consequently, three variables are required to model each active region, two describing the position of the region on the face of the Sun, and one variable describing the effective area of the active region. With these assumptions and simplifications in mind, the fitting model can be introduced.

Following Lanza et al. (2003), this results in the following model for L, the photometric intensity of the Sun
\begin{eqnarray} L - L_0 &=& L_r + L_0 \mathcal {C} \sum _{i = 1:\mu _i > 0}^3 A_i \mu _i [ a_p + b_p \mu _i + c_p \mu _i^2] \nonumber\\ && \times \, [ (c_{\rm s}-1)+Q(c_{\rm f} + c_{\rm f}^{\prime } \mu _i - 1)], \end{eqnarray}
(33)
where the μi correspond to the μ values of each of the sunspots, where μi will be defined in equation (34). For this study the parameters relating to the intrinsic properties of the Sun, L0, |$\mathcal {C}$|⁠, ap, bp, cp, Q, cs, cf and c′f were set to the same values as used in Lanza et al. (2003). For completeness, the values and the purpose of each of these model parameters will be stated and explained. The limb darkening parameters, ap, bp, cp and |$\mathcal {C}$| were set to 0.36, 0.84, −0.20 and 4.88, respectively. In addition, the parameter cs, which describes the dependence of sunspot luminosity on position was set to 0.67, and the parameters cf and c′f which describe the dependence of facular luminosity as a function of position were set to the solar values of 1.115 and −0.115 (Foukal, Harvey & Hill 1991). Q, the ratio of sunspot area to faculae area, was set to 10. As discussed in Chapman et al. (1997), this ratio can change throughout the 11 yr solar cycle.
In addition to the variables remaining constant for all fits, 11 variables are allowed to change. First, the additional background intensity is described by Lr. Secondly, the relative areas of the three sunspots are given by A1, A2 and A3. Finally, the effect of the position of the sunspots is parametrized by their μ value, defined as
\begin{eqnarray} \mu _i = \cos i_{{\rm Sun}} \sin \theta _i + \sin i_{{\rm Sun}} \cos \theta _i \cos (\lambda _i + \Omega t - l_0), \end{eqnarray}
(34)
where Ω is the angular velocity of the Sun due to its rotation, l0 is the longitude of the central meridian of the solar disc and λi and θi are the longitude and latitude of the ith sunspot. Consequently, the 11 variables which must be fitted for this model are A1, λ1, θ1, A2, λ2, θ2, A3, λ3, θ3, Lr and Ω for each 14 d segment of data. The fitted value of these variables is such that the χ2 value, defined as
\begin{eqnarray} \chi ^2 = \frac{1}{M}\sum _{i=1}^M \frac{(L(t_i) - L_{{\rm fit}}(t_i))^2}{\sigma ^2} \end{eqnarray}
(35)
is minimized, where L is the observed luminosity, Lfit is the fitted luminosity and σ = 2 × 10−5L0.

In addition to fitting these 11 variables, there are a number of constraints imposed by the physics of the problem on the values the variables can take, in particular, with respect to sunspot areas and the rotation rate. The values of the sunspot areas were constrained to be positive and below a threshold size. Lanza et al. (2003) calculated this threshold size to be 8.2 × 10−4 by assuming that the largest dip in the data were due to the rotational modulation of a single active region. However, as the span of SoHO data used for this work is longer than that used by Lanza et al. (2003), the upper limit derived may not be able to explain all the behaviour in the light curve analysed. In particular, there is a region of apparently high sunspot activity occurring between 2003 October 15 and November 11 containing dips which correspond to spots with a relative area of 1.7 × 10−3. Consequently, the upper limit of 8.2 × 10−4 on sunspot area was used for all 14 d blocks except for the two blocks between the 2003 October 15 and the November 11, where the limit 1.7 × 10−3 was used. In addition to sunspot area, solar rotation rate is an observationally constrained quantity. For this work, the limits of 23–33.5 d on the solar rotation period, derived by Lanza et al. (2003), were used without modification.

For this work, the simplex method described by Lagarias et al. (1998), implemented using the multidimensional matlab fitting function fminsearch was used to complete this constrained minimization. This approach required that starting values and a function for calculating χ2 were provided to the method. The starting values for each fit were either taken from the previous fit or manually estimated. As suggested by Lanza et al. (2003), the variables, A1, λ1, θ1, A2, λ2, θ2, A3, λ3, θ3 and Lr, were fitted independently to Ω, which was then optimized. In addition, to ensure that the sunspot areas remained within the physical bounds, the function which returned the χ2 value was modified such that it returned a large value if active region areas became too large or negative. Unfortunately, while these inputs resulted in a set of acceptable values for the fitting parameters being returned, issues with the simplex method itself, such as the fact that it may not converge (e.g. McKinnon 1999), required that a number of tests were conducted to ensure that the true minimum had been found.

To ensure that the fit had converged, three checks were made. First, each fit was checked by eye. Secondly, for each block of data, the fitting procedure was repeated, that is, the output of the preceding fit was used as the starting variables for the next fit, until the fitted variables remained approximately the same between two successive fits. Thirdly, the dependence of χ2 on each of the 11 fitting parameters was checked for 29 randomly selected blocks. All curves inspected indicated that for these blocks the simplex method had converged to the χ2 minimum.

Once the fitting had been performed, the best-fitting parameters were recorded. These parameters were in turn used to produce a model light curve. By subtracting the model from the data and then adding the average intensity, a detrended light curve was constructed.

5.3 Derivation of ϵj

This set of detrended data was then subjected to the same procedure as that of the unfiltered red noise (see Section 4.3) to determine σϵ as a function of transit area, transit duration and exposure time. The results are presented in Table 3 and Figs 7 and 8. To provide a reality check, these results were compared to results obtained using a different filtering method. For simplicity, the high-pass filter described in Carpano et al. (2003) was selected. The calculated values of σϵ produced by both methods agree to within 5 per cent.

Figure 7.
The observationally determined distribution of ϵ⊙ (grey bar) for the case of solar photometric noise filtered using the method of Lanza et al. (2003), for six different length observing windows. Note that the distribution of ϵ⊙ is very nearly a normal distribution (black line). Note the different scales.
Open in new tabDownload slide

The observationally determined distribution of ϵ⊙ (grey bar) for the case of solar photometric noise filtered using the method of Lanza et al. (2003), for six different length observing windows. Note that the distribution of ϵ⊙ is very nearly a normal distribution (black line). Note the different scales.

Figure 8.
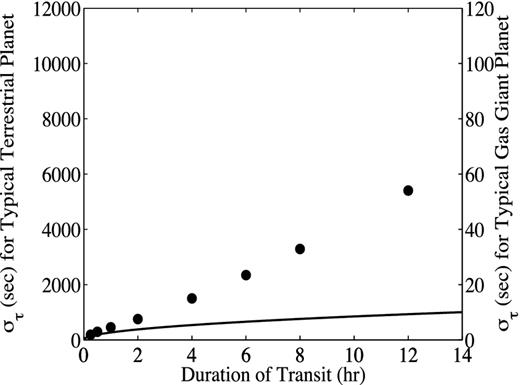
Comparison between measured errors, ϵj using solar light curves which have been ‘filtered’ using the method of Lanza et al. (2003) (dots) and theoretically predicted ϵj using white noise with the same power as the noise in the solar light curves (thick line). These relations are shown for the case of the transit of a gas giant (Ap/L0Ntra = 10− 2) and a terrestrial planet (Ap/L0Ntra = 10− 4), assuming Tobs ≈ 2Ttra.
Open in new tabDownload slide

Comparison between measured errors, ϵj using solar light curves which have been ‘filtered’ using the method of Lanza et al. (2003) (dots) and theoretically predicted ϵj using white noise with the same power as the noise in the solar light curves (thick line). These relations are shown for the case of the transit of a gas giant (Ap/L0Ntra = 10− 2) and a terrestrial planet (Ap/L0Ntra = 10− 4), assuming Tobs ≈ 2Ttra.

Table 3

The size of σ⊙ for the case of realistic stellar noise which has been filtered using the method of Lanza et al. (2003), as a function of length of observation window, Tobs, and exposure time, Δt. The value in parentheses is the error in the last significant figure.

TobsΔt = 3 minΔt = 30 min
30 min9.440(5) × 10−3 s–
1 h1.4433(2) × 10−2 s1.244(1) × 10−2 s
2 h2.264(1) × 10−2 s2.181(2) × 10−2 s
4 h3.77(1) × 10−2 s3.77(1) × 10−2 s
8 h7.48(1) × 10−2 s7.417(7) × 10−2 s
12 h1.169(2) × 10−1 s1.157(3) × 10−1 s
16 h1.640(8) × 10−1 s1.639(6) × 10−1 s
24 h2.71(2) × 10−1 s2.72(2) × 10−1 s
36 h4.3(2) × 10−1 s4.2(2) × 10−1 s
TobsΔt = 3 minΔt = 30 min
30 min9.440(5) × 10−3 s–
1 h1.4433(2) × 10−2 s1.244(1) × 10−2 s
2 h2.264(1) × 10−2 s2.181(2) × 10−2 s
4 h3.77(1) × 10−2 s3.77(1) × 10−2 s
8 h7.48(1) × 10−2 s7.417(7) × 10−2 s
12 h1.169(2) × 10−1 s1.157(3) × 10−1 s
16 h1.640(8) × 10−1 s1.639(6) × 10−1 s
24 h2.71(2) × 10−1 s2.72(2) × 10−1 s
36 h4.3(2) × 10−1 s4.2(2) × 10−1 s
Open in new tab
Table 3

The size of σ⊙ for the case of realistic stellar noise which has been filtered using the method of Lanza et al. (2003), as a function of length of observation window, Tobs, and exposure time, Δt. The value in parentheses is the error in the last significant figure.

TobsΔt = 3 minΔt = 30 min
30 min9.440(5) × 10−3 s–
1 h1.4433(2) × 10−2 s1.244(1) × 10−2 s
2 h2.264(1) × 10−2 s2.181(2) × 10−2 s
4 h3.77(1) × 10−2 s3.77(1) × 10−2 s
8 h7.48(1) × 10−2 s7.417(7) × 10−2 s
12 h1.169(2) × 10−1 s1.157(3) × 10−1 s
16 h1.640(8) × 10−1 s1.639(6) × 10−1 s
24 h2.71(2) × 10−1 s2.72(2) × 10−1 s
36 h4.3(2) × 10−1 s4.2(2) × 10−1 s
TobsΔt = 3 minΔt = 30 min
30 min9.440(5) × 10−3 s–
1 h1.4433(2) × 10−2 s1.244(1) × 10−2 s
2 h2.264(1) × 10−2 s2.181(2) × 10−2 s
4 h3.77(1) × 10−2 s3.77(1) × 10−2 s
8 h7.48(1) × 10−2 s7.417(7) × 10−2 s
12 h1.169(2) × 10−1 s1.157(3) × 10−1 s
16 h1.640(8) × 10−1 s1.639(6) × 10−1 s
24 h2.71(2) × 10−1 s2.72(2) × 10−1 s
36 h4.3(2) × 10−1 s4.2(2) × 10−1 s
Open in new tab

This agreement suggests that the behaviour of ϵ⊙ is not a strong function of the filtering method selected.

In addition, from Table 3 it can be seen that as the data for 3 and 30 min are effectively equivalent, only one of these data sets needs to be used. Fitting a line to the 3 min data points gives
\begin{eqnarray} \sigma _{\odot } = -2.16 \times 10^{-3}\, {\rm s} + 1.21 \times 10^{-3} {\rm \,s h}^{-1} T_{\rm obs}. \end{eqnarray}
(36)
Substituting this into equation (30) and using the expression Nobs = Ntra(Tobs/Ttra) gives
\begin{eqnarray} \sigma _\epsilon &=& 53.2{\rm \,s} \left[\frac{100(A_{\rm p} + A_{\rm m})}{L_{0}N_{{\rm tra}}}\right]^{-1} \left[\frac{T_{\rm tra}}{13 {\rm \,h}}\right]^{-1} \nonumber\\ && \times \left[ \left(-8 \times 10^{-3} \left(\frac{T_{\rm obs}}{24\,{\rm h}}\right) + 1.008 \left(\frac{T_{\rm obs}}{24 {\rm \,h}}\right)^2 \right)\right], \end{eqnarray}
(37)
where we note that comparison system is a Jupiter-like planet orbiting a Sun-like star at 1 au where the pre-filtering noise budget is dominated by solar-like photometric noise. In addition, the autocorrelation (see Fig. 9) was again calculated, and it was found that ϵj is again effectively uncorrelated from transit to transit.
Figure 9.
Normalized autocorrelation function of ϵj (black line) calculated using filtered stellar noise for the case where the observing window is 8 h. For reference, the one sigma error bars (grey) are also shown. As short period planets are more likely to be discovered by the transit technique, the inner section of the autocorrelation function is shown in the main plot. For completeness, the full autocorrelation function is shown in the inset.
Open in new tabDownload slide

Normalized autocorrelation function of ϵj (black line) calculated using filtered stellar noise for the case where the observing window is 8 h. For reference, the one sigma error bars (grey) are also shown. As short period planets are more likely to be discovered by the transit technique, the inner section of the autocorrelation function is shown in the main plot. For completeness, the full autocorrelation function is shown in the inset.

6 SIGNAL TO NOISE AS A FUNCTION OF TRANSIT DURATION

Szabó et al. (2006) found that when the noise on the light curve was white, the further a transiting planet was from its host star, the more detectable are its moons by the TTVp method. As discussed previously, not all noise sources relevant to transit surveys are white. Consequently, it would be useful to investigate whether this result holds for realistic or filtered stellar noise.

The detectability of moons is defined by the size of the timing perturbation they produce relative to the timing noise. So, to determine how the detectability of a moon changes with the transit duration Ttra, the relationship between the size of the timing signal due to a moon and Ttra must be determined and compared with the relationship between the timing noise and Ttra.

Simon, Szatmáry & Szabó (2007) investigated the approximate size of Δτ for the case where the orbit of the satellite was not inclined and where orbital motion of the moon during transit could be neglected. From equation 15 of Simon et al. (2007) we have that the maximum value of Δτ is approximately given by
\begin{eqnarray} \Delta \tau _{\rm max} = \frac{a_{\rm {pm}}}{v_{\rm {tr}}}\left| \frac{R_{\rm m}^2}{R_{\rm p}^2} - \frac{M_{\rm m}}{M_{\rm p}} \right|, \end{eqnarray}
(38)
where apm is the distance between the planet and the moon, vtr is the velocity of the planet–moon barycentre across the face of the star, Rp and Rm are the radii of the planet and moon and Mp and Mm are the masses of the planet and moon, respectively.
While this equation was derived specifically for the case of maximum projected separation between the planet and the moon, it can be modified to describe Δτ for the case where the moon is at any other position in its orbit. In particular, replacing apm with apm, proj, the projected separation between the planet and the moon, gives
\begin{eqnarray} \Delta \tau \approx T_{\rm tra}\frac{a_{\rm {pm,proj}}}{R_{\rm ch}}\left| \frac{R_{\rm m}^2}{R_{\rm p}^2} - \frac{M_{\rm m}}{M_{\rm p}} \right|, \end{eqnarray}
(39)
where vtr has been written as Rch/Ttra, where Rch is the length of the chord the planet traverses across the star's face. Thus, given that the assumption that moon orbital motion during transit can be neglected holds e.g. due to a short planetary transit or low moon orbital velocity, the size of Δτ will be proportional to the transit duration.
As ϵj is defined in terms of the observing duration, Tobs, not the transit duration, Ttra, equations (28), (31) and (36) must be rewritten in terms of Ttra. As the size of the region of light curve affected by the transit of a given planet–moon system is proportional to Ttra, we choose the relationship between Tobs and Ttra to be
\begin{eqnarray} T_{\rm obs} = \gamma T_{\rm tra}, \end{eqnarray}
(40)
where γ is a constant larger than 1.
Substituting this definition into equations (29), (31) and (36) gives
\begin{eqnarray} \sigma _\epsilon &=& 47.9{\rm \,s} \left[\left(\frac{\sigma _L/L_0}{3.95 \times 10^{-4}}\right)\left(\frac{\Delta t}{1 {\rm \,min}}\right)^{1/2}\right] \nonumber\\ && \times \, \left[\frac{100(A_{\rm p} + A_{\rm m})}{N_{{\rm tra}} L_0} \right]^{-1} \left[\left(\frac{\gamma T_{\rm tra}}{24 {\rm \,h}}\right)^{3/2} \left(\frac{T_{\rm tra}}{13 {\rm \,h}}\right)^{-1}\right], \end{eqnarray}
(41)
\begin{eqnarray} \sigma _\epsilon &=& 56.2 {\rm \,s} \left[\frac{L_{0}N_{{\rm tra}}}{100(A_{\rm p} + A_{\rm m})}\right]\nonumber\\ && \times \, \gamma \left[0.010 + 0.277 \left(\frac{\gamma T_{\rm tra}}{24\, {\rm h}}\right) + 0.714 \left(\frac{\gamma T_{\rm tra}}{24 {\rm \,h}}\right)^2\right], \end{eqnarray}
(42)
\begin{eqnarray} \sigma _\epsilon &=& 28.8{\rm \,s} \left[\frac{L_{0}N_{{\rm tra}}}{100(A_{\rm p} + A_{\rm m})}\right]\nonumber\\ && \times \, \gamma \left[ \left(-8 \times 10^{-3} + 1.008 \left(\frac{\gamma T_{\rm tra}}{24\, {\rm h}}\right) \right)\right]. \end{eqnarray}
(43)
In addition, for equations (42) and (43), for Ttra > 4 h, the constant terms in the Taylor expansion are small compared to the remaining terms. Neglecting these terms, equations (42) and (43) become
\begin{eqnarray} \sigma _\epsilon &=& 56.2 {\rm \,s} \left[\frac{L_{0}N_{{\rm tra}}}{100(A_{\rm p} + A_{\rm m})}\right]\nonumber\\ && \times \, \gamma \left[ 0.277 \left(\frac{\gamma T_{\rm tra}}{24\, {\rm h}}\right) + 0.714 \left(\frac{\gamma T_{\rm tra}}{24 {\rm \,h}}\right)^2\right], \end{eqnarray}
(44)
\begin{eqnarray} \sigma _\epsilon = 28.8{\rm \,s} \left[\frac{L_{0}N_{{\rm tra}}}{100(A_{\rm p} + A_{\rm m})}\right] \gamma \left[ 1.008 \left(\frac{\gamma T_{\rm tra}}{24 {\rm \,h}}\right) \right]. \end{eqnarray}
(45)

For the case of white noise it can be seen from equations (41) and (39) that as the amplitude of the timing signal increases as Ttra and the standard deviation of the timing noise increases as |$\sqrt{T_{\rm tra}}$|⁠, moons become more detectable as Ttra increases. This is in direct agreement with the work of Szabó et al. (2006). For the case where the noise is realistic stellar noise, from equation (44) we have that for short transit durations the standard deviation of the noise increases as Ttra, while for longer transit durations it increases as T2tra. Recalling from equation (39) that the amplitude of the timing signal increases as Ttra, we have that for short transit durations moon detectability is relatively independent of transit duration while for longer transit durations it decreases with increasing transit duration. Finally, for the case of filtered realistic noise, from equations (45) and (39) we have that both the timing signal and noise are proportional to Ttra, so for this case, moon detectability is independent of transit duration.

7 LIMITATIONS OF THIS ANALYSIS

The main assumption in this analysis is that the variability of a light curve during transit is the same as that out of transit. As light from a star is not uniformly distributed across its surface, this assumption will not always be valid. Indeed, finite structures such as starspots were predicted to (Hui & Seager 2002; Silva 2003) and do (e.g. Pont et al. 2007; Sanchis-Ojeda & Winn 2011) alter transit light curves. However, as discrete structures on the stellar surface should act to increase the variability of the light curve during transit, including effects due to these structures will act to make moons even less detectable than in the cases explored in this paper.

8 CONCLUSIONS

The effect of three different types of photometric noise, white, solar and filtered solar, on the TTVp moon detection technique are investigated. In particular, it is found that

  • the TTVp timing noise is approximately normally distributed and uncorrelated for most physically realistic planet–moon systems.

  • for the case of white photometric noise, where the noise budget is dominated by photon noise, as well as the cases of solar and filtered solar photometric noise, the timing error is approximately independent of the exposure time.

  • the timing noise for the case of solar photometric noise is dramatically larger than that for the equivalent amplitude white noise, and while filtering the light curve reduces this effect, it does not remove it.

  • assuming that the number of observed transits is held constant, for the case where the light curve is dominated by white, solar and filtered solar photometric noise, moon detectability using the TTVp technique increases with increasing transit duration, decreases with increasing transit duration and is independent of transit duration, respectively.

As a result of these findings, non-white photometric variability of host stars needs to be taken into account when analysing TTVp data or deriving moon detection thresholds. In addition, as this work focuses on the TTVp technique, research into the effect of non-white photometric noise on moon detection using other techniques is strongly recommended.

I thank Dr. Daniel Bayliss for informing me of the effect stellar red noise has on planetary transit detectability. In addition, I would like to thank Dr. Rosemary Mardling and Dr. Aidan Sudbury for their invaluable discussions and help improving the transparency of the derivations. Finally, my research was funded through the Faculty of Science Dean's Postgraduate Research Scholarship Scheme at Monash University. This financial assistance is gratefully acknowledged.

1

See, for example, http://exoplanet.eu/catalogue.php.

2

Kepler was designed to achieve a relative photometric precision of 2 × 10−5 over a 6.5 h exposure for the case of the 12th magnitude Sun-like host star (e.g. Basri, Borucki & Koch 2005). For the case of white noise, this translates to a relative photometric precision of 3.95 × 10−4 for a 1 min exposure.

3

A similar argument can be constructed for the case of dark noise, the noise caused by electron motion in the CCD chip during an exposure.

4

For the case where the relative photometric noise is independent of exposure time, such as the case explored by Szabó et al. (2006), σϵ will decrease with decreasing exposure time, which is in agreement with their findings.

5

http://seal.nascom.nasa.gov/cgi-bin/gui_plop

6

ftp://ftp.pmodwrc.ch/pub/data/irradiance/virgo/TSI/korr_tot6_001_0804.dat

7

Derived in Appendix B.

8

For this work the autocorrelation is defined as ∑jϵjϵj + k/Nk, where ϵj and ϵj + k represent all ϵj pairs separated by k × 8 h and Nk is the number of such pairs. This unbiased definition was selected to allow ease of comparison between values calculated for different lag times.

9

CoRoT-2 and CoRoT-4 were referred to as CoRoT-Exo-2 and CoRoT-Exo-4, respectively, at the time of publication of Lanza et al. (2009b) and Lanza et al. (2009a). These systems were renamed, along with a number of other CoRoT planetary systems in March 2009.

10

The optimum block length depends on the characteristics of the host star. For example, for the case of the Sun the optimal length is 14 d, while for the case of CoRoT-4 a length of 8.2 d (Lanza et al. 2009a) was used.

11

As there are twice as many terms in the sum in the numerator of the third term in equation (7) for the case of the short exposure time compared to that of the long exposure time, the numerator for the case of the short exposure time should be double that for the long exposure time. As the number of terms affects the denominator of the sum in exactly the same way, this effect will not affect τ.

REFERENCES

Agol
E.
, 
Steffen
J.
, 
Sari
R.
, 
Clarkson
W.
. , 
MNRAS
, 
2005
, vol. 
359
 pg. 
567
 
Crossref
Search ADS
 
Aigrain
S.
, et al. , 
A&A
, 
2009
, vol. 
506
 pg. 
425
 
Crossref
Search ADS
 
Alonso
R.
, et al. , 
A&A
, 
2008
, vol. 
482
 pg. 
L21
 
Crossref
Search ADS
 
Barnes
J. W.
, 
O'Brien
D. P.
. , 
AJ
, 
2002
, vol. 
575
 pg. 
1087
 
Crossref
Search ADS
 
Basri
G.
, 
Borucki
W. J.
, 
Koch
D.
. , 
New Astron. Rev.
, 
2005
, vol. 
49
 pg. 
478
 
Crossref
Search ADS
 
Basri
G.
, et al. , 
ApJ
, 
2010
, vol. 
713
 pg. 
L155
 
Crossref
Search ADS
 
Bogdan
T. J.
, 
Gilman
P. A.
, 
Lerche
I.
, 
Howard
R.
. , 
ApJ
, 
1988
, vol. 
327
 pg. 
451
 
Crossref
Search ADS
 
Borucki
W. J.
, 
Scargle
J. D.
, 
Hudson
H. S.
. , 
ApJ
, 
1985
, vol. 
291
 pg. 
852
 
Crossref
Search ADS
 
Borucki
W. J.
, et al. 
Sun
Y.-S.
, 
Ferraz-Mello
S.
, 
Zhou
J.-L.
. , 
Proc. IAU Symp. 249, Finding Earth-size planets in the habitable zone: the Kepler Mission
, 
2008
Cambridge
Cambridge Univ. Press
pg. 
17
  
in  
Brown
T. M.
, 
Charbonneau
D.
, 
Gilliland
R. L.
, 
Noyes
R. W.
, 
Burrows
A.
. , 
ApJ
, 
2001
, vol. 
552
 pg. 
699
 
Crossref
Search ADS
 
Carpano
S.
, 
Aigrain
S.
, 
Favata
F.
. , 
A&A
, 
2003
, vol. 
401
 pg. 
743
 
Crossref
Search ADS
 
Cassidy
T. A.
, 
Mendez
R.
, 
Arras
P.
, 
Johnson
R. E.
, 
Skrutskie
M. F.
. , 
ApJ
, 
2009
, vol. 
704
 pg. 
1341
 
Crossref
Search ADS
 
Chapman
G. A.
, 
Cookson
A. M.
, 
Dobias
J. J.
. , 
ApJ
, 
1997
, vol. 
482
 pg. 
541
 
Crossref
Search ADS
 
Dorren
J. D.
, 
Guinan
E. F.
. , 
AJ
, 
1982
, vol. 
87
 pg. 
1546
 
Crossref
Search ADS
 
Elser
S.
, 
Moore
B.
, 
Stadel
J.
, 
Morishima
R.
. , 
Icarus
, 
2011
, vol. 
214
 pg. 
357
 
Crossref
Search ADS
 
Fabrycky
D.
, 
Tremaine
S.
. , 
ApJ
, 
2007
, vol. 
669
 pg. 
1298
 
Crossref
Search ADS
 
Faigler
S.
, 
Mazeh
T.
. , 
MNRAS
, 
2011
, vol. 
415
 pg. 
3921
 
Crossref
Search ADS
 
Foukal
P.
, 
Harvey
K.
, 
Hill
F.
. , 
ApJ
, 
1991
, vol. 
383
 pg. 
L89
 
Crossref
Search ADS
 
Fröhlich
C.
, et al. , 
Sol. Phys.
, 
1995
, vol. 
162
 pg. 
101
 
Crossref
Search ADS
 
Fröhlich
C.
, et al. , 
Sol. Phys.
, 
1997
, vol. 
175
 pg. 
267
 
Crossref
Search ADS
 
Gillon
M.
, 
Pont
F.
, 
Moutou
C.
, 
Bouchy
F.
, 
Courbin
F.
, 
Sohy
S.
, 
Magain
P.
. , 
A&A
, 
2006
, vol. 
459
 pg. 
249
 
Crossref
Search ADS
 
Guis
V.
, 
Barge
P.
. , 
PASP
, 
2005
, vol. 
117
 pg. 
160
 
Crossref
Search ADS
 
Henry
G. W.
, 
Baliunas
S. L.
, 
Donahue
R. A.
, 
Fekel
F. C.
, 
Soon
W.
. , 
ApJ
, 
2000
, vol. 
531
 pg. 
415
 
Crossref
Search ADS
 
Holman
M. J.
, 
Murray
N. W.
. , 
Sci
, 
2005
, vol. 
307
 pg. 
1288
 
Crossref
Search ADS
 
Hui
L.
, 
Seager
S.
. , 
ApJ
, 
2002
, vol. 
572
 pg. 
540
 
Crossref
Search ADS
 
Jenkins
J. J.
. , 
ApJ
, 
2002
, vol. 
575
 pg. 
493
 
Crossref
Search ADS
 
Kipping
D. M.
. , 
MNRAS
, 
2009
, vol. 
396
 pg. 
1797
 
Crossref
Search ADS
 
Kipping
D.
, 
Bakos
G.
. , 
ApJ
, 
2011
, vol. 
733
 pg. 
36
 
Crossref
Search ADS
 
Knaack
R.
, 
Fligge
M.
, 
Solanski
S. K.
, 
Unruh
Y. C.
. , 
A&A
, 
2001
, vol. 
376
 pg. 
1080
 
Crossref
Search ADS
 
Kokoska
S.
, 
Zwillinger
D.
. , 
CRC Standard Probability and Statistics Tables and Formulae Student Edition
, 
2000
Boca Raton
Chapman & Hall

Google Scholar

OpenURL Placeholder Text

 
Lagarias
J. C.
, 
Reeds
J. A.
, 
Wright
M. H.
, 
Wright
P. E.
. , 
SIAM J. Optim.
, 
1998
, vol. 
9
 pg. 
112
 
Crossref
Search ADS
 
Lanza
A. F.
, 
Rodonò
M.
, 
Pagano
I.
, 
Barge
P.
, 
Llebaria
A.
. , 
A&A
, 
2003
, vol. 
403
 pg. 
1135
 
Crossref
Search ADS
 
Lanza
A. F.
, 
Rodonò
M.
, 
Pagano
I.
. , 
A&A
, 
2004
, vol. 
425
 pg. 
707
 
Crossref
Search ADS
 
Lanza
A. F.
, et al. , 
A&A
, 
2009a
, vol. 
506
 pg. 
255
 
Crossref
Search ADS
 
Lanza
A. F.
, 
Pagano
I.
, 
Leto
G.
, 
Messina
S.
, 
Barge
P.
, 
Baglin
A.
. 
Stempels
E.
. , 
AIP Proc. Conf. Vol. 1094, CoRoT and stellar activity: preliminary results from the modelling of CoRoT-Exo-2a
, 
2009b
New York
Am. Inst. Phys.
pg. 
684
  
in  
Le Bouquin
J.-B.
, 
Absil
O.
, 
Benisty
M.
, 
Massi
F.
, 
Mérand
A.
, 
Stefl
S.
. , 
A&A
, 
2009
, vol. 
498
 pg. 
L41
 
Crossref
Search ADS
 
Lockwood
G. W.
, 
Skiff
B. A.
, 
Radick
R. R.
. , 
ApJ
, 
1997
, vol. 
485
 pg. 
789
 
Crossref
Search ADS
 
Lockwood
G. W.
, 
Skiff
B. A.
, 
Henry
G. W.
, 
Henry
S.
, 
Radick
R. R.
, 
Baliunas
S. L.
, 
Donahue
R. A.
, 
Soon
W.
. , 
ApJSS
, 
2007
, vol. 
171
 pg. 
260
 
Crossref
Search ADS
 
Marcy
G. W.
, 
Butler
R. P.
. , 
PASP
, 
1992
, vol. 
104
 pg. 
270
 
Crossref
Search ADS
 
McKinnon
K. I. M.
. , 
SIAM J. Optim.
, 
1999
, vol. 
9
 pg. 
148
 
Crossref
Search ADS
 
McQuillan
A.
, 
Aigrain
S.
, 
Roberts
S.
. , 
A&A
, 
2012
, vol. 
539
 pg. 
A137
 
Crossref
Search ADS
 
Miralda-Escudé
J.
. , 
ApJ
, 
2002
, vol. 
564
 pg. 
1019
 
Crossref
Search ADS
 
Moutou
C.
, et al. , 
A&A
, 
2005
, vol. 
437
 pg. 
355
 
Crossref
Search ADS
 
Narita
N.
, et al. , 
PASJ
, 
2007
, vol. 
59
 pg. 
763
 
 
Oshagh
M.
, 
Boué
G.
, 
Haghighipour
N.
, 
Montalto
M.
, 
Figueira
P.
, 
Santos
N. C.
. , 
A&A
, 
2012
, vol. 
540
  
id.A62
Pont
F.
, 
Zucker
S.
, 
Queloz
D.
. , 
MNRAS
, 
2006
, vol. 
373
 pg. 
231
 
Crossref
Search ADS
 
Pont
F.
, et al. , 
A&A
, 
2007
, vol. 
476
 pg. 
1347
 
Crossref
Search ADS
 
Queloz
D.
, 
Eggenberger
A.
, 
Mayor
M.
, 
Perrier
C.
, 
Beuzit
J. L.
, 
Naef
D.
, 
Sivan
J. P.
, 
Udry
S.
. , 
A&A
, 
2000
, vol. 
359
 pg. 
L13
 
 
Quentin
C. G.
, 
Barge
P.
, 
Cautain
R.
, 
Meunier
J.-C.
, 
Moutou
C.
, 
Savalle
R.
, 
Surace
C.
. 
Fridlund
M.
, 
Baglin
A.
, 
Lochard
J.
, 
Conroy
L.
. , 
SP-1306, Software Application for Oversampling of Transit Candidates
, 
2006
Noordwijk
ESA
pg. 
409
  
in  

Google Scholar

OpenURL Placeholder Text

 
Radick
R. R.
, 
Mihalas
D.
, 
Hartmann
L.
, 
Worden
S. P.
, 
Africano
J. L.
, 
Klimke
A.
, 
Tyson
E. T.
. , 
PASP
, 
1982
, vol. 
94
 pg. 
934
 
Crossref
Search ADS
 
Radick
R. R.
, 
Lockwood
G. W.
, 
Skiff
B. A.
, 
Baliunas
S. L.
. , 
ApJSS
, 
1998
, vol. 
118
 pg. 
239
 
Crossref
Search ADS
 
Sanchis-Ojeda
R.
, 
Winn
J. N.
. , 
ApJ
, 
2011
, vol. 
743
 pg. 
61
 
Crossref
Search ADS
 
Sartoretti
P.
, 
Schneider
J.
. , 
A&AS
, 
1999
, vol. 
134
 pg. 
553
 
Crossref
Search ADS
 
Sasaki
T.
, 
Stewart
G. R.
, 
Ida
S.
. , 
ApJ
, 
2010
, vol. 
714
 pg. 
1052
 
Crossref
Search ADS
 
Schatten
K. H.
. , 
J. Geophys. Res.
, 
1993
, vol. 
98
 pg. 
18907
 
Crossref
Search ADS
 
Silva
A. V. R.
. , 
ApJ
, 
2003
, vol. 
585
 pg. 
L147
 
Crossref
Search ADS
 
Simon
A.
, 
Szatmáry
K.
, 
Szabó
G. M.
. , 
A&A
, 
2007
, vol. 
420
 pg. 
727
 
Crossref
Search ADS
 
Simon
A. E.
, 
Szabó
G. M.
, 
Kiss
L. L.
, 
Szatmáry
K.
. , 
MNRAS
, 
2012
, vol. 
419
 pg. 
164
 
Crossref
Search ADS
 
Steffen
J. H.
, 
Agol
E.
. , 
MNRAS
, 
2005
, vol. 
364
 pg. 
L96
 
Crossref
Search ADS
 
Struve
O.
. , 
The Observatory
, 
1952
, vol. 
72
 pg. 
199
 
 
Szabó
G. M.
, 
Szátmary
K.
, 
Divéki
Z.
, 
Simon
A.
. , 
A&A
, 
2006
, vol. 
450
 pg. 
395
 
Crossref
Search ADS
 
Triaud
A. H. M. J.
. , 
A&A
, 
2011
, vol. 
534
 pg. 
L6
 
Crossref
Search ADS
 
Triaud
A. H. M. J.
, et al. , 
A&A
, 
2010
, vol. 
524
 pg. 
A25
 
Crossref
Search ADS
 
Wada
K.
, 
Kokubo
E.
, 
Makino
J.
. , 
ApJ
, 
2006
, vol. 
638
 pg. 
1180
 
Crossref
Search ADS
 
Willson
R. C.
, 
Gulkis
S.
, 
Janssen
M.
, 
Hudson
H. S.
, 
Chapman
G. A.
. , 
Sci
, 
1981
, vol. 
211
 pg. 
700
 
Crossref
Search ADS
 

APPENDIX A: EFFECT OF THE DURATION AND TIMING OF EXPOSURES ON τ

As mentioned in Section 3.3, the timing and duration of exposures may affect the value of τ calculated for a given transit. This effect will be discussed using equation (7), restated here for convenience,
\begin{equation*} \Delta \tau = - t_0 - jT_{\rm p} + \frac{\sum _{i}t_i \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)\right)}{\sum _{i} \alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)}. \end{equation*}
Looking at this equation, we have that the first and second terms do not depend on the exposure time. In addition, the denominator of the third term represents the amount of light blocked by the planet as a result of the transit. This number should not depend on the timing or duration of the exposures, and thus is also independent of exposure time. The numerator of the third term is a different story.
To understand the effect of altering the timing and duration of exposures on the sum in the numerator, we compare the sum for the case of a long exposure time to that for the same system but with half the exposure time (see Fig. A1) by writing them in the same format and comparing the expressions. We begin by considering the sum for the long exposure times,
\begin{eqnarray} \sum _{i} t_i (\alpha _{\rm p}&(t_i) + \alpha _{\rm m}(t_i)) = \displaystyle\frac{1}{2} \sum _{i} 2t_i \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)\right) \end{eqnarray}
(A1)
\begin{eqnarray} =\displaystyle\frac{1}{2}\sum _{i} & \displaystyle\left(t_i + \frac{1}{4}\Delta t + t_i - \frac{1}{4}\Delta t \right) \left(\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)\right) \end{eqnarray}
(A2)
\begin{eqnarray} &=& \displaystyle\frac{1}{2}\sum _{i} \left(t_i + \frac{1}{4}\Delta t \right) (\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i))+ \frac{1}{2}\sum _{i} \left(t_i - \frac{1}{4}\Delta t \right) \nonumber \\ &&\times\, (\alpha _{\rm p}(t_i) + \alpha _{\rm m}(t_i)), \end{eqnarray}
(A3)
\begin{eqnarray} &\approx& \frac{1}{2}\sum _{i} \left(t_i + \frac{1}{4}\Delta t \right)\left(\alpha _{\rm p}\left(t_i + \frac{1}{4}\Delta t \right) + \alpha _{\rm m}\left(t_i + \frac{1}{4}\Delta t \right)\right) \nonumber \\ &&+ \frac{1}{2}\sum _{i} \left(t_i - \frac{1}{4}\Delta t \right)\left(\alpha _{\rm p}\left(t_i + \frac{1}{4}\Delta t \right) + \alpha _{\rm m}\left(t_i + \frac{1}{4}\Delta t \right)\right),\nonumber\\ \end{eqnarray}
(A4)
where we note that the last line is exactly equal to half11 the equivalent sum for short exposures. By comparing equation (A3), the sum for the long exposures, and equation (A4), the sum for the short exposures, we see that when (αp(ti) + αm(ti)) changes significantly from one exposure to the next, these two expressions are less likely to agree and errors may be introduced due to the timing and duration of exposures. To demonstrate that this is not an issue for a reasonable selection of physically realistic planet–moon parameters, the Monte Carlo simulation described in Section 3.2 was run for a range of exposure times and offsets from the transit centre. Some representative results from this process are shown in Fig. A2. As can be seen, a longer exposure time slightly distorts the distribution of σϵ away from the theoretically predicted one, in particular, by flattening the top of the distribution. This near-invariance of τ is partially as a result of the characteristic relative sizes of planets and stars (which define the relative transit depth), transit durations and exposure times, and partially as errors incurred during ingress and egress (the two periods when αp changes most from exposure to exposure) more or less cancel as the slope of the light curve during these two periods is equal and opposite. Consequently, any relationship between moon detectability and exposure time would be due to changes in σϵ as a function of exposure time.
Figure A1.
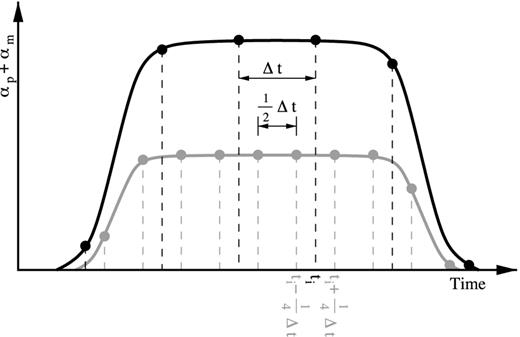
Schematic diagram showing αp + αm, the photon deficit due to the transit of the planet and the moon as a function of time, for two different exposure times. The long exposure time (black) is twice as long as the short exposure time (grey) and the exposures are indicated by vertical dashed lines. Note that the black curve is approximately twice as high as the grey curve as approximately twice as many photons are collected during the longer exposure.
Open in new tabDownload slide

Schematic diagram showing αp + αm, the photon deficit due to the transit of the planet and the moon as a function of time, for two different exposure times. The long exposure time (black) is twice as long as the short exposure time (grey) and the exposures are indicated by vertical dashed lines. Note that the black curve is approximately twice as high as the grey curve as approximately twice as many photons are collected during the longer exposure.

Figure A2.
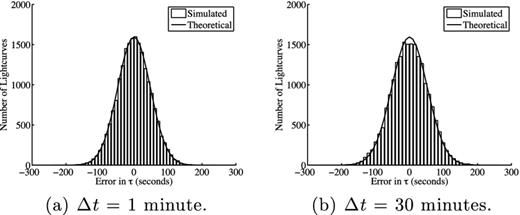
Comparison between results of the Monte Carlo simulation described in Section 3 for two different values of the exposure time. For these simulations it was assumed that the transit ingress and egress both lasted 1 hr, that the transit duration, Ttra, was 13 h, that the observing duration, Tobs, was 24 h and that σL was 0.54 and 0.10 times the transit depth for the case of 1 and 30 min exposures, respectively.
Open in new tabDownload slide

Comparison between results of the Monte Carlo simulation described in Section 3 for two different values of the exposure time. For these simulations it was assumed that the transit ingress and egress both lasted 1 hr, that the transit duration, Ttra, was 13 h, that the observing duration, Tobs, was 24 h and that σL was 0.54 and 0.10 times the transit depth for the case of 1 and 30 min exposures, respectively.

APPENDIX B: DERIVATION OF EQUIVALENT WHITE NOISE AMPLITUDE

In order to compare white noise with raw and filtered solar photometric noise, a method is needed to select the white noise which is the same as the solar photometric noise. For this work, it was decided to compare white and solar photometric noise with the same power. To ensure that photometric variation on time-scales relevant to transiting systems was included but variation due to longer term phenomenon such as the solar cycle were not, a three month span of data was used to determine the amount of power per unit time in the raw and filtered solar data sets. Using the definition of power
\begin{eqnarray} P_n = \sum _{i=1}^{N} \left| \alpha _{\rm n}(t_i) \right|^2, \end{eqnarray}
(B1)
this was found to be 6491 and 5644 W m−2, respectively. Consequently, a three month segment of white noise which is equivalent to the raw and filtered solar data should show a power of 6491 and 5644 W m−2, respectively.
Noting that for the case of white noise,
\begin{eqnarray} \sum _{i=1}^{N} \left| \alpha _{\rm n}(t_i) \right|^2 = N \left\langle \alpha _{\rm n}^2 \right\rangle , \end{eqnarray}
(B2)
where N is large and 〈α2n〉 is the expectation value of (αn)2. From equation (16), the definition of a Gaussian distribution, and the definition of expectation value we have that
\begin{eqnarray} \left\langle \alpha _{\rm n}^2\right\rangle &= \displaystyle\frac{1}{\sigma _L \sqrt{2\pi }} \int _{-\infty }^{\infty } x^2 {\rm e}^{-\frac{x^2}{2\sigma _L^2}} {\rm d}x \end{eqnarray}
(B3)
\begin{eqnarray} &=\sigma _L^2. \end{eqnarray}
(B4)
Consequently,
\begin{eqnarray} \sigma _L = \sqrt{\frac{P_n}{N}} \end{eqnarray}
(B5)
Thus, σL is equal to 0.0518 W m−2 for the case of raw solar photometric noise and 0.0483 W m−2 for the case of filtered solar photometric noise. Noting that L0 is equal to 1367.3 W m−2, this gives a relative photometric variability of 3.79 × 10−5 and 3.53 × 10−5, respectively.
© 2013 The Author Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides