Abstract
Plasma electromagnetic (EM) kinetic simulation faces two unavoidable difficulties. One arises from the fact that Maxwell equations determine a simultaneity relation between transverse electric field 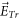 and local growth rates of probability distribution function (PDF)
and local growth rates of probability distribution function (PDF) 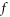 in Vlasov-Maxwell (V-M) simulation in Eulerian approach, so does that between
in Vlasov-Maxwell (V-M) simulation in Eulerian approach, so does that between 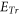 and Lagrangian particles' time-varying rates which refers to displacement of
and Lagrangian particles' time-varying rates which refers to displacement of 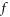 -element in
-element in 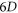 phase space in V-M simulation in Lagrangian approach, and macroparticles' accelerating rates in Particle-in-Cell (PIC) simulation. These simultaneous with
phase space in V-M simulation in Lagrangian approach, and macroparticles' accelerating rates in Particle-in-Cell (PIC) simulation. These simultaneous with 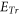 are termed as bottom objects' growth rates (BOGRs) in this work. Directly solving the BOGRs needs to diagonalize a large full matrix, and hence often be approximated. The other arises from the fact that Lagrangian particles' time-histories should uniformly converge with respect to the time-step. This severe requirement is difficult to be satisfied and hence some of Lagrangian particles' time-histories lose fidelity. We propose a strict alternative method free from two difficulties. The initial-value problem of V-M system can be interpreted by
are termed as bottom objects' growth rates (BOGRs) in this work. Directly solving the BOGRs needs to diagonalize a large full matrix, and hence often be approximated. The other arises from the fact that Lagrangian particles' time-histories should uniformly converge with respect to the time-step. This severe requirement is difficult to be satisfied and hence some of Lagrangian particles' time-histories lose fidelity. We propose a strict alternative method free from two difficulties. The initial-value problem of V-M system can be interpreted by 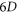 phase space allowed deformation of an initial
phase space allowed deformation of an initial 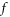 -profile. By virtue of a more compact description of
-profile. By virtue of a more compact description of 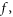 in which a conditional probability density function (C-PDF) well reflects some macroscopic conservation laws behind the V-M system, we can interpret the initial-value problem of
in which a conditional probability density function (C-PDF) well reflects some macroscopic conservation laws behind the V-M system, we can interpret the initial-value problem of 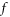 in terms of
in terms of 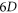 standing-wave oscillation in the C-PDF. A key subtle difference between microscopic scalar field and microscopic vector field can also lead to a similar scheme of particle simulation.
standing-wave oscillation in the C-PDF. A key subtle difference between microscopic scalar field and microscopic vector field can also lead to a similar scheme of particle simulation.
PACS: 52.65.-y.
Export citation and abstract BibTeX RIS
1. Introduction
Collective modes are common conceptions in plasma fluid theory. They usually exhibit as strict mathematic solutions of fluid equations with given initial conditions and 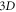 real space boundary conditions. For example, travelling-wave type electronic density oscillation is a familiar example of collective modes. In contrast, in plasma microscopic theory, similar conceptions are nearly unexploited and people tend to resort to kinetic simulation. No matter its detailed form is in Particle-in-Cell (PIC) code [1–16] or Vlasov code [17–39], the kinetic simulation treats both Vlasov-Maxwell/Poisson system and Newton-Maxwell system as an initial-value problem, and hence often hires one of two mainstream methods of numerical experiments on partial differential equations (PDEs): Eulerian approach and Lagrangian one. The Eulerian approach is based on a fixed numerical mesh. Compared with Lagrangian one, a drawback of the mesh-based method is its significant increase in computational cost as the problem dimension increases even though it is of the advantage of high order accuracy. Therefore, the Lagrangian approach, which is based on tracing time-histories of Lagrangian particles, receives more attention. Here, the phrase 'Lagrangian particle' refers to macroparticles in the PIC simulation and
real space boundary conditions. For example, travelling-wave type electronic density oscillation is a familiar example of collective modes. In contrast, in plasma microscopic theory, similar conceptions are nearly unexploited and people tend to resort to kinetic simulation. No matter its detailed form is in Particle-in-Cell (PIC) code [1–16] or Vlasov code [17–39], the kinetic simulation treats both Vlasov-Maxwell/Poisson system and Newton-Maxwell system as an initial-value problem, and hence often hires one of two mainstream methods of numerical experiments on partial differential equations (PDEs): Eulerian approach and Lagrangian one. The Eulerian approach is based on a fixed numerical mesh. Compared with Lagrangian one, a drawback of the mesh-based method is its significant increase in computational cost as the problem dimension increases even though it is of the advantage of high order accuracy. Therefore, the Lagrangian approach, which is based on tracing time-histories of Lagrangian particles, receives more attention. Here, the phrase 'Lagrangian particle' refers to macroparticles in the PIC simulation and 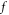 -elements, where
-elements, where 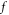 stands for probability density distribution (PDF), of
stands for probability density distribution (PDF), of 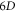 phase space in the Vlasov-Maxwell (V-M) simulation in Lagrangian approach.
phase space in the Vlasov-Maxwell (V-M) simulation in Lagrangian approach.
However, from basic mathematics perspective, both the Lagrangian approach and the Eulerian approach face two serious difficulties when applied to electromagnetic (EM) kinetic simulation. One is raised by simultaneity relation among physics fields. As expounded latter, the simultaneity relation between transverse electric field 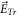 and bottom objects' growth rates (BOGRs) which refer to
and bottom objects' growth rates (BOGRs) which refer to 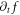 -values in the V-M simulation in Eulerian approach, displacement of
-values in the V-M simulation in Eulerian approach, displacement of 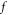 -element in the V-M simulation in Lagrangian approach and macroparticles' accelerating rate in the PIC simulation, makes the calculation on these BOGRs involving in high-dimension matrix. Here, the transverse electric field
-element in the V-M simulation in Lagrangian approach and macroparticles' accelerating rate in the PIC simulation, makes the calculation on these BOGRs involving in high-dimension matrix. Here, the transverse electric field 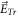 satisfies
satisfies 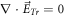 but
but 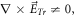 and is a fraction of self-consistent electric field
and is a fraction of self-consistent electric field  Usually, the dimension of such a matrix is so high that people have to resort to approximations. The common of these approximations is to ignore the simultaneity relation among
Usually, the dimension of such a matrix is so high that people have to resort to approximations. The common of these approximations is to ignore the simultaneity relation among 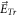 and BOGRs and hence avoid the difficulty in dealing with the high-dimension matrix. Clearly, such an ignorance is equal to ignoring some of Maxwell equations (MEs) which yield this simultaneity relation. It makes electromagnetic (EM) kinetic simulation to be approximated as electrostatic (ES) kinetic simulation and hence to be of very limited reliability in simulating hot plasmas even though such an approximation is good enough for simulating a cold plasma. On the other hand, many topics on light-matter interaction have urgent demands on the EM kinetic simulation. Even though suitable ansatz of
and BOGRs and hence avoid the difficulty in dealing with the high-dimension matrix. Clearly, such an ignorance is equal to ignoring some of Maxwell equations (MEs) which yield this simultaneity relation. It makes electromagnetic (EM) kinetic simulation to be approximated as electrostatic (ES) kinetic simulation and hence to be of very limited reliability in simulating hot plasmas even though such an approximation is good enough for simulating a cold plasma. On the other hand, many topics on light-matter interaction have urgent demands on the EM kinetic simulation. Even though suitable ansatz of 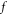 might be applicable to some special issues [40–42], its universal applicability cannot be warranted. Therefore, how to overcome this difficulty is of significant importance.
might be applicable to some special issues [40–42], its universal applicability cannot be warranted. Therefore, how to overcome this difficulty is of significant importance.
The other is raised by uniform convergence (with respect to the time-step 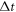 ) requirement on calculated Lagrangian particles' time-histories. If each electron is identified by its initial position and initial velocity
) requirement on calculated Lagrangian particles' time-histories. If each electron is identified by its initial position and initial velocity 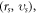 where subscript
where subscript 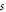 means 'starting', the particle simulation is to deal with
means 'starting', the particle simulation is to deal with  mono-variable functions of
mono-variable functions of 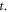 Each mono-variable function, or each particle's trajectory, obeys a relativistic Newton equation (RNE), a
Each mono-variable function, or each particle's trajectory, obeys a relativistic Newton equation (RNE), a 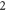 -nd differential equation with respect to the variable
-nd differential equation with respect to the variable 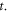 When updating these mono-variable functions, we face an unavoidable difficulty: how large the time-step
When updating these mono-variable functions, we face an unavoidable difficulty: how large the time-step 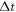 should be? If expressing each function as a power series of the variable
should be? If expressing each function as a power series of the variable 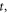 one can easily find that each power series, (identified by
one can easily find that each power series, (identified by 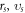 ), has its own convergence radius, denoted as
), has its own convergence radius, denoted as 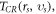 and hence naturally define a scalar field
and hence naturally define a scalar field 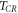 over the initial phase space
over the initial phase space 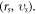 Each calculated trajectory, (identified by
Each calculated trajectory, (identified by 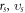 ), can be viewed as loyal if
), can be viewed as loyal if 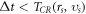 otherwise as losing fidelity. Thus, a loyal updating all particles requires
otherwise as losing fidelity. Thus, a loyal updating all particles requires  or
or 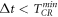 where
where  is defined as the minimum of all
is defined as the minimum of all 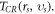 We call this requirement as uniform convergence requirement. Clearly, this is a quite severe requirement (because
We call this requirement as uniform convergence requirement. Clearly, this is a quite severe requirement (because 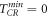 is easily to occur). Of course, ignoring this uniform convergence requirement implies the updating of all particles at the cost of some calculated trajectories losing fidelity. This might be an important reason for many PIC simulations violating MEs [17, 43–50]. For Eulerian approach, similar uniform convergence requirement for ensuring
is easily to occur). Of course, ignoring this uniform convergence requirement implies the updating of all particles at the cost of some calculated trajectories losing fidelity. This might be an important reason for many PIC simulations violating MEs [17, 43–50]. For Eulerian approach, similar uniform convergence requirement for ensuring  anywhere is also required.
anywhere is also required.
Initial-value problem can be expressed/interpreted in a more suitable form free from two difficulties. In plasma microscopic theory, a conception similar to the collective mode in plasma fluid theory is 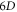 phase space time-dependent deformation of given initial
phase space time-dependent deformation of given initial 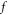 -profile. This conception can be used to express/interpret the initial-value problem. In plasma fluid theory, detailed mathematic form of a collective mode is derived from conservation laws behind fluid equation,
-profile. This conception can be used to express/interpret the initial-value problem. In plasma fluid theory, detailed mathematic form of a collective mode is derived from conservation laws behind fluid equation, 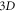 real space boundary condition and initial condition. Likewise, in plasma microscopic theory, conservation laws behind the V-M system,
real space boundary condition and initial condition. Likewise, in plasma microscopic theory, conservation laws behind the V-M system,  phase space boundary condition and initial condition can also be used to figure out the detailed mathematic form of time-dependent deformation of given initial
phase space boundary condition and initial condition can also be used to figure out the detailed mathematic form of time-dependent deformation of given initial 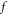 -profile. By virtue of a new compact expression of the
-profile. By virtue of a new compact expression of the 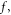 the initial-value problem of
the initial-value problem of 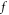 is expressed/interpreted as consistent evolutions of
is expressed/interpreted as consistent evolutions of 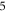 functions constituting this new expression. The new compact expression fully utilizes geometric/toplogical nature of the
functions constituting this new expression. The new compact expression fully utilizes geometric/toplogical nature of the 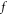 -profile due to some global conservation laws, and local conservation laws which reflects some fixed points (of
-profile due to some global conservation laws, and local conservation laws which reflects some fixed points (of 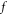 ) in
) in 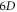 phase space existing. Its necessity, advantage over other methods, uniqueness and technical details will be presented in following sections. A subtle difference between microscopic scalar field and microscopic vector field a similar scheme of particle simulation.
phase space existing. Its necessity, advantage over other methods, uniqueness and technical details will be presented in following sections. A subtle difference between microscopic scalar field and microscopic vector field a similar scheme of particle simulation.
2. Theory and Method
For outstanding the emergency of overcoming two difficulties mentioned before, we first expound them in section 2.1. Then, we explain, in section 2.2, why others methods fail to overcome them. These explanations point out the importance of a suitable expression of the 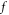 in overcoming two difficulties. Technical details of a new EM kinetic theory/simulation method free from two difficulties are presented in section 2.3 and 2.4. A numerical example of the application of such a new method is presented in section 2.5. A comparison with other methods ignoring two difficulties is presented in section 2.6.
in overcoming two difficulties. Technical details of a new EM kinetic theory/simulation method free from two difficulties are presented in section 2.3 and 2.4. A numerical example of the application of such a new method is presented in section 2.5. A comparison with other methods ignoring two difficulties is presented in section 2.6.
2.1. Crucial difficulty in EM kinetic simulation
According to MEs, scalar potential 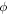 and vector potential
and vector potential 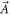 satisfy wave equations with different 'source' terms:
satisfy wave equations with different 'source' terms: 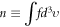 for
for  and
and  for
for 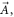 where
where 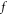 is the PDF. Lorentz gauge condition
is the PDF. Lorentz gauge condition  relates
relates 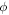 and
and  and agrees with continuity equation
and agrees with continuity equation  reflecting conservation of total particles number. According to standard partial differential equation (PDE) theory,
reflecting conservation of total particles number. According to standard partial differential equation (PDE) theory, 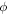 and
and  solutions can be expressed in a general form [51]:
solutions can be expressed in a general form [51]:
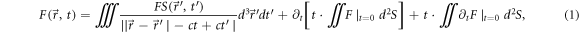
where 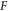 stands for
stands for  or
or 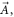
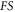 stands for its source term charge density
stands for its source term charge density 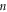 or current density
or current density 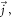 and
and 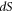 is a sphere surface which is centered at
is a sphere surface which is centered at 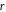 and of a radius
and of a radius 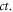 This general form indicates that
This general form indicates that 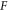 depends on its two initial conditions:
depends on its two initial conditions: 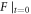 and
and 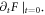 Due to Lorentz gauge condition,
Due to Lorentz gauge condition, 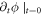 can be simultaneous with
can be simultaneous with 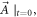 and further with
and further with 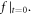 But
But 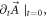 or initial transverse electric field profile
or initial transverse electric field profile 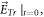 has a different simultaneous partner. Now that
has a different simultaneous partner. Now that 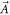 satisfies a wave equation with a source
satisfies a wave equation with a source 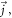
 will satisfy a wave equation with a source
will satisfy a wave equation with a source 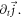 Thus,
Thus, 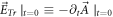 is simultaneous with
is simultaneous with 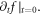 Moreover, when
Moreover, when 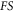 in equation (1) obeys an equation dependent on
in equation (1) obeys an equation dependent on 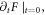 such as Vlasov equation (VE) containing
such as Vlasov equation (VE) containing 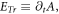 by setting the result of the operator
by setting the result of the operator 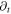 on the formula equation (1) of
on the formula equation (1) of 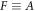 at
at 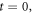 we can easily obtain a complicated self-consistent equation of
we can easily obtain a complicated self-consistent equation of 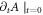 (because
(because 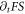 depends on
depends on 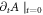 ). Namely, it is not an easy task to solve an initial condition
). Namely, it is not an easy task to solve an initial condition 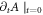 consistent with others such as
consistent with others such as 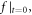
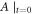 etc
etc
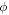 and
and 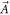 appearing in the VE of
appearing in the VE of 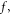 which formally is a PDE defined over a
which formally is a PDE defined over a 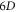 phase space plus a time coordinate, can be completely expressed, through above formula, in terms of
phase space plus a time coordinate, can be completely expressed, through above formula, in terms of 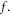 This makes the VE finally to become a differential-integral equation of
This makes the VE finally to become a differential-integral equation of 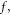 or an integral equation of local time growth-rate
or an integral equation of local time growth-rate 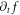 because
because  is simultaneous with
is simultaneous with 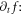
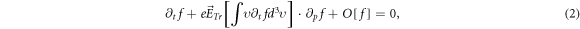
where  is electronic charge, and
is electronic charge, and ![${\vec{E}}_{{Tr}}\left[\int \upsilon {\partial }_{t}f{d}^{3}\upsilon \right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn116.gif) represents
represents 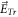 being a functional of
being a functional of 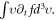 Moreover, all other terms in the VE are represented by a functional of
Moreover, all other terms in the VE are represented by a functional of  which is denoted as
which is denoted as ![$O\left[f\right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn120.gif) and
and 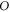 is the initial letter of
is the initial letter of  Its detailed form is easily written out but somewhat long for being presented here. Here, magnetic field
Its detailed form is easily written out but somewhat long for being presented here. Here, magnetic field 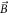 and longitudinal electric field
and longitudinal electric field 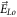 are simultaneous with
are simultaneous with 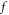 and hence contained in
and hence contained in 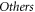 -functional.
-functional.
Once specifying the value of 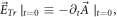 we have implicitly specified the value of
we have implicitly specified the value of  to some extent. Thus, when conducting the V-M simulation in Eulerian approach, substituting this
to some extent. Thus, when conducting the V-M simulation in Eulerian approach, substituting this 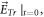 (i.e., the specified
(i.e., the specified 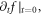 ) into the VE which is treated as an 'algebra' equation of
) into the VE which is treated as an 'algebra' equation of 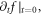 it is necessary to examine whether the implicitly-specified
it is necessary to examine whether the implicitly-specified 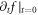 agrees with the calculated
agrees with the calculated  For brevity, we denote them as
For brevity, we denote them as 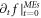 and
and 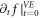 (where upper index 'MEs' means it being determined by MEs and 'VE' by VE), respectively. If they are different or
(where upper index 'MEs' means it being determined by MEs and 'VE' by VE), respectively. If they are different or 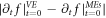 is not small enough, using the
is not small enough, using the 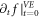 to calculate
to calculate 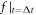 is futile. (In other words, because we can construct, according to the simultaneity relation above-mentioned, a
is futile. (In other words, because we can construct, according to the simultaneity relation above-mentioned, a 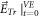 from
from 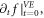 we should examine whether
we should examine whether 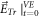 agreeing with the specified value of
agreeing with the specified value of 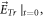 or
or 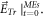 ) Once disagreement occur, we have to try a new trial of
) Once disagreement occur, we have to try a new trial of 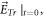 as well as a new trial of
as well as a new trial of 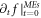 -profile, and calculate its yielded
-profile, and calculate its yielded 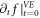 -profile, and then compare them. Repeating such a cycle until
-profile, and then compare them. Repeating such a cycle until 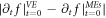 being small enough (if can). For example,
being small enough (if can). For example, 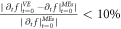 is a tolerable level of the relative error. Clearly, such iterative manner is very time-consuming in computer experiment but strictly speaking unable to be omitted.
is a tolerable level of the relative error. Clearly, such iterative manner is very time-consuming in computer experiment but strictly speaking unable to be omitted.
Of course, if not specifying the 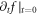 but taking the VE as an integral equation of
but taking the VE as an integral equation of 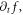 discrete expression of the integral
discrete expression of the integral 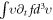 in the VE will lead to a high-dimension matrix, or those values of
in the VE will lead to a high-dimension matrix, or those values of 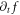 at different
at different 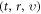 -coordinates will form, (because discretization of the integral with respect to
-coordinates will form, (because discretization of the integral with respect to 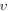 needs
needs 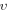 -points in sufficient amount), a
-points in sufficient amount), a 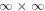 matrix equation nearly impossible to-be-solved. Moreover, singularities associated with
matrix equation nearly impossible to-be-solved. Moreover, singularities associated with 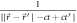 and
and 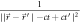 also make the calculation more complicated.
also make the calculation more complicated.
The V-M simulation in Lagrangian approach [43–50, 52–54] is to use displacements of 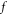 -elements in
-elements in 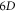 phase space to describe time-evolution of
phase space to describe time-evolution of 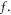 Here, the phrase 'displacement' represents a
Here, the phrase 'displacement' represents a 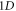 'coordinate' along a phase space contour defined by
'coordinate' along a phase space contour defined by 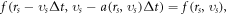 where
where 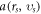 stands for accelerating rate and hence depends on
stands for accelerating rate and hence depends on 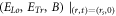 and relativistic factor
and relativistic factor 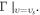 These displacements also need to be examined whether their yielded
These displacements also need to be examined whether their yielded 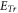 (through MEs) agrees with
(through MEs) agrees with 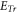 in the accelerating rate
in the accelerating rate ![$a\left({r}_{s},{\upsilon }_{s}\right)=a\left[\left({E}_{{Lo}},{E}_{{Tr}},B\right){{\rm{| }}}_{\left(r,t\right)=\left({r}_{s},0\right)},{\rm{\Gamma }}{{\rm{| }}}_{\upsilon ={\upsilon }_{s}}\right].$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn169.gif) Here
Here 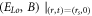 are functions of
are functions of 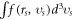 but
but  is a function of
is a function of 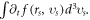
Similar difficulty also exists for Newton-Maxwell system. In the PIC code [1–15],  on any macroparticle is of a simultaneity relation with 'accelerating rate' of other macroparticles within adjacent cells (because two interpolation functions, one for from particle to grid and the other for from grid to particle, are taken as only dependent on space coordinates). If using this
on any macroparticle is of a simultaneity relation with 'accelerating rate' of other macroparticles within adjacent cells (because two interpolation functions, one for from particle to grid and the other for from grid to particle, are taken as only dependent on space coordinates). If using this 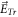 to calculate the 'accelerating rate' of a macroparticle, we will have a similar equation (where
to calculate the 'accelerating rate' of a macroparticle, we will have a similar equation (where 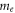 is static electronic mass and a macroparticle shares a same charge/mass ratio with an electron)
is static electronic mass and a macroparticle shares a same charge/mass ratio with an electron)
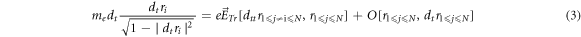
and hence need to diagonalize a matrix whose dimension is the number of macroparticles within adjacent cells.
This consistency-examination of 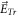 is absent in various algorithms. For example, in the PIC code [1–16], although particles' information and fields' information are alternatively updated, such a consistency-examination should be made per two time-steps. Unfortunately, it is omitted. This omission might be an important factor causing various 'violations of physics laws' [17]. Moreover, it will also affect implicit EM PIC scheme which utilizes particle enslavement technique [55] because iteratively solving the root of enslaved residual
is absent in various algorithms. For example, in the PIC code [1–16], although particles' information and fields' information are alternatively updated, such a consistency-examination should be made per two time-steps. Unfortunately, it is omitted. This omission might be an important factor causing various 'violations of physics laws' [17]. Moreover, it will also affect implicit EM PIC scheme which utilizes particle enslavement technique [55] because iteratively solving the root of enslaved residual 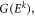 where
where 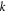 is iteration number, will encounter a difficulty arising from uncertain initial form of
is iteration number, will encounter a difficulty arising from uncertain initial form of 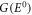 due to
due to 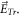
Because 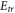 is taken as playing less role in these issues [4–39], it is often not taken into account and hence EM kinetic simulations in these works are actually approximated [4–39]. For example, in some issues on plasmas in magnetic fusion device involving in kinetic simulation on ionic PDF, the self-consistent magnetic field generated by plasma currents, (which is mainly determined by electronic PDF), is neglected and hence
is taken as playing less role in these issues [4–39], it is often not taken into account and hence EM kinetic simulations in these works are actually approximated [4–39]. For example, in some issues on plasmas in magnetic fusion device involving in kinetic simulation on ionic PDF, the self-consistent magnetic field generated by plasma currents, (which is mainly determined by electronic PDF), is neglected and hence  is indeed not taken into account [23, 28–30, 33, 34]. Some kinetic simulations are based on Vlasov-Poisson (VP) code to study electronic PDF [39–42] and ionic PDF [35, 38]. Some simulations are on 1D model and hence not take into account
is indeed not taken into account [23, 28–30, 33, 34]. Some kinetic simulations are based on Vlasov-Poisson (VP) code to study electronic PDF [39–42] and ionic PDF [35, 38]. Some simulations are on 1D model and hence not take into account 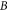 and
and  [38]. Some kinetic simulations on electronic PDF through Eulerian Vlasov code ignored
[38]. Some kinetic simulations on electronic PDF through Eulerian Vlasov code ignored 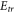 [18, 21], so did Semi-Lagrangian (SL) Vlasov code on discharge plasmas [31, 32] and PIC code for hot electron [22]. In some
[18, 21], so did Semi-Lagrangian (SL) Vlasov code on discharge plasmas [31, 32] and PIC code for hot electron [22]. In some  EM PIC simulations on kinetic-scale plasma, even though fluctuating magnetic field is taken into account,
EM PIC simulations on kinetic-scale plasma, even though fluctuating magnetic field is taken into account, 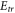 is still not strictly taken into account [15, 16].
is still not strictly taken into account [15, 16].
Even though many authors have been aware of some inherent drawbacks of current popular simulation schemes, such as hiring truncation approximation [20], statistical noise [35, 38] etc, the most urgent task, i.e. strictly taking 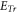 into account, have not win sufficient attention. This makes these simulation schemes under the risk of violating MEs [17] and hence discounts their effort in improving these simulation schemes [19, 23, 25]. For example, usually the kinetic simulation is taken as an initial problem evolution of an initial PDF
into account, have not win sufficient attention. This makes these simulation schemes under the risk of violating MEs [17] and hence discounts their effort in improving these simulation schemes [19, 23, 25]. For example, usually the kinetic simulation is taken as an initial problem evolution of an initial PDF  but people often choose
but people often choose 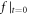 as having a non-zero vortex of the current density or
as having a non-zero vortex of the current density or 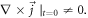 For example,
For example, 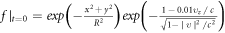 means the initial PDF having a Gaussian space transverse shape and is a typical example of
means the initial PDF having a Gaussian space transverse shape and is a typical example of 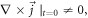 which will inevitably, according to MEs, trigger
which will inevitably, according to MEs, trigger 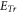 to be present. Namely, the choice of the initial PDF is inconsistent with hiring the ES approximation or using the VP code.
to be present. Namely, the choice of the initial PDF is inconsistent with hiring the ES approximation or using the VP code.
The V-M simulation in Eulerian approach is finally inevitably frustrated by the simultaneity relation between 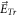 and
and 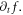 Ignoring this simultaneity relation can make the simulation going-on and speed-up but the reliability of yielded results is limited. Therefore, even though this Eulerian approach is applicable for electrostatic (ES) kinetic simulation [30–39, 41, 42], its suitability to EM kinetic simulation is still uncertain. This simultaneity relation also have profound effect on the V-M simulation in Lagrangian approach.
Ignoring this simultaneity relation can make the simulation going-on and speed-up but the reliability of yielded results is limited. Therefore, even though this Eulerian approach is applicable for electrostatic (ES) kinetic simulation [30–39, 41, 42], its suitability to EM kinetic simulation is still uncertain. This simultaneity relation also have profound effect on the V-M simulation in Lagrangian approach.
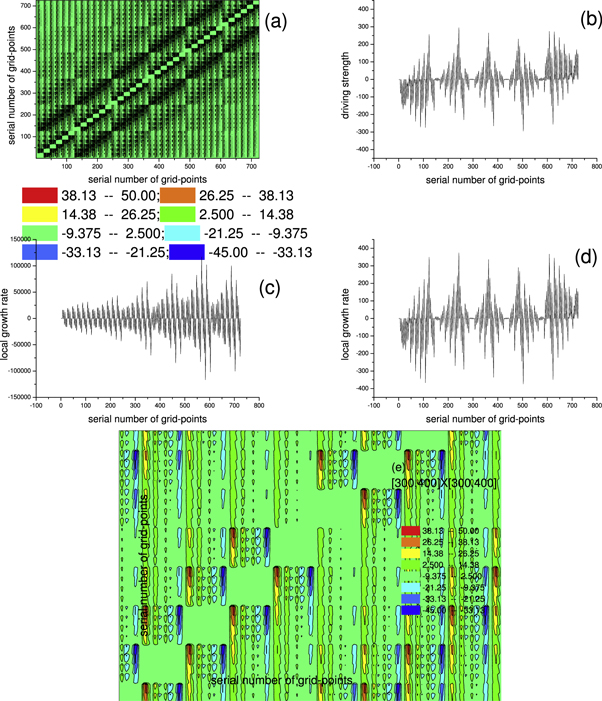
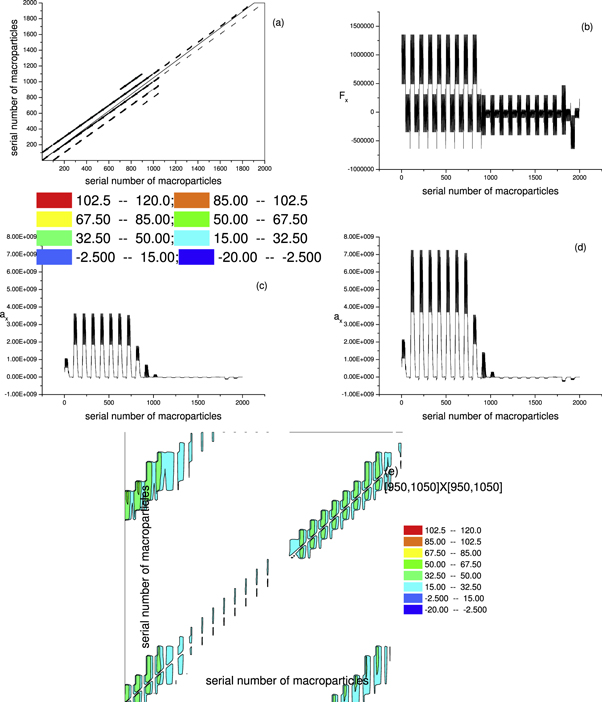
For illustrating the effect of the simultaneity relation described above on simulation, we display results based on strict treatment on the simultaneity relation and those based on approximate treatment in figures 1, 2. Here, the phrase 'strict treatment' refers to BOGRs being linked by a matrix, and the phrase 'approximate treatment' refers to simplifying this matrix as a diagonal one by approximating its non-diagonal elements as being of a different simultaneity relation (alike that between 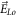 and
and 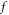 ) and hence merging them into the functional
) and hence merging them into the functional  in equations (2), (3). Figure 1 is for the V-M simulation in Eulerian approach and figure 2 for the PIC simulation. In figure 1,
in equations (2), (3). Figure 1 is for the V-M simulation in Eulerian approach and figure 2 for the PIC simulation. In figure 1, 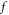 starts from a familiar Gaussian initial profile
starts from a familiar Gaussian initial profile 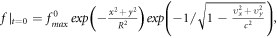 and all discrete grid-points in the phase space are numbered. Likewise, in figure 2, all macroparticles are numbered. Moreover, the term 'driving strength' in figure 1(b) stands for
and all discrete grid-points in the phase space are numbered. Likewise, in figure 2, all macroparticles are numbered. Moreover, the term 'driving strength' in figure 1(b) stands for 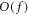 in equation (2) and
in equation (2) and  in figure 2(b) for
in figure 2(b) for  -component of
-component of 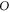 in equation (3). Parameters in figure 1 are chosen as
in equation (3). Parameters in figure 1 are chosen as 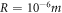 and
and 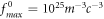 (where
(where 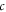 is speed of light in vacuum).
is speed of light in vacuum).
Figure 1. Examples of 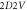 Vlasov simulation in Eulerian approach. The profile of dimensionless probability density function
Vlasov simulation in Eulerian approach. The profile of dimensionless probability density function 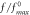 is represented by its values at discrete points of a grid in the dimensionless
is represented by its values at discrete points of a grid in the dimensionless 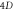 phase space
phase space 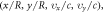 the projection of the grid on the
the projection of the grid on the 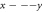 plane is a square whose each side contains
plane is a square whose each side contains 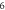 points, and that on the
points, and that on the 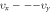 plane is a circle
plane is a circle 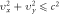 whose diameter contains
whose diameter contains 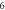 points, where
points, where 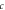 is speed of light in vacuum,
is speed of light in vacuum, 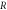 is the characteristic length proportional to the value of the density
is the characteristic length proportional to the value of the density 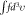 and
and 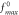 represents the maximum of the initial
represents the maximum of the initial 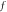 -profile
-profile  (a) is for values of these elements of the matrix in equation (2);(b) is for the driving at each grid-point; (c) is for 'local growth rate'
(a) is for values of these elements of the matrix in equation (2);(b) is for the driving at each grid-point; (c) is for 'local growth rate' 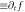 at each grid-point under strict treatment; (d) is the counterpart of (c) under approximate treatment.(e) is the amplification of the regime around the point
at each grid-point under strict treatment; (d) is the counterpart of (c) under approximate treatment.(e) is the amplification of the regime around the point 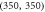 in (a).
in (a).
Download figure:
Standard image High-resolution imageFigure 2. Examples of 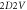 PIC simulation. Initially,
PIC simulation. Initially, 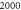 macroparticles are assigned into a
macroparticles are assigned into a 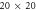 grid on the
grid on the 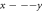 plane. Self-consistent magnetic field is taken as along
plane. Self-consistent magnetic field is taken as along 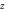 -direction. (a) is for values of these elements of the matrix in equation (3); (b) is for the driving force on each macroparticle; (c) is for macroparticles' accelerating rate according to strict treatment; (d) is the counterpart of (c) according to approximate treatment. (e) is the amplification of the regime around the point
-direction. (a) is for values of these elements of the matrix in equation (3); (b) is for the driving force on each macroparticle; (c) is for macroparticles' accelerating rate according to strict treatment; (d) is the counterpart of (c) according to approximate treatment. (e) is the amplification of the regime around the point 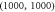 in (a).
in (a).
Download figure:
Standard image High-resolution imageClearly, marked differences exist between results based on different treatments. As shown in figures 1(c), (d), the difference is so large that results in figure 1(c) is higher several orders of magnitude than those in figure 1(d). Moreover, although the curve in figure 1(c) and that in figure 1(d) are in same unit, their shapes are obviously different. Using finer mesh in phase space still faces same problem. Even though results in figures 2(c), (d) are at a same order of magnitude, their relative error is nearly 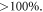 Figures 1, 2 display examples in
Figures 1, 2 display examples in 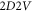 format. Similar marked differences between results based on different treatments exist universally for EM problem in all formats (from the simplest
format. Similar marked differences between results based on different treatments exist universally for EM problem in all formats (from the simplest 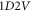 format to
format to 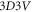 one) because there is always a high-dimension matrix (due to
one) because there is always a high-dimension matrix (due to 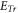 ) no matter which of these formats is studied. For example, a typical
) no matter which of these formats is studied. For example, a typical 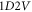 initial PDF
initial PDF 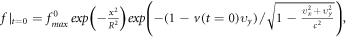 where
where  is space-independent, can be represented by a mesh in the
is space-independent, can be represented by a mesh in the  phase space, and the number of points in this mesh are usually chosen to be up to
phase space, and the number of points in this mesh are usually chosen to be up to 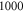 or higher. Because
or higher. Because  implies
implies  being an asymmetric function of
being an asymmetric function of  and only a space variable
and only a space variable  exists, there are initially a current vortex
exists, there are initially a current vortex 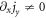 and hence a
and hence a 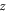 -direction component of
-direction component of 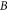 and a fast growing
and a fast growing 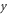 -direction component of
-direction component of 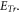 As previously mentioned, the presence of
As previously mentioned, the presence of  means a high-dimension matrix to be treated when calculating subsequent time evolution of
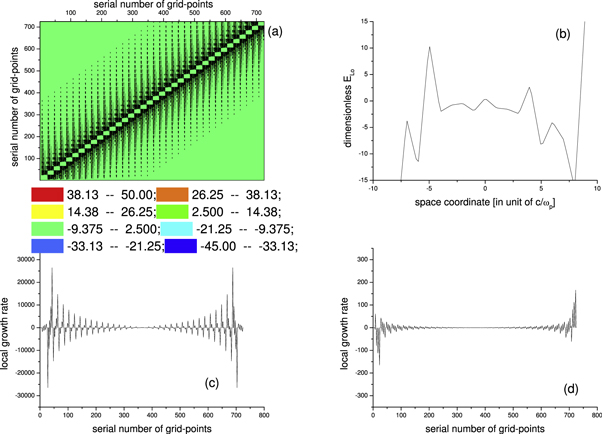
means a high-dimension matrix to be treated when calculating subsequent time evolution of 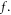 According to figures 3(c), (d), strict treatment and approximated one yield obviously different results of the local growth rate. This is similar to what are displayed by figures 1(c),(d). Figure 3(b) displays
According to figures 3(c), (d), strict treatment and approximated one yield obviously different results of the local growth rate. This is similar to what are displayed by figures 1(c),(d). Figure 3(b) displays 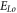 -profile after two time steps
-profile after two time steps  which exhibits marked space oscillation and hence implies marked density wave.
which exhibits marked space oscillation and hence implies marked density wave.
Figure 3. Examples of 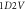 Vlasov simulation in Eulerian approach. The profile of dimensionless probability density function
Vlasov simulation in Eulerian approach. The profile of dimensionless probability density function  is represented by its values at discrete points of a grid in the dimensionless
is represented by its values at discrete points of a grid in the dimensionless 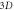 phase space
phase space 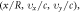 the projection of the grid on the
the projection of the grid on the 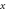 axis is a line containing
axis is a line containing 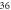 points, and that on the
points, and that on the 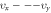 plane is a circle
plane is a circle 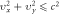 whose diameter contains
whose diameter contains 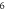 points, where
points, where 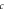 is speed of light in vacuum,
is speed of light in vacuum, 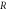 is the characteristic length proportional to the value of the density
is the characteristic length proportional to the value of the density 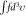 and
and 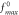 represents the maximum of the initial
represents the maximum of the initial 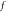 -profile
-profile 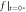 (a) is for values of these matrix elements;(b) is for
(a) is for values of these matrix elements;(b) is for 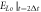 calculated through strict treatment, where
calculated through strict treatment, where 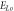 is in unit of
is in unit of 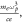
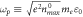 and
and 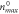 represents the maximum of initial density profile
represents the maximum of initial density profile 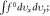 (c) is for 'local growth rate'
(c) is for 'local growth rate' 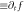 at each grid-point under strict treatment; (d) is the counterpart of (c) under approximate treatment.
at each grid-point under strict treatment; (d) is the counterpart of (c) under approximate treatment.
Download figure:
Standard image High-resolution imageThe root reason for limiting scientific validity of older approximated methods/approaches is to adopt approximation on the coefficient matrix needing diagonalization in discrete expression of the VE, which consists of 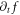 -values at
-values at  mesh points of
mesh points of 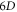 phase space:
phase space:
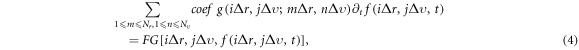
where 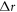 and
and 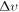 are steps of the mesh/grid in the phase space, and detailed forms of the function
are steps of the mesh/grid in the phase space, and detailed forms of the function 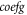 and the functional
and the functional 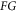 can be directly derived from MEs and the functional
can be directly derived from MEs and the functional 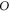 in equations (1), (2). After being aware of this root reason, we diagonalize this coefficient matrix, even though doing so is rather time-consuming, to obtain a set of equations, which are straightforward expressions of
in equations (1), (2). After being aware of this root reason, we diagonalize this coefficient matrix, even though doing so is rather time-consuming, to obtain a set of equations, which are straightforward expressions of 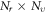 functions
functions 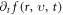 in terms of
in terms of 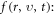
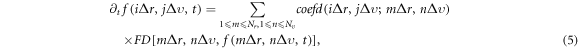
where detailed forms of the coefficient function 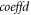 and the functional
and the functional 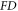 are easily written out but somewhat long for being presented here. Although this straightforward expression is now available, another difficulty still hinders calculating the
are easily written out but somewhat long for being presented here. Although this straightforward expression is now available, another difficulty still hinders calculating the 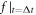 -profile from the
-profile from the 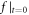 -profile and the
-profile and the 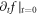 -profile (because the time-step
-profile (because the time-step 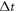 should ensure
should ensure 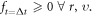 ) Because the discrete expression is through
) Because the discrete expression is through 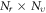 mesh points in
mesh points in 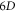 phase space, the allowed value of
phase space, the allowed value of 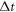 should be less than the minimum of
should be less than the minimum of 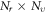 values of
values of 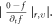 Usually, a comprehensive discrete expression of a
Usually, a comprehensive discrete expression of a 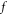 -profile should contain those boundary mesh points where
-profile should contain those boundary mesh points where 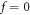 satisfies. Because not all
satisfies. Because not all 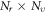 values of
values of 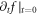 are
are 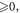 once at some boundary mesh points the values of
once at some boundary mesh points the values of 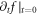 are negative, the allowed value of
are negative, the allowed value of 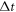 will be confined to be
will be confined to be  This difficulty is analogous to the uniform convergence requirement mentioned before.
This difficulty is analogous to the uniform convergence requirement mentioned before.
For the V-M simulation, two difficulties drive us to seek for new ways of describing the evolution of 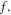 As shown latter, in a geometric expression of
As shown latter, in a geometric expression of 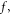
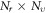 expression formulas of
expression formulas of  are converted into those of
are converted into those of 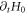 in a same amount. Unlike
in a same amount. Unlike 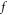 -values mandatory to be
-values mandatory to be 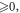
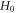 -value are allowed to be negative. This overcomes the difficulty arising from the requirement that
-value are allowed to be negative. This overcomes the difficulty arising from the requirement that 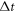 should warrant
should warrant 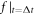 being non-negative anywhere.
being non-negative anywhere.
2.2. Main difficulty in V-M simulation and advantages of combination of different expressions of 
A main difficulty in simulating the V-M system, both in Eulerian approach and Lagrangian one, is to find an efficient expression of 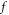 free from being supplemented by unnecessary approximations. In the Eulerian approach, if
free from being supplemented by unnecessary approximations. In the Eulerian approach, if 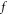 is expressed by a power expansion formula
is expressed by a power expansion formula
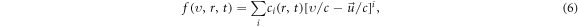
the VE will act as a recurrence relation/formula defining a set of expansion coefficient functions 
 constructed from this
constructed from this 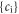 -set obviously satisfy the VE. The recurrence relation/formula can lead to a general relation between two expansion coefficient functions with adjacent subindex
-set obviously satisfy the VE. The recurrence relation/formula can lead to a general relation between two expansion coefficient functions with adjacent subindex
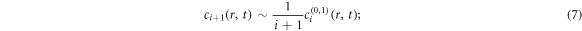
which implies 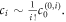 Here,
Here,  and
and  are common expressions of high-order derivatives of
are common expressions of high-order derivatives of 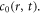 The convergence condition
The convergence condition ![${li}{m}_{i\to {\rm{\infty }}}{\rm{| }}\frac{{c}_{i+1}{\left[\upsilon -u\right]}^{i+1}}{{c}_{i}{\left[\upsilon -\vec{u}\right]}^{i}}{\rm{| }}\lt 1,$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn329.gif) whose detailed form is
whose detailed form is 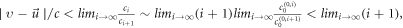 can be warranted if
can be warranted if 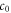 can satisfy
can satisfy 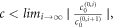 where
where 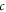 is speed of light in vacuum. Namely, once
is speed of light in vacuum. Namely, once 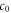 is convergent with respect to
is convergent with respect to 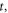 it can lead to a set
it can lead to a set 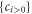 warranting the expansion series
warranting the expansion series 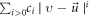 convergent over the region
convergent over the region 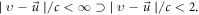
The power expansion can be converted into another form
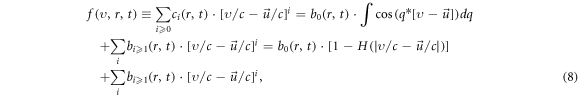
where Heviside function is defined as 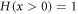 and
and 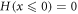 and satisfies
and satisfies 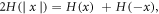 and the coefficient function
and the coefficient function 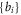 -set can be straightforward transformed from the
-set can be straightforward transformed from the 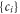 -set.
-set.
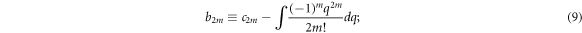
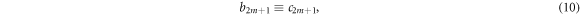
where 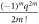 is from Taylor expansion of
is from Taylor expansion of 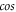 function. The non-negative-probability requirement demands
function. The non-negative-probability requirement demands 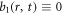 mandatory to be fulfilled [56–58]. Thus, complete microscopic description, which consists of the VE and the non-negative-probability requirement, implies following relation:
mandatory to be fulfilled [56–58]. Thus, complete microscopic description, which consists of the VE and the non-negative-probability requirement, implies following relation:
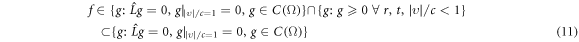
where 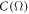 represents the set of all continuous functions defined over
represents the set of all continuous functions defined over 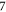 -D space
-D space 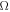 whose coordinates are
whose coordinates are 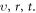
Note that when the operator 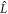 acts on
acts on 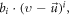 relevant terms will be in three classes: rising-order terms
relevant terms will be in three classes: rising-order terms  keeping-order terms
keeping-order terms  and decreasing-order ones
and decreasing-order ones 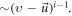 Thus, there will be a mono-variable recurrence relation/formula chain
Thus, there will be a mono-variable recurrence relation/formula chain
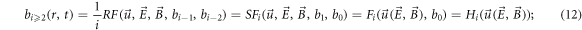
where the functional 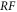 represents the recurrence formula reflected by the VE, and expressing
represents the recurrence formula reflected by the VE, and expressing 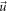 as
as 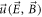 is due to the fact that
is due to the fact that  can lead to an equation among
can lead to an equation among 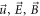 [56–58]
[56–58]
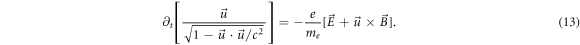
The relation between 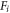 and
and 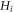 is described as follows: substituting the power series expansion back into Gauss law (where these
is described as follows: substituting the power series expansion back into Gauss law (where these 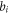 and
and 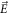 are space-time inhomogeneous functions and
are space-time inhomogeneous functions and 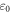 is permittivity of free space)
is permittivity of free space)
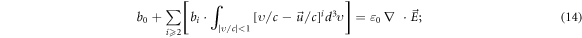
and utilizing 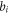 's expression equation (12), we can express
's expression equation (12), we can express  in terms of
in terms of 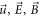 and hence convert
and hence convert 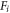 into
into 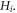 Note that equation (14) is indeed an infinite-order PDE (with respect to
Note that equation (14) is indeed an infinite-order PDE (with respect to 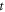 ) of
) of 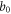 and hence often inevitably trigger approximations.
and hence often inevitably trigger approximations.
Semi-Lagrangian approaches [43–50, 52–54] face similar difficulty which refers to exact integration of contour of 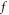 over
over 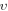 -space difficult to be conducted. As a result, even exact functional dependence of
-space difficult to be conducted. As a result, even exact functional dependence of 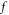 on
on 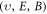 can be known from the contour form, it is difficult to obtain exact solution of
can be known from the contour form, it is difficult to obtain exact solution of 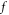 in terms of
in terms of 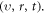
The VE reflects global conservation law 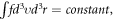 and the non-negative-probability requirement
and the non-negative-probability requirement 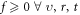 reflects local positivity-preserving law/requirement [43–50] which is mandatory for applying probability theory to various application issues. Many authors try to take this local positivity-preserving law/requirement into account by adjusting key technical details used in Lagrangian approaches [43–50], such as using more interpolation functions and dividing a time-step into more sub-steps etc Mathematically, these effort choose to update
reflects local positivity-preserving law/requirement [43–50] which is mandatory for applying probability theory to various application issues. Many authors try to take this local positivity-preserving law/requirement into account by adjusting key technical details used in Lagrangian approaches [43–50], such as using more interpolation functions and dividing a time-step into more sub-steps etc Mathematically, these effort choose to update 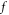 in a more complicated manner in which the displacement of a
in a more complicated manner in which the displacement of a 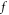 -element in
-element in 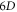 phase space is a nonlinear function of the time-step
phase space is a nonlinear function of the time-step 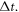 But these effort also cause computation cost increasing significantly.
But these effort also cause computation cost increasing significantly.
Historically, in theoretical plasmas physics, investigations are merely around the VE and hence often drop in a logic contradiction: Starting from the VE,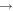 deriving its equivalent equation
deriving its equivalent equation 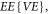 (where
(where 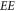 is the acronym of 'equivalent equation' and the phrase 'equivalent' means no any mathematics approximation being applied and hence can share common solutions with the VE),
is the acronym of 'equivalent equation' and the phrase 'equivalent' means no any mathematics approximation being applied and hence can share common solutions with the VE), then truncating this equivalent equation to obtain an equation
then truncating this equivalent equation to obtain an equation 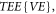 (where
(where 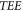 is the acronym of 'truncated equivalent equation' and the phrase 'truncating' means discarding some non-zero terms in the equation and hence cannot share common solutions with the equivalent equation),
is the acronym of 'truncated equivalent equation' and the phrase 'truncating' means discarding some non-zero terms in the equation and hence cannot share common solutions with the equivalent equation), then combining the amputated
then combining the amputated 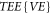 and the VE to obtain solutions of the VE. Obviously, such a procedure is contradict with the fact the a
and the VE to obtain solutions of the VE. Obviously, such a procedure is contradict with the fact the a 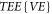 cannot share solutions with the equivalent equation
cannot share solutions with the equivalent equation 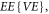 as well as the VE. Actually, people have been aware of that 'the 'truncation approximation' is a delicate operation, which might lead to a numerical failure of the solution for later times' [20]. Therefore, ignoring the non-negative-probability requirement delays a sound kinetic simulation scheme to be found.
as well as the VE. Actually, people have been aware of that 'the 'truncation approximation' is a delicate operation, which might lead to a numerical failure of the solution for later times' [20]. Therefore, ignoring the non-negative-probability requirement delays a sound kinetic simulation scheme to be found.
There are different expressions of the PDF 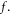 For example, the set
For example, the set ![$\{\int {\left[\upsilon -\vec{u}\right]}^{i}f{d}^{3}\upsilon {\rm{;}}i\geqslant 0\},$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn396.gif) where
where 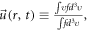 is convenient to reflect the global conservation law, and the set
is convenient to reflect the global conservation law, and the set  is convenient to reflect the local positivity-preserving law/requirement. Compared with sole usage of these expressions, combinative usage of them can avoid unnecessary approximations and is more efficient for establishing a universal and sound scheme of the EM kinetic simulation.
is convenient to reflect the local positivity-preserving law/requirement. Compared with sole usage of these expressions, combinative usage of them can avoid unnecessary approximations and is more efficient for establishing a universal and sound scheme of the EM kinetic simulation.
2.3. A compact self-consistent Eulerian expression of 
Among different expressions of  choosing the most suitable is important to obtain exact solutions of
choosing the most suitable is important to obtain exact solutions of 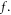 An unsuitable expression will inevitably lead to unnecessary mathematical approximations supplemented. As far as
An unsuitable expression will inevitably lead to unnecessary mathematical approximations supplemented. As far as  is concerned, previously mentioned two Eulerian expressions: mesh expression and power series expressions are far from suitable ones. For example, to make the
is concerned, previously mentioned two Eulerian expressions: mesh expression and power series expressions are far from suitable ones. For example, to make the 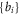 -set certain needs to first make the
-set certain needs to first make the 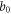 certain from equation (14)), an infinite-order PDE (with respect to
certain from equation (14)), an infinite-order PDE (with respect to 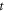 ) of
) of 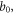 and hence often triggers approximations. In contrast, respecting some mathematical features of
and hence often triggers approximations. In contrast, respecting some mathematical features of 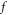 and targeted introducing more suitable Eulerian expression is feasible. For example, because equation (14), or Gauss law, must be respected, the
and targeted introducing more suitable Eulerian expression is feasible. For example, because equation (14), or Gauss law, must be respected, the 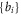 -set expression can be further improved into a more suitable expression in which
-set expression can be further improved into a more suitable expression in which  is expressed in term of
is expressed in term of 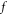 itself [59]:
itself [59]:

where 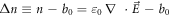 is always
is always 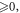 non-negative function
non-negative function ![$\left[{H}_{1}+{H}_{0}\right],$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn413.gif) which acts as a conditional probability density function (C-PDF), describes the allocation of particles contained in the
which acts as a conditional probability density function (C-PDF), describes the allocation of particles contained in the 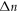 -profile into different values of
-profile into different values of  It is straightforward, from the definition formula equation (15), to derive that the non-negative function
It is straightforward, from the definition formula equation (15), to derive that the non-negative function ![$\left[{H}_{1}+{H}_{0}\right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn416.gif) satisfies
satisfies ![$\int \left[{H}_{1}+{H}_{0}\right]{d}^{3}\upsilon =1,\int \left[\upsilon -\vec{u}\right]\cdot \left[{H}_{1}+{H}_{0}\right]{d}^{3}\upsilon =0,\left[{H}_{1}+{H}_{0}\right]\left(\vec{u},r,t\right)\equiv 0\equiv \left[{H}_{1}+{H}_{0}\right]\left({\rm{| }}\upsilon {\rm{| }}=c,r,t\right).$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn417.gif) Clearly, such a non-negative function can be constructed from functions in two different classes, one class is denoted as
Clearly, such a non-negative function can be constructed from functions in two different classes, one class is denoted as 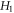 and the other
and the other 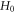 [56]:
[56]:
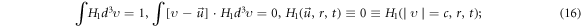
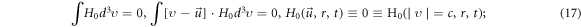
and 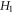 is
is  while
while 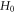 is not. Moreover, it is easy to find, by applying
is not. Moreover, it is easy to find, by applying 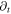 -operator and
-operator and 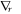 -operator on the definition formulas equations (16), (17), that,
-operator on the definition formulas equations (16), (17), that, 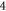 functions:
functions: 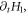
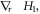
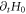 and
and 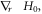 (denoting them as
(denoting them as 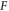 ), are alike to
), are alike to  or satisfy
or satisfy ![$\int F{d}^{3}\upsilon =0=\int \left[\upsilon -\vec{u}\right]* F{d}^{3}\upsilon .$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn432.gif) Note that any solution of equation (17) multiplying a
Note that any solution of equation (17) multiplying a  -independent function is still a solution of equation (17), but this important property does not hold for solutions of equation (16).
-independent function is still a solution of equation (17), but this important property does not hold for solutions of equation (16).
If an initial profile 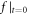 can correspond to a
can correspond to a 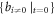 -set convergent with respect to
-set convergent with respect to  it will yield at least
it will yield at least 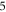 initial profiles:
initial profiles: 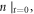
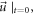
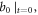
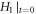 and
and  Because
Because ![$W\left(\vec{u},m\right)\equiv {\int }_{{\rm{| }}\upsilon {{\rm{| }}}^{2}\lt {c}^{2}}{\left[\upsilon -\vec{u}\right]}^{m}{d}^{3}\upsilon $](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn443.gif) is a function of
is a function of 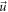 and
and 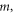
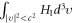 is therefore a combination of these functions of
is therefore a combination of these functions of 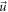 and
and 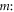
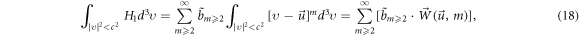
where  and its value equaling to
and its value equaling to 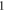 implies an equation of combination coefficients
implies an equation of combination coefficients 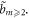 Likewise,
Likewise, ![${\int }_{{\rm{| }}\upsilon {{\rm{| }}}^{2}\lt {c}^{2}}\left[\upsilon -\vec{u}\right]* {H}_{1}{d}^{3}\upsilon =0,$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn452.gif)
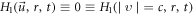 and equation (18) also imply equation of combination coefficients
and equation (18) also imply equation of combination coefficients 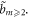 If expressing these combination coefficients in terms of power series of
If expressing these combination coefficients in terms of power series of 
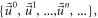 equations (14), (16) will imply that the
equations (14), (16) will imply that the 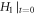 -profile naturally defines a matrix
-profile naturally defines a matrix 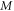 linking the set
linking the set 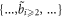 with the set
with the set 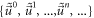
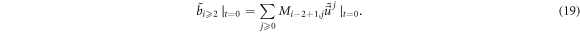
Now that ![${\sum }_{i\geqslant 2}{\tilde{b}}_{i}\left(\vec{u}\left(r,t=0\right)\right)* {\left[\upsilon -\vec{u}\left(r,t=0\right)\right]}^{i}$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn461.gif) can satisfy equations (14), (16), (17) at
can satisfy equations (14), (16), (17) at 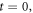 it is easy to prove its counterpart, which is to replace
it is easy to prove its counterpart, which is to replace 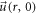 with
with 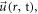 to still satisfy equations (14), (16), (17) at
to still satisfy equations (14), (16), (17) at 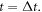 We term it as translation operation on the
We term it as translation operation on the 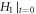 -profile and denote it as
-profile and denote it as 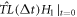 in which
in which 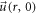 in
in  is replaced by
is replaced by 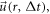 but the matrix linking
but the matrix linking 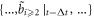 and
and 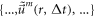 is as same as that linking
is as same as that linking 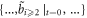 and
and  Such an operation can be expressed via a formula
Such an operation can be expressed via a formula
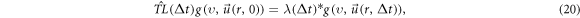
and the function  if
if  represents
represents 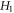 (because
(because 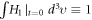 and
and 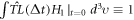 do not allow
do not allow 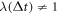 ), but
), but 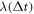 can be not constant-valued if
can be not constant-valued if  represents
represents 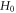 (because
(because 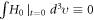 and
and 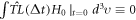 allow
allow 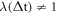 ).
).
The matrix linking the 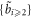 -set and the
-set and the 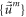 -set reflects geometric/toplogical nature/shape of the
-set reflects geometric/toplogical nature/shape of the 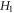 -profile, and likewise the
-profile, and likewise the 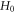 -profile also has a matrix reflecting its geometric/toplogical nature/shape. If this matrix is unchanged during evolution, the related profile is viewed as keeping geometric/toplogical nature/shape. Thus, the phrase 'deformation' refers to this matrix varying with respect to
-profile also has a matrix reflecting its geometric/toplogical nature/shape. If this matrix is unchanged during evolution, the related profile is viewed as keeping geometric/toplogical nature/shape. Thus, the phrase 'deformation' refers to this matrix varying with respect to 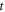 and hence the geometric/toplogical nature/shape is not fixed relative to an observer in the
and hence the geometric/toplogical nature/shape is not fixed relative to an observer in the 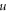 -frame. Namely, the
-frame. Namely, the 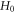 -profile can allow deformation, (relative to an observer in the
-profile can allow deformation, (relative to an observer in the 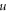 -frame), varying with respect to
-frame), varying with respect to 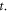
2.4. Interpreting the initial-value problem of V-M system in Eulerian-like approach as collective mode in  phase space
phase space
Because of 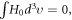
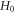 is therefore not a function positivity-preserving, and hence has zeros, beside
is therefore not a function positivity-preserving, and hence has zeros, beside 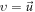 and
and 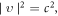 in
in 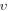 -space. Thus, a typical form of
-space. Thus, a typical form of 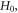 or that of functions satisfying equation (17), is
or that of functions satisfying equation (17), is
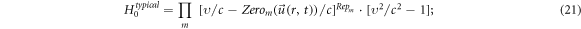
each root 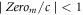 is mono-variable functional of
is mono-variable functional of  and each number
and each number 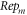 is repetition index of the root
is repetition index of the root  (and at least a root satisfies
(and at least a root satisfies 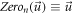 ). Such a product
). Such a product 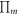 represents a class of
represents a class of  -space geometric/toplogic nature/shape. Any
-space geometric/toplogic nature/shape. Any  -independent function multiplying this typical form still satisfies equation (17). From
-independent function multiplying this typical form still satisfies equation (17). From
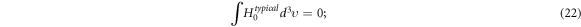
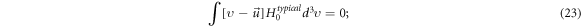
we can find
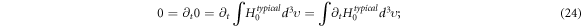
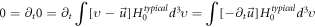
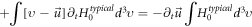
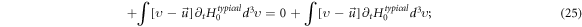
and (in similar procedure)
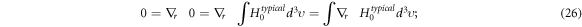
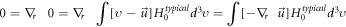
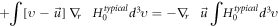
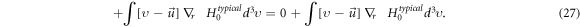
Because of
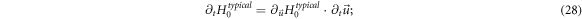

Equations (24)–(29) will yield
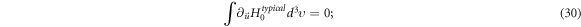
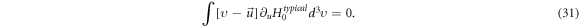
If we use the symbol '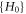 ' to represent the set of functions satisfying equation (17), equations (30), (31) imply that if
' to represent the set of functions satisfying equation (17), equations (30), (31) imply that if 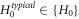 exists, so does
exists, so does 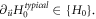
The VE is indeed an expression of the local growth rate ![${\partial }_{t}\left[{H}_{1}+{H}_{0}\right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn514.gif) [59]:
[59]:

where the effect of the operator 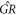 on a function
on a function  obey following formula [59]
obey following formula [59]
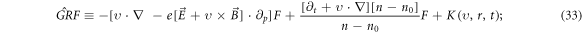
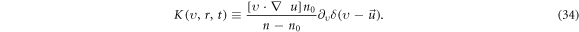
Note that a fraction of the local growth rate
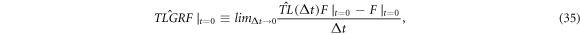
is responsible for  and another fraction
and another fraction
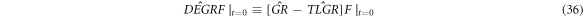
is responsible for the deformation of 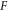 relative to an observer in the
relative to an observer in the 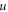 -frame.
-frame.
Because 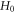 must satisfy equation (17), its general form reads
must satisfy equation (17), its general form reads 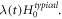 Substituting this general form into the VE, we have
Substituting this general form into the VE, we have
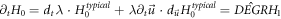
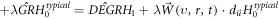
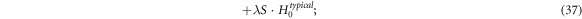
or
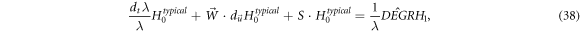
where

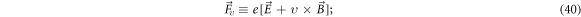
and the functional 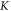 defined by equation (34) has been contained in
defined by equation (34) has been contained in 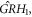 as well as in
as well as in 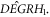
Because of equations (16), (17), (32)–(36), it is easy to find that
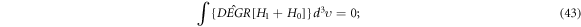
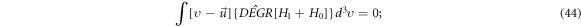
, or ![$\hat{{DEGR}}\left[{H}_{1}+{H}_{0}\right]\in \{{H}_{0}\}.$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn525.gif) Therefore, the VE reflects a relation among these members of the set
Therefore, the VE reflects a relation among these members of the set 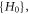 and has been converted into equation (38), a formal
and has been converted into equation (38), a formal 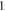 st-order ordinary differential equation (ODE) of
st-order ordinary differential equation (ODE) of 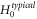 with respect to variable
with respect to variable 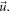 Its formal strict solution
Its formal strict solution

reflects a relation between 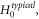 a member of
a member of 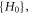 and another member
and another member 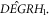
Asymptotic behavior of 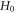 at
at 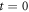 are
are 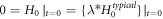 and
and 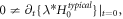 and lead to
and lead to
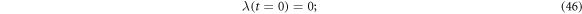
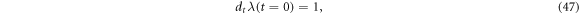
which can easily lead to

where 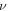 is a constant corresponding to the minimum of all time scales (each represents the time for
is a constant corresponding to the minimum of all time scales (each represents the time for ![$\left[{H}_{1}+{H}_{0}\right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn538.gif) at a given coordinate
at a given coordinate  decreasing to
decreasing to 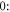
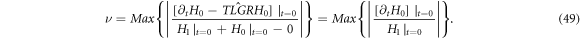
Such a choice of 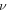 is for warranting
is for warranting 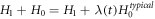 non-negative always. Thus, equations (45), (48), (49) reveal that the C-PDF
non-negative always. Thus, equations (45), (48), (49) reveal that the C-PDF 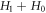 corresponds to a time-dependent global oscillation of
corresponds to a time-dependent global oscillation of 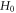 around
around 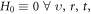 or that of
or that of 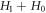 around
around 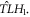 Because these fixed points, which correspond to
Because these fixed points, which correspond to 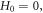 exist, the collective mode exhibits as a 'standing-wave' in
exist, the collective mode exhibits as a 'standing-wave' in 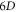 phase space.
phase space.
Considering the phrase 'Eulerian' is often for describing 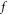 by its values at a mesh of the
by its values at a mesh of the 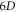 phase space, we term above procedure as 'Eulerian-like' because it is based on the description of
phase space, we term above procedure as 'Eulerian-like' because it is based on the description of 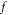 by specified functions defined over the
by specified functions defined over the 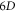 phase space. These specified functions reflect geometric/toplogial nature of initial
phase space. These specified functions reflect geometric/toplogial nature of initial 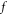 -profile. The well-known drawback of the Eulerian approach, i.e., too huge mount of mesh points and corresponding discrete values, is avoided by high-efficiently expressing them through collective mode, represented by the
-profile. The well-known drawback of the Eulerian approach, i.e., too huge mount of mesh points and corresponding discrete values, is avoided by high-efficiently expressing them through collective mode, represented by the 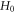 -profile, in the
-profile, in the 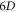 phase space. Namely, the Eulerian approach is in a one-by-one manner, to update a mesh
phase space. Namely, the Eulerian approach is in a one-by-one manner, to update a mesh 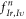 to another mesh
to another mesh 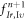 through a mesh
through a mesh 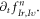 Each mesh has its own geometric/tpolgical nature. In contrast, our approach is to utilize respective geometric/topologic nature of three meshes and high-efficiently express the difference
Each mesh has its own geometric/tpolgical nature. In contrast, our approach is to utilize respective geometric/topologic nature of three meshes and high-efficiently express the difference 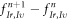 as a collective mode
as a collective mode 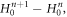 which is determined by
which is determined by 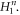 One-by-one mesh points calculation on individual
One-by-one mesh points calculation on individual 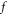 -values is replaced by calculating amplitude of the collective mode. Moreover, compared with various ansatz of
-values is replaced by calculating amplitude of the collective mode. Moreover, compared with various ansatz of 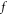 [40] used in simulating the V-M system,
[40] used in simulating the V-M system, ![$f=n* \left[{H}_{1}+{H}_{0}\right]$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn565.gif) is a strict expression. On the other hand, the Lagrangian approach is to express the initial-value problem of the V-M system or the N-M system as those of many initial mono-variable functions (of
is a strict expression. On the other hand, the Lagrangian approach is to express the initial-value problem of the V-M system or the N-M system as those of many initial mono-variable functions (of 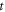 ), or Lagrangian particles, identified by different points on a
), or Lagrangian particles, identified by different points on a 
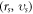 -profile. By now, the calculation in the Lagrangian approach is rarely to take into account the geometrical/toplogical nature of this
-profile. By now, the calculation in the Lagrangian approach is rarely to take into account the geometrical/toplogical nature of this 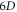 initial-values-profile, and to choose a rough treatment in which all initial-value problems of these Lagrangian particles are uniformly/equally treated as having a same time-convergence. This might be an unavoidable difficulty for the Lagrangian approach.
initial-values-profile, and to choose a rough treatment in which all initial-value problems of these Lagrangian particles are uniformly/equally treated as having a same time-convergence. This might be an unavoidable difficulty for the Lagrangian approach.
2.5. Example of application of this simulation based on the 5-function expression of 
Here, we present some examples of application of this new simulation method. It simulates an electron bunch (e-bunch) travelling within a space inhomogeneous DC-fields configuration. The DC-fields configuration is described as follows: 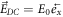 and
and 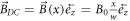 if
if  and
and 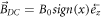 elsewhere. Namely,
elsewhere. Namely, 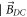 drops from
drops from  at
at 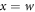 to
to 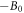 at
at 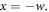 The initial PDF of the e-bunch is
The initial PDF of the e-bunch is 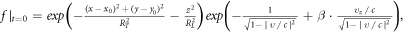 where
where 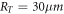 and
and 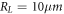 are transverse and longitudinal radius respectively and
are transverse and longitudinal radius respectively and 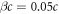 is the global moving velocity (along the
is the global moving velocity (along the 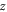 -direction) of the e-bunch,
-direction) of the e-bunch, 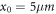 and
and 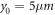 are initial transverse coordinates of the symmetric axis of the e-bunch relative to the
are initial transverse coordinates of the symmetric axis of the e-bunch relative to the 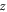 -axis. Note that this
-axis. Note that this 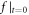 -profile corresponds to initial current profile having a vortex
-profile corresponds to initial current profile having a vortex 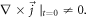 As described in last subsection, we can derive, from this initial PDF,
As described in last subsection, we can derive, from this initial PDF, 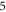 derivative initial profiles and calculate their evolutions. Some examples are presented in figures 4, 5. Velocity subspace boundary conditions are
derivative initial profiles and calculate their evolutions. Some examples are presented in figures 4, 5. Velocity subspace boundary conditions are 
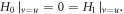
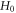 and
and 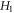 are finite-valued and
are finite-valued and 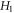 are always non-negatively-valued. These examples well illustrate that phase space details of the evolving
are always non-negatively-valued. These examples well illustrate that phase space details of the evolving 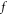 -profile can be well reflected by those of the evolving
-profile can be well reflected by those of the evolving 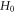 -profile.
-profile.
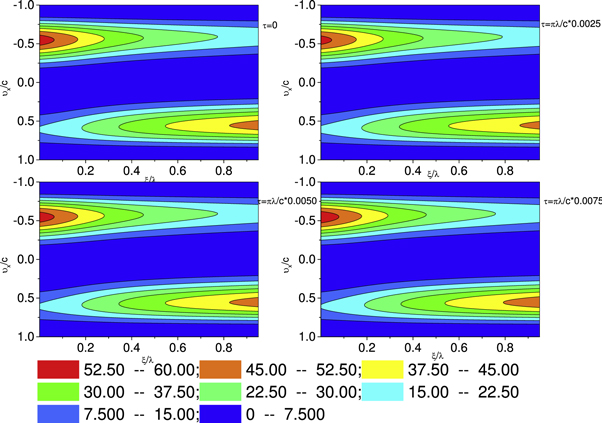
Figure 4. Snapshots of 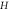 at
at 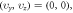 where
where 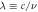 and
and  is the frequency of the oscillation in the off-center density
is the frequency of the oscillation in the off-center density 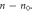
Download figure:
Standard image High-resolution imageFigure 5. Snapshots of ![$f\left(t,r,{\rm{\upsilon }}\ne u\right)\equiv \left[n-{n}_{0}\right]H$](https://content.cld.iop.org/journals/2516-1067/4/2/025005/revision2/prexac743eieqn603.gif) at
at 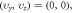 where
where 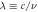 and
and  is the frequency of the oscillation in the off-center density
is the frequency of the oscillation in the off-center density 
Download figure:
Standard image High-resolution image2.6. Comparison with others
For comparison with other kinetic simulation schemes, we present, in figure 6, results of applying this method to laser wakefield, a topic attracting many PIC simulations [60, 61]. Electronic density wake of a laser with a triangular-function-type vector potential initial envelope 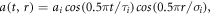 which is displayed in figure 6(a), has a shape similar to that displayed in figure 1 of [60], For a laser with a Gaussian-function-type initial envelope
which is displayed in figure 6(a), has a shape similar to that displayed in figure 1 of [60], For a laser with a Gaussian-function-type initial envelope  electronic density wake displayed in figure 6(c) has a shape similar to that displayed in figure 19 of [61].
electronic density wake displayed in figure 6(c) has a shape similar to that displayed in figure 19 of [61].
Figure 6. Snapshots of electronic density profile and longitudinal electric field profile of the wakefield of a laser propagating in a plasma layer from left-to-right. (a,b) are at 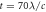 and for laser initial envelope and plasma parameters in figure 1 of [60]:
and for laser initial envelope and plasma parameters in figure 1 of [60]: 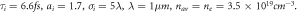 (c,d) are at
(c,d) are at 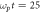 and for initial laser initial envelope and plasma parameters in figure 19 of [61]:
and for initial laser initial envelope and plasma parameters in figure 19 of [61]: 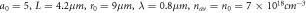 and same numerical parameters:
and same numerical parameters: 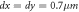 and
and 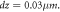
Download figure:
Standard image High-resolution imageBecause of incomplete information disclosure in these refs, such as missing detailed forms of the interpolation functions used in PIC simulations, it is only possible to make a qualitative comparison. Our results presented in figure 6 also display 'bubble structure' displayed in figure 19 of [61]. But the depth and longitudinal position of density valley differ from those in figure 19 of [61]. For example, in the upper-left panel, the region 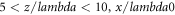 is a density valley, it is spaced by a density peak from another density valley at the region
is a density valley, it is spaced by a density peak from another density valley at the region  Likewise, in the down-left panel, a large density valley is at the region
Likewise, in the down-left panel, a large density valley is at the region 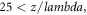 another small valley is at the region
another small valley is at the region 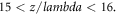
But in-depth understanding the unavoidable difficulty in particle simulation and seeking for possible solution for it are necessary. A possible solution might arise from a subtle, dual role of an electron. Each electron can be both the source of a scalar potential and that of a vector potential. A notable fact is that scalar potentials from different source electrons will not offset mutually but vector potentials will. This fact implies that the microscopic vector field exerted by an electron can be divided into two parts:  where the subscript 'c' represents 'contributed' (to macroscopic vector field) and 'o' represents 'offset'. For all electrons, there are at least a scalar field and two vector fields defined over the initial phase space
where the subscript 'c' represents 'contributed' (to macroscopic vector field) and 'o' represents 'offset'. For all electrons, there are at least a scalar field and two vector fields defined over the initial phase space  giving a description on the system. One vector field is from those
giving a description on the system. One vector field is from those 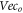 and the other from those
and the other from those 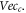 For example, accelerating rate of each electron
For example, accelerating rate of each electron 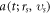 is a vector, and hence there should be
is a vector, and hence there should be

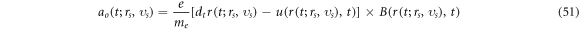
These unique properties of the 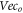 -field can be utilized for solving difficulties mentioned before.
-field can be utilized for solving difficulties mentioned before.
Note that the MEs do not couple with 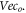 The uniform convergence requirement forces us to re-consider the role of those RNEs. It is appropriate to view them as a definition of respective
The uniform convergence requirement forces us to re-consider the role of those RNEs. It is appropriate to view them as a definition of respective 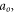 or all those RNEs yield the expression of an
or all those RNEs yield the expression of an 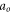 -field, which does not couple with the MEs. In other words, the particle simulation can be in a more efficient scheme if noticing the division
-field, which does not couple with the MEs. In other words, the particle simulation can be in a more efficient scheme if noticing the division  and the fact that the MEs do not couple with
and the fact that the MEs do not couple with  Ignoring them will make the particle simulation entangled by exactly solving
Ignoring them will make the particle simulation entangled by exactly solving 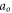 from those RNEs. Once the
from those RNEs. Once the  field cannot be exactly solved, the whole particle simulation is ruined. Actually, it is unnecessary to bind the particle simulation with this nearly impossible task (because of the uniform convergence requirement). The condition for
field cannot be exactly solved, the whole particle simulation is ruined. Actually, it is unnecessary to bind the particle simulation with this nearly impossible task (because of the uniform convergence requirement). The condition for 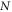 expression formula of
expression formula of 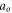 able to be simultaneously solved, or the fact that those
able to be simultaneously solved, or the fact that those 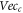 (such as
(such as 
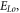
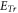 and
and 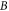 ) allow so diverse, even opposite, values of
) allow so diverse, even opposite, values of 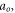 lead to an equation of these
lead to an equation of these 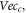 and this equation couples with the MEs to form a natural closure of these
and this equation couples with the MEs to form a natural closure of these 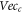 (because the MEs do not couple with
(because the MEs do not couple with 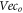 ) [56].
) [56].
3. Summary
Two difficulties previously mentioned limit the validity and efficiency of the EM kinetic simulation in both Eulerian approach and Lagrangian one. This forces us to try more efficient methods on kinetic theory. Starting from a compact expression of 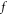 and utilizing geometrical/toplogical nature of initial conditions and conservation laws behind the V-M system, we can take a more efficient form of the initial-value problem of the V-M system. Difference among these
and utilizing geometrical/toplogical nature of initial conditions and conservation laws behind the V-M system, we can take a more efficient form of the initial-value problem of the V-M system. Difference among these 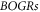 in the EM kinetic simulation in both Eulerian approach and Lagrangian one are contained in the geometrical/toplogical nature of the
in the EM kinetic simulation in both Eulerian approach and Lagrangian one are contained in the geometrical/toplogical nature of the  -profile and are taken into account. The initial-value problem of V-M system is therefore condensed into that of the magnitude of the
-profile and are taken into account. The initial-value problem of V-M system is therefore condensed into that of the magnitude of the  -profile. In short, this new method enables us to consistently treat these
-profile. In short, this new method enables us to consistently treat these 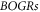 while treating them through the EM kinetic simulation in both Eulerian approach and Lagrangian one is always perplexed by two difficulties.
while treating them through the EM kinetic simulation in both Eulerian approach and Lagrangian one is always perplexed by two difficulties.
Acknowledgments
This work is supported by NSFC.Grant.No.12074398.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).