Abstract
By means of a canonical generalized momentum and a canonical conjugate spin variable, a complete canonical Hamiltonian formalism is designed to describe a coulomb field with electronic spin–orbit coupling in a semi-classical and non-relativistic way. After this operation, unlike the existing Lagrange formulation, the concepts of hidden momentum, hidden angular momentum and spin kinetic energy are not used in the canonical formalism. Besides, it is easy to find that there are four first integrals involving the conserved total energy and the conserved total angular momentum vector in an 8-dimensional phase space of the system. In this sense, the global dynamics is typically integrable, regular and non-chaotic, and each orbit in the phase space is a quasi-periodic 4-dimensional Kolmogorov-Arnold-Moser(KAM) torus.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
It is interesting to discuss electron spin–orbit couplings in electro-dynamics. A magnetic moment and the Thomas procession [1–4] are usually used as the description of an electron spin. In terms of quantum theory, the Bargmann-Michel-Telegdi(BMT) equation with electron spin and perturbation [5–7] is derived to study a hydrogen atomic coupled phenomenon associated to electron spin [8]. In addition, electronic spin–orbit coupling interactions in a non-relativity condition in relativity theory [9–12] are considered so that the Lagrangian function of a weak field is given [10]. It should be emphasized that the Thomas precession plays an important role in establishing the concept of electron spin, and the concept of the hidden momentum [13] agrees well with the theory of modern electrodynamics and Newton's laws of motion. However, the classical electromagnetic theory does not give the hidden momentum a satisfactory explanation. Instead, the relativistic covariant theory does. Besides this, semi-classical physics is consistent with quantum mechanics in the conservation of angular momentum of the system [10]. Here are some details. According to semi-classical physical theory [10], in the non-relativity condition the spin variable is expressed as a cross product of two vectors, where each vector and its derivative vs time are viewed as a pair of variables similar to a pair of generalized coordinate and velocity. At once, a Lagrange formulation of the system is obtained in the non-relativity limit, and the spin-evolution equations can be derived from the spin kinetic energy in the Lagrange function. It is shown in [14] that the total angular momentum in the Lagrange system is not conserved if the orbital angular momentum is defined as the kinetic angular momentum, but it is conserved when the canonical momentum including the general momentum and the hidden momentum.
On the other hand, the spin effects play an important role in the evolution of celestial bodies, and are a rich source for the occurrence of highly nonlinear phenomena including chaotic behaviors. It has been confirmed in many references [15–18] that the spin effects can cause chaos in the post-Newtonian dynamics for spinning compact binaries. Note that there have been a long history of some doubt about the problem whether the system is chaotic or not. In fact, the conflict is caused by two points. One is the post-Newtonian Lagrange dynamics for spinning compact binaries [19] different from the post-Newtonian Hamiltonian dynamics [20], and the other is the absence of a criterion on the integrability of the post-Newtonian dynamics of spinning compact binaries because the spin variables are non-canonical. As far as the first point is concerned, the two formulations use distinct coordinate gauges. The former uses the harmonic coordinate gauge, while the latter adopts the Arnowitt-Deser-Misner(ADM) coordinate gauge. It should be emphasized that there are some differences between them. In the conservative case, the total energy integral and angular momentum integral are approximately accurate to certain post-Newtonian order for the former, but they are exactly conserved. This difference may lead to different dynamical behaviors between the two approaches. For example, the conservative post-Newtonian Lagrangian dynamics of the binary system with one body spinning is possible to yield chaos [15, 21], but the conservative post-Newtonian Hamiltonian one is integrable and not at all chaotic [22]. These results are also suitable for the two approaches when the spin effects are only limited to spin–orbit coupling interactions to the leading two terms [23, 24]. It is shown clearly from the facts that the conflict should be explicit if the difference between the two formulations is neglected. As to the second point, the use of non-canonical spinning variables makes the relationship between the integrability of the system and the number of independent isolating integrals unclear. In order to work out this problem, Wu and Xie [25] proposed a set of canonical spinning variables so as to obtain a complete canonical post-Newtonian Hamiltonian formalism of the spinning compact binary system. At once, several integrable models can be found directly from the canonical formalism. In addition, it is easy to see the existence of the integrability of the dynamics either for the conservative post-Newtonian Hamiltonian binary system with one body spinning or for one with spin–orbit coupling interactions to the leading two terms On the contrary, their corresponding Lagrange formulations are not integrable for the lack of sufficient numbers of isolating integrals. Besides these, there are many other advantages for the analysis of dynamical behaviors in the canonical formalism. Up to now, the doubt of chaos in the spinning compact binary system has been explored completely [18, 25–29]. These are attributed to some examples on the spin effects increasing the extension of chaos of objects. Of course, there are reports on the spinning parameter of the Kerr black hole weakening chaos [30, 31].
Due to the above-mentioned points, a main motivation of this paper is to improve the work of [14], and to establish a complete canonical Hamiltonian formalism of a non-relativistic coulomb field with semi-classical electronic spin–orbit coupling in terms of the canonical spinning variables presented in [25]. In this way, the concepts of the hidden momentum and the hidden angular momentum are not necessary to be used, and the spin evolution equations are not necessary to be derived from the spin kinetic energy. In particular, the conservation laws of the system can be directly used to provide some insight into the dynamics of the complete canonical formalism. That is to say, the relationship between the integrability and the number of isolating integrals will be used to estimate the global dynamics of the system. This is the most important aim of the present paper.
First, let us introduce a Lagrangian formulation of classical charged particles with spin–orbit coupling, which can be found in [14]. Then a Hamiltonian formulation is used instead of the Lagrangian one, and all conserved quantities of the Hamiltonian system are given. Finally, the Hamiltonian is rewritten in a completely canonical formalism that uses canonical spin variables as well as canonical momentum.
2. Lagrangian formulation
Suppose that a charged particle moves in a non-relativistic semi-classical coulomb field with mass m, charge q, spin s = a × b (In non-relativistic limit, the spin is parameterized in terms of a and b), and coulomb potential ϕ. In the inertial frame, the Lagrangian formulation is written in the form [14]

In the above equation, v is the velocity of the particle in an electromagnetic field (E, B), A is a magnetic vector potential, r = ∣r∣, c is the velocity of light in vacuum, and the value of g-factor of the electron near the hydrogen atom is 2. In addition, 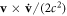 denotes the angular frequency of Thomas procession ωT
, and s · ωT
is just a spin–orbit coupling interaction.
denotes the angular frequency of Thomas procession ωT
, and s · ωT
is just a spin–orbit coupling interaction.
For an electron near the hydrogen atom in the inertial frame, one has q = − e(e > 0), and ϕ = e/r. Then it is easy to obtain E = − ▽ϕ = e
r/r3, and  . If there is no external field, A = B = 0. Hence, the Lagrangian function is rewritten as
. If there is no external field, A = B = 0. Hence, the Lagrangian function is rewritten as
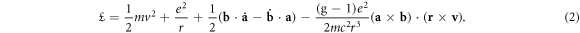
Where -1 in the factor (g − 1) is from the Thomas precession. For simplicity, we take G = (g − 1)e2/(2mc2). According to the Lagrangian equation, the orbital evolution equations and spin evolution equations are expressed as follows:
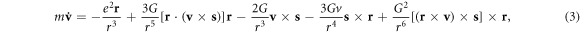
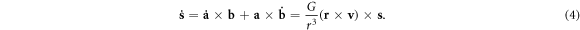
They are the non-relativistic dynamical evolution model of the hydrogen atom with electron spin–orbit coupling, given in [14].
It should be noted that the third term in the equation (2) is the electron spin kinetic energy. For the spin variables, each pair of 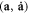 and
and 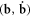 are similar to a pair of generalized coordinates and velocities (r, v). Obviously, the expressions of
are similar to a pair of generalized coordinates and velocities (r, v). Obviously, the expressions of 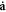 and
and  can be derived from the Lagrangian function, respectively, and the spin evolution equation (4) is obtained. Perhaps, one has some difficulty in understanding the spin kinetic energy in the Lagrangian. It is also clear that neither the orbital angular momentum L = r × m
v nor the total angular momentum J = L + s is conserved. Only when the hidden angular momentum is included [13], the total angular momentum of the system may be conserved. Here it is necessary to use the concept of a canonical generalized momentum consisting of the orbital angular momentum, the hidden angular momentum and others. This shows that the use of the concept of canonical momentum is very convenient to investigate the conservation laws of the system. Because of these, we shall directly use the canonical momentum to reexpress the system as a Hamiltonian formulation, where the concept of the spin kinetic energy does not at all appear.
can be derived from the Lagrangian function, respectively, and the spin evolution equation (4) is obtained. Perhaps, one has some difficulty in understanding the spin kinetic energy in the Lagrangian. It is also clear that neither the orbital angular momentum L = r × m
v nor the total angular momentum J = L + s is conserved. Only when the hidden angular momentum is included [13], the total angular momentum of the system may be conserved. Here it is necessary to use the concept of a canonical generalized momentum consisting of the orbital angular momentum, the hidden angular momentum and others. This shows that the use of the concept of canonical momentum is very convenient to investigate the conservation laws of the system. Because of these, we shall directly use the canonical momentum to reexpress the system as a Hamiltonian formulation, where the concept of the spin kinetic energy does not at all appear.
3. Hamiltonian formulation
Turning off the spin kinetic energy in equation (2), we modify slightly the Lagrangian in the version
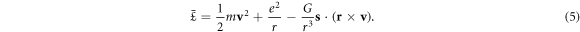
A canonical generalized momentum of the system is difined as
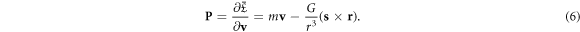
As an illustration, m v represents the kinetic momentum, − ge2(s × r)/(2mc2 r3) stands for the hidden momentum [13], and e2(s × r)/(2mc2 r3) is an additional momentum from the Thomas precession. Then the Hamiltonian of the system is in the form of

The evolutions of a pair of canonical variables (r, P) satisfy the Hamiltonian canonical equations
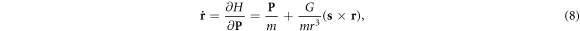
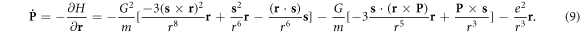
Meantime, the electron spin evolution equations are determined by [20],
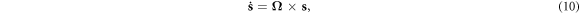
where
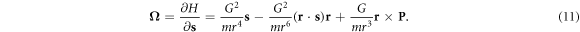
Obviously, equations (8) and (9)are equivalent to equation (3). It is easy to verify that equation (4) can be obtained by substituting equations (6) into (10). Thus, it can be concluded that although the Lagrangian (5) does not contain the electron spin kinetic energy, the Hamiltonian system (7) is completely equivalent with the Lagrangian system (2) from the point of view of the dynamics. Note that the equivalence of the two formulations is based on the use of the same coordinate gauges. Otherwise, different coordinate gauges may lead to the two formulations having inconsistent dynamical behaviors, as is mentioned in the Introduction.
4. Integrals of motion
The Hamiltonian (7), as a function of the state variables (r, P, s), is labeled as H(r, P, s). Its derivative with respect to time is

Namely, equation (7) is an integral of motion, called as the total energy integral of the system.
The derivative of the square of the spin vector is
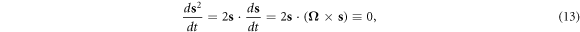
therefore, the magnitude of the spin vector is conserved. In other words, the length of s, s = ∣s∣, is always a constant.
Let the orbit angular momentum be L = r × P. Its derivative to time is
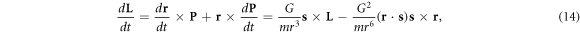
so L is not conserved. For the square of orbital angular momentum L2, we have
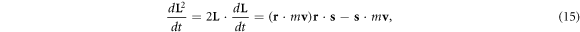
In quantum mechanics, it has [L2, H] = 0, the square of orbital angular momentum L2 is conserved if the potential energy V(r) is central symmetric. In this model, if and only if s is always perpendicular to the orbital plane (r, v), it has 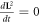 . In fact, this is not always the case. The essential difference between classical mechanics and quantum mechanics lies in the definition of spin direction. That is, L2 is not conserved here.
. In fact, this is not always the case. The essential difference between classical mechanics and quantum mechanics lies in the definition of spin direction. That is, L2 is not conserved here.
In addition, the derivative of the total angular momentum J = L + s is zero, i.e.
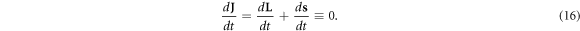
This means that the total angular momentum is conserved. It should be pointed out that the conservation of the total angular momentum vector corresponds to the existence of three conserved components of the vector.
In short, the Hamiltonian system (7) contains five integrals of motion, including the total energy, the length of the spin vector and the total angular momentum. It should be emphasized that the coordinate and momentum (r, P) in Hamiltonian (7) are canonical because they satisfy the equations (8) and (9) but the spin variable s is not. Therefore, the Hamiltonian (7) cannot be regarded as a complete canonical representation. The spin variable s of the Hamiltonian (7) should be expressed in a canonical form.
5. Construction of a canonical formalism
It has been reported in [25] that the non-canonical spinning variables in the post-Newton Hamiltonian formulations of compact spinning binaries could be replaced by canonical ones. In our opinion, the transformation should be also fit for the present problem. Details of the implementation are listed in the following.
The spin vector s can be readjusted as 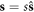 , where the unit vector
, where the unit vector 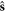 in cylindrical-like coordinates (ρ, θ, ξ) is given by [25],
in cylindrical-like coordinates (ρ, θ, ξ) is given by [25],
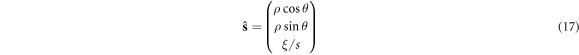
Here, ρ is a function of ξ in the form  . Clearly, s is a two-dimensional vector with three components. Substituting equation (17) into equation (7), we obtain a complete canonical Hamiltonian formalism, marked as Γ(r, θ; P, ξ). Notice that (r, θ) are regarded as a set of generalized coordinates in a four-dimensional space, and (P, ξ) are corresponded to their generalized momenta. For the canonical formalism Γ, (r, P) still satisfy the canonical equations (8) and (9) in which s should give place to
. Clearly, s is a two-dimensional vector with three components. Substituting equation (17) into equation (7), we obtain a complete canonical Hamiltonian formalism, marked as Γ(r, θ; P, ξ). Notice that (r, θ) are regarded as a set of generalized coordinates in a four-dimensional space, and (P, ξ) are corresponded to their generalized momenta. For the canonical formalism Γ, (r, P) still satisfy the canonical equations (8) and (9) in which s should give place to 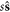 , but the new spin variable (θ, ξ) evolve according to the canonical equations
, but the new spin variable (θ, ξ) evolve according to the canonical equations
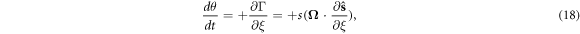
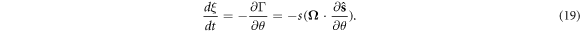
It is easy to check the above expressions equivalent to equation (10).
The Hamiltonian Γ is a completely canonical representation in an eight-dimensional phase space generated by (r, θ; P, ξ). It contains four integrals of motion, the total energy integral and the three components of the total angular momentum. As a point to illustrate, the length of the spin vector s is no longer an integral of the new Hamiltonian. In spite of this, the conserved length of the spin vector is not meant to be lost, and in fact it is hidden in the design of the new spin variable 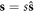 . This canonical representation will be useful to qualitatively analyze the dynamics. See the following demonstrations for more information.
. This canonical representation will be useful to qualitatively analyze the dynamics. See the following demonstrations for more information.
6. Properties of the canonical system
As is well-known, Hamiltonian mechanics that uses canonical variables is a geometry of the phase space generated by generalized coordinates and generalized momenta. It is also a symplectic geometry of the phase space [32]. Many symplectic geometric properties are suitable for the canonical formalism Γ. That is to say, the representation of the canonical formalism Γ has more advantages in the analysis of dynamics system theories than that of the Lagrangian formulation (2). Hereafter we list several points.
Without doubt, the Hamiltonian phase flow for a canonical system remains a symplectic structure. Meanwhile, the symplectic structure is an integral invariant of the Hamiltonian phase flow. This requires naturally that a numerical integration can always maintain the symplectic structure. Symplectic integration methods [33–39] can arrive at this aim. Based on the second-order implicit midpoint rule, several symplectic integrators for the post-Newtonian canonical Hamiltonian formulations of spinning compact binaries [28, 29] should be valid to solve the canonical system Γ. In the case, they are able to maintain the symplectic structure, ω2 = d r ∧ d P + d θ ∧ d ξ [34], and to make the total energy of the system have no a secular change with time. This implies that the use of the canonical formalism has a contribution in the improvement of numerical integration. Even if conventional numerical integration algorithms like Runge-Kutta type methods are used in place of symplectic integration schemes, the numerical accuracy should be better for the use of the canonical formalism than for that of the Lagrangian formulation. The result is supported by [40] regarding numerical comparisons of a second-order post-Newtonian three-body problem.
It should be emphasized particularly that there is a close relation between the canonical formalism and dynamics system theories. A conservative canonical Hamiltonian system with n degrees of freedom has a 2n-dimensional phase space. It holds 2n Lyapunov exponents, labeled as λi and λ2n−i+1(i = 1, 2, ...n). They satisfy the relations λi = − λ2n−i+1, and λi ≥ λj (1 ≤ i < j ≤ n) [41]. λ1 is called as the largest Lyapunov exponent [42–45]. If λ1 > 0, a bounded system is chaotic. If all the Lyapunov exponents are zero, the bounded system is ordered. A cyclic coordinate means its conjugate variable being a constant, so the phase space is decreased 2 dimensions, and two Lyapunov exponents become zero. It is clear that when the system has n independent isolating integrals, all Lyapunov exponents are zero. In this case, the system is integrable, regular and non-chaotic. Therefore, these n independent isolating integrals can be used as a criterion to estimate the integrability of the canonical system having n degrees of freedom. The criterion indicates that the dynamical system is not integrable, and even produce chaos if the number of independent isolating integrals is less than n, but the dynamical system should be integrable If the number of independent isolating integrals is more than or equal to n. This belongs to the classical Liouville integrability criterion [32, 41]. Here is the twofold to be noted. First, the integrability of a 2n-dimensional conservative non-canonical system needs 2n isolating integrals. Second, only n isolating integrals are sufficient to determine the integrability of a conservative canonical system with a 2n-dimensional phase space. There are n independent frequencies that are incommensurable to each other. Quasi-periodic orbits filled with the phase space are n-dimensional rings but not closed. When the number of isolating integrals is n + 1, the system is still integrable, but two frequencies are commensurable and not independent. Resonance phenomena may occur. If the number of isolating integrals is 2n − 1, the orbits in the phase space are closed, and strictly periodic. These properties are completely fit for the present electronic spin–orbit coupling canonical system Γ with 4 degrees of freedom since there are the four isolating integrals of motion, involving the total energy integral and the total angular momentum integrals, in the 8-dimensional phase space. This system is integrable and regular. Four frequencies are independent and incommensurable, and each orbit in the phase space is a four-dimensional quasi-periodic KAM torus. This is the global dynamics of the canonical system Γ.
7. Conclusions
Inspired by literatures of [14–25], in the non-relativistic and semi-classical conditions, a spin–orbit coupling system of an electron near the hydrogen atom can be described by a completely canonical Hamiltonian formalism in which the canonical generalized momenta and the canonical conjugate spin variables are used. The canonical formalism is greatly superior to the original Lagrangian formulation in the analysis of dynamical properties. The concepts of the hidden momentum, the hidden angular momentum and the kinetic energy are not necessary to use. In addition, there is a close relationship between the integrability of the canonical system and the number of isolating integrals. Because the canonical formalism has four integrals of motion consisting of the total energy integral and the total angular momentum integrals in an 8-dimensional phase space, its global dynamics is integrable and regular. It is can be concluded that the quantum-mechanical operator corresponds to the canonical variable of classical mechanics, and the dynamic analysis method of classical mechanics can be applied to quantum mechanical systems. In the future investigations, a clearer dynamic description will be given by the canonical formalism of Hamiltonian system with spin–orbit coupling in the framework of quantum physics.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant Nos. 12 073 008, 11 703 005. Da-Zhu Ma is supported by the Young Top-notch Talent Cultivation Program of Hubei Province.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.

