Abstract
In this paper, we report on the behavior of intersubband optical absorption and emission spectrum in quantum well structures with an asymmetrical potential profile in a quantizing magnetic field tilted with respect to the layers in the considered structure. The analysis of the effect of both the magnetic field value and orientation and potential profile of a quantum well structure on the intensity of the 'forbidden' (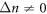 ) intersubband optical transitions is presented. We also present the approximate analytical expression for the estimation of the contribution to the absorption/emission coefficient of intersubband transitions with different
) intersubband optical transitions is presented. We also present the approximate analytical expression for the estimation of the contribution to the absorption/emission coefficient of intersubband transitions with different 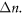
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Application of a quantizing magnetic field to a quantum well leads to a substantial change in the single-electron spectrum. Each of the continuous 2D subbands of the quantum well is split into a discrete set of equidistant Landau levels (LL). The discrete nature of the Landau spectrum leads to an essential transformation of electron scattering [1–4] and relaxation processes [5–7], which can be used to improve the characteristics of THz and far-infrared optoelectronic devices [1–16].
The other appealing aspect is a possibility of tuning the frequency of optical transitions between Landau levels of different subbands [17, 18]. The frequency of transition between 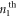 LL in
LL in 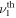 subband (LL
subband (LL 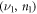 ) and
) and  LL in
LL in 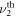 subband (LL
subband (LL 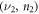 )
)
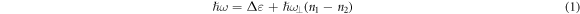
(where 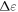 is intersubband spacing and
is intersubband spacing and 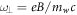 is the cyclotron frequency) can be tuned by varying magnetic field strength, if
is the cyclotron frequency) can be tuned by varying magnetic field strength, if  However, there is the selection rule
However, there is the selection rule 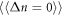 which forbids any transitions with
which forbids any transitions with 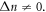 This selection rule can be violated by tilting the magnetic field with respect to the layers of quantum well structure [17, 19]. The numerical calculations carried out in the [19] for some fixed quantum well structure while varying the magnitude and direction of the magnetic field, demonstrated that the intensity of peaks induced by transitions with
This selection rule can be violated by tilting the magnetic field with respect to the layers of quantum well structure [17, 19]. The numerical calculations carried out in the [19] for some fixed quantum well structure while varying the magnitude and direction of the magnetic field, demonstrated that the intensity of peaks induced by transitions with  can exceed that of the peak with
can exceed that of the peak with 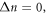 attaining the values close to those in the absence of a magnetic field. On the contrary in the [17], the potential profile of the quantum well structure was varied, while fixing the magnetic field magnitude and direction, and the importance of the potential asymmetry for the effect was established.
attaining the values close to those in the absence of a magnetic field. On the contrary in the [17], the potential profile of the quantum well structure was varied, while fixing the magnetic field magnitude and direction, and the importance of the potential asymmetry for the effect was established.
So both the magnetic field and potential profile are the critical parameters determining the intensity of the 'forbidden' transitions.
The primary aim of our present investigation is to study the violation of the selection rule 'Δn = 0' in a tilted magnetic field while simultaneously taking into account of both the critical parameters which determines the effect: tilting angle and the potential profile of the quantum well structure. We also aimed to obtain analytical expressions which give the transition intensities for different Δn, structure parameters as well as the magnetic field strength and direction. The expressions make it possible to estimate the contribution of intersubband transitions with different  to the absorption/emission coefficient and to understand the nature of the observed features in the optical spectra.
to the absorption/emission coefficient and to understand the nature of the observed features in the optical spectra.
2. Optical transitions in a quantizing tilted magnetic field
We consider the intersubband optical transitions of electrons in the quantum well structures with a potential profile  in a magnetic field
in a magnetic field  tilted with respect to growth axis z by an angle
tilted with respect to growth axis z by an angle 
In the Landau gauge  the electron envelope-function Hamiltonian in parabolic approximation has the form [18]
the electron envelope-function Hamiltonian in parabolic approximation has the form [18]
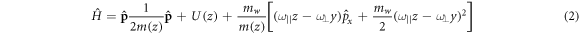
where,  is the electron effective mass,
is the electron effective mass,  and
and  are the cyclotron frequency for longitudinal (
are the cyclotron frequency for longitudinal ( ) and transverse (
) and transverse ( ) components of the applied magnetic field respectively.
) components of the applied magnetic field respectively.
Since the Hamiltonian operator commutes with the operator  of momentum projection on the x-axis, i. e.,
of momentum projection on the x-axis, i. e.,  we can construct a basis from the stationary states with definite values
we can construct a basis from the stationary states with definite values  in this momentum projection. The wave-functions of such basis has the form [18]
in this momentum projection. The wave-functions of such basis has the form [18]
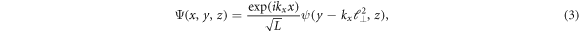
where L is the cross section of the sample,  is the magnetic length for the magnetic field component
is the magnetic length for the magnetic field component  The electron energies
The electron energies  and functions
and functions 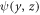 are the eigenenergies and the eigenfunctions of the two-dimensional Hamiltonian [18]
are the eigenenergies and the eigenfunctions of the two-dimensional Hamiltonian [18]
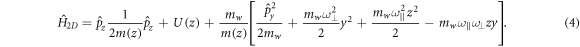
Since the Hamiltonian (4) is independent on 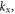 the electron energy levels are degenerate with respect to
the electron energy levels are degenerate with respect to 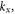 the matrix of the Hamiltonian (2) in the basis of wave functions (3) is diagonal in
the matrix of the Hamiltonian (2) in the basis of wave functions (3) is diagonal in  and the matrix element for
and the matrix element for 
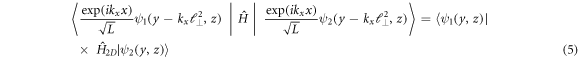
does not depend on 
In a magnetic field perpendicular to the structure layers (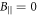 ), the electron energy levels and wave functions are given by the expressions [20]
), the electron energy levels and wave functions are given by the expressions [20]
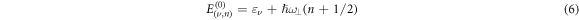
and
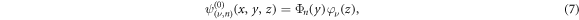
where Φn(y) is the wave function for nth energy level of the linear harmonic oscillator of the cyclotron frequency 
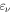 and φv(z) are vth energy level and wave function in the 1D quantum well
and φv(z) are vth energy level and wave function in the 1D quantum well  In the considered structures (GaAs/AlGaAs), the effective mass in the barrier is larger than that in the well. Therefore, the addition to the quantum well potential
In the considered structures (GaAs/AlGaAs), the effective mass in the barrier is larger than that in the well. Therefore, the addition to the quantum well potential 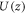 leads to an increment of barrier height with the Landau level number n [19]. However, we consider sufficiently deep subbands, therefore, this effect is neglected.
leads to an increment of barrier height with the Landau level number n [19]. However, we consider sufficiently deep subbands, therefore, this effect is neglected.
In the basis (7), the matrix element of Hamiltonian for electron in a tilted magnetic field has the form

Here we assumed that 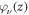 is mostly localized within the quantum well, and, therefore we can write
is mostly localized within the quantum well, and, therefore we can write

The matrix (8) can be analytically diagonalized, if the couplings between the subbands (elements with  ) are neglected. In this approximation, the energy levels and wave functions are given by the analytic expressions [21–23]
) are neglected. In this approximation, the energy levels and wave functions are given by the analytic expressions [21–23]
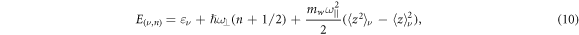
and

In the dipole approximation [24], the Fermi rule leads to the following expression for the number of electron transition events per unit time (absorption or emission intensity) from the Landau level 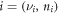 to the Landau level
to the Landau level  due to the absorption or emission of photons
due to the absorption or emission of photons

Here the negative sign represents the absorption, and the positive sign represents the emission. 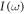 is the intensity of the incident radiation,
is the intensity of the incident radiation,  is the photon energy,
is the photon energy,  is the refractive index, and
is the refractive index, and  is the polarization vector of radiation,
is the polarization vector of radiation,
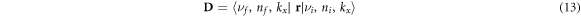
is dipole matrix element,  is the population of the Landau level i (2D concentration of electrons on the Landau level),
is the population of the Landau level i (2D concentration of electrons on the Landau level),  is the degeneracy of the Landau level.
is the degeneracy of the Landau level.
The expression (12) gives the following expressions for the power of the absorbed 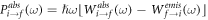 or emitted
or emitted  radiation at the frequency
radiation at the frequency 
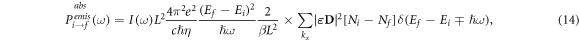
and thus, the absorption 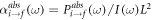 and emission
and emission  coefficients are
coefficients are
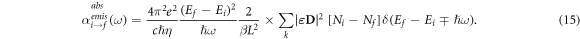
Since the component of the dipole matrix element parallel to the structure layers 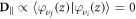 for intersubband optical transitions, we consider the electromagnetic wave polarization along the structure growth axis.
for intersubband optical transitions, we consider the electromagnetic wave polarization along the structure growth axis.
The substitution of wave-functions (11) into (13) leads to the following analytical expression for the z-component of the dipole matrix element
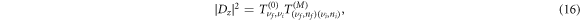

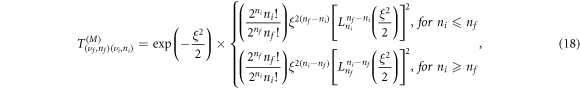

is the associated Legendre polynomial,

and 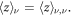
Lyo et al also obtained expressions similar to (16–20) for tunneling transitions in a magnetic field [22].
Since  does not depend on
does not depend on  the sum
the sum
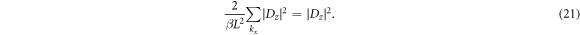
As it is seen from the obtained expressions, the contribution of the longitudinal component 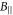 of the magnetic field is determined by the parameter
of the magnetic field is determined by the parameter  which is proportional to the difference
which is proportional to the difference  of the mean coordinates of an electron along the structure growth axis in the final and the initial states. This results in diverse effects on the absorption and emission depending on the symmetry of the quantum well structure potential.
of the mean coordinates of an electron along the structure growth axis in the final and the initial states. This results in diverse effects on the absorption and emission depending on the symmetry of the quantum well structure potential.
3. Symmetric well potential
In the case of the symmetric potential profile of the structure,  the subband wave functions
the subband wave functions  are either even or odd. Therefore, the mean value of the coordinate
are either even or odd. Therefore, the mean value of the coordinate  is the same for all subbands, and the parameter
is the same for all subbands, and the parameter  As a result, we get
As a result, we get

Thus, in a symmetric quantum well structure the selection rule 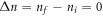 still holds for the zero order in the intersubband coupling, i.e., intersubband transitions are only possible between Landau levels with the same numbers.
still holds for the zero order in the intersubband coupling, i.e., intersubband transitions are only possible between Landau levels with the same numbers.
Moreover, some transitions remain forbidden even if the coupling between the subbands is completely taken into account. Indeed, in the case of  the Hamiltonian (4) does not change under inversion of the coordinates in the
the Hamiltonian (4) does not change under inversion of the coordinates in the  plane:
plane: 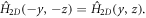 Consequently, the exact electron wave-function
Consequently, the exact electron wave-function  is even or odd with respect to the simultaneous inversion of both y and z coordinates:
is even or odd with respect to the simultaneous inversion of both y and z coordinates:  As a result, the dipole matrix element is exactly equal to zero for the transitions between states with the same parity with respect to the inversion in
As a result, the dipole matrix element is exactly equal to zero for the transitions between states with the same parity with respect to the inversion in  plane. Since
plane. Since  and
and 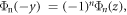 the expansion
the expansion  of an even wave-function in the basis (7) includes only terms with different parity of
of an even wave-function in the basis (7) includes only terms with different parity of 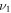 and
and  and that of an odd wave-function
and that of an odd wave-function  —only terms with the same parity of
—only terms with the same parity of 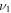 and
and 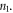 Thus, the dipole matrix element between the states
Thus, the dipole matrix element between the states  and Landau Levels
and Landau Levels 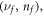 calculated with using the exact wave-functions is equal to zero in the cases when: (1) the parity of
calculated with using the exact wave-functions is equal to zero in the cases when: (1) the parity of 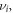
 is same, also, the parity of
is same, also, the parity of 
 is alike; (2),
is alike; (2), 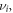
 have dissimilar parity, and,
have dissimilar parity, and, 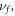
 also do not have the same parity. For example, the transitions between the ground Landau level (1, 0) and any odd-numbered Landau level in the second subband ((2, 1), (2, 3), (2, 5) and so on) are always forbidden even if the coupling between subbands is exactly taken into account.
also do not have the same parity. For example, the transitions between the ground Landau level (1, 0) and any odd-numbered Landau level in the second subband ((2, 1), (2, 3), (2, 5) and so on) are always forbidden even if the coupling between subbands is exactly taken into account.
For the remaining transitions, the coupling between the subbands leads to a violation of the selection rule  To estimate the magnitude of this violation, we consider an infinitely deep quantum well. In this case, the matrix (8) of the Hamiltonian (4) takes the form
To estimate the magnitude of this violation, we consider an infinitely deep quantum well. In this case, the matrix (8) of the Hamiltonian (4) takes the form
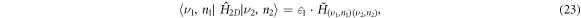
where  is ground subband energy,
is ground subband energy,  is the quantum well width,
is the quantum well width,

Thus, the diagonalization of the matrix (8) of the Hamiltonian (4) reduces to that of the matrix  The eigenvectors of this matrix coinсide with the coefficients
The eigenvectors of this matrix coinсide with the coefficients 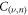 of the expansion of the electron wave-function
of the expansion of the electron wave-function  with respect to the basis (7), and its eigenvalues
with respect to the basis (7), and its eigenvalues 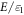 are the electron energy
are the electron energy  in the units of
in the units of  Since the matrix elements
Since the matrix elements  do not depend on the width
do not depend on the width 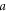 of the quantum well, the magnetic field and the quantum well width enter into the matrix only in the form of the ratios
of the quantum well, the magnetic field and the quantum well width enter into the matrix only in the form of the ratios  and
and 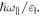 Consequently, the dimensionless energy
Consequently, the dimensionless energy 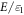 and the coefficients of the wave function expansion depend on the width of the quantum well and the magnetic field strength only via these ratios.
and the coefficients of the wave function expansion depend on the width of the quantum well and the magnetic field strength only via these ratios.
The dipole matrix element is expressed in term of C as
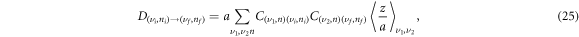
and, hence, the ratio 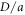 depends on the magnetic field and the quantum well width only in terms of the ratios of the Landau energies to the confined energy
depends on the magnetic field and the quantum well width only in terms of the ratios of the Landau energies to the confined energy  In figure 1, the ratio of the module of the dipole matrix elements between (1, 0) and (2, n) LLs to the width of the GaAs quantum well is shown as a function of
In figure 1, the ratio of the module of the dipole matrix elements between (1, 0) and (2, n) LLs to the width of the GaAs quantum well is shown as a function of 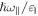 for the fixed value
for the fixed value 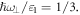 As it is seen, considering the coupling between the subbands leads to a violation of the selection rule. However, this effect is very small even when the intersubband spacing is equal to the Landau energy.
As it is seen, considering the coupling between the subbands leads to a violation of the selection rule. However, this effect is very small even when the intersubband spacing is equal to the Landau energy.
Figure 1. The module of the dipole matrix elements between the LLs (1, 0) and (2, n) divided by width  of the GaAs quantum well as a function of
of the GaAs quantum well as a function of  for the fixed value
for the fixed value 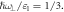
Download figure:
Standard image High-resolution image4. Asymmetric well potential
A completely different situation occurs in the structures with an asymmetric potential profile. The asymmetry leads to the subband wave-functions no longer having a definite parity. As a consequence, the mean coordinates 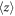 in different subbands are not the same, and the parameter ξ becomes nonzero, which results in a violation of the
in different subbands are not the same, and the parameter ξ becomes nonzero, which results in a violation of the  selection rule already in the zero order of coupling between the subbands.
selection rule already in the zero order of coupling between the subbands.
To see the extent of the selection rule violation, we compare the amplitudes of absorption/emission coefficients for transitions with 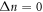 and
and 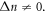 Let us consider the following transitions: absorption from ground Landau level of the lowest subband and emission from zeroth Landau level of the upper subband. The absorption/emission coefficients for the transition
Let us consider the following transitions: absorption from ground Landau level of the lowest subband and emission from zeroth Landau level of the upper subband. The absorption/emission coefficients for the transition 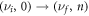 from the ground Landau level of the
from the ground Landau level of the  subband to the nth Landau level of the
subband to the nth Landau level of the  subband are
subband are
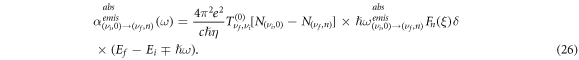
where

The transition frequency 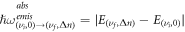 is
is

Here 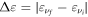 is the intersubband spacing,
is the intersubband spacing,
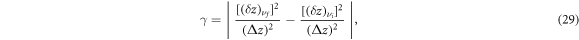
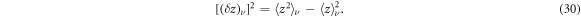
Thus, the ratio of amplitudes for the transition with  and
and  (i.e., the ratio of the intensities of the corresponding lines in the absorption or the emission spectrum) is
(i.e., the ratio of the intensities of the corresponding lines in the absorption or the emission spectrum) is

In the case of absorption (the positive sign), the expression in brackets always exceeds 1, and therefore
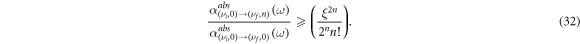
The parameter  and therefore it can be varied by changing the magnetic field strength and orientation. Accordingly, when
and therefore it can be varied by changing the magnetic field strength and orientation. Accordingly, when ![$| \xi | \gt \sqrt[2n]{{2}^{n}n!}$](https://content.cld.iop.org/journals/2399-6528/2/8/085019/revision2/jpcoaad885ieqn127.gif) the right part of (32) exceeds 1, i.e., the transition intensity for
the right part of (32) exceeds 1, i.e., the transition intensity for  dominates.
dominates.
In case of the emission (the negative sign):

and the transition intensity for  exceeds that for
exceeds that for 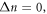 when
when ![$\xi \gt \sqrt[2n]{{2}^{n}n!\displaystyle \frac{{\rm{\Delta }}\varepsilon }{{\rm{\Delta }}\varepsilon -\hslash {\omega }_{\perp }n}}.$](https://content.cld.iop.org/journals/2399-6528/2/8/085019/revision2/jpcoaad885ieqn131.gif)
Thus, we conclude that in both the considered cases, the intensities of peaks with 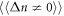 can exceed those with
can exceed those with 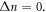
The effect of selection rule violation in tilted magnetic field is caused by the shift of the initial and final wave functions with respect to each other in the plane of layers. This relative shift can qualitatively explain the decrease in the transition intensity for Δn = 0. For the transitions with Δn ≠ 0, the in-plane wave functions are initially orthogonal, and the corresponding matrix elements are equal to zero. When the parallel component of the magnetic field arises, these in-plane wave functions are no longer orthogonal due to their relative shift and the matrix elements become non zero, that is, start to increase. With the increasing strength of the parallel component, the relative shift of the wave function also increases. Finally, for high values of the parallel component, the matrix elements start to go down. The details of the process are described by the formulas obtained.
The dependence of the line intensity on  is determined by the product of transition frequency and function
is determined by the product of transition frequency and function 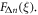 The value of the transition frequency is a monotonous function of
The value of the transition frequency is a monotonous function of  while the function
while the function  has an explicit maximum when
has an explicit maximum when  It leads to the following behavior of the line intensities. When
It leads to the following behavior of the line intensities. When  there is only one line in the spectrum that corresponds to the transitions with
there is only one line in the spectrum that corresponds to the transitions with  If
If  becomes non-zero, the lines from
becomes non-zero, the lines from  appear and their intensities grow with the increase of
appear and their intensities grow with the increase of 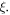 When
When  the intensity of a line with
the intensity of a line with  reaches the maximum. The intensity of this line decreases with further increase in
reaches the maximum. The intensity of this line decreases with further increase in 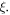 However, the line amplitude from
However, the line amplitude from  rises and reaches the maximum when
rises and reaches the maximum when 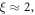 then goes down, and so on. Besides, the intensity of the line corresponding to
then goes down, and so on. Besides, the intensity of the line corresponding to  decreases close to exponentially.
decreases close to exponentially.
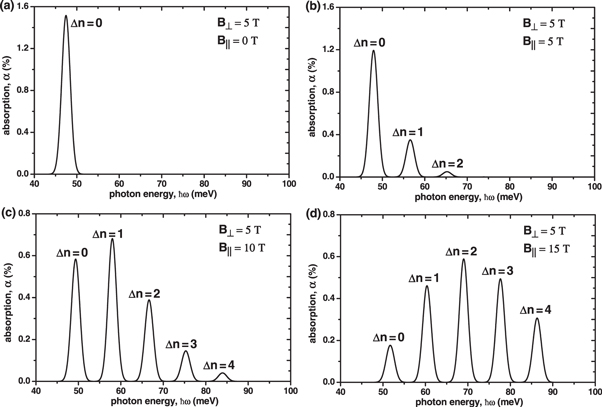
This behavior is illustrated in figure 2, where the absorption spectra caused by the transitions between Landau levels of the first and second subband are shown for an asymmetric structure consisting of two tunnel-coupled quantum wells GaAs/Al0.3Ga0.7As of different widths (12 and 5 nm), separated by the 2 nm barrier (figure 3). The calculation was performed for the fixed component  and the parameter
and the parameter  is varied via changing
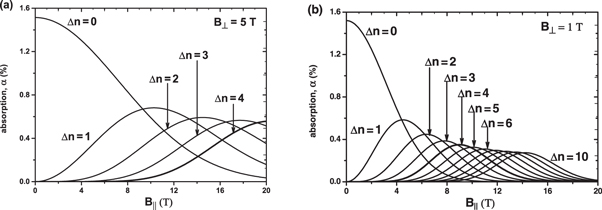
is varied via changing  The dependence of line intensities on
The dependence of line intensities on 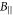 are shown in figure 4. For illustrative purposes, we use the Gaussian shape of the absorption line with a typical value of Γ = 1 meV. Thus, for any of the peaks with
are shown in figure 4. For illustrative purposes, we use the Gaussian shape of the absorption line with a typical value of Γ = 1 meV. Thus, for any of the peaks with 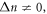 it is demonstrated that high intense peaks in the spectrum can be obtained by selecting the suitalbe structure parameters, the magnetic field magnitude and orientation.
it is demonstrated that high intense peaks in the spectrum can be obtained by selecting the suitalbe structure parameters, the magnetic field magnitude and orientation.
Figure 2. The absorption spectrum in the asymmetrical double quantum well on (1, 0) → (2, n) transitions with the fixed  and different values of
and different values of 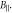 N(1,0) = 1011 cm−2, N(2,n) = 0.
N(1,0) = 1011 cm−2, N(2,n) = 0.
Download figure:
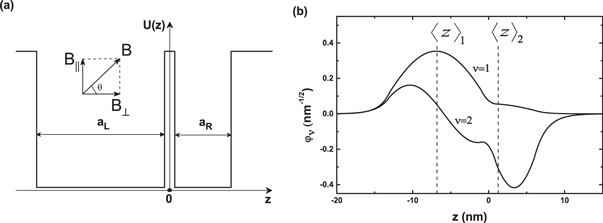
Standard image High-resolution imageFigure 3. (a) The potential profile of the asymmetrical double quantum well and (b) respective subband wave functions.
Download figure:
Standard image High-resolution imageFigure 4. The line intensity dependence on  when
when  5 T (a) and
5 T (a) and  1 T (b).
1 T (b).
Download figure:
Standard image High-resolution image5. Conclusion
The nature of the violation of the selection rule 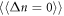 for optical transitions between Landau levels of different subbands in tilted magnetic field is studied. Neglecting the intersubband coupling, the analytical expression is obtained for the absorption/emission intensities, which makes it possible to estimate the contribution of the 'forbidden' intersubband transitions with different
for optical transitions between Landau levels of different subbands in tilted magnetic field is studied. Neglecting the intersubband coupling, the analytical expression is obtained for the absorption/emission intensities, which makes it possible to estimate the contribution of the 'forbidden' intersubband transitions with different  The magnitude of the violation of the selection rule for transitions with
The magnitude of the violation of the selection rule for transitions with 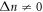 is shown to be essentially determined by the symmetry of the potential profile of the structure. In a symmetric structure, the selection rule remains in the zeroth approximation of intersubband coupling. Moreover, some transitions are forbidden in the tilted magnetic field even with taking account of intersubband coupling. For other transitions with
is shown to be essentially determined by the symmetry of the potential profile of the structure. In a symmetric structure, the selection rule remains in the zeroth approximation of intersubband coupling. Moreover, some transitions are forbidden in the tilted magnetic field even with taking account of intersubband coupling. For other transitions with 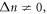 the intersubband coupling gives rise to the violation of the selection rule in the tilted magnetic field, but the degree of violation and the magnitude of the corresponding matrix elements are insignificant in the considered range of magnetic field strength. In asymmetric structures, the selection rule
the intersubband coupling gives rise to the violation of the selection rule in the tilted magnetic field, but the degree of violation and the magnitude of the corresponding matrix elements are insignificant in the considered range of magnetic field strength. In asymmetric structures, the selection rule  is significantly violated in zero order of the intersubband coupling, and the intensity of the transitions with
is significantly violated in zero order of the intersubband coupling, and the intensity of the transitions with  can even exceed those with
can even exceed those with 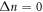 for an appropriate choice of the strengths of the magnetic field components and the structure potential profile. The intensity of the 'forbidden' intersubband transitions is traced as a function of the magnitude and orientation of the magnetic field.
for an appropriate choice of the strengths of the magnetic field components and the structure potential profile. The intensity of the 'forbidden' intersubband transitions is traced as a function of the magnitude and orientation of the magnetic field.
Acknowledgments
The work was carried out with financial support from the Ministry of Education and Science of the Russian Federation in the framework of increase Competitiveness Program of NUST 'MISIS', implemented by a governmental decree dated 16th of March 2013, No. 211, and by Russian Foundation for Basic Research (Project No. 18-02-00874).