Abstract
A chirped-pulse quantum control scheme applicable to coherent anti-Stokes Raman scattering spectroscopy, named as C-CARS, is presented aimed at maximizing the vibrational coherence in molecules. It implies chirping of three incoming pulses in the four-wave mixing process of CARS, the pump, the Stokes and the probe, to fulfill the conditions of adiabatic passage. The scheme is derived in the framework of rotating wave approximation and adiabatic elimination of excited state manifold simplifying the four-level model system into a 'super-effective' two level system. We demonstrate that the selectivity of excitation of vibrational degrees of freedom can be controlled by carefully choosing the spectral chirp rate of the pulses. The robustness, spectral selectivity and adiabatic nature of this method are advantageous for improving the existing methods of CARS spectroscopy for sensing, imaging and detection.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Discovery of Raman scattering in the 1920s, which coincided with major developments in quantum mechanics followed by the advancements in laser technology since 1960s, paved new ways for understanding the chemical compounds and structure of molecular systems. Modern Raman spectroscopy, that uses spontaneous Raman scattering at their core, is characterized by a sufficiently low intensity signal, which is incoherent and isotropic. Being one of the leading non-linear optics techniques, coherent anti-Stokes Raman scattering (CARS) spectroscopy makes use of stimulated Raman process resulting in a directional anti-Stokes signal of intensity many orders of magnitude higher than an isotropic spontaneous Raman signal. Because CARS addresses inherent properties of matter, such as vibrational degrees of freedom, it belongs to one of the well-suited and frequently used spectroscopic methods for imaging, sensing and detection without labeling or staining [1–5]. High sensitivity, high resolution and noninversiveness of CARS have been exploited for imaging of chemical and biological samples [6–16], standoff detection [17–20] and combustion thermometry [21, 22]. Recent developments in the applications of CARS in biology include imaging and classification of cancer cells that help early diagnosis [23–25], and rapid and label-free detection of the SARS-CoV-2 pathogens [26]. CARS has also been used recently for observing real-time vibrations of chemical bonds within molecules [27], direct imaging of molecular symmetry [28], graphene imaging [29], and femtosecond spectroscopy [30, 31].
In this work, we present a theoretical description of a general and robust technique of creating maximal-coherence superpositions of quantum states that can be used to optimize the signals in CARS-based applications.
In the four-wave mixing process of CARS, the pump and Stokes pulses having frequencies ωp
and ωs
respectively excite the molecular vibrations to create a coherent superposition which a probe pulse having frequency ωpr
then interacts with and generates an anti-Stokes signal. The output signal is blue-shifted and has a frequency of  . It is about six orders of magnitude higher in amplitude compared to the spontaneous process and its direction is determined by the phase-matching condition [32–35]. However, one of the main challenges in CARS has been the presence of non-resonant background appearing in the spectra which limits the image contrast and chemical sensitivity. Another coherent, multi-photon Raman process called stimulated Raman scattering (SRS) has an advantage over CARS because of the absence of nonresonant background [36]. In SRS, the frequency difference of pump and Stokes (
. It is about six orders of magnitude higher in amplitude compared to the spontaneous process and its direction is determined by the phase-matching condition [32–35]. However, one of the main challenges in CARS has been the presence of non-resonant background appearing in the spectra which limits the image contrast and chemical sensitivity. Another coherent, multi-photon Raman process called stimulated Raman scattering (SRS) has an advantage over CARS because of the absence of nonresonant background [36]. In SRS, the frequency difference of pump and Stokes ( ) is matched with the vibrational frequency of the molecule to excite the vibrational transitions. However, the detection of compounds using SRS requires a scheme that is more complicated than CARS as the input and output signals in SRS have the same frequencies. In CARS, the signal can be easily extracted by an optical filter due to the anti-Stokes component having a frequency blue-shifted compared to the incoming pulses [37]. To overcome the limitations of CARS, there have been tremendous efforts on removing the background from nonresonant processes and enhancing the signal amplitude [38–47].
) is matched with the vibrational frequency of the molecule to excite the vibrational transitions. However, the detection of compounds using SRS requires a scheme that is more complicated than CARS as the input and output signals in SRS have the same frequencies. In CARS, the signal can be easily extracted by an optical filter due to the anti-Stokes component having a frequency blue-shifted compared to the incoming pulses [37]. To overcome the limitations of CARS, there have been tremendous efforts on removing the background from nonresonant processes and enhancing the signal amplitude [38–47].
In the framework of Maxwell's equations, the amplitude of the anti-Stokes field is related to coherence between the electronic vibrational states of the target molecules. Thus, maximizing coherence is the key to optimizing the intensity of anti-Stokes signal [20, 48]. Chirped pulses have been often used in CARS-based imaging techniques as demonstrated in, e.g. the high spectroscopic resolution experiments [49, 50] and theoretical works on maximizing coherence [51–53]. A method for selective excitation in a multimode system using a transform-limited pump pulse and a lineraly chirped Stokes pulse in stimulated Raman scattering is proposed in [54]. The effects of chirped pump and Stokes pulses on the nonadiabatic coupling between vibrational modes are discussed in [55]. A 'roof' method of chirping to maximize coherence is introduced in [56] based on adiabatic passage in an effective two-level system. In this method, the Stokes pulse is linearly chirped at the same rate as that of the pump pulse during the first half of the pulse duration and is oppositely chirped afterwards.
Here, we discuss a chirping scheme in CARS, in which all the incoming pulses are chirped to achieve the maximum coherence and suppress the background via adiabatic passage. The selectivity, robustness and adiabatic nature of this control scheme make it a viable candidate for improving the current methods for imaging, sensing and detection using CARS. We examined in detail the impact of the two-photon detuning on the mechanism of adiabatic passage, and analyzed the controllability of the generation of the maximum coherence depending on the magnitude of the two-photon detuning.
2. Theoretical framework
The variables used in our theory are summarized below.
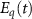 , , 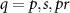
| The pump, Stokes and probe fields |
 , , 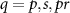
| The Rabi frequencies of the pump, Stokes and probe fields |
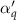 , αq
, , αq
, 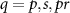
| Spectral and temporal chirp rates of the pump, Stoke and probe fields |
| τ0, τ | Transform-limited pulse duration and chirp-dependent pulse duration |
Ω3, 
| The effective and peak effective Rabi frequencies |
 , ,  , , 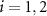
| The bare and dressed state energies |
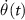
| The non-adiabatic coupling parameter |
A schematic diagram of the CARS process is given in figure 1. We consider the chirped pump, Stokes and probe pulses with temporal chirp rates αq
, 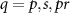
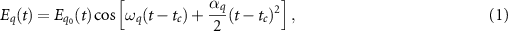
and having Gaussian envelopes
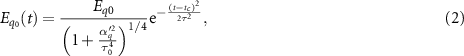
where τ0 is the transform-limited pulse duration, τ is the chirp-dependent pulse duration given by ![$\tau = \tau_0[1+\alpha_q^{^{\prime} 2}/\tau_0^4]^{1/2}$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn19.gif) and
and  is the spectral chirp rate, which is related to the temporal chirp rate as
is the spectral chirp rate, which is related to the temporal chirp rate as  . The interaction Hamiltonian of the four-level system, after defining the one photon detunings,
. The interaction Hamiltonian of the four-level system, after defining the one photon detunings, 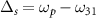 and
and  , reads:
, reads:
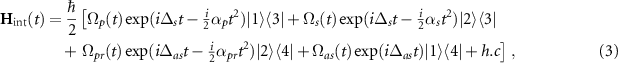
where 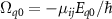 . This Hamiltonian can be simplified to a two-level 'super-effective' Hamiltonian by eliminating states
. This Hamiltonian can be simplified to a two-level 'super-effective' Hamiltonian by eliminating states 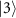 and
and 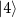 adiabatically under the assumption of large one-photon detunings. The dynamics of the four-level system interacting with the fields in equation (1) is described by the Liouville-von Neumann equation
adiabatically under the assumption of large one-photon detunings. The dynamics of the four-level system interacting with the fields in equation (1) is described by the Liouville-von Neumann equation ![$ i\hbar \dot{\boldsymbol{\rho}}(t) = [\mathbf{H}_\mathrm{int}(t), \boldsymbol{\rho}(t)].$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn27.gif) We define the two-photon detuning as
We define the two-photon detuning as 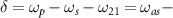
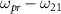 , make the transformations in the interaction frame
, make the transformations in the interaction frame 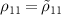 ,
, 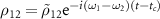 ,
, 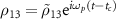 ,
, 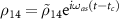 ,
, 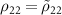 ,
, 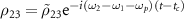 ,
, 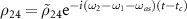 ,
, 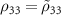 ,
, 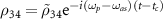 ,
,  and obtain a system of differential equations for the density matrix elements:
and obtain a system of differential equations for the density matrix elements:
As the next step, the condition for chirping of the probe pulse such that  is imposed, which is required to equate the exponentials. The above set of equations is then modified by applying the adiabatic elimination,
is imposed, which is required to equate the exponentials. The above set of equations is then modified by applying the adiabatic elimination,  and substituting for
and substituting for 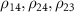 and ρ24 in the equations of
and ρ24 in the equations of 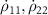 and
and 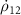 . After defining the new Rabi frequencies:
. After defining the new Rabi frequencies:
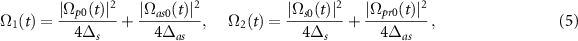
and
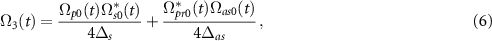
the density matrix equations cast into a set of equations describing the dynamics in the super-effective two-level systemml:
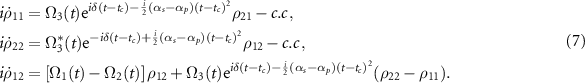
Figure 1. Schematic of CARS, where an anti-Stokes signal is generated by the four-wave-mixing process. Maximizing the coherence between states 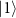 and
and  , ρ21, is the key to amplifying the signal response from the system. Here,
, ρ21, is the key to amplifying the signal response from the system. Here, 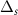 and
and 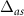 are the one-photon detunings, and δ is the two-photon detuning.
are the one-photon detunings, and δ is the two-photon detuning.
Download figure:
Standard image High-resolution imageFurther transformations of the density matrix elements such as 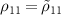 ,
, 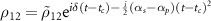 , and
, and 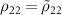 , and shifting the diagonal elements lead to the following super-effective Hamiltonian for the two-level system in the field-interaction representation:
, and shifting the diagonal elements lead to the following super-effective Hamiltonian for the two-level system in the field-interaction representation:
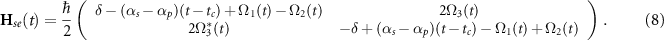
The amplitudes of incoming fields are manipulated to make the AC Stark shifts equal, 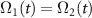 , and cancel out. This condition is satisfied by taking
, and cancel out. This condition is satisfied by taking 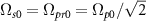 , considering the fact that the anti-Stokes signal is absent in the beginning of the process,
, considering the fact that the anti-Stokes signal is absent in the beginning of the process, 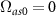 . The effective Rabi frequency
. The effective Rabi frequency 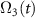 reads:
reads:
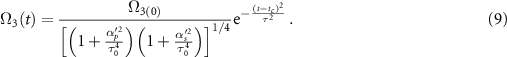
The peak effective Rabi frequency is given by 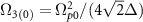 . It is reduced when chirping is applied to the pump and Stokes pulses with the spectral rates
. It is reduced when chirping is applied to the pump and Stokes pulses with the spectral rates 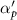 and
and 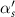 respectively. The relative amplitudes of all the Rabi frequencies related to three incoming pulses applied simultaneously are shown in figure 2. In this paper, all the frequency parameters are defined in the units of the frequency ω21 and time parameters are defined in the units of
respectively. The relative amplitudes of all the Rabi frequencies related to three incoming pulses applied simultaneously are shown in figure 2. In this paper, all the frequency parameters are defined in the units of the frequency ω21 and time parameters are defined in the units of 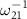 .
.
Figure 2. The evolution of different Rabi frequencies in the C-CARS scheme. The Stokes and the probe peak Rabi frequencies 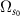 and
and 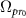 have the same amplitude, which is less than the pump Rabi frequency
have the same amplitude, which is less than the pump Rabi frequency 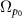 by a factor of
by a factor of 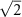 .
. 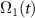 and
and 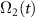 are canceled out in the Hamiltonian due to the complete overlap making
are canceled out in the Hamiltonian due to the complete overlap making 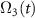 the only relevant quantity in the control scheme.
the only relevant quantity in the control scheme.
Download figure:
Standard image High-resolution imageDuring the interaction, at time 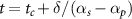 , the diagonal elements become equal to zero creating a coherent superposition state having equal populations of states
, the diagonal elements become equal to zero creating a coherent superposition state having equal populations of states 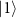 and
and 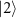 and, therefore, a maximum value of coherence ρ21. This time can be determined for a fixed value of two-photon detuning, δ. At the two-photon resonance, the system reaches this maximum coherence at the central time tc
. It is further preserved in the state of the maximum coherence by imposing the condition of
and, therefore, a maximum value of coherence ρ21. This time can be determined for a fixed value of two-photon detuning, δ. At the two-photon resonance, the system reaches this maximum coherence at the central time tc
. It is further preserved in the state of the maximum coherence by imposing the condition of 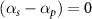 in the second half of the pulse duration. A smooth realization of this scheme is possible by choosing the temporal chirp rates of the pump and Stokes pulses to be the same in magnitude and opposite in sign before the central time and equal in sign after that, along with the condition imposed for the chirp rate of probe pulse such that
in the second half of the pulse duration. A smooth realization of this scheme is possible by choosing the temporal chirp rates of the pump and Stokes pulses to be the same in magnitude and opposite in sign before the central time and equal in sign after that, along with the condition imposed for the chirp rate of probe pulse such that 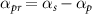 , which was deduced to arrive into the Hamiltonian in equation (8). This chirping scheme, namely C-CARS, is summarized as follows:
, which was deduced to arrive into the Hamiltonian in equation (8). This chirping scheme, namely C-CARS, is summarized as follows: 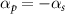 and
and 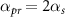 for
for 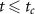 , and
, and  and
and 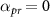 for
for 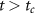 . The Wigner–Ville distributions of the incident pulses are found to be
. The Wigner–Ville distributions of the incident pulses are found to be
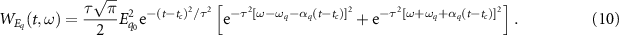
The positive solutions of these equations are depicted in figure 3. The 'turning off' of chirping in the second half of the pulse duration is the essence of this scheme, resulting in a selective excitation of the molecules and suppressing any off-resonant background. If αp
is not reversed, the coherence is not preserved leading to population inversion between states 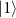 and
and 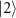 .
.
Figure 3. Wigner plots of the incident pulses; pump (a), Stokes (b) and probe (c). Note that the Stokes and probe have the same amplitudes, which is different from that of pump. The parameters used in this figure are ![$\omega_p = 4.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn63.gif) ,
, ![$\omega_s = 3.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn64.gif) ,
, ![$\omega_{pr} = 4.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn65.gif) ,
, ![$\tau = 3.0[\omega_{21}^{-1}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn66.gif) ,
, ![$\alpha_s = -0.2[\omega_{21}^{2}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn67.gif) , and
, and ![$t_c = 7.5[\omega_{21}^{-1}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn68.gif) .
.
Download figure:
Standard image High-resolution image3. Numerical results
3.1. Super-effective two-level system
To demonstrate the selective excitation of molecules using C-CARS, the time evolution of populations ρ11 and ρ22 and coherence ρ12 is presented in figure 4 for four different cases described below. The C-CARS control scheme is applied for the resonant (δ = 0) and off-resonant (δ ≠ 0) case respectively in figures 4(a) and (b). The coherence reaches maximum at the central time in the resonant case, and is preserved till the end of dynamics owing to the zero net chirp rate attained by reversing the sign of αp
. On the contrary, the time of the maximum coherence does not coincide with the central time in the non-resonant case, which results in a population transfer to the upper state and zero coherence. To emphasize the significance of reversing the sign of αp
in C-CARS control scheme we compare it with the scheme when the pump and Stokes are oppositely chirped for the whole pulse duration, 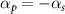 . For this case the dynamics of the system is plotted in figures 4(c) and (d) for δ = 0 and δ = 0.1 respectively. In (c), even though the system reaches a perfect coherence at
. For this case the dynamics of the system is plotted in figures 4(c) and (d) for δ = 0 and δ = 0.1 respectively. In (c), even though the system reaches a perfect coherence at 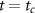 , it decreases to zero because population is further adiabatically transferred to state
, it decreases to zero because population is further adiabatically transferred to state 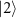 . Coherence in (d) behaves similar to that of (b).
. Coherence in (d) behaves similar to that of (b).
Figure 4. The evolution of the populations and coherence demonstrating selective coherent excitation in C-CARS: in (a) and (b), C-CARS scheme is applied to the resonant case (δ = 0) (a) and off-resonant (δ = 0.1) case (b). Coherence is preserved at the maximum value in the case of resonance, while it is destroyed in the detuned case. This is in contrast with the chirping scheme where the pump and Stokes pulses are oppositely chirped, 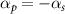 , for the whole pulse duration, shown for the resonant case (δ = 0) in (c) and off-resonant (δ = 0.1) case in (d). The dynamics is similar and the coherence is zero in both these cases demonstrating the need for turning off the chirp at central time. The parameters are
, for the whole pulse duration, shown for the resonant case (δ = 0) in (c) and off-resonant (δ = 0.1) case in (d). The dynamics is similar and the coherence is zero in both these cases demonstrating the need for turning off the chirp at central time. The parameters are ![$\Omega_{3(0)} = 5.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn83.gif) ,
, ![$\tau_0 = 10[\omega^{-1}_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn84.gif) ,
, ![$\Delta = 1.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn85.gif) and
and 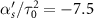 .
.
Download figure:
Standard image High-resolution image3.2. Exact four-level system
The validity of adiabatic approximation, which led to the derivation of the super-effective Hamiltonian, can be tested by comparing the results of the super-effective two-level system with the exact solution using the Liouville von Neumann equation for the four-level system. To this end, the condition for chirping of the probe pulse 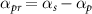 is applied to the field-interaction Hamiltonian of the four level systemml:
is applied to the field-interaction Hamiltonian of the four level systemml:
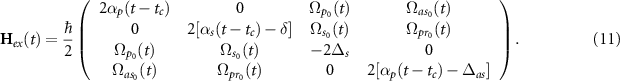
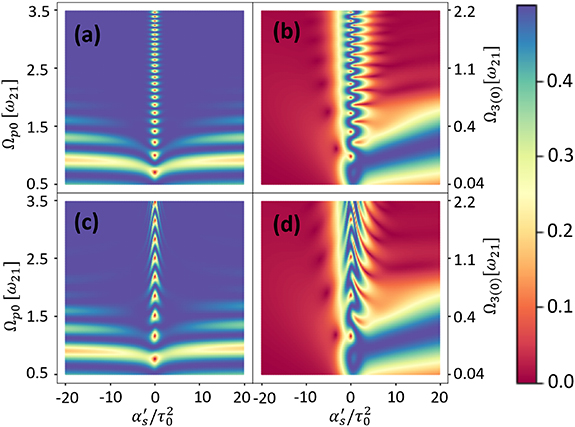
Figure 5 shows the contour-plot of vibrational coherence ρ12 at the end of dynamics as a function of the peak Rabi frequency 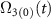 and dimensionless spectral chirp rate
and dimensionless spectral chirp rate 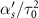 . Figures (a) and (b) represent the δ = 0 and δ = 0.1 cases, respectively, of the super-effective two level system, and (c) and (d) represent the same cases obtained by the exact solution of the four-level system using the same set of parameters. In all the figures, the one-photon detuning is
. Figures (a) and (b) represent the δ = 0 and δ = 0.1 cases, respectively, of the super-effective two level system, and (c) and (d) represent the same cases obtained by the exact solution of the four-level system using the same set of parameters. In all the figures, the one-photon detuning is  . Around the region where
. Around the region where 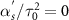 , adiabatic passage breaks down and the approximate solution disagrees with the exact solution. As the magnitude of spectral chirp rate increases, the adiabatic approximation coincides with the exact one because the Landau- Zener parameter is well in the adiabatic range,
, adiabatic passage breaks down and the approximate solution disagrees with the exact solution. As the magnitude of spectral chirp rate increases, the adiabatic approximation coincides with the exact one because the Landau- Zener parameter is well in the adiabatic range, 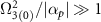 . In the resonant cases (a) and (c), the coherence is at the maximum, (blue color), for the most part, indicating the robustness of C-CARS chirping scheme in preparing the system in a coherent superposition. In the off-resonant case, zero coherence, (red color), is observed for the most part, which is in a stark contrast with the resonant case, revealing the selective nature of coherent excitation using the C-CARS control scheme.
. In the resonant cases (a) and (c), the coherence is at the maximum, (blue color), for the most part, indicating the robustness of C-CARS chirping scheme in preparing the system in a coherent superposition. In the off-resonant case, zero coherence, (red color), is observed for the most part, which is in a stark contrast with the resonant case, revealing the selective nature of coherent excitation using the C-CARS control scheme.
Figure 5. Vibrational coherence as a function of spectral chirp and the peak Rabi frequency when C-CARS chirping scheme is used: figures (a) and (b) are plotted using super-effective two-level Hamiltonian, equation (8), and figures (c) and (d) are plotted using the exact four-level Hamiltonian, equation (11). In figures (a) and (c) δ = 0 and (b) and (d) δ = 0.1. The similarity between the results of two Hamiltonians indicates the validity of adiabatic approximation which is used to derive the chirping scheme. In the case of resonance, the coherence is maximum, color blue, for most of the Rabi frequencies and spectral chirp rates, meaning that the chirping scheme is very robust against changes in the input parameters. In the absence of resonance, the coherence is zero, color red, for most values of parameters, implying that the chirping scheme is effective in selectively exciting the system. The parameters used in this figure are: ![$\tau_0 = 10[\omega^{-1}_{21}] $](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn90.gif) and
and ![$\Delta_s = \Delta_{as} = 1.0[\omega_{21}]\,.$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn91.gif)
Download figure:
Standard image High-resolution image3.3. Analysis of dressed states and adiabatic passage
When the electromagnetic field interacts with any quantum system, the eigenstates undergo a rearrangement resulting in a set of quantum states that are said to be 'dressed' by the light. These states are called dressed states and the initial states that were 'untouched' by the light are called bare states [57]. The robustness of the C-CARS control scheme stems from the adiabatic nature of the light–matter interaction, which can be demonstrated by analyzing the evolution of dressed state energies in the super-effective two-level system. To this end, the density matrix  is transformed to a dressed density matrix using the transformation
is transformed to a dressed density matrix using the transformation 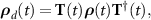 where
where 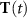 is an orthogonal matrix given by:
is an orthogonal matrix given by:

The Liouville-von Neumann equation for the dressed density matrix is derived from the bare state density matrix equation and reads
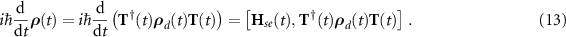
After expanding this equation and using 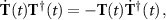 we arrive at
we arrive at
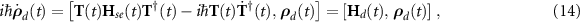
where  is a diagonal matrix. For adiabatic passage to occur, the dressed state Hamiltonian
is a diagonal matrix. For adiabatic passage to occur, the dressed state Hamiltonian 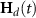 should give the dressed state energies separation greater than
should give the dressed state energies separation greater than 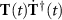 to avoid coupling between dressed states [57–59]. The dressed state Hamiltonian is found to be
to avoid coupling between dressed states [57–59]. The dressed state Hamiltonian is found to be
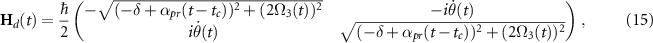
where the non-adiabatic parameter 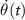 , which comes from the matrix
, which comes from the matrix  , is given by
, is given by
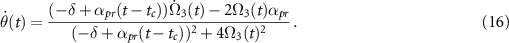
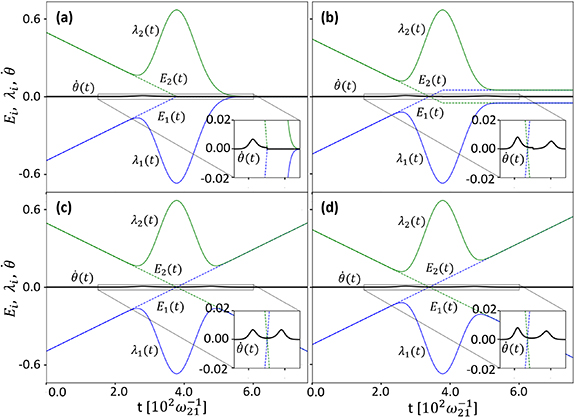
Analyzing the equation for  reveals the selective nature of adiabatic passage in the case of resonance. In the resonant case, the C-CARS chirping scheme ensures the process to be adiabatic in the second half of the pulse by keeping the non-adiabatic coupling parameter
reveals the selective nature of adiabatic passage in the case of resonance. In the resonant case, the C-CARS chirping scheme ensures the process to be adiabatic in the second half of the pulse by keeping the non-adiabatic coupling parameter 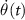 at zero during this time period. But adiabaticity is not guaranteed in the off-resonant case due to the non-zero factor δ in the equation. This is demonstrated in figure 6, where the bare state energies are given by
at zero during this time period. But adiabaticity is not guaranteed in the off-resonant case due to the non-zero factor δ in the equation. This is demonstrated in figure 6, where the bare state energies are given by 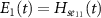 and
and 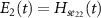 and the dressed state energies are given by
and the dressed state energies are given by 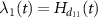 and
and 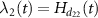 . The figures (a) and (b) represent resonant (δ = 0) and off-resonant (δ ≠ 0) cases when C-CARS control scheme is used. Clearly, the
. The figures (a) and (b) represent resonant (δ = 0) and off-resonant (δ ≠ 0) cases when C-CARS control scheme is used. Clearly, the 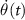 , dark sold line, has non-zero values in the second half when the system is detuned. The perfectly adiabatic nature of interaction in figure 6(a) corresponds to the maximum coherence in figure 4(a) and the non-adiabatic nature in figure 6(b) corresponds to the population inversion in figure 4(b). The parameters used in figure 6 are the same as that used in figure 4. In figures 6(c) and (d), the same quantities are plotted for δ = 0 and δ ≠ 0 respectively for the scheme when the pump and Stokes are chirped oppositely for the whole pulse duration. The process is perfectly adiabatic only in the second half of (a) since a smooth realization of
, dark sold line, has non-zero values in the second half when the system is detuned. The perfectly adiabatic nature of interaction in figure 6(a) corresponds to the maximum coherence in figure 4(a) and the non-adiabatic nature in figure 6(b) corresponds to the population inversion in figure 4(b). The parameters used in figure 6 are the same as that used in figure 4. In figures 6(c) and (d), the same quantities are plotted for δ = 0 and δ ≠ 0 respectively for the scheme when the pump and Stokes are chirped oppositely for the whole pulse duration. The process is perfectly adiabatic only in the second half of (a) since a smooth realization of  was made possible owing to the developed C-CARS control scheme. The dynamics is much different and the selective excitation does not happen when the effective Rabi frequency,
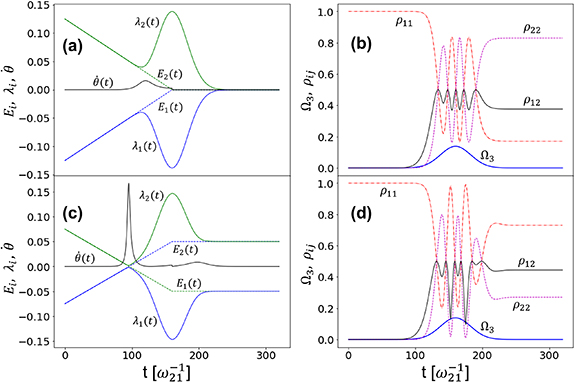
was made possible owing to the developed C-CARS control scheme. The dynamics is much different and the selective excitation does not happen when the effective Rabi frequency, 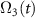 , is not strong enough as shown in figure 7 where
, is not strong enough as shown in figure 7 where 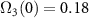 ,
,  and
and ![$\tau_0 = 25[\omega^{-1}_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn136.gif) . In both (a), δ = 0 and (b), δ = 0.1 cases, the non-adiabatic coupling parameter is much greater compared to figure 6. In the off-resonant case (d), the coherence oscillates much stronger compared to the resonant case (c) showing the absence of adiabatic passage.
. In both (a), δ = 0 and (b), δ = 0.1 cases, the non-adiabatic coupling parameter is much greater compared to figure 6. In the off-resonant case (d), the coherence oscillates much stronger compared to the resonant case (c) showing the absence of adiabatic passage.
Figure 6. The evolution of the bare state and the dressed state energies and the non-adiabatic parameter: 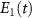 and
and 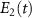 (dashed lines) are the bare state energies and
(dashed lines) are the bare state energies and 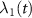 and
and  (solid lines) are the dressed state energies. Figures (a) and (b) are the resonant and off-resonant cases respectively when C-CARS scheme is used. Figures (c) and (d) show the resonant and off-resonant cases, when the pump and Stokes pulses are oppositely chirped for the whole pulse duration. In contract to all the other cases, figure (a) shows the non-adiabatic parameter
(solid lines) are the dressed state energies. Figures (a) and (b) are the resonant and off-resonant cases respectively when C-CARS scheme is used. Figures (c) and (d) show the resonant and off-resonant cases, when the pump and Stokes pulses are oppositely chirped for the whole pulse duration. In contract to all the other cases, figure (a) shows the non-adiabatic parameter 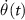 , the dark solid line, remaining at zero after the central time. The parameters used are
, the dark solid line, remaining at zero after the central time. The parameters used are ![$\Omega_{3(0)} = 5.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn103.gif) ,
, ![$\tau_0 = 10[\omega^{-1}_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn104.gif) ,
, ![$\Delta = 1.0[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn105.gif) and
and 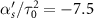
Download figure:
Standard image High-resolution imageFigure 7. Evolution of energies, populations and coherence for a weak Rabi frequency. Here the parameters are: 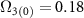 ,
,  and
and 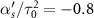 . Figure (a) show the dressed and bare state energies and (b) show the population dynamics in the case of resonance (δ = 0). Figures (c) and (d) show the same plots in the absence of resonance (δ = 0.1).
. Figure (a) show the dressed and bare state energies and (b) show the population dynamics in the case of resonance (δ = 0). Figures (c) and (d) show the same plots in the absence of resonance (δ = 0.1).
Download figure:
Standard image High-resolution image3.4. The dependence of state selectivity on the chirp rate
To investigate how the value of two-photon detuning and spectral chirp rate are related to the selectivity in C-CARS method, the end-of-pulse vibrational coherence is plotted as a function of δ and 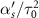 in figure 8. At the two-photon resonance, coherence is at the maximum for all the values of chirp rate. If the detuning is large, a small chirp rate can selectively excite the system while for smaller values of detuning, the chirp rate needs to be increased in order to suppress excitation of close vibrational frequencies and the non-resonant background. This provides a way to control the selectivity by adjusting the values of chirp rate. The plot is symmetric across the diagonal lines as flipping the signs of both αs
and δ will not change the dynamics; it would only result in switching of the diagonal elements in Hamiltonian (8). The plot is also nearly symmetric across the δ = 0 line, indicating that the selectivity holds for both red and blue detunings. When the chirp rate is close to zero, the pulses are transform-limited, implying that the maximum coherence and selectivity provided by the chirping scheme is absent in this region. This explains the vertical line present at the 0 of abscissa.
in figure 8. At the two-photon resonance, coherence is at the maximum for all the values of chirp rate. If the detuning is large, a small chirp rate can selectively excite the system while for smaller values of detuning, the chirp rate needs to be increased in order to suppress excitation of close vibrational frequencies and the non-resonant background. This provides a way to control the selectivity by adjusting the values of chirp rate. The plot is symmetric across the diagonal lines as flipping the signs of both αs
and δ will not change the dynamics; it would only result in switching of the diagonal elements in Hamiltonian (8). The plot is also nearly symmetric across the δ = 0 line, indicating that the selectivity holds for both red and blue detunings. When the chirp rate is close to zero, the pulses are transform-limited, implying that the maximum coherence and selectivity provided by the chirping scheme is absent in this region. This explains the vertical line present at the 0 of abscissa.
Figure 8. Coherence as a function of two-photon detuning and dimensionless spectral chirp rate. As the chirp rate increases, the system becomes selective to lesser values of δ. For the values of spectral chirp rate close to zero,  , a vertical line is present as the selectivity is degraded where effectively there is no chirping. Flipping the signs of detuning and chirp rates results in flipping of energy levels in the two-level Hamiltonian, creating a symmetry for the coherence values of (
, a vertical line is present as the selectivity is degraded where effectively there is no chirping. Flipping the signs of detuning and chirp rates results in flipping of energy levels in the two-level Hamiltonian, creating a symmetry for the coherence values of (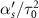 , δ) and (
, δ) and (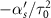 ,
, 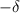 ). The parameters used in the figure are
). The parameters used in the figure are ![$\Omega_{3(0)} = 1.6[\omega_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn123.gif) and
and ![$\tau_0 = 4.66[\omega^{-1}_{21}]$](https://content.cld.iop.org/journals/2058-9565/8/4/045005/revision2/qstace3edieqn124.gif) .
.
Download figure:
Standard image High-resolution image4. Conclusion
We presented a control scheme to prepare the ground electronic-vibrational states in the four-level system of CARS in a maximally coherent superposition. We derived the Hamiltonian for a 'super-effective' two-level system employing the adiabatic approximation. This two-level Hamiltonian is used to derive the conditions for adiabatic passage necessary for the implementation of the selective excitation of spectrally close vibrations. The amplitudes of the Stokes and probe pulses have to be equal and should be 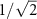 times that of the pump pulse. The pump pulse should be chirped at the same rate as the Stokes pulse before the central time and at the opposite rate after that. The probe pulse has to be chirped at a rate equal the difference between the chirp rates of the Stokes and the pump pulses for the whole pulse duration. The solutions of Liouville-von Neumann equation show that vibrational coherence is preserved until the end of dynamics in the resonant case due to the adiabatic nature of the interaction. At two-photon resonance, vibrational coherence is at the maximum, 0.5, for a wide range of field parameters revealing the robustness of the method. Conversely, coherence is almost zero in the two-photon off-resonant case for most of the peak Rabi frequency values and the chirp parameters. A comparison of coherence in the four-level and the two-level systems reveals that the adiabatic approximation is valid except for when the chirp rate is almost equal to zero. A dressed-state analysis reveals the details of the mechanism of adiabatic passage using C-CARS control scheme.
times that of the pump pulse. The pump pulse should be chirped at the same rate as the Stokes pulse before the central time and at the opposite rate after that. The probe pulse has to be chirped at a rate equal the difference between the chirp rates of the Stokes and the pump pulses for the whole pulse duration. The solutions of Liouville-von Neumann equation show that vibrational coherence is preserved until the end of dynamics in the resonant case due to the adiabatic nature of the interaction. At two-photon resonance, vibrational coherence is at the maximum, 0.5, for a wide range of field parameters revealing the robustness of the method. Conversely, coherence is almost zero in the two-photon off-resonant case for most of the peak Rabi frequency values and the chirp parameters. A comparison of coherence in the four-level and the two-level systems reveals that the adiabatic approximation is valid except for when the chirp rate is almost equal to zero. A dressed-state analysis reveals the details of the mechanism of adiabatic passage using C-CARS control scheme.
Notably, the proposed chirping scheme for maximum coherence is not exclusive to CARS; it can be applied to other coherent Raman techniques such as SRS. However, the amplitudes of the interacting fields must satisfy the condition that the AC Stark shifts cancel out in equation (8). In SRS, for example, equal amplitudes for the pump and the Stokes fields will satisfy this condition.
The presented C-CARS method can find important applications in sensing and imaging of molecular species because it creates a maximally coherent superposition of vibrational states in coherent anti-Stokes Raman scattering allowing the system to emit an optimized signal suitable for detection. The robustness of this method against changes in Rabi frequencies and chirp rates is helpful in experiments. The method permits suppressing the background species and excite only the desired ones; the resolution needed for this distinction can be controlled by the chirp parameter.
Acknowledgments
S M and J Ch acknowledge support from the Office of Naval Research under Awards N00014-20-1-2086 and N00014-22-1-2374. S M acknowledges the Helmholtz Institute Mainz Visitor Program. The work of D B was supported in part by the European Commission's Horizon Europe Framework Program under the Research and Innovation Action MUQUABIS GA No. 101070546.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).