ABSTRACT
We derive new limits on the cold dark matter properties for weakly interacting massive particles (WIMPs), potentially trapped in the solar core by using for the first time the central temperature constrained by boron neutrinos and the central density constrained by the dipolar gravity modes detected with the Global Oscillations at Low Frequency/Solar Helioseismic Observatory instrument. These detections disfavor the presence of non-annihilating WIMPs for masses ⩽10 GeV and spin dependent cross-sections >5 × 10−36 cm2 in the solar core but cannot constrain WIMP annihilation models. We suggest that in the coming years helio- and asteroseismology will provide complementary probes of dark matter.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
What is the nature of dark matter (DM) in the universe? Resolving this question is one of the most important issues in astrophysics today and is one which has had no definitive answer until now. On the one hand, there is a claim for direct annual modulation of the DM detection signal with Na i detectors in the DAMA/LIBRA experiment (Bernabei et al. 2011). This result is potentially compatible with germanium direct detection signatures in the CoGeNT and CDMS experiments (Aalseth et al. 2011) and also in CRESST-II (Brown et al. 2011), although these claims remain controversial (Fitzpatrick et al. 2010; Savage et al. 2011). On the other hand, a modified gravitational interaction, as an alternative to DM, continues to find support in resolving some hitherto unresolved observational issues in cosmology, for example, in reconciling observations of satellite galaxies with predictions of the Concordance Cosmological Model (CCM; Kroupa et al. 2010). The present situation encourages us to look for any additional indirect evidence of DM.
This paper examines for the first time some properties of cold DM (CDM) in the form of weakly interacting massive particles (WIMPs) trapped in the solar core at the light of the most recent detections of neutrinos and gravity modes. We focus on light non-annihilating WIMPs for the following reasons: (1) WIMP masses ⩽10 GeV fill the solar core and hence potentially affect solar structure via elastic scattering on nuclei; (2) this mass range is favored by recent data from experiments such as DAMA/LIBRA, CoGeNT, and CRESST-II; and (3) annihilating WIMPs in this mass range with a thermal freeze-out cross-section are in conflict with WMAP7 and Fermi data on the CMB angular power spectrum (Galli et al. 2011) and dwarf galaxy gamma ray upper limits, respectively (Geringer-Sameth & Koushiappas 2011).
Helioseismology is now a mature discipline thanks to two satellites, the Solar Helioseismic Observatory (SOHO; Domingo et al. 1995) and the Solar Dynamical Observatory (SDO; Pesnell et al. 2011), and asteroseismology has confirmed its capability to detect acoustic and mixed modes for thousands of stars thanks to the satellites COROT (Convection Rotation; Baglin et al. 2006) and Kepler (Borucki et al. 2009), and their interpretation justifies a new interest for the possible role of DM in stellar evolution (Casanellas & Lopes 2011).
In this Letter, we focus on the solar core as a unique probe. Thousands of acoustic modes have been detected and identified with both the Global Oscillations at Low Frequency (GOLF; Gabriel et al. 1995) and the Michelson Doppler Imager (MDI; Scherrer et al. 1995). A precise sound-speed profile has been derived from the surface down to the core (Turck-Chièze et al. 2001; Couvidat et al. 2003). This profile has then been confirmed by the combination of the BiSON network and the MDI instrument (Basu et al. 2009). In parallel, six different terrestrial neutrino detectors count the number of neutrinos coming from the nuclear region of the Sun, in particular from the very central region within 0.1 R☉. The confrontation of these detections through the seismic model shows a remarkable agreement between the two probes, within the error bars (Turck-Chièze et al. 2010; Turck-Chièze & Couvidat 2011), and strongly constrains the central temperature.
The GOLF instrument has also unveiled the existence of several patterns that have been interpreted as gravity modes (Turck-Chièze et al. 2004b; García et al. 2007, 2008, 2011). The first ones, located above 150 mHz, have mixed characteristics, making them sensitive to the core and to the surface of the Sun. These modes are individually difficult to identify due to their low amplitude, the ambiguity among several splitting components of different degrees, and their possible sensitivity to magnetic activity. Thus, their proper use needs complementary work that is now under way. The second series of papers are devoted to dipole gravity modes and their asymptotic properties. The first step was to analyze globally the power of 20 consecutive dipole modes (García et al. 2007) in a way that is now successfully generalized to other stars using Kepler observation (Beck et al. 2011; Bedding et al. 2011). Then, a detailed analysis of the individual modes, which appear as multiplets split by rotation, has recently been accomplished by García et al. (2011), using several techniques including collapsograms (Salabert et al. 2009). This recent detection puts additional constraint on the central density. So new insights into the very center of the Sun are revealed.
In Section 2, we review the properties of DM studied in this Letter and the induced central temperature deduced from neutrinos and the seismic model. In Section 3, we compare the detected individual gravity modes with the seismic model predictions. In Section 4, we explore the properties of the real Sun with respect to the properties of models including different masses of WIMPs and interaction cross-sections. We conclude with a discussion of our results and the perspectives for future work.
2. WIMP PROPERTIES AND NEUTRINOS
The effects of the accumulation of WIMPs in the Sun have been studied for many years. These particles collide with nuclei (hydrogen and heavy constituents), losing momentum and drifting into the solar core. The redistribution of the thermal energy lowers the central temperature by a small amount, with the kinetic energy of DM particles being in equilibrium with the local gravitational potential (Spergel & Press 1985). Several papers have discussed the impact of these particles on the solar core characteristics (Cox et al. 1990; Giraud-Heraud et al. 1990; Dearborn et al. 1991; Kaplan et al. 1991). These studies sought to understand the low values detected for the solar neutrino fluxes via helioseismology probes that put other constraints on the solar core. They focused on a mass domain between 2 and 7 GeV and cross-sections on protons in the range 10−36–10−33.5 cm2 for which effects are clearly visible. We know now that the discrepancy between prediction and detection of neutrinos was partly due to the extreme sensitivity to the physics of the solar model and dominated by the oscillations of neutrinos between different flavors (Turck-Chièze & Couvidat 2011).
Nevertheless, the idea that seismic probes of the Sun or stars can help to constrain the WIMP properties is still relevant. Figures 2 and 3 of Cox et al. (1990) and Figure 5 of Kaplan et al. (1991) have both shown that these particles can only influence the solar core below 0.1 R☉. The accumulation of WIMPs in the center of the Sun decreases its central temperature and increases its density, which can lead to the formation of an isothermal core in extreme cases (Lopes et al. 2002; Lopes & Silk 2002). Recent studies have revisited the effect of WIMPs on neutrino fluxes (Cumberbatch et al. 2010; Lopes & Silk 2010a; Taoso et al. 2010). Recently, Lopes & Silk (2010b) have pointed out the interest in considering gravity modes which are more sensitive to the very inner part of the Sun than acoustic modes and performed a new analysis of the WIMP impact on the properties of these modes for a range of masses between 4 and 12 GeV, both for annihilating models and spin-dependent cross-sections as large as 10−32 cm2 and for non-annihilating models with a range of masses between 5 and 50 GeV and spin-dependent cross-sections down to 2 × 10−35 cm2. The largest effect is obtained for low mass WIMPs, decreasing with the annihilation cross-section interaction and the spin-dependent cross-section.
Here we use the same prescriptions as in these preceding studies but obtain more stringent limits by considering both neutrinos, which are very sensitive to the temperature, and the discovery of dipolar gravity modes, which are very sensitive to the density (García et al. 2011). This new and rich information justifies an extended domain of models exploring the WIMP properties. The final result of the Sudbury National Observatory puts strong constraints on the solar central temperature because this flux depends on this temperature to the 24th power. The Solar Seismic Model (SSeM; Turck-Chièze et al. 2004a, 2011; Turck-Chièze & Couvidat 2011) deduced from acoustic modes (see below) predicts a flux in agreement with this detection and fluxes in agreement with the other five neutrino detections with a central temperature of 15.75 × 106 K, 1.5% greater than the temperature of the standard model.
3. THE OBSERVED SOLAR GRAVITY MODES COMPARED WITH PREDICTIONS
The solar radiative zone represents at least 0.92 M☉. In this vast region, the microscopic ingredients (nuclear reaction rates, opacity coefficients associated with the composition) largely imprint the theoretical sound-speed profile. The observed profile has been established down to 0.06 R☉ by using the acoustic mode frequencies of both GOLF and MDI instruments aboard SOHO (Turck-Chièze et al. 2001) and confirmed by Basu et al. (2009). The SSeM has been built to precisely reproduce this profile (Turck-Chièze et al. 2001; Couvidat et al. 2003). As described in the previous section, this model nicely predicts the different neutrino fluxes as presently observed.
This means that the very central region (below 0.05 R☉), which is not probed by acoustic modes, is not so badly reproduced by the SSeM. That model is also useful for predicting the low degree gravity mode frequencies (Couvidat et al. 2003; Mathur et al. 2007). These modes are particularly sensitive to the solar core. Most of the gravity mode frequencies of the well-documented SSM differ by less than 5 μHz from the SSeM model predictions. The largest differences appear for frequencies above 120 μHz (periods below 2 hr) where the mixed modes are located. Below this limit (higher periods), they agree within about 3 μHz (see Table 1 and Figure 1). The gravity modes are mainly sensitive to the density profile, so the observed differences naturally follow the difference in density; see Figures 2 and 3 of Mathur et al. (2007). For orders n > 4, the gravity modes start to follow an asymptotic regime, which means that the modes are almost equally spaced in period. For dipolar modes (i.e., modes with degree ℓ = 1), the period spacing reads as (Tassoul 1980)
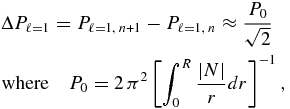
where N is the Brunt Väissälä frequency defined by N2 = g[(1/Γ1(d/dr)log P(r) − (d/dr)logρ(r))].
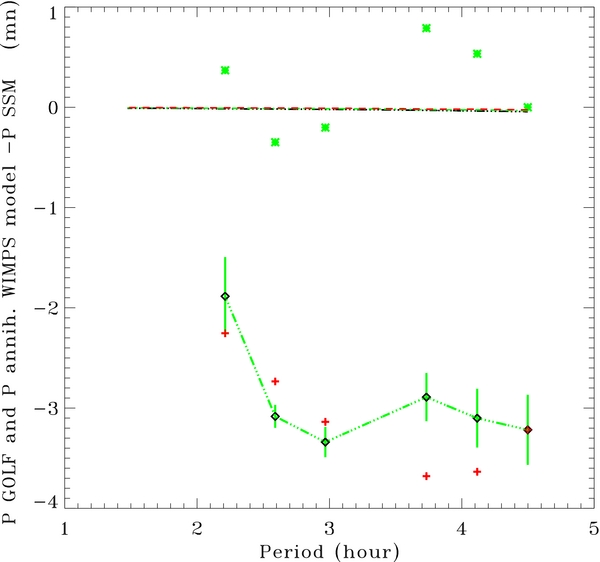
Figure 1. Difference between dipole gravity mode periods of GOLF (diamonds connected by triple dot-dashed lines with error bars) or SSeM (crosses) and the SSM of Lopes & Silk (2010b). The difference between GOLF and SSeM is represented by stars; see Table 1. The WIMPs models using an annihilation cross-section of 10−27 cm3 s−1 show no difference with the SSM on which the calculation has been built (horizontal dashed lines) The different symbols for 5, 7, and 10 GeV are superimposed.
Download figure:
Standard image High-resolution imageThe progress in solar modeling leads to a fundamental period P0 of 34.4 ± 1 mn for all the models computed. This represents important progress in comparison with the situation before the launch of SOHO where values between 30 and 60 mn were considered. This theoretical fact helps us to guide the g-mode search in SOHO data (Mathur et al. 2007).
Following this property of dipole modes, one has put in evidence a broad theoretical structure around 24 mn corresponding to the equidistant periods between the dipole modes for orders between n = 4 and 26. The deviation from a Dirac peak is a manifestation of the incomplete asymptotic behavior of the modes and the enlargement due to the rotation in the core knowing that the components with an azimuthal order m = ±1 dominate the solar dipole signal. Depending on the core rotation axis, the mode m = 0 is absent or smaller and its frequency is the mean value at the first order.
A corresponding signal has been found in the GOLF/SOHO data with an extremely high confidence level after 10 years of continuous observation (García et al. 2007). This is the first significant evidence of detected dipole gravity modes. This signal has been followed in time and its probability of positive detection has continued to increase (García et al. 2008). It is important to note that because these oscillations are pure g-modes, their frequency does not vary with the solar cycle, in contrast with the mixed modes. The broad observed peak reflects the increased rotation in the core and the order of magnitude of this rotation has consequently been extracted. This method for detecting gravity-dominated modes is now being extended to other stars with success for a large number of solar-like stars of slightly higher mass and for red giants (Beck et al. 2011; Bedding et al. 2011). A detailed analysis of the power spectrum has recently shown that the component m = ±1 peaks rise above the background noise in the power spectrum, confirming, for at least six modes, the strong rotation increase in the core through their splitting values (García et al. 2011).
Table 1 compares different prediction frequencies (SSM from Lopes & Silk (2010b) and SSM and SSeM from Mathur et al. (2007), with the mean frequency between the two observed GOLF m = ±1 components in the frequency band where they can be identified without ambiguity as dipole modes. These values are attributed to the component m = 0 of these dipole modes. In this study, an error bar of 41 nHz is attributed to the observed frequencies, corresponding to the boxcar used to extract the components. A rotational analysis at second order is useful for estimating the shift due to the core rotation of the m = 0 component following Ballot et al. (2010). Considering Equation (19) of that work, the shift due to a mean core rotation of four times the mean rotation of the rest of the radiative zone amounts to about −40 nHz for n = 4 and to +10 nHz for n = 10, so this effect is presently smaller than the error bar of 58 nHz attributed to the modes and negligible in the difference of periods of successive same order (Table 2). In another study, Rashba et al. (2007) have shown that the magnetic shift of a potential fossil field must be smaller than 100 nHz. We have not introduced this effect in the absence of any observational evidence of such a fossil field.
Table 1. Comparison of Dipole Gravity Mode Frequencies: Gravity Mode Order, SSM Predictions for Lopes & Silk (2010b) and Mathur et al. (2007) and Corresponding Periods, SSeM Predictions, then Differences GOLF-SSeM and GOLF-SSM from Lopes & Silk (2010b) Expressed + Observational Error Bars
| n | SSM | Period | SSeM | GOLF-SSeM | GOLF-SSM |
|---|---|---|---|---|---|
| (μHz) | (hour) | (μHz) | (mn) | (mn) | |
| −10 | 61.7–61.75 | 4.53 | 62.50 | 0 ± 0.25 | −3.23 ± 0.25 |
| −9 | 67.5–67.48 | 4.14 | 68.49 | 0.75 ± 0.21 | −3.11 ± 0.21 |
| −8 | 74.6–74.42 | 3.76 | 75.66 | 0.76 ± 0.22 | −2.9 ± 0.22 |
| −7 | 83.0–82.92 | 3.37 | 84.38 | ... | ... |
| −6 | 93.8–93.55 | 2.99 | 95.23 | −0.2 ± 0.1 | −3.35 ± 0.1 |
| −5 | 107.6–107.23 | 2.59 | 109.15 | −0.36 ± 0.08 | −3.09 ± 0.08 |
| −4 | 126.0–125.57 | 2.21 | 127. 74 | 0.37 ± 0.3 | −1.9 ± 0.3 |
Download table as: ASCIITypeset image
Table 2. Equidistance between Dipole Modes in μHz and in Minutes for GOLF, SSeM, and the WIMPs Models Showing the Smallest Effect for Masses 5, 7, and 10 GeV
| n | Period | Δν Measured | Δ P Measured | ΔP sismique | WIMPs1 | WIMPs2 | WIMPs3 |
|---|---|---|---|---|---|---|---|
| (hour) | (μHz) | (mn) | (mn) | (mn) | (mn) | (mn) | |
| −10 −9 | 4.53–4.14 | 5.8 | 22.8 ± 0.3 | 23.32 | 20.68 | 21.48 | ... |
| −9 −8 | 4.14–3.76 | 7.17 | 22.8 ± 0.2 | 23.06 | 20.89 | 21.74 | 22.17 |
| −8 −7 | 3.76–3.37 | 9.17 | ... | 22.76 | 20.89 | 21.70 | 22.19 |
| −7 −6 | 3.36–2.99 | 10.7 | ... | 22.51 | 20.87 | 21.67 | 22.15 |
| −6 −5 | 2.97–2.59 | 14.16 | 22.5 ± 0.1 | 22.31 | 20.86 | 21.59 | 22.02 |
| −5 −4 | 2.59–2.21 | 18.36 | 21.50 ± 0.34 | 22.2 | 20.78 | 21.65 | 22.02 |
| −4 −3 | 2.21 | ... | ... | 21.73 | 20.24 | 20.91 | 21.48 |
| −3 −2 | 1.84 | ... | ... | 22.02 | 20.74 | 21.45 | 21.74 |
Download table as: ASCIITypeset image
Table 1 and Figure 1 clearly show that the observed values agree well with the SSeM predictions. Their differences are largely smaller than the difference with the recent predictions of SSM using recent re-estimates of CNO abundances. The mentioned difference between the different estimates of SSM given in Table 1 is due to the tachocline treatment and the adopted versions of the new abundances that have slightly varied over the last 5 years: see discussions and values used in Turck-Chièze et al. (2004a), Mathur et al. (2007), and Lopes & Silk (2010b). So, the density of 153.6 g cm−3 of the SSeM is not far from the central density of the real Sun, it is slightly smaller than the SSM central density (Turck-Chièze et al. 2011).
4. COMPARISON WITH DARK MATTER PREDICTIONS
This work is the first attempt to put so many constraints on light DM by looking at the properties of the very inner solar core (below 0.1 R☉) with both boron neutrinos, acoustic modes, and dipole gravity modes. The considered frequency range strongly reduces the range of WIMP masses and cross-sections compatible with the observations.
At first glance, the results of GOLF are not in favor of DM as the temperature and density of the corresponding SSeM in comparison with SSM vary in the opposite way than expected from WIMPs trapped in the solar core (see Figures 1 and 2 of Lopes & Silk 2010b). In this Letter, we extend this previous work to more realistic WIMP cross-section interactions as suggested by Kappl & Winkler (2011) and compare them directly to the GOLF dipole gravity mode observations. Figure 1 illustrates first that the DM model using a standard annihilation cross-section 〈σann〉 = 10−27 cm3 s−1 shows no modification of the central conditions with respect to the SSM.
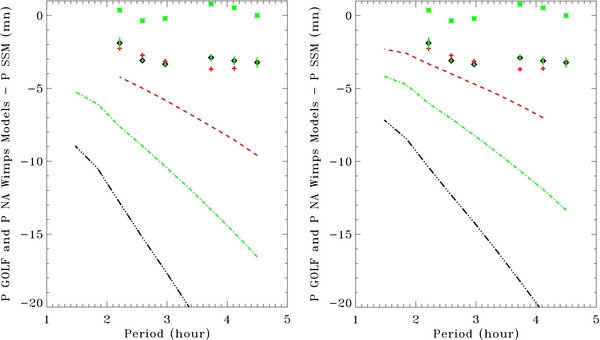
Next, we study non-annihilating particle models—with annihilating cross-sections 〈σann〉 = 10−50 cm3 s−1—for 5, 7, 10 GeV WIMPs with spin-independent cross-sections of 10 −40 cm2 and spin-dependent cross-sections varying between 2 × 10−35 cm2 and 5 × 10−36 cm2 starting from the SSM. Figure 2 shows the effect for the lowest of these cross-sections that produce the smallest effect: 7 and 5 × 10−36 cm2. Other cases lead to a difference of up to 20 mn instead of about 3 mn for the SSeM. We note that the WIMP models are very far from the models compatible with the GOLF data. This allows us to exclude all of these models. We infer that these DM models of low-mass WIMPs are not supported by our knowledge of the solar core.
Figure 2. Gravity mode period differences expressed in minutes between GOLF (circle with error bar) or SSeM (crosses) and the SSM of Lopes & Silk (2010b) or between GOLF and SSeM (stars). Superimposed are DM non annihilation models with spin dependent cross-section of 7 × 10−36 cm2 (left) and 5 × 10−36 cm2 (right) for, respectively, 5, 7, and 10 Gev (black line, green line, and red line).
Download figure:
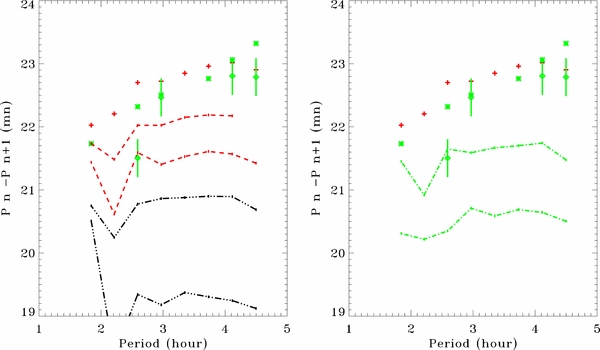
Standard image High-resolution imageTo avoid the criticism that this comparison is model dependent, Figure 3 and Table 2 illustrate the asymptotic behavior, discussed in Section 3, for the different masses compared to SSM and GOLF data. We show for the masses 5, 7, 10 GeV the range of models for spin-dependent cross-section non-annihilating between 2 × 10−35 cm2 and 5 × 10−36 cm2. A specific behavior is clearly visible in all the WIMP models at low period (high frequencies). Such signature is not visible in the GOLF data, and so one can exclude this range of parameters as not being observed in the present Sun. Of course, the present error bars are still large and the range of the observations needs to be enlarged. We are continuing to work on the GOLF data and in parallel we have shown that a reduction of the solar noise is possible with a new generation of space instrument like GOLF-NG (Turck-Chièze et al. 2008 and references therein) designed specifically for a better determination of gravity modes over a larger range of periods and for a better description of the low atmosphere of the Sun.
Figure 3. Difference in minutes between successive dipole gravity periods for SSM (crosses), SSeM (stars) and GOLF (diamonds +error bars). These values are compared to the range of results for the WIMP mass of 10 and 5 GeV, respectively (left) and a spin-dependent cross-section between 2 × 10−35 cm2 and 5 × 10−36 cm2. Idem for mass 7 GeV (right). Same symbols as Figure 2.
Download figure:
Standard image High-resolution imageIn the range of frequencies considered in this Letter, all of the differences between GOLF and the seismic model predictions are smaller than 0.3 μHz. This is an important result of the SOHO satellite and leaves little room for any solar signature of the CDM.
However, Figure 3 shows that a very central signature in the solar core justifies a larger band of detection to confirm this preliminary result. Moreover, the physical processes that lead to the seismic model are not yet under control despite specific studies of the transport of momentum by rotation (Turck-Chièze et al. 2010), of opacity coefficients and energy transfer, of the present and past energy balance, and of the effects of mass loss (Guzik et al. 2010; Turck-Chièze et al. 2011) and fossil magnetic fields in the young Sun (Duez et al. 2010; Turck-Chièze & Couvidat 2011). The discrimination between all these processes in combination with possible DM signatures will be possible only through a generalization of the physics of the Sun to other stars.
It is now well established that gravity modes are detectable with greater amplitudes in solar-like stars of greater masses and also in red giant stars, and it is evident that new constraints from asteroseismology will arrive rather soon.
SOHO is a mission of international cooperation between ESA and NASA, we are particularly thankful to our colleagues at ESA who take care of the satellite and to CNES for the CNES/GOLF grant at SAp/CEA-Saclay. S.C. acknowledges financial support from the NASA SDO grants. S.M. acknowledges financial support from the National Science Foundation.