Abstract
This work introduces the concept and experimentation of reversible optical coherence conversion, and outlines optical coherency matrix tomography as a method for measuring the full coherence of a field. To date, coherence conversion has only been demonstrated between the spatial and polarization degrees-of-freedom (DoFs). Coherence conversion offers a new control over an optical field's DoFs—protecting against deleterious scrambling effects.
Export citation and abstract BibTeX RIS
1. Introduction
Optical coherence is often studied through the lens of interference, a tangible phenomenon that is exhibited in nature and often described using the Young's double slit experiment. The possibility of interference is dictated by correlations between different points of the field in space (spatial coherence), correlations between different points of the field in time (temporal coherence), and correlations of electric field vector orientations within the field at points in space and time (polarization coherence) [1]. Coherence has been thoroughly, yet not exhaustively, investigated in the quantum and classical optical regimes. In fact, recent developments such as classical entanglement (analogous to the better-known and further-explored quantum entanglement) have spurred from ruminations on quantum and classical optics, rather than one exclusively [2–4]. The result of which is a research-rich area in which multiple degrees-of-freedom (DoFs) of light (e.g. temporal, spatial, polarization) are correlated, manipulated, and measured simultaneously [5–11]. Classical optical fields with unique correlations between DoFs may be transformative in optical communications (e.g. overcoming current bandwidth limits) [12], optical microscopy via tighter focusing [13, 14], near-diffraction-free propagation [15–18], speckle resistance [19], and polarimetry [6, 20].
Quite often, the DoFs of coherence are assessed separately; a Young's double slit experiment to measure spatial coherence, a Michelson or Mach–Zehnder interferometer to measure temporal coherence, and calculations of the Stokes parameters to measure polarization. However, there exists an approach to measure the full coherence of a field called optical coherence matrix tomography (OCmT), inspired by quantum state tomography, that can be used to assess coherence such that multiple DoFs are measured simultaneously—accounting for correlations between DoFs [21, 22]. The process of OCmT will be detailed in this tutorial. Furthermore, the treatment of coherence as a multi-DoF property permits its sharing, as a resource, across DoFs through the process of coherence conversion [23, 24]. Introduced by Okoro et al in 2017, coherence conversion reversibly and unitarily transfers coherence between two DoFs of an optical field via a reorganization of the field's statistical fluctuations (entropy) from a less coherent DoF to a more coherent one [23]. To date, the conversion has only been demonstrated between the spatial DoF and polarization, the reversibility of which was recently validated experimentally [24].
This work serves as a comprehensive introduction to the concept of coherence conversion for nonexpert researchers. Typically, optical coherence is discussed while focusing on a single DoF, here, we will discuss intra- and inter-DoF correlations in optical fields. To date, unitary coherence conversion is limited to simple DoFs that can be described using 2 × 2 coherence matrices and carry up to 1 bit of entropy. We hope that by establishing this tutorial, we may offer inspiration and guidance for future studies in this area that may extend the boundaries of current investigations.
2. Optical coherence
2.1. Polarization coherence
The polarization of an optical field corresponds to its electric field vector orientations. Determining the state of polarization is often done by calculating the Stokes parameters, 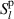 , where l is an integer value from 0 to 3 [1]. To find these parameters experimentally requires measuring the intensity (or power) of an optical field, using a polarization analyzer and a quarter wave plate, for instance, along certain polarization projections;
, where l is an integer value from 0 to 3 [1]. To find these parameters experimentally requires measuring the intensity (or power) of an optical field, using a polarization analyzer and a quarter wave plate, for instance, along certain polarization projections; 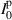 ,
, 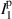 ,
, 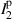 , and
, and  which correspond to the intensity of the horizontal component plus the intensity of the vertical component (the total intensity of the field), the intensity of the horizontal component, the intensity of the (+45∘)-projection, and the intensity of the right-handed circular projection, respectively. The Stokes parameters are calculated using the equation
which correspond to the intensity of the horizontal component plus the intensity of the vertical component (the total intensity of the field), the intensity of the horizontal component, the intensity of the (+45∘)-projection, and the intensity of the right-handed circular projection, respectively. The Stokes parameters are calculated using the equation  , and the degree of polarization
, and the degree of polarization 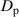 is calculated using the Stokes parameters:
is calculated using the Stokes parameters: 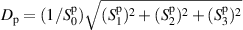 [21]. The degree of polarization should be interpreted as a ratio of intensities; the polarized part of the field over the total intensity. For an unpolarized field, the normalized Stokes parameters are
[21]. The degree of polarization should be interpreted as a ratio of intensities; the polarized part of the field over the total intensity. For an unpolarized field, the normalized Stokes parameters are ![$[S^{\mathrm{p}}_{0} \; S^{\mathrm{p}}_{1} \; S^{\mathrm{p}}_{2} \; S^{\mathrm{p}}_{3}] = [1 \; 0 \; 0 \; 0]$](https://content.cld.iop.org/journals/2040-8986/25/5/053502/revision5/joptacc74eieqn9.gif) , and
, and 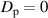 . The state of polarization, or polarization coherence, at a point in an optical field may also be described using a coherency matrix which is a product of the Stokes parameters and the Pauli spin matrices (
. The state of polarization, or polarization coherence, at a point in an optical field may also be described using a coherency matrix which is a product of the Stokes parameters and the Pauli spin matrices (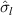 ),
),
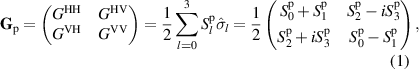
where H and V correspond to the horizontal and vertical polarization components, respectively,  ,
,  H,V, and
H,V, and  is an ensemble average [1, 23]. The Pauli spin matrices are defined as
is an ensemble average [1, 23]. The Pauli spin matrices are defined as 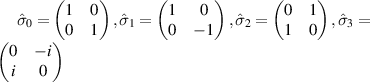 , and are used in this context because they underly the geometry of the Poincar
, and are used in this context because they underly the geometry of the Poincar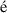 sphere, the 3D geometric representation of all the possible states of polarization, although another complete set of four basis matrices may be used [25]. Here,
sphere, the 3D geometric representation of all the possible states of polarization, although another complete set of four basis matrices may be used [25]. Here, 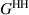 and
and 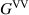 are the contributions of H and V to the total power of the field, respectively, whereas
are the contributions of H and V to the total power of the field, respectively, whereas  and
and 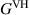 are correlations between the H and V components. For a horizontally polarized field
are correlations between the H and V components. For a horizontally polarized field 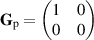 , under the normalization
, under the normalization 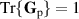 , where
, where ![$\mathrm{Tr}\{[\cdot]\}$](https://content.cld.iop.org/journals/2040-8986/25/5/053502/revision5/joptacc74eieqn23.gif) is the matrix trace. For a vertically polarized field
is the matrix trace. For a vertically polarized field 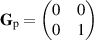 , for a 45∘ polarized field
, for a 45∘ polarized field  , and for an unpolarized field
, and for an unpolarized field  .
.
The coherency matrix 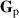 is Hermitian and positive-semidefinite such that it is equal to its conjugate transposed matrices, and has real, non-negative eigenvalues. These eigenvalues determine the entropy of the polarization DoF and the degree of polarization. We define the polarization entropy as
is Hermitian and positive-semidefinite such that it is equal to its conjugate transposed matrices, and has real, non-negative eigenvalues. These eigenvalues determine the entropy of the polarization DoF and the degree of polarization. We define the polarization entropy as 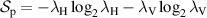 , where
, where 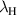 and
and 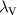 are the eigenvalues of
are the eigenvalues of 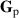 [23]. Entropy in this context is a measure of the total disorder in the polarization DoF [26]. We can relate the degree of polarization to the eigenvalues of
[23]. Entropy in this context is a measure of the total disorder in the polarization DoF [26]. We can relate the degree of polarization to the eigenvalues of 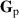 by
by  [1]. By imposing the normalization
[1]. By imposing the normalization  , we have
, we have  [27] and
[27] and 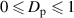 . When the field is fully polarized
. When the field is fully polarized 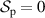 ,
, 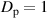 , and when unpolarized
, and when unpolarized 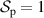 ,
, 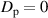 . Another relation of the eigenvalues to
. Another relation of the eigenvalues to 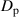 is
is 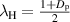 and
and  when
when 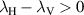 , and
, and 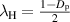 and
and 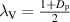 when
when 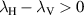 [25]. When
[25]. When 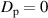 ,
, 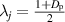 . The relationship of the polarization entropy and the degree of polarization is
. The relationship of the polarization entropy and the degree of polarization is 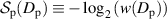 where
where 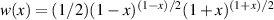 , such that there is a nonlinear dependence of
, such that there is a nonlinear dependence of 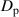 on
on 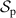 ; as
; as 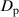 ranges from 0 to 1,
ranges from 0 to 1,  ranges from 1 to 0. This is the red curve in figure 1. Also shown in figure 1 is a portion of the circle defined by
ranges from 1 to 0. This is the red curve in figure 1. Also shown in figure 1 is a portion of the circle defined by 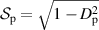 , drawn in blue. These two functions correspond to the left y-axis. One can quantitatively compare
, drawn in blue. These two functions correspond to the left y-axis. One can quantitatively compare  to the definition of
to the definition of 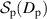 by plotting the absolute values of the first derivatives of each function which are shown as dashed curves in figure 1 and correspond to the right y-axis. These derivatives trend toward
by plotting the absolute values of the first derivatives of each function which are shown as dashed curves in figure 1 and correspond to the right y-axis. These derivatives trend toward 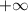 as
as 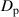 approaches 1, and highlight that
approaches 1, and highlight that 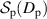 does not have the same rate of change as a circular function.
does not have the same rate of change as a circular function.
Figure 1. The relationship between polarization entropy and degree of polarization. The red curve represents 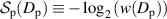 . The blue curve represents part of the circle defined by
. The blue curve represents part of the circle defined by 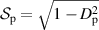 . The red dashed curve represents the absolute value of the first derivative of
. The red dashed curve represents the absolute value of the first derivative of 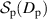 . The blue dashed curve represents the absolute value of the first derivative of
. The blue dashed curve represents the absolute value of the first derivative of 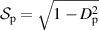 .
.
Download figure:
Standard image High-resolution image2.2. Spatial coherence
While the spatial DoF is a continuous variable, it may be reduced to just two points to assess its coherence—evaluating the statistical correlation between said points. Spatial points are said to be correlated if they are within the field's spatial coherence width or coherence area [1]. Spatial coherence for a pair of points in an optical field may also be described in a similar manner as polarization coherence using a 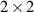 coherency matrix:
coherency matrix: 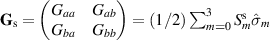 , where a and b are two points of a scalar field in space,
, where a and b are two points of a scalar field in space, 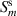 are two-point 'spatial Stokes' parameters,
are two-point 'spatial Stokes' parameters, 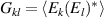 ,
, 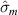 are the Pauli spin matrices, and
are the Pauli spin matrices, and 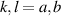 [21]. Here,
[21]. Here, 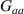 and
and  are the contributions of a and b to the total power of the field, respectively, whereas
are the contributions of a and b to the total power of the field, respectively, whereas 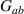 and
and 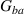 are correlations between the points a and b. The experimental process to calculate the spatial Stokes parameters requires measuring the intensity (or power) of the field along certain spatial projections;
are correlations between the points a and b. The experimental process to calculate the spatial Stokes parameters requires measuring the intensity (or power) of the field along certain spatial projections; 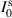 ,
, 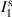 ,
,  , and
, and 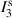 correspond to the total intensity of the field, the intensity at a or b, the intensity after symmetric mixing of a and b, and the intensity after a
correspond to the total intensity of the field, the intensity at a or b, the intensity after symmetric mixing of a and b, and the intensity after a 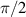 phase shift is applied to b, respectively, furthermore, the two-point spatial Stokes parameters can be found using the equation
phase shift is applied to b, respectively, furthermore, the two-point spatial Stokes parameters can be found using the equation 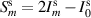 [21].
[21].
For a spatially coherent field made up of one point (point a) 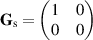 , under the normalization
, under the normalization 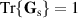 , where
, where ![$\mathrm{Tr}\{[\cdot]\}$](https://content.cld.iop.org/journals/2040-8986/25/5/053502/revision5/joptacc74eieqn84.gif) is the matrix trace. For a spatially coherent field made up of just point b
is the matrix trace. For a spatially coherent field made up of just point b
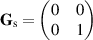 , for a spatially coherent field in which two points can be used to assess coherence
, for a spatially coherent field in which two points can be used to assess coherence 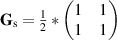 , and for a spatially incoherent field
, and for a spatially incoherent field  . The coherency matrix
. The coherency matrix 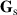 is Hermitian and positive-semidefinite. Such is the case with the polarization coherency matrix, the spatial coherency matrix determines the entropy of the spatial DoF and the degree of spatial coherence. We define the spatial entropy as
is Hermitian and positive-semidefinite. Such is the case with the polarization coherency matrix, the spatial coherency matrix determines the entropy of the spatial DoF and the degree of spatial coherence. We define the spatial entropy as 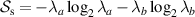 , where λa
and λb
are the eigenvalues of
, where λa
and λb
are the eigenvalues of 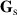 [24]. We define the degree of spatial coherence as
[24]. We define the degree of spatial coherence as 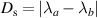 [28]. By imposing the normalization
[28]. By imposing the normalization 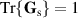 , we have
, we have 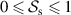 and
and  . When the field is spatially coherent
. When the field is spatially coherent 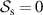 ,
, 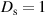 , and when spatially incoherent
, and when spatially incoherent  ,
, 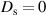 .
.
2.3. Multi-DoF coherence
As will be outlined in section 3, a key feature of coherence conversion is the correlating and uncorrelating of the spatial DoF and polarization, enabling the sharing of entropy between DoFs and the concentration of entropy in a single DoF [24]. When entropy is shared between two DoFs simultaneously, these DoFs are non-separable. Consider an optical field in which there exists correlations between the spatial and polarization DoFs. For cases in which the two DoFs are not separable (correlated), such is the case for classically entangled cylindrical vector beams [29, 30],  and
and 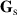 are not sufficient descriptors [23, 28]. Instead the spatial and polarization coherence must be considered jointly. Using a
are not sufficient descriptors [23, 28]. Instead the spatial and polarization coherence must be considered jointly. Using a 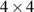 coherency matrix that describes the full vector-field coherence in terms of discretized space and polarization,
coherency matrix that describes the full vector-field coherence in terms of discretized space and polarization,

where 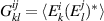 ,
, 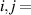 H,V, and
H,V, and 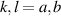 , one can account for correlations between the spatial and polarization DoFs [4, 21–23]. The elements of
, one can account for correlations between the spatial and polarization DoFs [4, 21–23]. The elements of 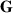 therefore represent normalized correlations between field projections in space and polarization. In cases that exhibit said correlations,
therefore represent normalized correlations between field projections in space and polarization. In cases that exhibit said correlations, 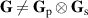 ; this equality is only achieved when the two DoFs are independent of each other (separable). This coherency matrix has proved useful in a variety of contexts, such as evaluating the visibility of Young's double slit interference in the presence of polarization effects [28, 31, 32]. From the Hermitian and non-negative matrix (equation (2)) we can derive the field entropy
; this equality is only achieved when the two DoFs are independent of each other (separable). This coherency matrix has proved useful in a variety of contexts, such as evaluating the visibility of Young's double slit interference in the presence of polarization effects [28, 31, 32]. From the Hermitian and non-negative matrix (equation (2)) we can derive the field entropy 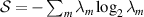 , where λm
are the real eigenvalues of G:
, where λm
are the real eigenvalues of G: 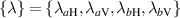 , and
, and 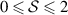 with the normalization
with the normalization 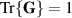 . Therefore, the field can carry up to a total of 2 bits of entropy across the two DoFs.
. Therefore, the field can carry up to a total of 2 bits of entropy across the two DoFs.
2.4. Evaluating multi-DoF coherence via OCmT
2.4.1. Introduction to OCmT.
OCmT is a method used to measure the full 4 × 4 coherence matrix of an optical field in which two DoFs are of interest; it is especially useful when investigating the coherence of DoFs with respect to one another [21, 22]. While this method can be used for a variety of DoFs, this tutorial will only cover OCmT in the context of the spatial and polarization DoFs. The expression for the full coherence matrix represented by equation (2) can be rewritten as
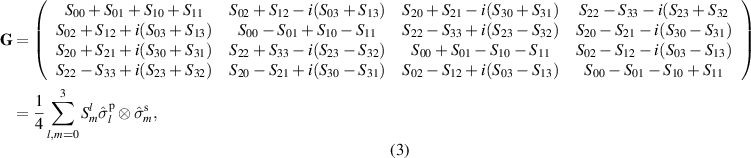
where the elements are made up of multi-DoF Stokes parameters 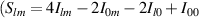 ,
, 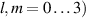 [21]. Here Ilm
represents joint intensity projections; to calculate these projections and ultimately the coherence matrix,
[21]. Here Ilm
represents joint intensity projections; to calculate these projections and ultimately the coherence matrix,  , 16 tomographic projections are needed. The procedure for finding the intensity projections is outlined in figure 2 and table 1.
, 16 tomographic projections are needed. The procedure for finding the intensity projections is outlined in figure 2 and table 1.
Figure 2. The process for one set of projective measurements on an optical field of arbitrary coherence and polarization state to reconstruct G. Here, the polarization optics (quarter wave plate and linear polarizer) are set to measure the horizontal projection, through which spatial projections are collected. By collecting these four spatial projections for each polarization projection (horizontal, vertical, 45∘, and circular), the 16 tomographic measurements are found.
Download figure:
Standard image High-resolution imageTable 1. The tomographic intensity measurements necessary for calculating the joint Stokes parameters, and ultimately G. H: horizontal, V: vertical, D: 45∘, R: right-handed circular.
| Polarization projection | |||||
|---|---|---|---|---|---|
| H | V | D | R | ||
| Spatial projection | a |
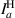
|
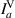
|
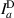
|
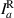
|
| b |
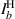
|
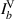
|
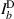
|
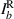
| |
| a + b |
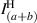
|
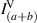
|
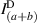
|
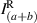
| |
| a + ib |

|
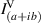
|
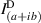
|
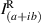
| |
The 16 tomographic measurements in table 1 can be found using the setup in figure 2 and taking a cross-section of intensity images. The first row of the spatial projection section corresponds to the joint polarization-spatial projections when b is blocked, likewise the second row corresponds to the joint polarization-spatial projections when a is blocked. The third row of the spatial projection section corresponds to the zero-spatial-phase-shift joint spatial-polarization projections when both a and b are superposed, and if coherent: interfere. The fourth row of the spatial projection section corresponds to the joint polarization-spatial projections when b experiences a ( )-spatial-phase-shift with respect to a. The fourth column of the polarization projection section corresponds to the joint polarization-spatial projections when b experiences a (
)-spatial-phase-shift with respect to a. The fourth column of the polarization projection section corresponds to the joint polarization-spatial projections when b experiences a (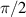 )-polarization-phase-shift with respect to a. These values are used to calculate the 16 intensity projections (Ilm
) in the following manner:
)-polarization-phase-shift with respect to a. These values are used to calculate the 16 intensity projections (Ilm
) in the following manner: 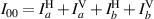 ;
; 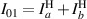 ;
; 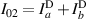 ;
; 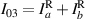 ;
; 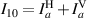 ;
; 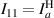 ;
; 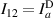 ;
; 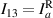 ;
; 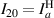 ;
;  ;
; 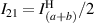 ;
; 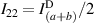 ;
; 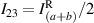 ;
; 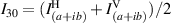 ;
; 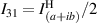 ;
; 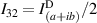 ;
; 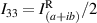 . Once these intensity projections are obtained, the joint Stokes parameters (Slm
) can be calculated, and the full optical coherence matrix (equation (3)) can be constructed.
. Once these intensity projections are obtained, the joint Stokes parameters (Slm
) can be calculated, and the full optical coherence matrix (equation (3)) can be constructed.
2.4.2. OCmT example 1.
Consider a field that is randomly polarized and spatially coherent. To determine the field's coherence properties, one can apply the OCmT procedure from figure 2. The mutual coherence of the electric field components are summarized in table 2. The field's horizontal and vertical components are equal in intensity due to the randomness of the polarization state. The field should be assessed at two spatial points (a and b) that are equal in intensity; these points can be selected using a Young's double slit with separation less than the spatial coherence width of the field. In this case, 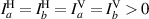 . The interference equation for the vertical projection is
. The interference equation for the vertical projection is 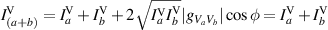 , here the normalized cross-correlation
, here the normalized cross-correlation 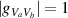 , and the cosine of the phase difference (φ) equals 1 because the field is spatially coherent and, for measurement purposes, polarized along the vertical projection. For the uninitiated, note that the wave nature of light is mathematically represented by a phase variable inside a cosine term. Therefore, in this context, φ is the difference in phase between
, and the cosine of the phase difference (φ) equals 1 because the field is spatially coherent and, for measurement purposes, polarized along the vertical projection. For the uninitiated, note that the wave nature of light is mathematically represented by a phase variable inside a cosine term. Therefore, in this context, φ is the difference in phase between  and
and  . Similar interference equations are written for the horizontal, 45∘, and circular projections, all of which are theoretically equal in magnitude due to the random state of polarization. The interference equation for the vertical projection containing a (
. Similar interference equations are written for the horizontal, 45∘, and circular projections, all of which are theoretically equal in magnitude due to the random state of polarization. The interference equation for the vertical projection containing a ( )-spatial phase shift is
)-spatial phase shift is 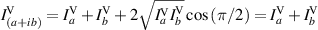 . Similar interference equations with (
. Similar interference equations with (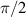 )-spatial phase shifts are written for the horizontal and 45∘-projection, and even for the circular projection which adds a (
)-spatial phase shifts are written for the horizontal and 45∘-projection, and even for the circular projection which adds a ( )-polarization phase shift between the horizontal and vertical components which already exhibit a random phase relationship and thus the equation is unaffected by polarization phase shifts. These measurements result in the coherence matrix:
)-polarization phase shift between the horizontal and vertical components which already exhibit a random phase relationship and thus the equation is unaffected by polarization phase shifts. These measurements result in the coherence matrix: 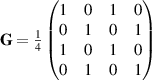 . If this field is restricted to one spatial point (a) such that the field is still unpolarized and spatially coherent, the resulting coherency matrix would be equation (4).
. If this field is restricted to one spatial point (a) such that the field is still unpolarized and spatially coherent, the resulting coherency matrix would be equation (4).
Table 2. Comparing the mutual coherence of electrical field components for the OCmT example from section 2.4.2.
| Mutually coherent? | ||
|---|---|---|
|
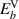
| |
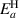
| Yes | No |
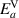
| No | Yes |
2.4.3. OCmT example 2.
Consider a field that is linearly polarized along a vertical projection and made up of two mutually incoherent spatial modes. The mutual coherence of the electric field components are summarized in table 3. It is expected that 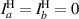 , and the field is linearly polarized along the vertical projection;
, and the field is linearly polarized along the vertical projection; 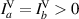 . Furthermore,
. Furthermore, 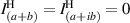 . The interference equation for the vertical projection:
. The interference equation for the vertical projection: 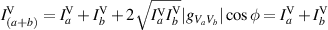 does not include a third term because the spatial modes (a and b) are mutually incoherent, therefore,
does not include a third term because the spatial modes (a and b) are mutually incoherent, therefore, 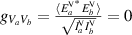 . Furthermore,
. Furthermore, 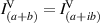 , because a spatial phase shift, in this case of
, because a spatial phase shift, in this case of 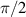 , to one arm (b) does not alter the tomographic measurement if a and b are mutually incoherent, i.e. there exists a random phase relationship between the two points.
, to one arm (b) does not alter the tomographic measurement if a and b are mutually incoherent, i.e. there exists a random phase relationship between the two points.
Table 3. Comparing the mutual coherence of electrical field components for the OCmT example from section 2.4.3.
| Mutually coherent? | ||
|---|---|---|

|
| |

| No | No |

| No | No |
The physical result of superposing a and b at a vertical projection is an incoherent sum—no fringes are present. A 45∘-projection (D) results in 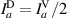 , likewise for b, and
, likewise for b, and 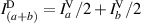 . Similar equations can be written for the circular projection. These measurements result in the coherence matrix shown in equation (5).
. Similar equations can be written for the circular projection. These measurements result in the coherence matrix shown in equation (5).
3. Coherence conversion
3.1. Concept of optical coherence conversion
Now that we have described the 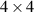 coherency matrix and a method to measure it, the concept of optical coherence conversion can be discussed. A coherence conversion between the spatial and polarization DoFs relies on the field's ability to transfer entropy between the two DoFs, therefore, the field at the input of the system must be curated with this ability. The field must contain entropy, and thus cannot be fully coherent (
coherency matrix and a method to measure it, the concept of optical coherence conversion can be discussed. A coherence conversion between the spatial and polarization DoFs relies on the field's ability to transfer entropy between the two DoFs, therefore, the field at the input of the system must be curated with this ability. The field must contain entropy, and thus cannot be fully coherent (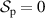 ,
,  ). The field should also not be fully incoherent (
). The field should also not be fully incoherent (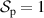 ,
, 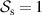 ). Two appropriate options, for example, are a polarized (
). Two appropriate options, for example, are a polarized (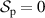 ) and spatially incoherent (
) and spatially incoherent (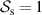 ) field (e.g. a polarized LED), or an unpolarized (
) field (e.g. a polarized LED), or an unpolarized (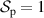 ) and spatially coherent (
) and spatially coherent ( ) field.
) field.
The concept of a reversible coherence converter is outlined in figure 3. In the case of the input field being unpolarized and spatially coherent, i.e. having 1 bit of entropy in the polarization DoF and 0 bits of entropy in the spatial DoF, as the field passes through coherence conversion α, the entropy will move from the polarization DoF to the spatial DoF, thus the output is a polarized and spatially incoherent field. For the case in which the input is polarized and spatially incoherent, as the field passes through coherence conversion β, the entropy will move from the spatial DoF to the polarization DoF, thus the output is unpolarized and spatially coherent. A key feature of this conversion is that it is unitary—no energy is lost during the conversion as is observed in typical filtering procedures to establish coherence in an optical field. Thus, the conversion can continue indefinitely between the DoFs. Also, the total entropy of the field is invariant throughout the coherence conversion.
Figure 3. A reversible coherence converter consists of two coherence conversions (α and β) that transfer the entropy across the spatial and polarization DoFs such that the degree of coherence is converted between the DoFs.
Download figure:
Standard image High-resolution image3.2. Experimental process of optical coherence conversion
The case in figure 3 of the input to the converter being unpolarized and spatially coherent is shown in the experimental setup in figure 4. An example of an appropriate source would be an unpolarized HeNe laser. The first step is to isolate the beam in a single spatial mode using a small aperture on the µm-scale. Because the field encounters a small aperture, it will diffract in space necessitating the use of lenses to relay the beam—maintaining reasonable dimensions as the field encounters optics of finite size; generally on the scale of 25.4 cm. The field after the aperture at the input of coherence conversion α can then be described with the coherence matrix:
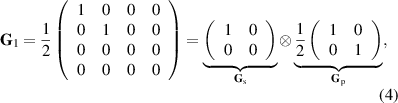
here the field exists as one point and has no correlations between H and V. As the field encounters the polarization beam splitter (PBS) in coherence conversion α, the random polarization is spatially split into two paths (a and b), each containing a now fully polarized eigenmode; H or V of the original unpolarized state. In doing so, the two DoFs become correlated (non-separable) and entropy is shared between the polarization and spatial DoF, such that 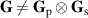 . With the addition of the half-wave plate (HWP) to rotate the polarization in one arm to be parallel to the polarization in the other arm, the entropy is fully transferred from the polarization DoF to the spatial DoF, and the field is separable once again. The field can be described with the coherence matrix:
. With the addition of the half-wave plate (HWP) to rotate the polarization in one arm to be parallel to the polarization in the other arm, the entropy is fully transferred from the polarization DoF to the spatial DoF, and the field is separable once again. The field can be described with the coherence matrix:
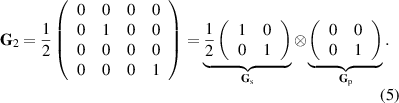
At this point, the field is linearly polarized and spatially incoherent (there is mutual incoherence between the two arms). In other words, the random phase relationship that exists between H and V prior to PBS is exhibited between a and b after the PBS; the respective elements of  and
and  have completely interchanged in this coherence conversion.
have completely interchanged in this coherence conversion.
Figure 4. The experimental setup of a reversible coherence converter. Coherence conversion α moves the entropy from the polarization DoF to the spatial DoF. Coherence conversion β moves the entropy from the spatial DoF to the polarization DoF. The inset shows OCmT components used to measure the G matrices.  : half-wave plate;
: half-wave plate; 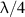 : quarter wave plate; PBS: polarizing beam splitter; BS: beam splitter; L: spherical lens; LP: linear polarizer; Cam: camera.
: quarter wave plate; PBS: polarizing beam splitter; BS: beam splitter; L: spherical lens; LP: linear polarizer; Cam: camera.
Download figure:
Standard image High-resolution imageAt the plane of G2 the field is linearly polarized and there exists mutual incoherence between a and b (equation (5)). Now the field is to pass through coherence converter β. Lenses L2 and L3 are used to relay the field from the plane of G2 to its conjugate plane: the plane of G3. The field first encounters the HWP and then the PBS. The HWP rotates the polarizations such that they are perpendicular to one another, but a constant phase difference still remains in the polarization DoF. When entering the PBS through orthogonal ports, the orthogonal polarizations overlap in a single spatial mode and the random phase relationship between a and b now exists between H and V, resulting in a spatially coherent and unpolarized field that can be represented by equation (4), here 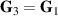 . To benchmark coherence in these contexts, we use OCmT.
. To benchmark coherence in these contexts, we use OCmT.
Here, we have presented an experimental example in which the input to the coherence converter is spatially coherent and unpolarized. There is also the case in which the input to the system is linearly polarized and spatially incoherent, such as a field represented by equation (5). An example of this would be a linearly polarized LED. If this is the starting field, a reversible coherence converter would be setup by first isolating two mutually spatially incoherent spatial modes from the LED, then passing the field through coherence conversion β, resulting in a spatially coherent and unpolarized field (G3). This should be followed by coherence conversion α to reconstitute the field's original properties.
In both examples, it is crucial that care is taken in the alignment of the paths' respective relay lenses, such that a and b are the same size. For sources of low temporal coherence length, it is vital that a delay line is implemented in one of the optical paths to minimize the path length difference; without it, any mutual temporal incoherence between the two paths may lead to confounding or misleading results.
3.3. Engineering immunity to phase-scrambling
Coherence converters have demonstrated unique protective effects against scrambling media. Generally, when coherent light encounters a phase-scrambling medium, its phase in one or more DoFs is randomized or becomes more disordered. To counteract this undesirable disorder, prior to the medium one can transfer the ordered phase in a coherent DoF that is to experience scrambling to an incoherent DoF that is not expected to be scrambled, via a coherence conversion. After the medium, a second coherence conversion can be implemented to transfer the ordered phase back into its original DoF. Thus, coherence conversion can protect specific DoFs from the deleterious effects of scrambling media.
Consider a depolarizing medium that is described by the Mueller matrix 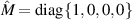 and converts any incoming state of polarization to one that is completely random. There are many practical cases in which maintaining a field's initial polarization is desired (e.g. in optical communications) [33–35]. For a field that is completely polarized and encountering this depolarizing medium, e.g. one that is represented by equation (5), its polarization DoF can be protected by a reversible coherence converter. To protect the polarization DoF from randomization, two mutually spatially incoherent points of the field should be isolated and passed through coherence conversion β which transfers the entropy from the spatial DoF to the polarization DoF. The coherence that existed in the polarization DoF is transferred to the spatial DoF. The field can then encounter the depolarizing medium without suffering any deleterious effects. Following the medium with coherence conversion α reconstitutes the field's original coherence properties. Okoro et al demonstrated a proof-of-concept experiment which aimed to protect the polarization DoF in such a case [23]. A linearly polarized and spatially incoherent field was passed through a coherence conversion (organized identical to coherence conversion β) to swap entropy between the DoFs, such that the output is unpolarized and spatially coherent. This was done prior to a depolarizing medium. It was shown that the field's coherence properties are invariant when passed through the depolarizer; this invariance is attributed to the transfer of entropy into the polarization DoF [23]. In this experiment, the reversibility of the coherence conversion was not demonstrated; however the reversibility was successfully demonstrated by Harling et al [24].
and converts any incoming state of polarization to one that is completely random. There are many practical cases in which maintaining a field's initial polarization is desired (e.g. in optical communications) [33–35]. For a field that is completely polarized and encountering this depolarizing medium, e.g. one that is represented by equation (5), its polarization DoF can be protected by a reversible coherence converter. To protect the polarization DoF from randomization, two mutually spatially incoherent points of the field should be isolated and passed through coherence conversion β which transfers the entropy from the spatial DoF to the polarization DoF. The coherence that existed in the polarization DoF is transferred to the spatial DoF. The field can then encounter the depolarizing medium without suffering any deleterious effects. Following the medium with coherence conversion α reconstitutes the field's original coherence properties. Okoro et al demonstrated a proof-of-concept experiment which aimed to protect the polarization DoF in such a case [23]. A linearly polarized and spatially incoherent field was passed through a coherence conversion (organized identical to coherence conversion β) to swap entropy between the DoFs, such that the output is unpolarized and spatially coherent. This was done prior to a depolarizing medium. It was shown that the field's coherence properties are invariant when passed through the depolarizer; this invariance is attributed to the transfer of entropy into the polarization DoF [23]. In this experiment, the reversibility of the coherence conversion was not demonstrated; however the reversibility was successfully demonstrated by Harling et al [24].
In this case, a spatially coherent and unpolarized field was set to encounter a spatially scrambling medium. Protecting a field's spatial properties from scrambling would be beneficial in image transmission, space division multiplexing applications, and other coherence coding schemes [36, 37]. This experiment more closely resembled the setup shown in figure 4. Firstly, the PBS in coherence conversion α was replaced with a regular beam splitter (BS), outputting two mutually spatially coherent points. These points were sent to a simulated spatially scrambling medium using a spatial light modulator (SLM) not shown in figure 4. The simulated medium was a hologram exhibiting the full dynamic phase range of the SLM from 0 to  over columns that extended vertically in the y-direction and were ten pixels wide in the x-direction. The random phase patterns changed randomly at 10 fps for 1 s. Following the SLM, a and b were overlapped to interfere, and images were acquired by a camera that collected multiple frames at 50 fps, resulting in stacks of 50 images. When the SLM was idle, the mutually coherent points demonstrated high visibility, but when the scrambling pattern was present, the visibility decreased by 35% suggesting a large reduction in spatial coherence. These results are shown in figures 5(a) and (b). To avoid this deleterious effect, a field that was spatially coherent and unpolarized, represented by equation (4), was passed through coherence conversion α to protect the spatial DoF by transferring the entropy from the polarization DoF to the spatial DoF. Following the SLM, the field was sent to the SLM and passed through coherence conversion β which reversed the entropy back to the polarization DoF, leaving the spatial DoF coherent; thus reconstituting the field's original coherence properties. Using a BS and mirrors not shown in figure 4, the field was separated and then the two points were overlapped to interfere. These results are shown in figures 5(c) and (d). The visibility remained high when the spatial scrambling medium was imparted to the SLM. Thus, similarly to the previous case of protecting polarization, the field's coherence properties were found to be invariant upon scrambling. We encourage readers to refer to [23, 24] for further experimental details.
over columns that extended vertically in the y-direction and were ten pixels wide in the x-direction. The random phase patterns changed randomly at 10 fps for 1 s. Following the SLM, a and b were overlapped to interfere, and images were acquired by a camera that collected multiple frames at 50 fps, resulting in stacks of 50 images. When the SLM was idle, the mutually coherent points demonstrated high visibility, but when the scrambling pattern was present, the visibility decreased by 35% suggesting a large reduction in spatial coherence. These results are shown in figures 5(a) and (b). To avoid this deleterious effect, a field that was spatially coherent and unpolarized, represented by equation (4), was passed through coherence conversion α to protect the spatial DoF by transferring the entropy from the polarization DoF to the spatial DoF. Following the SLM, the field was sent to the SLM and passed through coherence conversion β which reversed the entropy back to the polarization DoF, leaving the spatial DoF coherent; thus reconstituting the field's original coherence properties. Using a BS and mirrors not shown in figure 4, the field was separated and then the two points were overlapped to interfere. These results are shown in figures 5(c) and (d). The visibility remained high when the spatial scrambling medium was imparted to the SLM. Thus, similarly to the previous case of protecting polarization, the field's coherence properties were found to be invariant upon scrambling. We encourage readers to refer to [23, 24] for further experimental details.
Figure 5. (a) Interference pattern of two mutually coherent points overlapped. The points are generated by replacing the PBS of coherence conversion α with a BS when the SLM is idle; lower panel is its corresponding interferogram along x after integrating along y. (b) The sum of 50 interference patterns collected after the SLM while the SLM imparted the scrambling phase pattern on the two mutually coherent points; lower panel is its corresponding interferogram along x after integrating along y. (c) Interference pattern from spatially overlapping points using a BS and mirrors following the coherence converter shown in figure 4 in absence of the scrambling phase; bottom panel is the corresponding interferogram along x after integrating along y. (d) The sum of 50 frames collected while the SLM imparted the scrambling phase pattern to the field; lower panel is its corresponding interferogram along x after integrating along y.
Download figure:
Standard image High-resolution image4. Conclusion
Here, we have discussed the concept of coherence conversion, highlighting the capability of coherence converters to be used in engineering immunity to randomizing operations, and the method in which to benchmark coherence in this context. We showed that measuring the coherence of optical fields in which multiple DoFs are of interest has found a useful approach (OCmT) that borrows from the mathematical formalism of multipartite quantum mechanical states. Furthermore, OCmT is particularly useful in measuring the coherence of fields that are classically entangled, i.e. have non-separable DoFs. Coherence conversion relies on classical entanglement to temporarily correlate two DoFs so that entropy can be transferred between them. This transfer of entropy enables a new control of optical fields—protection against randomizing media (e.g. depolarizers)—that may eventually be a promising capability for optical communications. However, coherence conversion is currently at a basic research stage. Thus far, coherence conversion has only been demonstrated between polarization and the two-point spatial DoF which can be attributed to the convenient coupling operations of a PBS. More work is needed to find analogous devices that can convert coherence between other continuous DoFs. Furthermore, exciting opportunities of coherence conversion may manifest between DoFs that are carried by two different systems, e.g. swapping of entropy between photons and phonons. Current limitations and future potential add to the importance of tutorials like this one; supplying exposure for these concepts while brandishing an instructional approach will hopefully inspire future studies and the development of technologies in this area.
Acknowledgments
We acknowledge financial support from U.S. Office of Naval Research (N00014-20-1-2789).
Data availability statement
The data cannot be made publicly available upon publication because they are not available in a format that is sufficiently accessible or reusable by other researchers. The data that support the findings of this study are available upon reasonable request from the authors.






