Abstract
We investigate the evolution of vortex and quadrupole solitons in the parity-time (PT)-symmetric optical lattices with self-focusing saturable nonlinearity. It is found that the saturable parameter plays a significant role on the existence and stability of vortex solitons. There exists a threshold for saturable parameter, above which the single-charged vortex solitons can be stable. The strength of gain–loss component of the PT-symmetric potential can affect the existence and stability of vortex solitons dramatically. We find that the single-charged vortex solitons can exist even at the phase transition point of the PT-symmetric potential, but diffuse fast during propagation. In addition, it is also found that the direction of the angular momentum has little effect on the properties of vortex solitons. Dramatically, the stable regions of out-of-phase quadrupole solitons are broader than that of the single-charged vortex solitons, while the stable regions of in-phase quadrupole solitons are narrower than that of the single-charged vortex solitons.
Export citation and abstract BibTeX RIS
1. Introduction
Vortex solitons which are associated with the phase singularities in the center and carrying the angular momentum have been demonstrated to be stabilized in homogeneous media, such as nonlocal nonlinear media [1] and cubic-quintic competing nonlinear media [2]. But they will generally break into several fundamental solitons due to the azimuthal instability. With the introduction of the periodic optical lattice, the stability of lattice vortex solitons enhances. In particular, it has been theoretically shown that both on-site (vortices with their phase singularities located on a site) and off-site (vortices with their phase singularities located between sites) vortex solitons can be stable in an optical lattice based on Kerr nonlinearity within certain range of parameters [3, 4]. Following the theoretical study, these lattice vortex solitons are quickly observed by experiments in photorefractive crystals [5, 6]. Besides, both on-site and off-site solitons have also been demonstrated to propagate stably in some regions in a photorefractive crystal [7]. One of the most important characters of vortex soliton is the topological charge, which affects the spiral structures of soliton phase, and its value determines the number of the branch of the spiral phase structures.
In 1998, Bender and Boettcher showed that certain non-Hermitian Hamiltonian can have entirely real spectra if the parity-time (PT)-symmetry is satisfied [8]. In the context of PT-symmetry, it requires that the complex potential satisfies  [8]. This indicates that the real part of a complex potential must be an even function while the imaginary part should be an odd one. In recent years, the notion of PT-symmetry was introduced into optics due to the judicious designs which involve both optical gain–loss regions and process of index guiding [9, 10]. Since then, light propagating in PT-symmetric potentials have been attracted extensive investigations. It has been revealed that some unusual features of solitons, such as double refraction, energy oscillations, and secondary emissions, will exhibit during evolution [11]. With the PT-symmetry, the existence, stability, and propagation dynamics of various types of solitons, such as fundamental [12], multi-peak [13, 14], Bragg [15], gap [16], and temporal solitons [17], have been widely investigated. In addition, the evolution of defect solitons in both one- [18–20] and two- [21] dimensional optical lattices have been analyzed. Recently, we investigated the propagation dynamics of vortex solitons in the PT-symmetric optical lattices based on the self-defocusing Kerr nonlinearity [22]. In addition, the on-site discrete vortex solitons also have been reported [23]. Very recently, a comprehensive review about various types of PT-symmetric solitons has been made [24–26].
[8]. This indicates that the real part of a complex potential must be an even function while the imaginary part should be an odd one. In recent years, the notion of PT-symmetry was introduced into optics due to the judicious designs which involve both optical gain–loss regions and process of index guiding [9, 10]. Since then, light propagating in PT-symmetric potentials have been attracted extensive investigations. It has been revealed that some unusual features of solitons, such as double refraction, energy oscillations, and secondary emissions, will exhibit during evolution [11]. With the PT-symmetry, the existence, stability, and propagation dynamics of various types of solitons, such as fundamental [12], multi-peak [13, 14], Bragg [15], gap [16], and temporal solitons [17], have been widely investigated. In addition, the evolution of defect solitons in both one- [18–20] and two- [21] dimensional optical lattices have been analyzed. Recently, we investigated the propagation dynamics of vortex solitons in the PT-symmetric optical lattices based on the self-defocusing Kerr nonlinearity [22]. In addition, the on-site discrete vortex solitons also have been reported [23]. Very recently, a comprehensive review about various types of PT-symmetric solitons has been made [24–26].
The work mentioned above focused mainly on the solitons in the PT-symmetric potentials with Kerr nonlinearity. It has been reported that the defect [27, 28] and gap [29] solitons can propagate stably based on the saturable nonlinearity and the saturable parameter has a great effect on the properties of solitons. However, dynamics of vortex solitons in the PT-symmetric lattices with the saturable nonlinearity have not been investigated. It is still an open question on how saturable parameter affects the properties of vortex solitons.
In this paper, we investigate the evolution of vortex and quadrupole solitons in the PT-symmetric optical lattices with saturable nonlinearity. The influence of the saturable parameter on the existence, stability, and propagation dynamics of single-charged vortex solitons, of which the topological charge is ±1, are detailedly analyzed. Moreover, the effect of the strength of gain–loss component of PT-symmetric potential on vortex solitons is discussed. Finally, the evolutions of out-of-phase and in-phase quadrupole solitons are also investigated.
2. Theoretical model
The light propagation along the z axis in the Kerr-type saturable nonlinear medium with transverse refractive index modulation can be described by the following nonlinear Schrödinger equation with a normalized complex field U [30]:
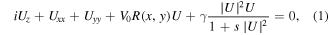
where transverse x, y and longitudinal z coordinates are scaled to the width and the diffraction length of the input beam, respectively. The parameter V0 describes the lattice depth. γ = ±1 represents the nonlinearity is self-focusing or defocusing. In this paper, we set γ = 1 (self-focusing nonlinearity). The saturable parameter s, which is related to the maximum value of the light-induced refractive index change, is a positive constant [31].
The equation (1) holds in the condition that the crystal is based on a strong electric field, and the intensities of soliton and lattice-creating beams are small compared with the background illumination level [32]. In addition, the equation (1) holds also for the case that the refractive index modulation is imprinted in nonlinear medium. In particular, discrete solitons in waveguide arrays imprinted in saturable LiNbO3 crystal have been observed [33]. R(x, y) is the PT-symmetric optical lattice, which can be described as follows:
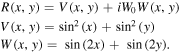
Here W0 is the strength of gain–loss component of the PT-symmetric lattice potential. According to [8], there exists a threshold for W0. Below this threshold, all eigenvalues of the PT-symmetric are real. On the contrary, some complex eigenvalues appear above this threshold and hence the intensity of a beam cannot propagate stably [9, 10]. It has been demonstrated that the threshold of W0 for our PT-symmetric complex potential is 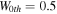 [34].
[34].
In this paper, we set potential parameter V0 = 7, W0 = 0.1 and alter the values of saturable parameter s to investigate the properties of single-charged vortex solitons.
We search for the stationary solutions of equation (1) in the form of  where μ is the propagation constant,
where μ is the propagation constant,  is a complex-valued and localized function. In such case,
is a complex-valued and localized function. In such case, 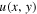 satisfies the following equation:
satisfies the following equation:
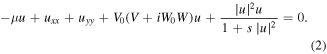
These single-charged vortex solitons can be resolved by the modified squared-operator iteration method [35]. In this method, the 'squared-operator' evolution equation, in which the positive-definite and Hermitian operator is used to accelerate the convergence, should be numerically integrated. The power of a lattice vortex soliton is defined as  [9].
[9].
In order to investigate the linear stability of these single-charged vortex solitons, we add the perturbations  and
and 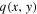 into the solution, which is written as:
into the solution, which is written as:
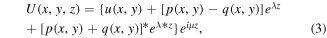
where 
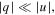 λ is the perturbation growth rate. Substituting equation (3) into (1) and linearizing, we can get the following coupled equations:
λ is the perturbation growth rate. Substituting equation (3) into (1) and linearizing, we can get the following coupled equations:
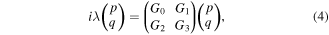
where
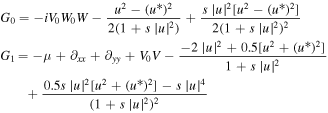
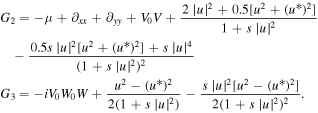
Solving the above equation (4) by the Fourier collocation method [35], we can obtain the complex-valued λ. If 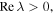 the solitons are linearly unstable; otherwise they are linearly stable.
the solitons are linearly unstable; otherwise they are linearly stable.
3. Numerical results
3.1. Single-charged vortex solitons
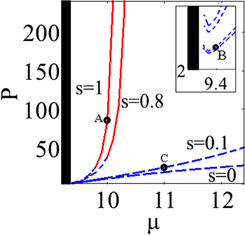
Firstly, we investigate the properties of single-charged vortex soliton having the direction of its angular momentum counterclockwise. Two methods are utilized to investigate the stability of solitons in our work. One is the split-step method to directly simulate the propagation of solitons [35]. If the solitons can maintain their profiles or powers during the propagation, they are stable. The other one is the analysis of the linear stability. If the real part of the eigenvalue of the perturbation equation (4) is zero, the corresponding soliton is linearly stable. These two criterions are used together to judge the stability of solitons. We set saturable parameters  and the corresponding power diagrams versus the propagation constant μ are displayed in figure 1. It is found that the single-charged vortex solitons can exist in the semi-infinite gap. For
and the corresponding power diagrams versus the propagation constant μ are displayed in figure 1. It is found that the single-charged vortex solitons can exist in the semi-infinite gap. For  the single-charged vortex solitons are unstable in their whole existence regions. However, for
the single-charged vortex solitons are unstable in their whole existence regions. However, for 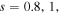 the single-charged vortex solitons are stable in the high power regions while they are unstable in the lower power regions. This is completely different from the properties of single-charged vortex solitons in the PT-symmetric optical lattices with self-defocusing cubic nonlinearity, in which the single-charged vortex solitons are stable in some lower power regions [22]. In addition, the single-charged vortex solitons in the two-dimensional superlattice with self-focusing cubic nonlinearity have also been reported. It is shown that they are unstable in their whole existence regions [36]. On the other hand, we also investigate the stability of vortex solitons in self-focusing cubic nonlinear medium (
the single-charged vortex solitons are stable in the high power regions while they are unstable in the lower power regions. This is completely different from the properties of single-charged vortex solitons in the PT-symmetric optical lattices with self-defocusing cubic nonlinearity, in which the single-charged vortex solitons are stable in some lower power regions [22]. In addition, the single-charged vortex solitons in the two-dimensional superlattice with self-focusing cubic nonlinearity have also been reported. It is shown that they are unstable in their whole existence regions [36]. On the other hand, we also investigate the stability of vortex solitons in self-focusing cubic nonlinear medium (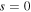 ) and find that they are unstable in their whole existence regions. However, our study shows that the vortex solitons can be stable in the higher power regions with the saturable nonlinearity if the saturable parameter is larger enough. That is to say, saturable nonlinearity is helpful to stabilize the propagation of vortex solitons in self-focusing media with PT-symmetric potential. It is found that the single-charged vortex solitons can be stable only if the saturable parameter is above a threshold
) and find that they are unstable in their whole existence regions. However, our study shows that the vortex solitons can be stable in the higher power regions with the saturable nonlinearity if the saturable parameter is larger enough. That is to say, saturable nonlinearity is helpful to stabilize the propagation of vortex solitons in self-focusing media with PT-symmetric potential. It is found that the single-charged vortex solitons can be stable only if the saturable parameter is above a threshold 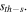 Here,
Here, 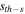 is a threshold of saturable parameter above which the single-charged vortex solitons can propagate stably within some range of propagation constant as other parameters fixed. Also, it has been found that this threshold is
is a threshold of saturable parameter above which the single-charged vortex solitons can propagate stably within some range of propagation constant as other parameters fixed. Also, it has been found that this threshold is  for
for 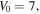
 and it will be discussed in detail hereafter. Besides, the larger saturable parameter leads to the larger power of single-charged vortex solitons for a fixed propagation constant. One prominent feature is that the power of the single-charged vortex solitons increases fast with the increase of propagation constant μ, and with the larger saturable parameter, the power curves of single-charged vortex solitons become steeper. It is due to the fact that the large saturable parameter weakens the focusing nonlinearity. Then it needs larger power to compensate this nonlinearity and to balance the diffraction induced by the complex potential.
and it will be discussed in detail hereafter. Besides, the larger saturable parameter leads to the larger power of single-charged vortex solitons for a fixed propagation constant. One prominent feature is that the power of the single-charged vortex solitons increases fast with the increase of propagation constant μ, and with the larger saturable parameter, the power curves of single-charged vortex solitons become steeper. It is due to the fact that the large saturable parameter weakens the focusing nonlinearity. Then it needs larger power to compensate this nonlinearity and to balance the diffraction induced by the complex potential.
Figure 1. The power curves of single-charged vortex solitons versus the propagation constant. The black shaded region is the first Bloch band. The blue dash lines indicate the solitons are unstable, and the red solid lines indicate the solitons are stable. The inset shows the power curves near the first Bloch band.
Download figure:
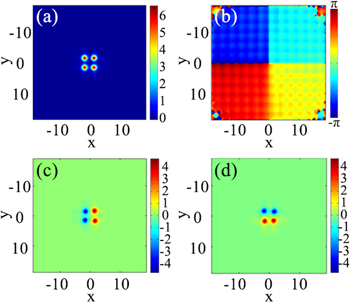
Standard image High-resolution imageThe intensity profiles of single-charged vortex solitons are shown in figure 2, and the parameters are chosen as 
 The intensity profile
The intensity profile  of single-charged vortex soliton is shown in figure 2(a). Figure 2(b) is the corresponding phase profile of the single-charged vortex solitons, and the real and imaginary parts of the single-charged vortex solitons are displayed in figures 2(c) and (d), respectively.
of single-charged vortex soliton is shown in figure 2(a). Figure 2(b) is the corresponding phase profile of the single-charged vortex solitons, and the real and imaginary parts of the single-charged vortex solitons are displayed in figures 2(c) and (d), respectively.
Figure 2. The field profiles of single-charged vortex solitons for 
 (a) The intensity profile
(a) The intensity profile  (b) the phase of the single-charged vortex soliton, (c) and (d) are the corresponding real and imaginary parts, respectively.
(b) the phase of the single-charged vortex soliton, (c) and (d) are the corresponding real and imaginary parts, respectively.
Download figure:
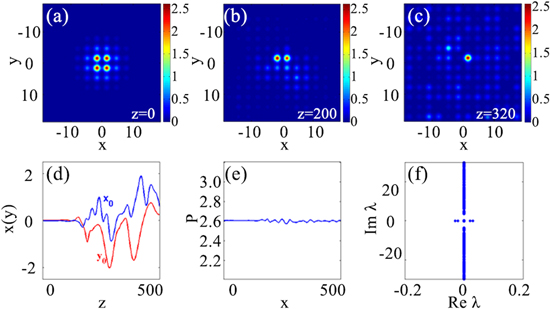
Standard image High-resolution imageIn order to investigate the longitudinal evolution of these single-charged vortex solitons, we add a random noise (5% of the soliton amplitude) to the soliton to simulate the propagation of the solitons. We first investigate the smaller saturable parameter 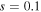 and take
and take 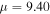 as solitons in the lower power region, in which the solitons are unstable. The evolution is displayed in figure 3. It is found that its linear stability spectrum (figure 3(f)) contains two couples of unstable eigenvalues. It indicates the soliton is linearly unstable. From figures 3(a)–(c), we learn that this single-charged vortex soliton is unstable and its four peaks will reduce to one peak during propagation. However, the power of the soliton has little change. It indicates the energy of the four peaks of soliton shift to one peak instead of dissipation. In addition, we also investigate the evolution of the center of the soliton during the propagation, where the center of the solitons is defined as
as solitons in the lower power region, in which the solitons are unstable. The evolution is displayed in figure 3. It is found that its linear stability spectrum (figure 3(f)) contains two couples of unstable eigenvalues. It indicates the soliton is linearly unstable. From figures 3(a)–(c), we learn that this single-charged vortex soliton is unstable and its four peaks will reduce to one peak during propagation. However, the power of the soliton has little change. It indicates the energy of the four peaks of soliton shift to one peak instead of dissipation. In addition, we also investigate the evolution of the center of the soliton during the propagation, where the center of the solitons is defined as 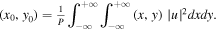 It is shown in figure 3(e) and it is found that the center of the soliton first has little change and then oscillates irregularly.
It is shown in figure 3(e) and it is found that the center of the soliton first has little change and then oscillates irregularly.
Figure 3. The evolution of single-charged vortex solitons for 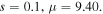 (a)–(c) The intensity profiles of soliton propagating to
(a)–(c) The intensity profiles of soliton propagating to 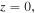
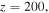 and
and  respectively. (d) The center of the soliton versus the propagation distance, and the blue and red lines represent the component of
respectively. (d) The center of the soliton versus the propagation distance, and the blue and red lines represent the component of  and
and 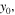 respectively. (e) The power of the soliton along the propagation distance, and (f) is the corresponding linear stability spectrum.
respectively. (e) The power of the soliton along the propagation distance, and (f) is the corresponding linear stability spectrum.
Download figure:
Standard image High-resolution imageIn the higher power regime of smaller saturable parameter 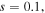 we take
we take  as an example. The evolution of the soliton is displayed in figure 4. Its linear stability spectrum contains a couple of real eigenvalues and the soliton is unstable. It is found that it will present some different properties, such as the profile of the soliton maintain its four peaks except some peaks weakened, during the evolution. Furthermore, the power of the soliton oscillates irregularly. The
as an example. The evolution of the soliton is displayed in figure 4. Its linear stability spectrum contains a couple of real eigenvalues and the soliton is unstable. It is found that it will present some different properties, such as the profile of the soliton maintain its four peaks except some peaks weakened, during the evolution. Furthermore, the power of the soliton oscillates irregularly. The 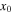 component of the center oscillates irregularly while the
component of the center oscillates irregularly while the 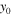 component of the center has little change except having a little oscillation during first propagation distance.
component of the center has little change except having a little oscillation during first propagation distance.
Figure 4. The evolution of single-charged vortex solitons for  (a)–(c) The intensity profiles of soliton propagates to
(a)–(c) The intensity profiles of soliton propagates to 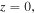
 and
and 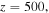 respectively. (d) The center of the soliton along with the propagation distance, the blue and red lines represent the component of
respectively. (d) The center of the soliton along with the propagation distance, the blue and red lines represent the component of  and
and 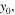 respectively. (e) The power of the soliton versus the propagation distance. (f) The corresponding linear stability spectrum.
respectively. (e) The power of the soliton versus the propagation distance. (f) The corresponding linear stability spectrum.
Download figure:
Standard image High-resolution imageNext, we set 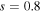 and
and 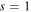 to investigate the influence of the saturable parameter on the properties of single-charged vortex solitons. It is found that the single-charged vortex solitons can stably exist in the higher power region with the larger saturable parameter. It indicates that the saturable parameter can suppress the instability of the vortex solitons to some extent. However, the existence region of the soliton shrinks by increasing of the saturable parameter. We take
to investigate the influence of the saturable parameter on the properties of single-charged vortex solitons. It is found that the single-charged vortex solitons can stably exist in the higher power region with the larger saturable parameter. It indicates that the saturable parameter can suppress the instability of the vortex solitons to some extent. However, the existence region of the soliton shrinks by increasing of the saturable parameter. We take 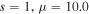 as an example to understand the evolution of the stable single-charged vortex solitons. The evolution of the soliton is displayed in figure 5. It is found that its linear stability spectrum contains no unstable eigenvalues and the soliton is stable. When it propagates to
as an example to understand the evolution of the stable single-charged vortex solitons. The evolution of the soliton is displayed in figure 5. It is found that its linear stability spectrum contains no unstable eigenvalues and the soliton is stable. When it propagates to 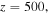 it maintains its original shape; see figures 5(a) and (b). Besides, the power and the center of the soliton have little change along with the propagation distance.
it maintains its original shape; see figures 5(a) and (b). Besides, the power and the center of the soliton have little change along with the propagation distance.
Figure 5. The evolution of single-charged vortex solitons for 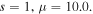 (a), (b)The intensity profiles of soliton propagating to
(a), (b)The intensity profiles of soliton propagating to  and
and  respectively. (c) The power of the soliton versus the propagation distance. (d), (e) The component of
respectively. (c) The power of the soliton versus the propagation distance. (d), (e) The component of  and
and 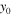 of the center of the soliton along with the propagation distance, respectively. (f) The corresponding linear stability spectrum.
of the center of the soliton along with the propagation distance, respectively. (f) The corresponding linear stability spectrum.
Download figure:
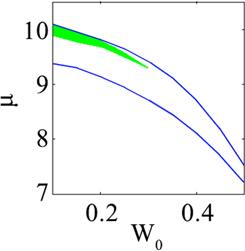
Standard image High-resolution imageIn order to understand the effect of the saturable parameter on the existence and stability of single-charged vortex solitons extensively, we plot the existence and stable regions of the single-charged vortex solitons versus the saturable parameter. It is shown in figure 6. It is found that the existence region of the single-charged vortex solitons shrinks with the increase of the saturable parameter, and there exists a threshold of saturable parameter, above which the single-charged vortex solitons will not exist. It can be explained as that the term 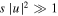 with the lager saturable parameter leads the nonlinear term approximated as
with the lager saturable parameter leads the nonlinear term approximated as  which is linear. In addition, it has been found that the existence threshold of saturable parameter is
which is linear. In addition, it has been found that the existence threshold of saturable parameter is 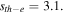 Furthermore, it is seen that the stable single-charged vortex solitons can be found only when the saturable parameter is above a threshold
Furthermore, it is seen that the stable single-charged vortex solitons can be found only when the saturable parameter is above a threshold  and it has been shown that this threshold is
and it has been shown that this threshold is  with potential parameter
with potential parameter 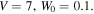 In addition, the relation between lattice depth and the threshold of saturable parameter
In addition, the relation between lattice depth and the threshold of saturable parameter  is investigated. We take
is investigated. We take 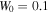 and
and 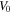 changes from
changes from 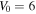 to
to 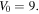 The dependence of
The dependence of 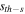 on lattice depth is shown figure 7. It is found that the threshold of saturable parameter
on lattice depth is shown figure 7. It is found that the threshold of saturable parameter  decreases with the increase of lattice depth. It is due to the fact that deeper lattice depth is helpful to stabilize solitons.
decreases with the increase of lattice depth. It is due to the fact that deeper lattice depth is helpful to stabilize solitons.
Figure 6. The existence and stable regions of single-charged vortex solitons versus the saturable parameter. The region between the blue curves is the existence region and the green shaded region is the stable region.
Download figure:
Standard image High-resolution imageFigure 7. The dependence of the threshold of saturable parameter  on lattice depth with
on lattice depth with 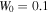 and
and 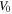 changing from 6 to 9.
changing from 6 to 9.
Download figure:
Standard image High-resolution imageThe stable region of the single-charged vortex solitons first expands then shrinks with the increase of the saturable parameter. This indicates the moderate saturable parameter can suppress the instability of the single-charged vortex solitons. Here, the first expanding of the stable region of vortex solitons is due to the fact that the saturable nonlinearity approximates to cubic-quintic nonlinearity [ ] in our model when
] in our model when 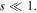 However, in the condition of
However, in the condition of  the defocusing quintic nonlinearity is so tiny that it can be neglected. The nonlinear term in our model can be seen as self-focusing cubic nonlinearity. In self-focusing Kerr nonlinear medium, it has been shown that the single-charged vortex solitons are unstable in their whole existence regions in the two-dimensional superlattice [36]. In our investigation, the stability of vortex solitons in self-focusing cubic nonlinear medium (
the defocusing quintic nonlinearity is so tiny that it can be neglected. The nonlinear term in our model can be seen as self-focusing cubic nonlinearity. In self-focusing Kerr nonlinear medium, it has been shown that the single-charged vortex solitons are unstable in their whole existence regions in the two-dimensional superlattice [36]. In our investigation, the stability of vortex solitons in self-focusing cubic nonlinear medium ( ) is also discussed. It is found that the vortex solitons are unstable in its whole existence regions. This further indicates the idea that vortex solitons are unstable when
) is also discussed. It is found that the vortex solitons are unstable in its whole existence regions. This further indicates the idea that vortex solitons are unstable when 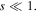 With the increase of saturable parameter S, the nonlinear term tends to approximate to cubic-quintic or saturable nonlinearity and the vortex solitons can stably exist within some range of parameters, and the stable regions of vortex solitons first expand with the increase of saturable. However, the nonlinear term approximates to linear term as saturable parameter s being large enough. The existence regions of vortex solitons shrink. On the other hand, the stable regions of vortex solitons also shrink as the nonlinear term weakens and cannot compensate the diffraction of beams for
With the increase of saturable parameter S, the nonlinear term tends to approximate to cubic-quintic or saturable nonlinearity and the vortex solitons can stably exist within some range of parameters, and the stable regions of vortex solitons first expand with the increase of saturable. However, the nonlinear term approximates to linear term as saturable parameter s being large enough. The existence regions of vortex solitons shrink. On the other hand, the stable regions of vortex solitons also shrink as the nonlinear term weakens and cannot compensate the diffraction of beams for 
In addition, the influence of the strength of gain–loss component of PT-symmetric potential on single-charged vortex solitons is investigated. We take saturable parameter as  and the existence and stable regions of vortex solitons versus the strength of gain–loss component of PT-symmetric potential are displayed in figure 8. It is shown that both the existence and stable regions of vortex solitons shrink with the increase of gain–loss component of PT-symmetric potential. Moreover, at the phase transition point of PT-symmetric potential
and the existence and stable regions of vortex solitons versus the strength of gain–loss component of PT-symmetric potential are displayed in figure 8. It is shown that both the existence and stable regions of vortex solitons shrink with the increase of gain–loss component of PT-symmetric potential. Moreover, at the phase transition point of PT-symmetric potential 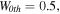 the vortex soliton can also exist and its intensity, real, imaginary and phase profiles are displayed in figure 9. From figure 9, we see that when vortex soliton propagates to
the vortex soliton can also exist and its intensity, real, imaginary and phase profiles are displayed in figure 9. From figure 9, we see that when vortex soliton propagates to 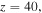 its shape changes and it diffuses fast. In addition, its power increases fast during propagation, and its center oscillates seriously during propagation. Its corresponding linear-stability spectrum is shown in figure 9(i). It is found that it contains many unstable eigenvalues.
its shape changes and it diffuses fast. In addition, its power increases fast during propagation, and its center oscillates seriously during propagation. Its corresponding linear-stability spectrum is shown in figure 9(i). It is found that it contains many unstable eigenvalues.
Figure 8. At saturable parameter 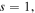 the existence and stable regions of vortex soliton versus the strength of gain–loss component of PT-symmetric potential.
the existence and stable regions of vortex soliton versus the strength of gain–loss component of PT-symmetric potential. 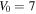 and
and 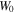 changes from 0.1 to 0.5. The region between two blue lines is the existence region of vortex soliton. The green shaded region is the stable region.
changes from 0.1 to 0.5. The region between two blue lines is the existence region of vortex soliton. The green shaded region is the stable region.
Download figure:
Standard image High-resolution imageFigure 9. The vortex soliton with parameters 
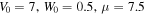 , (a) intensity profile, (b) real part, (c) imaginary part, (d) phase. The intensity profile of soliton propagates to (e)
, (a) intensity profile, (b) real part, (c) imaginary part, (d) phase. The intensity profile of soliton propagates to (e)  and (f)
and (f) 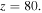 (g) The power of soliton versus propagation distance, (h) is the center of soliton versus propagation distance, and (i) the linear stability spectrum.
(g) The power of soliton versus propagation distance, (h) is the center of soliton versus propagation distance, and (i) the linear stability spectrum.
Download figure:
Standard image High-resolution imageFurthermore, the evolution of single-charged vortex soliton having the direction of its angular momentum clockwise is also investigated. The field profiles of single-charged vortex solitons are shown in figure 10 and the parameters are chosen as 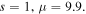 The intensity profile
The intensity profile 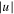 of single-charged vortex soliton is shown in figure 10(a). Figure 10(b) is the corresponding phase profile of the single-charged vortex solitons, and the real and imaginary parts of the single-charged vortex solitons are displayed in figures 10(c) and (d), respectively. Since the vortex solitons having the direction of its angular momentum clockwise have the same properties with the vortex soliton having the direction of its angular momentum counterclockwise, we will not discussed it in detail.
of single-charged vortex soliton is shown in figure 10(a). Figure 10(b) is the corresponding phase profile of the single-charged vortex solitons, and the real and imaginary parts of the single-charged vortex solitons are displayed in figures 10(c) and (d), respectively. Since the vortex solitons having the direction of its angular momentum clockwise have the same properties with the vortex soliton having the direction of its angular momentum counterclockwise, we will not discussed it in detail.
Figure 10. The field profiles of single-charged vortex solitons for  (a) The intensity profile
(a) The intensity profile  (b) the phase of the single-charged vortex soliton, (c) and (d) are the corresponding real and imaginary parts, respectively.
(b) the phase of the single-charged vortex soliton, (c) and (d) are the corresponding real and imaginary parts, respectively.
Download figure:
Standard image High-resolution image3.2. The out-of-phase and in-phase quadrupole solitons
Finally, we investigate the evolution of out-of-phase and in-phase quadrupole solitons. We take the saturable parameter as 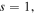 and the power of the in-phase quadrupole, single-charged and out-of-phase quadrupole solitons versus the propagation constant are displayed in figure 11. It is found that these two types of solitons also exist in the semi-infinite gap. Dramatically, the out-of-phase quadrupole soliton can be stable in its whole existence region while the in-phase quadrupole soliton only can be stable in a very small region near the first Bloch band. Moreover, the out-of-phase quadrupole solitons have the largest power with the same propagation constant, while the in-phase quadrupole solitons have the smallest power for a fixed propagation constant.
and the power of the in-phase quadrupole, single-charged and out-of-phase quadrupole solitons versus the propagation constant are displayed in figure 11. It is found that these two types of solitons also exist in the semi-infinite gap. Dramatically, the out-of-phase quadrupole soliton can be stable in its whole existence region while the in-phase quadrupole soliton only can be stable in a very small region near the first Bloch band. Moreover, the out-of-phase quadrupole solitons have the largest power with the same propagation constant, while the in-phase quadrupole solitons have the smallest power for a fixed propagation constant.
Figure 11. The power of in-phase quadrupole (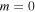 ), single-charged vortex (
), single-charged vortex (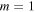 ), and out-of-phase quadrupole (out-of-phase) solitons depend on the propagation constant. The saturable parameter is
), and out-of-phase quadrupole (out-of-phase) solitons depend on the propagation constant. The saturable parameter is 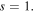 The stable and unstable regions are indicated by red solid lines and blue dash lines, respectively. The shaded region is the first Bloch band. The insert shows the power curves near the first Bloch band.
The stable and unstable regions are indicated by red solid lines and blue dash lines, respectively. The shaded region is the first Bloch band. The insert shows the power curves near the first Bloch band.
Download figure:
Standard image High-resolution imageThe longitudinal evolution of in-phase quadrupole and out-of-phase quadrupole solitons is investigated by adding a random noise (5% of the soliton amplitude) to the soliton to simulate the propagation. For out-of-phase quadrupole solitons, we take the propagation constant 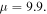 The intensity profile and the evolution of the out-of-phase quadrupole soliton are displayed in figure 12. It is clearly seen that the intensity profile of out-of-phase quadrupole soliton contains four peaks and these four peaks have the adjacent peaks out-of-phase while the diagonal peaks in-phase. The linear-stability spectrum of the soliton contains no unstable eigenvalues and so it is linearly stable. On the other hand, the soliton will maintain its original shape when it propagates to
The intensity profile and the evolution of the out-of-phase quadrupole soliton are displayed in figure 12. It is clearly seen that the intensity profile of out-of-phase quadrupole soliton contains four peaks and these four peaks have the adjacent peaks out-of-phase while the diagonal peaks in-phase. The linear-stability spectrum of the soliton contains no unstable eigenvalues and so it is linearly stable. On the other hand, the soliton will maintain its original shape when it propagates to  In addition, the power and the center of the soliton have little change along with the propagation distance.
In addition, the power and the center of the soliton have little change along with the propagation distance.
Figure 12. The evolution of out-of-phase quadrupole solitons at 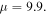 (a) The intensity profile of soliton at
(a) The intensity profile of soliton at 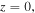 (b) real part, (c) imaginary part, (d) phase, (e) the intensity profile of soliton at
(b) real part, (c) imaginary part, (d) phase, (e) the intensity profile of soliton at  (f) the power of the soliton versus the propagation distance, (g) and (h) the
(f) the power of the soliton versus the propagation distance, (g) and (h) the 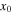 - and
- and 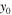 -component of the center of the soliton versus the propagation distance, and (i) the corresponding linear stability spectrum.
-component of the center of the soliton versus the propagation distance, and (i) the corresponding linear stability spectrum.
Download figure:
Standard image High-resolution imageThe intensity profile and the evolution of the in-phase quadrupole soliton are displayed in figure 13. This in-phase quadrupole soliton is formed by ring-shaped beam without the angular momentum and it has four peaks which are in-phase. We take the propagation constant 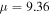 and
and 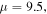 at which the solitons are stable and unstable respectively. It can be seen from figure 13 that at
at which the solitons are stable and unstable respectively. It can be seen from figure 13 that at  (the bottom two rows of figure 13), the linear-stability spectrum of the soliton contains no unstable eigenvalues, and the soliton will maintain its original shape during propagation. The power and the center of the soliton have little change along with the propagation distance. At
(the bottom two rows of figure 13), the linear-stability spectrum of the soliton contains no unstable eigenvalues, and the soliton will maintain its original shape during propagation. The power and the center of the soliton have little change along with the propagation distance. At  (the upper two rows of figure 13), the in-phase quadrupole soliton is unstable. Its linear-stability spectrum contains two couples of unstable eigenvalues and it changes from four peaks into one peak. Interestingly, its power has little change along with the propagation distance, while its center oscillates irregularly during the propagation.
(the upper two rows of figure 13), the in-phase quadrupole soliton is unstable. Its linear-stability spectrum contains two couples of unstable eigenvalues and it changes from four peaks into one peak. Interestingly, its power has little change along with the propagation distance, while its center oscillates irregularly during the propagation.
Figure 13. The evolution of in-phase quadrupole solitons, the upper two rows correspond to  and the bottom two rows correspond to
and the bottom two rows correspond to 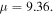 (a) Real part, (b) imaginary part, (c) the intensity profile of soliton at
(a) Real part, (b) imaginary part, (c) the intensity profile of soliton at 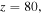 (d) and (e) the evolution of the power and center of soliton along with the propagation distance, respectively. (f) The corresponding linear-stability spectrum. (g), (h) The intensity profiles of soliton at
(d) and (e) the evolution of the power and center of soliton along with the propagation distance, respectively. (f) The corresponding linear-stability spectrum. (g), (h) The intensity profiles of soliton at  and
and 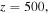 respectively. (i) The power of soliton versus the propagation distance, (j) and (k) the
respectively. (i) The power of soliton versus the propagation distance, (j) and (k) the 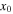 - and
- and 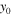 -component of center of the soliton versus the propagation distance. (l) The corresponding linear stability spectrum.
-component of center of the soliton versus the propagation distance. (l) The corresponding linear stability spectrum.
Download figure:
Standard image High-resolution image4. Conclusions
In this paper, we investigate the vortex and quadrupole solitons in the PT-symmetric optical lattices with self-focusing saturable nonlinearity in detail. It is shown that the single-charged vortex solitons can be stable unless the saturable parameter higher than a threshold. Moreover, the single-charged vortex solitons will not exist if the saturable parameter is too large. The existence region of single-charged vortex solitons shrinks with the increase of saturable parameter while the stable region of single-charged vortex solitons first expands and then shrinks with the increase of saturable parameter. In addition, the influence of the strength of gain–loss component on vortex solitons is also discussed. We also find that the single-charged vortex soliton can also exist at phase transition point of PT-symmetric potential, but it diffuses fast during propagation. It is shown that the direction of the angular momentum of vortex solitons has little effect on the properties of solitons. Dramatically, the stable regions of out-of-phase quadrupole solitons are broadest, while the stable regions of in-phase quadrupole solitons are narrowest.
Acknowledgments
This work was supported by Science and Technologies Projects of Guangdong Province (Nos. 2017B010112003, 2017A050506013), and by Applied technologies R&D Projects of Guangdong Province (Nos. 2015B010127013, 2016B010123004), and by Science and Technologies Projects of Guangzhou City (Nos. 201504291502518, 201604046021, 201704030139), and by Science and Technology Development Special Fund Projects of Zhongshan City (Nos. 2017F2FC0002, 2017A1009), and in part by Union Fund of Guizhou Science and Technology Department & Guizhou Mizu University (No. 20157221).