Abstract
Natural classes of integrability-preserving reductions of a 4+4-dimensional generalisation (TED equation) of the general heavenly equation are recorded. In particular, these reductions lead to integrable 'deformations' of various other avatars of the heavenly equation governing self-dual Einstein spaces. The known deformed heavenly equations which give rise to half-flat conformal structures are retrieved in this manner. Moreover, Plebański's link between the first and second heavenly equations is extended to their deformed counterparts.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
 spaces (heavens) [1], that is, self-dual solutions of the (complex) Einstein vacuum equations (for vanishing cosmological constant) have attracted a considerable amount of attention since it was established by Plebański [2] that these self-dual Einstein spaces are governed by a single partial differential equation of second order. This equation adopts a variety of avatars, including Plebański's original first and second heavenly equations (see, e.g. [3] and references therein). In [4, 5], a novel form of this equation was derived in connection with a superposition principle associated with the integrable (discrete) Tzitzéica equation [6]. This integrable equation, now known as the general heavenly equation [3], turns out to be privileged in that it constitutes the generic form of an eigenfunction equation for
spaces (heavens) [1], that is, self-dual solutions of the (complex) Einstein vacuum equations (for vanishing cosmological constant) have attracted a considerable amount of attention since it was established by Plebański [2] that these self-dual Einstein spaces are governed by a single partial differential equation of second order. This equation adopts a variety of avatars, including Plebański's original first and second heavenly equations (see, e.g. [3] and references therein). In [4, 5], a novel form of this equation was derived in connection with a superposition principle associated with the integrable (discrete) Tzitzéica equation [6]. This integrable equation, now known as the general heavenly equation [3], turns out to be privileged in that it constitutes the generic form of an eigenfunction equation for  spaces [7]. Its coefficients are canonically parametrised in terms of four parameters
spaces [7]. Its coefficients are canonically parametrised in terms of four parameters 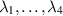 so that it adopts the form
so that it adopts the form
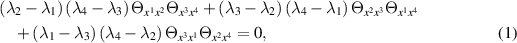
where 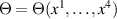 .
.
Remarkably, the general heavenly equation admits a 4+4-dimensional integrable generalisation which may be obtained by formally replacing the parameters λi
by additional derivatives 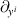 . Indeed, it is readily verified that the TED equation [8]
. Indeed, it is readily verified that the TED equation [8]
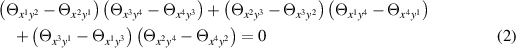
becomes the general heavenly equation (1) on application of the symmetry reduction 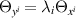 . It is observed that this formal substitution in the Lax pair for the general heavenly equation generates the Lax pair for the TED equation, which was, in fact, the origin of the discovery of the TED equation. The TED equation admits a variety of reductions which are significant in mathematical physics [8]. In particular, various heavenly equations, including the first and second Plebański equations, are captured by the TED equation. On the other hand, it has been shown that the general heavenly equation (1) remains integrable if one assumes that its 'parameters' constitute arbitrary functions of the form
. It is observed that this formal substitution in the Lax pair for the general heavenly equation generates the Lax pair for the TED equation, which was, in fact, the origin of the discovery of the TED equation. The TED equation admits a variety of reductions which are significant in mathematical physics [8]. In particular, various heavenly equations, including the first and second Plebański equations, are captured by the TED equation. On the other hand, it has been shown that the general heavenly equation (1) remains integrable if one assumes that its 'parameters' constitute arbitrary functions of the form 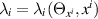 . In fact, this 'deformed' general heavenly equation has been shown to give rise to half-flat conformal structures [9].
. In fact, this 'deformed' general heavenly equation has been shown to give rise to half-flat conformal structures [9].
Here, we present a systematic way of generating natural classes of reductions of the TED equation which either directly contain deformed heavenly equations or may be mapped to deformed heavenly equations via Legendre-type transformations. In particular, the deformed heavenly equations presented in [9] in connection with half-flat conformal structures are retrieved in this manner. In order to isolate the deformed second heavenly equation recorded therein, the original connection between Plebański's first and second heavenly equations is generalised and applied to their deformed counterparts. By construction, the reductions considered here preserve the integrable nature of the partial differential equations. This is achieved by exploiting the fact that the TED equation is multi-dimensionally consistent.
Multi-dimensional consistency plays a fundamental role in the theory of discrete integrable systems [10–12]. In fact, in this context, multi-dimensional consistency often captures the integrable nature of a discrete equation. In the case of discrete equations defined on the quadrilaterals of a 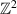 lattice, multi-dimensional consistency may be algorithmically exploited to construct a Lax pair and an associated Bäcklund transformation for the given quad equation (see, e.g. [13] and references therein). In the current context, we adopt a similar approach in that we demonstrate how the existence of a Lax pair for any of the reductions considered here is implied by the multi-dimensional consistency property of the TED equation. The relation between the multi-dimensional consistency of the TED equation and its Lax pair has been discussed in [8]. The latter has also formed the basis for the application of the
lattice, multi-dimensional consistency may be algorithmically exploited to construct a Lax pair and an associated Bäcklund transformation for the given quad equation (see, e.g. [13] and references therein). In the current context, we adopt a similar approach in that we demonstrate how the existence of a Lax pair for any of the reductions considered here is implied by the multi-dimensional consistency property of the TED equation. The relation between the multi-dimensional consistency of the TED equation and its Lax pair has been discussed in [8]. The latter has also formed the basis for the application of the 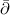 -dressing method to the TED equation [14], thereby reinforcing its integrable nature.
-dressing method to the TED equation [14], thereby reinforcing its integrable nature.
2. The TED equation
The TED equation [8] is a 4+4-dimensional integrable partial differential equation which adopts the algebraic form of a Plücker relation, namely

The latter may be regarded as the Pfaffian of a skew-symmetric 4×4 matrix 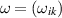 and is therefore completely symmetric in all indices. It is recalled that the Pfaffian of a skew-symmetric even-dimensional matrix ω is related to its determinant by
and is therefore completely symmetric in all indices. It is recalled that the Pfaffian of a skew-symmetric even-dimensional matrix ω is related to its determinant by 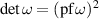 [15]. The TED equation for a function
[15]. The TED equation for a function 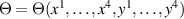 is obtained by setting
is obtained by setting

so that (3) becomes
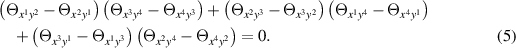
There exist various useful avatars of the TED equation encoded in identities such as

where εiklm constitutes the totally antisymmetric Levi-Civita symbol. Here, all indices run from 1 to 4 and Einstein's summation convention over repeated indices has been adopted.
The TED equation has the remarkable property that it is multi-dimensionally consistent, that is, if we regard Θ as a function of independent variables xi
and yi
, where 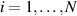 then the
then the 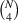 4+4-dimensional TED equations
4+4-dimensional TED equations
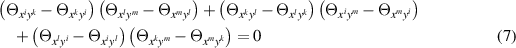
obtained by replacing the indices in (5) by any four distinct indices 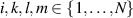 are in involution in the sense of Riquier-Janet (Cartan-Kähler) theory [16, 17]. For instance, in the case N = 5, all compatibility conditions for the five TED equations
are in involution in the sense of Riquier-Janet (Cartan-Kähler) theory [16, 17]. For instance, in the case N = 5, all compatibility conditions for the five TED equations

are satisfied so that the Cauchy data for any individual TED equation are not constrained by the other four TED equations.
Multi-dimensional consistency has a variety of interesting and useful implications. In particular, it may be used to construct Lax pairs [18]. In the current setting, the four equations corresponding to  in (8) may be formulated as
in (8) may be formulated as

The fifth equation (n = 5) is the TED equation (5). If we now consider the 'travelling wave' reduction
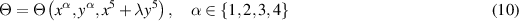
then
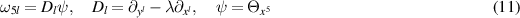
and the system (9) may be formulated as
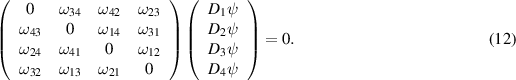
This system of linear differential equations for ψ has rank 2 since the above matrix is skew-symmetric and its determinant is 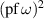 and, hence, vanishes. By construction, it is compatible modulo the TED equation so that any two equations constitute a Lax pair for the TED equation (5) with the constant λ playing the role of the spectral parameter. Moreover, the eigenfunction ψ is a symmetry of the TED equation since the latter is preserved by the flow
and, hence, vanishes. By construction, it is compatible modulo the TED equation so that any two equations constitute a Lax pair for the TED equation (5) with the constant λ playing the role of the spectral parameter. Moreover, the eigenfunction ψ is a symmetry of the TED equation since the latter is preserved by the flow  [8].
[8].
3. Canonical admissible constraints
As indicated in the preceding, the TED equation has been shown to admit a variety of reductions which are significant in mathematical physics. In particular, it is evident that it is admissible to impose individually and simultaneously linear constraints of 'travelling wave'-type

on the TED equation (5), where i may take up to 4 values in 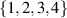 . The simplest set of four linear constraints is given by
. The simplest set of four linear constraints is given by

Here, and in the following, indices on 'parameters' such as λi are not taken into account when Einstein's summation convention is applied so that, in particular, there is no summation in (14). The TED equation then reduces to
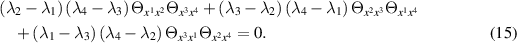
The latter was originally derived [4, 5] as the continuum limit of the superposition principle associated with the Bäcklund transformation for the integrable (discrete) Tzitzéica equation of affine (discrete) differential geometry [6]. Its multi-dimensional consistency [19] may be regarded as being inherited from the TED equation. Indeed, if one extends the reduction (14) to the system (9) of five TED equations then one obtains five compatible general heavenly equations and one may formulate the additional four TED equations as a Lax representation for the original general heavenly equation (15) in the manner described in section 2.
Other heavenly-type equations, including Plebański's heavenly equations, have also been shown to be encapsulated in the TED equation [8]. In particular, different linear constraints of the type (13) have been shown to lead to Plebański's first heavenly equation and the Husain-Park equation via Legendre-type transformations [7]. In this connection, it is observed that the general heavenly equation has been shown to be invariant under the Legendre transformation

and the above-mentioned three heavenly-type equations arise naturally in the classification of eigenfunction equations for self-dual Einstein spaces [7]. Against this background, it is natural to investigate to what extent nonlinear generalisations of the constraints (13) may be shown to be admissible and, in particular, lead to 'deformations' of these heavenly-type equations. Accordingly, we here consider constraints of the form

on the TED equation (5), where, once again, up to 4 constraints of this type may be present. For these constraints to be admissible, these have to be both consistent amongst themselves and compatible with the TED equation. Moreover, it turns out appropriate to consider the admissibility of these constraints in the more general setting of compatible TED equations so that 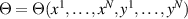 . We begin by stating that 'internal' consistency of constraints of the type (17) is always guaranteed.
. We begin by stating that 'internal' consistency of constraints of the type (17) is always guaranteed.
Lemma 3.1. Any pair of differential equations
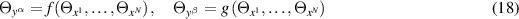
is compatible for fixed and distinct 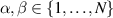 .
.
Even though it is straightforward to verify the above lemma by evaluating the compatibility condition 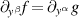 , it is enlightening to present an alternative proof which sheds light on the non-triviality of 'external' consistency with the TED equations. Thus, as in (16), we denote the derivatives of Θ by
, it is enlightening to present an alternative proof which sheds light on the non-triviality of 'external' consistency with the TED equations. Thus, as in (16), we denote the derivatives of Θ by 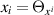 and
and 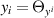 so that
so that

Hence, on introduction of the (partial) Legendre transform

we obtain

and the constraints (18) become
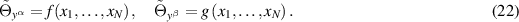
The latter are evidently compatible and may, in fact, be integrated. Accordingly, the constraints (18) are equivalent to demanding that the Legendre transform 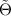 be linear in the independent variables yα
and yβ
. Since it is not difficult to show that the TED equations (7) are quartic when formulated in terms of
be linear in the independent variables yα
and yβ
. Since it is not difficult to show that the TED equations (7) are quartic when formulated in terms of 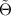 , we conclude that, in general, this linearity assumption leads to a highly overdetermined system of differential equations for
, we conclude that, in general, this linearity assumption leads to a highly overdetermined system of differential equations for 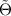 which may only be made consistent by carefully choosing the functions f and g. It is emphasised that the existence of solutions is guaranteed since it is known, a priori, that linear constraints of the form (13) are admissible.
which may only be made consistent by carefully choosing the functions f and g. It is emphasised that the existence of solutions is guaranteed since it is known, a priori, that linear constraints of the form (13) are admissible.
It turns out that, in principle, one may derive an overdetermined system of partial differential equations for the functions Fi , the solutions of which guarantee compatibility with the TED equations. However, the general solution of this system is unknown. Here, we focus on two cases which are natural and indicate how one may proceed in more general situations. These are presented in the following two theorems.
Theorem 3.2. The differential equation

where 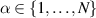 is fixed, constitutes an admissible constraint on the system of compatible TED equations (7).
is fixed, constitutes an admissible constraint on the system of compatible TED equations (7).
Theorem 3.3. The pair of differential equations
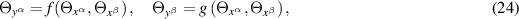
where 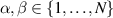 are fixed and distinct, constitute admissible constraints on the system of compatible TED equations (7) provided that
are fixed and distinct, constitute admissible constraints on the system of compatible TED equations (7) provided that
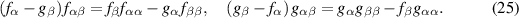
Here, the subscripts on f and g denote derivatives with respect to the corresponding arguments.
The proof of the above theorems is based on the following lemma.
Lemma 3.4. For any solution Θ of the compatible system of TED equations (7),

where 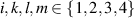 and
and  .
.
Proof. Without loss of generality, we may assume that m = 4 and 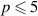 and replace the statement (26) by
and replace the statement (26) by

If p = 4 then the left-hand side of (27) is exactly (6)3. If p = 5 then the statement coincides with (9) for n = 4. If p < 4 then the only non-zero contributions arise if i = p or k = p. If k = p then the two non-zero terms in the sum

(no summation over p) cancel each other. The same applies to the case i = p. □
Proof of theorems 3.2 and 3.3. For convenience, we set 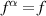 and
and 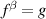 and confine ourselves, without loss of generality, to proving compatibility with the TED equation (5). If we set
and confine ourselves, without loss of generality, to proving compatibility with the TED equation (5). If we set

then we first need to show that 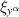 evaluated modulo the constraints (23) or (24) vanishes on the solution set of the system (7) of TED equations. Thus,
evaluated modulo the constraints (23) or (24) vanishes on the solution set of the system (7) of TED equations. Thus,

Here, we adopt the summation convention that expressions of the form 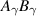 denote
denote 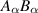 in the case of the constraint (23) and
in the case of the constraint (23) and 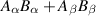 if the constraints (24) apply. Further evaluation now leads to
if the constraints (24) apply. Further evaluation now leads to
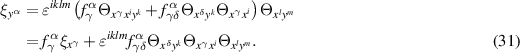
On the solution set of (7), the first term in the above sum vanishes and the two indices in the derivative 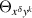 may be exchanged by virtue of lemma 3.4. Hence,
may be exchanged by virtue of lemma 3.4. Hence,

so that  if
if

due to the antisymmetry 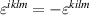 . It is evident that only the condition for
. It is evident that only the condition for 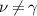 is not identically satisfied. In the case of the constraint (23), where
is not identically satisfied. In the case of the constraint (23), where 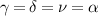 , the function fα
is therefore arbitrary and for the constraints (24),
, the function fα
is therefore arbitrary and for the constraints (24), 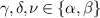 and (33) reduces to
and (33) reduces to

The latter coincides with (25)1. For reasons of symmetry, 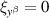 if (25)2 holds. This concludes the proof. □
if (25)2 holds. This concludes the proof. □
4. Deformation of the general heavenly equation
The simplest application of the admissible constraints established in the preceding is the imposition of a nonlinear analogue of the 'travelling wave' reduction (14), that is,

In this case, the quantities ωik as defined by (4) become
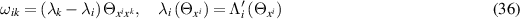
so that the resulting reduction of the TED equation is of the same algebraic form as the general heavenly equation, namely
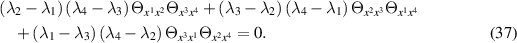
However, the coefficients λi
now constitute arbitrary functions of their arguments  . Moreover, since it has been shown that the constraints (35) are compatible with systems of TED equations and, in particular, the system (9) of five TED equations, the additional compatible constraint
. Moreover, since it has been shown that the constraints (35) are compatible with systems of TED equations and, in particular, the system (9) of five TED equations, the additional compatible constraint

may be employed to derive a Lax representation for the deformed general heavenly equation (37) in the manner described in section 2. Specifically, one obtains the linear system (12) with 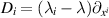 .
.
It turns out that the Lax pair for the deformed general heavenly equation remains valid if the coefficients λi
are assumed to be arbitrary functions of both  and xi
. The associated deformed general heavenly equation given by (37), wherein
and xi
. The associated deformed general heavenly equation given by (37), wherein 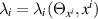 , has been shown to give rise to half-flat conformal structures in [9]. Therein, it has been stated that for any non-constant λk
, there exists a contact transformation which preserves the algebraic form of the deformed general heavenly equation but maps λk
to the coordinate xk
. It is illuminating to verify this assertion by formulating the deformed general heavenly equation in terms of differential forms according to
, has been shown to give rise to half-flat conformal structures in [9]. Therein, it has been stated that for any non-constant λk
, there exists a contact transformation which preserves the algebraic form of the deformed general heavenly equation but maps λk
to the coordinate xk
. It is illuminating to verify this assertion by formulating the deformed general heavenly equation in terms of differential forms according to
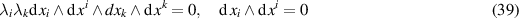
with  . The second equation guarantees the existence of a potential
. The second equation guarantees the existence of a potential 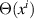 such that
such that

and, hence,  as before. (39)1 then becomes the deformed general heavenly equation (37) with
as before. (39)1 then becomes the deformed general heavenly equation (37) with  . In fact, since the pair (39) is completely symmetric in the variables xi
and xi
, one may also introduce a potential
. In fact, since the pair (39) is completely symmetric in the variables xi
and xi
, one may also introduce a potential 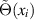 defined by
defined by

so that 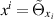 and the deformed general heavenly equation
and the deformed general heavenly equation
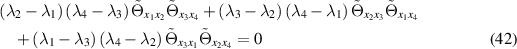
is obtained. It is important to note that this also exchanges the roles of xi
and xi
in the coefficients 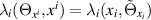 . In particular, in the case of the autonomous deformed general heavenly equation (37), the deformed general heavenly equation (42) is non-autonomous with
. In particular, in the case of the autonomous deformed general heavenly equation (37), the deformed general heavenly equation (42) is non-autonomous with 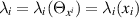 . It is observed that the potentials Θ and
. It is observed that the potentials Θ and 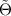 are related by
are related by

up to an irrelevant constant of integration. Thus, the transition between the two deformed general heavenly equations (37) (with 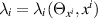 ) and (42) is generated by a Legendre transformation which generalises that for the general heavenly equation alluded to in the previous section.
) and (42) is generated by a Legendre transformation which generalises that for the general heavenly equation alluded to in the previous section.
We now introduce the change of variables

In order to preserve the deformed general heavenly equation in the form (39), the functions Fi and Gi are constrained by

wherein the suffix 0 has been used to indicate that Einstein's summation convention does not apply and the subscripts 1 and 2 denote derivatives with respect to the first and second arguments respectively of the functions Fi and Gi . Indeed, the above constraints guarantee that

which, in turn, implies that (39) is invariant under the transformation 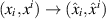 with the coefficients λi
now being regarded as functions
with the coefficients λi
now being regarded as functions

It is observed that the change of variables (44) is invertible due to the associated Jacobian determinants (45) being non-vanishing. Moreover, for any locally non-constant coefficient λk
, functions Fk
and Gk
obeying the constraint (45) may be chosen such that, locally, 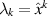 , which proves the above-mentioned assertion.
, which proves the above-mentioned assertion.
We conclude this section by observing that the discussion in the preceding implies that the deformed general heavenly equation may be obtained directly form the TED equation for any coefficients  . For instance, the ansatz
. For instance, the ansatz

where the functions zi are defined by the decoupled system of differential equations

leads to

so that the TED equation (3) reduces to the deformed general heavenly equation
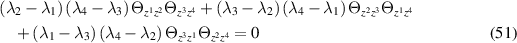
for  , which coincides with the 'Legendre transform' of the autonomous deformed general heavenly equation (37) as pointed out in the preceding.
, which coincides with the 'Legendre transform' of the autonomous deformed general heavenly equation (37) as pointed out in the preceding.
5. Deformation of the first Plebański equation
In [7], it has been shown how Plebański's first heavenly equation and the Husain-Park equation [3] may be obtained from the TED equation by means of a combination of 'travelling wave' reductions and Legendre transformations. It turns out that this approach may be generalised to construct deformations of these heavenly-type equations. Here, we focus on the derivation of a class of deformed first Plebański equations. To this end, we consider a pair of admissible constraints of the type (24), namely,
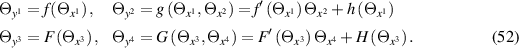
The restrictions (25) are indeed satisfied and if the functions  and
and 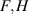 are proportional to their arguments then linear constraints of the form (13) are obtained. Now, evaluation of (4) yields
are proportional to their arguments then linear constraints of the form (13) are obtained. Now, evaluation of (4) yields

so that the TED equation (3) becomes
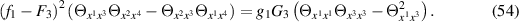
In view of the application of an appropriate Legendre-type transformation, it turns out convenient to write this differential equation in terms of differential forms. Thus, as usual, we consider the one-form

and formulate (54) as
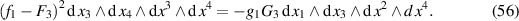
If we now interchange the roles of 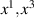 and
and 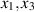 and introduce the partial Legendre transform
and introduce the partial Legendre transform

leading to
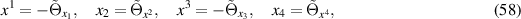
then the differential equation for 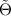 is given by
is given by
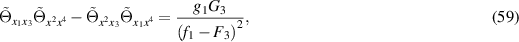
wherein
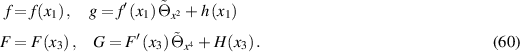
We illustrate the significance of the reduction (59) and (60) of the TED equation with three examples. In the 'linear' case, that is,
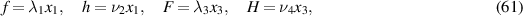
we obtain Plebański's first heavenly equation
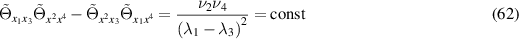
governing self-dual Einstein spaces. In this case, the constraints (52) coincide with those presented in [7] in connection with the classification of canonical eigenfunction equations for self-dual Einstein spaces. Accordingly, (59) constitutes a deformation of the first Plebański equation. On the other hand, if we make the choice

then the deformed first Plebański equation reads
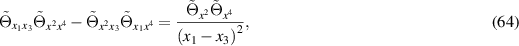
which is exactly one of the normal forms of deformed first Plebański equations which give rise to half-flat conformal structures as discussed in [9]. The remaining normal form contained therein may be obtained by setting
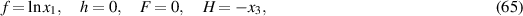
corresponding to the deformed Plebański equation

It is emphasised that Lax pairs associated with the reductions presented in this section may again be constructed algorithmically in the manner indicated in section 2.
In conclusion, the connections established in this and the previous sections suggest that it is desirable to investigate in more detail the link between (reductions of) the TED equation and half-flat conformal structures.
6. Deformation of the Husain–Park equation
In [7], it has been established that the Husain–Park equation [3], which constitutes another avatar of the equation governing self-dual Einstein spaces, may be obtained from the TED equation by imposing a 'hybrid' of the constraints leading to the general heavenly and first Plebański equations. The 'nonlinear' analogue of this mixture of constraints is given by
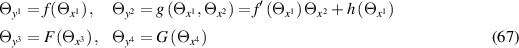
which may be regarded as either a hybrid of the constraints (35) and (52) or two particular pairs of constraints which obey the admissibility conditions (25). In this case, the quantities ωik are given by
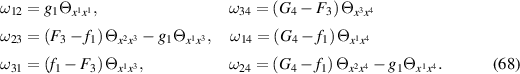
The TED equation (3) now becomes
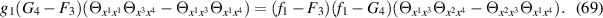
In terms of differential forms, the differential equation (69) may be formulated as
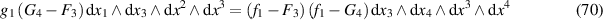
so that a partial Legendre transformation with associated potential

where

generates the transformed equation
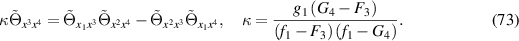
In terms of the new (in)dependent variables, the functions 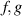 and
and 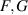 are now of the form
are now of the form
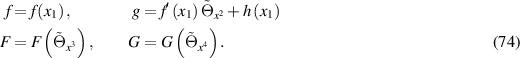
In the 'linear' case given by
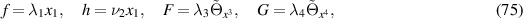
we obtain the Husain-Park equation since

Accordingly, in general, one may regard (73) and (74) as a deformed Husain-Park equation. As an illustration, we make the choice
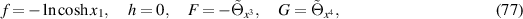
leading to the deformed Husain–Park equation

which is homogeneous in 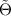 . Once again, the reductions of the TED equation derived in this section admit Lax pairs which may be constructed by means of the procedure indicated in section 2.
. Once again, the reductions of the TED equation derived in this section admit Lax pairs which may be constructed by means of the procedure indicated in section 2.
7. Deformation of the second Plebański equation
It has been shown that Plebański's second heavenly equation also resides in the TED equation as a reduction. However, it is not evident how this may be generalised to deformed second heavenly equations. On the other hand, one may inquire to what extent the original connection between Plebański's first and second heavenly equations may be modified so that the deformed first Plebanśki equations discussed in the preceding may be linked to deformed second Plebański equations. Here, we demonstrate (cf [7]) that such a link exists in the case of a particular deformed second heavenly equation which, once again, arises in connection with half-flat conformal structures. To this end, we consider the closed two-form

where q is an arbitrary function of u1 and 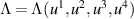 satisfies the differential equation
satisfies the differential equation
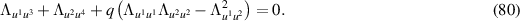
If q is constant, that is, q = 1 without loss of generality then Plebański's second heavenly equation is obtained. If q is a linear function so that 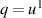 without loss of generality then, once again,
without loss of generality then, once again,
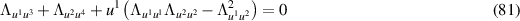
constitutes a deformed second Plebański equation associated with a particular class of half-flat conformal structures [9].
On expanding the differentials 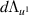 and
and 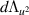 in (79), one may verify that the two-form Ω factorises into
in (79), one may verify that the two-form Ω factorises into
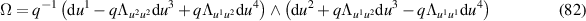
modulo the deformed second Plebański equation (79) so that

Darboux's theorem then states that, locally, there exist functions z1 and z2 such that

Comparison with (82) shows that the 'factors' therein must admit expansions of the form
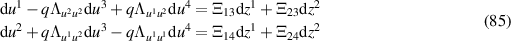
with the coefficients Ξik being constrained by

We now regard  and
and 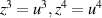 as the independent variables so that u1 and u2 become functions of these variables. Accordingly, (85) implies that
as the independent variables so that u1 and u2 become functions of these variables. Accordingly, (85) implies that 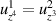 and, hence, there exists a potential Ξ such that
and, hence, there exists a potential Ξ such that

This leads to the parametrisation

by virtue of (85) and (86) becomes, in turn, the deformed first Plebański equation

In particular, in the case  , the associated deformed second heavenly equation (81) is mapped to the deformed first Plebański equation
, the associated deformed second heavenly equation (81) is mapped to the deformed first Plebański equation

which coincides with (66) on appropriate identification of the (in)dependent variables.
Acknowledgment
B K acknowledges the financial support of the project MMNLP of the CSN IV of INFN (Italy).
Data availability statement
No new data were created or analysed in this study.
