Abstract
Neoclassical properties in quasi-axisymmetric (QA) stellarators are analogous to these in tokamaks. Consequently, a substantial bootstrap current could significantly modify the MHD equilibrium properties of a QA stellarator, which is an important characteristic in this type of stellarator. This paper is dedicated to systemically investigate the effects of bootstrap current on the magnetic configuration in Chinese first quasi-axisymmetric stellarator (CFQS). For the first time, self-consistent bootstrap currents in free-boundary equilibria are calculated with an accurate Fokker–Planck neoclassical numerical mode in CFQS. Several important results are achieved: (a) as the bootstrap current grows with increasing volume-averaged normalized pressure 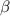 , magnetic shear develops in the bulk plasma and meanwhile, a deep magnetic well is robustly sustained, which leads to improved stabilization of interchange modes up to
, magnetic shear develops in the bulk plasma and meanwhile, a deep magnetic well is robustly sustained, which leads to improved stabilization of interchange modes up to 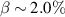 . (b) In the analysis of global ideal MHD instability, as the bootstrap current rises to 39 kA (
. (b) In the analysis of global ideal MHD instability, as the bootstrap current rises to 39 kA (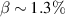 ), external kink modes become destabilized and the unstable mode with m/n = 2/1 is dominant. (c) From
), external kink modes become destabilized and the unstable mode with m/n = 2/1 is dominant. (c) From 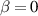 to 1.5%, the bootstrap current hardly changes the QA property and a low neoclassical transport is maintained. However, as
to 1.5%, the bootstrap current hardly changes the QA property and a low neoclassical transport is maintained. However, as 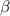 is enhanced beyond 2.0%, the substantial bootstrap current gives rise to an increase of non-QA magnetic field components, which weakens the neoclassical transport properties. (d) An increase of the negative magnetic shear at the core region by the bootstrap currents has a favorable effect on the properties of J (second adiabatic invariant). The maximum-J region can be extended by raising bootstrap currents.
is enhanced beyond 2.0%, the substantial bootstrap current gives rise to an increase of non-QA magnetic field components, which weakens the neoclassical transport properties. (d) An increase of the negative magnetic shear at the core region by the bootstrap currents has a favorable effect on the properties of J (second adiabatic invariant). The maximum-J region can be extended by raising bootstrap currents.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
An essential optimization strategy for a stellarator is to achieve omnigenity [1], meaning the particle radial drift vanishes on a time average [2]. In quasi-symmetric configurations the omnigenious property can be realized. The quasi-symmetric configurations include quasi-axisymmetric (QA), quasi-helical symmetric and quasi-poloidal symmetric magnetic field topologies [3]. To date, the QA configuration has been accomplished in many physics designs e.g. CHS-qa [4], NCSX [5], ESTELL [6], etc, none of which, however, has been successfully fabricated and operated. The Chinese first quasi-axisymmetric stellarator (CFQS) will represent the first operational quasi-axially symmetric stellarator in the world, which has been constructed as a collaborative project between the National Institute for Fusion Science and Southwest Jiaotong University to prove the intrinsic advantages of quasi-axisymmetry [7–11]. The principal parameters of CFQS are as follows: the major radius is 1.0 m, the magnetic field strength is 1.0 T, the aspect ratio is 4.0, and the toroidal periodic number is 2 [7]. A magnetic field coil system consists of 16 modular coils (MCs), 12 toroidal field coils (TFCs), and 4 poloidal field coils (PFCs). It has been designed to possess a number of advanced features in fixed and free-boundary equilibria. The MHD equilibrium of the CFQS configuration is stable up to β ∼ 1.1% in the plasma-current-free scenario [9]. Rotational transform profiles with weak magnetic shear were always sustained, which did not contribute to stabilization of Mercier modes. The resistive ballooning modes were simulated in CFQS equilibria with magnetic islands [10]. For the high-resistivity regimes, the modes were unstable, whereas in the low-resistivity regimes, the modes were stabilized. With bootstrap current effects, in β ∼ 1.0% plasma the low-order islands (2/4) were generated, which may lead to a stochastization of magnetic field lines [10]. Moreover, the effects of the bootstrap current on neoclassical transport were investigated and a satisfactory neoclassical transport maintained up to β = 1.5% [11]. Now the fabrication of the CFQS device is steadily progressing to achieve its first plasma [12]. It is noted in previous work [9–12], that the bootstrap current was estimated with the BOOTSJ code, which uses a semi-analytic formula in the collision-less limit [13]. The bootstrap current density predicted with this code is usually noisy or has 'spikes' near the rational surfaces [10, 14], which results from the shortcoming of the low-collisionality bootstrap analytical formula. Even though these spikes can be smoothed over with a damping parameter, the current profile still does not closely match the accurate Fokker–Planck neoclassical numerical results in high β plasma [14].
The bootstrap current is a net toroidal current driven by the temperature and density gradients, which was predicted and calculated in tokamak geometry five decades ago by Galeev [15] and Bickerton, Connor, and Taylor [16]. A proper estimation of the bootstrap current in a stellarator configuration was first done by Shaing and Callen [17], using the Hirshman-Sigmar moment method, which was improved by a more direct calculation by Boozer and Gardner [18]. Both in tokamaks and stellarators the bootstrap current has been observed experimentally [19, 20]. Since then, it has proven to be of great importance to both tokamaks and stellarators [21, 22], especially in QA stellarators [10, 23]. A new analytic expression of bootstrap current in a low-collisionality stellarator plasma was given by Helander [24], which was suitable for all low-collisionality regimes. The QA configuration has neoclassical properties that are similar to those in tokamaks [25], since the physics of the bootstrap current is the same in the Boozer coordinates, which indicates this current may significantly change the equilibrium properties in a QA configuration. Previous studies in NCSX [26, 27] and CHS-qa [28, 29] had shown that large bootstrap currents dramatically impacted the rotational transform profile, magnetic shear, MHD modes, etc. Recently, a magnetic configuration (a 1 Tesla mean field) with precise QA for plasma confinement has been achieved in which the axisymmetry-breaking fields throughout the torus of aspect ratio 6 are as small as the 50 μT geomagnetic field [30].
In addition, a discrepancy between accurate Fokker–Planck neoclassical numerical results and the analytical model, for higher collisionality, was identified in the studies by Koh et al [31] and Landreman and Ernst [32]. In W7-X experiments, the neoclassical effects were frequently observed and studied [33], which could be precisely predicted with the code SFINCS (the Stellarator Fokker–Planck Iterative Neoclassical Conservative Solver). This code solves the steady-state drift-kinetic equation for multiple species, allowing arbitrary collisionality, and using the full linearized Fokker–Planck–Landau collision operator. In this paper, we use the SFINCS code to accurately calculate bootstrap currents in CFQS and systematically study bootstrap current effects on MHD instabilities and plasma transport behaviors.
2. MHD equilibria with bootstrap currents
The simulation of 3D ideal MHD equilibria is executed using the free-boundary VMEC code [34]. The code approaches an equilibrium state by minimization of the plasma energy. The bootstrap current is estimated with the SFINCS code. A convergent iteration operation between VMEC and SFINCS codes is performed to self-consistently calculate the bootstrap current in CFQS. After several iterations a self-consistent equilibrium state is obtained. The plasma β is scanned from 0% to 2.03%. Problems of convergence towards an equilibrium state with VMEC arise partially due to the large Shafranov shift for β > 2.03%. The plasma temperature and density profiles are assumed as T = T0 (1 − ρ2) and ne = ni = n0 (1 − ρ2), respectively and set Te0 /Ti0 = 3/2. 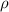 represents the normalized minor radius. n0 is scanned form 0 to
represents the normalized minor radius. n0 is scanned form 0 to  and Ti0 is fixed at 1.3 keV. The dependence of rotational transform (
and Ti0 is fixed at 1.3 keV. The dependence of rotational transform ( ) on bootstrap currents and bootstrap current density as a function of the normalized minor radius are shown in figures 1(a) and (b), respectively. As the plasma β increases to 2.03% the bootstrap current is enhanced to 54 kA. In the regions with ρ from 0.4 to 0.6 a peak exists in the profile of the bootstrap current density, which results in generation of magnetic shear in the bulk plasma. This could be beneficial for the stabilization of MHD modes, e.g. interchange modes. Meanwhile, the rotational transform crosses the low-order rational surfaces with n/m = 1/2 as β increases to 1.0%, which may lead to the generation of magnetic islands.
) on bootstrap currents and bootstrap current density as a function of the normalized minor radius are shown in figures 1(a) and (b), respectively. As the plasma β increases to 2.03% the bootstrap current is enhanced to 54 kA. In the regions with ρ from 0.4 to 0.6 a peak exists in the profile of the bootstrap current density, which results in generation of magnetic shear in the bulk plasma. This could be beneficial for the stabilization of MHD modes, e.g. interchange modes. Meanwhile, the rotational transform crosses the low-order rational surfaces with n/m = 1/2 as β increases to 1.0%, which may lead to the generation of magnetic islands.
Figure 1. Profiles of (a) rotational transform and (b) bootstrap current density for β = 0.00%, 0.50 %, 1.00 %, 1.50% and 2.03% with plasma bootstrap current = 0, 15, 30, 42 and 54 kA, respectively. These results are obtained with the self-consistent iterations between SFINCS and VMEC codes.
Download figure:
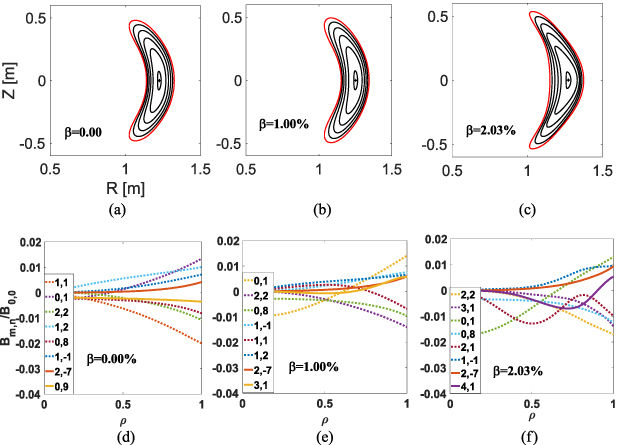
Standard image High-resolution imageThe impact of increasing β and bootstrap currents on the equilibria is shown in figure 2 which displays cross sections of magnetic flux surfaces with the bean shape in equilibrium states with various bootstrap currents and corresponding magnetic field strength spectra Bm,n normalized by B0,0 in the Boozer coordinates. In order to demonstrate clearly the emergence of non-axisymmetric magnetic field components, the dominant component B1,0 with a large amplitude is not shown. Figures 2(a)–(c) show as β is increased, that the magnetic axis is shifted horizontally by the net toroidal current because the effective vertical field is changed. Meanwhile, the flux surfaces become deformed and compressed towards the outside of the torus. The core region develops a B0,1 symmetry breaking component from β > 1% in figure 2(e) and from β > 2% the B2,1 term becomes significant in figure 2(f), which indicates as β increases beyond 2.0%, the deformation of magnetic flux surfaces may degrade the quasi-axisymmetry of the magnetic configuration in the core. This phenomenon is further studied in section 4.
Figure 2. Cross sections of magnetic flux surfaces with the bean shape and magnetic field strength spectra with n ≠ 0 normalized by B0,0 in the Boozer coordinates for three of the cases: (a) and (d) for  , (b) and (d) for
, (b) and (d) for  with a 30 kA bootstrap current, and (c) and (f) for
with a 30 kA bootstrap current, and (c) and (f) for 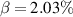 with a 54 kA bootstrap current.
with a 54 kA bootstrap current.
Download figure:
Standard image High-resolution image3. Effects of bootstrap current on MHD stability
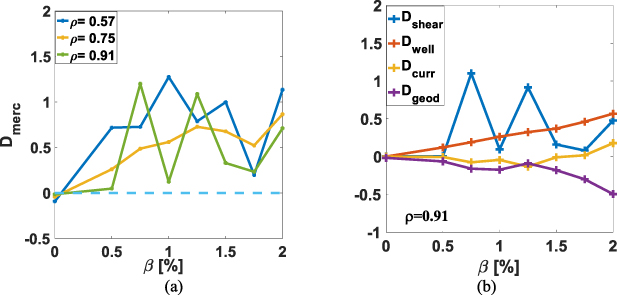
The Mercier criterion and global linear MHD stability are estimated with the VMEC and TERPSICHORE codes [34, 35]. The Mercier criterion for the stable interchange modes is expressed by Dmerc = Dshear + Dwell + Dcurr + Dgeod > 0 where they represent magnetic shear term, magnetic well term, current term and geodesic curvature term, respectively [36]. At three different radial positions, the variations of Mercier stabilities with β are given in figure 3(a), which illustrates that the interchange modes are stable up to β = 2.03% at least. What is interesting is that in the equilibria with bootstrap currents the stabilization of interchange modes is attributed to the enhancement of magnetic shear and the magnetic well, as shown in figure 3(b). These two stabilization effects enable to robustly suppress the destabilization effect of the geodesic curvature term. The previous study [10] found that free boundary equilibria without bootstrap currents, they were also stable when β ⩽ 2.0% in CFQS. However in that case, a flat  profile was well sustained as β increased. Thus, interchange modes were merely stabilized by magnetic well structures. In addition, the stabilization effect of a net toroidal current on interchange modes in heliotron plasmas was also observed [37]. The resistive ballooning mode was also studied in CFQS [10] and its stability is dependent on the MHD resistivity. If the resistivity is not large, the ballooning modes can be stabilized well.
profile was well sustained as β increased. Thus, interchange modes were merely stabilized by magnetic well structures. In addition, the stabilization effect of a net toroidal current on interchange modes in heliotron plasmas was also observed [37]. The resistive ballooning mode was also studied in CFQS [10] and its stability is dependent on the MHD resistivity. If the resistivity is not large, the ballooning modes can be stabilized well.
Figure 3. (a) Mercier stabilities versus β at three different radial positions ρ = 0.57, 0.75 and 0.91 respectively; (b) magnetic shear, magnetic well, current and geodesic curvature terms versus β at ρ = 0.91 in various free-boundary equilibria with bootstrap currents.
Download figure:
Standard image High-resolution imageA global linear MHD stability analysis of CFQS equilibria is computed with respect to n = 1 and n = 2 family of modes with the TERPSICHORE code, which evaluates the variational energy principle. Figure 4 displays bootstrap currents as a function of β and it is approximately proportional to β. The ranges of Fourier modes for the global MHD stability analysis are m < 49 and n < 14 for the poloidal and toroidal modes, respectively. The typical marginal stability is represented by a threshold value of λ = −1 × 10−4 and more negative eigenvalues than this crucial number are thought to be more unstable [38]. The simulation results reveal that a global MHD stability is obtained for  up to 1.35% (Ibc = 38 kA). The stability is determined by the rotational transform at the edge, i.e. the iota value higher than 0.5 is unstable. As
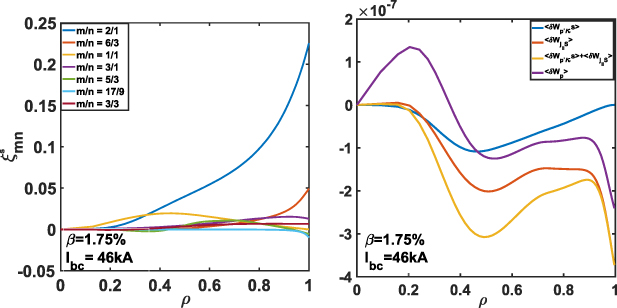
up to 1.35% (Ibc = 38 kA). The stability is determined by the rotational transform at the edge, i.e. the iota value higher than 0.5 is unstable. As 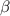 increases beyond 1.35%, global instabilities arise. As an instance, the Fourier amplitudes of the radial component of the displacement vector (
increases beyond 1.35%, global instabilities arise. As an instance, the Fourier amplitudes of the radial component of the displacement vector (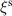 ) profiles are displayed in figure 5(a). In this equilibrium the plasma
) profiles are displayed in figure 5(a). In this equilibrium the plasma  and bootstrap current are 1.75% and 46 kA, respectively. The unstable mode structure is dominated by the m/n = 2/1 term with the eigenvalue λ = −3.8724 × 10−4. In order to identify the category of these unstable modes, figure 5(b) shows radial profiles of surface-averaged plasma potential energy
and bootstrap current are 1.75% and 46 kA, respectively. The unstable mode structure is dominated by the m/n = 2/1 term with the eigenvalue λ = −3.8724 × 10−4. In order to identify the category of these unstable modes, figure 5(b) shows radial profiles of surface-averaged plasma potential energy  which mainly includes two instability drive terms,
which mainly includes two instability drive terms,  and
and 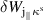 [38, 39]. The former drive term associates with ballooning modes in which the plasma pressure gradient interacts with the curvature of magnetic field lines. The latter describes kink modes which are caused by the parallel current density interacting with the local magnetic shear. In the unstable regions with
[38, 39]. The former drive term associates with ballooning modes in which the plasma pressure gradient interacts with the curvature of magnetic field lines. The latter describes kink modes which are caused by the parallel current density interacting with the local magnetic shear. In the unstable regions with  , the second term completely exceeds the first term. Hence, the 2/1 mode is mainly current-driven external kink mode.
, the second term completely exceeds the first term. Hence, the 2/1 mode is mainly current-driven external kink mode.
Figure 4. Bootstrap currents versus β in CFQS, calculated with the self-consistent iterations between SFINCS and VMEC codes.
Download figure:
Standard image High-resolution imageFigure 5. Fourier amplitudes of the radial component of the displacement vector 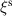 (a) and surface-averaged plasma potential energy
(a) and surface-averaged plasma potential energy 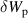 , ballooning mode driven energy
, ballooning mode driven energy 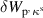 and kink modes driven energy
and kink modes driven energy  (b) as a function of
(b) as a function of  for
for  = 1.75% and Ibc = 46 kA. These results are calculated with TERPSICHORE.
= 1.75% and Ibc = 46 kA. These results are calculated with TERPSICHORE.
Download figure:
Standard image High-resolution image4. Effects of bootstrap current on neoclassical transport and J
The neoclassical transport study of the quasiaxisymmetric stellarator is implemented to evaluate how close it is to a axisymmetric configuration during increasing plasma bootstrap currents. The estimation of the neoclassical transport can be characterized by the effective helical ripple strength 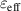 [40] and neoclassical transport matrix [41]. In the 1/ν regime the neoclassical diffusion coefficient is proportional to
[40] and neoclassical transport matrix [41]. In the 1/ν regime the neoclassical diffusion coefficient is proportional to 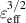 which is investigated with the NEO code [40]. The NEO code solves for the radial profile of
which is investigated with the NEO code [40]. The NEO code solves for the radial profile of 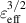 using an analytic solution of the banana kinetic equation. Figure 6 shows the radial profiles of
using an analytic solution of the banana kinetic equation. Figure 6 shows the radial profiles of 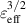 in the free boundary equilibria with various
in the free boundary equilibria with various 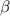 . As a comparison with CFQS, the
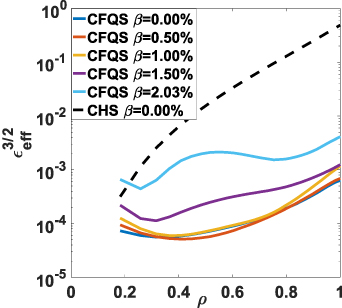
. As a comparison with CFQS, the 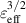 profile in the fixed boundary equilibrium of CHS [42] is given by a black dashed curve. From
profile in the fixed boundary equilibrium of CHS [42] is given by a black dashed curve. From  to 1.50%, the
to 1.50%, the  in the CFQS configurations is approximately two orders lower than that in CHS, which is in good agreement with A.Shimizu's, et.al results [11]. In their study, they used a flatter density profile to estimate the bootstrap current. However, as
in the CFQS configurations is approximately two orders lower than that in CHS, which is in good agreement with A.Shimizu's, et.al results [11]. In their study, they used a flatter density profile to estimate the bootstrap current. However, as  increases beyond 2.0% the
increases beyond 2.0% the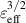 gets enhanced notably in the core region due to an increase of non-axisymmetric components of B, e.g. B0,1, B2,1, etc, which results from the deformation of magnetic flux surfaces by high
gets enhanced notably in the core region due to an increase of non-axisymmetric components of B, e.g. B0,1, B2,1, etc, which results from the deformation of magnetic flux surfaces by high  and bootstrap currents, as displayed in figures 2(c) and (f).
and bootstrap currents, as displayed in figures 2(c) and (f).
Figure 6. Radial profiles of effective helical ripple calculated with NEO for various β in the free-boundary equilibria with bootstrap currents. The CHS result is shown as a reference, plotted by a black dashed curve.
Download figure:
Standard image High-resolution imageFurthermore, in order to reveal impacts of bootstrap currents on neoclassical transport in various plasma collisional regimes, the transport matrix is computed with the SFINCS code with the full linearized Fokker–Planck–Landau collision operator. In this collision operator, the momentum conservation property is adequately sustained, which can more accurately describe the collisional effects than the pitch-angle scattering collision operator [43]. Figure 7 shows two transport matrix elements L1,1 and L1,2 as a function of ν* for the CFQS and CHS geometries at half-radius. The quantities L1,1, L1,2 and ν* are defined by formula 40 and 41 in [43], which represent the radial particle and heat transport coefficients and normalized collisionality, respectively. Here the ambipolar electric field on transport coefficients is not considered. At high collisionality ν* > 10°, L1,1 and L1,2 are quite low and basically independent of the toroidal current in CFQS. The neoclassical transport in CHS is comparable with that in CFQS. In the rare collision regime ν* < 10−1, however, as the current increases to 54 kA ( ) these two coefficients are approximately one order of magnitude higher than that in low bootstrap current equilibria in CFQS, which indicate a degradation of neoclassical transport properties in high bootstrap current equilibria. Overall, when
) these two coefficients are approximately one order of magnitude higher than that in low bootstrap current equilibria in CFQS, which indicate a degradation of neoclassical transport properties in high bootstrap current equilibria. Overall, when 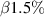 the neoclassical transport in CFQS is much lower than that in CHS and the quasi-axisymmetry is robustly sustained. This is in good agreement with the results from NEO in figure 6. The operational parameters of CFQS were estimated using the ISS95 scaling law [9, 12]. With a heating power of 1.0 MW, the
the neoclassical transport in CFQS is much lower than that in CHS and the quasi-axisymmetry is robustly sustained. This is in good agreement with the results from NEO in figure 6. The operational parameters of CFQS were estimated using the ISS95 scaling law [9, 12]. With a heating power of 1.0 MW, the 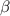 ranged from 1.0% to 2.0% in high-density plasmas. Our results are also consistent with the expected operation.
ranged from 1.0% to 2.0% in high-density plasmas. Our results are also consistent with the expected operation.
Figure 7. The radial particle and heat transport coefficients L1,1 and L2,1 as a function of the normalized collisionality in CFQS for various β in the free-boundary equilibria with bootstrap current. The CHS result is shown as a reference, plotted by a black curve. These results are calculated with SFINCS.
Download figure:
Standard image High-resolution imageQuasi-axisymmetry makes a stellarator as analogous as possible to a tokamak, in some sense, which is not an essential condition for achieving good plasma confinement. Mathematically, the necessary condition is to require parallel adiabatic invariant 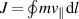 to be (approximately) constant on flux surfaces for trapped particle orbits [2]. If the magnetic field has been written as
B
= ∇ψ × ∇α and ψ measures the toroidal flux and
to be (approximately) constant on flux surfaces for trapped particle orbits [2]. If the magnetic field has been written as
B
= ∇ψ × ∇α and ψ measures the toroidal flux and 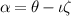 labels the different field lines on each flux surface, a configuration with vanishing bounce-averaged drift, ∂J/∂α = 0, is called omnigenous. Meanwhile, J decreases away from the center, i.e. ∂J/∂ψ < 0, it is the so-called the maximum-J condition [44], which is very beneficial for stabilizing trapped-particle-driven micro-instability modes [45, 46]. The perfectly omnigenous configurations with the maximum-J property cannot be exactly achieved. Alternatively, the wave vector perpendicular to the magnetic field is expressed by
k⊥
= kψ
∇ψ + kα
∇α and if kψ
is very small, ∂J/∂ψ < 0 is able to suppress these micro instabilities in incompletely omnigenous configurations at least [46, 47]. The maximum-J capability has been broadly investigated in QA and quasi-isodynamic configurations [29, 45, 48]. It is of importance to evaluate the maximum-J capability in CFQS.
labels the different field lines on each flux surface, a configuration with vanishing bounce-averaged drift, ∂J/∂α = 0, is called omnigenous. Meanwhile, J decreases away from the center, i.e. ∂J/∂ψ < 0, it is the so-called the maximum-J condition [44], which is very beneficial for stabilizing trapped-particle-driven micro-instability modes [45, 46]. The perfectly omnigenous configurations with the maximum-J property cannot be exactly achieved. Alternatively, the wave vector perpendicular to the magnetic field is expressed by
k⊥
= kψ
∇ψ + kα
∇α and if kψ
is very small, ∂J/∂ψ < 0 is able to suppress these micro instabilities in incompletely omnigenous configurations at least [46, 47]. The maximum-J capability has been broadly investigated in QA and quasi-isodynamic configurations [29, 45, 48]. It is of importance to evaluate the maximum-J capability in CFQS.
To obtain the distribution of J, the guiding center trajectories of tracer particles are calculated in Boozer coordinates, which are reflected at the same B. The motion equations used in the simulation were expressed in [49]. The tracing particle energy is W = 10 eV and set the magnetic field strength at the bounce point equal to 0.95 T. The initial positions of these particles are distributed in the ( ) plane. The J contours on the (
) plane. The J contours on the (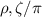 ) plane are calculated in various equilibria, as shown in figure 8. The J contour values are normalized to the largest J. The color bar represents the normalized J values. The areas on the left side of the red solid curve represent the maximum-J criterion satisfied. In low bootstrap current equilibria with
) plane are calculated in various equilibria, as shown in figure 8. The J contour values are normalized to the largest J. The color bar represents the normalized J values. The areas on the left side of the red solid curve represent the maximum-J criterion satisfied. In low bootstrap current equilibria with  the maximum-J region can hardly be generated in figure 8(a). As the bootstrap current increases, the negative magnetic shear in the core region is enhanced in figure 1(a), leading to a decrease of J away from the center, which is to extend maximum-J regions in figures 8(b) and (c). A similar result was also observed in reversed shear tokamaks [50] that the maximum-J region coincides with the region of the reversed q profile (negative shear). Meanwhile, with increasing β, it is found that
the maximum-J region can hardly be generated in figure 8(a). As the bootstrap current increases, the negative magnetic shear in the core region is enhanced in figure 1(a), leading to a decrease of J away from the center, which is to extend maximum-J regions in figures 8(b) and (c). A similar result was also observed in reversed shear tokamaks [50] that the maximum-J region coincides with the region of the reversed q profile (negative shear). Meanwhile, with increasing β, it is found that 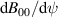 decreases monotonically with radius, which could make poloidal drift decrease with radius. This process is also beneficial for obtaining ∂J/∂ψ < 0. Notably, an inhomogeneity of maximum-J regions in the
decreases monotonically with radius, which could make poloidal drift decrease with radius. This process is also beneficial for obtaining ∂J/∂ψ < 0. Notably, an inhomogeneity of maximum-J regions in the  direction arises due to the existence of the non-axisymmetry of B.
direction arises due to the existence of the non-axisymmetry of B.
Figure 8. Contours of normalized J on the ( ) plane for (
) plane for ( ) = (0.30%, 11 kA) (a), (0.75%, 24 kA) (b) and (1.50%, 42 kA) (c) in CFQS configurations, respectively. The J is normalized to the largest J. The areas on the left side of the red solid curve represent the maximum-J criterion satisfied.
) = (0.30%, 11 kA) (a), (0.75%, 24 kA) (b) and (1.50%, 42 kA) (c) in CFQS configurations, respectively. The J is normalized to the largest J. The areas on the left side of the red solid curve represent the maximum-J criterion satisfied.
Download figure:
Standard image High-resolution imageTo assess the capability of the maximum-J in CFQS, linear gyrokinetic simulations using the GENE code [51] are performed to explore electrostatic trapped electron modes (TEMs) in these equilibria. The code GENE solves the gyrokinetic equation along with Maxwell's equations. In this study, both electrons and ions are kinetically treated with a resolution of nx
× nky
× nz
× nv
× nw
= 30 × 1 × 128 × 64 × 16. The wave number  (
(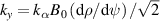 ) is scanned from 0.5 to 2.0 with an interval = 0.1. The local flux-tube is fixed at the position at (
) is scanned from 0.5 to 2.0 with an interval = 0.1. The local flux-tube is fixed at the position at (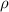 ,
, 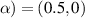 . The stability study is simulated with the same temperature for ions and electrons Ti = Te, while setting the ion–temperature normalized gradient a/LTi and the density normalized gradient a/Ln
to zero and the electron–temperature normalized gradient a/LTe = 7. Figure 9 shows the growth rate spectrum of electrostatic TEMs in three equilibria with β = 0.0%, 0.75%, and 1.50%, respectively. The propagating direction of these modes is the electron diamagnetic drift direction. In the plasma-pressure-free equilibrium, the TEMs are significantly excited, displayed by the blue curve. As
. The stability study is simulated with the same temperature for ions and electrons Ti = Te, while setting the ion–temperature normalized gradient a/LTi and the density normalized gradient a/Ln
to zero and the electron–temperature normalized gradient a/LTe = 7. Figure 9 shows the growth rate spectrum of electrostatic TEMs in three equilibria with β = 0.0%, 0.75%, and 1.50%, respectively. The propagating direction of these modes is the electron diamagnetic drift direction. In the plasma-pressure-free equilibrium, the TEMs are significantly excited, displayed by the blue curve. As  increases to 0.75%, weak maximum-J regions are produced in the core, which slightly mitigate the TEMs, denoted by the red curve. In the equilibrium with β = 1.50%, the development of the core maximum-J becomes prominent, which remarkably suppresses the TEMs, as shown by the black curve. This numerical result is consistent with the above analytical analysis that even though the perfect omnigeneity is not achieved in CFQS, the TEMs in maximum-J regions can be effectively mitigated. In addition, in low
increases to 0.75%, weak maximum-J regions are produced in the core, which slightly mitigate the TEMs, denoted by the red curve. In the equilibrium with β = 1.50%, the development of the core maximum-J becomes prominent, which remarkably suppresses the TEMs, as shown by the black curve. This numerical result is consistent with the above analytical analysis that even though the perfect omnigeneity is not achieved in CFQS, the TEMs in maximum-J regions can be effectively mitigated. In addition, in low  plasmas a stability-valley-like structure was found along the transition boundary of the ion temperature gradient mode and TEM, where the growth rate is quite low [52].
plasmas a stability-valley-like structure was found along the transition boundary of the ion temperature gradient mode and TEM, where the growth rate is quite low [52].
Figure 9. The growth rates of electrostatic TEM modes as a function of 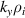 in three equilibra with
in three equilibra with  ,
,  and
and 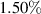 , respectively.
, respectively.
Download figure:
Standard image High-resolution imageThe magnetic islands and chaos could modify the properties of MHD equilibria, which may result in enhanced radial transport [53]. In CFQS the magnetic islands emerge in edge plasma region at  ∼ 1.0%. This is due to the rotational transform crossing the rational surface with ι = 2/4 = 1/2. An equilibrium with 2/4 magnetic islands was found in the simulation results with the HINT code [10]. 12 planar TFC have been designed to adjust the rotational transform profile [54], healing magnetic islands. Moreover, active control of islands is also available by electron cyclotron heating and tailoring the pressure profile [55, 56]. In the
∼ 1.0%. This is due to the rotational transform crossing the rational surface with ι = 2/4 = 1/2. An equilibrium with 2/4 magnetic islands was found in the simulation results with the HINT code [10]. 12 planar TFC have been designed to adjust the rotational transform profile [54], healing magnetic islands. Moreover, active control of islands is also available by electron cyclotron heating and tailoring the pressure profile [55, 56]. In the 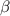 = 1.0%, the 2/4 magnetic islands are fully suppressed by TFC. How to control magnetic islands is an interesting and important research topic, which will be further studied in future work.
= 1.0%, the 2/4 magnetic islands are fully suppressed by TFC. How to control magnetic islands is an interesting and important research topic, which will be further studied in future work.
5. Conclusion
Characteristics of MHD activities and plasma transport affected by self-consistent bootstrap currents are studied in free boundary equilibria of CFQS. The bootstrap currents are calculated accurately with the SFINCS code. The volume-averaged normalized pressure is scanned from 0.00% to 2.03% and the bootstrap current is enhanced to 54 kA.
The interchange modes are stabilized by the magnetic shear and magnetic well effects, which are able to suppress the unfavorable effect of the geodesic curvature till β = 2.03%. In the free boundary equilibria without bootstrap currents, interchange modes were also stable up to β = 2.0% in CFQS [9]. However, the magnetic shear has not been produced as β increased and these modes were merely stabilized by a magnetic well structure. Furthermore, with β exceeding 1.35%, the current-driven kink modes become unstable and the dominant mode is m/n = 2/1. This instability is sensitive to the rotational transform at the edge and as the iota value is higher than 0.5, this instability arises. Such a dependence was also found in the CHS-qa configuration [29].
From 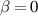 to 1.5%, the
to 1.5%, the 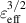 , L1,1 and L1,2 in the CFQS configurations are quite low and the QA property is sustained well. Whereas, as plasma
, L1,1 and L1,2 in the CFQS configurations are quite low and the QA property is sustained well. Whereas, as plasma 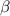 increases to 2.0%, these neoclassical transport coefficients grow significantly in the core regions, which result from an increase of non-axisymmetric magnetic field components due to unfavorable deformations of the QA configuration.
increases to 2.0%, these neoclassical transport coefficients grow significantly in the core regions, which result from an increase of non-axisymmetric magnetic field components due to unfavorable deformations of the QA configuration.
Additionally, the extension of maximum-J regions can be achieved by increasing bootstrap currents, which is beneficial for mitigating trapped-electron-driven microinstabilities. The numerical result is consistent with the analytical studies.
In conclusion, a stable plasma with good confinement properties in  equilibria is expected to be experimentally accomplishable in CFQS.
equilibria is expected to be experimentally accomplishable in CFQS.
Acknowledgments
The authors are very grateful and indebted to M Landreman, S A Lazerson, T Goerler and P Xanthopoulos for useful discussions and support. The research was supported by National Supercomputing Center in Chengdu. This work was partly supported by the National Natural Science Foundation of China under Grant Nos. 12175185, 11820101004 and U22A20262, the Chinese National Fusion Project for ITER under Grant No.2022YFE03070001, the Advanced Foreign Expert Introduction Program under Grant No. G20200023025, the Sichuan International Science and Technology Innovation Cooperation Project under Grant No. 2021YFH0066, NIFS international collaborations with overseas laboratories (UFEX105), NIFS promotion of magnetic confinement research using helical devices in Asia (URSX401), the NIFS general collaboration project, NIFS18KBAP041, NIFS20KBAP067, NIFS20KBAE001, NIFS22KIPH009, NIFS22KIPH011 and NIFS22KIEE001 and 'PLADyS', JSPS Core-to-Core Program, A Advanced Research Networks.
Appendix:
In order to assess the possible formation of magnetic islands and chaotic magnetic fields in CFQS, we apply the multi-region relaxed MHD (MRXMHD) framework based on the Taylor's relaxation theory [57] to develop MHD equilibria with the stepped-pressure equilibrium code (SPEC) [58]. SPEC allows the plasma to undergo possible magnetic reconnection events that would minimize the plasma potential energy. In this work, we consider two interfaces so that the entire plasma volume is divided into three distinct sub-volumes in CFQS equilibria. Given that both relaxed regions and ideal interfaces exist in MRXMHD, two types of toroidal currents coexist, namely currents flowing in sub-volumes and current sheets in ideal interfaces [59]. Meanwhile, the spatially distributed current density in each sub-volume can change self-consistently with variations of magnetic islands and stochasticities. The stepped pressure profile is interpolated from the VMEC output. Figure A1 displays Poincaré sections of the equilibrium magnetic fields calculated from the SPEC code with increasing values of  and self-consistent bootstrap currents. The magnetic islands emerge in the edge plasma domain at around
and self-consistent bootstrap currents. The magnetic islands emerge in the edge plasma domain at around  = 1.0% in figure A1(a). This is due to the rotational transform crossing the rational surface with ι = 2/4 = 1/2 (see figure 1). In the CFQS device, 12 planar TFC have been designed to adjust the rotational transform profile, healing magnetic islands. With the ratio of the current in TFC to that in MC, ITFC/ IMC = 15%, a strong resilience against magnetic islands and chaos is produced and the 2/4 magnetic islands are well suppressed in figure A1(b).
= 1.0% in figure A1(a). This is due to the rotational transform crossing the rational surface with ι = 2/4 = 1/2 (see figure 1). In the CFQS device, 12 planar TFC have been designed to adjust the rotational transform profile, healing magnetic islands. With the ratio of the current in TFC to that in MC, ITFC/ IMC = 15%, a strong resilience against magnetic islands and chaos is produced and the 2/4 magnetic islands are well suppressed in figure A1(b).
Figure A1. (a) Without and (b) with considering TFC, Poincaré plots of the poloidal cross section with the bean shape in the MHD equilibria with 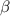 = 1.0%. The ratio of the current in TFC to that in MC ITFC/ IMC = 15%.
= 1.0%. The ratio of the current in TFC to that in MC ITFC/ IMC = 15%.
Download figure:
Standard image High-resolution image