Abstract
A new type of fast particle instability involving axisymmetric modes in magnetic fusion tokamak plasmas is presented. The relevant dispersion relation involves three roots. One corresponds to a vertical plasma displacement that, in the absence of active feedback stabilization, grows on the wall resistivity time scale. The other two, oscillating close to the poloidal Alfvén frequency, are normally damped by wall resistivity. The resonant interaction with fast ions can drive the oscillatory roots unstable. Resonance conditions, stability thresholds and experimental evidence are discussed.
Export citation and abstract BibTeX RIS
It is well known that tokamak plasmas with non-circular cross sections are prone to an instability, involving axisymmetric modes with toroidal mode number n = 0, which, if left uncontrolled, would lead to vertical displacement events (VDE) and plasma current disruptions. As shown in the pioneering work by Laval et al [1], a nearby perfectly conducting wall can provide passive feedback stabilization. For the realistic case of a resistive wall, the relevant dispersion relation is cubic [2]. Two roots correspond to weakly damped oscillations, with a frequency close to the poloidal Alfvén frequency and damping rate of the order of the inverse of the resistive wall time. The third one is unstable, growing on the resistive wall time, and its complete suppression requires an active feedback stabilization system, whose principle and practical implementation have been the subject of several contributions (see, e.g., references [3–9]). Here, we focus our attention on the two oscillatory roots, and show that they can be driven unstable by the resonant interaction with energetic ions. This fast-ion-driven vertical mode (in brief, FIDVM; see reference [10] for a preliminary account) adds to the catalog of potentially dangerous fast ion instabilities in tokamak fusion plasmas [11, 12]. We suggest that the FIDVM may provide a possible explanation for the saturated n = 0 Alfvén oscillations observed in recent beam-injected JET experiments with additional ICRF heating, tentatively interpreted in reference [13] in terms of n = 0 global Alfvén eigenmodes (GAEs). We point out that the FIDVM is a mode with a discrete frequency below the minimum value of the poloidal Alfvén frequency, not affected by continuum damping. Thus, its frequency does not depend on transient details of the safety factor profile, and as such it appears to be also a robust candidate, on the same footing as GAE, for the interpretation of the JET n = 0 observations.
The FIDVM dispersion relation is derived within the framework of the hybrid kinetic-MHD model [14]. The bulk thermal plasma is described according to ideal-MHD, while the fast particles are modelled by the collisionless drift-kinetic equation [15]. We study the resonant interaction between the oscillatory branch of the n = 0 dispersion relation and fast ions. We evaluate the contributions of particles with trapped and passing orbits to the mode growth rate and the conditions under which these can overcome the damping associated with wall resistivity. We show that instability requires a fast ion distribution function with positive derivative as function of energy. The experimental conditions under which such distribution can be realized are discussed below.
The magnetic field is represented as B = eϕ
× ∇ψ + Bϕ
eϕ
, where eϕ
is the unit vector along the toroidal direction, and Bϕ
is nearly constant. The plasma flow is v = eϕ
× ∇φ. The magnetic flux function, ψ, and the stream function, φ, obey the dimensionless equations: ![${\partial }_{t}\psi +\left[\varphi ,\psi \right]=0$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn1.gif) ;
; ![${\partial }_{t}\,\nabla \cdot \left(\varrho \,\nabla \varphi \right)+\left[\varrho ,{(\nabla \varphi )}^{2}\right]/2+U\left[\varphi ,\varrho \right]+\left[\varphi ,U\right]=\left[\psi ,J\right]-{\boldsymbol{e}}_{\phi }\cdot \nabla \times \nabla \cdot {\boldsymbol{\mathcal{P}}}_{\text{h}}$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn2.gif) , where
, where ![$\left[\chi ,\eta \right]={\mathbf{e}}_{\phi }\cdot \nabla \chi \times \nabla \eta $](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn3.gif) , J = ∇2
ψ is the current density, and U = ∇2
φ is the flow vorticity. The fast particles pressure tensor is defined as
, J = ∇2
ψ is the current density, and U = ∇2
φ is the flow vorticity. The fast particles pressure tensor is defined as 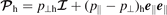 , where
e
∥
=
B
/B, p⊥h and p∥h are moments of the fast ions distribution function, which obeys the collisionless drift-kinetic equation. The normalization is standard, see reference [10] for details. Time is normalized to the poloidal Alfvén time,
, where
e
∥
=
B
/B, p⊥h and p∥h are moments of the fast ions distribution function, which obeys the collisionless drift-kinetic equation. The normalization is standard, see reference [10] for details. Time is normalized to the poloidal Alfvén time, 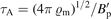 , with ϱm the on-axis mass density and
, with ϱm the on-axis mass density and 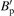 the on-axis derivative of the equilibrium poloidal field; space is normalized to a convenient equilibrium scale length,
the on-axis derivative of the equilibrium poloidal field; space is normalized to a convenient equilibrium scale length, ![${r}_{0}=a\,b/{[\left({a}^{\,2}+{b}^{\,2}\right)/2]}^{1/2}$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn7.gif) with a and b the minor and major semi-axes of the elliptical plasma boundary.
with a and b the minor and major semi-axes of the elliptical plasma boundary.
At equilibrium, we assume stationary fields, no flows, and isotropic fast ions (p∥h,eq = p⊥h,eq). To allow for analytic work, and since toroidal effects and current density gradients are not expected to affect the MHD response of the bulk plasma to axisymmetric perturbations, the particle and current densities are taken uniform up to an elliptical boundary, μ = μb, where (μ, ϑ) are elliptical coordinates: x = A sinh(μ)cos(ϑ); y = A cosh(μ)sin(ϑ);  . The equilibrium current density is Jeq(μ) = 2H(μb − μ), where H(x) is the unit step function. The equilibrium magnetic flux is ψeq = (x2/a2 + y2/b2)/2 for μ ⩽ μb,
. The equilibrium current density is Jeq(μ) = 2H(μb − μ), where H(x) is the unit step function. The equilibrium magnetic flux is ψeq = (x2/a2 + y2/b2)/2 for μ ⩽ μb, ![${\psi }_{\text{eq}}=1/2+{{\alpha }_{0}}^{2}\left\{\mu -{\mu }_{b}-{e}_{0}\,\mathrm{sinh}\left[2(\mu -{\mu }_{\text{b}})\right]\mathrm{cos}(2\vartheta )\right\}/2$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn9.gif) for μ > μb, where
for μ > μb, where 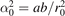 and e0 = (b2 − a2)/(b2 + a2) is the ellipticity parameter. The equilibrium flux exhibits X-points outside the plasma, located at μ = 2μb, ϑ = (π/2, 3π/2). More details on the equilibrium solution can be found in references [16, 17].
and e0 = (b2 − a2)/(b2 + a2) is the ellipticity parameter. The equilibrium flux exhibits X-points outside the plasma, located at μ = 2μb, ϑ = (π/2, 3π/2). More details on the equilibrium solution can be found in references [16, 17].
Let 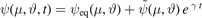 and
and  , where the over-tilde denotes small perturbations. To first order in perturbed quantities,
, where the over-tilde denotes small perturbations. To first order in perturbed quantities,
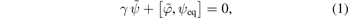
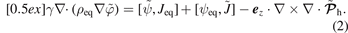
We multiply equation (2) by 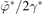 and integrate over the whole volume. After straightforward algebra, we obtain a standard expression for the dispersion relation in terms of quadratic forms,
and integrate over the whole volume. After straightforward algebra, we obtain a standard expression for the dispersion relation in terms of quadratic forms,
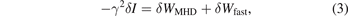
where  ,
, 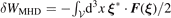 and
and 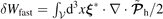 . All the integrals extend over the plasma volume
. All the integrals extend over the plasma volume 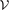 , the displacement vector is
, the displacement vector is  and the reduced MHD force operator is
and the reduced MHD force operator is  .
.
Firstly, we neglect energetic particles. As shown in [10], the rigid-shift vertical displacement,  , with ξ = const, is the exact solution of equations (1) and (2) for the considered equilibrium. The perturbed flux in the plasma region is obtained from equation (1). In the vacuum region, the flux is modified by the presence of a nearby resistive wall, assumed to lie on an elliptical surface, μ = μw, confocal with the plasma elliptical boundary, as in reference [1]. Considering a thin wall, we solve analytically for
, with ξ = const, is the exact solution of equations (1) and (2) for the considered equilibrium. The perturbed flux in the plasma region is obtained from equation (1). In the vacuum region, the flux is modified by the presence of a nearby resistive wall, assumed to lie on an elliptical surface, μ = μw, confocal with the plasma elliptical boundary, as in reference [1]. Considering a thin wall, we solve analytically for  and obtain the expected cubic dispersion relation for the n = 0 mode:
and obtain the expected cubic dispersion relation for the n = 0 mode:
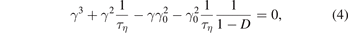
where  and
and
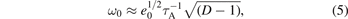
with τη
the resistive wall time and ![$D=\left[\mathrm{exp}(4{\mu }_{\text{b}})+1\right]/\left[\mathrm{exp}(2{\mu }_{\text{w}})+1\right]$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn23.gif) a geometrical factor that depends on the distance between the plasma boundary and the wall [1]. If μw = 2μb, the wall intercepts the X-points and D = 1. Values of D > 1 are obtained if the X-points lie outside the wall, 2μb > μw > μb. The criterion D > 1 corresponds to passive feedback stabilization of the n = 0 mode in the ideal wall limit (τη
→ ∞) and it is the scenario assumed in the remainder of this article. In an actual tokamak with a divertor separatrix, the plasma extends to the X-points, which lie inside the wall, and additional plasma facing components are introduced inside the vacuum chamber to ensure passive feedback stabilization. Furthermore, as shown in [18], even in the no-wall limit (μw → ∞), the ideal-MHD constraint imposed on the X-points leads to current sheets, localized on the magnetic separatrix, adding an important ingredient to the n = 0 stability properties. The latter scenario requires careful treatment of the ideal-MHD X-point resonance and is beyond the scope of the present article.
a geometrical factor that depends on the distance between the plasma boundary and the wall [1]. If μw = 2μb, the wall intercepts the X-points and D = 1. Values of D > 1 are obtained if the X-points lie outside the wall, 2μb > μw > μb. The criterion D > 1 corresponds to passive feedback stabilization of the n = 0 mode in the ideal wall limit (τη
→ ∞) and it is the scenario assumed in the remainder of this article. In an actual tokamak with a divertor separatrix, the plasma extends to the X-points, which lie inside the wall, and additional plasma facing components are introduced inside the vacuum chamber to ensure passive feedback stabilization. Furthermore, as shown in [18], even in the no-wall limit (μw → ∞), the ideal-MHD constraint imposed on the X-points leads to current sheets, localized on the magnetic separatrix, adding an important ingredient to the n = 0 stability properties. The latter scenario requires careful treatment of the ideal-MHD X-point resonance and is beyond the scope of the present article.
Solving for γ = −iω in the limit D > 1 and small resistivity γ0 τη ≫ 1, we obtain the three relevant roots.
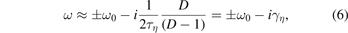

The two stable roots in (6) oscillate at frequency ω = ±ω0. As anticipated, the damping rate ![${\gamma }_{\eta }=D/\left[2{\tau }_{\eta }(D-1)\right]$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn24.gif) is related to the resistive wall time, but the resonant interaction with fast ions can destabilize these modes, as shown in the following. The third root corresponds to the unstable n = 0 resistive wall mode, which is normally suppressed by active feedback stabilization.
is related to the resistive wall time, but the resonant interaction with fast ions can destabilize these modes, as shown in the following. The third root corresponds to the unstable n = 0 resistive wall mode, which is normally suppressed by active feedback stabilization.
Let us now consider the effects of energetic particles, represented by the last term in equation (3). We adopt a perturbative approach. We introduce the small expansion parameter,  h = βh/βc ≪ 1, i.e., the ratio between energetic particle and core plasma pressures. In this limit, |δWMHD| ≫ |δWfast|. The cubic dispersion relation, equation (4), is recovered to zeroth order in
h = βh/βc ≪ 1, i.e., the ratio between energetic particle and core plasma pressures. In this limit, |δWMHD| ≫ |δWfast|. The cubic dispersion relation, equation (4), is recovered to zeroth order in  h. Following a standard procedure [15, 19], the quadratic term related to energetic particles can be written as δWfast = δWh,ad + δWh,nad. Here, the first term (the 'adiabatic' part) is fluid-like and purely real; the second term ('non-adiabatic') has both real and imaginary parts, the latter contributed by the resonant fast ions. The real part of δWfast gives rise to
h. Following a standard procedure [15, 19], the quadratic term related to energetic particles can be written as δWfast = δWh,ad + δWh,nad. Here, the first term (the 'adiabatic' part) is fluid-like and purely real; the second term ('non-adiabatic') has both real and imaginary parts, the latter contributed by the resonant fast ions. The real part of δWfast gives rise to 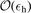 corrections to the n = 0 oscillation frequency and thus can be neglected. On the other hand, the imaginary part of δWfast contributes to the n = 0 growth rate, competing with the damping term γη
. Accordingly, only the imaginary part of δWfast is retained in the following.
corrections to the n = 0 oscillation frequency and thus can be neglected. On the other hand, the imaginary part of δWfast contributes to the n = 0 growth rate, competing with the damping term γη
. Accordingly, only the imaginary part of δWfast is retained in the following.
Thus, we are led to the following dispersion relation for the two oscillatory n = 0 modes modified by fast ions:
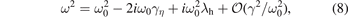
where 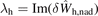 is a dimensionless parameter and
is a dimensionless parameter and 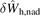 the properly normalized quadratic form. Leading order solutions for the real and imaginary parts of the mode frequency are ω = ±ω0 + iγtot, where γtot = ω0
λh/2 − γη
. In order to determine the stability threshold, detailed analysis of δWh,nad is necessary. For n = 0 modes:
the properly normalized quadratic form. Leading order solutions for the real and imaginary parts of the mode frequency are ω = ±ω0 + iγtot, where γtot = ω0
λh/2 − γη
. In order to determine the stability threshold, detailed analysis of δWh,nad is necessary. For n = 0 modes:
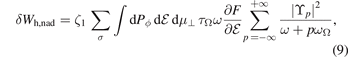
where ζ1 = −(2π2
c)/(Zem2) and F is the unperturbed fast ion distribution function. The σ-summation is over co- and counter-circulating particle orbits, and integration is performed over the three invariants of particle motion: toroidal canonical momentum Pϕ
, energy  , and magnetic moment μ⊥; ωΩ is the bounce frequency of trapped/passing particle orbits, and τΩ = 2π/ωΩ. The p-summation is the Fourier expansion of the perturbed Lagrangian over the harmonics of the unperturbed particle orbits, labelled by integer p, with Fourier coefficients
, and magnetic moment μ⊥; ωΩ is the bounce frequency of trapped/passing particle orbits, and τΩ = 2π/ωΩ. The p-summation is the Fourier expansion of the perturbed Lagrangian over the harmonics of the unperturbed particle orbits, labelled by integer p, with Fourier coefficients
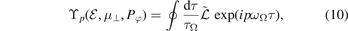
where the loop integral is over a closed banana/transit orbit, and the perturbed Lagrangian is 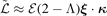 , with r the radial variable and
κ
the curvature vector [15]. We consider the 'thin-orbit' approximation, where the radial excursion of both passing and trapped orbits from a reference magnetic surface is negligibly small.
, with r the radial variable and
κ
the curvature vector [15]. We consider the 'thin-orbit' approximation, where the radial excursion of both passing and trapped orbits from a reference magnetic surface is negligibly small.
To leading order in the parameter  h, the displacement vector
ξ
corresponds to the rigid-shift vertical displacement, which is orthogonal to the main direction of toroidal curvature. Since the perturbed Lagrangian is proportional to the scalar product
ξ
⋅
κ
, the interesting consequence is that toroidal curvature contributions to
h, the displacement vector
ξ
corresponds to the rigid-shift vertical displacement, which is orthogonal to the main direction of toroidal curvature. Since the perturbed Lagrangian is proportional to the scalar product
ξ
⋅
κ
, the interesting consequence is that toroidal curvature contributions to 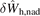 are negligibly small. The perturbed Lagrangian can be rewritten as
are negligibly small. The perturbed Lagrangian can be rewritten as  with
with  = r/R0, R0 the tokamak major radius and θ the standard poloidal angle. The pitch angle variable
= r/R0, R0 the tokamak major radius and θ the standard poloidal angle. The pitch angle variable  ranges from 0 ⩽ Λ ⩽ 1 −
ranges from 0 ⩽ Λ ⩽ 1 −  for passing orbits, to 1 −
for passing orbits, to 1 −  ⩽ Λ ⩽ 1 +
⩽ Λ ⩽ 1 +  for trapped orbits.
for trapped orbits.
The mode-particle resonant condition is ω + pωΩ = 0. Note that the p = 0 harmonic is non resonant. The resonant frequency is proportional to the particle velocity, v, as we can write ωΩ = vhΩ(r, Λ)/(R0 q), where the safety factor q = rBϕ /(R0 Bp) is approximately constant and the dimensionless function hΩ involves well-known combinations of elliptic integrals. Changing integration variables, the pole contribution yields
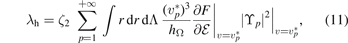
where 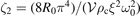 , ρc is the core mass density and
, ρc is the core mass density and ![${v}_{p}^{\ast }={\omega }_{0}{R}_{0}q/\left[p{h}_{{\Omega}}(r,{\Lambda})\right]$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn34.gif) is the resonant velocity.
is the resonant velocity.
Clearly, the sign of λh depends on the derivative of the fast particles equilibrium distribution function with respect to energy. Instability requires  , giving rise to a positive λh. Such a distribution can be obtained, for instance, from Fokker–Plank calculations including a fast particles loss term, as shown in reference [20]. We consider a simplified model with a monochromatic source term at velocity vfast, and a velocity-independent loss frequency, νloss. Assuming a uniform radial distribution of fast ions up to r = rh, and solving the relevant Fokker–Plank equation, we obtain
, giving rise to a positive λh. Such a distribution can be obtained, for instance, from Fokker–Plank calculations including a fast particles loss term, as shown in reference [20]. We consider a simplified model with a monochromatic source term at velocity vfast, and a velocity-independent loss frequency, νloss. Assuming a uniform radial distribution of fast ions up to r = rh, and solving the relevant Fokker–Plank equation, we obtain
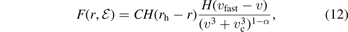
where C is a normalization constant, α = νloss
τs/3 and vc ≪ vfast is the critical velocity. With this model, when the fast particle slowing down time, τs, is larger than the loss time, τloss = 1/νloss, the usual, monotonically decreasing slowing down distribution cannot form, and F develops a positive slope as function of energy. Experimental evidence indicates that  can also be induced by a time-dependent source, see reference [21] for the case of modulated neutral beam injection. Another relevant scenario is discussed in [22], where source modulation is caused by sawtooth oscillations. Finally, as discussed in [23] in connection with the excitation of n = 0 geodesic acoustic modes, a fast ion distribution arising from neutral beam injection, with a positive slope as function of energy, can be observed on time intervals, following neutral beam injection time, that are short compared with the fast ion slowing down time.
can also be induced by a time-dependent source, see reference [21] for the case of modulated neutral beam injection. Another relevant scenario is discussed in [22], where source modulation is caused by sawtooth oscillations. Finally, as discussed in [23] in connection with the excitation of n = 0 geodesic acoustic modes, a fast ion distribution arising from neutral beam injection, with a positive slope as function of energy, can be observed on time intervals, following neutral beam injection time, that are short compared with the fast ion slowing down time.
Next, we investigate the Fourier coefficients ϒp
. We are going to show that passing particles contribute mostly to the p = 1 harmonic, trapped particles mostly to the p = 1 and p = 2 harmonics, while all other harmonics can be neglected. This result is obtained in the thin-orbit limit, where r ≈ const along the particle orbit and the perturbed Lagrangian depends on time only through the poloidal angle θ. Therefore, we can set 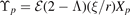 , where Xp
= ⟨sin(θ)exp(ipωΩ
τ)⟩ and ⟨⟩ means orbit averaging.
, where Xp
= ⟨sin(θ)exp(ipωΩ
τ)⟩ and ⟨⟩ means orbit averaging.
Let us consider the transit frequency of passing particles, ![${\omega }_{{\Omega}}\to {\omega }_{t}=\pi v\kappa \sqrt{{\epsilon}/2}/\left[{R}_{0}qK(1/{\kappa }^{2})\right]$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn38.gif) , where K(x) is the complete elliptic integral of the first kind and κ2 = 1/2 + (1 − Λ)/(2
, where K(x) is the complete elliptic integral of the first kind and κ2 = 1/2 + (1 − Λ)/(2 ) (for passing orbits, κ ⩾ 1). We find that ωt
τ = πF(θ/2|1/κ2)/K(1/κ2) ≈ θ, where F(ϕ|x2) is the incomplete elliptic integral of the first kind and the last equality is valid for most values of κ, with the exception of κ very close to unity, which corresponds to the barely passing limit. Since for barely passing particles ωt
→ 0, these particles are non-resonant, and so their contribution to λh can be safely neglected. In this way, Xp
reduces to
) (for passing orbits, κ ⩾ 1). We find that ωt
τ = πF(θ/2|1/κ2)/K(1/κ2) ≈ θ, where F(ϕ|x2) is the incomplete elliptic integral of the first kind and the last equality is valid for most values of κ, with the exception of κ very close to unity, which corresponds to the barely passing limit. Since for barely passing particles ωt
→ 0, these particles are non-resonant, and so their contribution to λh can be safely neglected. In this way, Xp
reduces to ![$i(1/4K(1/{\kappa }^{2})){\int }_{0}^{2\pi }\mathrm{d}\theta \left[\mathrm{sin}(\theta )\mathrm{sin}(p\theta )\right]/\sqrt{1-{\mathrm{sin}}^{2}(\theta /2)/{\kappa }^{2}}$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn39.gif) , and in the asymptotic limit κ ≫ 1,
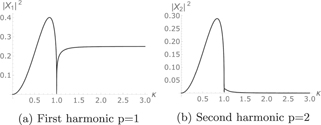
, and in the asymptotic limit κ ≫ 1, 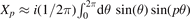 . It is clear that the only harmonic that contributes in this limit is p = 1, while the average is zero for all other p values. Figure 1 displays |Xp
|2 for the first two harmonics as functions of κ, showing that even considering all κ values the contribution of passing particles for harmonics with p > 1 is indeed negligible.
. It is clear that the only harmonic that contributes in this limit is p = 1, while the average is zero for all other p values. Figure 1 displays |Xp
|2 for the first two harmonics as functions of κ, showing that even considering all κ values the contribution of passing particles for harmonics with p > 1 is indeed negligible.
Figure 1. Plots of |Xp |2 = |⟨sin(θ)exp(ipωΩ τ)⟩|2 as a function of κ for p = 1 and p = 2 harmonics.
Download figure:
Standard image High-resolution imageFor trapped particles, 0 ⩽ κ ⩽ 1, the bounce frequency is ![${\omega }_{{\Omega}}\to {\omega }_{\text{b}}=\pi v\sqrt{{\epsilon}/2}/\left[2{R}_{0}qK({\kappa }^{2})\right]$](https://content.cld.iop.org/journals/0029-5515/62/6/064002/revision2/nfac5ad0ieqn41.gif) . Then, ωb
τ = π/2F(ζ|κ2)/K(κ2), where sin(θ/2) = κ sin(ζ). For κ sufficiently far from the barely trapped limit κ = 1, where the bounce frequency drops to 0, it is possible to approximate ωb
τ ≈ ζ. Therefore, one obtains
. Then, ωb
τ = π/2F(ζ|κ2)/K(κ2), where sin(θ/2) = κ sin(ζ). For κ sufficiently far from the barely trapped limit κ = 1, where the bounce frequency drops to 0, it is possible to approximate ωb
τ ≈ ζ. Therefore, one obtains 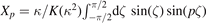 . As shown in figure 1, this is zero for both barely trapped (κ = 1) and deeply trapped (κ = 0) particles. It can be shown that all even-p harmonics yield a non-zero Xp
; however, values of Xp
with p ⩾ 4 are negligibly small. For odd-p values, Xp
= 0, with the only exception of p = 1. Thus, we conclude that only the p = 1 and p = 2 harmonics are of interest. In figure 1, values of |Xp
|2 for the p = 1 and p = 2 harmonics are plotted as functions of κ.
. As shown in figure 1, this is zero for both barely trapped (κ = 1) and deeply trapped (κ = 0) particles. It can be shown that all even-p harmonics yield a non-zero Xp
; however, values of Xp
with p ⩾ 4 are negligibly small. For odd-p values, Xp
= 0, with the only exception of p = 1. Thus, we conclude that only the p = 1 and p = 2 harmonics are of interest. In figure 1, values of |Xp
|2 for the p = 1 and p = 2 harmonics are plotted as functions of κ.
The reason why deeply trapped (κ = 0) as well as barely trapped/passing (κ = 1) particles do not contribute to ϒp , and thus to λh, is very simple. For n = 0 vertical displacements, ξ ⋅ κ ∼ sin θ. Deeply trapped particles are localized near θ = 0; barely trapped particles spend most of their time near θ = π; hence, the orbit-averaged value of the scalar product ξ ⋅ κ vanishes in both these limits.
In order to determine stability thresholds, we consider the model distribution function in equation (12), where the normalization constant is determined by ∫d3 vF = nh, with nh the fast particle density. After straightforward algebra, we obtain

where nc is the core plasma density, mc and mh are the core and fast particle mass, respectively, and  is the resonant velocity of passing particles with Λ = 0. We can write
is the resonant velocity of passing particles with Λ = 0. We can write  , where
, where  is a dimensionless factor that depends on three parameters. Inserting this expression for λh in equation (8), the instability threshold can be cast in the form
is a dimensionless factor that depends on three parameters. Inserting this expression for λh in equation (8), the instability threshold can be cast in the form
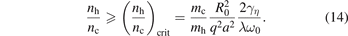
To gain further insight on realistic numerical values for the critical density threshold, we consider the parameters of the JET experiments discussed in reference [13], where saturated n = 0 oscillations were observed, and MeV fast ions were produced by a combination of ICRH and NBI. Some parameters are experimentally well known, e.g., R0 = 3 m, a = 0.9 m, elongation b/a ≈ 1.3, which corresponds to e0 ≈ 0.3, toroidal magnetic field BT = 2.2 T, q ≈ 1, and deuterium main ion species, yielding an inverse poloidal Alfvén time 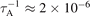 s−1. The experimentally observed n = 0 oscillation frequency is in the range f0 = ω0/2π ≈ 300 kHz, which compares well with the theoretical predicted value of the frequency ω0, defined below equation (4), if we assume realistic values for the geometrical factor, D ≈ 3. Fast ions in the mentioned JET experiments are also mostly deuterium, thus we take mh/mc = 1. We assume rh/a = 0.5 and α ≈ 2. The remaining parameter to be evaluated,
s−1. The experimentally observed n = 0 oscillation frequency is in the range f0 = ω0/2π ≈ 300 kHz, which compares well with the theoretical predicted value of the frequency ω0, defined below equation (4), if we assume realistic values for the geometrical factor, D ≈ 3. Fast ions in the mentioned JET experiments are also mostly deuterium, thus we take mh/mc = 1. We assume rh/a = 0.5 and α ≈ 2. The remaining parameter to be evaluated,  , depends on the fast ion cut-off energy,
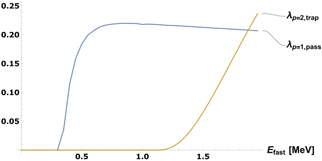
, depends on the fast ion cut-off energy,  . Realistic JET estimates indicate values of Efast in the MeV range. We can see that the p = 1 harmonic, contributed by the passing particles, is the leading contribution for fast ion energies up to ∼1.5 MeV. At higher energies, the p = 2 harmonic contributed by trapped particles can also give a significant contribution. On the other hand, for the considered parameters, the p = 1 harmonic contributed by trapped particles gives a non-zero contribution only for cut-off energy Efast ⩾ 5 MeV. Let us write λ = λp=1,pass + λp=2,trap. In figure 2, we present plots of these quantities as functions of Efast, having fixed all the other parameters to the JET-relevant values indicated above. The overall value of the parameter λ is estimated of order 3 × 10−1 for the JET experiments of interest.
. Realistic JET estimates indicate values of Efast in the MeV range. We can see that the p = 1 harmonic, contributed by the passing particles, is the leading contribution for fast ion energies up to ∼1.5 MeV. At higher energies, the p = 2 harmonic contributed by trapped particles can also give a significant contribution. On the other hand, for the considered parameters, the p = 1 harmonic contributed by trapped particles gives a non-zero contribution only for cut-off energy Efast ⩾ 5 MeV. Let us write λ = λp=1,pass + λp=2,trap. In figure 2, we present plots of these quantities as functions of Efast, having fixed all the other parameters to the JET-relevant values indicated above. The overall value of the parameter λ is estimated of order 3 × 10−1 for the JET experiments of interest.
Figure 2. Coefficients λp=1,pass and λp=2,trap as function of fast ion cut-off energy Efast.
Download figure:
Standard image High-resolution imageThe damping rate due to the resistive wall can be estimated of the order of γη
∼ 3 × 102 s−1. As a consequence, the critical instability threshold for the relevant JET experiments can be estimated to be 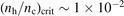 .
.
In this analysis, we have restricted ourselves to fast ion distribution functions that are isotropic in velocity space. In principle, pitch-angle anisotropy may also contribute to the instability drive. This should make the instability more ubiquitous in many tokamak experiments, where fast ions are produced by neutral beam injection and/or by ion cyclotron radio frequency heating. The effect of velocity space anisotropy will be investigated in a future article.
As we have already pointed out, the theory presented in this article is motivated in part by the observation of saturated n = 0 fluctuations, with a frequency of the order of the poloidal Alfvén frequency, in recent JET experiments where fast ions are produced by auxiliary heating, see reference [13]. At that time, the FIDVM instability was not a known concept, and the observations were tentatively interpreted in [13] in terms of a saturated n = 0 GAE. It is early for us to conclude whether, in fact, the mode observed at JET is a FIDVM rather than a GAE: more experiments are required, but also, the theory developed here ought to be developed further. Nevertheless, we can indicate what are the main points of distinction between GAE and FIDVM that may facilitate the experimental identification. These are basically three. First, the GAE mode frequency for n = 0 is given by [24]  , where τA is the poloidal Alfvén as defined in the first page of this article. On the other hand, the FIDVM mode frequency is given by equation (5), and, taking the parameter D of order unity, it falls below the GAE mode frequency, since the ellipticity parameter e0 is typically below unity. Secondly, the FIDVM scales as the square root of e0, while the n = 0 GAE mode frequency is independent of elongation. Indeed, the GAE would survive in the circular limit, while the FIDVM would not. Thirdly, and perhaps most importantly, the FIDVM mode structure is different from that of the GAE. The FIDVM is a vertical mode, corresponding to a vertical shift of the plasma cross section. This signature would be easily detected by magnetic perturbation coils placed top and bottom of the tokamak midplane. The GAE mode structure favours instead a ballooning type of parity, with the relevant perturbed flux being an even function of the poloidal angle. It also happened at JET, as reported in reference [13], that the GAE mode frequency was close to the frequency of ellipticity-induced Alfvén eigenmodes (EAE) [25]. In this case, however, the distinction between the FIDVM and the EAE is easy, because EAEs are not axisymmetric (their toroidal mode number is n ≠ 0).
, where τA is the poloidal Alfvén as defined in the first page of this article. On the other hand, the FIDVM mode frequency is given by equation (5), and, taking the parameter D of order unity, it falls below the GAE mode frequency, since the ellipticity parameter e0 is typically below unity. Secondly, the FIDVM scales as the square root of e0, while the n = 0 GAE mode frequency is independent of elongation. Indeed, the GAE would survive in the circular limit, while the FIDVM would not. Thirdly, and perhaps most importantly, the FIDVM mode structure is different from that of the GAE. The FIDVM is a vertical mode, corresponding to a vertical shift of the plasma cross section. This signature would be easily detected by magnetic perturbation coils placed top and bottom of the tokamak midplane. The GAE mode structure favours instead a ballooning type of parity, with the relevant perturbed flux being an even function of the poloidal angle. It also happened at JET, as reported in reference [13], that the GAE mode frequency was close to the frequency of ellipticity-induced Alfvén eigenmodes (EAE) [25]. In this case, however, the distinction between the FIDVM and the EAE is easy, because EAEs are not axisymmetric (their toroidal mode number is n ≠ 0).
In conclusion, we have presented a new type of fast ion instability, dubbed FIDVM, involving n = 0 axisymmetric modes in a tokamak plasma, with a well defined, discrete frequency, 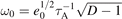 , determined by passive feedback stabilization of vertical displacements in plasma with elongated cross-section. The mode is driven unstable by a mode-particle resonant interaction involving fast ions on both trapped and passing orbits. Instability requires a fast ion distribution with a positive slope as function of energy. The critical fast ion density threshold for instability is determined by the competition between the mode-particle resonance drive and damping introduced by the resistive wall.
, determined by passive feedback stabilization of vertical displacements in plasma with elongated cross-section. The mode is driven unstable by a mode-particle resonant interaction involving fast ions on both trapped and passing orbits. Instability requires a fast ion distribution with a positive slope as function of energy. The critical fast ion density threshold for instability is determined by the competition between the mode-particle resonance drive and damping introduced by the resistive wall.
Even though the theory presented in this article is linear, it is appropriate to speculate on what might be the nonlinear consequences of this instability. Typically, n = 0 perturbations do not cause a direct radial transport of resonant particles; at most, we might expect that they induce a faster relaxation of the fast ion distribution function, by eliminating 'bumps' in the tail of the distribution, thus relaxing it faster to a standard slowing down distribution. On the other hand, vertical displacements are potentially dangerous, because of their connection with VDEs. One aspect of axisymmetric MHD modes that deserves further attention is the fact that these modes are resonant at the X-point(s) of a tokamak divertor [18]. The resonance is likely to drive perturbed current sheets in the vicinity of the X-points and extending along the separatrix, as numerical simulations reported, e.g., in reference [5] also seem to indicate. These current sheets may in turn affect the stability of edge-localized modes and, more in general, the dynamics of plasma flows in the divertor region.
The theoretical model presented in this article is a proof of concept, indicating that the FIDVM is a potential instability in fusion burning tokamak plasmas. Preliminary estimates indicate that the theoretically predicted mode frequency and stability threshold compare favourably with JET experimental results [13, 22]. However, a more detailed comparison between theory and experiments requires numerical work using realistic equilibria and a careful assessment of the fast ion distribution function.
Acknowledgments
The authors would like to thank Boris Breizman (University of Texas at Austin) and Sergei Sharapov (JET) for useful discussions. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under Grant Agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.