Abstract
Coherence distillation and dilution are two core problems in the manipulation of quantum resources. In this paper, we propose deterministic coherent distillation and dilution protocols, which fully demonstrate the change from the pure state to the maximum coherent state and vice versa. Our protocols can reach the theoretical value introduced in the upper bound proposed by Liu et al recently [Liu C L and Zhou D L Phys. Rev. Lett. 123 070 402 (2019)]. In particular, we propose pure distillation and dilution protocols through the majorization of the relation, which can be obtained by using the strictlyincoherent operators.
Export citation and abstract BibTeX RIS
1. Introduction
As a basic property of quantum mechanics, quantum coherence plays a major role in many quantum information processing tasks [3, 5, 6, 11] such as quantum resource theory [1, 4, 7], quantum cryptography [12], metrology [13], and randomness generation [2, 14, 15]. Recently, a restricted theoretical framework of resource of coherence has been introduced [5–9, 16–20]. Many researchers have focused on how to establish accurate physical and mathematical laws to guide the generation, manipulation, and transformation of quantum coherence and have achieved great progress in this field. There are two main ingredients in the resource theory of coherence: free states and free operations [5, 6, 10, 17]. The free states in the coherence theory are the density matrices which are diagonal in a fixed basis  ; free operations are some specified classes of physically realizable operations that act invariantly on the set of incoherent states. For the resource theory of coherence, a variety of free operations have been proposed based on different physical settings, and different free operations have different characteristics under different operations and applications [16–20]. In this work, we focus on the incoherent operation proposed by Baumgratz et al [20], and the strictly incoherent operation proposed by Winter and Yang [16].
; free operations are some specified classes of physically realizable operations that act invariantly on the set of incoherent states. For the resource theory of coherence, a variety of free operations have been proposed based on different physical settings, and different free operations have different characteristics under different operations and applications [16–20]. In this work, we focus on the incoherent operation proposed by Baumgratz et al [20], and the strictly incoherent operation proposed by Winter and Yang [16].
Coherence distillation and dilution are two important issues of quantum information processing. Coherence distillation is the process of extracting the pure coherent state of the general state by free operation, and the dilution problem is to convert a unit resource pure coherent state to the target state by free operation. For these two problems, one can consider two cases: the asymptotic regime and one-shot regime [21, 22, 26, 27]. Since the one-shot coherence dilution problem was proposed and fully addressed in [22], more and more attention has been paid to one-shot coherence manipulation. The standard one-shot distillation problem was fully addressed in [21] and [6]. Then, one-shot coherence distillation was extended to a few modified versions: probabilistic distillation, deterministic distillation, and distillation with catalysts. In this paper, we mainly discuss pure-state deterministic coherence distillation and coherence dilution under the one-shot regime, and present a protocol to calculate the explicit free operator under the maximum conversion rate. Our conclusion is consistent with that of Liu et al, when we distill a two-dimensional maximum coherent state [25]. Furthermore, we give deterministic coherent distillation and dilution protocols, which can achieve the optimal distillation dilution rate. We present an example to illustrate our result.
The remainder of the paper is organized as follows. In section 2, we briefly review the basic preliminaries used in this paper. In section 3, we introduce the majorization relation of the maximum proportion of deterministic pure state. In section 4, we propose the maximum proportion of deterministic pure-state dilution by majorization. We summarize our results in section 5.
2. Preliminaries
We first recall some necessary notations. We consider a Hilbert space  of finite dimension d. The incoherent basis of
of finite dimension d. The incoherent basis of  is fixed and denoted as
is fixed and denoted as  throughout this paper. A general resource theory for a quantum system has two components: free states and free operations. In the resource theory of coherence, a free state σ (incoherent state) can be written as
throughout this paper. A general resource theory for a quantum system has two components: free states and free operations. In the resource theory of coherence, a free state σ (incoherent state) can be written as  for a fixed basis
for a fixed basis  . A d dimensional pure coherent state is where
. A d dimensional pure coherent state is where  is a non-negative real number and
is a non-negative real number and  . The d dimensional maximum coherent state is
. The d dimensional maximum coherent state is  , and
, and
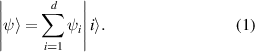
Different forms of the free operations in the resource theory of coherence have been proposed. A completely positive and trace-preserving (CPTP) map Φ is said to be incoherent operations (IO) if its Kraus operators Kn are of the form  , with j(i) being a (possibly many-to-one) function from the index set of the basis onto itself, and coefficients c(i) satisfying
, with j(i) being a (possibly many-to-one) function from the index set of the basis onto itself, and coefficients c(i) satisfying  [20]. If every
[20]. If every  satisfies that π(i) is a permutation, then the corresponding operation is a strictly incoherent operation (SIO) [16]. From their definitions, it is obvious that the relation SIO ⊂ IO holds.
satisfies that π(i) is a permutation, then the corresponding operation is a strictly incoherent operation (SIO) [16]. From their definitions, it is obvious that the relation SIO ⊂ IO holds.
Let us recall the notion of the majorization relationship, which plays an important role in pure-state transformation. Let  and
and  be two d-dimensional vectors. We use
be two d-dimensional vectors. We use  to indicate that the elements of x are rearranged in descending order, where
to indicate that the elements of x are rearranged in descending order, where  is the largest element of x. If
is the largest element of x. If  holds for
holds for  with equality holding when k = d, then x is majorized y (y majorizes x), written x ≺ y. When x ≺ y, only if
with equality holding when k = d, then x is majorized y (y majorizes x), written x ≺ y. When x ≺ y, only if  are pairs of a certain probability distribution pj and a permutation matrix Pj established. Du et al proved that the transformation of pure coherent states is also related to the majorization relationship [11]. Pure coherent state
are pairs of a certain probability distribution pj and a permutation matrix Pj established. Du et al proved that the transformation of pure coherent states is also related to the majorization relationship [11]. Pure coherent state  can be determined to be transformed into another pure coherent state
can be determined to be transformed into another pure coherent state  by incoherent operations if and only if
by incoherent operations if and only if  is majorized by
is majorized by  , written
, written  . We write µ(ψ) down as
. We write µ(ψ) down as  .
.
As is well known, it is important to study the coherence distillation and dilution. Next, we will introduce the notions of the one-shot coherence distillation and dilution.
The one-shot coherence distillation with error ε under general incoherent operation is defined as the maximum over all distillation rates, where  . When ε = 0, it is deterministic one-shot coherence distillation
. When ε = 0, it is deterministic one-shot coherence distillation
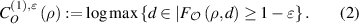
One-shot coherence cost measures the minimal length d such that  can be converted into a target state ρ via incoherent operations within some error. The one-shot coherence cost with an error tolerance of ε under general incoherent operation is defined as, where
can be converted into a target state ρ via incoherent operations within some error. The one-shot coherence cost with an error tolerance of ε under general incoherent operation is defined as, where ![$F(\rho, \sigma) = (\operatorname{\textrm{Tr}}[\sqrt{\sqrt{\rho} \sigma \sqrt{\rho}}])^{2}$](https://content.cld.iop.org/journals/1612-202X/17/8/085201/revision1/lplab7f3aieqn28.gif) is the fidelity measure between two states ρ and σ. When ε = 0, it is deterministic one-shot coherence dilution
is the fidelity measure between two states ρ and σ. When ε = 0, it is deterministic one-shot coherence dilution
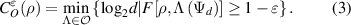
3. Deterministic pure-state distillation
Recently, Liu et al proposed a protocol of deterministic coherent distillation and gave the optimal distillation rate of the two-dimensional maximum coherent state. Base on their work, we study the deterministic coherent distillation of the pure state, and give the distillation rate of the d-dimensional maximum coherent state. As a follow-up study of their work, we further give a deterministic coherent distillation protocol and obtain the maximum coherent state obtained by the protocol. In this section, we discuss deterministic one-shot coherence distillation under SIO. Next, we give the general condition of any pure state  conversion to coherent state
conversion to coherent state  by majorization.
by majorization.
Proposition 1. The maximum number of d-dimensional maximally coherent states  that can distill from pure state
that can distill from pure state  is
is  . In particular, the maximum number of two-dimensional maximally coherent states
. In particular, the maximum number of two-dimensional maximally coherent states  that can distill from pure state
that can distill from pure state  is
is  . Here
. Here  represents the largest integer equal to or less than x.
represents the largest integer equal to or less than x.
Proof. By the condition of pure state for deterministic transformation by majorization condition when  , we can transform
, we can transform  deterministically to
deterministically to  . Suppose
. Suppose  , and
, and  are real vectors whose components are in decreasing order. If the maximum value is made to be
are real vectors whose components are in decreasing order. If the maximum value is made to be  , it must be that
, it must be that  , i.e.
, i.e.  . Then , when
. Then , when  , the maximum number of d-dimensional maximally coherent states
, the maximum number of d-dimensional maximally coherent states  that can distill from pure state
that can distill from pure state  . Similarly, when
. Similarly, when  , the maximum number of two-dimensional maximally coherent states
, the maximum number of two-dimensional maximally coherent states  that can distill from pure state
that can distill from pure state  . Thus, we complete our proof.
. Thus, we complete our proof.
Proposition 1 on optimal one-shot zero-error coherence distillation are directly implied by [PRL 121.010 401] [21]. This paper solves the problem of one-shot coherence distillation for general mixed states, allowing a small fidelity error. By setting this error parameter to zero and focusing on pure states, we immediately get proposition 1 presented here. However, our proposition uses the majorization relationship to define the maximum coherent state of coherent distillation. The pure-state distillation problem is transformed into the general pure-state transformation problem, and a new protocol is given by majorization relationship. In [21], the authors are more concerned about the transformation conditions from the initial state to the maximum coherent state. Unlike those protocols, we give the definite SIO operator on the basis of known transformation conditions. The main purpose of our protocol is to compute the certain SIO operator according to permutation relation, which can transform general state to maximally coherent state.
Next, we present a deterministic coherence distillation protocol for the pure staste  to coherent state
to coherent state  . First, let us introduce a SIO map Φs. Map Φs will be
. First, let us introduce a SIO map Φs. Map Φs will be  . Where
. Where  and
and ![$p_{s}^{i} = \operatorname{\textrm{Tr}}\left[K_{s}^{i} \rho_{\psi} K_{s}^{i}\right]$](https://content.cld.iop.org/journals/1612-202X/17/8/085201/revision1/lplab7f3aieqn56.gif) , it is obvious quantum operation Φs is a strictly incoherent operation, and its Kraus operators are also strictly incoherent.
, it is obvious quantum operation Φs is a strictly incoherent operation, and its Kraus operators are also strictly incoherent.  is a set of permutation arrangements, and there are multiple sets of different permutation relations corresponding to different
is a set of permutation arrangements, and there are multiple sets of different permutation relations corresponding to different  and
and  . cs denotes the matrix under different permutations, where csij is the element of the (ij)th under the matrix cs:
. cs denotes the matrix under different permutations, where csij is the element of the (ij)th under the matrix cs:
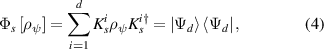
We first need to determine the permutation set  and use them to get the probability
and use them to get the probability  and a set of Kraus operators. The following equation can be obtained by
and a set of Kraus operators. The following equation can be obtained by 
wherethe coefficient csij is
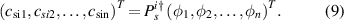
The first step is to find the permutation relationship. In the majorization relationship, x ≺ y if and only if  for some probability distribution pj and some permutation matrix Pj [28]. According to this, we can give all possible permutations. For all permutation relationships, we have
for some probability distribution pj and some permutation matrix Pj [28]. According to this, we can give all possible permutations. For all permutation relationships, we have  and ψn≥ 0. In the specific distillation process, from proposition 1 we can determine the optimal relations
and ψn≥ 0. In the specific distillation process, from proposition 1 we can determine the optimal relations  and
and  , but for the initial coherent state and other coefficients of the final coherent state, there are still d × (n − d) relations.
, but for the initial coherent state and other coefficients of the final coherent state, there are still d × (n − d) relations.
Table 1. All permutation relationships d × (n − d) of  .
.
| ψd + 1≥ 0 |  |
 |
... |  |
| ψd + 2≥ 0 |  |
 |
... |  |
| ... | ... | ... | ... | ... |
| ψn≥ 0 |  |
 |
... |  |
We first determine the set of all possible permutation relationships, and then we show how to choose our permutation relationship. (1) All permutation sets contain  , and the corresponding measurement probability is
, and the corresponding measurement probability is  . Because there are only a few sets satisfying the conditions on the measurement, positivity of
. Because there are only a few sets satisfying the conditions on the measurement, positivity of  and
and  . (2) When
. (2) When  happens in the table, it must be an element of all the arranged sets. (3) There must be
happens in the table, it must be an element of all the arranged sets. (3) There must be  in all the permutations. (4) The permutation
in all the permutations. (4) The permutation  exists in all the sets of permutations if
exists in all the sets of permutations if  is the only permutation in a column of the resulting table. (5) The permutation
is the only permutation in a column of the resulting table. (5) The permutation  exists in all the sets of permutations if
exists in all the sets of permutations if  is the only permutation in a row of the resulting table. Using the pictorial representation of the table of permutations, we observe that equation (9) has a solution with positive probabilities for all sets with no intersection of permutations. More importantly, the collection of the solutions of equation (9) for all subcases forms the complete solution, and the collection of the set with no intersection in the pictorial representation forms what we call the complete set. So, we get the sets of permutations of the form
is the only permutation in a row of the resulting table. Using the pictorial representation of the table of permutations, we observe that equation (9) has a solution with positive probabilities for all sets with no intersection of permutations. More importantly, the collection of the solutions of equation (9) for all subcases forms the complete solution, and the collection of the set with no intersection in the pictorial representation forms what we call the complete set. So, we get the sets of permutations of the form  , where the rest are permutations without intersection.
, where the rest are permutations without intersection.
The second step is finding the probability and SIO operator through the permutation relationship. In order to get the probability, we first need the relational cij. In equation (9), we can get the coefficient cij through the permutation relation and the target state, where the target state is the maximum coherent state. Then, the coefficient cij can find a set of linear equations, and we calculate the probability of linear equations. Finally, we bring the obtained cij, probability, and permutation relation groups into the operators, and we can get the definite SIO operators.
Next, we give some examples to illustrate the distillation protocol. We give a state to be distilled  where
where  . According to proposition 1, it can be obtained that when d = 2 ,
. According to proposition 1, it can be obtained that when d = 2 ,  can be deterministicly distilled to
can be deterministicly distilled to  . First we construct table 2, which contains all possible permutations of
. First we construct table 2, which contains all possible permutations of  in this case.
in this case.
Table 2. All possible permutations of  .
.
| ψ3≥ 0 |  |
 |
We get the substitution relations  and
and  . All permutation sets contain an identity transformation
. All permutation sets contain an identity transformation  , the probability corresponding to this permutation is
, the probability corresponding to this permutation is  , and the resulting permutation relationship is
, and the resulting permutation relationship is
We identify the pair and get a set of Kraus operators as follows, where  and
and ![$p^{i} = \operatorname{\textrm{Tr}}\left[K^{i} \rho_{\psi} K^{i}\right]$](https://content.cld.iop.org/journals/1612-202X/17/8/085201/revision1/lplab7f3aieqn106.gif) . We represent the coefficient cij as the element of the (ij)th of the matrix c,
. We represent the coefficient cij as the element of the (ij)th of the matrix c,  . The matrix of c is the condition (12) from the following set of linear equations:
. The matrix of c is the condition (12) from the following set of linear equations:
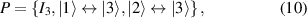
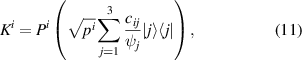
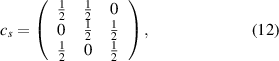
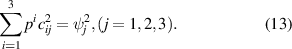
Finally, pi can be found by solving a linear system of equations, where  and p2 = 0. Then,
and p2 = 0. Then,


4. Deterministic pure-state dilution
In this section, we will study the deterministic coherent dilution of pure states and give the optimal dilution consumption under d-dimension. Corresponding to deterministic coherent distillation, we also give the optimal dilution consumption in two dimensions. Then, we use the specific protocol for deterministic coherent dilution under the one-shot system, and we can achieve the optimal dilution rate.
Proposition 2. The minimum number of d-dimensional maximally coherent states  that can be diluted from pure state
that can be diluted from pure state  under SIO is d = n. In particular, the minimum number of two-dimensional maximally coherent states
under SIO is d = n. In particular, the minimum number of two-dimensional maximally coherent states  that can be diluted from pure state
that can be diluted from pure state  under SIO is
under SIO is  . Here,
. Here,  represents the least integer equal to or greater than x.
represents the least integer equal to or greater than x.
Proof. When  , we can transform
, we can transform  deterministically to
deterministically to  . Suppose
. Suppose  , and
, and  are real vectors whose components are in decreasing order by the condition of majorization condition. When d ≤ n, the pure state
are real vectors whose components are in decreasing order by the condition of majorization condition. When d ≤ n, the pure state  can be deterministically distilled by
can be deterministically distilled by  , and when d > n, the pure state
, and when d > n, the pure state  cannot be deterministically distilled by
cannot be deterministically distilled by  . Then, the minimum value is d = n and
. Then, the minimum value is d = n and  , and the pure state
, and the pure state  can be definitely distilled by
can be definitely distilled by  . Thus, we complete our proof.
. Thus, we complete our proof.
Proposition 2 on optimal one-shot zero-error coherence dilution are directly implied by [PRL 120.070 403] [21]. Like proposition 1, proposition 2 can be used to find the minimum value of the maximum coherent state under the majorization relationship.
Table 3. All permutation relationships of  .
.
 |
 |
- | - | ... | - |
 |
 |
 |
- | ... | - |
 |
 |
 |
 |
... | - |
| ... | ... | ... | ... | ... | ... |
 |
 |
 |
 |
... |  |
It is obvious that coherent dilution and coherent distillation are the same protocols in solving the definite SIO operator. Because of their different properties, there are also some differences in solving substitution. For all permutation relationships, we have  and
and  . In the specific dilution process, we can determine the optimal relations
. In the specific dilution process, we can determine the optimal relations  and
and  , but for the initial coherent state and other coefficients of the final coherent state, there are still (n − 1) to
, but for the initial coherent state and other coefficients of the final coherent state, there are still (n − 1) to  relations.
relations.
Then, we use examples to understand deterministic coherent dilution protocols more clearly. We introduce a state to be diluted  where
where  . From proposition 2, we can get the smallest d = 3, and
. From proposition 2, we can get the smallest d = 3, and  can dilute from pure state
can dilute from pure state  . First, we construct table 4, which contains all possible permutations of
. First, we construct table 4, which contains all possible permutations of  in this case.
in this case.
Table 4. All possible permutations of  .
.
 |
 |
 |
 |
We get the substitution relations  and
and  . All permutation sets contain an identity transformation
. All permutation sets contain an identity transformation  , the metric probability corresponding to this permutation is
, the metric probability corresponding to this permutation is  , and the resulting permutation relationship is
, and the resulting permutation relationship is  . Similar to the coherent distillation process, we identified the pair and got a set of Kraus operators and the matrix. The condition can obtain a set of linear equations. Finally, deterministic Kraus operators can be found by solving a linear system of equations, where
. Similar to the coherent distillation process, we identified the pair and got a set of Kraus operators and the matrix. The condition can obtain a set of linear equations. Finally, deterministic Kraus operators can be found by solving a linear system of equations, where  and Kraus operators are
and Kraus operators are
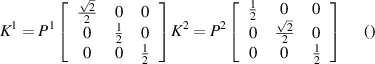
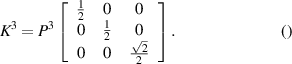
5. Discussion and conclusion
In this paper, we have obtained the optimal rate of pure-state deterministic coherent distillation and dilution. For coherent distillation, we have given the maximum number of d-dimensional maximally coherent states. For coherent dilution, we have given the minimum number of d-dimensional maximally coherent states. Then, we have given the protocols of coherent distillation and dilution to achieve optimal coherent distillation and dilution rates. It can also be said that our main work is to propose a method to achieve the optimal rate, and our protocols can reach the theoretical value introduced in the upper bound proposed by Liu et al. At the same time, we give examples to prove the flow of the protocol more clearly, which shows that the method is feasible and practical. In our future studies, we will focus on more efficient distillation and dilution protocols, and consider whether the operators of distillation and dilution can be deterministic in the mixed state.












