Abstract
We study the propagation of polarized light through turbid media with high scattering coefficient (μs = 50 cm−1) and disclose the physical processes involved in the evolution of Stokes vector. The results show that the components of the Stokes vector can be expressed as the superimposition of the generalized divergence and the generalized curl of the two orthogonal electric field vectors. The components I, Q, and U can be represented as the superimposition of the generalized divergence. The components V can be conveyed as the superimposition of the generalized curl omitting the direction. Further, the depolarization of the linearly polarized light corresponds to the alteration of the generalized divergence, while the depolarization of the circularly polarized light coincides with the variability of the generalized curl omitting the direction. The evolutions of the scattering electric fields arise from the scattering of the particles, followed by the polarization state transition of the incident light and the change of the scattering phase function. Further, the circularly polarized light can preserve the polarization state better than that of the linearly polarized light with an increase of the thickness of the scattering volume.
Export citation and abstract BibTeX RIS
1. Introduction
The study of light wave propagation and control through turbid media has attracted growing attention due to its fundamental importance in a wide range of applications in astronomy [1], ocean optics [2], biological optics [3] and materials [4, 5]. A rigorous description of the interaction of light with turbid media requires Maxwell theory, considering the vector nature of light. However, the major drawback of this theory is extremely high computational needs to investigate the volumetric turbid media, which makes it inappropriate for many areas [6]. To accelerate the speed of calculation and simplify the analysis process of light through turbid media, many researchers treat light as a transport of particles or energy and neglect any correlation and interference effects. Then the transport of light in turbid media is governed by the radiation transport equation (RTE), with an emphasis on the variability of the incident light intensity distribution [7, 8]. In highly scattering environments, the RTE can even be simplified to the diffusion equation with analytical solutions [9, 10]. The information carried by the spatial intensity distribution of the exiting light has been used to determine the parameters of scattering particles including the size, the anisotropy factor, and the scattering coefficient of turbid media [11, 12].
Compared with the specific spatial intensity distribution information delivered by the outgoing light, the polarization state can give additional information about turbid media, such as the optical rotatory dispersion and the circular dichroism [13, 14]. In the imaging area, except the intensity information, the polarization can serve as a supplementary dimension to extract the imaging information of embedded objects in turbid media [15–17]. Generally, the physical processes of light wave propagation through various turbid media are more completely described by the vector RTE (VRTE) including the polarization information of the transmitted light. A few researchers focus on the analytical solution of the VRTE, which has a clear physical meaning and can be used as the benchmark solution to verify the applicability of the existing numerical computational methods [18].
However, owing to the intricate nature of this equation, a significant proportion of studies have focused on developing numerical solutions rather than analytical solutions of the VRTE. An incomplete list of these methods includes the Chebyshev spectral method [19], the vector Fokker–Planck approximation [20], and the lattice Boltzmann method [21]. Because the computation time of these numerical methods increases dramatically with an increase of the dimension. Then a typically method named the polarization sensitive Monte Carlo (MC) method has been introduced and widely used to investigate the transport of polarized light through turbid media [22–24]. Schmitt et al reported on the loss of the degrees of linear and circular polarization as linearly and circularly polarized light propagates in light scattering media [25]. On the basis of the above work, researchers presented a study of the transition of linearly polarized light into randomly polarized light during light propagation through tissues, taking into account of the birefringent effect [26]. Further, researchers pointed out that the depolarization effects were different in continuous random medium and turbid media with discrete spherical scatterers [27]. Additionally, a paper described the use of degree of polarization to discriminate unscattered and weakly scattered light from multiply scattered light in an optically turbid material [28]. Most of the existing researches about the polarized light through turbid media concentrate on the quantitative alteration of the degree of the polarization derived from the Stokes vector ( S ) that is an important parameter to track the polarization state of light through turbid media [29].
However, the physical picture underlying the Stokes vector has not been clearly addressed. In this letter, we disclose the physical processes involved in the evolution of Stokes vector. Here, the polarization sensitive MC method is used to study the interaction of light fields and the polarization state transition mechanism through highly turbid media. The method used in our simulation is with the polarization information based on the classical MC model of light transport in multi-layered tissues and the volumetric turbid media [30, 31].
2. MC simulation method and model
Light transfer can be characterized utilizing the concept of electromagnetic fields propagating as wave through turbid media. The electric field  of a pencil beam can be represented by two independent field components,
of a pencil beam can be represented by two independent field components, 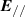 and
and 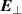 orthogonal to each other and lying in the plane perpendicular to the direction of propagation as shown in figure 1. Given to the pencil beam perpendicularly incident on the turbid media, we can decompose mathematically the propagating light with two transverse components in the input plane.
orthogonal to each other and lying in the plane perpendicular to the direction of propagation as shown in figure 1. Given to the pencil beam perpendicularly incident on the turbid media, we can decompose mathematically the propagating light with two transverse components in the input plane.
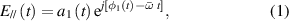
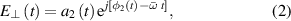
Figure 1. Schematic of the polarized light through turbid media. (a) Simulation configuration. The central wavelength of the incident laser was 632.8 nm; The thickness (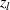 ) of the volume along the optical axis was varied from 0 to 1.00 cm. The half-acceptance angle of the detection area was about θ = 5°. (b) A random scattering event in the meridian plane's geometry. The photon's directions of propagation before and after scattering were
) of the volume along the optical axis was varied from 0 to 1.00 cm. The half-acceptance angle of the detection area was about θ = 5°. (b) A random scattering event in the meridian plane's geometry. The photon's directions of propagation before and after scattering were 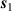 and
and 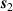 , respectively.
, respectively.
Download figure:
Standard image High-resolution imagewhere 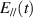 and
and 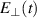 are the parallel and perpendicular components of the incident electric field, respectively;
are the parallel and perpendicular components of the incident electric field, respectively; 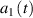 and
and  are the moduli of parallel and perpendicular components of the incident electric field, respectively; j is the unit of the imaginary number;
are the moduli of parallel and perpendicular components of the incident electric field, respectively; j is the unit of the imaginary number; 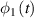 and
and  are the initial phases of the horizontal and perpendicular light, respectively; and
are the initial phases of the horizontal and perpendicular light, respectively; and 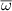 is the average frequency of the incident light. Then the Stokes vector and its components of the input light are linked to the components of the incident electric field and can be defined as [32]:
is the average frequency of the incident light. Then the Stokes vector and its components of the input light are linked to the components of the incident electric field and can be defined as [32]:
where the angle brackets represent vector time averages over time periods longer than the period of light electric field, and * represents the complex conjugate.
The change of the Stokes vector in turbid media can be obtained by tracking the scattering process using the polarization sensitive MC method as shown in figure 1(b). Assuming before scattering the light propagation's direction is  . When a random scattering event occurs, a new meridian plane is created by the new direction of propagation
. When a random scattering event occurs, a new meridian plane is created by the new direction of propagation  and the z-axis. Two rotations of the Stokes vector, in and out of the scattering plane, are required by this method [33]. Then the relationship between the new and old Stokes vector can be obtained by
and the z-axis. Two rotations of the Stokes vector, in and out of the scattering plane, are required by this method [33]. Then the relationship between the new and old Stokes vector can be obtained by
where 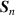 and
and  are the new and old Stokes vectors, respectively;
are the new and old Stokes vectors, respectively;  is the scattering angle;
is the scattering angle; 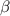 or
or  is the angle between the scattering plane and the meridian plane;
is the angle between the scattering plane and the meridian plane; 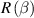 and
and  are the two rotation matrices; and
are the two rotation matrices; and 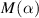 is the scattering matrix or Mueller matrix.
is the scattering matrix or Mueller matrix.
In our polarization sensitive MC simulation as shown in figure 1, the Stokes vectors of the incident linearly and circularly polarized light were [1 0 1 0]T and [1 0 0 1]T, respectively. The number of the incident photon packet for each simulation was 1 million to minimize the statistical error arising from the different number of input photon packets. The incident laser had a central wavelength of 632.8 nm. The incident laser propagated along the z-axis, and the xoy plane was the detecting plane. The turbid media consisted of a polystyrene microspheres' solution contained in a scattering volume with 50 mm in length and 50 mm in width. The thickness ( ) of the volume along the optical axis was varied from 0 to 1.00 cm at intervals of 0.01 cm. The diameter of the polystyrene microspheres was 2 μm. The refractive indices of the ambient medium (deionized water) na and the polystyrene microspheres np were 1.33 and 1.58, respectively. The anisotropy factor (g) of the microspheres was 0.91. The absorption of turbid media could be neglected compared with the scattering. The scattering coefficient μs of the polystyrene microsphere suspension was 50 cm−1. The half-acceptance angle of the detection area was θ = 5°.
) of the volume along the optical axis was varied from 0 to 1.00 cm at intervals of 0.01 cm. The diameter of the polystyrene microspheres was 2 μm. The refractive indices of the ambient medium (deionized water) na and the polystyrene microspheres np were 1.33 and 1.58, respectively. The anisotropy factor (g) of the microspheres was 0.91. The absorption of turbid media could be neglected compared with the scattering. The scattering coefficient μs of the polystyrene microsphere suspension was 50 cm−1. The half-acceptance angle of the detection area was θ = 5°.
3. Results and discussion
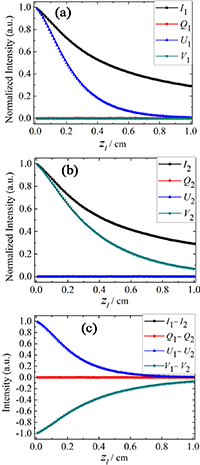
In figure 2, we show the components of the Stokes vector varying with the thickness of the scattering volume. From figure 2(a), we can see that with an increase of the thickness of the scattering volume, the intensities of components I1 and U1 both decrease appreciably, while the intensities of components Q1 and V1 have very small values and keep nearly unchanged. From figure 2(b), it can be seen that with increased thickness of the scattering volume, the intensities of components I2 and V2 both obviously drop, while the intensities of components Q2 and U2 are with very small values and remain stable. To examine the degrees of the alteration of the components of Stokes vectors of linearly and circularly polarized incident light through turbid media, we subtract the Stokes vector of circularly polarized light from the Stokes vector of linearly polarized light and the differential intensities are shown in figure 2(c). From figure 2(c), we can see that the change tendencies of components I and Q of the Stokes vector for linearly and circularly polarized light are very similar, while the change tendencies of components U and V are opposite. It means that the decline of the intensity of the incident light is independent of the polarization state. Further, the decline of the intensity of the component U1 for linearly polarized light is faster than that of the component V2 for circularly polarized light. Therefore, the degree of the polarization of the exiting light depends on the polarization state of the incident light and the circularly polarized light can preserve the polarization state better than that of the linearly polarized light with an increase of the thickness of the scattering volume.
Figure 2. Components of the Stokes vector varying with the thickness of the scattering volume. (a) Linearly polarized light; (b) circularly polarized light; (c) difference of the components of the Stokes vectors of the linearly and circularly polarized light through turbid media.
Download figure:
Standard image High-resolution imageThe difference of the capability to preserve the initial polarization state can be explained as follows. Firstly, we analyze the underlying physics of components of the Stokes vector. The parallel and perpendicular components of the incident electric field can be simplified as 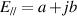 , and
, and 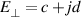 ,where
,where  ,
,  ,
,  , and
, and 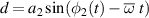 . Then the corresponding electric field vectors can be expressed as
. Then the corresponding electric field vectors can be expressed as 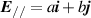 and
and  , where
, where  and
and  are unit vectors in two orthogonal directions. From the relation between the complex numbers and the vectors [34], we can deduce
are unit vectors in two orthogonal directions. From the relation between the complex numbers and the vectors [34], we can deduce
where  represents the inner product of the two orthogonal electric field vectors, and
represents the inner product of the two orthogonal electric field vectors, and  represents the outer product of the two orthogonal electric field vectors but not considering the direction. Here, we define the generalized divergence and the generalized curl as the inner and outer product of the two orthogonal electric field vectors, respectively. Then the Stokes vector can be represented by the generalized divergence and the generalized curl of the two orthogonal electric field vectors as shown in equation (7)
represents the outer product of the two orthogonal electric field vectors but not considering the direction. Here, we define the generalized divergence and the generalized curl as the inner and outer product of the two orthogonal electric field vectors, respectively. Then the Stokes vector can be represented by the generalized divergence and the generalized curl of the two orthogonal electric field vectors as shown in equation (7)
The components I and Q contain the self-interaction ( and
and  ) and the interaction (
) and the interaction ( ) of two orthogonal electric fields vector, while the components U and V only contain the interaction of two orthogonal electric fields. Further, the linear polarization component U corresponds to the generalized divergence. The circular polarization component V corresponds to the generalized curl omitting the direction. Therefore, we can examine the polarization transition mechanism in turbid media by tracking the generalized divergence and the generalized curl omitting the direction.
) of two orthogonal electric fields vector, while the components U and V only contain the interaction of two orthogonal electric fields. Further, the linear polarization component U corresponds to the generalized divergence. The circular polarization component V corresponds to the generalized curl omitting the direction. Therefore, we can examine the polarization transition mechanism in turbid media by tracking the generalized divergence and the generalized curl omitting the direction.
According to equation (7), we can see that the depolarization of the linearly polarized light is related to the alteration of the generalized divergence, while the depolarization of the circularly polarized light can be assessed by the variability of the generalized curl omitting the direction. Since the generalized divergence and the generalized curl can be expressed as the inner and outer product of the two orthogonal electric field vectors, respectively, we analyze the evolution of the two orthogonal electric field vectors. For a spherical scattering particle with diameter longer than the wavelength of the incident light, the relation between incident and scattered electric field amplitudes satisfies [35]
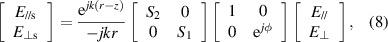
where 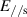 and
and 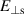 are the parallel and perpendicular components of the scattered electric fields, respectively; k is the wave number of the incident light; r is the distance between the scattering particle and the observation point of the scattering electric filed; z is the distance between the source and the scattering particle;
are the parallel and perpendicular components of the scattered electric fields, respectively; k is the wave number of the incident light; r is the distance between the scattering particle and the observation point of the scattering electric filed; z is the distance between the source and the scattering particle; 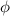 is the phase difference of the two orthogonal electric field vectors; and the elements S1 and S2 of the amplitude scattering matrix depend, in general, on the scattering angle. The mathematic expresses of the scattering amplitudes can be obtained by Mie theory.
is the phase difference of the two orthogonal electric field vectors; and the elements S1 and S2 of the amplitude scattering matrix depend, in general, on the scattering angle. The mathematic expresses of the scattering amplitudes can be obtained by Mie theory.
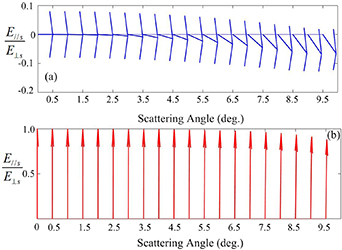
The incident intensities of the linearly and circularly polarized light both are 1. The phase differences of the two orthogonal electric fields for the linearly and circularly polarized light are 0 and π/2, respectively. Then we can get the ratios of the two orthogonal scattering electric fields as a function of the scattering angle as shown in figure 3. The horizon axis corresponds to the scattering angle of the incident light and the longitude axis corresponds to the ratio of the two orthogonal scattering electric fields. Noted that the ratio of the two orthogonal electric fields is a complex number instead of a real number. The length of the arrow stands for the module of the ratio and the angle between the arrow and the horizon axis stands for the argument. The moduli of the ratios of two orthogonal electric fields are both 1 for the linearly and circularly polarized incident light when the scattering angles are 0°. The corresponding arguments of the ratios of two orthogonal electric fields for the linearly and circularly polarized light are 0° and 90°, respectively.
Figure 3. Ratios of the two orthogonal scattering electric fields. (a) Linearly polarized light; (b) circularly polarized light.
Download figure:
Standard image High-resolution imageAs shown in figure 3(a), the module and the argument of the ratio hardly change when the scattering angle is smaller than 2°. Then with increased scattering angle, the module of the ratio gradually grows while the argument of the ratio decreases. It means that the polarization state of the scattering light depends on the scattering angle. Further, with the scattering angle increasing from 0° to 9.5°, the polarization state of the incident light is changing from the linear polarization to the elliptical polarization state, because the length of the ratio is not equal to 1 and the argument of the ratio decreases from 0° to −3.4°. In figure 3(b), we can see the alteration of the polarization state of the incident circularly polarized light scattered by a microsphere. The module and argument of the ratio are almost invariable when the scattering angle is less than 5°. With a further increase of the scattering angle, the module of the ratio declines. It can also be seen from figure 3(b) that the argument of the ratio scarcely decreases with an increase of the scattering angle from 5° to 9.5°. It means that the polarization state of the initial light is gradually changing from the circular polarization state to the elliptical polarization state with increased scattering angle. Further, from figures 3(a) and (b), we can infer that the transition velocity of the initial circularly polarized light is slower than that of the linearly polarized light and that is the reason for the difference of the capability to preserve the initial polarization state.
To clearly see the effect of the scattering on the different incident polarized light, we provide the physical flow configuration of light over the geometry. The physical flow configuration of light is also called the scattering phase function (P) for incident light and can be obtained by [36]
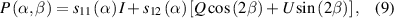
where the parameters  and
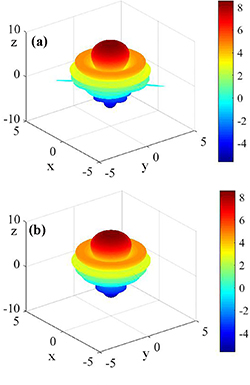
and 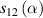 are related to the scattered amplitudes S1 and S2. The parameters I, Q, and U are the components of the Stokes vector for the incident light. The scattering phase functions of a microsphere for the linearly polarized light and the circularly polarized light are shown in figures 4(a) and (b), respectively. From figures 4(a) and (b), we see that the forward scattering of a microsphere for the linearly polarized light increases distinctively compared with that for the circularly polarized light, which results in more scattered photons collected and the big change of the initial polarization state.
are related to the scattered amplitudes S1 and S2. The parameters I, Q, and U are the components of the Stokes vector for the incident light. The scattering phase functions of a microsphere for the linearly polarized light and the circularly polarized light are shown in figures 4(a) and (b), respectively. From figures 4(a) and (b), we see that the forward scattering of a microsphere for the linearly polarized light increases distinctively compared with that for the circularly polarized light, which results in more scattered photons collected and the big change of the initial polarization state.
Figure 4. Scattering phase function of a microsphere for incident light. (a) Linearly polarized light; (b) circularly polarized light.
Download figure:
Standard image High-resolution image4. Conclusions
In conclusion, we find that the components of the Stokes vector can be expressed as the superimposition of the generalized divergence and the generalized curl of the two orthogonal electric field vectors. The components I, Q, and U can be expressed as the superimposition of the generalized divergence. The components V can be expressed as the superimposition of the generalized curl omitting the direction. The depolarization of the linearly polarized light corresponds to the alteration of the generalized divergence, while the depolarization of the circularly polarized light can be reflected by the variability of the generalized curl omitting the direction. Further, the generalized divergence and the generalized curl depend on the amplitude and phase difference of the two orthogonal electric fields. The evolutions of the scattering electric fields arise from the scattering of the particles, followed by the polarization state transition of the incident light and the change of the scattering phase function. For the light through turbid media with big particles (diameter longer than the wavelength of the incident light), the circularly polarized light can preserve the polarization state better than that of the linearly polarized light.
Acknowledgments
The authors gratefully acknowledge the financial support for this work provided by National Natural Science Foundation of China (Grant No. 61905090); Shandong Provincial Natural Science Foundation under the Grant No. ZR2023MA024.