Optimized loading of ultracold Cs atoms in a magnetic levitated optical dipole trap

In recent years, an increasing interest in the development of optical traps for cold atoms with applications to fundamental physical issues [1, 2], nanotechnology [3, 4], high–resolution microwave [5, 6], optical spectroscopy [7, 8], frequency standards [9, 10] as well as atom optics [11]. Far-off-resonance optical dipole trap is one of the most prevalent technologies for preparing and manipulating atoms and can provide the opportunity to investigate numerous physical including double potentials [12], microscopic traps [13, 14], and optical lattices [15–17]. Optical dipole trap producing a near conservation well for atoms, is pivotal to the study of Bose–Einstein condensations [18, 19], magnetically tunable Feshbach resonances [20, 21], as well as formation of cold molecules [22, 23]. Except for that, an optical dipole trap is typically utilized to trap and cool all spin states of the trapped atoms, which provides a favorable environment for studies of spinor condensates and multicomponent Fermi degenerate gas [24, 25]. Furthermore, an optical dipole trap is applied to manipulate the atoms according by shifting the trapping geometries, including three-dimensional (3D) to (1D) optical lattice for quantum simulation and quantum information application [26, 27]. Nonetheless, incorporating the inevitable heating caused by the photo recoil of the scattered laser light, the atom loss in the dipole tape is not insignificant [28, 29].

For the purpose of preparing a large number of atoms in an optical dipole trap for further exploration, numerous schemes have been proposed for increasing the loading efficiency, typical techniques include loading atoms into a large-volume trap [30] and modifying trapping geometries [26]. Magnetic levitation [18, 31] has been employed to compensate for the destructive potential created by the gravity of atoms, making an effective loading in a large and shallow dipole trap. The dimple trap [32] is applied for changing the trapping geometries to increase trap depth on the basis of a typical optical dipole trap. There has been a growing fascination with the advancement of optical traps for cold atoms [1, 31]. Nonetheless, the effect of the 'pre-loading process' for loading atoms into a dipole trap still lacks a comprehensive experimental study, which is substantial to the loading efficiency.

In this paper, we examined the 'pre-loading process' for loading atoms into the magnetic levitated dipole trap, and the number of atoms as a function of the opening time prior to loading the atoms into the dipole trap of distinct laser power intensities were obtained. Furthermore, the variation of trapped atoms as the function of the fixed opening time was measured with divergent sweep ranges from one laser power intensity to the final fixed one, which has not yet been observed in previous reports. To explain our experimental results, a simple analysis is provided.

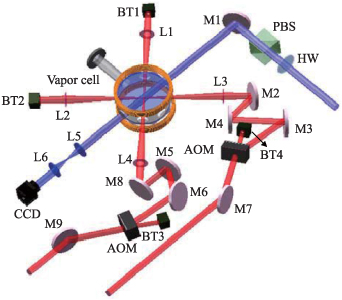
The study starts with ultracold Cs atoms in a vapor-loaded magneto-optical trap (MOT) at a background pressure of 3 × 10⁻⁸ Pa, the experimental setup is illustrated in figure 1. Following accomplishing a compressed MOT and optical molasses, 3 × 10⁷ atoms are obtained with a peak density of ∼10¹¹ cm⁻³. Subsequently, the atoms are transferred to a 3D optical lattice, and degenerated Raman sideband cooling is applied to cool the atoms to a low temperature of ∼1.7 μK. Moreover, the atoms are loaded into the magnetically levitated dipole trap, which is constructed by utilizing a 1070 nm, collimated multiple-longitudinal-mode, linearly polarized beam from an Yb: fiber laser. As depicted in figure 1, the dipole trap consists of two crossing lasers with an angle of 90°. The corresponding trap-center beam waists are w_x = 230 µm and w_y = 240 µm, respectively. Regarding each laser beam, an acousto-optical modulator is employed for intensity stabilization and rapidly switching off the beam in less than 1 µs. For the purpose of preventing any interference between the two laser beams, one is downshifted in frequency by 110 MHz, whereas the other is upshifted by 110 MHz [33], and the magnetic levitated dipole trap has been theoretically and experimentally studied in detail in [31].

Zoom In Zoom Out Reset image size

The loading of a large-volume shallow dipole trap without a magnetic field, directly impacted by the anti-trapping potential induced by atomic gravity, the loading rate is roughly zero. For a typical loading process in our experiment, the dipole laser and the magnetic field were switched on simultaneously, ∼0.59 × 10⁶ atoms were loaded in the magnetic levitated dipole trap, as measured by the horizontal absorption image (Apogee CCD camera) taken after 3 ms of expansion following the release from the levitated dipole trap. To achieve optimized loading of ultracold Cs atoms in a magnetically levitated dipole trap, the dipole laser was activated beforehand, preceding the utilization of the magnetic field to compensate for gravity. As previously mentioned, the large-volume dipole trap exhibited minimal atom loading. It should be pointed out that the studies here are before the loading process begins, on the condition that the atoms were loaded into the magnetic levitated dipole trap, the laser power intensity would be unchanged, and subsequently, the number of atoms was acquired by the absorption image.

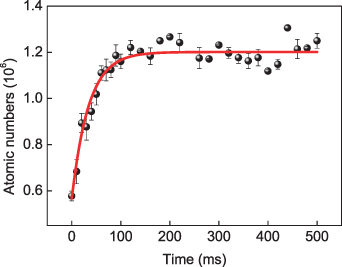
In the first place, we explored the influence of the opening time in advance on the loading, the variation of the atomic numbers in the dipole trap is revealed in figure 2, and the red solid curve fits with the exponential function. In the beginning, with the increase of the opening time, the atom in the dipole trap has a large growth rate. On the condition that the time approaches 100 ms, the atomic number stops increasing, and it is accessible to obtain maximum ∼1.26 × 10⁶ atoms in the dipole trap, which is more than twice the situation of the dipole laser, and concurrently, the magnetic field was switched on.

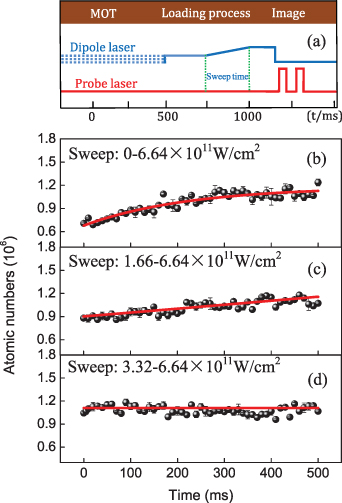
Zoom In Zoom Out Reset image size

Following obtaining the optimized opening time (greater than 100 ms), the open way of the dipole laser has become the focus of this research. Thus, the atomic numbers as the function of sweep time from one laser power intensity to the other were measured during the opening time. We subsequently opened the dipole laser in advance (at 500 ms), and set a fixed value, then the dipole laser power intensity in the loading process was set to 6.64 × 10¹¹ W cm⁻², we are interested in the time between the initial laser power intensity and the final laser power intensity. Figure 3(a) indicates the experimental sequence. The initial laser power intensity was set to 0 W cm⁻², 1.66 × 10¹¹ W cm⁻², and 3.32 × 10¹¹ W cm⁻², as revealed in figures 3(b)–(d). The red solid lines were the fitting curves by the exponential function. With increasing the sweep time, the number of atoms in the dipole trap presented a growth tendency. On the condition that the sweep time reaches the 500 ms, the maximum number of atoms was obtained, figure 3(b) was 1.24 × 10⁶ and figure 3(c) was 1.19 × 10⁶, and yet for the figure 3(d), the number of atoms was almost 1.09 × 10⁶. It could be predicted that the same tendency if the laser power intensity increase to 6.64 × 10¹¹ W cm⁻², the further increase of laser power intensity would contribute to the effect of heating with the number of atoms tending to decrease.

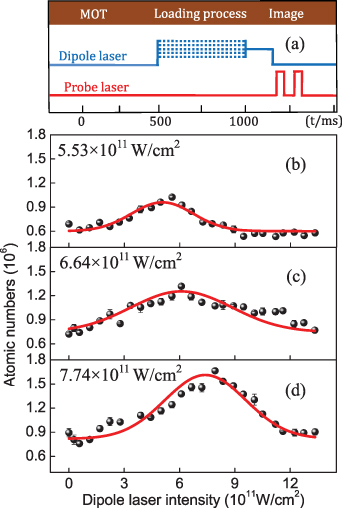
Zoom In Zoom Out Reset image size

We noticed that the initial laser power intensity equal to half of the final intensity, and the number of atoms stay nearly constant. On the condition that the linear sweep time reaches 500 ms, the number of atoms would get saturation. Based on this way, we employed the dependence of the loading of the atoms on the laser power intensity, and figure 4(a) depicts the experimental sequence. Besides, the opening time was set as 500 ms, we consequently shifted the laser intensity and linearly sweep to a fixed intensity, and subsequently, the dipole laser intensity in the magnetically levitated process kept unchanged (after 1000 ms). Figures 4(b)–(d) show atomic numbers as the function of the dipole laser intensity, with the fixed value of 11.06 × 10¹¹ W cm⁻² (b), 13.26 × 10¹¹ W cm⁻² (c) and 15.48 × 10¹¹ W cm⁻² (d). Initially, as the intensity of the dipole laser increases, the number of atoms in the dipole trap exhibits a growth trend; when the laser power intensity reaches half of the final intensity in magnetic levitation, the maximum number of atoms is attained. For the figures 4(b)–(d), the corresponding maximum number of atoms is 1.02 × 10⁶ for 5.53 × 10¹¹ W cm⁻², 1.32 × 10⁶ for 6.64 × 10¹¹ W cm⁻² and 1.67 × 10⁶ for 7.74 × 10¹¹ W cm⁻². Based on the dependence of the number of trapped atoms on the trap depth as demonstrated in [34], the atomic numbers are proportional to the trap depth of a shallow dipole trap under our experimental parameters. With the increase of trap depth, the maximum atomic numbers increase, and the number of trapped atoms will decrease with a further increase in the laser power intensity; the red solid line is a fitting curve by the Gaussian function. It can be easily comprehended that the further increase of the laser power intensity leads to the result that the atoms are heated prior to the effective loading process, which induces the loss of the number of atoms in the dipole trap.

Zoom In Zoom Out Reset image size

We consequently provided a brief theoretical description of the optical potential. The optical potential in a dipole trap with the gravity of the pre-loading [31] is

$$\begin{align}{U_0}(x,y,z)& = -\,\, \frac{{3{c^3}}}{{\omega _0^3}}\left(\frac{\Gamma }{{{\omega _0} - \omega }} + \frac{\Gamma }{{{\omega _0} + \omega }}\right)\left[\frac{{{P_1}}}{{{\omega ^2}(x)}}{{\text{e}}^{ - 2\left({y^2} + {z^2}\right){\text{/}}{\omega ^2}(x)}}\right.\notag\\ &\quad \left. +\, \,\frac{{{P_2}}}{{{\omega ^2}(y)}}{{\text{e}}^{ - 2\left({x^2} + {z^2}\right)/ - 2\left({x^2} + {z^2}\right){\omega ^2}(y)}}\right] - mgz\end{align} \tag{ 1 }$$

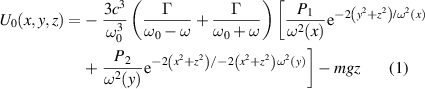
where (x, y, z) is the Cartesian spatial coordinates of the atom with the z-axis oriented downward, c denotes the speed of light, $\omega = 2\pi c/\lambda$ implies the circular frequency of the dipole trap laser, ${\omega _0}$ represents an effective transition circular frequency defined by a weighted average of both D lines for the Cs atoms, P₁ and P₂ signify the powers of the two beams of the dipole trap laser, $\omega (x)$ and $\omega (y)$ embody the corresponding beam waists. The total potential of the magnetically levitated dipole trap is

$$\begin{align}{U_1}(x,y,z)& = - \,\,\frac{{3{c^3}}}{{\omega _0^3}}\left(\frac{\Gamma }{{{\omega _0} - \omega }} + \frac{\Gamma }{{{\omega _0} + \omega }}\right)\left[\frac{{{P_1}}}{{{\omega ^2}(x)}}{{\text{e}}^{ - 2\left({y^2} + {z^2}\right)/{\omega ^2}(x)}}\right. \notag\\ & \quad \left.+\,\, \frac{{{P_2}}}{{{\omega ^2}(y)}}{{\text{e}}^{ - 2\left({x^2} + {z^2}\right)/{\omega ^2}(y)}}\right]\! - \frac{3}{4}{\mu _{\text{B}}}{B_{{\text{bias}}}} \notag\\ & \quad - \,\frac{1}{6}\frac{{{m^2}{g^2}}}{{{\mu _{\text{B}}}{B_{{\text{bias}}}}}}\left({x^2}{{ + }}{{\text{y}}^2}\right)\end{align} \tag{ 2 }$$

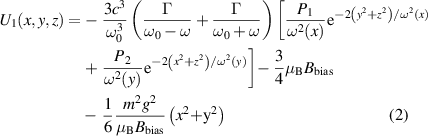
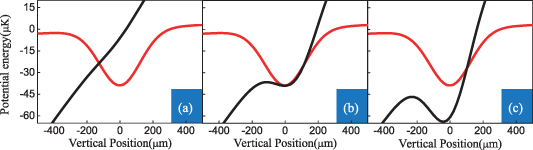
where μ_B is the Bohr magneton, and B_bias is the bias magnetic field contributed to the magnetic levitation. By employing equations (1) and (2), we computed the theoretical potentials acting on the Cs atoms in the vertical direction, and the results are indicated in figure 5. Furthermore, the solid red line represents the total potential of the magnetically levitated dipole trap, whereas the solid black line represents the potential of the dipole laser pre-loading. In figure 5(a), it is obvious that the potentials of the dipole trap barely coincide. Figure 5(b) gives the potential curve for a power intensity of 6.64 × 10¹¹ W cm⁻², a portion of the line has an overlap, which corresponds to the experimental results in figure 4. As depicted in figure 5(c), the number of trapped atoms will decrease as the laser power intensity is increased further, causing them to move further apart from the two potentials.

Zoom In Zoom Out Reset image size

In summary, employing a straightforward optimization approach for loading ultracold Cs atoms in a magnetically levitated optical dipole trap led to a notable increase in the loading efficiency of atoms during the pre-loading process. The laser intensity is swept about 500 ms in advance prior to loading atoms in an optical dipole trap, and the optimized laser power intensity is half of the intensity of the dipole trap. Furthermore, a qualitatively theoretical explanation has been provided by considering the potential of the optical dipole trap in the pre-loading process.

In this work, a comprehensive study of optimized pre-loading process loading of ultracold Cs atoms in a magnetic levitated dipole trap was examined. Consequently, the experimental optimized parameter of the opening time, as well as the dependence of the atomic numbers on the sweep time and the laser power intensity for the loading process has been obtained. On the condition that the opening time was 500 ms, the linear sweep time was set as 500 ms, and the initial laser power intensity reached half of the final intensity, the maximum atomic numbers are up to  ∼1.67 × 10⁶, which are  ∼2.88 times than the atomic numbers of opening the dipole laser directly without the optimization. Our optimized pre-loading procedure has numerous benefits. On one hand, the loading efficiency of the optical dipole trap was increased in the optimized condition. On the other hand, the method can be adapted and realized for the efficient loading of distinct species of atoms.

This work was supported by the Shanxi Natural Science Foundation of China (No. 202203021212376).