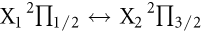Spectroscopic properties and laser cooling feasibility with the ${{\rm{X}}}_{1}{{}^{2}{\rm{\prod }}}_{1/2}\leftrightarrow {{\rm{X}}}_{2}{{}^{2}{\rm{\prod }}}_{3/2}$ transition for the PbX (X = F, Cl, Br, and I) molecules

The production of ultracold molecules has received growing interest and emerged as an important research goal for experimentalists, at the same time, these molecules have broad applications in chemical dynamics [1], atom-ion sympathetic cooling [2–4], high-precision spectroscopic measurements [5–7], and quantum simulation of many-body interactions [8, 9]. In 2004, Di Rosa [10] proposed three conditions that diatomic candidates for laser cooling need to satisfy: (1) short radiative lifetimes for the upper states, (2) highly diagonal Frank–Condon factors (FCFs), and (3) no interference from intermediate states. Since the SrF molecule was experimentally cooled to the μK level using three lasers by Shuman et al [11] in 2010, YO [12], CaF [13], YbF [14], CaH [15], and BaH [16] molecules have also been successively cooled. Especially, the direct laser cooling of the BaH [16] molecule indicates the feasibility of laser cooling and trapping heavy molecules with relatively long-lived excited electronic states, despite previously unexplored this technical challenge. Theoretical investigations on laser cooling of diatomic molecules have also attracted the interest of many researchers. For example, the laser cooling optical schemes of BeF [17], ScO [18], CuH [19], AuH [20], and NH [21] were proposed. Moreover, Li et al [22] assessed the direct laser cooling feasibility of XH (X = Si, Ge, Sn, and Pb) and CS molecules, and found that SiH and CS molecules are promising for laser cooling candidates. Moussa et al [23] built the four-laser optical scheme for the CaCs molecule based on the X²Σ⁺ ↔ (2)²Π transition with an intermediate state of (2)²Σ⁺. Madi et al [24] investigated the low-lying electronic states of the BeX⁻ (Cl, Br, F, and I) molecules and constructed a laser cooling scheme for BeF⁻. Osika et al [25] reported that the effective cooling scheme for the RaF molecule can be realized using only one pump laser. Very recently, El-Kork et al [26] reported a three-laser cooling scheme including intervening electronic states for LuF. Bigagli et al [27] built a cycling scheme for Doppler cooling of trapped OH⁺ ions using X³Σ⁻ ↔ A³Π transition. The BeFr⁺ molecule was reported as a good candidate for laser cooling by Zrafi et al [28]. Moreover, a four-laser optical scheme of laser cooling was constructed for the AuAl molecule by Zhu et al [29].

The above investigations indicate that a small difference between the equilibrium bond lengths (|ΔR_e |) of the two electronic states involved in the pumping transitions can usually result in highly diagonal FCFs. For example, for BeF [17], LiRb [30], BH⁺ [31], and BH⁻ [31] molecules, the |ΔR_e | for pseudo-closed transitions are 0.035, 0.085, 0.042, and 0.038 Å, the corresponding FCFs of the main transitions are 0.897, 0.872, 0.943, and 0.942, respectively. Yan et al [21] calculated the R_e s for the X³Σ⁻ and ³Π₁ states of NH molecule are 1.0363 Å and 1.0364 Å, respectively, and constructed the optical scheme based on the 0.99972 of FCF for the X³Σ⁻ (ν'' = 0) ↔ ³Π₁ (ν' = 0) transition. The A²Π_1/2 ↔ ${{\rm{X}}}^{2}{{\rm{\Sigma }}}_{1/2}^{+}$ transition was used for the laser cooling scheme for SrCl molecule by Xiao et al [32], in which the |ΔR_e | of the X²Σ⁺ _1/2 and A²Π_1/2 states is 0.028 Å, and the corresponding FCF of the A²Π_1/2 (ν' = 0) ↔ ${{\rm{X}}}^{2}{{\rm{\Sigma }}}_{1/2}^{+}$ (ν'' = 0) transition reaches 0.9124. The laser cooling scheme for the LuF molecule [26] was constructed using (1)³Π₀₊ (ν'' = 0) ↔ X¹Σ₀₊ (ν = 0) transition with 0.021 Å of |ΔR_e | and 0.930636 of FCF. Therefore, to screen a molecule with a small ΔR_e | is a helpful way to find potential molecules for laser-cooling. So, we throw our light on the PbX (X = F, Cl, Br, and I) molecules because the spin–orbit coupling (SOC) states are expected to be small |ΔR_e |. Moreover, researchers have been interested in these molecules for a long time [33]. In 1936, the band spectra of PbF and PbCl molecules were analyzed and described experimentally by Rochester [34]. In the same year, Morgan [35] performed a vibrational analysis of the absorption band systems due to the PbF, PbCl, and PbBr molecules and estimated that the ground state would be expected to be a ²Π state with a splitting energy gap of 7000 cm⁻¹ for PbCl. The ultraviolet band systems (B ← X) of PbCl and PbBr were obtained by Wieland et al [36] in 1952. The rotational spectra of (4, 0), (6, 0), (1, 1), and (3, 1) bands of PbCl were studied by Rao et al [37], while the emission spectrum of the A – X system of PbBr was obtained by Lal et al [38]. In 1992, Ziebarth et al [39] observed the emission spectra of the X₂ ²Π_3/2 ↔ X₁ ²Π_1/2 transitions for the PbX molecules in the near-infrared spectral region and obtained the harmonic vibrational constants (ω_e s), the anharmonic vibrational constants (ω_e χ_e s) and the spectroscopic terms (T_e s) of the X₁ ²Π_1/2 and X₂ ²Π_3/2 states. The laser-induced fluorescence excitation spectrum of PbBr and PbBr was reported by Drake et al [40] in 1995. The high-resolution studies of the X₂ ²Π_3/2 ↔ X₁ ²Π_1/2 emission spectra for ²⁰⁸PbF, ²⁰⁷PbF, ²⁰⁶PbF, and ²⁰⁸Pb^{35, 37}Cl molecules were investigated by Ziebarth et al [41] in 1998. Moreover, for the low-lying states of the PbX molecules, the spectroscopic properties such as R_e s, ω_e s, and T_e s were calculated theoretically [42–48]. Das et al [42] also obtained the radiative lifetimes of the X₂ ²Π_3/2 and ${{\rm{A}}}^{2}{{\rm{\Sigma }}}_{1/2}^{+}$ states for PbF. The transition dipole moment of the X₁ ²Π_1/2 → B²Σ_1/2 transition, the radiative lifetime of the B²Σ_1/2 state, and the spectroscopic constants for the B, D, E, and F states were determined for PbF by McRaven et al [49, 50]. The Franck–Condon factors of B²Σ⁺ ↔ X₁ ²Π_1/2 transition PbF were calculated by Chen et al [33] in 2022. In the same year, Zhu et al [51] recorded the high-resolution laser-induced fluorescence spectra of the B²Σ⁺ ↔ X₁ ²Π_1/2 transition for PbF under jet-cooled conditions. In addition, the previous research [35–48] showed that the SOC effect of the X²Π state of the PbX molecules is very significant, and the spin–orbit splitting energy difference can reach 8000 cm⁻¹, and the |ΔR_e | of the SOC splitting states are about 0.01 ∼ 0.04 Å. Thus, the X₁ ²Π_1/2 ↔ X₂ ²Π_3/2 transitions of the PbX molecules are expected to achieve highly diagonal FCFs.

The cooling of PbF was paid attention. For example, a cold PbF molecular beam was produced by laser-ablating a Pb rod under jet-cooled conditions, followed by the reaction with SF₆ [51]. The Ne buffer gas instead of He can induce the molecular beam to undergo significant translational cooling, but little or no rotational cooling [52]. Bichsel et al [53] experimentally assess the two-state Stark shifts for NO and recommend that the two-state model be used for lased cooling except that some special treats are desired. These quantitative assessments along with their two-state equations for the Stark shifts in conjunction with the equations for the rovibronic energies and for the splitting of the Λ doublet can constitute a reliable resource for cold-molecule experiments involving ²Π molecules with an odd number of electrons (e.g, LiO, OH, ClO, BeH, SH, PbF, YbF, and CH), which suggests that we can constructed optical scheme of laser cooling for these molecules with the two-state model. Inspired by these findings, we determined to explore the laser cooling feasibility with the X₁ ²Π_1/2 ↔ X₂ ²Π_3/2 transition of the PbX molecules. The potential energy curves (PECs) are obtained by four-component relativistic calculations with the multireference configurations interaction (MRCI) [54, 55]. By solving the Schrödinger equation of nuclear motion with the calculated PECs, we have obtained the rovibrational energy levels and the spectroscopic parameters. For the X₁ ²Π_1/2 ↔ X₂ ²Π_3/2 transition, the FCFs of the PbX molecules are close to 1.0. Thus, we constructed optical schemes for direct laser cooling for these molecules and found that the schemes can produce 10⁵ scattering photons for PbF and 10⁴ ones for PbCl, PbBr, and PbI before leaking. The Doppler/recoil temperatures are 19.05 / 57.55, 9.63 / 61.20, 4.95 / 49.98, and 0.71 / 40.17 nK for the four molecules, indicating these laser cooling schemes are expected to reach temperatures below microkelvin orders of magnitude.

The quantum chemical calculations on molecules containing heavy elements have to include relativistic effects to obtain high-accuracy results [56]. DIRAC22 [57] is a program system for one-, two-, and four-component relativistic molecular calculations at the level of Hartree–Fock, Kohn–Sham (including range-separated theory), multiconfigurational self-consistent-field, multireference configuration interaction, electron propagator, and various flavors of coupled cluster theory [58]. For heavy molecules, DIRAC22 is computationally less efficient, especially for the all-electron basis sets. The lowest-order relativistic effect on atomic and molecular energies is the spin-free relativistic effect (also known as scalar relativistic effect), which consists of single-electron relativistic effects. For light atoms, this effect is relatively easy to evaluate using mass-velocity and Darwin operators or direct perturbation theory. In addition, many standard non-relativistic basis sets are available for use with lighter elements in DIRAC22. These kinds of calculations need smaller computational consumption in comparison with the all-relativistic effect method for the heavy-element-containing molecules.

By using the DIRAC22 program package [57], we calculate the PECs and the transition dipole moments (TDMs) of the PbX molecules. For each molecule, 9 Ω states are considered although the low-lying five of them are presented. The Dyall-3zp basis sets [59–61] are employed, which correspond to the large component 30s26p17d11f for Pb, 14s8p2d for F, 18s11p3d for Cl, 23s16p10d2f for Br, and 28s21p15d2f for I atom. Based on the molecular orbitals produced by the four-component Hartree–Fock method, the MRCI calculations in the Kramers-restricted relativistic large-scale configuration interaction module (KRCI) [62–64] are used to generate the convincing data of the PECs and TDMs for the PbX molecules. A Generalized Active Space (GAS) approach [65] was employed to account for electronic correlations of the MRCI calculations, and we use a 3-GAS space (8, 10/ 5), (19, 21/ 8), (21, 21/ 16). The distributions of 11 among 8 Kramers pairs in a complete active space (GAS II). Up to two holes were allowed in the 5d shell of the heavy elements (GAS I) to account for core-valence and core-core correlations. Further, the electronic dynamic correlation was considered through the inclusion of single and double excitations from the GAS I and GAS II spaces into the virtual spinor space (GAS III). For the PbF, PbCl, PbBr, and PbI molecules, the remaining 35, 39, 48, and 57 electrons were kept frozen and occupied during the configuration interaction procedure, and the calculated PECs span internuclear distance ranges of 1.60 ∼ 3.80, 1.85 ∼ 3.85, 2.00 ∼ 4.00, and 2.15 ∼ 3.95 Å with a step size of 0.05Å, respectively.

By solving the Schrödinger equation of nuclear motion based on the calculated PECs, we have calculated the wavefunctions of each electronic state, and the rovibrational energy levels. The spectroscopic parameters are obtained by fitting the vibrational-rotational energy levels with Dunham expansion [66]. The Einstein coefficients (A_ν'ν'' ) and FCFs (f_ν'ν'' ) of the X₁ ²Π_1/2 (_ν'' ) ↔ X₂ ²Π_3/2 (_ν' ) transitions are calculated to understand the laser cooling feasibility of the PbX molecules. These calculations are completed by the LEVEL8.0 program [67] that can give the width of the quasi-binding energy level and the inertial rotation constants and centrifugal distortion constants of diatomic molecules at a given energy level. It should be noted that the S (J'; J'') expression is only valid for the transition between singlet and singlet states, but can be generalized to other situations. For example, it can treat the ²Π ↔ ²Δ transition because the spectral structure is the same as that of ¹Π ↔ ¹Δ transition when the splitting constants of the electronic states are small.

3.1. Potential energy curves and spectroscopic parameters

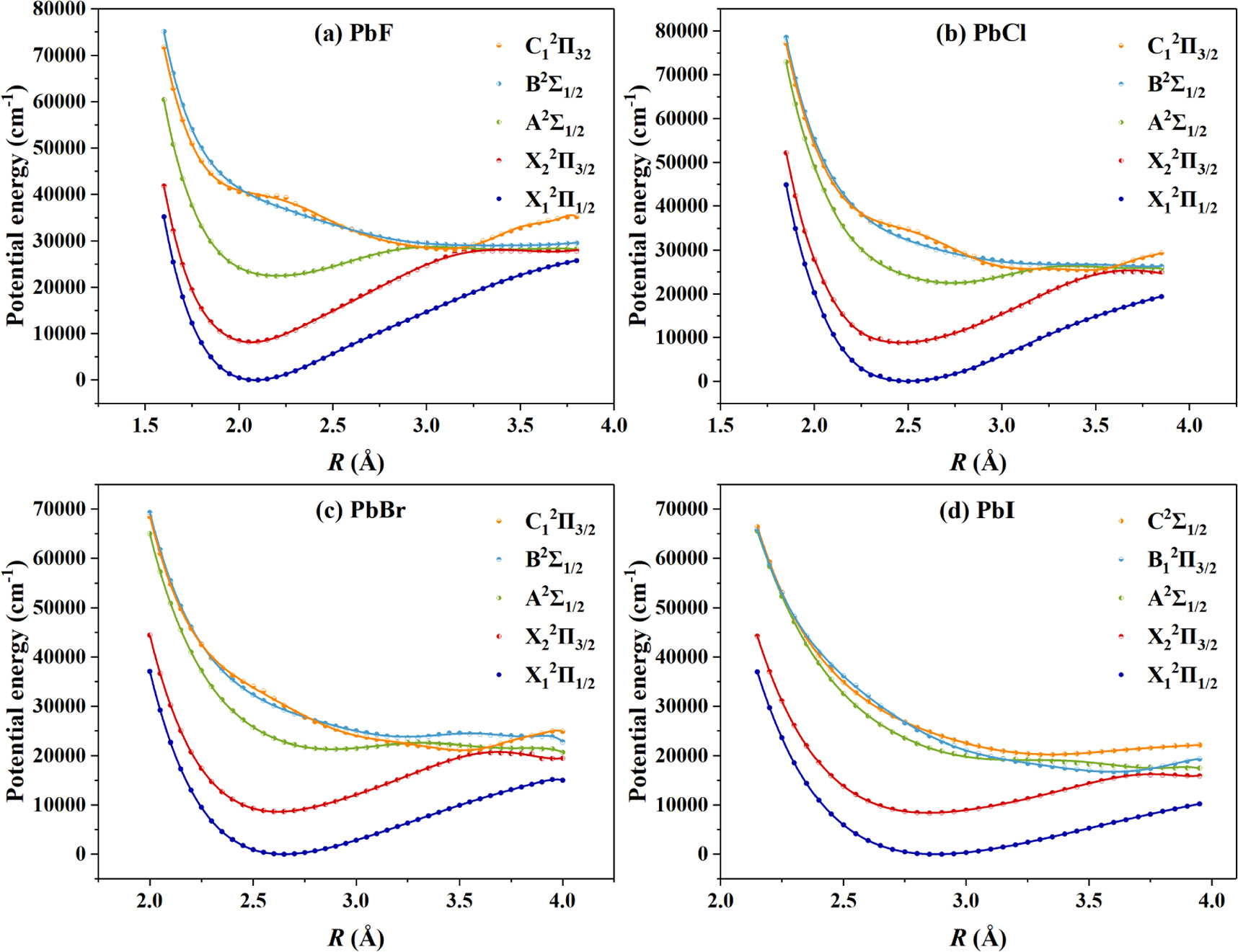
The PECs of the PbX molecules of the five low-lying states by DIRAC22 [57] with Dyall-3zp basis sets are shown in figure 1. They are attributed to the X₁ ²Π_1/2/ X₂ ²Π_3/2/ A²Σ_1/2/ B²Σ_1/2/ C₁ ²Π_3/2 states for the PbF, PbCl, and PbBr molecules, and the X₁ ²Π_1/2/ X₂ ²Π_3/2/ A²Σ_1/2/B₁ ²Π_3/2/ C²Σ_1/2 states for the PbI one. Based on the calculated PECs, the rovibrational energy levels are obtained by solving the Schrödinger equation of nuclear motion. There are 51/ 49 vibrational energy levels for the X₁ ²Π_1/2/ X₂ ²Π_3/2 states of the PbF molecule, and 51/ 51 ones for those of the PbCl, PbBr, and PbI molecules. For the sake of brevity, the vibrational energy levels over 8 are omitted in tables 1 and 2.

Zoom In Zoom Out Reset image size

Table 1. The vibrational energy levels of the PbF and PbCl molecules (in cm⁻¹).

	PbF		PbCl
	X1 2∏1/2	X2 2∏3/2	X1 2∏1/2	X2 2∏3/2
ν = 0	228.1557	240.9362	147.8020	135.6125
ν = 1	707.5739	742.2173	441.9110	444.9914
ν = 2	1182.7644	1239.3312	736.4642	754.8542
ν = 3	1653.7346	1732.3179	1031.2126	1025.6471
ν = 4	2120.4831	2221.1571	1308.6427	1254.2053
ν = 5	2582.9888	2705.8179	1554.8247	1522.6548
ν = 6	3041.2235	3186.2818	1796.5914	1813.8198
ν = 7	3495.1515	3662.5439	2060.2448	2104.3958
ν = 8	3944.7368	4134.5976	2333.9940	2393.6734

Table 2. The vibrational energy levels of the PbBr and PbI molecules (in cm⁻¹).

	PbBr		PbI
	X1 2∏1/2	X2 2∏3/2	X1 2∏1/2	X2 2∏3/2
ν = 0	101.0078	88.3004	59.5426	78.2719
ν = 1	303.1707	299.5909	209.5371	234.4211
ν = 2	504.4429	509.9825	358.9903	390.0046
ν = 3	704.8271	719.477	507.9032	545.0222
ν = 4	904.3269	928.0753	656.2762	699.4746
ν = 5	1102.9435	1135.782	804.111	853.3602
ν = 6	1300.6829	1342.5952	951.4077	1006.6806
ν = 7	1497.5474	1548.5192	1098.1661	1159.4354
ν = 8	1693.5376	1753.5577	1244.3901	1311.6227

The spectroscopic parameters for the lowest two Ω states are fitted from the obtained energy levels with Dunham expansion [66], as shown in table 3. In fact, we have tested the small basis sets and the larger Dyall-4zp basis sets [59, 60, 68] for the PbF molecule and found the remarkable increase in computational consumption has not substantially improved the results in comparison with the experimental data. As shown in table 3, the results with Dyall-4zp basis sets only a little improvement than those with Dyall-3zp basis sets, and the latter are also in good agreement with the experimental data [39, 69]. Generally, the larger active space can get more sufficient electron correlation energy and should give accurate results, but the computational consumption also increases rapidly. The valence electrons of 6s²6p² of Pb and 2s²2p⁵ of F in the active space, together with the 5d¹⁰ of Pb core electron as the reference space, need ∼10⁷ determinants per double group irrep for the present core-valence project with Dyall-3zp basis sets. The calculations with larger reference space of inner shells (All 14 electrons of the f shell of Pb should be included if they are considered.) are difficult to perform because the huge memory is needed (Of course, only 1s² of F is included, the calculational consume increase is not remarkable, but the impact is also small). Considering the results of the present core-valence project are in agreement with the available experimental values, the projects with larger reference space have not been explored. For the PbF molecule, the spectroscopic term T_e of 8144 cm⁻¹ for the X₂ ²Π_3/2 state is only 1.430% and 1.452% smaller than the experimental values of 8262.11 [39] and 8264 cm⁻¹ [69] respectively, and consistent with the other theoretical ones [42, 43, 47, 48]. Meanwhile, for the PbCl, PbBr, and PbI molecules, the experimental T_e s of 8272.78, 8197.92, and 7969.15 cm⁻¹ by Ziebarth et al [39] and the theoretical ones [44–47] in the literature are close to the present 8830, 8636, and 8404 cm⁻¹, respectively. The equilibrium positions of 2.086/ 2.065 Å for the X₁ ²Π_1/2/ X₂ ²Π_3/2 states of the PbF molecule well correspond to the experimental [69] and theoretical [42, 43, 47, 48] values available in the literature. At the same time, the calculated R_e s of the X₁ ²Π_1/2/ X₂ ²Π_3/2 states for the PbCl, PbBr, and PbI molecules are 2.493/ 2.464, 2.647/ 2.619, and 2.875/ 2.846 Å, respectively, which deviate from the theoretical values [44–47] with percent differences from 0.244% to 4.483%. The absolute differences between the R_e s for the X₁ ²Π_1/2 and X₂ ²Π_3/2 states are 0.021, 0.029, 0.028, and 0.029 Å for the PbF, PbCl, PbBr, and PbI molecule, respectively. These close R_e s indicate that the highly diagonal FCFs for the X₁ ²Π_1/2 ↔ X₂ ²Π_3/2 transition of the PbX molecules are feasible, which is necessary for laser cooling. Moreover, the calculated ω_e s for the X₁ ²Π_1/2 and X₂ ²Π_3/2 states in the present work of the PbX molecules are also close to the previous experimental [39, 69] and theoretical [42–48] values. For example, the present ω_e s of the PbBr molecule for the X₁ ²Π_1/2 and X₂ ²Π_3/2 states deviate from the experimental values of Ziebarth et al [39] by 1.804% and 2.834%, respectively, which are better than the other theoretical result reported by Benavides-Garcia et al [46]. The present results of the ω_e χ_e values of the X₁ ²Π_1/2 and X₂ ²Π_3/2 states for the PbX molecules also match the previous experimental results by Ziebarth et al [39].

Table 3. The calculated spectroscopic parameters of the X₁ ²Π_1/2/ X₂ ²Π_3/2 states for PbX (X = F, Cl, Br, and I) (R_e in Å, the other variables are in cm⁻¹).

Molecules	States	Methods	Te	Re	ωe	ωe χe
PbF	X1 2∏1/2	This work a	0	2.086	484.892	2.547
		This work b	0	2.076	489.837	2.391
		Expt. c	0		506.97	2.200
		Expt. d	0	2.0575	503
		Calc. e	0	2.050	521
		Calc. f	0	2.084	530
		Calc. g	0	2.08	540
		Calc. h	0	2.08	494
	X2 2∏3/2	This work a	8144	2.065	505.508	2.235
		This work b	8359	2.051	510.809	2.269
		This work i	5068	1.892
		Expt. c	8262.11		533.12	2.200
		Expt. d	8264	2.0342	529
		Calc. e	7417	2.038	533
		Calc. f	7805	2.066	542
		Calc. g	7895	2.06	547
		Calc. h	8259	2.07	522
PbCl	X1 2∏1/2	This work a	0	2.493	262.121	0.807
		Expt. c	0		304.17	0.904
		Calc. e	0	2.475	310
		Calc. j	0	2.61	304
	X2 2∏3/2	This work a	8830	2.464	277.775	0.835
		Expt. c	8272.78		322.52	0.878
		Calc. e	7526	2.458	317
		Calc. j	8473	2.58	313
PbBr	X1 2∏1/2	This work a	0	2.647	203.039	0.444
		Expt. c	0		206.77	0.446
		Calc. e	0	2.603
		Calc. k	0	2.712	195
	X2 2∏3/2	This work a	8636	2.619	212.162	0.445
		Expt. c	8197.92		218.35	0.433
		Calc. e	7577	2.588
		Calc. k	7220	2.674	205
PbI	X1 2∏1/2	This work a	0	2.875	150.535	0.271
		Expt. c	0		161.02	0.287
		Calc. e	0	2.772	168
		Calc. l	0	2.885	153
	X2 2∏3/2	This work a	8404	2.846	156.564	0.257
		Expt. c	7969.15		169.28	0.323
		Calc. e	7659	2.760	171
		Calc. l	8255	2.859	162

^a Based on the PECs with the Dyall-3zp basis sets. ^b Based on the PECs with the Dyall-4zp basis sets. ^c Ref. [39]. ^d Ref. [69]. ^e Ref. [47]. ^f Ref. [42]. ^g Ref. [43]. ^h Ref. [48]. ⁱ Based on the PECs with the MRCI method and x2c-TZVPPall-2c basis sets free of relativistic effects. ^j Ref. [44]. ^k Ref. [46]. ^l Ref. [45].

Meanwhile, we performed test calculations for PbF with non-relativistic effects and found the results for the equilibrium position and spectroscopic term (1.8916 Å and 5068.30 cm⁻¹ at MRCI/x2c-TZVPPall-2c [70]) are apparently different from the experimental values, while the ones with the relativistic effects are substantially improved, as shown in table 3. Overall, the calculations with the relativistic four-component method can give accurate spectroscopic parameters in comparison with the previous experimental and theoretical values.

3.2. Franck–Condon factors and laser cooling schemes

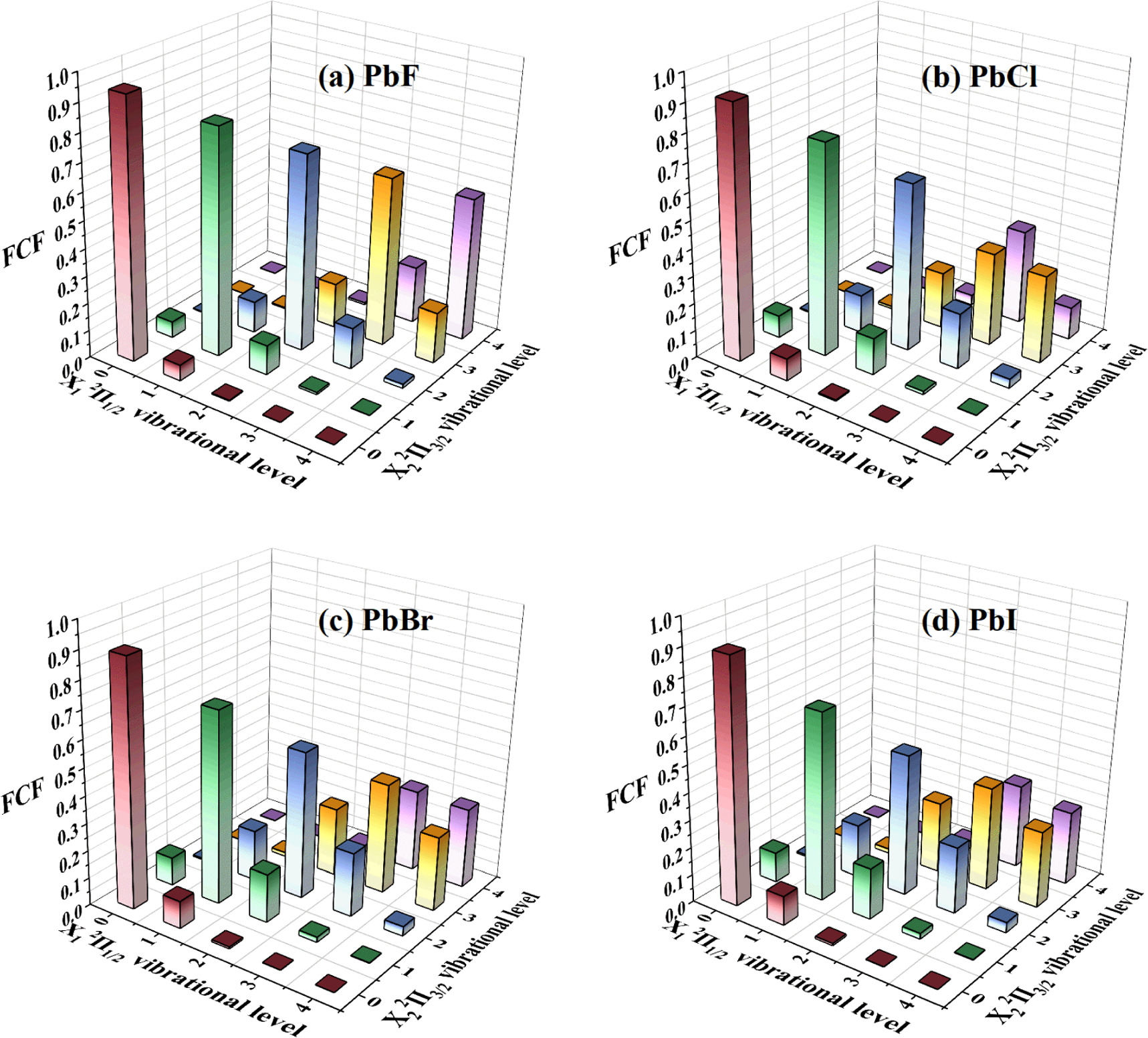
The FCFs (f_ν'ν'' ) for the X₁ ²Π_1/2 ($\nu$ '' ≤ 4) ↔ X₂ ²Π_3/2 (ν' ≤ 4) transitions of the PbX molecules are calculated based on the vibrational wavefunctions evaluated by solving the nuclear motion Schrödinger equation with the obtained PECs. Figure 2 shows that the FCFs of the X₁ ²Π_1/2 (ν'' ≤ 4) ↔ X₂ ²Π_3/2 (ν' ≤ 4) transitions of the PbX molecules are highly diagonal. For example, the f₀₀ values of the X₁ ²Π_1/2 (ν'' = 0) ↔ X₂ ²Π_3/2 (ν' = 0) are respectively 0.939125, 0.914541, 0.892669, and 0.885371. Therefore, these transitions are pseudo-closed transitions and suitable for constructing laser cooling schemes for the PbX molecules.

Zoom In Zoom Out Reset image size

The laser cooling scheme is constructed for the PbF molecule according to the obtained spectroscopic properties, as shown in figure 3(a), and the actual values of f_ν'ν''s are presented in table 4. A laser with the wavelength of λ₀₀ = 1213.16 nm is used to pump the main X₁ ²Π_1/2 (ν'' = 0) ↔ X₂ ²Π_3/2 (ν' = 0) transition. Considering that there are small probabilities of decaying from the X₂ ²Π_3/2 (ν' = 0, 1, 2) states to the X₁ ²Π_1/2 states (ν'' = 1, 2, 3), we added three pump lasers with the wavelengths of 1209.95, 1206.75, and 1279.47 nm to ensure the pseudo-closed loop transition more efficiently. As a result, the accumulated FCFs for PbF can reach 0.999994 which can provide 1.779 × 10⁵ scattered photons before leaking. These scattered photons are enough to exert an obvious cooling effect. In the present work, the accumulated FCFs are calculated with the sum of f₀₀, f₀₁, f₀₂, and f₀₃, and number of the scattered photons is evaluated by $1/\left(1-{f}_{00\left(\mathrm{1,2,3}\right)}\right).$

Zoom In Zoom Out Reset image size

Table 4. The FCFs (f_ν'ν''s ) of the X₁ ²Π_1/2 (ν'' ≤ 4) ↔ X₂ ²Π_3/2 (ν' ≤ 2) transitions for the PbF, PbCl, PbBr, and PbI molecules, respectively.

	PbF	PbCl	PbBr	PbI
f00	0.939125	0.914541	0.892669	0.885371
f01	0.058087	0.081338	0.100140	0.106555
f02	0.002667	0.003962	0.006803	0.007627
f03	1.17 × 10−4	1.45 × 10−4	3.69 × 10−4	4.25 × 10−4
f04	5.28 × 10−6	8.23 × 10−6	1.79 × 10−5	2.05 × 10−5
f10	0.059678	0.082538	0.102390	0.108891
f11	0.823645	0.769645	0.700327	0.682352
f12	0.108539	0.135067	0.176987	0.186194
f13	0.007658	0.011698	0.018813	0.020870
f14	4.53 × 10−4	9.84 × 10−4	0.001393	0.001589
f20	0.001188	0.002863	0.004817	0.005581
f21	0.114667	0.139731	0.185295	0.194763
f22	0.716662	0.614080	0.538306	0.514772
f23	0.151666	0.205450	0.233447	0.242896
f24	0.014641	0.033863	0.034592	0.037989

Similarly, the optical schemes pumping with four lasers are built for the PbCl, PbBr, and PbI molecules with the X₁ ²Π_1/2 (ν'' = 0) ↔ X₂ ²Π_3/2 (ν' = 0) as the main transition, which is shown in figures 3(b)–(d), respectively, and table 4 shows the corresponding values of f_ν'ν''s . For the PbCl molecule, the pumping laser wavelength for the main transition is 1135.87 nm, and those of the additional ones are 1133.68 (λ₁₁), 1131.62 (λ₂₂), and 1171.04 nm (λ₂₃), respectively, inducing 6.975 × 10⁴ of the scattered photons. For the PbBr and PbI molecules, the driven lasers with the wavelengths of 1155.44 and 1186.88 nm to pump the main X₁ ²Π_1/2 (ν'' = 0) ↔ X₂ ²Π_3/2 (ν' = 0) transition respectively, in addition, those of the additional wavelengths are 1154.22, 1153.01, 1180.28 for the PbBr and 1186.02, 1185.15, and 1206.45 nm for the PbI molecules to re-pump the photons falling on the auxiliary vibrational energy levels (ν' = 1, 2, 3). As a result, the accumulated FCFs are 0.999982 and 0.999978, and the correspondingly scattered photons are 5.424 × 10⁴ and 4.568 × 10⁴ for the PbBr and PbI molecules, respectively. The scattered photons are enough to perform remarkable cooling effects for the three molecules. Meanwhile, all required laser-cooling wavelengths are in the infrared region which the continuous wave laser can easily achieve.

3.3. The validities of the constructed optical schemes

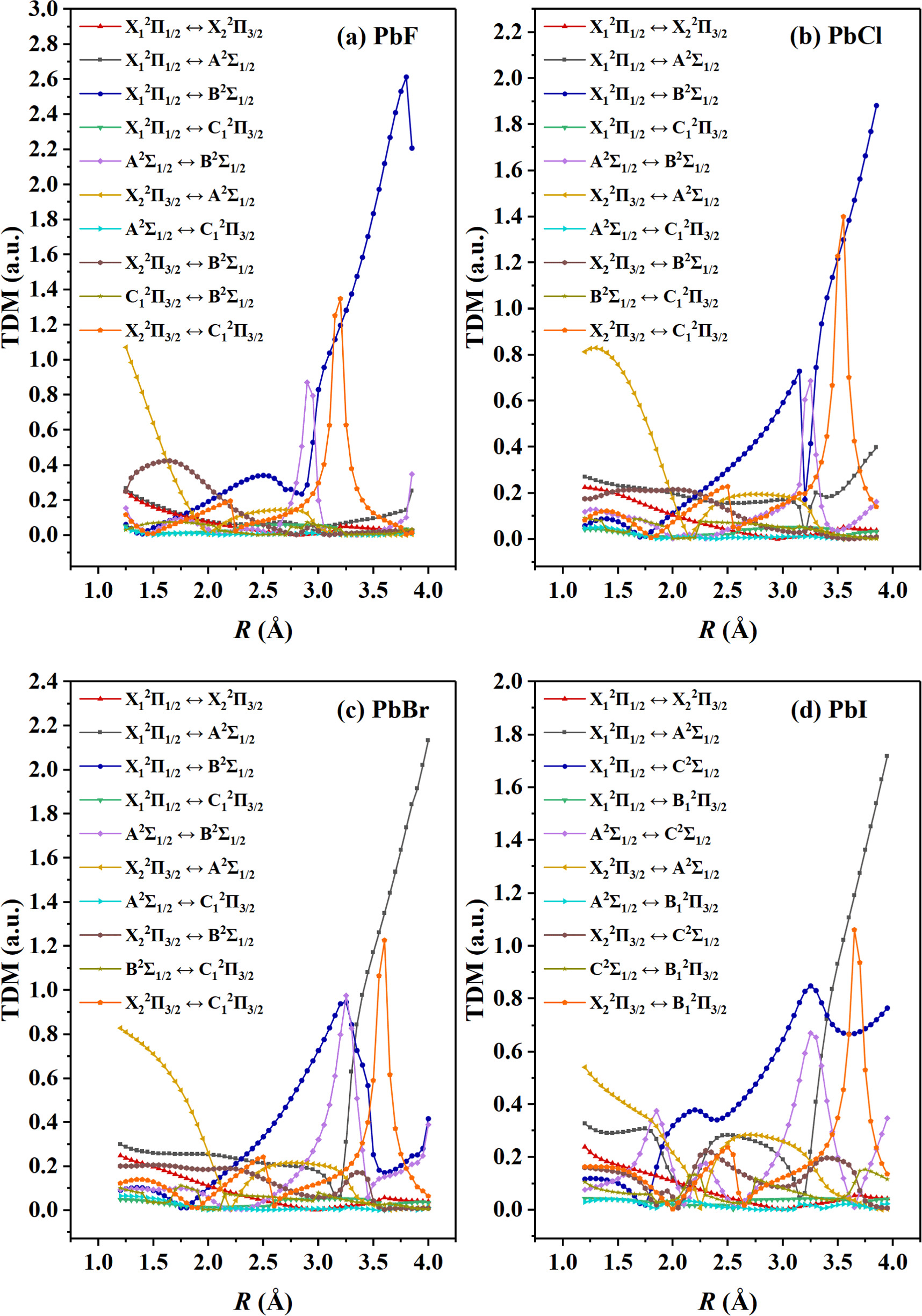
The TDMs of all possible transitions for the 5 lowest-lying Ω states of the PbX molecules are calculated, the results are shown in figure 4. Based on the obtained TDMs, we calculated the Einstein coefficients (A_ν'ν'' ) and radiative lifetimes (τs) for the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0, 1, 2) transitions involving in the optical schemes for laser cooling the PbX molecules, as shown in tables 5–8. For the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0) transitions, the sums of the A_ν'ν''s are the order of magnitude of 10³ for the PbF, PbCl, and PbBr molecules while the corresponding τs reach 10⁻⁴ s, and the sums of the A_ν'ν''s and the calculated τs for the PbI molecule are respectively the order of magnitude of 10² and 10⁻³. The smaller A_ν'ν''s and longer τs indicate that the driving forces of the optical schemes for the PbX molecules are limited, and a lower pre-cooling temperature for each molecule is required to achieve good cooling effects. The vibrational branch ratios (R_ν'ν''s ) are calculated for the X₁ ²Π_1/2 (ν'' ≤ 4) ↔ X₂ ²Π_3/2 (ν' ≤ 2) transitions by [71]:

$$\begin{eqnarray}&&{R}_{{\nu }^{{\prime} }{\nu }^{{\prime\prime} }}={A}_{{\nu }^{{\prime} }{\nu }^{{\prime\prime} }}/\displaystyle \sum _{{\nu }^{{\prime\prime} }}{A}_{{\nu }^{{\prime} }{\nu }^{{\prime\prime} }},\end{eqnarray} \tag{ 1 }$$

Zoom In Zoom Out Reset image size

Table 5. The Einstein coefficients A_ν'ν'' and radiative lifetimes τ of the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0, 1, 2) vibrational transitions for PbF.

ν'' (X1 2∏1/2)	ν' (X2 2∏3/2)
	ν' = 0	ν' = 1	ν' = 2
ν'' = 0	4.55 × 103	5.97 × 10−2	1.19 × 10−3
ν'' = 1	4.11 × 102	0.82	0.11
ν'' = 2	22.91	0.11	0.72
ν'' = 3	1.07	7.66 × 10−3	0.15
ν'' = 4	5.40 × 10−2	4.53 × 10−4	1.46 × 10−2
ν'' = 5	3.52 × 10−3	2.58 × 10−5	1.10 × 10−3
ν'' = 6	2.64 × 10−4	1.50 × 10−6	7.57 × 10−5
ν'' = 7	1.78 × 10−5	8.92 × 10−8	5.15 × 10−6
ν'' = 8	9.17 × 10−7	5.27 × 10−9	3.55 × 10−7
ν'' = 9	2.91 × 10−8	3.09 × 10−10	2.49 × 10−8
∑ Α ν'ν'' (s−1 )	4.98 × 103	4.85 × 103	4.73 × 103
τ = 1/∑ Α ν'ν'' (s)	2.01 × 10−4	2.06 × 10−4	2.11 × 10−4

Table 6. The Einstein coefficients A_ν'ν'' and radiative lifetimes τ of the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0, 1, 2) vibrational transitions for PbCl.

ν'' (X1 2∏1/2)	ν' (X2 2∏3/2)
	ν' = 0	ν' = 1	ν' = 2
ν'' = 0	2.17 × 103	83.46	0.77
ν'' = 1	3.23 × 102	1.78 × 103	1.31 × 102
ν'' = 2	23.96	5.30 × 102	1.38 × 103
ν'' = 3	1.43	68.91	7.80 × 102
ν'' = 4	0.10	7.32	1.85 × 102
ν'' = 5	1.05 × 10−2	0.41	24.35
ν'' = 6	7.60 × 10−5	2.51 × 10−4	1.22
ν'' = 7	1.18 × 10−3	8.22 × 10−4	7.03 × 10−2
ν'' = 8	7.96 × 10−4	6.32 × 10−5	3.04 × 10−2
ν'' = 9	3.77 × 10−6	5.10 × 10−4	1.87 × 10−2
∑ Α ν'ν'' (s−1 )	2.52 × 103	2.47 × 103	2.50 × 103
τ = 1/∑ Α ν'ν'' (s)	3.97 × 10−4	4.05 × 10−4	4.00 × 10−4

Table 7. The Einstein coefficients A_ν'ν'' and radiative lifetimes τ of the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0, 1, 2) vibrational transitions for PbBr.

ν'' (X1 2∏1/2)	ν' (X2 2∏3/2)
	ν' = 0	ν' = 1	ν' = 2
ν'' = 0	1.06 × 103	50.14	0.42
ν'' = 1	2.07 × 102	8.13 × 102	87.06
ν'' = 2	21.32	3.58 × 102	6.09 × 102
ν'' = 3	1.60	57.80	4.62 × 102
ν'' = 4	0.10	5.93	1.04 × 102
ν'' = 5	5.66 × 10−3	0.47	13.73
ν'' = 6	3.00 × 10−4	3.25 × 10−2	1.34
ν'' = 7	1.54 × 10−5	2.03 × 10−3	0.11
ν'' = 8	7.79 × 10−7	1.20 × 10−4	7.83 × 10−3
ν'' = 9	3.86 × 10−8	6.88 × 10−6	5.25 × 10−4
∑ Α ν'ν'' (s−1 )	1.30 × 103	1.29 × 103	1.28 × 103
τ = 1/∑ Α ν'ν'' (s)	7.72 × 10−4	7.77 × 10−4	7.83 × 10−4

Table 8. The Einstein coefficients A_ν'ν'' and radiative lifetimes τ of the X₁ ²Π_1/2 (ν'' = 0 ∼ 9) ↔ X₂ ²Π_3/2 (ν' = 0, 1, 2) vibrational transitions for PbI.

ν'' (X1 2∏1/2)	ν' (X2 2∏3/2)
	ν' = 0	ν' = 1	ν' = 2
ν'' = 0	1.06 × 103	50.14	0.42
ν'' = 1	2.07 × 102	8.13 × 102	87.06
ν'' = 2	21.32	3.58 × 102	6.09 × 102
ν'' = 3	1.60	57.80	4.62 × 102
ν'' = 4	0.10	5.93	1.04 × 102
ν'' = 5	5.66 × 10−3	0.47	13.73
ν'' = 6	3.00 × 10−4	3.25 × 10−2	1.34
ν'' = 7	1.54 × 10−5	2.03 × 10−3	0.11
ν'' = 8	7.79 × 10−7	1.20 × 10−4	7.83 × 10−3
ν'' = 9	3.86 × 10−8	6.88 × 10−6	5.25 × 10−4
∑ Α ν'ν'' (s−1 )	1.30 × 103	1.29 × 103	1.28 × 103
τ = 1/ ∑Α ν'ν'' (s)	7.72 × 10−4	7.77 × 10−4	7.83 × 10−4

The results in table 9 demonstrate that the ${R}_{{\nu }^{{\prime} }{\nu }^{{\prime\prime} }}$ from X₂ ²Π_3/2 (ν' = 0) to X₁ ²Π_1/2 (ν' = 0) is 91.26%, 86.18%, 82.20%, and 68.57% for PbF, PbCl, PbBr, and PbI, respectively. By using four lasers to pump the X₁ ²Π_1/2 (ν'' = 0) ↔ X₂ ²Π_3/2 (ν' = 0), X₁ ²Π_1/2 (ν' = 1) ↔ X₂ ²Π_3/2 (ν' = 1) and X₁ ²Π_1/2 (ν'' = 2, 3) ↔ X₂ ²Π_3/2 (ν' = 2) transitions, the total ${R}_{{\nu }^{{\prime} }{\nu }^{{\prime\prime} }}$ s of the pseudo-closed-loop transitions increase to 99.99% / 99.99% / 99.99% / 99.97% for the four molecules, which could significantly improve the cooling effect. Moreover, the scattering probabilities leaking into off-diagonal bands for the X₁ ²Π_1/2 (ν'') ↔ X₂ ²Π_3/2 (ν') transitions are low, which further demonstrates that these transitions of PbX are suitable for laser cooling.

Table 9. Vibrational branch ratios (R_ν'ν''s ) (in %) for the X₁ ²Π_1/2 (ν'' ≤ 4) ↔ X₂ ²Π_3/2 (ν' ≤ 2) vibrational transitions of PbX (X = F, Cl, Br, and I).

		ν' (X2 2∏3/2)
	ν'' (X1 2∏1/2)	ν' = 0	ν' = 1	ν' = 2
PbF	ν'' = 0	91.26	3.12	1.14 × 10−2
	ν'' = 1	8.25	79.87	5.91
	ν'' = 2	0.46	15.56	69.32
	ν'' = 3	2.14 × 10−2	1.36	21.87
	ν'' = 4	1.08 × 10−3	8.64 × 10−2	2.66
PbCl	ν'' = 0	86.18	3.38	3.07 × 10−2
	ν'' = 1	12.8	72.08	5.23
	ν'' = 2	0.95	21.44	55.15
	ν'' = 3	5.66 × 10−2	2.79	31.18
	ν'' = 4	4.15 × 10−3	0.3	7.38
PbBr	ν'' = 0	82.20	3.9	3.32 × 10−2
	ν'' = 1	16.02	63.24	6.81
	ν'' = 2	1.65	27.87	47.65
	ν'' = 3	0.12	4.49	36.16
	ν'' = 4	7.75 × 10−3	0.46	8.15
PbI	ν'' = 0	68.57	9.04 × 10−2	0.24
	ν'' = 1	27.07	46.37	9.79 × 10−2
	ν'' = 2	3.98	42.1	31.62
	ν'' = 3	0.35	10.17	47.81
	ν'' = 4	3.01 × 10−2	1.14 × 10−2	17.53

However, the smaller A_ν'ν'' will result in smaller Doppler (Τ_D s) and recoil temperatures (Τ_r s), which can be used to obtain lower cooling temperatures. The achievable Τ_D and Τ_r are estimated according to the following formulas [72]:

$$\begin{eqnarray}&&{T}_{D}=h/\left(4\pi \tau {k}_{B}\right),\end{eqnarray} \tag{ 2 }$$

$$\begin{eqnarray}&&{T}_{r}={h}^{2}/\left(m{\lambda }_{00}^{2}{k}_{B}\right),\end{eqnarray} \tag{ 3 }$$

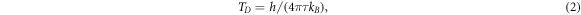
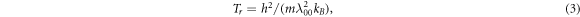
where m, h, and k_B are molecular mass, Planck's constant, and Boltzmann's constant, while λ₀₀ is the laser wavelength pumping the main transition of X₁ ²Π_1/2 (0) ↔ X₂ ²Π_3/2 (0). The calculated Τ_D / Τ_r are 19.05/ 57.55, 9.63/ 61.20, 4.95/ 49.98, and 0.71/ 40.17 nK for the PbX molecules, respectively. Equation (3) shows that the recoil temperature is strongly related to molecular mass, which indicates that heavy molecules are more likely to be cooled with lower recoil temperatures. Therefore, among the molecules considered, the PbI molecule can reach a minimum recoil temperature of 40.17 nK, which implies that this molecule is promising to achieve sub-micro-Kelvin temperature by Doppler cooling. On the whole, the present schemes can achieve the sub-micro-Kelvin temperatures for the PbX molecules but need lower pre-cooling temperatures.

In summary, the PECs and TDMs are obtained for the five low-lying Ω states of the PbX molecules by using the KRCI with the molecular orbitals produced by the relativistic four-component method in DIRAC22. The reliability of the present calculational level is confirmed by the calculated spectroscopic parameters for the two low-lying Ω states (X₁ ²Π_1/2 and X₂ ²Π_3/2) that are in good agreement with the theoretical and experimental values available in the literature. The four-laser cooling optical schemes with the close-loop X₁ ²Π_1/2 ↔ X₂ ²Π_3/2 transition are constructed for the PbX molecules based on the highly diagonal Frank–Condon factors. The pumping laser wavelengths are 1131.62 ∼ 1279.47 nm, which are available for common laser devices. Remarkably, the Doppler and recoil temperatures below microkelvin orders of magnitude can be achieved for all the constructed schemes. However, the radiative lifetimes of the upper levels are in the order of 10⁻⁴ or 10⁻³ s, which are not short enough to produce large spontaneous scattering forces for rapid cooling. Therefore, a lower pre-cooling temperature is needed to perform the present optical schemes. These results are expected to provide a helpful guide for designing experimental laser cooling programs for the PbX molecules.

This work is supported by the National Neutral Science Foundation of China (Grant Nos.12374232). C.L. Yang thanks the Xinjiang Tianchi Talent Program (2023).

All data that support the findings of this study are included within the article (and any supplementary files).

Jing-Zhen Luan: Data curation, Investigation, Writing-original draft. Chuan-Lu Yang: Conceptualization, Methodology, Supervision, Writing-review & editing. Xiao-Hu Li: Investigation. Wen-Wang Lu:Visualization. Yu-Liang Liu: Software. Wenkai Zhao: Supervision.