Abstract
The formation and propagation characteristics of the magnetosonic shocks are investigated in a three-component magnetoplasma, consisting of warm dynamical ions with hot inertialess electrons and positrons. By solving the well-known nonlinear magnetohydrodynamic equations within the framework of diagonalization method, a set of two exact nonlinear wave equations is derived, which permits for both analytical as well as numerical solutions. It is shown that coherent solitary structures are formed at time τ = 0, which transform into the magnetosonic shocklets with the passage of time (τ > 0) because of the rapid steepening of ion-fluid velocity and magnetic field perturbations. The nonlinear ponderomotive force could be the major responsible force behind the wave steepening and wave breaking in such plasmas. Furthermore, the variation of plasma β, the positron-to-electron density ratio p and the ion-to-electron temperature ratio σ significantly modifies the profiles of the ion-fluid velocity and magnetic field. The present study might be useful for understanding the nonlinear propagation of magnetosonic shocklets in interstellar medium and in laboratory plasma experiments, where an additional positron-component exist.
Export citation and abstract BibTeX RIS
1. Introduction
In the last few years, a considerable interest [1–4] has been developed in studying the linear and nonlinear phenomena in three-component electron-positron-ion (e-p-i) plasmas. The importance of positron component (that has an equal mass but opposite charge to electrons) has been recognized in many astrophysical and laboratory produced plasmas. An extensive literature can be found on the existence of positrons in natural environments, e.g., the early universe [5–7], the active galactic nuclei (AGN) [8–11], the neutron stars [12, 13], the solar atmosphere [14], the pulsar magnetospheres [15–17], supernova remnants, [18], gamma rays bursts [19] and at the center of Milky Way galaxy [20]. In particular, the positrons are produced in interstellar medium due to interaction of cosmic-ray nuclei with atoms [21, 22]. Apart from astrophysical plasmas, there are many observations that have confirmed the presence of positron component in laser-produced plasmas [23–26], and in laboratory experiments, where positrons have been used as a probe to study transport in tokamaks [27–30].
It is a well established fact that linear theory is valid only if the wave amplitude is taken small, so in this case higher order nonlinerarities are neglected. However, there are several reported phenomena in plasma in which unstable modes can saturate and attain large amplitudes. The study of nonlinear processes become important for the large amplitude waves leading to the localization of waves that yields different types of coherent structures, e.g., solitons, shocks, vortices etc. Many authors have shown their interest in investigating the properties of nonlinear waves propagating in electron positron ion plasma [31–34]. Rizzato [31] studied the localization of high-frequency electromagnetic waves in cold unmagnetized e-p-i plasmas and showed that low-frequency magnetic field may develop in the presence of oblique modulations and reported that the amplitude of the magnetic field and solitary wave is dependent on the angle between the direction of modulation and spatial dependence. Analytically, Berezhiani et al [32] investigated the nonlinear propagation of electromagnetic waves in an unmagnetized e-p-i plasma and also analyzed relativistically intense electromagnetic radiation in the presence of heavy ions that may lead to localized structures in unmagnetized e-p-i plasma in contrast to the case of e-p plasma. Nejoh [33] explored theoretically the effect of the ion temperature on large-amplitude ion acoustic waves in an e-p-i plasma. It was observed that with the increase of ion temperature, the maximum Mach number also increases while the amplitude of the ion-acoustic waves decreases. The region of existence of the ion-acoustic waves escalates as the ion temperature decreases and positron density increases. In 1995, Popel et al [34] explained the nonlinear properties of ion-acoustic solitons in e-p-i plasmas by considering the inertial ions and Boltzmann distributed electrons and positrons. They found that enhancement of the positron concentration leads to mitigation of the amplitude of ion-acoustic solitons.
The low-frequency magnetosonic mode is an important mode of the plasma that propagates in the direction perpendicular to the magnetic field. The magnetosonic wave is mostly called the 'fast' hydromagnetic wave as its phase velocity is larger as compared to the speed of Alfven waves. The fast magnetosonic mode exists in e-p (electron-positron) as well as in e-i (electron-ion) plasmas with a single branch but due to the presence of third component in e-p and e-i plasmas, it splits into two branches comprising of low and high frequency modes. There is an extensive literature on the investigation of nonlinear magnetosonic solitary and shock wave structures with their distinct propagation characteristics. [35–43], Gardner et al [35] analyzed the profiles of magnetosonic solitary waves in a collisionless plasma and inspected the influence of plasma temperature on the width of small-amplitude solitary waves while Kakutani et al, [36] discussed the small-amplitude magnetosonic waves in a collisionless cold plasma using the framework of nonlinear perturbation technique. Vito and Pantano [37] presented the two-dimensional magnetoacoustic waves in a collisionless plasma to obtain a Kadometsev Petviashvili (KP) equation and Ohsawa [39] derived a KdV (Korteweg de-Vries) equation for both nonlinear magnetosonic fast and slow waves by considering the two fluid description with finite electron and ion pressures. Ohsawa [40] also examined the time evolution of quasi-perpendicular magnetosonic shock profiles in 2-1/2 dimensional, fully relativistic plasmas by utilizing the electromagnetic particle simulations. Later, Hoshino et al [41] described theoretically the properties of relativistic magnetosonic collisionless shock waves in an e-p-i plasma and explored the spatial and kinetic structures of nonlinear flows using PIC simulations and quasi-linear theory. Hasegawa et al [42] studied the linear and nonlinear development of magnetosonic waves in an e–p–i plasma and showed magnetosonic waves in terms of low and high frequency modes. Deriving a KdV equation for low and high frequency modes, it has been established that width of the soliton for low-frequency solitary wave is much longer as compared to the electron skin depth, whereas, for high-frequency mode, the width of soliton is approximately equal to the electron skin depth. The electric potential is shown higher in case of low-frequency mode and smaller for high-frequency mode in comparison with an e–i plasma. In addition, Stasiewicz [43] revealed the electric field structures caused by the nonlinear magnetosonic waves and obtained convergent electric field structures associated with fast magnetosonic solitons and divergent electric field structures with slow solitons.
In this paper, we extend the work of [44] by incorporating an additional positron component to an e-i plasma and investigate the nonstationary nonlinear magnetoacoustic shock waves in terms of velocity and magnetic field profiles. The magnetohydrodynamical equations alongwith the charge-neutrality equation are solved by diagonalization method to obtain two characteristic wave equations. Analyzing numerically the latter, it is shown that positron concentration appreciably alters the profiles of the ion-fluid velocity and magnetic field.
The manuscript is organized in the following manner: In section 2, the nonlinear model equations are presented with a derivation of two-characteristic wave equations using the diagonalization technique. In section 3 derives the expressions for linear and nonlinear phase and shock speeds while section 4 shows the numerical illustration and discussion on nonstationary solutions for velocity and magnetic field profiles by varying the plasma β, positron-to-electron density ratio (p) and ion-to-electron temperature ratio (σ). Finally, section 4 summarizes the main findings of this manuscript.
2. Governing nonlinear equations and formulation
We study the dynamics of fast magnetosonic (FMS) shocks in a uniform three component magnetized e-p-i plasma, which is governed by the magnetohydrodynamic (MHD) equations. At ionic dynamical scale, the positrons and electrons are assumed to be inertialess while warm ions as dynamic. The complete set of MHD equations for describing the evolution of nonlinear FMS waves in an e-p-i magnetoplasma can be expressed, as
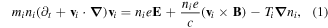
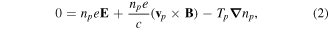


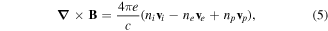
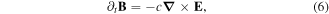
and

Equations (1)–(3) are the momentum equations for dynamical ions, inertialess positrons and electrons, respectively. Apart from momentum equations, the dynamics of FMS also includes the continuity equation equation (4). Equations (1)–(4) can be closed by considering the Ampere's and Faraday's laws alongwith the charge-neutrality condition through equations (5)–(7). Moreover nj, vj and Tj represent the number density, fluid velocity and temperature of the jth species (where j = i for positive ions, j = p for positrons and j = e for electrons), 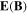 stands for electric (magnetic) field vector, and e is the magnitude of electronic charge. At equilibrium state, equation (7) can be expressed in terms of positron concentration as ni0/ne0 = 1−p, where p(=np0/ne0) denotes the ratio of positron-to-electron equilibrium densities (or positron concentration). Adding equations (2), (3) and using the charge-neutrality from equation (7), we get
stands for electric (magnetic) field vector, and e is the magnitude of electronic charge. At equilibrium state, equation (7) can be expressed in terms of positron concentration as ni0/ne0 = 1−p, where p(=np0/ne0) denotes the ratio of positron-to-electron equilibrium densities (or positron concentration). Adding equations (2), (3) and using the charge-neutrality from equation (7), we get
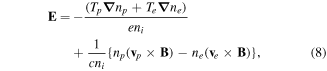
Eliminating 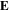 from equation (1) by equations (5) and (8), we easily arrive at
from equation (1) by equations (5) and (8), we easily arrive at
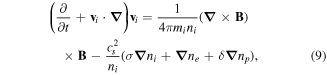
where ![${c}_{s}[={\left({T}_{e}/{m}_{i}\right)}^{1/2}]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn3.gif) is acoustic speed,
is acoustic speed, 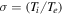 and
and 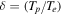 pinpoint the ratios of the ion-to-electron temperature and positron-to-electron temperature, respectively. By taking the gradient of charge-neutrality condition as
pinpoint the ratios of the ion-to-electron temperature and positron-to-electron temperature, respectively. By taking the gradient of charge-neutrality condition as 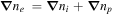 and upon substitution in equation (9), we come up with an equation as
and upon substitution in equation (9), we come up with an equation as
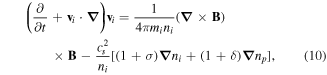
Now inserting equations (5), (8) into (6), we have
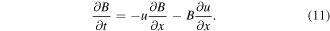
Similarly, we can express equations (10) in this form
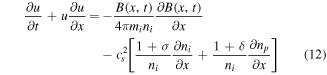
To investigate the nonlinear characteristics of one-dimensional FMS waves, we assume that 
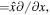
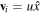 and
and 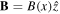 , where
, where 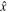 and
and 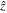 are the unit vectors along the x and z-axes. We also introduce different normalizations like τ = tωci,
are the unit vectors along the x and z-axes. We also introduce different normalizations like τ = tωci, 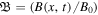 , Nj = nj/nj0, X = x/(VA/ωci) and U = u/VA, where
, Nj = nj/nj0, X = x/(VA/ωci) and U = u/VA, where ![${V}_{A}\left[={B}_{0}/\sqrt{4\pi {m}_{i}{n}_{i0}}\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn14.gif) and
and ![${\omega }_{{ci}}\left[={{eB}}_{0}/{m}_{i}c\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn15.gif) being the Alfven speed and ion-gyrofrequency, respectively. Thus, equations (4), (11) and (12) become simplified in the following form
being the Alfven speed and ion-gyrofrequency, respectively. Thus, equations (4), (11) and (12) become simplified in the following form
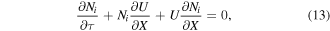
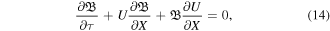
and
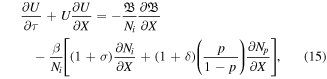
where ![$\beta \left[={c}_{s}^{2}/{V}_{A}^{2}\equiv 4\pi {n}_{i0}{T}_{e}/{B}_{0}^{2}\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn16.gif) is the plasma beta. The comparison of equations (13) and (14) leads to have
is the plasma beta. The comparison of equations (13) and (14) leads to have 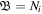 (a concept of frozen in field lines). As a consequence, in this model, the three plasma fluids are frozen in field to satisfy the relation
(a concept of frozen in field lines). As a consequence, in this model, the three plasma fluids are frozen in field to satisfy the relation
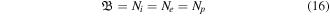
The above condition illustrates that the electron, positron, and ion fluids oscillate with magnetic field lines or plasma is frozen in field. Substituting equation (16) into equations (14) and (15), one obtains
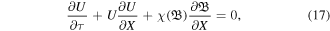
and
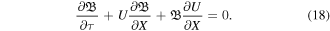
with
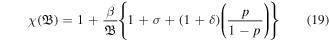
Equations (17) and (18) is the required set of governing normalized nonlinear coupled equations for FMS waves in a hot magnetoplasma, which result into the self-steepened profiles in terms of velocity and magnetic field variables. It is worth noticing that for taking β = 0, equations (17) and (18) completely coincide with the set of nonlinear coupled equations (2a) and (2b) of [45] for a cold magnetoplasma. To investigate the characteristics of FMS shocklets in a warm magnetoplasma, we express equations (17) and (18) in the following matrix form:
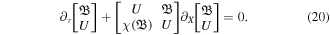
Now applying the diagonalization matrix technique to the square matrix in equation (20), we as a first step determine the eigen values by the formula det (A−λI) = 0, yielding
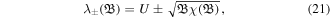
where ![$A=\left[\begin{array}{cc}U & {\mathfrak{B}}\\ \chi ({\mathfrak{B}}) & U\end{array}\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn18.gif) and
and ![$I=\left[\begin{array}{cc}1 & 0\\ 0 & 1\end{array}\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn19.gif) . Next, we determine the diagonalizing matrix C, whose columns are the eigenvectors of the square matrix A such that
. Next, we determine the diagonalizing matrix C, whose columns are the eigenvectors of the square matrix A such that
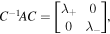
which results into the diagonal matrix with C, given by
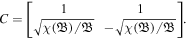
Multiplying equation (20) by C−1 from the left side and the second term with CC−1, we obtain
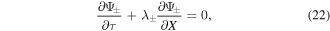
where the new variable Ψ±can be defined as 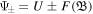 with
with  . This type of system admits a wave solution, which is determined by putting either Ψ+ or Ψ− equal to zero. Setting Ψ− = 0, one can find
. This type of system admits a wave solution, which is determined by putting either Ψ+ or Ψ− equal to zero. Setting Ψ− = 0, one can find 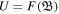 , which further gives rise to
, which further gives rise to 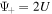 . Hence, from equation (22) the following form is obtained:
. Hence, from equation (22) the following form is obtained:

where the eigen value is now written in a new form as 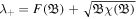 . Since we have U as a function of
. Since we have U as a function of 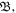 therefore we can have a similar equation to equation (23) for
therefore we can have a similar equation to equation (23) for 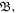 i.e.,
i.e.,
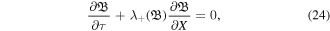
This result depicts the self-steepening of the magnetic field  The possible solution of equation (24) can be written as
The possible solution of equation (24) can be written as ![${\mathfrak{B}}={{\mathfrak{B}}}_{0}\left[X-{\lambda }_{+}\left({\mathfrak{B}}\right)\tau \right],$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn28.gif) where
where  is dependent on one-variable that is resolved by the initial condition for
is dependent on one-variable that is resolved by the initial condition for  at τ = 0. Here
at τ = 0. Here 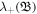 exhibits the nonlinear effective phase speed. Notice that the presence of nonlinearity is responsible to transform the pulse into shocklets with the development of time and this behavior is depicted in figures 2–4. It is important to mention here that the positron concentration enhances the amplitude of solitary and shock pulses and causes to enhance the wave self-steepening in comparison with the case when positron concentration is zero. Similarly, with the passage of time the profiles of compressional magnetic field perturbation are transformed to more steeper waves with the inclusion of positron concentration.
exhibits the nonlinear effective phase speed. Notice that the presence of nonlinearity is responsible to transform the pulse into shocklets with the development of time and this behavior is depicted in figures 2–4. It is important to mention here that the positron concentration enhances the amplitude of solitary and shock pulses and causes to enhance the wave self-steepening in comparison with the case when positron concentration is zero. Similarly, with the passage of time the profiles of compressional magnetic field perturbation are transformed to more steeper waves with the inclusion of positron concentration.
3. Linear/nonlinear phase and shock speeds
In order to find linear, nonlinear effective phase and shock speeds, we follow the well-known standard procedure [46, 47] and expand the phase speed 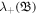 (as given by equation (21)) in the small-amplitude limit to the following form:
(as given by equation (21)) in the small-amplitude limit to the following form:
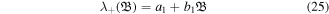
with a modified linear phase speed
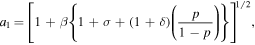
while the modified coefficient (b1) is defined as
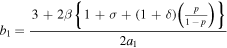
On the other hand, the shock speed can be determined by the Rankine-Hugoniot relation as
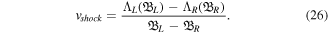
Here 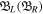 represents the value of B on the left (right) and
represents the value of B on the left (right) and 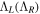 is the flux fluctuation, defined as
is the flux fluctuation, defined as 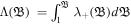 on the left (right) side of the shock front. After some simplifications, equation (26) can be simplified as
on the left (right) side of the shock front. After some simplifications, equation (26) can be simplified as
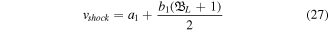
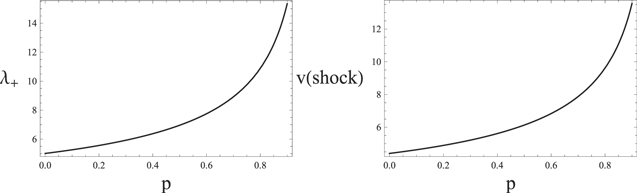
Figure 1 shows the variation of the normalized effective phase and shock speeds against the positron concentration. The magnitudes of effective phase and shock speeds are enhanced by increasing the positron concentration (p < 1).
Figure 1. Normalized effective phase and shock speeds against the positron concentration (p) with fixed β = 1.73, σ = 0.2 and 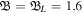 .
.
Download figure:
Standard image High-resolution image4. Numerical results and discussion
For numerical illustration, we solve equation (24) numerically and use the solution ![${\mathfrak{B}}=1+A{\rm{sech}} [X/d]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn37.gif) as an initial condition for the localized magnetic field pulse with fixed amplitude A = 0.5 and pulse width d = 20. We also choose typical numerical values that are consistent to interstellar medium [48], e.g., the ion number density ni0 ∼ 10−3 − 10−2cm−3, the positron number density np0 ∼1.5 × 10−4 − 1.5 × 10−3cm−3, and electron number density ne0 ∼1.15 × 10−3 − 1.15 × 10−2cm−3, the electron and positron temperatures Te = Tp = 107 K, the ion temperature
as an initial condition for the localized magnetic field pulse with fixed amplitude A = 0.5 and pulse width d = 20. We also choose typical numerical values that are consistent to interstellar medium [48], e.g., the ion number density ni0 ∼ 10−3 − 10−2cm−3, the positron number density np0 ∼1.5 × 10−4 − 1.5 × 10−3cm−3, and electron number density ne0 ∼1.15 × 10−3 − 1.15 × 10−2cm−3, the electron and positron temperatures Te = Tp = 107 K, the ion temperature 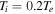 and magnetic field strength B0 = 10−5G. Relying on these values, we can further derive the physical quantities such as the ion-gyrofrequency ωci = 9.5 × 10−2 rad/sec, the Alfven speed VA = 2.18 × 107 − 6.90 × 107cm/s, the ion-acoustic speed cs = 2.87 × 107cm/s and plasma beta in the range β = 0.173 − 1.73 with a characteristic length VA/ωci = 2.29 × 108 − 7.26 × 108 cm. Since we are basically interested in the time evolution profiles that are associated with the fast magnetosonic (FMS) shocks, propagating along the positive X-direction in e-p-i magnetoplasmas and therefore set our initial condition for the ion-fluid velocity
and magnetic field strength B0 = 10−5G. Relying on these values, we can further derive the physical quantities such as the ion-gyrofrequency ωci = 9.5 × 10−2 rad/sec, the Alfven speed VA = 2.18 × 107 − 6.90 × 107cm/s, the ion-acoustic speed cs = 2.87 × 107cm/s and plasma beta in the range β = 0.173 − 1.73 with a characteristic length VA/ωci = 2.29 × 108 − 7.26 × 108 cm. Since we are basically interested in the time evolution profiles that are associated with the fast magnetosonic (FMS) shocks, propagating along the positive X-direction in e-p-i magnetoplasmas and therefore set our initial condition for the ion-fluid velocity 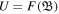 .
.
Figure 2 displays how the effect of plasma beta (β) modifies the temporal evolution of FMS shocklets in terms of compressional magnetic field. Here, different values of plasma beta such as (a) β = 0 (b) β = 0.17 and (c) β = 1.73 correspond to dashed, dotted and solid curves, respectively, for fixed of values of p = 0.13, σ = 0.2 and δ = 1. It is evident from the plot that the pulses in terms of compressional magnetic field propagate along the positive X-direction with a nonlinear phase speed 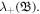 For a stationary situation (τ = 0), there appear the nonlinear excitations in the form of solitary pulses, which are later developed into the FMS shocklets, relying strongly on the time evolution. Because as long as the time (τ > 0) progresses, the solitary pulses start travelling with nonlinear phase speeds and lead to the wave self-steepening. The plasma beta
For a stationary situation (τ = 0), there appear the nonlinear excitations in the form of solitary pulses, which are later developed into the FMS shocklets, relying strongly on the time evolution. Because as long as the time (τ > 0) progresses, the solitary pulses start travelling with nonlinear phase speeds and lead to the wave self-steepening. The plasma beta 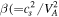 ) is the squared ratio of ion-acoustic speed to the Alfven speed
) is the squared ratio of ion-acoustic speed to the Alfven speed ![${V}_{A}[=({B}_{0}/\sqrt{4\pi {m}_{i}{n}_{i0}})]$](https://content.cld.iop.org/journals/1402-4896/95/7/075601/revision2/psab8652ieqn42.gif) . The larger the value of VA at constant cs, the smaller is the plasma beta (β < 1), which gives rise to purely transverse FMS waves. For smaller values of Alfven speed, we have larger beta (β > 1), which may result into the obliquely propagating magnetosonic waves. The wave becomes dispersive as long as it propagates at an angle with the direction of magnetic field and gets steepened with the passage of time. It is worth mentioning that ponderomotive force [49–51] could be responsible for the wave steepening and wave breaking in e-p-i plasmas. This force is a nonlinear force and essentially acts on the plasma fluids associated with coherent excitations to ultimately transform into the magnetosonic shocklets. Hence the large plasma β results into the wave dispersion involving the wave steepening and ponderomotive force might enhance the wave steepness. It is clear that by increasing the value of plasma β, it results in the faster development of shocks comprising of more self-steepened pulses in comparison with the case of zero/lower plasma β without showing any significant change in the magnitudes of magnetic field perturbation, see figures 2(a)–(c). It is vividly seen that increase in the plasma beta does not affect the profile of compressional magnetic field at X = 0 and τ = 0 but with the passage of time τ = (20, 40, 60), the nonlinear pulses are modified with the effective phase speeds and impact of plasma β is more significant for larger values of τ as compared to its smaller values. Thus, the effective phase speed
. The larger the value of VA at constant cs, the smaller is the plasma beta (β < 1), which gives rise to purely transverse FMS waves. For smaller values of Alfven speed, we have larger beta (β > 1), which may result into the obliquely propagating magnetosonic waves. The wave becomes dispersive as long as it propagates at an angle with the direction of magnetic field and gets steepened with the passage of time. It is worth mentioning that ponderomotive force [49–51] could be responsible for the wave steepening and wave breaking in e-p-i plasmas. This force is a nonlinear force and essentially acts on the plasma fluids associated with coherent excitations to ultimately transform into the magnetosonic shocklets. Hence the large plasma β results into the wave dispersion involving the wave steepening and ponderomotive force might enhance the wave steepness. It is clear that by increasing the value of plasma β, it results in the faster development of shocks comprising of more self-steepened pulses in comparison with the case of zero/lower plasma β without showing any significant change in the magnitudes of magnetic field perturbation, see figures 2(a)–(c). It is vividly seen that increase in the plasma beta does not affect the profile of compressional magnetic field at X = 0 and τ = 0 but with the passage of time τ = (20, 40, 60), the nonlinear pulses are modified with the effective phase speeds and impact of plasma β is more significant for larger values of τ as compared to its smaller values. Thus, the effective phase speed  increases for large values of plasma β and consequently leads to the development of faster shocks with increased self-steepness and wave-amplitudes.
increases for large values of plasma β and consequently leads to the development of faster shocks with increased self-steepness and wave-amplitudes.
Figure 2. Temporal evolution of compressional magnetic field against the normalized position X is shown for different values of plasma beta (a) β = 0 (dashed), 0.17 (dotted) and 1.73 (solid) with fixed p = 0.13, σ = 0.2 and δ = 1.
Download figure:
Standard image High-resolution imageFigure 3(a) exhibits the variation of positron concentration (p) on the profiles of compressional magnetic field as function of normalized position X with fixed values of β = 1.73, σ = 0.2 and δ = 1. The solid curves represent the profiles of magnetic field perturbation for finite positrons concentration at p = 0.13 and dashed curves correspond to compressional magnetic field perturbation without positron concentration p = 0. It may be observed that symmetrical solitary pulses exist at τ = 0 and this symmetry breaks down with the passage of time, τ > 0. As a result, shocklets are developed with enhanced wave-amplitudes and self-steepness. Specifically, at τ = 0, the solitary pulses converge without showing any affect of positron concentration and significantly change with τ > 0. This is because of the effective phase and shock speeds which are correlated with positron concentration and become strongly influenced by the large values of positron concentration (can be seen from figure 1). Thus, for higher values of p, the self- steepening of pulses is more dominant as compared to lower concentration p. Figure 3(b) shows how the ion-to-electron temperature ratio (σ) modifies the profiles of compressional magnetic field against the normalized position X with fixed values of β = 1.73, p = 0.13 and δ = 1. It is important to note that the behavior of pulses leads to the enhancement of self-steepening with increasing σ( = 0.02,0.87), which confirms that thermal effect enhances the effective phase speed of the solitary pulses which in turn amplifying the pulse-amplitude and wave-steepening with time evolution. For τ > 0, the shocklets associated with compressional magnetic field perturbations are developed faster and more steeper, depending strongly on the ion-to-electron temperature ratio in comparison with those shocklets obtained for variation of positron concentration (as shown in figure 3(a)).
Figure 3. Temporal evolution of compressional magnetic field against the normalized position X for different values of positron concentration (a) p = 0.13 (solid), p = 0 (dashed) with β = 1.73, σ = 0.2 and δ = 1 (b) σ = 0.87 (solid), σ = 0.02 (dashed) with p = 0.13.
Download figure:
Standard image High-resolution imageFigure 4 depicts the temporal change of the normalized ion-fluid velocity for different values of (a) β(=0,0.3) at fixed p = 0.13 and σ = 0.2 (b) p(=0,0.67) with β = 0.17 and σ = 0.2 (c) σ(=0.02,0.87) with β = 0.35 and p = 0.13. It can be seen that how the solitary waves resulting at τ = 0 transformed into shocklets with increasing τ = (30, 60). In the velocity profiles, as the plasma β increases, the wave-amplitude and pulse width also increase. The pulses get more self-steepened in comparison with the case of zero plasma beta. Further, it is examined that the behavior of plots with increasing p and σ values is found similar as that shown in figure 4(a) with varying plasma β. The solitary structures at τ = 0 transform into shocklets with increased wave-amplitudes and self-steepening by increasing the values of p and σ, respectively. This behavior is due to the effective phase speed 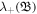 which becomes large by increasing the values of β, σ and p, thus, resulting into the enhancement of wave-amplitudes with an escalation in wave self-steepness.
which becomes large by increasing the values of β, σ and p, thus, resulting into the enhancement of wave-amplitudes with an escalation in wave self-steepness.
Figure 4. Plot of temporal progression of the normalized ion-fluid velocity versus the normalized position X for different values of (a) β = 0 (dashed), 0.3 (solid) with fixed p = 0.13, σ = 0.2 and δ = 1 (b) p = 0 (dashed), 0.67 (solid) with fixed β = 0.17, σ = 0.2 and δ = 1 (c) σ = 0.02 (dashed), 0.87 (solid) with fixed β = 0.35, p = 0.13 and δ = 1.
Download figure:
Standard image High-resolution image5. Summary
To summarize, we have studied the propagation characteristics of large-amplitude fast magnetosonic (FMS) waves in a three component magnetoplasma, whose constituents are the warm dynamical ions, hot inertialess electrons and positrons. For this purpose, we have solved the nonlinear MHD equations alongwith quasineutrality condition within the framework of diagonalization method and obtained a set of two characteristic wave equations to numerically depict the formation of FMS shocklets. It has been shown that concentration of positrons (p), plasma beta (β) and ion-to-electron temperature ratio (σ) affect the profiles of velocity and magnetic field perturbations significantly with the time evolution. This study can be beneficial to explain the evolution of magnetosonic shocklets in different environments of astrophysical plasmas where positrons are supposed to be generated by annihilation processes as observed in pulsars [17], active galaxies [8] and solar atmosphere [14], these highly magnetized dense astrophysical objects are responsible for the emission of strong electromagnetic radiations, relativistic jets and cosmic rays into interstellar medium. Thus the interactions involved are the main source of positron generation in low density space plasmas [21, 22]. Moreover, the results obtained in this study can be useful to understand laboratory-produced plasma experiments like those observed in Tokamaks [30], laser–plasma interaction [52–55] and single antimatter plasmas [56, 57]. In this context, it is suggested that our findings may prove useful in studying the nonlinear wave excitations and propagation in both astrophysical and laboratory plasmas.
Acknowledgments
This research was partly supported by the Higher Education Commission (HEC) under Grant 7632/Federal/NRPU/R&D/HEC/2017 and the Quaid-i-Azam University Research Fund, URF (2019-2020)