Abstract
The pressure-dependent lattice dynamics of 4H-SiC is investigated using diamond anvil cell, and compared with those of 3C- and 6H-SiC. It is found that both the zone-center longitudinal optical (LO) and transverse optical (TO) modes shift to higher frequencies with the increase of the applied pressures. This indicates that polymorph transitions are unlikely to happen under the (quasi-)hydrostatic pressure. The LO–TO splitting is described well by the cubic function with respect to the applied pressure. A decrease in the LO–TO splitting is observed above 33 GPa. The change of transverse effective charge and thus the ionic character of 4H-SiC exhibits a cubic dependence on the pressure due to the nonequivalent lattice dynamics parallel and perpendicular to the c-axis of 4H-SiC. Compared to what happens in 6H-SiC, the high pressure exerts higher effect on the ionic character of 4H-SiC because less nonequivalent bilayers are evolved. At last, the mode-Grüneisen parameters of the LO and TO modes at the Γ point are determined. Given the hexagonal lattice of 4H-SiC, the LO mode are softer than the TO mode.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Silicon carbide (SiC) is attracting great attention in power electronics, reinforced ceramics and quantum information technologies [1–9]. There exists over 250 polymorphs of SiC, with similar tetrahedral Si-C bonds but different stacking sequences [10, 11]. According to the Ramsdell's notation [12], polymorphs of SiC are denoted by the number of Si-C bilayers in the unit cell and the crystal symmetry. The most common polymorphs of SiC include 3C-SiC, 4H-SiC, 6H-SiC, where C and H represent cubic and hexagonal, respectively. The stacking sequences for the unit cells of 3C-, 4H- and 6H-SiC are ABC, ABCB and ABCACB, respectively [10]. The hexagonality is defined as the ratio of the number of hexagonal Si-C bilayers to the total number of bilayers per unit cell of SiC, which closely related to the lattice parameters of SiC polymorphs [13]. The hexagonality of 3C-, 4H- and 6H-SiC are 0, 1/2 and 1/3, respectively. It has been found that the lattice parameters, electrical and optical properties for the polymorphs of semiconductors show clear dependence on the hexagonality [14], while the elastic properties, equation of state and thermal conductivities are insensitive to the hexagonality because of the similar bonding among polymorphs in semiconductors [10].
Among the polymorphs of SiC, 4H-SiC has the highest Baliga's figure-of-merit [14], owing to its high critical field strength and high electron mobility. This endows 4H-SiC a great success in high-power electronics. During the growth of 4H-SiC single crystals, 6H-SiC is often incorporated as the secondary phase. Meanwhile, the wafering process gives rise to the local high pressure because of the high hardness of 4H-SiC, which induces a polymorph transitions [15, 16]. Therefore, understanding on the lattice dynamics of 4H-SiC, especially the pressure-dependent lattice dynamics of 4H-SiC, is critical to the growth and wafering of 4H-SiC. However, the understanding on the lattice dynamics of SiC under high-pressure processing mainly concentrates on 3C- and 6H-SiC [10, 17–21], which can be synthesized in a wide temperature range [14, 22]. It has been found the longitudinal optical (LO) and transverse optical (TO) phonon modes of both 3C- and 6H-SiC shift to higher wave numbers under high pressures up to 80 GPa. The splitting between the LO and TO modes of 3C-SiC increases with pressure, while the LO–TO splitting of 6H-SiC firstly increases rapidly as the pressure increases to 40 GPa and then decreases with the increase of the pressure [20]. This suggests that the lattice dynamics of SiC may be sensitive to its hexagonality.
In this work, we investigate the pressure-dependent lattice dynamics of 4H-SiC single crystal using diamond anvil cell (DAC). Both LO and TO modes shift to higher frequencies under high pressure due to reduced interatomic distances. The LO–TO splitting in 4H-SiC increases with rising pressure. This suggests that the polymorph transition is unlikely to happen under the (quasi-)hydrostatic pressure. The transverse effective charge has a cubic dependence on the pressure for 4H-SiC single crystal because of lattice anisotropy. Compared to what happens in 6H-SiC, the ionic character of 4H-SiC is more sensitive to applied pressure. At last, the mode-Grüneisen parameters of the LO and TO modes at the Γ point are determined. The LO mode is softer than the TO mode for 4H-SiC single crystal, which indicates that the structure of hexagonal SiC is unstable to shear stress.
2. Experimental methods
4H-SiC single crystal samples with the diameter of 50–60 μm and the thickness of below 30 μm were prepared from a 4H-SiC substrate wafer, which was grown by the physical vapor transport method and processed subsequently by slicing, lapping and chemical mechanical polishing. High-pressure experiments up to 50 GPa at room temperature were performed with DACs. The pressure was measured by the ruby pressure calibration [23]. The tiny ruby balls with a sizes of 10 μm and initial fluorescence spectra were simultaneously loaded along with the 4H-SiC sample in the DAC. The silicone oil was a polydimethylsiloxane oil (Baysilone oil M1000) with a viscosity of 1000 mPa s at 25 °C (the viscosity depends on the mean molecular weight). The silicone oil contributes to the formation of (quasi-)hydrostatic pressure and related Raman signal [24] were excluded from the data analysis. In situ high-pressure Raman spectroscopy experiments were performed using a micro-Raman spectroscopy system (inVia Reflex, Renishaw) with a 532 nm laser beam as the excitation source. The laser beam spot size was 5 μm. The wavenumber of both TO and LO modes were extracted by fitting the individual Raman peaks of modes with the Gaussian function.
3. Results and discussion
Figure 1 shows the in situ Raman spectra of 4H-SiC under pressures ranging from the ambient pressure to 50 GPa. The Raman spectra of 4H-SiC under the ambient pressure shows two Raman active modes from 750 to 1200 cm−1, that is, the zone-center LO and TO modes locating at 964 cm−1 and 776 cm−1, respectively [13] (figure 1(a)). It is clear that both the zone-center LO and TO modes shift to higher frequencies with the increase of the pressures. When the pressure increases from the ambient pressure to 50 GPa, the peak positions of the LO and TO modes shift to 1128.5 cm−1 and 912.9 cm−1, respectively (figure 1(b)). The non-linear behavior of the LO and TO modes can be expressed as:

where ωi
is the wavenumber of the LO and TO modes in cm−1, ω subscript 0 means the wavenumber at atmospheric pressure, P is the measured pressure in GPa, α1 and α2 are constants. During compression, the peak positions for the frequencies of the LO ( ) and TO (
) and TO ( ) modes are quadratically dependent on the loaded pressure by:
) modes are quadratically dependent on the loaded pressure by:


Figure 1. (a) In situ Raman spectra of 4H-SiC under pressures ranging from the ambient pressure to 50 GPa. (b) The zone-center LO and TO frequencies, and (c) the LO–TO splitting of 4H-SiC as functions of the pressure.
Download figure:
Standard image High-resolution imageWhen the 4H-SiC sample is decompressed, the pressure dependence for the peak positions for the frequencies of the LO ( ) and TO (
) and TO ( ) modes are quadratically fitted by:
) modes are quadratically fitted by:
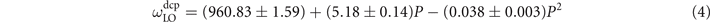

The continuous changes of the Raman modes with respect to the pressure indicate that the polymorph transition from 4H to 3C does not occur under the (quasi-)hydrostatic pressure [19].
The pressure dependence of LO–TO splitting during compression and decompression are then calculated. As shown in figure 1(c), the LO–TO splitting is 188 cm−1 at the ambient pressure. With the increase of the pressure, the LO–TO splitting rapidly increases and reaches the peak value under the pressure of 40 GPa. When the pressure further increases to 50 GPa, the LO–TO splitting exhibits a slight decrease. The LO–TO splitting can be described quite well by the cubic function with respect to the applied pressure.
The LO–TO splitting is caused by the non-zero macroscopic dipole polarization which is characterized by the transverse effective charge in zinc-blende and wurtzite semiconductors. The observed splitting of the optical mode frequencies in polar crystals, first noted by Lyddane and Herzfeld [25], and frequently associated with the names of Lyddane et al [26], who gave a theoretical account. The splitting may be understood physically by noting that when atoms of positive and negative charge move with respect to each other, a local polarization density leads to charge accumulation and extra rigidity for longitudinal waves but not for transverse waves. The transverse effective charge ( ) of 4H-SiC can be calculated by [19, 20, 27]:
) of 4H-SiC can be calculated by [19, 20, 27]:
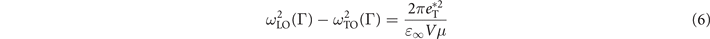
where  =
=  (Si) = −
(Si) = − (C) due to the charge neutrality condition; µ is the reduced mass of Si and C; V is the volume per atom; ε∞ is the high frequency dielectric constant with the value of 6.52 for SiC at the ambient pressure [19]. The volume dependence of ε∞ can be described by [20]:
(C) due to the charge neutrality condition; µ is the reduced mass of Si and C; V is the volume per atom; ε∞ is the high frequency dielectric constant with the value of 6.52 for SiC at the ambient pressure [19]. The volume dependence of ε∞ can be described by [20]:

The value of r in SiC remains controversial. The widely used assumption for the volume dependence of the high-frequency dielectric constant is only valid for semiconductors near the equilibrium volume. In other words, it is an approximate relationship. Moreover, the value of the logarithmic derivative of the high-frequency dielectric constant is not universal and differs considerably. The value of r depends on empirical values and theoretical calculations. In order to facilitate the comparison between our results on 4H-SiC and those of Olego et al's on 3C- and 6H-SiC, the same value of r is taken as 0.6 [19–21]. Therefore, the pressure dependence of is available with the equation-of-state data being applied.
First-principles calculations are then performed to calculated the equation-of-state data of 4H-SiC within the density functional theory framework, as implemented in the Vienna ab initio simulation package [28]. The projector-augmented wave method is adopted to describe the electron–ion interactions, with the cutoff energy for the wave function expansion of 600 eV. The structural optimization and electronic-property calculations are carried out using the Perdew–Burke–Ernzerhof exchange–correlation functional [29]. All structural relaxations proceed until the total energy per cell converges to less than 1 × 10−8 eV. Brillouin zone integrations were performed by Monkhorst–Pack k-point sampling of 21 × 21 × 5. The equilibrium lattice constants are determined by optimizing the geometry with lattice constants and internal atomic positions.
Figures 2(a) and (b) show the calculated lattice parameters and volume of the 4H-SiC unit-cell as functions of the pressure. It is found that the lattice parameters of a and c both decrease with increasing applied pressure. Meanwhile, the value of c/a is only weakly dependent upon pressure. The relative variation of c/a is less than 0.14% at pressures up to 50 GPa. Moreover, the variation of c/a of 2H-SiC within the same pressure range is less than 0.12% [30]. This tiny variation of c/a matches well with the calculated Poisson ratio of these SiC phases. The equilibrium values of c/a of 2H (1.644), 4H (3.274) and 6H (4.906) SiC are very close to the ideal value c/a = n
 and indicate an almost negligible structural anisotropy at atmospheric pressure. The third order Birch–Murnaghan equation of state (BM-EOS) describes the compression behavior of materials over the entire pressure range [31]. With the BM-EOS fitting, the isothermal bulk modulus (B0) of 213.61 ± 0.10 GPa and the pressure derivative (B0') of 3.82 are obtained for 4H-SiC, which agree well with previous results [32]. We note that 3C-, 4H- and 6H-SiC share similar bulk modulus and its pressure derivatives [32–36], because of the similar Si-C bonds in these polymorphs [10].
and indicate an almost negligible structural anisotropy at atmospheric pressure. The third order Birch–Murnaghan equation of state (BM-EOS) describes the compression behavior of materials over the entire pressure range [31]. With the BM-EOS fitting, the isothermal bulk modulus (B0) of 213.61 ± 0.10 GPa and the pressure derivative (B0') of 3.82 are obtained for 4H-SiC, which agree well with previous results [32]. We note that 3C-, 4H- and 6H-SiC share similar bulk modulus and its pressure derivatives [32–36], because of the similar Si-C bonds in these polymorphs [10].
Figure 2. Calculated (a) lattice parameters and (b) volumes of the 4H-SiC unit-cell as functions of the pressure.
Download figure:
Standard image High-resolution imageWith the pressure-dependent shifts of the TO and LO phonons (figure 1(b)) and the calculated volumes of 4H-SiC under different pressure (figure 2(b)), the values of  under different pressures are then calculated by equations (6) and (7). As shown in figure 3(a), the values of
under different pressures are then calculated by equations (6) and (7). As shown in figure 3(a), the values of  of 4H-SiC exhibits the cubic dependence on the applied pressure with the peak value of
of 4H-SiC exhibits the cubic dependence on the applied pressure with the peak value of  occurs under the pressure of 33 GPa. Because the value of
occurs under the pressure of 33 GPa. Because the value of  have been well correlated to the ionic character of the semiconductors [19]. The pressure dependence for
have been well correlated to the ionic character of the semiconductors [19]. The pressure dependence for  of 4H-SiC indicates that 4H-SiC becomes more ionic the applied pressure increases from 10 GPa to 33 GPa. During the compression of 4H-SiC, the axial Si-C bilayer is preferentially compressed. For nH polytypes, the planar modes (TO) propagate along the direction perpendicular to the c-axis, and the axial modes (LO) propagate along this direction. Compared with the planar modes, the axial modes are more sensitive to pressure which reduces the distance between the basal plane layers. Our calculation results also confirm this. When the pressure is increased to 60 GPa, the compression ratio of the c-axis (6.34%) is higher than that of the a- or b-axis (6.22%) which is parallel to the base plane. The planar hexagon in the basal plane of 4H-SiC increases the ionic nature of 4H-SiC when the pressure increases to 33 GPa. When the pressure further increases, the shortening of the distance between neighboring bilayers gives rise to the increased covalence of 4H-SiC, which is similar to what happens in compressed III–V and II–VI semiconductors [37–40]. It should be noted that the value of
of 4H-SiC indicates that 4H-SiC becomes more ionic the applied pressure increases from 10 GPa to 33 GPa. During the compression of 4H-SiC, the axial Si-C bilayer is preferentially compressed. For nH polytypes, the planar modes (TO) propagate along the direction perpendicular to the c-axis, and the axial modes (LO) propagate along this direction. Compared with the planar modes, the axial modes are more sensitive to pressure which reduces the distance between the basal plane layers. Our calculation results also confirm this. When the pressure is increased to 60 GPa, the compression ratio of the c-axis (6.34%) is higher than that of the a- or b-axis (6.22%) which is parallel to the base plane. The planar hexagon in the basal plane of 4H-SiC increases the ionic nature of 4H-SiC when the pressure increases to 33 GPa. When the pressure further increases, the shortening of the distance between neighboring bilayers gives rise to the increased covalence of 4H-SiC, which is similar to what happens in compressed III–V and II–VI semiconductors [37–40]. It should be noted that the value of  of 4H-SiC experienced a drop below 10 GPa. In above calculations, we neglected the tensor character of ε∞ and
of 4H-SiC experienced a drop below 10 GPa. In above calculations, we neglected the tensor character of ε∞ and  . Furthermore, there are two independent silicon (carbon) atomic sites in the unit cell of 4H-SiC (namely the h site and the k site). There exists two independent tensors of
. Furthermore, there are two independent silicon (carbon) atomic sites in the unit cell of 4H-SiC (namely the h site and the k site). There exists two independent tensors of  for these inequivalent atoms. In Wang et al's calculations, the value r = 0.3 is found to give the best fit to the calculated values [1]. In addition, Karch et al [41] found that the equation (7) describes the volume dependence of
for these inequivalent atoms. In Wang et al's calculations, the value r = 0.3 is found to give the best fit to the calculated values [1]. In addition, Karch et al [41] found that the equation (7) describes the volume dependence of  satisfactorily for volumes close to the equilibrium one using r = 0.37 (0.39) for the parallel (perpendicular) component of
satisfactorily for volumes close to the equilibrium one using r = 0.37 (0.39) for the parallel (perpendicular) component of  . In order to verify the tendency, we examined the effect of value of r on the pressure dependence of
. In order to verify the tendency, we examined the effect of value of r on the pressure dependence of  . As shown in figure 3(b), the decrease of
. As shown in figure 3(b), the decrease of  with increased pressures below 10 GPa are not observed when the value of r are taken as 0.3, 0.37 and 0.39. This indicates that the decrease of
with increased pressures below 10 GPa are not observed when the value of r are taken as 0.3, 0.37 and 0.39. This indicates that the decrease of  with increased pressures below 10 GPa is likely to be caused by the inaccuracy of the value of r rather than the inherent properties of SiC.
with increased pressures below 10 GPa is likely to be caused by the inaccuracy of the value of r rather than the inherent properties of SiC.
Figure 3. (a) The transverse effective charge ( ) at various pressures. The decrease in the transverse effective charge above 33 GPa indicates the increased covalent bonding in the material. The data of the values of
) at various pressures. The decrease in the transverse effective charge above 33 GPa indicates the increased covalent bonding in the material. The data of the values of  for 3C- and 6H-SiC under high pressures are extracted in references [18, 20]. (b) Comparison of the scaling relation in equation (7) for several values of r: 0.3, 0.37, 0.39, 0.6.
for 3C- and 6H-SiC under high pressures are extracted in references [18, 20]. (b) Comparison of the scaling relation in equation (7) for several values of r: 0.3, 0.37, 0.39, 0.6.
Download figure:
Standard image High-resolution imageIn order to investigate the effect of hexagonality on the values of  of SiC, the values for 3C- and 6H-SiC under the same pressures are incorporated as dashed lines in figure 3(a). For 3C-SiC with the hexagonality of 0, the values of
of SiC, the values for 3C- and 6H-SiC under the same pressures are incorporated as dashed lines in figure 3(a). For 3C-SiC with the hexagonality of 0, the values of  linearly increase with the increase of the pressure. Due to the difference between the electronegativity of Si and C, the distribution of electric cloud in 3C-SiC becomes more asymmetrical under high pressures. This gives rise to the increase of the ionic character of 3C-SiC with the increase of the pressure. For 6H-SiC with the hexagonality of 0.33, there are six nonequivalent stacking bilayers (ABCACB) along the c-axis. As the pressure increases, the change on the values of
linearly increase with the increase of the pressure. Due to the difference between the electronegativity of Si and C, the distribution of electric cloud in 3C-SiC becomes more asymmetrical under high pressures. This gives rise to the increase of the ionic character of 3C-SiC with the increase of the pressure. For 6H-SiC with the hexagonality of 0.33, there are six nonequivalent stacking bilayers (ABCACB) along the c-axis. As the pressure increases, the change on the values of  of 6H-SiC is more mild than what happens in 4H-SiC, because more stacking bilayers are involved in the compression or decompression process.
of 6H-SiC is more mild than what happens in 4H-SiC, because more stacking bilayers are involved in the compression or decompression process.
To understand the volume dependence of the phonon frequencies of 4H-SiC, the mode-Grüneisen parameter (γ) is then calculated by [42]:

where i is denoted as LO and TO; ωi is the wavenumber; V is the atomic volume. For 4H-SiC, we find that the values of the γ0(LO) and γ0(TO) are 1.04 and 0.94, respectively, which are lower than those of 3C-and 6H-SiC [19–21]. The mode softening with respect to the pressure, which can be derived from the density variation of γ, is regarded as a precursor for the phase transition [43]. The normalized mode-Grüneisen parameter (γ/γ0) for the LO and TO modes of 4H-SiC are shown in figure 4(a). It is clear that the LO modes of 4H-SiC are softer than the TO modes under high pressures. The LO mode and TO mode correspond to the lattice vibrations parallel and perpendicular to the c-axis [44]. Therefore, lattice vibrations along the c-axis are more sensitive to the variation of high pressures. It indicates that the polymorph transition of 4H-SiC is more sensitive to shear stress, which is consistent with previous experimental results [17, 45]. As to the effect of hexagonality on the volume dependence of the phonon frequencies, we find that both the LO and TO modes of 4H-SiC are softer than those of 6H-SiC, because less nonequivalent stacking bilayers are evolved during the compression of 4H-SiC. We also compared the value of γ/γ0 for the LO–TO splitting between 4H- and 6H-SiC. As shown in figure 4(b), the LO–TO splitting of 4H-SiC is softer than that of 6H-SiC. This indicates that the phase transition for SiC with higher hexagonality is more likely to happen, but the critical pressure of the phase transition exceeds the highest value in this work.
Figure 4. (a) The density variation of the normalized mode-Grüneisen parameters (γ/γ0) for 4H-SiC and 6H-SiC. The four (dash) lines at the bottom represent optical modes of 4H-SiC. The error bars are for four data points and are representative. (b) The density variation of the γ/γ0 of LO–TO splitting for 6H- and 4H-SiC. The data of the normalized mode-Grüneisen parameters of diamond, silicon and 6H-SiC are obtained from reference [18].
Download figure:
Standard image High-resolution image4. Conclusions
In conclusion, we have investigated the lattice dynamical properties of 4H-SiC single crystal under various high pressures using DACs. The TO and LO modes of 4H-SiC are observed up to 50 GPa. It has been found the structure of the 4H-SiC is stable under the (quasi-)hydrostatic pressure.  and thus the ionic character of 4H-SiC increase with the increase of pressure and reaches a maximum value at about 33 GPa due to the nonequivalent lattice dynamics parallel and perpendicular to the c-axis of 4H-SiC. Pressure exerts higher influence on lattice dynamic of 4H-SiC than 6H-SiC because of hexagonal Si-C bilayers. Furthermore, the mode-Grüneisen parameters for LO and TO modes of 4H-SiC are calculated from experimental data. The LO mode for 4H-SiC is softer than that of the TO mode, which is similar to 6H-SiC. The fact suggests that hexagonal polytypes of SiC likely undergo structural transformation under shear stress rather than hydrostatic pressure. The investigation of the high-pressure behavior of 4H-SiC provides us an effective approach to understand the mechanism of material deformation and structural transformation.
and thus the ionic character of 4H-SiC increase with the increase of pressure and reaches a maximum value at about 33 GPa due to the nonequivalent lattice dynamics parallel and perpendicular to the c-axis of 4H-SiC. Pressure exerts higher influence on lattice dynamic of 4H-SiC than 6H-SiC because of hexagonal Si-C bilayers. Furthermore, the mode-Grüneisen parameters for LO and TO modes of 4H-SiC are calculated from experimental data. The LO mode for 4H-SiC is softer than that of the TO mode, which is similar to 6H-SiC. The fact suggests that hexagonal polytypes of SiC likely undergo structural transformation under shear stress rather than hydrostatic pressure. The investigation of the high-pressure behavior of 4H-SiC provides us an effective approach to understand the mechanism of material deformation and structural transformation.
Acknowledgments
This work is supported by 'Pioneer' and 'Leading Goose' R&D Program of Zhejiang (Grant No. 2022C01021), National Key Research and Development Program of China (2018YFA0703400 and 2021YFA0718900) and Natural Science Foundation of China (Grant Nos. 91964107 and U20A20209). Partial support from Natural Science Foundation of China for Innovative Research Groups (Grant No. 61721005) is acknowledged. National Supercomputer Center in Tianjin is thanked for computational support.
Data availability statement
The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.







