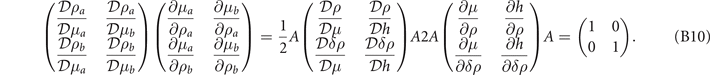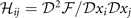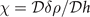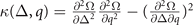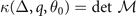Abstract
Finite-temperature phase structures for asymmetric two-component D-wave fermion superfluids in the weak coupling BCS regime are investigated. The Fulde–Ferrell–Larkin-Ovchinnikov (FFLO) state becomes non-degenerate with the orientation of Cooper pair momentum due to the anisotropic pairing gap for D-wave pairing. The new parameter θ0, corresponding to the orientation of Cooper pair momentum, greatly enriches the phase structures. Especially, the phase separation (PS) region in the phase diagram is significantly reduced comparing to that for S-wave pairing. Theoretically, the stability condition of solutions is equivalent to the positive definite Hessian matrix of free energy in the hyperplane defined by the number density constraints in the parameter space spanned by the average chemical potential μ, relative chemical potential h, paring gap Δ, pair momentum q, and θ0. In addition, the stability condition of the superfluid density is essentially included in the positive definite Hessian matrix. Moreover, the positiveness of imbalance number susceptibility  is always equivalent to the positiveness of the smaller eigenvalue λ− of the number susceptibility matrix. While the criteria ∂2Ω/∂Δ2 and
is always equivalent to the positiveness of the smaller eigenvalue λ− of the number susceptibility matrix. While the criteria ∂2Ω/∂Δ2 and 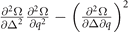 against PS in previous studies are equivalent to λ− only under the prerequisite that the solution is a local minimum in the corresponding hyperplane.
against PS in previous studies are equivalent to λ− only under the prerequisite that the solution is a local minimum in the corresponding hyperplane.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In the past two decades, the fermion pairing between different species with mismatched Fermi surfaces has promoted great interest in both experimental [1–6] and theoretical [7–14] researches owing to the exotic quantum phenomena, such as the non-zero Cooper pair momentum [15, 16], gapless excitation [17], the normal-superfluid phase separation (PS) [4, 7, 18], superfluid density instability [11, 19, 20] and so on. The easy tunability in terms of interaction [21, 22], population imbalance [18, 23–28] of the ultracold Fermi gases also provide good opportunities to study these exotic quantum phenomena. Except for the atomic Fermi gas, these interesting phenomena due to the mismatched Fermi surface are realized in asymmetric nuclear matter with neutron–proton pairing [29–31] and the neutral dense quark matter [32–34] as well.
In the exotic phenomena, stemming from the mismatched Fermi surface, the non-zero Cooper pair momentum corresponding to the anisotropic Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) states proposed by Fulde and Ferrell [15] and Larkin and Ovchinnikov [16] in an S-wave superconductor with Zeeman splitting about sixty years ago is especially concerned. While due to the sensitivity to impurities [35, 36] and orbital pair breaking [37], convincing evidence for experimental realization of FFLO state at low temperatures and high fields is still rather scare. However, the appearance has been suggested in the unconventional heavy fermion superconductors [35] and organic superconductors [38, 39] as well as Fe-pnictides [40, 41]. Particularly, the unconventional heavy fermion compound CeCoIn5 had been considered to be the most possible candidate for a FFLO state [35]. This heavy fermion superconductor together with pressured CeRhIn5 [42], NpPd5Al2 [43], and Tl-based cuprates [44] may share a couple of common features, such as the D-wave pairing and the strong paramagnetic effect [45]. In asymmetric nuclear matter, the neutron–proton pairings in 3 SD1 and 3 D2 channels are actually non S-wave pairing where 3 SD1 channel corresponds to the mixing of S-wave and D-wave pairing and 3 D2 channel corresponds to the pure D-wave pairing. To include the direction dependence of the pairing gap for non S-wave, the angle-dependent gap (ADG) has been proposed [30], which can reduce the suppression effect on the pairing gap from the mismatched Fermi surface. Once the anisotropic pairing gap for D-wave pairing is considered, the FFLO state becomes non-degenerate with the orientation of Cooper pair momentum. Different orientations may correspond to different superconductor phases and the change of orientation might lead to phase transition. In fact, in the investigation of D-wave superconductors with a quasi-two-dimensional Fermi surface, the change of orientation from the nodal direction to anti-nodal direction with increasing magnetic field has been reported in reference [46]. Due to the anisotropic pairing gap, the phase structure of non S-wave pairing (especially include FFLO state) is distinctly different from pure S-wave pairing [47]. Accordingly, a general discussion of asymmetric D-wave fermion superfluid may provide us new understanding of the exotic phenomena.
Another significant phenomenon of the asymmetric two-component fermion superfluid is the normal-superfluid PS which also attracted enormous attentions [4, 7, 10–14] after it is realized [18]. The stable regions of uniform superfluid state and FFLO state against PS in the T − α plane are seriously suppressed in the weak coupling BCS regime [12, 14] for S-wave pairing. But this PS for D-wave pairing remains unclear. Due to the angle dependence of the pairing for D-wave pairing, the FFLO state splits into three branches with different types of phase transition comparing to that of S-wave pairing and several unstable solutions arise at zero temperature [48]. Thus the corresponding PS might be interesting and distinctive owing to the ADG for D-wave pairing.
Additionally, once the FFLO state is taken into account for the ground state, an extra freedom, corresponding to the orientation of Cooper pair momentum, should be introduced. Consequently, the stability conditions for the solution of the gap equation and the superfluid density, and the stability constraint against PS may evolve into distinct formula.
Therefore, a generalized investigation of the D-wave pairing for asymmetric two-component fermion superfluid in the weak coupling region is presented in the current work, focusing on the temperature effects on the phase structures. The analysis is based on the mean field approximation which is believed to be a good treatment in weak coupling region even at finite temperature. Special attention is payed to the finite-temperature phase diagram of FFLO state. The current paper is organized as follows. A brief review of the formalism of FFLO state with ADG, thermodynamics, and the stability conditions of solutions, superfluid density, and number susceptibility are presented in section 2. The numerical results, are shown and discussed in section 3, where the phase diagrams of ADG state and FFLO state are performed. Finally, a summary and outlook are given in section 4.
2. Formalism
In the present paper, the physical system we interested in is an infinite system composed of two components of number density ρa
and ρb
and of chemical potential μa
and μb
, respectively. They interact via an anisotropic D-wave attractive interaction in three-dimensional free space. The full fermion Green's function is given by 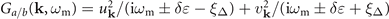 , with
, with  , ξk
= (ɛa
+ ɛb
)/2, δɛ = (ɛb
− ɛa
)/2 and
, ξk
= (ɛa
+ ɛb
)/2, δɛ = (ɛb
− ɛa
)/2 and 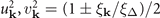 . Where
. Where 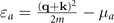 , and
, and 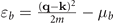 represents the single-particle energy of the two species of Fermions, respectively. ωm is odd Matsubara frequencies [49]. 2q corresponds to the nonzero center-of-mass momentum, i.e., the Cooper pair momentum in FFLO state. The off diagonal element, corresponding to the anomalous propagator, takes the form of
represents the single-particle energy of the two species of Fermions, respectively. ωm is odd Matsubara frequencies [49]. 2q corresponds to the nonzero center-of-mass momentum, i.e., the Cooper pair momentum in FFLO state. The off diagonal element, corresponding to the anomalous propagator, takes the form of 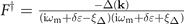 . The summation over the Matsubara frequencies provides the density matrix of particles in the condensate, i.e., the pairing probability,
. The summation over the Matsubara frequencies provides the density matrix of particles in the condensate, i.e., the pairing probability,
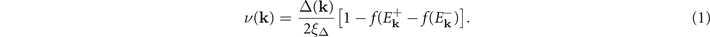
Accordingly, the gap equation is expressed as
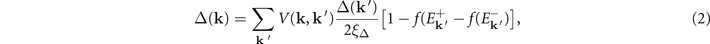
where 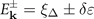 is the quasi-particle energy in the condensate and V(k, k') represents the anisotropic point contact interaction.
is the quasi-particle energy in the condensate and V(k, k') represents the anisotropic point contact interaction. ![$f(x)={\left[1+\mathrm{exp}(\frac{x}{T})\right]}^{-1}$](https://content.cld.iop.org/journals/1367-2630/24/10/103006/revision2/njpac94b4ieqn10.gif) is the well-known Fermi–Dirac distribution function. The fermion Green's function gives the number densities of the components
is the well-known Fermi–Dirac distribution function. The fermion Green's function gives the number densities of the components

with the density distributions
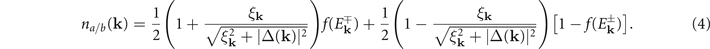
For fixed number densities, it is essential that the coupled equations (2) and (3) should be solved self-consistently.
2.1. Angle-dependent gap and the orientation of Cooper pair momentum
To investigate D-wave pairing conveniently, we simply consider the point contact pairing interaction of the form
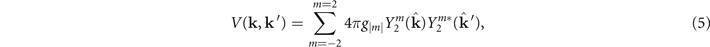
with 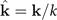 . We take the z axis in the direction of the quantization axis of the spherical harmonic function
. We take the z axis in the direction of the quantization axis of the spherical harmonic function 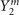 . Different from the S-wave pairing, the pairing gap, which is also anisotropic, can be expressed as
. Different from the S-wave pairing, the pairing gap, which is also anisotropic, can be expressed as

Generally, all components δm
should be taken into account in solving the gap equations. However, the thermodynamical stability investigation of D-wave pairing base on the Ginzburg–Landau energy functional indicates [50] that the stable D-wave state corresponds to cyclic D-wave phase or single component 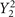 pairing phase in the weak coupling limit when the coupling constant g|m| are degenerate with m. For asymmetric case, the other single component (such as
pairing phase in the weak coupling limit when the coupling constant g|m| are degenerate with m. For asymmetric case, the other single component (such as 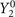 ) may as well turn into stable at certain asymmetries in weak coupling region. In addition, because of the crystal lattice, the pairing interaction of the heavyfermion superconductors [51] could be different with various m. Under such circumstances, the most energetically favored component may exclude the others. Therefore, it make sense to consider the pairing of single component. For simplicity, we suppose gm=0 ≫ gm=other, i.e., we only take m = 0 component pairing into account in the present work corresponding to
) may as well turn into stable at certain asymmetries in weak coupling region. In addition, because of the crystal lattice, the pairing interaction of the heavyfermion superconductors [51] could be different with various m. Under such circumstances, the most energetically favored component may exclude the others. Therefore, it make sense to consider the pairing of single component. For simplicity, we suppose gm=0 ≫ gm=other, i.e., we only take m = 0 component pairing into account in the present work corresponding to  . Which can ensure the axial symmetry of ξΔ and
. Which can ensure the axial symmetry of ξΔ and 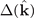 along the z axis (the symmetry axis of ADG). Substituting equations (5) and (6) in to gap equation (2), one can obtain the equation for δm
,
along the z axis (the symmetry axis of ADG). Substituting equations (5) and (6) in to gap equation (2), one can obtain the equation for δm
,
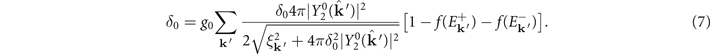
Noting that the pairing gap δ0 is a real number, we replace it by real parameter Δ for convenience hereafter. The pairing gap turn into  , which remains the rotational symmetry along the axis (θ = 0, ϕ = 0).
, which remains the rotational symmetry along the axis (θ = 0, ϕ = 0).
Once the pairing gap is anisotropic, the quasi-particle energy becomes non-degenerate with the orientation of Cooper pair momentum. To account this effect, the symmetric and asymmetric part of the spectrum can be expressed
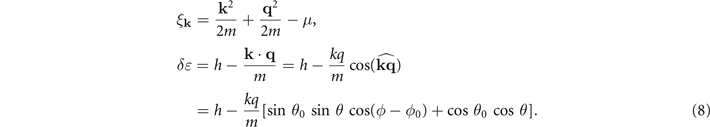
Where the average and relative chemical potentials are defined as μ = (μa
+ μb
)/2 and h = (μa
− μb
)/2, respectively. The orientations of 2q and k are related to (θ0, ϕ0) and (θ, ϕ) in spherical coordinate, respectively. One should note that the properties of spherical harmonics have been employed to expand the cosine of the angle between 2q and k. It is obvious that the term  due to the Cooper pair momentum can reduce the suppression from the mismatched Fermi surface h in certain direction. We stress here that the gap equation (7) and the densities (3) are independent of the constant ϕ0, i.e., ϕ0 can be eliminated by choosing a special spherical coordinate in which the orientation of 2q is represented as (θ0, ϕ0 = 0). Only θ0 as a parameter describes the direction of Cooper pair momentum. Different to the S-wave pairing, the FFLO states are non-degenerate for the orientation of Cooper pair momentum. And both the value q and the direction of Cooper pair momentum θ0 should be determined by minimizing the energy of the system. These two values are also embodied in the gap equation (7) via the symmetric and asymmetric part of the spectrum.
due to the Cooper pair momentum can reduce the suppression from the mismatched Fermi surface h in certain direction. We stress here that the gap equation (7) and the densities (3) are independent of the constant ϕ0, i.e., ϕ0 can be eliminated by choosing a special spherical coordinate in which the orientation of 2q is represented as (θ0, ϕ0 = 0). Only θ0 as a parameter describes the direction of Cooper pair momentum. Different to the S-wave pairing, the FFLO states are non-degenerate for the orientation of Cooper pair momentum. And both the value q and the direction of Cooper pair momentum θ0 should be determined by minimizing the energy of the system. These two values are also embodied in the gap equation (7) via the symmetric and asymmetric part of the spectrum.
2.2. Thermodynamics
For asymmetric two-component fermion systems with fixed the total number densities ρ = ρa + ρb and the asymmetry α = (ρa − ρb )/ρ at temperature T, the thermodynamic quantity describing the system is the free energy defined as
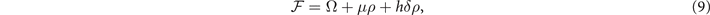
where δρ = ρa − ρb . The thermodynamic potential Ω takes the form of

Where the entropy can be expressed as
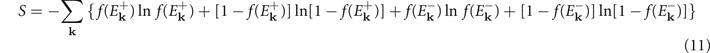
in the mean-filed approximation and the internal energy of the grand canonical ensemble reads
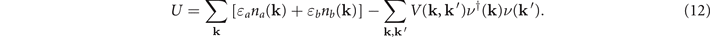
The chemical potential of quasiparticles is also embodied in the first term of the internal energy. The second term of the internal energy represents the BCS mean-field interaction energy among the particles in condensate. Using the particle pairing probability (1), density distribution (4), and gap equation (7), the thermodynamic potential can be expressed in the following form (noting the property ![$f(\omega )\mathrm{ln}\,f(\omega )+[1-f(\omega )]\mathrm{ln}[1-f(\omega )]=-\frac{\omega }{T}-\mathrm{ln}(1+{\text{e}}^{\frac{-\omega }{T}})$](https://content.cld.iop.org/journals/1367-2630/24/10/103006/revision2/njpac94b4ieqn19.gif) )
)
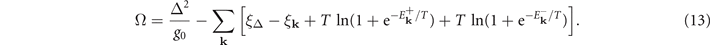
The gap equation (7) and density (3) can be equivalently expressed as
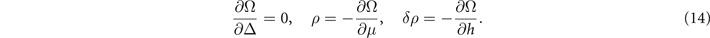
If the Cooper pair momentum q = 0, one easily finds that dF/dΔ = ∂Ω/∂Δ. As will be discussed in section 2.3 the gap equation is equivalent to the statement that the free energy reaches a minimum.
2.3. Solutions and stability conditions of the pairing solution for fixed ρ and δρ
For a fixed particle number system, the solution is equivalent to the minimum of 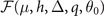 in the hyperplane
in the hyperplane 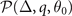 defined by the two number densities equation in the parameter space spanned by μ, h, Δ, q, θ0. The parameters μ and h can be treated as implicit functions of Δ, q, and θ0 as defined by the density constraints (14). In hyperplane
defined by the two number densities equation in the parameter space spanned by μ, h, Δ, q, θ0. The parameters μ and h can be treated as implicit functions of Δ, q, and θ0 as defined by the density constraints (14). In hyperplane 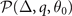 , the free parameters Δ, q, and θ0 are determined by minimizing the free energy. In order to make the expression more clear, we define
, the free parameters Δ, q, and θ0 are determined by minimizing the free energy. In order to make the expression more clear, we define
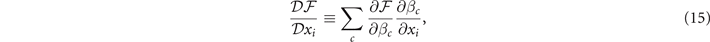
where xi
= Δ, q, θ0, and βc
= μ, h, Δ, q, θ0. The derivatives 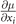 and
and 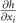 can be obtained from the implicit relations, i.e., density constraints (3). Whereas the
can be obtained from the implicit relations, i.e., density constraints (3). Whereas the 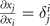 . From the relation (9) between the free energy
. From the relation (9) between the free energy 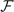 and the thermodynamic potential Ω, it is easy to check that
and the thermodynamic potential Ω, it is easy to check that 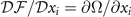 , which develops into
, which develops into 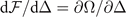 when q and θ0 are absent. Accordingly, the solutions of
when q and θ0 are absent. Accordingly, the solutions of 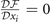 , corresponding to the minimum of free energy, turn into
, corresponding to the minimum of free energy, turn into
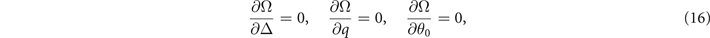
with the density constraints
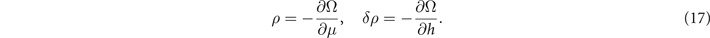
The stability of these solutions corresponds to positive definite Hessian matrix 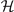 of the free energy. The elements of
of the free energy. The elements of 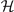 is
is
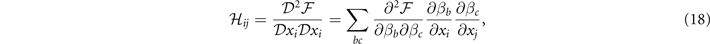
here xi,j
= Δ, q, θ0, and βb,c
= μ, h, Δ, q, θ0. The positive definite 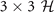 requires all the determinants of the sequential principal minor of
requires all the determinants of the sequential principal minor of 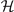 are positive, which imply that
are positive, which imply that 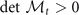 ,
, 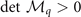 ,
, 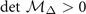 , and
, and 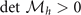 (see the appendix
(see the appendix 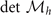 is always positive due to the number density constraints. For the other three constraints, only one key constraint remains to play crucial role in determining the stability of the solution under the circumstances considered, which will be discussed in section 3. As an example, if the solution is confined to q = 0, the stability condition of solutions [10] corresponds to the element of Hessian matrix
is always positive due to the number density constraints. For the other three constraints, only one key constraint remains to play crucial role in determining the stability of the solution under the circumstances considered, which will be discussed in section 3. As an example, if the solution is confined to q = 0, the stability condition of solutions [10] corresponds to the element of Hessian matrix 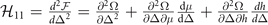 , which is always positive when the solution of the gap equation with fixed particle number exists for S-wave pairing. However, it is not true for D-wave pairing as will shown in section 3.1.
, which is always positive when the solution of the gap equation with fixed particle number exists for S-wave pairing. However, it is not true for D-wave pairing as will shown in section 3.1.
2.4. Superfluid density
For a superfluid state to be stable, the superfluid density must be positive [11]. Using the linear response theory, the superfluid density can be calculated via the response of the system to an external vector potential. Since the thermodynamics of the system with fixed number densities is the free energy, the supercurrent js and the superfluid density ρs should be defined via the Taylor expansion of 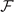 near the solution qs = (qs, θ0s, ϕ0s) (here supposing μs, hs, Δs, qs, θ0s represent certain solution of equations (16) and (17)), responding to a small velocity vs
near the solution qs = (qs, θ0s, ϕ0s) (here supposing μs, hs, Δs, qs, θ0s represent certain solution of equations (16) and (17)), responding to a small velocity vs
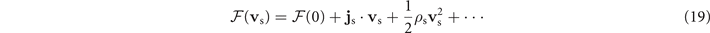
Where
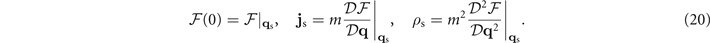
The equation (16) can ensure the zero of the supercurrent js. The positive superfluid density corresponds to the positive definite matrix  , which is also called as the Cooper pair momentum susceptibility [12]. One should note that in the previous works [10–12, 34] for S-wave pairing, the Cooper pair momentum susceptibility mainly focus on the appearance of the Cooper pair momentum, i.e., the linear response of the system to the value of q deviating from 0. In the present work, the Cooper pair momentum susceptibility refers in particular to the same focus point. In the spherical coordinates,
, which is also called as the Cooper pair momentum susceptibility [12]. One should note that in the previous works [10–12, 34] for S-wave pairing, the Cooper pair momentum susceptibility mainly focus on the appearance of the Cooper pair momentum, i.e., the linear response of the system to the value of q deviating from 0. In the present work, the Cooper pair momentum susceptibility refers in particular to the same focus point. In the spherical coordinates, 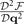 can be expressed as
can be expressed as
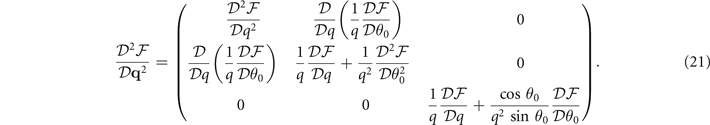
Here all the derivative with respect to ϕ0 vanishes due to the fact that the free energy is independent of azimuth angle ϕ0, indicating the superfluid density matrix (including the  component) is independent of ϕ0 as well.
component) is independent of ϕ0 as well.
Under the circumstance q = 0 for uniform superfluid state,  , the superfluid density developed into
, the superfluid density developed into
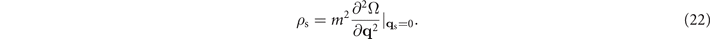
Due to the axial symmetry of the pairing gap we consider in the present work, the superfluid density tensor is no longer isotropic and can be decomposed into a transverse and a longitudinal part due to the O(2) symmetry. The superfluid density tensor can be expressed as
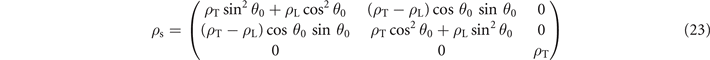
in the spherical coordinates with
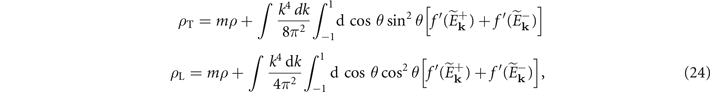
where 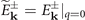 . It should be stressed that the forms
. It should be stressed that the forms 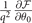 and
and 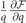 might be non-zero though the solutions require
might be non-zero though the solutions require 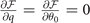 when q = 0. For S-wave pairing, Δ(k) is independent of θ, ρT = ρL. Thus the superfluid density is also isotropic. Due to the angle dependence of the pairing gap for D-wave pairing, the discrepancy between ρT and ρL result in the anisotropic ρs.
when q = 0. For S-wave pairing, Δ(k) is independent of θ, ρT = ρL. Thus the superfluid density is also isotropic. Due to the angle dependence of the pairing gap for D-wave pairing, the discrepancy between ρT and ρL result in the anisotropic ρs.
For the uniform superfluid state with q = 0, one essentially confines the gap equation 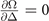 and the density equation (17) to the hyperplane
and the density equation (17) to the hyperplane 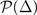 defined by the density constraint in the parameter space spanned by μ, h, Δ (the free parameter is Δ only). The stable solution corresponds to that the free energy reaches a minimum in hyperplane
defined by the density constraint in the parameter space spanned by μ, h, Δ (the free parameter is Δ only). The stable solution corresponds to that the free energy reaches a minimum in hyperplane 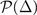 . And the stability condition of the solution is
. And the stability condition of the solution is 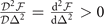 . However, the stable solution in hyperplane
. However, the stable solution in hyperplane 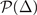 may become unstable in hyperplane
may become unstable in hyperplane 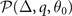 (the free parameters are Δ, q, θ0), namely, the stability condition
(the free parameters are Δ, q, θ0), namely, the stability condition 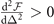 is insufficient once the solution (Δ, q = 0, θ0) is treated as a specific solution in hyperplane
is insufficient once the solution (Δ, q = 0, θ0) is treated as a specific solution in hyperplane 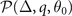 . Under this circumstances, the stability condition of the specific solution should be the positive definiteness of the
. Under this circumstances, the stability condition of the specific solution should be the positive definiteness of the 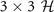 , which develop into
, which develop into
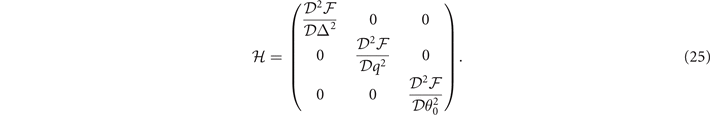
Where 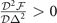 corresponds to the stability condition of solutions [10] in hyperplane
corresponds to the stability condition of solutions [10] in hyperplane 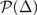 . The extra requirement
. The extra requirement 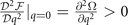 determines the appearance of the pairing momentum. If ρL > ρT, it is obvious that the
determines the appearance of the pairing momentum. If ρL > ρT, it is obvious that the  firstly reaches zero and changes sign along the orientation of
firstly reaches zero and changes sign along the orientation of 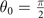 resulting in the first appearance of the FFLO state with q perpendicular to the symmetry axis of ADG. And the positive definiteness of the superfluid density result in the identical conclusion as
resulting in the first appearance of the FFLO state with q perpendicular to the symmetry axis of ADG. And the positive definiteness of the superfluid density result in the identical conclusion as 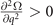 when ρL > ρT. This is also true for the case ρL < ρT. From the perspective of the occurrence of the FFLO state,
when ρL > ρT. This is also true for the case ρL < ρT. From the perspective of the occurrence of the FFLO state, 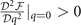 is equivalent to the positive definiteness of the superfluid density. As will discussed in section 3.2,
is equivalent to the positive definiteness of the superfluid density. As will discussed in section 3.2, 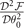 corresponds to the
corresponds to the 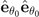 component of the superfluid density and describes the stability of the orientation of Cooper pair momentum.
component of the superfluid density and describes the stability of the orientation of Cooper pair momentum.
2.5. Number susceptibility and stability of homogeneous two-component superfluid against phase separation
Generally, the stability condition for a two-component system against changes in the densities of its component can be described by the total free energy of the system [12, 52], ![$F=\int {\mathrm{d}}^{3}\mathbf{r}\,\mathcal{F}[{\rho }_{\tau }(\mathbf{r})]$](https://content.cld.iop.org/journals/1367-2630/24/10/103006/revision2/njpac94b4ieqn67.gif) (τ = a, b). Supposing a tiny changes δρi
(r) deviate from uniform density distribution, due to the number conversation the first-order variation δF automatically vanishes. And the second-order variation δ2
F is expressed as
(τ = a, b). Supposing a tiny changes δρi
(r) deviate from uniform density distribution, due to the number conversation the first-order variation δF automatically vanishes. And the second-order variation δ2
F is expressed as
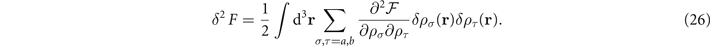
The stable homogeneous density distribution requires the 2 × 2 matrix 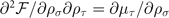 to be positively definite. As shown in appendix
to be positively definite. As shown in appendix 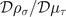 , where we define
, where we define
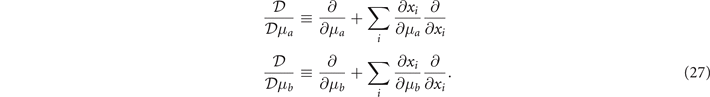
With the relationships 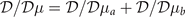 and
and 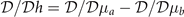 . One can find easily that
. One can find easily that
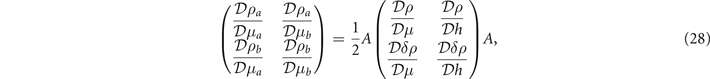
here 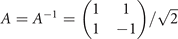 is a unitary transformation matrix. Therefore the stable homogeneous density distribution corresponds to the positive definite matrix
is a unitary transformation matrix. Therefore the stable homogeneous density distribution corresponds to the positive definite matrix
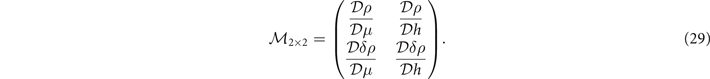
Which is equivalent to the statement that the eigenvalues λ± of 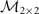 are both positive. Here
are both positive. Here
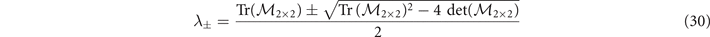
with the trace  . Fortunately, λ+ is always positive which roughly corresponds to
. Fortunately, λ+ is always positive which roughly corresponds to  . Another eigenvalue λ− roughly corresponds to
. Another eigenvalue λ− roughly corresponds to 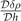 . The numerics shows λ− changes sign when
. The numerics shows λ− changes sign when  changes sign for S-wave pairing [10]. Our calculations for D-wave pairing also confirm this. Actually, the authors [11, 12] adopt
changes sign for S-wave pairing [10]. Our calculations for D-wave pairing also confirm this. Actually, the authors [11, 12] adopt 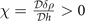 as the criterion for the stability of superfluid against the PS.
as the criterion for the stability of superfluid against the PS.
Since the appearance of 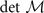 [see equation (B3) for the definition of
[see equation (B3) for the definition of 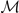 ] in the denominator of the expressions in equation (B7), each element of
] in the denominator of the expressions in equation (B7), each element of 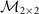 will change sign when
will change sign when 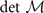 approaches zero and changes sign. Under this circumstance,
approaches zero and changes sign. Under this circumstance, 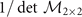 approaches zero and changes sign as discussed in reference [10]. Note that
approaches zero and changes sign as discussed in reference [10]. Note that 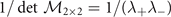 and λ+ is always positive, the stability condition that the eigenvalues of number susceptibility matrix are positive is equivalent to
and λ+ is always positive, the stability condition that the eigenvalues of number susceptibility matrix are positive is equivalent to 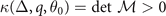 , which evolves into
, which evolves into 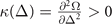 when q = 0 and
when q = 0 and 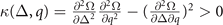 when q ≠ 0 for S-wave pairing. In reference [10], the numerics confirm that the stability condition
when q ≠ 0 for S-wave pairing. In reference [10], the numerics confirm that the stability condition 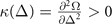 is equivalent to the imbalance number susceptibility
is equivalent to the imbalance number susceptibility 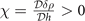 . However, as will be shown in section 3.4, it is true only when the solutions are the local minima in the considered parameter space.
. However, as will be shown in section 3.4, it is true only when the solutions are the local minima in the considered parameter space.
3. Results and discussions
As is well known, the point contact interaction adopted in the current work will result in the ultraviolet divergence of the gap equation. To avoid this, we employ a hard cutoff kΛ for three dimensional momentum which is usually used in the study of color superconductivity at moderate baryon density and isospin asymmetric nuclear matter. In this scheme, the normalization of the coupling constant  and the cutoff
and the cutoff 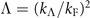 with
with 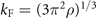 are also used to avoid the specific choice of model parameters. The value of Δ depend both on the cutoff Λ and the coupling constant
are also used to avoid the specific choice of model parameters. The value of Δ depend both on the cutoff Λ and the coupling constant 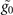 , however, the scaled quantities such as Δ/Δ0 and h/Δ0 (hereafter Δ0 is the value of Δ in the symmetric case with h = 0) are regularization scheme independent in the weak coupling region [18, 34, 53, 54]. In the present work, we take the weak coupling constant
, however, the scaled quantities such as Δ/Δ0 and h/Δ0 (hereafter Δ0 is the value of Δ in the symmetric case with h = 0) are regularization scheme independent in the weak coupling region [18, 34, 53, 54]. In the present work, we take the weak coupling constant 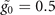 with the cutoff Λ = 4 as in the previous work [48, 55].
with the cutoff Λ = 4 as in the previous work [48, 55].
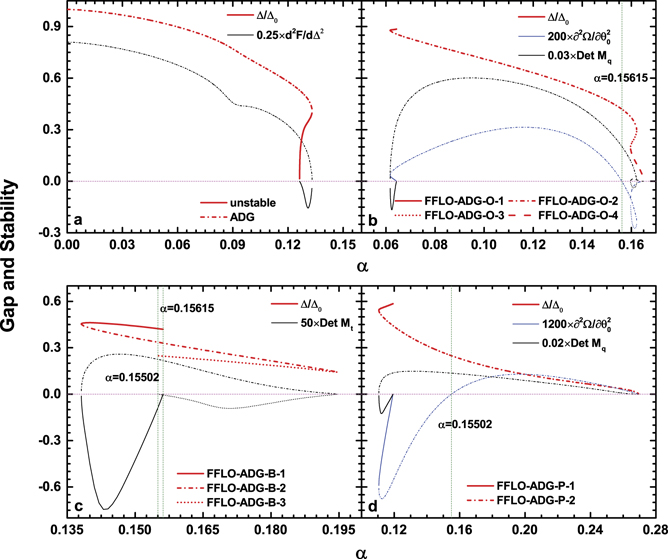
3.1. ADG state
We first consider the case without the pair momentum, i.e., q = 0, and we call this ADG state. The stability condition of the nontrivial solution is 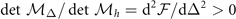 , which is always true when the solution of the gap equation with fixed number density exists for S-wave pairing. However, for D-wave pairing, there exist two solutions at low temperature, corresponding to a saddle point and a local minimum of
, which is always true when the solution of the gap equation with fixed number density exists for S-wave pairing. However, for D-wave pairing, there exist two solutions at low temperature, corresponding to a saddle point and a local minimum of 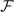 in hyperplane
in hyperplane 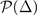 , respectively. The locally minimal solution satisfy the stability condition whereas the saddle point solution correspond to the negative
, respectively. The locally minimal solution satisfy the stability condition whereas the saddle point solution correspond to the negative 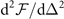 (as shown in figure 4(a)). The solution related to the local minimum (saddle point) is marked with red short dash doted (blue solid) line in figure 1. The normalized pairing gap Δ/Δ0 and the scaled difference of the free energy between superconducting and normal states
(as shown in figure 4(a)). The solution related to the local minimum (saddle point) is marked with red short dash doted (blue solid) line in figure 1. The normalized pairing gap Δ/Δ0 and the scaled difference of the free energy between superconducting and normal states  are shown in the upper and lower panel of figure 1, respectively. Where the constant
are shown in the upper and lower panel of figure 1, respectively. Where the constant 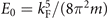 and the Fermi temperature
and the Fermi temperature 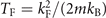 . One should note that this unstable solution is quite analogous to the Sarma state [17]. Both this unstable state in the present paper and Sarma state correspond to the saddle point of the thermodynamic quantities. Different as Sarma state which appears as the saddle point of the thermodynamic potential, the unstable state here corresponds to the saddle point of the free energy. Besides, since there exist gapless excitations in momentum space for D-wave pairing, the criteria of Sarma state for S-wave are difficult to be applied in D-wave pairing.
. One should note that this unstable solution is quite analogous to the Sarma state [17]. Both this unstable state in the present paper and Sarma state correspond to the saddle point of the thermodynamic quantities. Different as Sarma state which appears as the saddle point of the thermodynamic potential, the unstable state here corresponds to the saddle point of the free energy. Besides, since there exist gapless excitations in momentum space for D-wave pairing, the criteria of Sarma state for S-wave are difficult to be applied in D-wave pairing.
Figure 1. The scaled paring gap Δ/Δ0 and the scaled difference of the free energy between superconducting and normal states 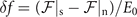 as a function of the asymmetry α. The temperatures are set to be T/TF = 0.0001, 0.01, and 0.02. The red short dash dotted and solid lines correspond to the stable ADG and unstable superconducting state, respectively.
as a function of the asymmetry α. The temperatures are set to be T/TF = 0.0001, 0.01, and 0.02. The red short dash dotted and solid lines correspond to the stable ADG and unstable superconducting state, respectively.
Download figure:
Standard image High-resolution imageThe existence of the unstable solution at low temperature indicate the first order transition from the superconduction state to the normal state since Δ does not approach to zero when α → αc (αc represent the critical asymmetry where the δf become positive). This is also confirmed from the free energy curve. It is obvious that the free energy of ADG state cross the free energy of normal state as exhibited in the insert at T/TF = 0.01. However, the first transition only occur at low temperature, with increasing temperature, the domain of the unstable state is getting smaller, and disappear when T/TF > 0.0125. The insert at T/TF = 0.02 implies a second order transition from the superconducting state to normal state.
The stability condition against PS develop into κ(Δ) = ∂2Ω/∂Δ2 when q = 0. Our numerics for D-wave pairing indicate that ∂2Ω/∂Δ2 > 0 is equivalent to 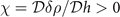 only if the solution is locally minimal in hyperplane
only if the solution is locally minimal in hyperplane  . Since the ground state corresponds to the locally minimal solution only, both ∂2Ω/∂Δ2 and χ can be adopted to distinguish the PS. The finite-temperature phase diagram for D-wave pairing without Cooper pair momentum are displayed in figure 2, which is significantly different from the phase diagram for S-wave pairing [10, 12]. There are two narrow yellow regions corresponding to the PS, one is settled around α = 0.09 at very low temperature. Another is located near the boundary of αc
. This difference from S-wave pairing may result from the existence of the nodes and zero-lines of the pairing gap which can provide phase-space for the excess particles. Under this circumstance, it might be unnecessary to destroy the pairing state to settle the excess particle. Therefore, the superconducting state in certain region which is unstable against PS for S-wave pairing becomes stable against PS for D-wave pairing.
. Since the ground state corresponds to the locally minimal solution only, both ∂2Ω/∂Δ2 and χ can be adopted to distinguish the PS. The finite-temperature phase diagram for D-wave pairing without Cooper pair momentum are displayed in figure 2, which is significantly different from the phase diagram for S-wave pairing [10, 12]. There are two narrow yellow regions corresponding to the PS, one is settled around α = 0.09 at very low temperature. Another is located near the boundary of αc
. This difference from S-wave pairing may result from the existence of the nodes and zero-lines of the pairing gap which can provide phase-space for the excess particles. Under this circumstance, it might be unnecessary to destroy the pairing state to settle the excess particle. Therefore, the superconducting state in certain region which is unstable against PS for S-wave pairing becomes stable against PS for D-wave pairing.
Figure 2. Phase diagram without Cooper pair momentum in the T − α plane. The yellow region represents the PS. The solid and the short dashed thick lines correspond to the second and first order transition from the superconducting state to normal state, respectively. The solid and short dashed thin lines correspond to the scaled longitudinal and transverse part of the superfluid density under the O(2) symmetry, respectively. The short dash-dotted thin lines corresponds to the imbalance number susceptibility.
Download figure:
Standard image High-resolution imageTo investigate pair momentum susceptibility, the scaled (scaled by 3mρ/8) transverse and longitudinal part of superfluid density are exhibited in figure 2 as well, corresponding to the red short dashed and black solid thin lines, respectively. On the whole, the transverse part ρT always reaches zero first, which indicates the FFLO state with pair momentum perpendicular to the symmetry axis of ADG appears earlier than that along the symmetry axis of ADG when the asymmetry α grows. Nevertheless, with increasing temperature, ρL reaches zero earlier than ρT when α get large, indicating a phase transition from the uniform superconducting state to the FFLO state with Cooper pair momentum along θ0 = 0. Figure 3 shows ρL reaches zero firstly at temperature T/TF = 0.0326. However, both ρT and ρL are positive for all the superconducting state when T/TF > 0.0332, indicating the vanishing of the FFLO state as shown in figure 7.
Figure 3. The scaled ∂2Ω/∂q2 as a function of the asymmetry α. The solid and short dash-dotted lines correspond to the scaled longitudinal and transverse part of the superfluid density under the O(2) symmetry, respectively. The insert shows the details near α = 0.152. The temperature is set to be T/TF = 0.0326.
Download figure:
Standard image High-resolution image3.2. FFLO state with Cooper pair momentum perpendicular/parallel to the symmetry axis of ADG
Due to the anisotropic pairing gap, the FFLO state is non-degenerate with the orientation of Cooper pair momentum. Two specific direction [47], corresponding to θ0 = 0 and 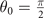 , are firstly discussed for neutron-proton pairing in asymmetric nuclear matter. Actually, one can easily find that θ0 = 0
, are firstly discussed for neutron-proton pairing in asymmetric nuclear matter. Actually, one can easily find that θ0 = 0 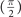 satisfies the equation of θ0
satisfies the equation of θ0
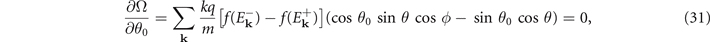
which corresponds to that the direction of q and the symmetry axis of ADG is parallel (orthogonal). And we call these two configurations, i.e., θ0 = 0 and 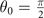 , the FFLO-ADG-P state and the FFLO-ADG-O state, respectively.
, the FFLO-ADG-P state and the FFLO-ADG-O state, respectively.
For the case θ0 = 0 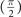 with nonzero Cooper pair momentum,
with nonzero Cooper pair momentum, 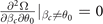 , the Hessian matrix turn into
, the Hessian matrix turn into
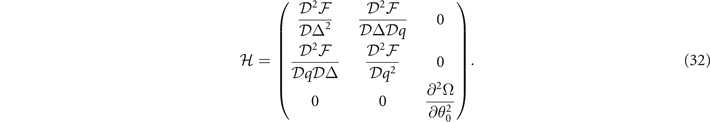
The positive definiteness corresponds to 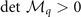 ,
, 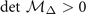 ,
, 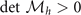 , and
, and 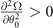 . Our numerics show that
. Our numerics show that  and
and 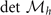 are always positive,
are always positive, 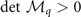 and
and 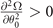 become the key stability condition. Where
become the key stability condition. Where  determines the stability of solutions in hyperplane
determines the stability of solutions in hyperplane  and
and  individually describes the stability of the orientation of the Cooper pair momentum. In addition to these constraints, the denominator in the number susceptibility (B7) evolves into
individually describes the stability of the orientation of the Cooper pair momentum. In addition to these constraints, the denominator in the number susceptibility (B7) evolves into 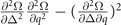 which corresponds to the stability condition against PS. It is obvious the constraint from PS is coincident with the FFLO state for S-wave pairing in reference [10], i.e.,
which corresponds to the stability condition against PS. It is obvious the constraint from PS is coincident with the FFLO state for S-wave pairing in reference [10], i.e., 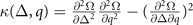 . In fact, on account of the vanishing of
. In fact, on account of the vanishing of 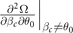 , the hyperplane
, the hyperplane 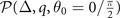 constitutes an individual subspace. If one confine the solution in hyperplane
constitutes an individual subspace. If one confine the solution in hyperplane 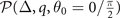 , the results are coincident with that in the hyperplane
, the results are coincident with that in the hyperplane 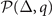 defined by the number density constraints in the parameter space spanned by μ, h, Δ, q for S-wave pairing. Therefore, both the stability conditions of solutions and against PS are identical to that for S-wave pairing.
defined by the number density constraints in the parameter space spanned by μ, h, Δ, q for S-wave pairing. Therefore, both the stability conditions of solutions and against PS are identical to that for S-wave pairing.
However, as discussed in section 2.4, the stability conditions are insufficient if the solutions are obtained in the subspace. And the superfluid density need to be supplemented to constrain the stability. Especially, the superfluid density in FFLO-ADG-P states reads
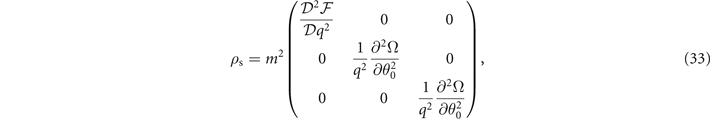
where 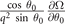 has been calculated by adopting the L'Hospital rule. Note that the positive definiteness of the 2 × 2 matrix
has been calculated by adopting the L'Hospital rule. Note that the positive definiteness of the 2 × 2 matrix 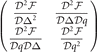 , corresponding to the stable solution in hyperplane
, corresponding to the stable solution in hyperplane  , require the positiveness of
, require the positiveness of 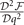 . Thus, only the
. Thus, only the 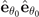 component can provide an extra constraint
component can provide an extra constraint 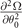 on orientation of the Cooper pair momentum, and we can call this the orientation susceptibility of the Cooper pair momentum similar as the Cooper pair momentum susceptibility. However, this constraint is essentially included in 3 × 3 Hessian matrix of the hyperplane
on orientation of the Cooper pair momentum, and we can call this the orientation susceptibility of the Cooper pair momentum similar as the Cooper pair momentum susceptibility. However, this constraint is essentially included in 3 × 3 Hessian matrix of the hyperplane 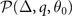 . For FFLO-ADG-O state, the
. For FFLO-ADG-O state, the 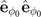 component of the superfluid density becomes to zero due to the fact
component of the superfluid density becomes to zero due to the fact 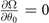 , the superfluid density might be positive semi-definite matrix. Nevertheless, the stability condition of the superfluid density can still provide the same constraint
, the superfluid density might be positive semi-definite matrix. Nevertheless, the stability condition of the superfluid density can still provide the same constraint 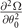 as FFLO-ADG-P state. Summarily, the stability conditions of superfluid density are essentially included in the positive definite Hessian matrix if the adopted parameter space is complete.
as FFLO-ADG-P state. Summarily, the stability conditions of superfluid density are essentially included in the positive definite Hessian matrix if the adopted parameter space is complete.
In order to have an entire inspection of the solutions, the scaled gap Δ/Δ0, the scaled (scaled by E0) 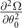 and the dimensionless
and the dimensionless 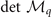 (Ω has been normalized by E0, μ, h, and Δ have been normalized by
(Ω has been normalized by E0, μ, h, and Δ have been normalized by 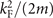 , and q has been normalized by kF in the calculation) at T/TF = 0.001 are displayed in figure 4. The FFLO-ADG-O and FFLO-ADG-P states are shown in figures 4(b) and (d), respectively. The red thick lines represent the scale pairing gap Δ/Δ0, where as the black thin lines correspond to the key stability conditions in hyperplane
, and q has been normalized by kF in the calculation) at T/TF = 0.001 are displayed in figure 4. The FFLO-ADG-O and FFLO-ADG-P states are shown in figures 4(b) and (d), respectively. The red thick lines represent the scale pairing gap Δ/Δ0, where as the black thin lines correspond to the key stability conditions in hyperplane  and the blue thin lines are related to the extra constraint
and the blue thin lines are related to the extra constraint 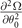 . And the short dash-dotted and short dashed lines correspond to the stable solutions in hyperplane
. And the short dash-dotted and short dashed lines correspond to the stable solutions in hyperplane  , while the solid and short dotted lines are related to the saddle point solutions. In addition, as discussed in section 3.1, there exists an unstable solution related to the saddle point for uniform ADG state in hyperplane
, while the solid and short dotted lines are related to the saddle point solutions. In addition, as discussed in section 3.1, there exists an unstable solution related to the saddle point for uniform ADG state in hyperplane 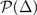 , corresponding to the negative
, corresponding to the negative  shown in figure 4(a).
shown in figure 4(a).
Figure 4. The scaled gap and the key stability conditions of the solutions at low temperature T/TF = 0.001. The red thick lines correspond to the scaled gap, while the thin lines are related to the stability conditions of the solutions. For the FFLO-ADG-O and FFLO-ADG-P states, the key stability conditions develop into the 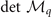 and
and 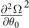 , corresponding to the black and blue lines, respectively. The solid, short dash-dotted, short dotted, and short dashed lines correspond to the different branches of solutions. The short dash-dotted lines correspond the possible candidates of the ground state.
, corresponding to the black and blue lines, respectively. The solid, short dash-dotted, short dotted, and short dashed lines correspond to the different branches of solutions. The short dash-dotted lines correspond the possible candidates of the ground state.
Download figure:
Standard image High-resolution imageIn figure 4(b), four branches of solution [48] for the FFLO-ADG-O state are displayed. Our numerics show that 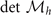 and
and 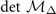 are always positive for these four branches of solution. Thus only
are always positive for these four branches of solution. Thus only 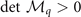 remains to determine the stability of the solutions in hyperplane
remains to determine the stability of the solutions in hyperplane 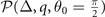 . Form this stability condition, one can find that the FFLO-ADG-O-1 and FFLO-ADG-O-3 states actually correspond to the saddle point due to the negative
. Form this stability condition, one can find that the FFLO-ADG-O-1 and FFLO-ADG-O-3 states actually correspond to the saddle point due to the negative 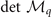 . This is also confirmed in the free energy surface
. This is also confirmed in the free energy surface 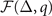 (here μ, h are obtained from the density constraint). Instead, the FFLO-ADG-O-2 and FFLO-ADG-O-4 are both related to the local minimum of
(here μ, h are obtained from the density constraint). Instead, the FFLO-ADG-O-2 and FFLO-ADG-O-4 are both related to the local minimum of 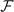 in hyperplane
in hyperplane 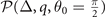 . And the free energy of FFLO-ADG-O-2 (FFLO-ADG-O-4) state get smaller than that of FFLO-ADG-O-4 (FFLO-ADG-O-2) state in the region 0.615 < α < 0.161 (α > 0.161). But the orientation susceptibility of the Cooper pair momentum
. And the free energy of FFLO-ADG-O-2 (FFLO-ADG-O-4) state get smaller than that of FFLO-ADG-O-4 (FFLO-ADG-O-2) state in the region 0.615 < α < 0.161 (α > 0.161). But the orientation susceptibility of the Cooper pair momentum 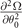 becomes negative when α > 0.1562, indicating that the FFLO-ADG-O-4 state is always unstable in hyperplane
becomes negative when α > 0.1562, indicating that the FFLO-ADG-O-4 state is always unstable in hyperplane 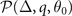 . Only the FFLO-ADG-O-2 state could be the candidate of the ground state, thus unless otherwise specified, the FFLO-ADG-O state refers to the FFLO-ADG-O-2 state hereafter. For the FFLO-ADG-P state shown in figure 4(d), two solutions corresponding to the saddle point and local minimum are labelled as the FFLO-ADG-P-1 and FFLO-ADG-P-2, respectively. Owing to the key stability condition
. Only the FFLO-ADG-O-2 state could be the candidate of the ground state, thus unless otherwise specified, the FFLO-ADG-O state refers to the FFLO-ADG-O-2 state hereafter. For the FFLO-ADG-P state shown in figure 4(d), two solutions corresponding to the saddle point and local minimum are labelled as the FFLO-ADG-P-1 and FFLO-ADG-P-2, respectively. Owing to the key stability condition 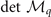 of solutions in hyperplane
of solutions in hyperplane 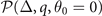 and the orientation susceptibility
and the orientation susceptibility 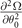 , only the FFLO-ADG-P-2 state becomes the local minimum and the possible ground state when α > 0.155 in hyperplane
, only the FFLO-ADG-P-2 state becomes the local minimum and the possible ground state when α > 0.155 in hyperplane  . For convenience, unless otherwise specified, the FFLO-ADG-P state refers to the FFLO-ADG-P-2 state hereafter.
. For convenience, unless otherwise specified, the FFLO-ADG-P state refers to the FFLO-ADG-P-2 state hereafter.
We now discuss the phase transition from uniform ADG state to FFLO state. Since the transverse part of the superfluid density ρT in ADG state reaches zero first in most case, a phase transition from the ADG state to FFLO-ADG-O state arises first. We call this phase transition the A-O phase transition for convenience in the present work. It is obvious that the FFLO-ADG-O-1 state is related to the emergence of FFLO state. Hence, the transverse part of the superfluid density ρT (scaled by 3mρ/8) in ADG state, the scaled Cooper pair momentum q/kF in FFLO state, and the scaled difference of the free energy between superconducting and normal state 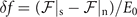 for the ADG (blue short dotted lines), FFLO-ADG-O-1 (black solid lines), and FFLO-ADG-O-2 (red short dash-dotted lines) states at different temperatures are exhibited in the upper, middle, and lower panel of figure 5, respectively. At low temperature T/TF = 0.001, ρT reaches zero at 0.0643 and change sign when α > 0.0643 indicating that the solution with q = 0 is no longer locally minimal in hyperplane
for the ADG (blue short dotted lines), FFLO-ADG-O-1 (black solid lines), and FFLO-ADG-O-2 (red short dash-dotted lines) states at different temperatures are exhibited in the upper, middle, and lower panel of figure 5, respectively. At low temperature T/TF = 0.001, ρT reaches zero at 0.0643 and change sign when α > 0.0643 indicating that the solution with q = 0 is no longer locally minimal in hyperplane 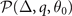 when α > 0.0643. However, in a small region 0.0616 < α < 0.0643 there are two local minima. One corresponds to the ADG state while the other corresponds to the FFLO-ADG-O-2 state. Between these two local minima, there exists a saddle point solution, i.e., the FFLO-ADG-O-1 state. The A-O phase transition must occur in this small region where the FFLO-ADG-O-1 exists, due to the fact that the ADG turn into unstable when α > 0.0643 and the FFLO-ADG-O state vanishes when α < 0.0616. The left vertical line in the middle panel at T/TF = 0.001/0.003 corresponds to the A-O transition asymmetry. Thanks to the coexistence region of ADG and FFLO-ADG-O state, the A-O phase transition is of the first order as shown in figure 7. One should note that the stable ADG and FFLO-ADG-O states coexist in the region where the FFLO-ADG-O-1 state exists. With increasing temperature, the existence region of the FFLO-ADG-O-1 state is getting smaller and vanishes when T/TF > 0.005 48. And the A-O phase transition turns into the second order as shown in figure 7.
when α > 0.0643. However, in a small region 0.0616 < α < 0.0643 there are two local minima. One corresponds to the ADG state while the other corresponds to the FFLO-ADG-O-2 state. Between these two local minima, there exists a saddle point solution, i.e., the FFLO-ADG-O-1 state. The A-O phase transition must occur in this small region where the FFLO-ADG-O-1 exists, due to the fact that the ADG turn into unstable when α > 0.0643 and the FFLO-ADG-O state vanishes when α < 0.0616. The left vertical line in the middle panel at T/TF = 0.001/0.003 corresponds to the A-O transition asymmetry. Thanks to the coexistence region of ADG and FFLO-ADG-O state, the A-O phase transition is of the first order as shown in figure 7. One should note that the stable ADG and FFLO-ADG-O states coexist in the region where the FFLO-ADG-O-1 state exists. With increasing temperature, the existence region of the FFLO-ADG-O-1 state is getting smaller and vanishes when T/TF > 0.005 48. And the A-O phase transition turns into the second order as shown in figure 7.
Figure 5. The scaled transverse part of the superfluid density ρT in ADG state, Cooper pair momentum q/kF, and difference of the free energy between superconducting and normal state 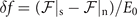 as a function of the asymmetry α. The left, middle, and right panel correspond to the temperature T/TF = 0.001, 0.003, and 0.006, respectively. The black solid, red short dash-dotted, and blue short dotted line are related to the FFLO-ADG-O-1, FFLO-ADG-O-2, and ADG state, respectively.
as a function of the asymmetry α. The left, middle, and right panel correspond to the temperature T/TF = 0.001, 0.003, and 0.006, respectively. The black solid, red short dash-dotted, and blue short dotted line are related to the FFLO-ADG-O-1, FFLO-ADG-O-2, and ADG state, respectively.
Download figure:
Standard image High-resolution image3.3. FFLO state with 
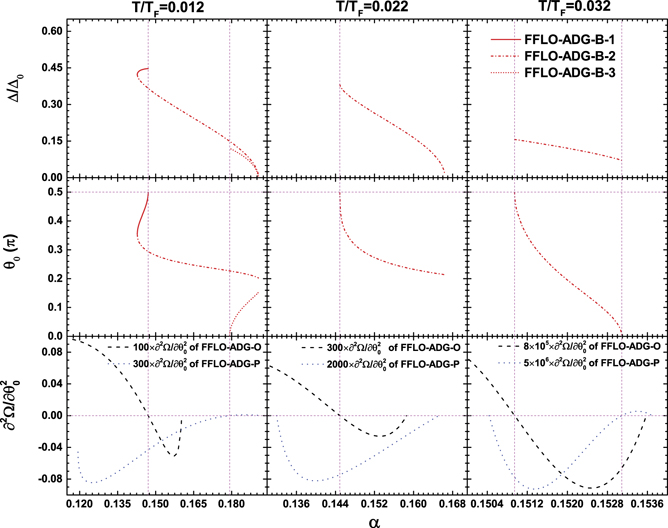
Except the two special directions of the Cooper pair momentum, the orientation between the two special direction may also survive as discussed in reference [48]. However, it might not be true for the neutron–proton pairing in attractive 3
SD1 channel [47]. To some extent, the possible orientation of the Cooper pair momentum depends on the configuration of the pairing gap. For the current pairing gap, the orientation between θ0 = 0 and  can survive in an appreciable region in the T − α phase diagram as displayed in figure 7. We call this state the FFLO-ADG-B state.
can survive in an appreciable region in the T − α phase diagram as displayed in figure 7. We call this state the FFLO-ADG-B state.
The stability condition of FFLO-ADG-B state require the Hessian matrix is positive definite, i.e.,  ,
, 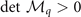 ,
, 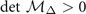 , and
, and 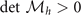 . Fortunately,
. Fortunately, 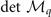 ,
, 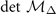 , and
, and  are always positive for all the possible solutions. The key stability condition becomes
are always positive for all the possible solutions. The key stability condition becomes 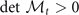 . At Low temperature, there are three branches of solutions labelled by FFLO-ADG-B-1, FFLO-ADG-B-2, and FFLO-ADG-B-3 in figure 4(c). It is obvious that only the FFLO-ADG-B-2 state is related to the local minimum of free energy in hyperplane
. At Low temperature, there are three branches of solutions labelled by FFLO-ADG-B-1, FFLO-ADG-B-2, and FFLO-ADG-B-3 in figure 4(c). It is obvious that only the FFLO-ADG-B-2 state is related to the local minimum of free energy in hyperplane  . While the other two branches correspond to the saddle point solution. Same as the FFLO-ADG-O state, unless otherwise specified, the FFLO-ADG-B state refers to the FFLO-ADG-B-2 state hereafter. One should note that the behavior of the FFLO-ADG-B-1 and FFLO-ADG-B-3 states are very similar to that of the FFLO-ADG-O-1 state, for instance, the FFLO-ADG-B-1 (FFLO-ADG-O-1) vanishes at the zero point of
. While the other two branches correspond to the saddle point solution. Same as the FFLO-ADG-O state, unless otherwise specified, the FFLO-ADG-B state refers to the FFLO-ADG-B-2 state hereafter. One should note that the behavior of the FFLO-ADG-B-1 and FFLO-ADG-B-3 states are very similar to that of the FFLO-ADG-O-1 state, for instance, the FFLO-ADG-B-1 (FFLO-ADG-O-1) vanishes at the zero point of 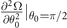
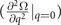 . This behavior indicates the first phase transition from the FFLO-ADG-O state to the FFLO-ADG-B state.
. This behavior indicates the first phase transition from the FFLO-ADG-O state to the FFLO-ADG-B state.
To understand the phase transition from the FFLO-ADG-B state to the FFLO-ADG-O (FFLO-ADG-P) state, the scaled pairing gap and the orientation of q for the FFLO-ADG-B state, and the scaled orientation susceptibility of the Cooper pair momentum 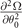 for the FFLO-ADG-O and FFLO-ADG-P states are exhibited in figure 6. At low temperature T/TF = 0.012, the existence of the FFLO-ADG-B-1 solution implies a sudden change of θ0 from the stable FFLO-ADG-O state to the stable FFLO-ADG-B state. This sudden change corresponds to the first phase transition from the FFLO-ADG-O state to the FFLO-ADG-B state. We call this transition the O-B phase transition. Similarly, we call the transition from the FFLO-ADG-B state to the FFLO-ADG-P state the B-P phase transition. The FFLO-ADG-B-3 state results in the first order B-P transition. With increasing temperature, the unstable FFLO-ADG-B-1 solution vanishes, indicating the second O-B phase transition. Interestingly, at temperature T/TF = 0.022, the orientation susceptibility is negative in the whole existing region, indicating that the FFLO-ADG-P state vanishes as shown in figure 7. But, however, the FFLO-ADG-P state reappears in a small temperature region 0.0318 < T/TF < 0.332 as displayed in the insert of figure 7. This can also be confirmed in right panel of figure 6, the orientation susceptibility for FFLO-ADG-P becomes positive when α > 0.153. The corresponding B-P phase transition at this small temperature region become the second order due to the vanishing of the FFLO-ADG-B-3 state at high temperature.
for the FFLO-ADG-O and FFLO-ADG-P states are exhibited in figure 6. At low temperature T/TF = 0.012, the existence of the FFLO-ADG-B-1 solution implies a sudden change of θ0 from the stable FFLO-ADG-O state to the stable FFLO-ADG-B state. This sudden change corresponds to the first phase transition from the FFLO-ADG-O state to the FFLO-ADG-B state. We call this transition the O-B phase transition. Similarly, we call the transition from the FFLO-ADG-B state to the FFLO-ADG-P state the B-P phase transition. The FFLO-ADG-B-3 state results in the first order B-P transition. With increasing temperature, the unstable FFLO-ADG-B-1 solution vanishes, indicating the second O-B phase transition. Interestingly, at temperature T/TF = 0.022, the orientation susceptibility is negative in the whole existing region, indicating that the FFLO-ADG-P state vanishes as shown in figure 7. But, however, the FFLO-ADG-P state reappears in a small temperature region 0.0318 < T/TF < 0.332 as displayed in the insert of figure 7. This can also be confirmed in right panel of figure 6, the orientation susceptibility for FFLO-ADG-P becomes positive when α > 0.153. The corresponding B-P phase transition at this small temperature region become the second order due to the vanishing of the FFLO-ADG-B-3 state at high temperature.
Figure 6. The scaled gap and the orientation of the Cooper pair momentum for the FFLO-ADG-B state, and the scaled 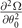 for the FFLO-ADG-O and FFLO-ADG-P state as a function of the asymmetry α. The left, middle, and right panel correspond to the temperature T/TF = 0.012, 0.022, and 0.032, respectively. The red solid, short dash-dotted, and dotted lines are related to the FFLO-ADG-B-1, FFLO-ADG-B-2, and FFLO-ADG-B-3 states, respectively. The black dashed and blue dotted line correspond to the FFLO-ADG-O and FFLO-ADG-P states, respectively.
for the FFLO-ADG-O and FFLO-ADG-P state as a function of the asymmetry α. The left, middle, and right panel correspond to the temperature T/TF = 0.012, 0.022, and 0.032, respectively. The red solid, short dash-dotted, and dotted lines are related to the FFLO-ADG-B-1, FFLO-ADG-B-2, and FFLO-ADG-B-3 states, respectively. The black dashed and blue dotted line correspond to the FFLO-ADG-O and FFLO-ADG-P states, respectively.
Download figure:
Standard image High-resolution imageFigure 7. Phase diagram with Cooper pair momentum in the T − α plane. The yellow region represent the PS. The solid and the short dashed thick lines correspond to the second and first order transition, respectively. The black, blue, red, and cyan olive lines are related to the A-O, O-B, B-P and A-P phase transition, respectively. The olive line correspond to the phase transition from the superconductiing state to the normal state. The insert shows the detail of T − α near the critical point where the FFLO state vanishes.
Download figure:
Standard image High-resolution imageIn addition, the stability against PS can be determined by the 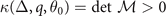 or
or 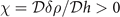 . Together with the constraints from the ADG, FFLO-ADG-O, and FFLO-ADG-P state, the T − α phase diagram is finally exhibited in figure 7. For convenience, the name of FFLO-ADG-O, FFLO-ADG-B, and FFLO-ADG-P have been shortened to ADG-O, ADG-B, and ADG-P in figure 7. We stress here the A-P phase transition (phase transition from the ADG state to the FFLO-ADG-P state) emerges near the critical temperature where the FFLO states disappear due to the fact that ρL < ρT occurs at high temperature as displayed in figure 3. The A-P phase transition is of second order because the unstable FFLO-ADG-P-1 solution disappears at high temperature. In the T − α phase diagram, two narrow PS regions are located near the occurrence region of the FFLO-ADG-O state and the FFLO-ADG-B state, respectively. These PS regions are obviously reduced comparing to that for ADG phase diagram. Moreover, this T − α phase diagram significantly differentiates from that for S-wave pairing [10, 12].
. Together with the constraints from the ADG, FFLO-ADG-O, and FFLO-ADG-P state, the T − α phase diagram is finally exhibited in figure 7. For convenience, the name of FFLO-ADG-O, FFLO-ADG-B, and FFLO-ADG-P have been shortened to ADG-O, ADG-B, and ADG-P in figure 7. We stress here the A-P phase transition (phase transition from the ADG state to the FFLO-ADG-P state) emerges near the critical temperature where the FFLO states disappear due to the fact that ρL < ρT occurs at high temperature as displayed in figure 3. The A-P phase transition is of second order because the unstable FFLO-ADG-P-1 solution disappears at high temperature. In the T − α phase diagram, two narrow PS regions are located near the occurrence region of the FFLO-ADG-O state and the FFLO-ADG-B state, respectively. These PS regions are obviously reduced comparing to that for ADG phase diagram. Moreover, this T − α phase diagram significantly differentiates from that for S-wave pairing [10, 12].
3.4. Comparing the stability constraints κ and χ against phase separation
The stability of the polarized superfluid against PS requires the number susceptibility matrix must be positive definite. As discussed in section 2.5, both  and
and 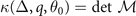 can be adopted as the criteria of the stability of the polarized superfluid against PS, and they are equivalent to each other for S-wave pairing [10]. For D-wave paring, these two stability constraints might be different from that for S-wave pairing owing to the emergence of the unstable states, such as FFLO-ADG-O-1 and FFLO-ADG-O-3 states.
can be adopted as the criteria of the stability of the polarized superfluid against PS, and they are equivalent to each other for S-wave pairing [10]. For D-wave paring, these two stability constraints might be different from that for S-wave pairing owing to the emergence of the unstable states, such as FFLO-ADG-O-1 and FFLO-ADG-O-3 states.
For the sake of verifying the validity of κ and χ, the scaled χ, κ, and the second eigenvalue λ− of number susceptibility matrix  for FFLO state with
for FFLO state with 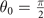 are plotted in figure 8. The denominator in the number susceptibility (B7) evolves into
are plotted in figure 8. The denominator in the number susceptibility (B7) evolves into 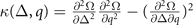 in hyperplane
in hyperplane 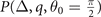 . The solid, short dash-dotted, short dotted, and short dashed lines label the FFLO-ADG-O-1, FFLO-ADG-O-2, FFLO-ADG-O-3, and FFLO-ADG-O-4 solutions, respectively. Since λ+ is always positive, λ− determines the positive definiteness of
. The solid, short dash-dotted, short dotted, and short dashed lines label the FFLO-ADG-O-1, FFLO-ADG-O-2, FFLO-ADG-O-3, and FFLO-ADG-O-4 solutions, respectively. Since λ+ is always positive, λ− determines the positive definiteness of 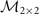 . One can realize from figure 8 that the imbalance number susceptibility χ and λ− always keep the same positiveness and change signs synchronously, signifying that the criterion
. One can realize from figure 8 that the imbalance number susceptibility χ and λ− always keep the same positiveness and change signs synchronously, signifying that the criterion 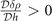 is completely equivalent to the positive eigenvalue λ−. In contrast, κ and λ− hold the same positiveness and alter signs only for the stable solutions in the adopted parameter space, i.e., the FFLO-ADG-O-2 and FFLO-ADG-O-4 solutions. In the FFLO-ADG-O-1 and FFLO-ADG-O-3 states corresponding to the saddle point in hyperplane
is completely equivalent to the positive eigenvalue λ−. In contrast, κ and λ− hold the same positiveness and alter signs only for the stable solutions in the adopted parameter space, i.e., the FFLO-ADG-O-2 and FFLO-ADG-O-4 solutions. In the FFLO-ADG-O-1 and FFLO-ADG-O-3 states corresponding to the saddle point in hyperplane 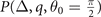 , κ is opposite to λ− and κ cannot provide available constraint against the PS. However, one may probably evaluate the stability condition against the PS after confirming the stability of the solution in the adopted parameter space. Under the prerequisite that the solution should at least be a local minimum of
, κ is opposite to λ− and κ cannot provide available constraint against the PS. However, one may probably evaluate the stability condition against the PS after confirming the stability of the solution in the adopted parameter space. Under the prerequisite that the solution should at least be a local minimum of 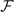 in the adopted parameter space, the criterion κ is equivalent to the criteria χ and λ−. The solutions in the S-wave pairing with fixed number density is always stable, and the two criteria are equivalent to each other [10]. Nevertheless one should treat the D-wave pairing with carefulness.
in the adopted parameter space, the criterion κ is equivalent to the criteria χ and λ−. The solutions in the S-wave pairing with fixed number density is always stable, and the two criteria are equivalent to each other [10]. Nevertheless one should treat the D-wave pairing with carefulness.
Figure 8. The scaled χ, κ(Δ, q), and λ− as a function of α for FFLO state with θ0 at the temperature T/TF = 0.001. The red solid, black short dash-dotted, blue short dotted, and olive short dashed line correspond to the FFLO-ADG-O-1, FFLO-ADG-O-2, FFLO-ADG-O-3, FFLO-ADG-O-4 solutions, respectively.
Download figure:
Standard image High-resolution image4. Summary and outlook
In summary, we have studied phase structure of a two-component D-wave fermion superfluid with density imbalance in the present work. The pairing gap becomes no longer isotropic owing to the anisotropic D-wave pairing interaction. As a result, the FFLO state develops into non-degenerate with the orientation of Cooper pair momentum. The extra freedom, i.e. the direction of Cooper pair momentum θ0, can significantly enrich the phase structures. Briefly, the FFLO state for S-wave pairing splits into three branches according to the possible orientations of Cooper pair momentum, i.e., the FFLO-ADG-O, FFLO-ADG-P, and FFLO-ADG-B states. The phase diagram significantly differentiate from that of S-wave pairing. To investigate the phase structure, the stability constraints are theoretically extended as well for D-wave pairing. The main conclusions are as follows.
- (a)For a fixed density system, the stable solutions are essentially correspond to the local minima of the free energy
 in the hyperplane defined by the density constraints in the parameter space. The solution is related to
in the hyperplane defined by the density constraints in the parameter space. The solution is related to  with xi
representing the free parameters such as Δ, q, θ0. The stability condition corresponds to that the Hessian matrix of the free energy
with xi
representing the free parameters such as Δ, q, θ0. The stability condition corresponds to that the Hessian matrix of the free energy  is positive definite.
is positive definite. - (b)The superfluid density consists of two parts, i.e., the response to the value of Cooper pair momentum and the orientation of Cooper pair momentum, due to the anisotropic pairing gap for D-wave pairing. These two parts correspond to the Cooper pair momentum susceptibility and orientation susceptibility. The constraints from superfluid density are effective only if the parameter space is sufficient. In fact, the stability condition of the super fluid density is essentially included in the positive definite Hessian matrix as long as the parameter space is complete.
- (c)The stability condition
 against PS is equivalent to the positiveness of eigenvalue λ− of the number susceptibility matrix. While the criteria κ(Δ) = ∂2Ω/∂Δ2,
against PS is equivalent to the positiveness of eigenvalue λ− of the number susceptibility matrix. While the criteria κ(Δ) = ∂2Ω/∂Δ2,  , and
, and  are equivalent to λ− only under the prerequisite that the Hessian matrix is positive definite in the adopted parameter space.
are equivalent to λ− only under the prerequisite that the Hessian matrix is positive definite in the adopted parameter space. - (d)At low temperature, the transition from the uniform ADG state to normal state is of first order and becomes the second order with increasing temperature. For FFLO state, the A-O, O-B, B-P phase transitions are of the first order at low temperature, and become the second order transition with increasing temperature as well. The transition from the FFLO state to normal state is of second order. Near the critical temperature where FFLO state vanishes, there exists a second order A-P phase transition. These diversified phase transitions might be distinguishing feature of the considered D-wave pairing. The specific heat and thermal expansion may offer a circumstantial evidence of the FFLO state for D-wave pairing via analyzing the phase transition type. Additionally, the node structures of these ADG-FFLO states in momentum space might be distinctive. Therefore, the scanning tunneling microscopy quasiparticle interference [56–59] can perhaps be adopted to investigate the pairing structure of ADG-FFLO states.
- (e)Both the phase diagrams with and without Cooper pair momentum in the T − α plane show there are two narrow PS regions which are significantly different from those for S-wave pairing. This difference of the S-wave pairing may result from the existence of the nodes and zero-line of the quasi-particle spectrum near Fermi surface which can provide phase-space for the excess particles. Accordingly, it might be unnecessary to destroy the pairing state to settle the excess particles. And the superconducting state in certain region which is unstable against PS for S-wave pairing turns into stable against PS for D-wave pairing.
The current calculations are carried in the framework of mean-field level, the pseudogap effect [13] should also be take into account at finite temperature to obtain the realistic phase diagram in future. In addition, we adopt only the m = 0 component pairing interaction of D-wave pairing in the current calculation, it remains for future work that whether the other components result in the same phase diagram and whether the single component pairing is stable.
Acknowledgments
The work is supported by the Youth Innovation Promotion Association of Chinese Academy of Sciences (No. Y2021414), the National Natural Science Foundation of China (Nos. 11875013 and 11505241), the Strategic Priority Research Program of Chinese Academy of Sciences, Grant No. XDB34000000, the fund of State Key Laboratory of Long-Life High Temperature Materials (No. DECSKL202111), the Scientific Research Program Funded by Hangzhou Dianzi University Information Engineering College (No. KYP0222007).
Appendix A
Note that  , we define the 5 × 5 matrix
, we define the 5 × 5 matrix 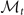 as
as

the 4 × 4 matrix 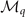 as
as
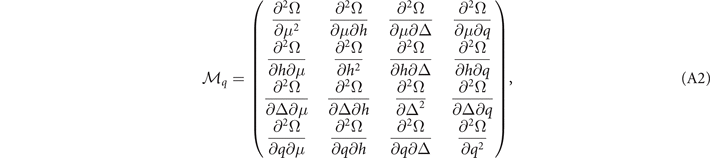
the 3 × 3 matrix 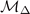 as
as

and the 2 × 2 matrix 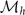 as
as
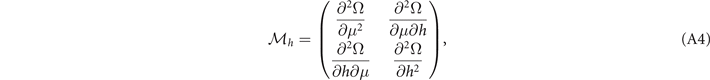
for convenience. Owing to the property  , there are 15 independent elements of matrix
, there are 15 independent elements of matrix 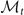 , which read
, which read
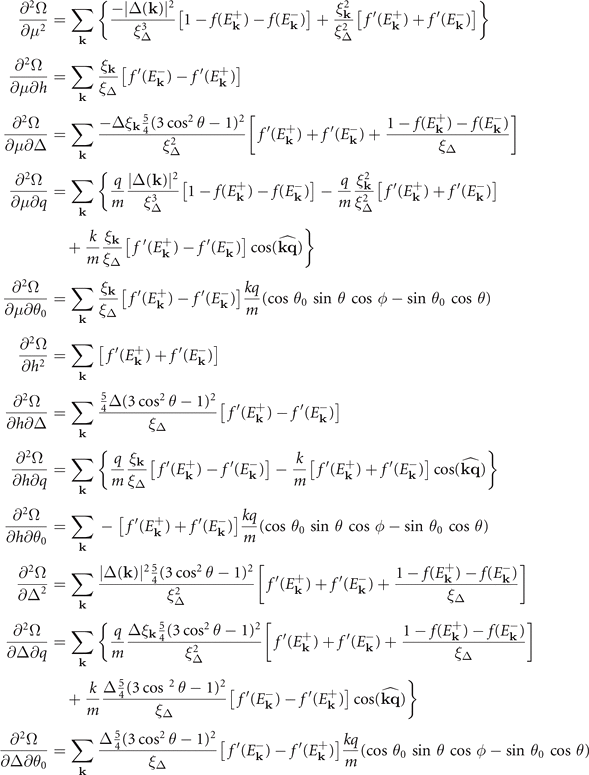
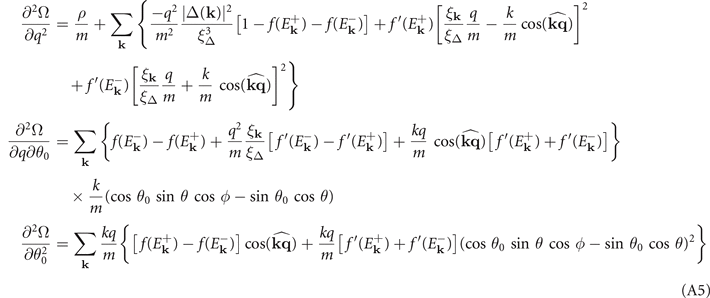
Where ![${f}^{\,\prime }(x)=-\mathrm{exp}(\frac{x}{T})/{\left[1+\mathrm{exp}(\frac{x}{T})\right]}^{2}/T$](https://content.cld.iop.org/journals/1367-2630/24/10/103006/revision2/njpac94b4ieqn203.gif) is the derivative of f(x).
is the derivative of f(x).
From the density constraints, we have
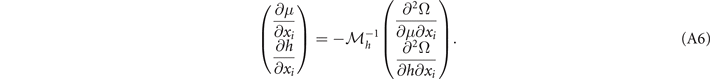
The elements of the Hessian matrix 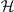 of the free energy can be expressed as
of the free energy can be expressed as
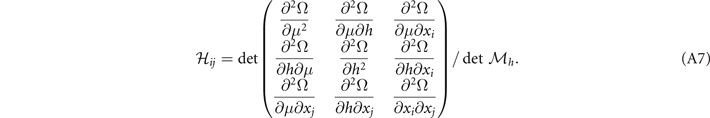
The positive definite 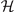 corresponds to the positiveness of all the determinant of the sequential principal minor of
corresponds to the positiveness of all the determinant of the sequential principal minor of 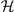 , i.e.,
, i.e., 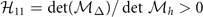 ,
, 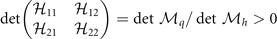 , and
, and 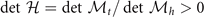 . Note that
. Note that 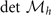 is always positive, the stability conditions turn in to
is always positive, the stability conditions turn in to 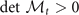 ,
, 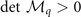 , and
, and 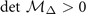 .
.
Appendix B
We start from the solutions (16) and the density constraints (17). Considering small fluctuations of the total densities dρ, the variations of μ, h, Δ, q, θ0 induced by dρ are determined by the following coupled equations
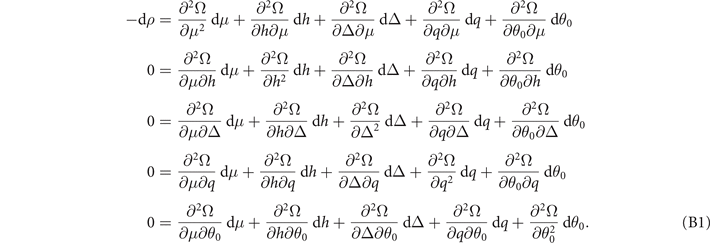
It is obvious that the variations of μ, and h induced by dρ are 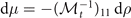 and
and 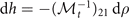 . Accordingly, the matrix elements corresponding to the total density are
. Accordingly, the matrix elements corresponding to the total density are 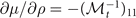 and
and 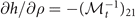 . Similarly, the matrix elements related to the asymmetry take the form of
. Similarly, the matrix elements related to the asymmetry take the form of 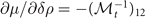 and
and 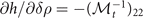 . Using the properties of inverse matrix, one can obtain
. Using the properties of inverse matrix, one can obtain

where 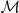 is the stability matrix for ADG-FFLO state defines as
is the stability matrix for ADG-FFLO state defines as

On the other hand, the solutions (16) result in
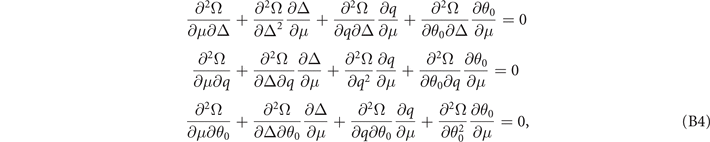
and we readily obtain
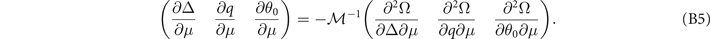
Similarly, the relation
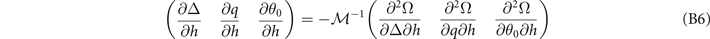
can also be obtained by replacing μ with h. Substituting ∂xi /∂μ (B5) and ∂xi /∂h (B6) into the definition (27), the number susceptibility matrix elements take the form of

One can easily find that
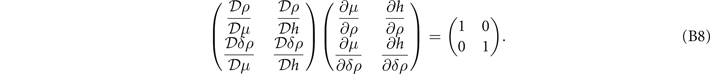
Moreover, note the relation ρ = ρa + ρa , δρ = ρa − ρa , and ∂/∂ρa = ∂/∂ρ + ∂/∂δρ, ∂/∂ρb = ∂/∂ρ − ∂/∂δρ,
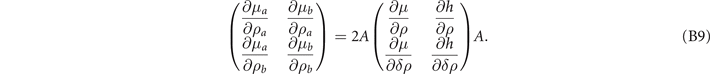
Therefore,