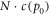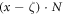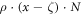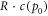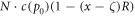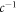Abstract
Biological information-processing usually runs at high precision. However, recent results from stochastic thermodynamics and biophysics indicate that though it is high, precision is intrinsically bounded to less than 100%. We explore the implications of such an intrinsic finite precision on dynamical systems which consist of an iterated production process that is required to run at high precision, and a correction process that is needed to maintain the accuracy of the production. Both processes are assumed to be inherently error-prone, defective and subject to a trade-off between cost and precision. The cost must be paid from refillable but limited resources like energy. As our bifurcation analysis shows, the errors of such a system then either converge to a desired low error threshold and constant success of repair, or they accumulate to a maximal ratio, while the success of repair decays to zero, or all resources are absorbed for repair so that none are left for subsequent production. We term the latter two fates 'aging' in reminiscence to natural systems. It depends then on the cost of production relative to the cost of repair and the maintenance cost of repair success whether aging is avoidable or not.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Usually the high precision of biological information-processing in genetic networks, signaling proteins or sensing cells is appreciated in view of the inherent stochastic fluctuations of various kinds. Apart from physical mechanisms [1, 2] such as anti-correlations between external and internal noise, sophisticated repair mechanisms like kinetic proofreading [3] prevent an immediate accumulation of errors on short time scales.
On the other hand, an increasing number of recent results indicate that though the precision is remarkably high, it is finite (less than 100%). A thermodynamic uncertainty relation was formulated in [4] and proven in [5]. It states that a more precise output requires a higher thermodynamic cost: The product of the total dissipation after time t and the square of the relative uncertainty of the measured observable is bounded from below by 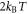 , with T the temperature of the system and kB the Boltzmann constant. Moreover, from a comparison between cellular copy protocols with canonical copy protocols in computational science it became clear [6–8] why cellular sensing systems can never reach the Landauer limit [9, 10] on the optimal trade-off between accuracy and energetic cost. Cellular systems have to dissipate more than thermodynamic processes that run according to ideal quasistatic protocols. Cellular copy protocols can only reach 100% precision for diverging costs.
, with T the temperature of the system and kB the Boltzmann constant. Moreover, from a comparison between cellular copy protocols with canonical copy protocols in computational science it became clear [6–8] why cellular sensing systems can never reach the Landauer limit [9, 10] on the optimal trade-off between accuracy and energetic cost. Cellular systems have to dissipate more than thermodynamic processes that run according to ideal quasistatic protocols. Cellular copy protocols can only reach 100% precision for diverging costs.
Although in principle an infinite amount of resources exists in external reservoirs, only a finite amount is accessible in a finite period of time, so that the precision is unavoidably not optimal. Even kinetic proofreading seems to be subject to a trade-off between cost and precision: The higher the specificity, the longer the proofreading reaction runs, the less efficient the correction process is [11].
In living organisms, many kinds of processes are ongoing in parallel with their own specific precision and costs for maintaining the precision, so that a prediction of the fate of complex organisms from first physical principles appears completely out of range. Instead, we focus on the impact of a lack of perfect precision in a simple model for a dynamical system that shares some features with living organisms, and more generally with systems that should perform some functions at high accuracy. We distinguish two kinds of processes. The first one is a repeated production process, here realized as copying of a bitstring that should represent the essential performance or function of the system and run at high but finite precision. The second process is chosen as error correction to guarantee the maintenance of the limited but high accuracy of the copying. The costs are paid from a finite but refillable reservoir. Since we assume a single type of required resources for simplicity, we term the cost 'energy'. The functional dependency of the cost on the required precision is only restricted by diverging cost for 100% precision and a lower finite amount for random copying and repair.
Under these constraints we determine the time evolution of errors and distinguish the following fates: Depending on the relation between cost for copying, cost for repair and success of repair, (i) the system may converge to a desired error fraction that is considered as tolerable for the functioning of the system. (ii) Since an accumulation of deleterious mutations is one of the basic manifestations of biological aging in living organisms, we call a fate with accumulating errors in our bitstring 'aging'. (If a bistring represents a code that steers the system, the system will lose its function if the number of errors in the code exceeds a certain threshold.) (iii) To avoid aging, a possible alternative fate may be an absorption of all energy for repair, at the price that no energy is left for the essential performance, here the copying process. For simplicity this fate is also called aging, ending with the termination of the copying.
Here some remarks are in order with respect to previous error catastrophe theories of aging. Originally the term 'error catastrophe' was introduced in [12] to describe specifically the effect of errors in amino acid incorporation during cellular protein synthesis, a process that can contribute to the collapse of regulatory networks in the process of aging. More generally, error catastrophe is termed the accumulation of errors in the process of information processing from genes to proteins. The catastrophe induces a malfunction of proteins and the extinction of an organism as a result of excessive mutations. It is also one of the hypotheses that have been suggested to explain senescence at the cellular level [13]. In the work of [13] (and references therein such as [14]), the very existence of an error threshold is discussed, arguments in favor or against its existence are presented. Below this threshold the system gets partially rid of errors and is stable, above the threshold errors continue to increase and produce an error catastrophe. The absence of such a threshold then automatically implies a catastrophe.
In contrast to these approaches, we do not explicitly model the emergence of an error threshold by biochemical processes. In analogy to defective software code we assume that a low error fraction is tolerable without inducing a malfunction of the whole system. The maximal tolerable ratio defines an error threshold. In general, this threshold may depend on the process itself, the species and the individual. We then focus on the question of whether the production process of the system (here the copying process) can be kept running below the assumed and desired threshold if the costs for achieving a certain precision are taken into account.
Novel at our perspective is to point to possible deeper and fundamental physical reasons for the very occurrence of errors, not only restricted to the genetic level. The conjecture is that because biological systems are in general information processing they are error-prone and defective as such if perfect precision requires an infinite amount of resources. This is in extrapolation of the results derived in [4, 6–8]. In our model we implement this inherent error-proneness by the boundary conditions of the cost-precision functions, which diverge for perfect precision. Importantly, both our processes are assumed to be inherently error-prone and defective, so that the copies have to be corrected and the correction is imperfect itself. This way we implement the assumed unavoidable thermodynamic cost for information-processing on an effective level of description. The functional form of the cost-precision functions is not assumed to be universal, but to depend on the process in question. Just the singular behavior for perfect precision is assumed to be a universal feature.
While here the threshold of a tolerable error fraction is assumed rather than derived, we derive thresholds in parameters instead. These are bifurcation parameters that determine the production costs in relation to costs for repair and the success of the repair investments. The regimes of the resulting bifurcation diagram then correspond to different fates of the system, mentioned before, changing from stable error ratios to error catastrophes.
Since we use the term 'aging' in particular in a biological context, some further remarks are in order about relations to phenomenological manifestations of biological aging. As described so far, we consider error accumulation as a typical, overarching characterization of aging on a fundamental level of description. On a phenomenological level, aging goes along with the process of decline of physiological function, e.g. a reduction of heart rate and respiratory variability, leading to decreased responsiveness and reduced sensitivity to external and internal stimuli, or sleep disorders in older age [15, 16]. The overall degree of cardio-respiratory phase synchronization is reduced by about 40% for elderly subjects [15], whereas certain complex features of multiple time scales and coupled cascades of feedback loops seem to be maintained upon healthy aging [17]. Similarly, aging of the central circadian clock located in the suprachiasmatic nucleus of the hypothalamus is manifest in altered physiology and function and in a decreased degree of flexibility to adapt to changes of the external conditions [18].
We consider it as a very challenge for future research to trace back these well established manifestations of biological aging to (accumulating) errors in the steering code, the regulation on the underlying genetic, cellular, metabolic, or neuronal level1 . In this paper we do not pursue the propagation of errors through different layers and levels of an organism, but focus on a single level.
The paper is organized as follows: In section 2 we present the model in the form of a stochastic algorithm, followed by the results of a mean-field calculation in section 3, before the conclusions and outlook are presented in section 4.
2. The model
Copying a bitstring. We start with a bitstring of length N that is initially correct with all bits set to zero. When the defective copies iteratively get further copied, errors accumulate. Each bit is copied with precision p0 that equals the probability of copying a bit correctly. The parameter p0 denotes the initial value of maximal precision, typically chosen as p0 = 0.90.
We choose a threshold ζ, such that repair sets in when the error ratio x exceeds ζ that is assumed to be tolerable. The repair is successful with probability ρ ≤ 1, so ρ = 1 corresponds to deterministic repair, ρ < 1 to probabilistic repair. Thus, on average, ρ gives the fraction of bits for which repair was attempted and successful. We keep ρ either constant, or let it decrease with time in steps of size d, or dynamically decrease ρ (when accounting for the maintenance cost for constant repair success).
For the energy costs per copy of a single bit at highest precision p0 we choose 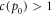 with c(p) a cost-precision function. The repair costs of a single bit are chosen as
with c(p) a cost-precision function. The repair costs of a single bit are chosen as 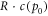 with R ≥ 0.
with R ≥ 0.
Choice of cost-precision functions. The cost-precision function c(p) for copying a single bit with precision p is only constrained by the boundary conditions such that 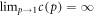 and
and 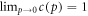 . The limit
. The limit  corresponds to perfect copying without errors and requires an infinite amount of energy, while random copying without any guarantee of correctness causes minimal nonzero costs set to 1. The first condition is an effective implementation of the kind of observations made in [4, 6–8] that perfect precision requires an infinite amount of energy unless the process runs adiabatically. We test different options for c(p), in particular power-like behavior
corresponds to perfect copying without errors and requires an infinite amount of energy, while random copying without any guarantee of correctness causes minimal nonzero costs set to 1. The first condition is an effective implementation of the kind of observations made in [4, 6–8] that perfect precision requires an infinite amount of energy unless the process runs adiabatically. We test different options for c(p), in particular power-like behavior
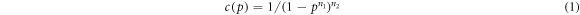
for n1 = 1, n2 = 1 or 2, or n1 = 2, n2 = 1 as well as a logarithmic dependence according to 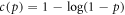 .
.
Choice of the energy reservoir. We equip the system with a temporary energy reservoir per 'sweep' that can be refilled: When we allow for correcting erroneously copied bits beyond the threshold ζ, one sweep amounts to the repair of a string with a fraction x of errors, where the fraction exceeds the tolerated threshold ζ, and the subsequent copying of all bits. As capacity of the energy reservoir we choose 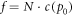 . These are the costs for copying the whole string at initially highest available precision p0 just once. It is a minimal choice. We shall keep the capacity of size f constant over time. This means that for each sweep (representing a fixed finite time interval), always the same finite amount of energy is accessible, independently of how the reservoir was depleted in the preceding sweep and independently of its actual large size. Our minimal choice as
. These are the costs for copying the whole string at initially highest available precision p0 just once. It is a minimal choice. We shall keep the capacity of size f constant over time. This means that for each sweep (representing a fixed finite time interval), always the same finite amount of energy is accessible, independently of how the reservoir was depleted in the preceding sweep and independently of its actual large size. Our minimal choice as 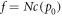 is for simplicity; adding initially a constant reserve would delay its depletion, letting it fluctuate may delay or accelerate its depletion.
is for simplicity; adding initially a constant reserve would delay its depletion, letting it fluctuate may delay or accelerate its depletion.
Importantly, the energy needed for the correction of the bitstring is taken from the very same energy reservoir that also serves to provide energy for the copying process. Since we assume a direct correlation between copying precision and energetic costs, the precision decreases as soon as energy has to be spent on repair. We analyze the conditions under which a stationary performance of the copying process is still possible that maintains the desired accuracy below the tolerated error threshold ζ.
The stochastic implementation can then be summarized in the following algorithm.
- (1)Choose the parameters c(p0), p0, ζ, R, ρ, d, starting from a bitstring
 of zeros, choose a cost-precision function and size of the energy reservoir.
of zeros, choose a cost-precision function and size of the energy reservoir. - (2)Copy the string with initial precision p0.
- (3)Compute the current error fraction
![$x\in [0,1]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , i.e. the fraction of bits that are 1. Also, set the energy available for this step to
, i.e. the fraction of bits that are 1. Also, set the energy available for this step to  .
. - (4)If x < ζ go to 2, else (for x ≥ ζ and d ≥ 0) decrease ρ by d and go to 5.
- (5)Make an attempt of repairing
 bits, with success probability ρ ≤ 1. (This means that on average
bits, with success probability ρ ≤ 1. (This means that on average  randomly chosen bits actually get repaired.) Even if a repair is not successful, the attempt of repair causes
randomly chosen bits actually get repaired.) Even if a repair is not successful, the attempt of repair causes  energy cost per bit, so that the remaining energy for the subsequent copying process decreases to
energy cost per bit, so that the remaining energy for the subsequent copying process decreases to  .
. - (6)If
 , stop; else, use the rest of accessible energy for copying the whole string with highest possible precision
, stop; else, use the rest of accessible energy for copying the whole string with highest possible precision  (with
(with  the inverse function) and go to 3.
the inverse function) and go to 3.
Typical choices are  , p0 = 0.9, ζ = 0.1; R and ρ will be used as bifurcation parameters. Important special cases are deterministic repair, that is, ρ = 1 and d = 0, and constant repair success rate with ρ < 1 and d = 0.
, p0 = 0.9, ζ = 0.1; R and ρ will be used as bifurcation parameters. Important special cases are deterministic repair, that is, ρ = 1 and d = 0, and constant repair success rate with ρ < 1 and d = 0.
In table 1 we summarize the parameters and variables, and their physical meaning, where the quantities below the horizontal line will be introduced later.
Table 1. Glossary.
| Symbol/term | Meaning |
|---|---|
| N | Length of the bitstring |
| n | Discrete time step |
| p0 | Highest initial precision of copying |
| p | Time dependent precision of copying |
| ζ | Tolerated error threshold above which repair sets in |
| ρ | Probability for a successful correction of an erroneous copy |
| c(p) | Cost-precision function that determines the costs for copying a single bit with precision p |
| R | Modulates the costs for the attempt of repair of a single bit |
| x | Error ratio |
| 1 sweep | Repair attempts of all bits of the string, followed by copying all bits of the string with reduced accuracy |
| d | Decrease of repair success probability per sweep |
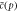
|
Cost-repair success function |
| C | Fraction of remaining energy to be used for copying |
| 1 − C | Fraction of remaining energy to be used for maintenance of repair success |
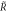
|
Modulates the maintenance costs of repair success |
3. Results
Figure 1 shows the time evolution of the error fraction x for two repair cost factors R, for ρ = 1 and two cost-precision functions 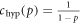 and
and  . As a first observation, the qualitative behavior of the error fraction sensitively depends on R, approaching a constant value xn < 1 at discrete time n for R below some 'critical' value Rcrit, or rapidly increasing towards 1 above this critical value. The critical parameter range, where the qualitative behavior of xn changes, depends on the choice of c(p).
. As a first observation, the qualitative behavior of the error fraction sensitively depends on R, approaching a constant value xn < 1 at discrete time n for R below some 'critical' value Rcrit, or rapidly increasing towards 1 above this critical value. The critical parameter range, where the qualitative behavior of xn changes, depends on the choice of c(p).
Figure 1. Numerical time evolution xn as function of discrete time n for two different cost functions (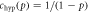 and
and  ), each one for R < Rcrit and R > Rcrit. Other parameters are p0 = 0.9, ζ = 0.1, N = 100 000.
), each one for R < Rcrit and R > Rcrit. Other parameters are p0 = 0.9, ζ = 0.1, N = 100 000.
Download figure:
Standard image High-resolution imageAlong with an increasing error fraction goes a decreasing precision pn and an increasing fraction ψn of energy which is used for repair.
Mean-field calculations. In the limit of large N we may use the probabilities for erroneous copies and successful repair as the actual mean values. For deterministic repair (ρ = 1) we obtain the discrete map from xn at time step n to xn+1 at time step n + 1
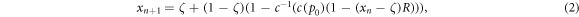
when a fraction ζ of errors is tolerated, the remaining (1 − ζ) fraction of the bits may get wrong during copying with precision p. This generates 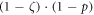 erroneous copies. The precision is determined via
erroneous copies. The precision is determined via
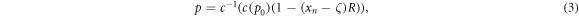
with c−1 the inverse cost-precision function. This way the whole string can be copied with a precision so that the energy cost per bit c(p) can be exactly covered by the remaining energy per bit after repair. Note that the discrete map holds only for xn ≥ ζ, which excludes the (linear) transient at early times when errors are allowed to accumulate toward the threshold that is assumed to be tolerable.
For ρ ≤ 1 and the cost-precision function chosen as 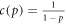 , the map becomes
, the map becomes
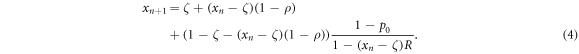
Here 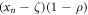 is the fraction of errors which were repaired without success, while from the remaining bits a fraction of
is the fraction of errors which were repaired without success, while from the remaining bits a fraction of 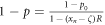 gets erroneously copied. Fixed points of this map are obtained by setting xn+1 = xn:
gets erroneously copied. Fixed points of this map are obtained by setting xn+1 = xn:
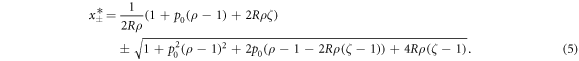
Since  , these are only physically relevant under the condition that the square root is real. For
, these are only physically relevant under the condition that the square root is real. For 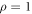 this condition leads to
this condition leads to
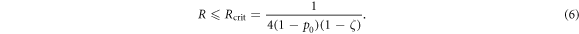
For discrete maps 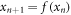 a fixed point x* is stable if
a fixed point x* is stable if 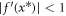 . Regarding the fixed points in equation (5), for ρ = 1 we find
. Regarding the fixed points in equation (5), for ρ = 1 we find
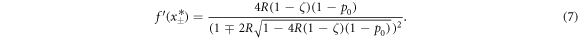
Since 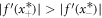 ,
, 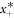 must be unstable and
must be unstable and  stable (there are only two fixed points, thus they must have opposite stability in one-dimensional phase space).
stable (there are only two fixed points, thus they must have opposite stability in one-dimensional phase space).
Figure 2(a) displays the location of both fixed points as a function of the repair cost factor R for ρ = 1.
Figure 2. Bifurcation diagrams (p0 = 0.9, ρ = 1), plotting the location of the stable (solid line) and unstable (dashed line) fixed points (a) against the size of the repair-cost factor R for ζ = 0.1 fixed; and (b) against the threshold ζ for 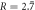 fixed.
fixed.
Download figure:
Standard image High-resolution imageThe solid (dashed) line marks the locations of the stable (unstable) fixed points, respectively. Since only values of x < 1 are physically meaningful, there exists only a stable fixed point in the shaded area between R = 0 and R = 1. For R > 1 we find a coexistence between a stable and an unstable fixed point for given R. States within the shaded region to the left of and below the unstable branch are stable in the sense that from all locations in this area the error fractions converge towards the line of stable fixed points. The fate of the system is then a stable repeating copying process at constant error ratio, given by the stable fixed point that is approached.
In the coexistence regime it depends on the initial value of x whether the system approaches a stable fixed point or ends up in the phase of deterioration or aging, where the error ratio of the copying process rapidly approaches 1. Even from the area below the line of unstable fixed points, stochastic fluctuations may kick the system across the line into the regime of deterioration.
A fold bifurcation happens at  (black dot in figure 2(a)), where stable and unstable fixed points collide and vanish. For R > Rcrit the system always deteriorates.
(black dot in figure 2(a)), where stable and unstable fixed points collide and vanish. For R > Rcrit the system always deteriorates.
If we plot the error fraction x for given R and ρ = 1 as a function of the tolerated error threshold ζ, we obtain the diagram of figure 2(b). We chose 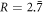 so that ζcrit = 0.1 (for comparability with figure 2(a)). Thus, for higher repair cost factor R the system may still be in the stable regime if the tolerance threshold ζ is large enough (i.e. larger than
so that ζcrit = 0.1 (for comparability with figure 2(a)). Thus, for higher repair cost factor R the system may still be in the stable regime if the tolerance threshold ζ is large enough (i.e. larger than 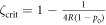 ).
).
Figure 3 shows the time evolution of the error fraction x for different repair costs factors R, for 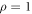 and
and 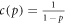 , above and below Rcrit. Similarly to the numerically determined time evolution of figure 1, the error fraction sensitively depends on R, approaching a constant value < 1 (solid curve), or slowly (red/dark-gray curve, R = 2.78) or rapidly (orange/light-gray curve R = 2.8) increasing towards 1. The slow increase of errors for a small interval of R is due to the 'felt' vicinity of the stable fixed point. If a stochastic fluctuation pushes the (otherwise stable) system beyond the unstable fixed points, it will deteriorate. As soon as the system leaves the vicinity of this fixed point, x rapidly approaches 1, so that the string consists of only erroneous bits. The dotted lines mark the unstable fixed points (that only exist for R < Rcrit) for the two R-values below Rcrit. Note that the analytically calculated value of
, above and below Rcrit. Similarly to the numerically determined time evolution of figure 1, the error fraction sensitively depends on R, approaching a constant value < 1 (solid curve), or slowly (red/dark-gray curve, R = 2.78) or rapidly (orange/light-gray curve R = 2.8) increasing towards 1. The slow increase of errors for a small interval of R is due to the 'felt' vicinity of the stable fixed point. If a stochastic fluctuation pushes the (otherwise stable) system beyond the unstable fixed points, it will deteriorate. As soon as the system leaves the vicinity of this fixed point, x rapidly approaches 1, so that the string consists of only erroneous bits. The dotted lines mark the unstable fixed points (that only exist for R < Rcrit) for the two R-values below Rcrit. Note that the analytically calculated value of 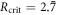 for ρ = 1 and
for ρ = 1 and 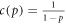 reproduces quite well the numerically observed threshold.
reproduces quite well the numerically observed threshold.
Figure 3. Mean-field error ratio xn as a function of time for different repair costs R. Dotted lines mark the location of the unstable fixed points. Other parameters are p0 = 0.9, ζ = 0.1.
Download figure:
Standard image High-resolution imageFor variable ρ ≤ 1, both ρ and R serve as bifurcation parameter. The formerly single fold bifurcation point becomes the line with a solid and dotted branch in figure 4(a), analytically obtained from the vanishing of the ± square root in equation (5) with the solid (dotted) branch for  (
(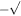 ), respectively. The bifurcation points constituting the dotted branch contain non-physical values (x > 1) as their fixed-point coordinates. The solid and dotted branches meet at R = 1, since for our choice of parameters p0 + ζ = 1 and
), respectively. The bifurcation points constituting the dotted branch contain non-physical values (x > 1) as their fixed-point coordinates. The solid and dotted branches meet at R = 1, since for our choice of parameters p0 + ζ = 1 and 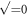 . For R < 1 and ρ > 0, all initial conditions for x lead to a stable fixed point with constant error fraction. In the striped area the fate of the system depends on the initial value for x. Finally, the vertical dotted line marks a possible way for fixed R that a system with decaying repair success would take towards the phase of deterioration. Figure 2(a) corresponds to a ρ = 1-slice of this figure.
. For R < 1 and ρ > 0, all initial conditions for x lead to a stable fixed point with constant error fraction. In the striped area the fate of the system depends on the initial value for x. Finally, the vertical dotted line marks a possible way for fixed R that a system with decaying repair success would take towards the phase of deterioration. Figure 2(a) corresponds to a ρ = 1-slice of this figure.
The three-dimensional plot of figure 4(b) shows the volume between the surfaces of stable (blue/dark-gray) and unstable (green/light-gray) fixed points. The crest where both surfaces meet is the line of fold bifurcations. From any point below this volume the system is attracted to a stable fixed point in the error fraction, as long as R is not too large; above the volume the phase is characterized by aging. Figure 2(a) is a cut of figure 4(b) through the (x, R)-plane for ρ = 1. When the repair costs are smaller than the copying costs (R < 1), it is plausible that a constant error ratio can be maintained. For R > Rcrit repair absorbs all energy after a few steps, so that no energy is left for copying. On the other hand, repair without success (ρ = 0) and R > 1 leads unavoidably to error accumulation, while for 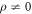 the chance for error stabilization at larger repair cost factors increases with increasing success ρ.
the chance for error stabilization at larger repair cost factors increases with increasing success ρ.
Via AUTO [20] we have checked that the analogous bifurcation diagrams for our other choices of cost-precision functions lead to qualitatively very similar (x, R)-diagrams as in figure 2(a), also when plotted for different choices of the success factor ρ. Therefore we expect our results as summarized in figure 4 not to be particularly sensitive to the choice of c(p) as long as the boundary conditions are the same.
Figure 4. (a) Bifurcation diagram as a function of varying repair success ρ and repair cost factor R. The solid line marks the critical value Rcrit of fold bifurcations, continued by the blue/darkgrey dotted line. In the shaded region the system approaches a stable error ratio, below the solid line the error fraction goes to 1. In the striped coexistence region both outcomes are possible. The vertical dotted line marks a possible path when the repair success ρ is decaying (d > 0). When the system crosses the line of fold bifurcations from above, it will deteriorate. Other parameters are p0 = 0.9, ζ = 0.1. (b) Bifurcation diagram in the R–ρ–x space. Figure 2(a) is a ρ = 1 cut of this plot.
Download figure:
Standard image High-resolution imageSo far we have assumed that repair is not perfect if 0 < ρ < 1, but constant over time. If a trade-off between cost and precision also applies to the repair mechanisms, these mechanisms will get less efficient over time with an increasing number of unsuccessful repair events, unless a superordinated repair mechanism controls and corrects the repair. An ad hoc choice is to let the repair success decrease with time, here after each sweep by an amount of d. Apart from the region with R < 1 this means that starting at ρ = 1, the surface of stable fixed points will be crossed towards the aging regime, unavoidably and sooner for larger R, later for smaller R ( > 1), as seen in figure 4(a).
A self-consistent implementation would require to account for the costs caused by the repair of repair, which we neglected so far when using constant ρ. Now we dynamically determine the time evolution of the repair success ρ and assume a cost-repair success function 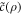 that diverges for perfect repair success ρ = 1 (all wrong bits beyond the threshold get corrected) and leads to non-zero costs without any guarantee of repair success (ρ = 0), so that a possible simple choice is given by
that diverges for perfect repair success ρ = 1 (all wrong bits beyond the threshold get corrected) and leads to non-zero costs without any guarantee of repair success (ρ = 0), so that a possible simple choice is given by
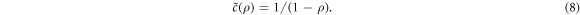
Starting from a refilled energy reservoir of size c(p0) per bit, after repairing (x − ζ) bits at cost 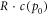 , an amount of
, an amount of 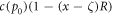 is in principle available for maintenance of repair and the subsequent new copying process. Now we use only a fraction C, (0 < C < 1) for the subsequent copying of the string and of
is in principle available for maintenance of repair and the subsequent new copying process. Now we use only a fraction C, (0 < C < 1) for the subsequent copying of the string and of  for maintenance of repair. In addition we introduce a parameter
for maintenance of repair. In addition we introduce a parameter 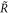 to modulate the maintenance costs
to modulate the maintenance costs 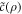 per bit, independently of the partitioning of energy via C. At step n + 1,
per bit, independently of the partitioning of energy via C. At step n + 1, 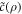 is then given by
is then given by
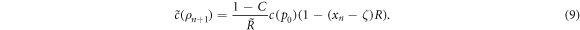
These costs determine the new ρn+1 via equation (8) to yield
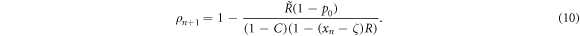
Note that ρn+1 depends on ρn only indirectly via xn, since the error fraction increases on average with less precision and decreased ρn. Now we have two dynamical variables x and ρ, so that deterioration as accumulation of errors means 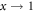 and
and 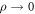 . The mean-field equation for ρn+1 is given by equation (10), while the one for xn+1 generalizes to
. The mean-field equation for ρn+1 is given by equation (10), while the one for xn+1 generalizes to
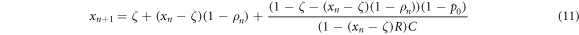
with initial conditions x0 = ζ and ρ0 = 0.99. Fixed points in xn and ρn mutually entail each other. We derived the bifurcation diagram with AUTO [20], including the additional parameters 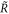 and C. What was a single fold bifurcation in figure 2(a) and a line of bifurcation points in figure 4(a), now becomes a surface, indicated by their blue coordinate lines in figure 5(a). Parameter combinations in C, R, and
and C. What was a single fold bifurcation in figure 2(a) and a line of bifurcation points in figure 4(a), now becomes a surface, indicated by their blue coordinate lines in figure 5(a). Parameter combinations in C, R, and 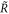 lead to fixed points in x and ρ behind this surface, while those in front of the surface lead to aging according to
lead to fixed points in x and ρ behind this surface, while those in front of the surface lead to aging according to 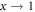 or
or 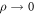 . The analogous diagram to figure 4(b), now for ρ as function of
. The analogous diagram to figure 4(b), now for ρ as function of 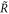 and R, is shown in figure 5(b). Here the part of the red lines above the blue bifurcation line indicate stable fixed points, below unstable ones. The larger the repair costs (parameterized by R), the more effort (larger C) on precise copying and the smaller the investment on maintenance (smaller
and R, is shown in figure 5(b). Here the part of the red lines above the blue bifurcation line indicate stable fixed points, below unstable ones. The larger the repair costs (parameterized by R), the more effort (larger C) on precise copying and the smaller the investment on maintenance (smaller 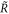 ) are required to have fixed points in R and ρ.
) are required to have fixed points in R and ρ.
Figure 5. (a) Surface of bifurcation points in the parameter space of C, 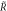 and R. Blue lines mark coordinate lines on this surface. (b) Phase portrait of ρ as a function of R and
and R. Blue lines mark coordinate lines on this surface. (b) Phase portrait of ρ as a function of R and  . The red lines indicate fixed points, the blue line marks the bifurcation between stable fixed points (above the blue line) and unstable fixed points (below the blue line).
. The red lines indicate fixed points, the blue line marks the bifurcation between stable fixed points (above the blue line) and unstable fixed points (below the blue line).
Download figure:
Standard image High-resolution imageIn case of an unavoidable accumulation of errors it is of interest whether repair and its maintenance can delay the accumulation of errors. Indeed, the decay of ρ can be slowed down by an appropriate choice of parameters, but also by the vicinity to the bifurcation point (being off from the fixed points, but still close to them): aging is slowed down the more, the closer the parameters are chosen to the fixed point parameters.
4. Conclusions and outlook
In summary, even if the energy for maintenance of repair, repair and copying are taken from the same reservoir so that repair is at the expense of its maintenance and the subsequent copying precision, errors need not automatically approach the maximal ratio 1, but may saturate at fixed points in x and ρ with values that are assumed to be tolerable. If we implement the first step towards a further iteration of repair and include the maintenance costs for keeping the primary repair success constant, we have to specify a new cost-precision function 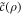 , here chosen in analogy to c(p) for the copying process. The phase diagram, now for two dynamic variables x and ρ, has still regions where aging can be prevented and error fractions and repair success approach fixed values, independently of the starting point. Again we find a coexistence region, where the fate of the system depends on the starting values, and a third region with deterioration or aging. In the aging regime errors accumulate (
, here chosen in analogy to c(p) for the copying process. The phase diagram, now for two dynamic variables x and ρ, has still regions where aging can be prevented and error fractions and repair success approach fixed values, independently of the starting point. Again we find a coexistence region, where the fate of the system depends on the starting values, and a third region with deterioration or aging. In the aging regime errors accumulate (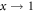 ) in the course of time, repair gets less and less successful (
) in the course of time, repair gets less and less successful (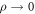 ), or, alternatively, all energy gets absorbed by successful repair, so that nothing remains for supporting the copying process.
), or, alternatively, all energy gets absorbed by successful repair, so that nothing remains for supporting the copying process.
Already simple extensions of our model toward a large (rather than minimal) and fluctuating energy reservoir may considerably delay the accumulation of errors. The extended model should be able to explain the large variance in lifetimes as well as the (on average) rather long time scale, on which aging emerges. This time is usually long as compared to the intrinsic time scales of the 'production' and maintenance processes.
Once the cost-precision functions for sufficiently simple organisms are identified, a balance along this kind of model may in particular predict that aging is an unavoidable fate of this organism, unless the cost-precision functions are changed. In the spirit of treating aging like a disease that can be cured like a disease [21] one may argue that what is needed is then to reprogram the genetic code such that the cost-precision functions get optimized to avoid aging. However, at this point it should be noticed that the best achievable trade-off may be bounded by unavoidable thermodynamic costs for the various types of information-processing, which may be easily overlooked. These costs are in general specific of an organism, a species or an individual, and whatever the costs are, they have to face finite accessible resources. Thus a change of the functional form via reprogramming may contradict fundamental physical bounds on the highest achievable precision that should be derived in the thermodynamics of the specific types of information processing. In such a case aging would be an intrinsically unavoidable fate of the dynamical system (where a different, more optimal choice of parameters would violate fundamental constraints), while in our model it is avoidable by a suitable choice of parameters.
It should be interesting to pursue the impact that the lack of perfect precision has on biological systems and to search for realizations of iterations of repair and estimate these 'maintenance' costs.
Acknowledgments
Financial support from the Deutsche Forschungsgemeinschaft DFG (grant no. ME-1332/28-1) is gratefully acknowledged.
Footnotes
- 1
For example, if synchronization on the population level of heart cells gets lost, because more and more individual cells lose their ability to oscillate (a transition termed aging-transition in [19]), the question remains of what causes the loss of this ability on the single cell level.




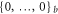
![$x\in [0,1]$](https://content.cld.iop.org/journals/1367-2630/21/4/043045/revision2/njpab1043ieqn11.gif)