Abstract
By the generalized gradient approximation in the framework of density functional theory, we find a new silicon allotrope (called dumbbell silicene) with high stability, which can turn a quantum spin Hall insulator with an inverted band gap through tuning external compression strain, just like in previous silicene. However, the obtained maximum topological nontrivial band gap about 12 meV under isotropic strain is much larger than that for previous silicene, and can be further improved to 36 meV by tuning extra anisotropic strain, which is sufficiently large to realize quantum spin Hall effect even at room-temperature, and thus is beneficial to the fabrication of high-speed spintronics devices. Furthermore, we confirm that the boron nitride sheet is an ideal substrate for the experimental realization of the dumbbell silicene under external strain, maintaining its nontrivial topology. These properties make the two-dimensional dumbbell silicene a good platform to study novel quantum states of matter, showing great potential for future applications in modern silicon-based microelectronics industry.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Two-dimensional (2D) materials have been a focus of intense research in recent years [1–4]. As opposed to three-dimensional (3D) one, its optical, electronic, mechanical and thermal properties are easily adjusted by external strains, defects, electric field, or stacking orders [5–8], and thus its realistic performance can also be readily improved through current microfabrication technology. 2D materials [9, 10] were first predicted with quantum spin Hall (QSH) effect, and recently more and more 2D materials have been confirmed as 2D topological insulators (TIs) [11–14], also known as QSH insulator. 2D TIs are novel materials characterized by a bulk energy gap and gapless spin-filtered edge states with the potential application in quantum computation and spintronics [15, 16]. Different from surface states of 3D TIs, which is only free from exact 1800-backscattering and suffers from scattering of other angles, the special edges of 2D TIs are topologically protected by the time reversal symmetry and can immune to nonmagnetic scattering and geometry perturbations, thus 2D TIs is better than 3D TIs for coherent nondissipative spin transport related applications.
Graphene, a monolayer of carbon atoms forming a similar honeycomb lattice, hosts a miraculous electronic system, and thus becomes a perfect breeding ground for a variety of exotic quantum phenomena, such as quantum anomalous Hall effect (QAHE), Majorana fermions and superconductor [17–19]. Furthermore, massless Dirac fermions endow graphene with superior carrier mobility [20, 21]. Unfortunately, its tiny band gap (about 8 × 10−4 meV [22]) opened by spin–orbit coupling (SOC) effect seriously limits its device applications. Subsequently, a new QSH insulator silicene was synthesized with a relatively large spin–orbit gap of 1.55 meV [23, 24]. Almost every striking property of graphene can be transferred to this innovative material. Indeed, these features together with the natural compatibility with current silicon-based microelectronics industry make silicene a promising candidate for future nanoelectronics application. However, its topological nontrivial band gap is still small and limits its room-temperature application in spintronics. Hence, there is great interest in searching for room temperature QSH insulator (topological band gap about 26 meV). Many valuable studies have been done for seeking large band gap TIs actually such as those containing heavy-metal atoms [25–27], or those tuned by chemical functionalization [28–32]. But, until now, there are very few room temperature QSH insulators to be found for silicon-based QSH insulator.
In this work, we propose a potential QSH insulator of new silicon allotrope (called dumbbell silicene) similar to the dumbbell configurations of other carbon-group elements [33–35], which is a local structural reconstruction of silicene induced by adatoms [36, 37]. Based on 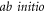 structure optimization, phonon vibration spectrum, and band structure calculations, we find that the dumbbell silicene can be stable and behave as a normal semiconductor. However, external strain can induce this material to turn a QSH insulator, accompanied by a band inversion at Γ point that changes Z2 number from 0 to 1. The maximum topological nontrivial band gap about 12 meV under isotropic strain can be further improved to 35 meV by tuning extra anisotropic strain, which is sufficiently large to realize QSH effect of the dumbbell silicene even at room temperature. In additional, we further show that the boron nitride (BN) substrate is suitable to support the dumbbell silicene under external strain, and the topologically nontrivial properties of the strained dumbbell silicene can be retained well in the realistic growth on the boron nitride (BN) substratproposee. Hence, we believe that this new silicon allotrope has great potential for future applications in modern silicon-based microelectronics industry.
structure optimization, phonon vibration spectrum, and band structure calculations, we find that the dumbbell silicene can be stable and behave as a normal semiconductor. However, external strain can induce this material to turn a QSH insulator, accompanied by a band inversion at Γ point that changes Z2 number from 0 to 1. The maximum topological nontrivial band gap about 12 meV under isotropic strain can be further improved to 35 meV by tuning extra anisotropic strain, which is sufficiently large to realize QSH effect of the dumbbell silicene even at room temperature. In additional, we further show that the boron nitride (BN) substrate is suitable to support the dumbbell silicene under external strain, and the topologically nontrivial properties of the strained dumbbell silicene can be retained well in the realistic growth on the boron nitride (BN) substratproposee. Hence, we believe that this new silicon allotrope has great potential for future applications in modern silicon-based microelectronics industry.
The first-principle calculations based on the density functional theory were performed using the Vienna ab simulation package [38, 39]. We use the generalized gradient approximations of Perdew–Burke–Ernzerhof (PBE) [40] for electron–electron interactions and the projector-augmented-wave [41] pseudo-potentials in the plane-wave basis with an energy cutoff of 700 eV. The Brillouin zone (BZ) was sampled using an 13 × 13 × 1 gamma-centered Monkhorst–Pack grid [42]. A slab model, together with a vacuum layer larger than 30 Å, was employed to avoid spurious interactions due to the nonlocal nature of the correlation energy [43]. SOC [44] is included in the calculations after the structural relaxations. In additional, we calculated the phonon vibration spectra by using the frozen phonon method as implemented in the PHONOPY code [45]. Long-range dispersion corrections have been taken into account within a semi-empirical van der Waals approach proposed by Grimme known as the DFT-D2 method [46](where D2 stands for the second generation of this method) to dealing with the interaction between the dumbbell silicene and the BN sheet. Hybrid Heyd–Scuseria–Emzerhof (HSE06) functional is adopted to correct the PBE bulk band gaps [47, 48].
Different from silicene (space group 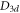 ) shown in figure 1(b), in the dumbbell silicene there are two types of Si atoms: one is fourfold coordinated (denoted by Si(α)), and the other one is only threefold coordinated with a dangling bond (denoted by Si(β)), as shown in figure 1(a). All the Si(α) atoms keep on the same plane, which is surrounded by the Si(β) atoms to form the dumbbell structure. The especial lattice structure of the dumbbell silicene is similar to that for dumbbell stanene [33] with the same space group
) shown in figure 1(b), in the dumbbell silicene there are two types of Si atoms: one is fourfold coordinated (denoted by Si(α)), and the other one is only threefold coordinated with a dangling bond (denoted by Si(β)), as shown in figure 1(a). All the Si(α) atoms keep on the same plane, which is surrounded by the Si(β) atoms to form the dumbbell structure. The especial lattice structure of the dumbbell silicene is similar to that for dumbbell stanene [33] with the same space group 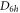 . The buckling height h of the dumbbell silicene about 2.71 Å is much larger than that in the silicene about 0.44 Å, which may result in the larger SOC strength for the dumbbell silicene. The obtained lattice constant and the distance between the neighboring dumbbell units (s in figure 1(a)) for the dumbbell silicene are 7.43 Å and 4.29 Å, respectively, which is smaller than that in the dumbbell stanene regardless of the lattice constant or the distance between the neighboring dumbbell units. These results including those for the silicene are in well agreement with those reported in previous published works [23, 36].
. The buckling height h of the dumbbell silicene about 2.71 Å is much larger than that in the silicene about 0.44 Å, which may result in the larger SOC strength for the dumbbell silicene. The obtained lattice constant and the distance between the neighboring dumbbell units (s in figure 1(a)) for the dumbbell silicene are 7.43 Å and 4.29 Å, respectively, which is smaller than that in the dumbbell stanene regardless of the lattice constant or the distance between the neighboring dumbbell units. These results including those for the silicene are in well agreement with those reported in previous published works [23, 36].
Figure 1. Top and side view of (a) the dumbbell silicene structure and (b) the silicene structure. 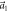 and
and 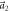 are the lattice unit vectors. (c) The first Brillouin zone.
are the lattice unit vectors. (c) The first Brillouin zone. 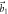 and
and 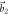 are the reciprocal lattice unit vectors. Γ, M and K refer to special points in the first Brillouin zone. (d) Total energies of the dumbbell silicene, silicene and siliconeet with different in-layer strain ratios.
are the reciprocal lattice unit vectors. Γ, M and K refer to special points in the first Brillouin zone. (d) Total energies of the dumbbell silicene, silicene and siliconeet with different in-layer strain ratios.
Download figure:
Standard image High-resolution imageTotal energies of the two silicon allotropes with different in-layer strain ratios are presented in figure 1(d). The minimum energy per Si atom for the dumbbell silicene is lower than that for the silicene, implying that the stability of the dumbbell silicene is over the silicene. Furthermore, we also calculate the minimum energy per Si atom of siliconeet which is predicted by Wang  [49] recently, as shown in figure 1(d). The minimum energy of the siliconeet is lower than that for the silicene, but is higher than that for the dumbbell silicene, indicating that the dumbbell silicene is the most stable among them. Because the HB configure is unstable due to its large imaginary phonon frequency [50] (see figure 1(d)), the mentioned silicene in our work refers to the LB silicene. Phonon vibration spectrums of the two silicon allotropes are presented in figures 2(a) and (b). The frequencies of all modes are positive over the whole BZ for the two silicon allotropes, which shows that the two lattice structures are thermodynamically stable and their stability do not depend on the substrates. This small imaginary frequency near the gamma point for the dumbbell silicene is extremely sensitive to the details of the calculation and in some cases disappears altogether. The absolute value of the imaginary frequency is similar to the amount by which the acoustic branch of the dispersion curve misses zero when Newton's third law is not imposed on the matrix of force constants, and in fact this small imaginary frequency appears to be a common issue in first-principles calculations for 2D materials [51]. The slopes of the longitudinal acoustic branches near Γ correspond to the speed of sound and reveal the in-plane stiffness. The calculated speed of sound along the Γ − M direction in the dumbbell silicene,
[49] recently, as shown in figure 1(d). The minimum energy of the siliconeet is lower than that for the silicene, but is higher than that for the dumbbell silicene, indicating that the dumbbell silicene is the most stable among them. Because the HB configure is unstable due to its large imaginary phonon frequency [50] (see figure 1(d)), the mentioned silicene in our work refers to the LB silicene. Phonon vibration spectrums of the two silicon allotropes are presented in figures 2(a) and (b). The frequencies of all modes are positive over the whole BZ for the two silicon allotropes, which shows that the two lattice structures are thermodynamically stable and their stability do not depend on the substrates. This small imaginary frequency near the gamma point for the dumbbell silicene is extremely sensitive to the details of the calculation and in some cases disappears altogether. The absolute value of the imaginary frequency is similar to the amount by which the acoustic branch of the dispersion curve misses zero when Newton's third law is not imposed on the matrix of force constants, and in fact this small imaginary frequency appears to be a common issue in first-principles calculations for 2D materials [51]. The slopes of the longitudinal acoustic branches near Γ correspond to the speed of sound and reveal the in-plane stiffness. The calculated speed of sound along the Γ − M direction in the dumbbell silicene, 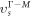 = 3.0 Km s−1, is lower than the
= 3.0 Km s−1, is lower than the 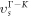 = 3.3 Km s−1 value along the
= 3.3 Km s−1 value along the 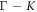 direction. The lower rigidity along the
direction. The lower rigidity along the 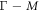 direction
direction 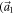 +
+ 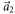 direction in figure 1(a)), indicates that compression along this direction requires primarily bond bending, which comes at a lower energy cost than stretching. On the contrary, the in-plane elastic response of the silicene is nearly isotropic, with nearly the same value
direction in figure 1(a)), indicates that compression along this direction requires primarily bond bending, which comes at a lower energy cost than stretching. On the contrary, the in-plane elastic response of the silicene is nearly isotropic, with nearly the same value 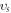 = 2.3 Km s−1 for the speed of sound along the
= 2.3 Km s−1 for the speed of sound along the 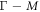 and the
and the 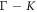 directions (see figure 2(b)). These results are advantageous when accommodating lattice mismatch during chemical vapor deposition growth on a substrate.
directions (see figure 2(b)). These results are advantageous when accommodating lattice mismatch during chemical vapor deposition growth on a substrate.
Figure 2. Vibrational band structure 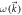 of (a) the dumbbell silicene and (b) the silicene. The slope of the red dashed lines along the longitudinal acoustic branches near Γ corresponds to the speed of sound and the in-plane stiffness. Electronic band structure of (c) the dumbbell silicene and (d) the silicene without SOC. Dirac cone is marked by black rectangular box. The green dots corresponding to Si-pz. The Fermi level is set to zero.
of (a) the dumbbell silicene and (b) the silicene. The slope of the red dashed lines along the longitudinal acoustic branches near Γ corresponds to the speed of sound and the in-plane stiffness. Electronic band structure of (c) the dumbbell silicene and (d) the silicene without SOC. Dirac cone is marked by black rectangular box. The green dots corresponding to Si-pz. The Fermi level is set to zero.
Download figure:
Standard image High-resolution imageOur DFT results for the electronic band structures without SOC of the two different silicon allotropes are presented in figures 2(c) and (d). Like to the dumbbell stanene [33], the dumbbell silicene is also a semiconductor with an indirect PBE band gap about 0.24 eV, which is much larger than almost zero band gap for the silicene. The dumbbell silicene also owns a Dirac cone at K point around the Fermi level, and more surprisingly, the Dirac cone of the dumbbell silicene also originates from the pz orbital like in the silicene (see the black rectangular box in figures 2(c) and (d)). The especial Dirac cone is closely related to the Si(β) atoms. Its three of four valence electrons form bonds with neighboring silicon atoms while the remaining one makes a contribution to pz state, which binds covalently with each other and develops into delocalized π and 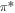 states. Such bands are responsible for Dirac points and linear band dispersion near the Fermi level. However, because other nodes of the dumbbell silicene throughout the band structure are parabolic instead of Dirac-type with linear dispersion, its Dirac cone may make less contribution to the transportation.
states. Such bands are responsible for Dirac points and linear band dispersion near the Fermi level. However, because other nodes of the dumbbell silicene throughout the band structure are parabolic instead of Dirac-type with linear dispersion, its Dirac cone may make less contribution to the transportation.
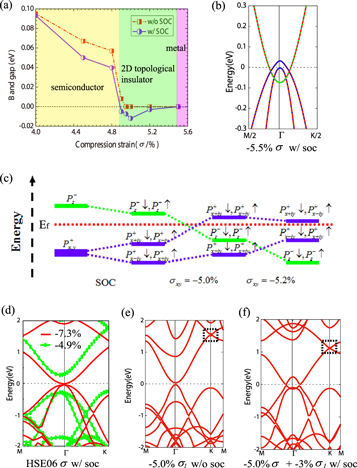
Previous theoretical and experimental studies have shown that the external strain is an excellent method to tune electronic structures of 2D materials. Our results also prove that the band gap of the dumbbell silicene depends sensitively on the applied in-layer isotropic strain σ, as shown in figure 3. The in-plane isotropic strain σ is loaded synchronously in the 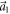 and
and  directions. Without SOC, the conduction band (CB) and the valence band (VB) at Γ point tend to approach together as σ increases, and compression beyond 5.0% shall turn the dumbbell silicene metallic. At Γ point, the top of VB is mainly contributed by the antibonding
directions. Without SOC, the conduction band (CB) and the valence band (VB) at Γ point tend to approach together as σ increases, and compression beyond 5.0% shall turn the dumbbell silicene metallic. At Γ point, the top of VB is mainly contributed by the antibonding 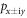 orbitals with fourfold degeneracy, and the bottom of CB is from the bonding pz orbital. However, by introducing SOC, the fourfold degenerate VBs are split (see figure 3(c)). Most remarkably, the closed band gap is reopened when σ =
orbitals with fourfold degeneracy, and the bottom of CB is from the bonding pz orbital. However, by introducing SOC, the fourfold degenerate VBs are split (see figure 3(c)). Most remarkably, the closed band gap is reopened when σ = 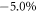 (
(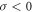 means the compression strain), and a band inversion occurs between the
means the compression strain), and a band inversion occurs between the  and pz orbitals with a 12 meV nontrivial band gap around Γ point, accompanied by the exchange of their parities, as illustrated in figure 3(d). The inverted states are labeled by
and pz orbitals with a 12 meV nontrivial band gap around Γ point, accompanied by the exchange of their parities, as illustrated in figure 3(d). The inverted states are labeled by 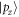 and
and 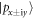 . Such band-inversion character may indicate that the topological phase transition from a trivial state to a nontrivial topological state is happened for the dumbbell silicene as σ increases, which is similar to the band-inversion character in bilayer phosphorene [11] and antimonene [52] induced by strain. The Fermi level sitting outside the bulk gap for the dumbbell silicene when σ =
. Such band-inversion character may indicate that the topological phase transition from a trivial state to a nontrivial topological state is happened for the dumbbell silicene as σ increases, which is similar to the band-inversion character in bilayer phosphorene [11] and antimonene [52] induced by strain. The Fermi level sitting outside the bulk gap for the dumbbell silicene when σ = 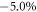 can be artificially adjusted inside the gap by applying a gate voltage.
can be artificially adjusted inside the gap by applying a gate voltage.
Figure 3. Electronic band structure of the dumbbell silicene when σ = 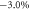 (a) without SOC and (c) with SOC, where the inset in (c) shows its enlarged views around the Fermi level in the vicinity of Γ point. Electronic band structure of the dumbbell silicene when σ =
(a) without SOC and (c) with SOC, where the inset in (c) shows its enlarged views around the Fermi level in the vicinity of Γ point. Electronic band structure of the dumbbell silicene when σ = 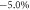 (b) without SOC and (d) with SOC, where the right-hand panels of (b) and (d) show their enlarged views around the Fermi level in the vicinity of Γ point. The green and blue dots corresponding to Si-pz and Si-
(b) without SOC and (d) with SOC, where the right-hand panels of (b) and (d) show their enlarged views around the Fermi level in the vicinity of Γ point. The green and blue dots corresponding to Si-pz and Si-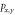 , respectively. (Even, odd) Parity is denoted by (+, −) and the Fermi level is set to zero.
, respectively. (Even, odd) Parity is denoted by (+, −) and the Fermi level is set to zero.
Download figure:
Standard image High-resolution imageFurther, we apply a rigid method of Fu and Kane [53] to judge whether or not the dumbbell silicene is a QSH insulator by calculating its Z2 number when σ = 0 and 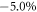 . Such method is valid since the dumbbell silicene has both spatial invention and time reversal symmetries. We state a time-reversal invariant periodic Hamiltonian H with
. Such method is valid since the dumbbell silicene has both spatial invention and time reversal symmetries. We state a time-reversal invariant periodic Hamiltonian H with 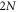 occupied bands characterized by Bloch wave functions. A time-reversal operator matrix relates time-reversed wave functions is defined by
occupied bands characterized by Bloch wave functions. A time-reversal operator matrix relates time-reversed wave functions is defined by
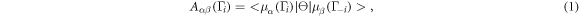
where 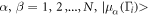 are cell periodic eigenstates of the Bloch Hamiltonian, Θ = exp(
are cell periodic eigenstates of the Bloch Hamiltonian, Θ = exp(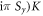 is the time-reversal operator (Sy is spin and K complex conjugation), which
is the time-reversal operator (Sy is spin and K complex conjugation), which  = −1 for spin 1/2 particles. Since
= −1 for spin 1/2 particles. Since 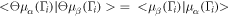 ,
, 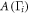 is antisymmetric at TRIM
is antisymmetric at TRIM 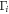 . The square of its Pfaffian is equal to its determinant, i.e., det[A] = Pf
. The square of its Pfaffian is equal to its determinant, i.e., det[A] = Pf ![${[A]}^{2}$](https://content.cld.iop.org/journals/1367-2630/18/4/043001/revision1/njpaa1a07ieqn40.gif) . Then
. Then 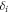 = (det
= (det ![$[A({{\rm{\Gamma }}}_{i})]$](https://content.cld.iop.org/journals/1367-2630/18/4/043001/revision1/njpaa1a07ieqn42.gif) )
) 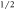 /Pf
/Pf ![$[A({{\rm{\Gamma }}}_{i})]$](https://content.cld.iop.org/journals/1367-2630/18/4/043001/revision1/njpaa1a07ieqn44.gif) = ±1. Therefore, the topological invariant Z2 can be defined as
= ±1. Therefore, the topological invariant Z2 can be defined as
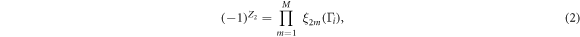
where ξ is the parities of all occupied bands at 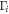 , and M is the number of Kramers pairs. Results show that the product of parities of occupied bands at the time reversal invariant points contributes to a +1 parity when σ = 0, yielding a trivial topological invariant Z2 = 0. However, as σ is increased up to σ =
, and M is the number of Kramers pairs. Results show that the product of parities of occupied bands at the time reversal invariant points contributes to a +1 parity when σ = 0, yielding a trivial topological invariant Z2 = 0. However, as σ is increased up to σ = 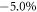 , the product of parities of occupied bands is −1 at Γ point but +1 at the three other time-reversal invariant momenta. Hence, like in the silicene, the dumbbell silicene also is a QSH insulator when the external isotropic compression strain is beyond 5.0% with Z2 = 1. The evolution of the band gap at Γ point with σ is presented in figure 4(a). We find that the character of the dumbbell silicene shall undergo a semiconductor, TI to metal process with the increase of σ. The dumbbell silicene can maintain to be the QSH insulator under the isotropic strain
, the product of parities of occupied bands is −1 at Γ point but +1 at the three other time-reversal invariant momenta. Hence, like in the silicene, the dumbbell silicene also is a QSH insulator when the external isotropic compression strain is beyond 5.0% with Z2 = 1. The evolution of the band gap at Γ point with σ is presented in figure 4(a). We find that the character of the dumbbell silicene shall undergo a semiconductor, TI to metal process with the increase of σ. The dumbbell silicene can maintain to be the QSH insulator under the isotropic strain  . Because the electronic band gap by the PBE method is usually underestimated, we adopt the more accurate HSE06 functional to correct it in our work. The results show that the PBE band gap is underestimated about 0.462 eV for the dumbbell silicene without external strain and SOC. Hence, we think that the HSE06 critical strain value from normal insulator to TI must be relatively larger than that within the PBE calculations. The unclosed band gaps under
. Because the electronic band gap by the PBE method is usually underestimated, we adopt the more accurate HSE06 functional to correct it in our work. The results show that the PBE band gap is underestimated about 0.462 eV for the dumbbell silicene without external strain and SOC. Hence, we think that the HSE06 critical strain value from normal insulator to TI must be relatively larger than that within the PBE calculations. The unclosed band gaps under  (∼0.525 eV) and
(∼0.525 eV) and 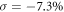 (∼0.03 eV) without SOC confirm this hypothesis, as shown in figure 4(d). Like to the case in the PBE calculations, the closed HSE06 band gap for the dumbbell silicene can also be reopened by introducing SOC when
(∼0.03 eV) without SOC confirm this hypothesis, as shown in figure 4(d). Like to the case in the PBE calculations, the closed HSE06 band gap for the dumbbell silicene can also be reopened by introducing SOC when 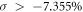 , and the isotropic strain range where the dumbbell silicene can maintain to be the QSH insulator is about
, and the isotropic strain range where the dumbbell silicene can maintain to be the QSH insulator is about 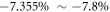 for the HSE06 method. The dependence of the band gap for the silicene with SOC on the applied isotropic strain σ is also analyzed. The band gap of the silicene is not sensitive to σ. Its Dirac cone at K point is protected by the crystal symmetry, and thus can hardly be eliminated by σ. Under
for the HSE06 method. The dependence of the band gap for the silicene with SOC on the applied isotropic strain σ is also analyzed. The band gap of the silicene is not sensitive to σ. Its Dirac cone at K point is protected by the crystal symmetry, and thus can hardly be eliminated by σ. Under 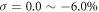 , the band gap of the silicene only changes from 1.52 to 1.56 meV, which is smaller than the maximum topological band gap about 12 meV of the dumbbell silicene when σ =
, the band gap of the silicene only changes from 1.52 to 1.56 meV, which is smaller than the maximum topological band gap about 12 meV of the dumbbell silicene when σ = 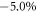 . Hence, it is quite promising for the achievement of the QSH effect of the dumbbell silicene at higher temperatures than the silicene.
. Hence, it is quite promising for the achievement of the QSH effect of the dumbbell silicene at higher temperatures than the silicene.
Figure 4. (a) Dependence of the fundamental band gap for the dumbbell silicene on the in-plane isotropic compression strain σ. Yellow, green and pink shaded regions indicate its characters of semiconductor, topological insulator and metal under σ, respectively. (c) Schematic diagram of the electronic band evolution of the dumbbell silicene under σ with SOC for the orbitals around the Fermi level at Γ point. Electronic band structure of the dumbbell silicene (b) under 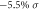 with SOC, (d) under
with SOC, (d) under 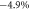 and
and 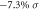 without SOC by HSEO6 method, (e) under
without SOC by HSEO6 method, (e) under 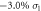 without SOC, and (f) under
without SOC, and (f) under 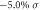 +
+ 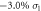 with SOC. In (b) the green and blue dots corresponding to Si-pz and Si-
with SOC. In (b) the green and blue dots corresponding to Si-pz and Si- , respectively. The Fermi level is set to zero.
, respectively. The Fermi level is set to zero.
Download figure:
Standard image High-resolution imageWe find that the incorporating band inversion in dumbbell silicene could be created solely by external isotropic strain, even without considering the SOC, as shown in figure 3(b). As σ is increased up to  , the top of VB (
, the top of VB ( state) and the bottom of CB (
state) and the bottom of CB (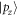 state) is inversion, and then the exchanged bottom of VB (
state) is inversion, and then the exchanged bottom of VB (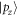 state) and the previous degenerate top of VB (
state) and the previous degenerate top of VB (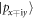 state) is rapidly once again inversion due to the existence of the fourfold degenerate VBs at Γ point, which turns the dumbbell silicene metallic. Hence, it is impossible that the dumbbell silicene can turn 2D TI solely by external isotropic strain. SOC plays a vital role in lifting the band degeneracy for the VBs at Γ point, and thus creating a gap at the crossing points originating from the band inversion. However, the SOC in Si is too weak, leading to a tiny energy difference between the
state) is rapidly once again inversion due to the existence of the fourfold degenerate VBs at Γ point, which turns the dumbbell silicene metallic. Hence, it is impossible that the dumbbell silicene can turn 2D TI solely by external isotropic strain. SOC plays a vital role in lifting the band degeneracy for the VBs at Γ point, and thus creating a gap at the crossing points originating from the band inversion. However, the SOC in Si is too weak, leading to a tiny energy difference between the 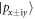 and
and 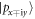 states. As seen in figures 4(b) and (c), the exchanged
states. As seen in figures 4(b) and (c), the exchanged 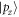 state and the
state and the 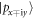 state shall exchange quickly once again as the compression strain σ is increased, similar to the case without SOC. This character is different to the dumbbell configurations of other carbon-group elements [33–35] with large SOC strength. Without any external strain or electric field, the dumbbell stanene is still QSH insulator with a large topological band gap, and its nontrivial band gap can be further increased with hydrogenation. Hence, the weak SOC strength and the fourfold degenerate VBs at Γ point are the main restricted factors for the dumbbell silicene to create larger topological band gap.
state shall exchange quickly once again as the compression strain σ is increased, similar to the case without SOC. This character is different to the dumbbell configurations of other carbon-group elements [33–35] with large SOC strength. Without any external strain or electric field, the dumbbell stanene is still QSH insulator with a large topological band gap, and its nontrivial band gap can be further increased with hydrogenation. Hence, the weak SOC strength and the fourfold degenerate VBs at Γ point are the main restricted factors for the dumbbell silicene to create larger topological band gap.
The calculated results for the dumbbell silicene under anisotropic strain 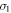 are presented in figures 4(e) and (f). The anisotropic strain
are presented in figures 4(e) and (f). The anisotropic strain 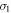 is only along the
is only along the 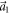 direction. We find that the fourfold degenerate VB at Γ point for the dumbbell silicene can be lifted solely by anisotropic strain
direction. We find that the fourfold degenerate VB at Γ point for the dumbbell silicene can be lifted solely by anisotropic strain  (see figure 4(e)).
(see figure 4(e)). 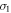 may create the larger topological band gap than that only induced by σ. Hence, we apply an extra anisotropic strain
may create the larger topological band gap than that only induced by σ. Hence, we apply an extra anisotropic strain 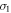 about
about 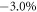 on the previous lattice structure under
on the previous lattice structure under 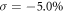 , as shown in figure 4(f). The optimized lattice structure of the dumbbell silicene under
, as shown in figure 4(f). The optimized lattice structure of the dumbbell silicene under 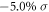 and
and 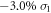 still has both spatial invention and time reversal symmetries, and hence its topological property still can be judged by the previous method of Fu and Kane. Results show that the character of 2D TI for the dumbbell silicene is retained and the topological band gap is increased up to 36 meV, which is sufficiently larger to realize QSH effect at room-temperature. With the further increase of
still has both spatial invention and time reversal symmetries, and hence its topological property still can be judged by the previous method of Fu and Kane. Results show that the character of 2D TI for the dumbbell silicene is retained and the topological band gap is increased up to 36 meV, which is sufficiently larger to realize QSH effect at room-temperature. With the further increase of 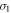 , the topological band gap for the dumbbell silicene under
, the topological band gap for the dumbbell silicene under 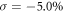 is decreased. In addition, the Dirac cone for the dumbbell silicene under
is decreased. In addition, the Dirac cone for the dumbbell silicene under 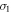 is destroyed as a result of spatial symmetry breaking (see figure 4(f)), different from the previous case under σ, which indicates that hexagonal symmetry is the main precondition for the present of Dirac cone in the dumbbell silicene.
is destroyed as a result of spatial symmetry breaking (see figure 4(f)), different from the previous case under σ, which indicates that hexagonal symmetry is the main precondition for the present of Dirac cone in the dumbbell silicene.
The in-plane strain on the dumbbell silicene can be realized by bending its flexure substrate in experiment, similar to graphene [54], where the amount of the strain is proportional to 2D mode position of the dumbbell silicene. It is important to find a proper substrate for the dumbbell silicene on which its exotic topological properties under high external strain can be retained for future applications. Because the BN sheet has a close lattice structure and large band gap and high dielectric constant, here we use it as a substrate to support DB stanene. Figure 5(a) shows the geometrical structure of the dumbbell silicene on the (3 × 3) BN sheet, where the lattice mismatch is less than 1.5%. The dumbbell silicene almost retains the original structure with lattice constant about 7.50 Å and a buckling height h about 2.69 Å. The distance between the adjacent layers (d in figure 5(b)) is about 3.16 Å. Cohesive energy ESi for the dumbbell silicene on the hexagonal BN sheet is defined by ESi = 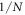 (Etotal − EDS − EBN), where EDS and EBN are the total energy of dumbbell silicene and hexagonal BN sheet, respectively, and Etotal is the total energy of the dumbbell silicene/substrate system, and N is the number of Si atoms in the dumbbell silicene. The obtained cohesive energy ESi is only about −0.26 eV per Si atom, which is larger than those of the silicene and hexagonal BN system proposed by previous works [55–57], indicating that the interaction between the dumbbell silicene and substrate system is stronger. But the obtained cohesive energy per atom about −0.029 eV can be compared with those of the dumbbell configurations for other carbon-group elements/hexagonal BN systems [33, 35]. The interaction between the dumbbell silicene and the BN sheet is relatively weak and can be considered as van der Waals type. The dumbbell silicene on BN sheet with SOC under σ = 0 remains semiconducting (see figure 5(b)). There is essentially no charge transfer between the adjacent layers, and the states around the Fermi level are dominantly contributed by the dumbbell silicene. As σ is increased up to −6.2%, the top of VB and the bottom of CB for the dumbbell silicene on BN sheet are inversion, and thus opens a small topological band gap (see the inset of figure 5(c)), accompanied by the exchange of their parities. Evidently, the dumbbell silicene on the (3 × 3) BN substrate also is a QSH insulator whose band inversion is not affected by the substrate.
(Etotal − EDS − EBN), where EDS and EBN are the total energy of dumbbell silicene and hexagonal BN sheet, respectively, and Etotal is the total energy of the dumbbell silicene/substrate system, and N is the number of Si atoms in the dumbbell silicene. The obtained cohesive energy ESi is only about −0.26 eV per Si atom, which is larger than those of the silicene and hexagonal BN system proposed by previous works [55–57], indicating that the interaction between the dumbbell silicene and substrate system is stronger. But the obtained cohesive energy per atom about −0.029 eV can be compared with those of the dumbbell configurations for other carbon-group elements/hexagonal BN systems [33, 35]. The interaction between the dumbbell silicene and the BN sheet is relatively weak and can be considered as van der Waals type. The dumbbell silicene on BN sheet with SOC under σ = 0 remains semiconducting (see figure 5(b)). There is essentially no charge transfer between the adjacent layers, and the states around the Fermi level are dominantly contributed by the dumbbell silicene. As σ is increased up to −6.2%, the top of VB and the bottom of CB for the dumbbell silicene on BN sheet are inversion, and thus opens a small topological band gap (see the inset of figure 5(c)), accompanied by the exchange of their parities. Evidently, the dumbbell silicene on the (3 × 3) BN substrate also is a QSH insulator whose band inversion is not affected by the substrate.
Figure 5. (a) Top and side view of the dumbbell silicene structure on the (3 × 3) BN sheet. Electronic band structure of the dumbbell silicene on the (3 × 3) BN sheet with SOC when (b) σ = 0 and (c) σ = 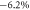 . The red and blue dots stand for the contribution from the BN sheet and Si-
. The red and blue dots stand for the contribution from the BN sheet and Si-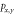 , respectively. The right-hand panel of (c) show its enlarged view around the Fermi level in the vicinity of Γ point. (Even, odd) Parity is denoted by (+, −) and the Fermi level is set to zero.
, respectively. The right-hand panel of (c) show its enlarged view around the Fermi level in the vicinity of Γ point. (Even, odd) Parity is denoted by (+, −) and the Fermi level is set to zero.
Download figure:
Standard image High-resolution imageIn summary, the dumbbell silicene has been proven as an excellent QSH insulator when the isotropic compression strain 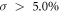 based on the first-principles calculations. Electronic band of the dumbbell silicene can be inverted between the VB maximum of
based on the first-principles calculations. Electronic band of the dumbbell silicene can be inverted between the VB maximum of 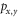 orbitals and the CB maximum of pz orbital at Γ point by tuning σ. The obtained maximum topological band gap about 12 meV under isotropic compression strain σ can be further improved to 35 meV by tuning extra anisotropic strain
orbitals and the CB maximum of pz orbital at Γ point by tuning σ. The obtained maximum topological band gap about 12 meV under isotropic compression strain σ can be further improved to 35 meV by tuning extra anisotropic strain 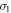 , which is useful for the application of QSH effect at room temperature. In additional, we confirm that BN substrate is suitable to support the dumbbell silicen under external strain, maintaining its nontrivial topology. We expect that the previous silicene can be replaced by the dumbbell silicene in modern silicon-based microelectronics industry, and the QAHE and topological superconductivity can also be realized in the dumbbell silicene, which shall make supported dumbbell silicene an ideal platform to study quantum states of matter and show great potential for future applications.
, which is useful for the application of QSH effect at room temperature. In additional, we confirm that BN substrate is suitable to support the dumbbell silicen under external strain, maintaining its nontrivial topology. We expect that the previous silicene can be replaced by the dumbbell silicene in modern silicon-based microelectronics industry, and the QAHE and topological superconductivity can also be realized in the dumbbell silicene, which shall make supported dumbbell silicene an ideal platform to study quantum states of matter and show great potential for future applications.
Acknowledgments
The work was supported by the National Natural Science Foundation of China and the Chinese Academy of Engineering Physics (Grant Nos. U1430117, U1230201).