Abstract
The energetics and atomic structure associated with the localized hole formed near an Al-atom dopant in α-quartz are calculated using a variational, self-consistent implementation of the Perdew–Zunger self-interaction correction with complex optimal orbitals. This system has become an important test problem for theoretical methodology since generalized gradient approximation energy functionals, as well as commonly used hybrid functionals, fail to produce a sufficiently localized hole due to the self-interaction error inherent in practical implementations of Kohn–Sham density functional theory. The self-interaction corrected calculations are found to give accurate results for the energy of the defect state with respect to both valence and conduction band edges as well as the experimentally determined atomic structure where only a single Al–O bond is lengthened by 11%. The HSE hybrid functional, as well as the PW91 generalized gradient approximation functional, however, gives too small an energy gap between the defect state and the valence band edge, overly delocalized spin density and lengthening of more than one Al–O bond.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
While Kohn–Sham density functional theory (KS-DFT) has been extremely successful and is now widely used in studies of molecules and condensed matter [1, 2], there are several shortcomings of this approach of which the description of localized electronic states in semiconductors and insulators is particularly problematic [3]. An important issue is the energy of the defect state with respect to the valence and conduction band edges as well as structural changes due to the introduction of the defect. A widely studied and well documented case is the Al-atom substitutional defect in α-quartz. Since the Al-atom has three valence electrons while the Si-atom it replaces has four, an electron hole is introduced in the electronic structure.
Extensive electron paramagnetic resonance (EPR) experiments have been interpreted in terms of a localized hole on one of the O-atoms neighboring the Al-atom and a 12% lengthening of the corresponding Al–O bond [4, 5]. An experimental estimate of the defect energy level has been obtained from optical absorption measurements where an electron is excited from a lone pair of an O-atom adjacent to the Al-atom into the localized defect state, a light-induced transfer of the hole between oxygen atoms of the AlO4 tetrahedron. The estimate obtained for the energy difference between the defect level and valence band edge is 1.96 eV [16]. The band gap of α-quartz is estimated experimentally to be 9 eV so the defect level is much closer to the valence band edge than the conduction band edge. Both the energetics as well as atomic structure related to the Al substitutional defect in α-quartz are, therefore, well established from experimental measurements.
Theoretical calculations of clusters using the Hartree–Fock (HF) approximation have supported the interpretation of the EPR data while DFT calculations have predicted a more delocalized hole. Pacchioni et al [5] have presented a review of calculations of the atomic structure using various theoretical methods as well as systematic computational studies of finite clusters of varying size. Comparison of the calculated hyperfine splitting with the EPR data has shown conclusively that the original interpretation of the EPR measurements was correct while the DFT calculations were in error. HF calculations and DFT calculations based on the generalized gradient approximation (GGA) such as the PBE and PW91 functionals [7] tend to have errors of opposite sign. For example, HF calculations predict the band gap of α-quartz to be 17 eV [8], while the energy difference between conduction and valence band edges is 5.9 eV in results obtained using the PBE functional [9]. By mixing different theoretical approaches that have errors of opposite sign to form a hybrid functional, the errors can be made to cancel to some extent and a number of such mixtures have been proposed for various different purposes. Calculations of small clusters using the B3LYP functional which includes 20% exact exchange have given a delocalized hole spread over two O-atoms, while calculations using the BB1K functional which includes 42% exact exchange have given localization on a single O-atom [6]. The construction of hybrid functionals, however, does not address the root of the problem inherent in KS-DFT functionals.
The basic reason for the instability of the localized hole is the self-interaction error in commonly used KS-DFT functionals. Lægsgaard and Stokbro illustrated how the self-interaction destabilizes the localized hole using a model calculation [10]. Even though Perdew and Zunger proposed a method for self-interaction correction (SIC) more than 30 years ago [11], there have been few attempts to make use of this approach in calculations of defect states in solids. Several perfect crystals have been studied with a linear-muffin-tin-orbital implementation of SIC and the local density approximation (LDA) functional, were the correction was applied selectively to d- or f-electrons, and good results in terms of band gaps, f- and d-state occupation and magnetic properties obtained [12–14]. The full implementation of SIC, including structural optimization, is challenging in many respects, as described in the following section. A limited SIC procedure has been applied to Al-doped α-quartz where the correction was only applied to the spin density, i.e. a single unpaired electron, while the rest of the electrons were described with the PBE functional in a spin restricted formulation [15]. Such a limited version of the Perdew–Zunger correction was shown to help stabilize the localized hole to some extent, but made it only metastable. The valence band energy is still too high in such calculations because of the remaining self-interaction error in the rest of the occupied orbitals. The method cannot give an accurate estimate of the energy of the defect state with respect to the valence band edge since the two are treated at a different level of theory.
A semi-empirical DFT + U approach has been used to estimate the energy of the defect state. There, a penalty is added to inhibit fractional occupation of atomic orbitals and, thereby, stabilizing localized states on atoms [17]. By tuning the U parameter to 7.0 eV, a localized hole was produced 1.1 eV above the valence band. A larger value of the U parameter would presumably shift the defect state even higher in energy. But, a significant correction is not made to the energy of the valence band and the band gap obtained from DFT + U calculations using a U value of 7.0 eV is only 6.5 eV [9].
We present here results of variational, self-consistent calculation using the Perdew–Zunger SIC applied equally to all the valence electrons in the system. The electronic structure as well as the atomic structure is analyzed and found to be in close agreement with the experimental estimates, while calculations with commonly used GGA (PBE, PW91) and hybrid (HSE) functionals are found to give results that are not consistent with the experimental results. In the following section, section 2, the SIC and its implementation are discussed. Section 3 describes the simulated system and in section 4 the results are presented. The article concludes with a discussion and summary in section 5.
2. Self-interaction correction
In KS-DFT [1], the energy of the ground state of an electronic system is estimated as a functional of the total electron density for each spin,  and
and 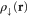 , as
, as
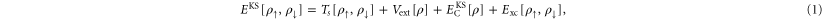
where  . Here, Ts is the kinetic energy of an independent electron reference system having the same electron density as the real system, Vext is the external potential representing the interaction of the electrons with the nuclei,
. Here, Ts is the kinetic energy of an independent electron reference system having the same electron density as the real system, Vext is the external potential representing the interaction of the electrons with the nuclei, 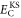 is an estimate of the Coulomb repulsion between the electrons, and Exc is the exchange and correlation energy. While a set of orthonormal orbitals is introduced in order to obtain a better estimate of the kinetic energy, the rest of the terms in the functional involve just the total electron density of each spin component. The total energy only depends on the space spanned by the orbitals i.e. the energy is invariant to unitary transformations of the orbitals. A mathematically convenient choice of orbitals can be made so as to diagonalize the orthonormalization constraint matrix and this set of orbitals is referred to as the Kohn–Sham orbitals.
is an estimate of the Coulomb repulsion between the electrons, and Exc is the exchange and correlation energy. While a set of orthonormal orbitals is introduced in order to obtain a better estimate of the kinetic energy, the rest of the terms in the functional involve just the total electron density of each spin component. The total energy only depends on the space spanned by the orbitals i.e. the energy is invariant to unitary transformations of the orbitals. A mathematically convenient choice of orbitals can be made so as to diagonalize the orthonormalization constraint matrix and this set of orbitals is referred to as the Kohn–Sham orbitals.
The electron–electron Coulomb repulsion is estimated in KS-DFT from the total electron density as

Written in terms of orbital densities, the total electron density is  , where
, where  is the density associated with orbital m with spin σ, and
is the density associated with orbital m with spin σ, and  can be expressed as
can be expressed as
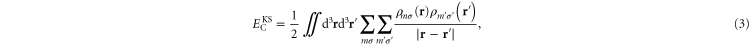
where the double sum includes the diagonal, self-interaction terms
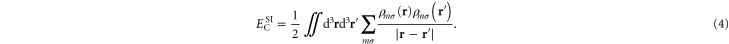
These diagonal terms represent Coulomb interaction of the orbital densities with themselves. This is the Coulomb part of the so-called self-interaction error in KS-DFT. The term  is often referred to as the 'Hartree energy', even though Hartree in his early calculations of electronic structure of atoms did not include the diagonal, self-interaction terms [18].
is often referred to as the 'Hartree energy', even though Hartree in his early calculations of electronic structure of atoms did not include the diagonal, self-interaction terms [18].
One of the tasks of the ![${E}_{\mathrm{xc}}[{\rho }_{\uparrow },{\rho }_{\downarrow }]$](https://content.cld.iop.org/journals/1367-2630/17/8/083006/revision1/njp517597ieqn9.gif) term in the KS-DFT functional is to cancel out these unphysical self-interaction terms in the estimate of the electron–electron Coulomb energy. Such a cancellation does occur in HF theory where exchange is calculated exactly. However, functionals developed for KS-DFT typically only give partial cancellation and, therefore, include a self-interaction error which is the source of several inaccuracies in results obtained from such calculations, in particular the destabilization of localized electronic states. The more localized an orbital is, the larger the repulsive self-interaction Coulomb energy is and, thereby, an artificial tendency towards delocalization.
term in the KS-DFT functional is to cancel out these unphysical self-interaction terms in the estimate of the electron–electron Coulomb energy. Such a cancellation does occur in HF theory where exchange is calculated exactly. However, functionals developed for KS-DFT typically only give partial cancellation and, therefore, include a self-interaction error which is the source of several inaccuracies in results obtained from such calculations, in particular the destabilization of localized electronic states. The more localized an orbital is, the larger the repulsive self-interaction Coulomb energy is and, thereby, an artificial tendency towards delocalization.
Perdew and Zunger proposed a procedure where a KS-DFT functional (originally the LDA) is corrected by explicitly subtracting an orbital based estimate of the self-interaction [11]. The corrected energy functional, ESIC, is
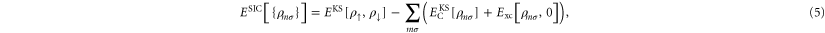
where the spin density for spin component σ is  . This correction procedure cancels out the diagonal terms in
. This correction procedure cancels out the diagonal terms in  and gives a self-interaction free functional for one-electron systems where Exc vanishes, but for many-electron systems this orbital based estimate of the self-interaction in
and gives a self-interaction free functional for one-electron systems where Exc vanishes, but for many-electron systems this orbital based estimate of the self-interaction in ![${E}_{\mathrm{xc}}[{\rho }_{\uparrow },{\rho }_{\downarrow }]$](https://content.cld.iop.org/journals/1367-2630/17/8/083006/revision1/njp517597ieqn12.gif) is only approximate. Unlike a KS-DFT functional, the total energy given by ESIC depends on the orbital densities,
is only approximate. Unlike a KS-DFT functional, the total energy given by ESIC depends on the orbital densities, 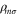 . Because of this, the total energy is not unitary invariant and the variational minimization of the energy is mathematically more challenging than for KS-DFT. No longer can a convenient linear combination be chosen for the orbitals and a new inner loop needs to be added to the self-consistency procedure to find the set of optimal orbitals. The variational minimization is, therefore, more challenging. As a result, most calculations involving some form of SIC have not been variational and in many cases not even self-consistent. Rather, the PZ-SIC has mostly been applied only to selected electrons (d- and f-electrons, or only unpaired electron), and in many cases assuming a priori some form for the optimal orbitals (Foster-Boys or Wannier localized orbitals), applied perturbatively without correcting the electron density, etc For a recent review of PZ-SIC calculations, see [19].
. Because of this, the total energy is not unitary invariant and the variational minimization of the energy is mathematically more challenging than for KS-DFT. No longer can a convenient linear combination be chosen for the orbitals and a new inner loop needs to be added to the self-consistency procedure to find the set of optimal orbitals. The variational minimization is, therefore, more challenging. As a result, most calculations involving some form of SIC have not been variational and in many cases not even self-consistent. Rather, the PZ-SIC has mostly been applied only to selected electrons (d- and f-electrons, or only unpaired electron), and in many cases assuming a priori some form for the optimal orbitals (Foster-Boys or Wannier localized orbitals), applied perturbatively without correcting the electron density, etc For a recent review of PZ-SIC calculations, see [19].
The present calculations make use of a variational, self-consistent implementation of PZ-SIC applied equally to all occupied orbitals. The method has been described elsewhere [21, 22] and will only be reviewed here briefly. Two orthonormal basis sets are used in the variational minimization of the energy. The first set consists of the optimal orbitals 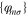 that minimize the self-interaction corrected energy functional, equation (5), and define the SIC potential
that minimize the self-interaction corrected energy functional, equation (5), and define the SIC potential

which enters the Hamiltonian as shown below. The second set consists of canonical orbitals 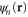 that are eigenfunctions of the Hamiltonian operator
that are eigenfunctions of the Hamiltonian operator
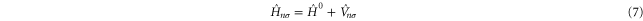
which is now comprised of a part  that is unitary invariant and an orbital density dependent term
that is unitary invariant and an orbital density dependent term 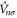 . The
. The 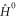 Hamiltonian is of KS-DFT form
Hamiltonian is of KS-DFT form

and depends only on the total electron density for each spin component ![$[{\rho }_{\uparrow },{\rho }_{\downarrow }]$](https://content.cld.iop.org/journals/1367-2630/17/8/083006/revision1/njp517597ieqn19.gif) , while the orbital density dependent part
, while the orbital density dependent part 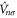 is defined by the SIC potential
is defined by the SIC potential 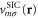 of the optimal orbitals as
of the optimal orbitals as
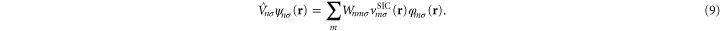
The matrix,  , gives the unitary transformation relating the two basis sets
, gives the unitary transformation relating the two basis sets
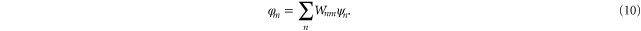
In order to minimize ESIC, an iterative procedure is followed where the eigenvalue problem

is solved and a unitary optimization [21] carried out to find the  that minimizes the energy. It has recently been realized that it is important to allow the orbitals be complex valued functions [23, 24].
that minimizes the energy. It has recently been realized that it is important to allow the orbitals be complex valued functions [23, 24].
Previous calculations of molecules and solids have shown that the accuracy of ESIC depends strongly on the KS-DFT functional it is applied to. While the correction is too small when applied to LDA, it is too large when applied to the PBE [7] and PW91 [25] functionals, as judged from atomization energy of molecules and band gaps [24, 26]. Ideally, a new exchange enhancement factor in the generalized gradient functional form should be developed for use with PS-SIC, that has a weaker enhancement factor than PBE or PW91 [27]. Here, a scaling with a factor of 1/2 will be used as has been justified based on the adiabatic connection formula and has been shown to work well for a wide range of properties and various different types of systems [24, 26]

We choose to use the PW91 functional rather than the PBE functional because the exchange enhancement factor goes to zero for large values of the reduced gradient. Since the corrected energy functional depends on orbital densities which have nodal planes, the reduced gradient of the orbital densities can become large even if the total electron density only has a small reduced gradient.
While variational, self-consistent calculations of  using complex optimal orbitals have been used to study molecules and even clusters of molecules [24, 28, 29], the present work represents the first application of this implementation to a defect in an extended solid.
using complex optimal orbitals have been used to study molecules and even clusters of molecules [24, 28, 29], the present work represents the first application of this implementation to a defect in an extended solid.
3. Methodology
The calculations were performed using a 72 atom cell subject to periodic boundary conditions. Only the gamma point for this extended cell was included in the k-point sampling. For the perfect α-SiO2 crystal, optimization of the lattice constants using the SIC-PW91 functional gave a = b = 4.972 Å and c = 5.473 Å which is in good agreement with measurements, the former being 1.19% and the latter 1.08% larger than experimental values [30]. Without the SIC, the PW91 functional gives lattice constants that are 1.43% and 2.36% larger than the experiment. The calculations were performed with a real space grid with a spacing of 0.2 Å, and an orthogonal cell of size 9.94 Å × 8.61 Å × 10.93 Å using the GPAW software [31]. The cell size was not changed after substituting one of the Si-atoms with an Al-atom.
The PAW method was used to represent the ion core [32]. The optimal orbitals are then written as
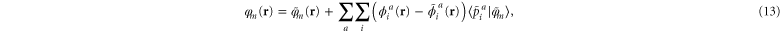
where the smooth projector function 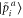 determines the expansion coefficients for the orbitals inside an augmentation sphere around each atom a. The smooth optimal orbital
determines the expansion coefficients for the orbitals inside an augmentation sphere around each atom a. The smooth optimal orbital 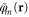 is given by a rotation of the smooth canonical orbitals through the transformation
is given by a rotation of the smooth canonical orbitals through the transformation  , and the same goes for the projections
, and the same goes for the projections 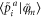 . A more detailed description of the PAW implementation for SIC calculations is given elsewhere [33].
. A more detailed description of the PAW implementation for SIC calculations is given elsewhere [33].
The PZ-SIC calculations were started by constructing first highly localized orbitals. This is accomplished by including initially only the Coulomb term in the SIC. Then, the contribution of Exc is gradually increased. The reason is that highly delocalized orbitals can also represent a local minimum for the ESIC functional when applied to periodic systems. In order to converge on the global minimum corresponding to localized orbitals, the iterative self-consistency calculation needs to be started with sufficiently localized orbitals [33].
For comparison with the PW91 and SIC-PW91 results, calculations using the HSE hybrid functional [34] were carried out using the VASP software [35].
4. Results
The band gap estimated from the calculated eigenvalues of the perfect α-SiO2 crystal is 8.87 eV, in good agreement with the experimental measurements [36]. The gap increases when the SIC is applied mainly because of a lowering of the valence band edge. The energy of valence band orbitals is too high in KS-DFT because of the repulsive self-interaction error. Similar accuracy of band gap estimates has been obtained in SIC calculations for several semiconductors and insulators [26].
The properties of an Al-doped crystal were calculated by replacing one of the Si-atoms with an Al-atom and minimizing the energy given by the  functional with respect to both orbitals and atomic structure. The resulting atomic structure and spin density are shown in figure 1. The spin density,
functional with respect to both orbitals and atomic structure. The resulting atomic structure and spin density are shown in figure 1. The spin density, 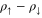 , is highly localized on a single O-atom and the distance between that atom and the Al-atom becomes 11% longer than the short Al–O distances, as listed in table 1. This is in good agreement with the EPR experiments from which the lengthening has been estimated to be 12% [4, 5]. Embedded HF calculations using large clusters have given slightly larger value, 14% [5]. Bader analysis of the spin density [37, 38] gives integrated spin of 0.77 unpaired electrons on the O-atom, showing that the hole is mainly localized on this single atom. The shape of the spin density shows that the hole largely corresponds to a p-orbital. As has been discussed in detail previously, GGA functionals give a delocalized hole spread over all four O-atoms neighboring the Al-atom, the PW91 functional being no exception, as shown in figure 1 and listed in table 1.
, is highly localized on a single O-atom and the distance between that atom and the Al-atom becomes 11% longer than the short Al–O distances, as listed in table 1. This is in good agreement with the EPR experiments from which the lengthening has been estimated to be 12% [4, 5]. Embedded HF calculations using large clusters have given slightly larger value, 14% [5]. Bader analysis of the spin density [37, 38] gives integrated spin of 0.77 unpaired electrons on the O-atom, showing that the hole is mainly localized on this single atom. The shape of the spin density shows that the hole largely corresponds to a p-orbital. As has been discussed in detail previously, GGA functionals give a delocalized hole spread over all four O-atoms neighboring the Al-atom, the PW91 functional being no exception, as shown in figure 1 and listed in table 1.
Figure 1. (a) The simulation cell used in the calculations, subject to periodic boundary conditions, and the spin density obtained in a PZ-SIC calculation with the PW91 functional rendered at a value that is 10% of the maximum value. A close-up of the Al-atom and its neighbours comparing KS-DFT calculations with the PW91 functional in (b) where the hole is delocalized over all four neighbouring oxygen atoms, and (c) the results of PZ-SIC calculations with the PW91 functional, showing the hole sitting on a single O-atom.
Download figure:
Standard image High-resolution imageTable 1. Distance (in Å) from the Al-atom to its four O-atom neighbors calculated with the PW91 functional, the HSE functional and the PZ-SIC applied to the PW91 functional. The PW91 calculations distribute the hole nearly evenly over the four O-atom neighbors and all four Al–O bonds are lengthened. The PZ-SIC calculation localizes the hole on one of the O-atoms and lengthens that Al–O bond by 11%, in good agreement with experimental EPR estimates [4, 5]. The HSE functional gives intermediate results, with two Al–O bonds lengthened.
| Bond | PW91 | HSE | PW91-SIC |
|---|---|---|---|
| Al–Oa | 1.73 | 1.80 | 1.88 |
| Al–Ob | 1.73 | 1.72 | 1.71 |
| Al–Oc | 1.73 | 1.69 | 1.70 |
| Al–Od | 1.73 | 1.69 | 1.70 |
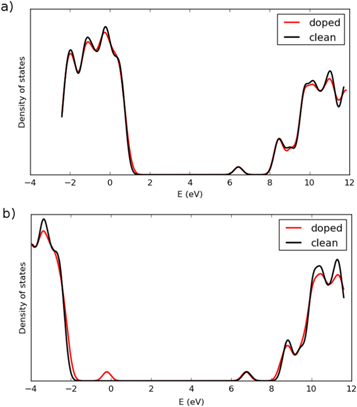
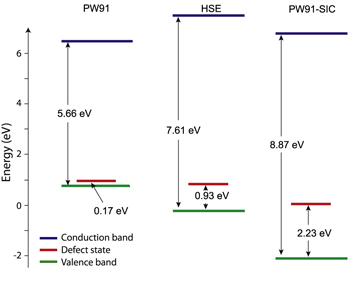
The calculated DOS is shown in figure 2. After applying some broadening, the results of the PW91 calculation do not show a distinct peak corresponding to the defect state in the band gap. Furthermore, the energy difference between the valence and conduction band edges is only 5.7 eV, much smaller than the experimentally estimated band gap. When PZ-SIC is applied, however, a band gap of 8.87 eV is obtained, in good agreement with measured value of 9 eV [36]. The DOS is quite similar in shape to that obtained with GW calculations [39], where the band gap was estimated to be 9.4 eV. In the SIC calculation, a peak corresponding to the defect state appears 2.2 eV above the valence band edge. This is in good correspondence with the optical absorption experiments which gave an estimate of 1.96 eV [16]. Without the SIC, the valence band is too high in energy and the defect state calculated with the PW91 functional is only 0.17 eV above the valence band edge, as shown in figure 3.
Figure 2. Calculated density of states for clean and Al-atom doped α-SiO2. (a) Using PW91 functional. (b) Using PZ-SIC applied to PW91. The valence band is too high in the PW91 calculation because of the repulsive self-interaction and a distinct defect state corresponding to the electron hole is not seen. When the self-interaction correction is included, a large band gap is obtained, mainly because of a lowering of the valence band. A distinct peak due to the localized hole associated with the Al-atom defect appears.
Download figure:
Standard image High-resolution imageFigure 3. Orbital energy values of canonical orbitals calculated with the PW91 functional, the HSE hybrid functional and PZ-SIC applied to PW91. The valence band is too high in the PW91 calculation because of repulsive self-interaction. The defect state corresponding to the electron hole is only slightly above the valence band edge and the spin density is delocalized over all four O atoms neighboring the Al atom (as shown in figure 1(b)). When the self-interaction correction is included, the energy of the valence band is lowered and a band gap of 8.87 eV is obtained in good agreement with measurements [36]. A defect state 2.2 eV above the valence band edge is obtained, which corresponds well with an estimate of 1.96 eV from optical measurements [16]. The HSE hybrid functional both lowers the valence band edge and raises the conduction band edge as compared with the PW91 results, but the band gap is still significantly smaller than the experimental value. Furthermore, the defect state is only 0.93 eV over the valence band edge.
Download figure:
Standard image High-resolution imageFigure 3 shows the calculated electronic energy levels using the HSE hybrid functional, which contains 20% exact exchange, as well as the PW91 and PZ-SIC results. The inclusion of exact exchange both lowers the valence band edge and raises the conduction band edge as compared with the PW91 results, but the band gap obtained, 7.61 eV, is still significantly smaller than the experimental value. Furthermore, the defect state is only 0.93 eV over the valence band edge, significantly lower than the experimental estimate. The spin density obtained from the HSE functional is delocalized over two of the O-atoms neighboring the Al-atom. The corresponding Al–O bonds are 1.72 and 1.80 Å while the remaining two are 1.69 Å (see table 1). This is quite consistent with results of previously reported calculations of small clusters using the B3LYP hybrid functional [10]. In order to increase the band gap sufficiently and move the defect energy level high enough above the valence band edge, a larger fraction of exact exchange would need to be included in order to get agreement with the experimental results on this system. For other systems, 20% exact exchange can work well. This mixing factor is increasingly being treated as a free parameter in hybrid calculations, making the approach semi-empirical.
5. Discussion
The calculations presented here, as well as other calculations using the same approach [24, 26], illustrate that an orbital density dependent form of the energy functional, of which the PZ-SIC is an example, can significantly improve the accuracy of density functional calculations. The electron hole introduced by the Al-dopant atom is properly localized, the band gap is estimated accurately from the orbital energies and the energy of the defect state above the valence band edge is consistent with optical absorption experiments. Elimination of the self-interaction terms in the electron–electron Coulomb interaction is clearly an important improvement over the KS-DFT functional form. Interestingly, the early calculations of Hartree [18] also excluded these self-interaction terms, but the interaction was calculated using canonical orbitals. In the variational, self-consistent implementation of PZ-SIC used here, the Coulomb interaction between the electrons is estimated using optimal orbitals, which in the present case resemble sp3 hybrid orbitals rather than the more delocalized canonical orbitals. The optimization of the orbital densities introduces additional computational effort, but has the advantage that meaningful, energy optimal orbitals are obtained from the calculation. The scaling of the computational effort of PZ-SIC calculations is the same as for GGA functional calculations, i.e. it scales as the system size cubed, but there is a large prefactor due to the fact that an effective potential needs to be evaluated for each orbital. These calculations can, however, readily be carried out in parallel and the wall clock time can, thereby, be reduced quite easily by using a larger number of processors.
The exchange and correlation term of the PW91 functional is, however, not optimal for PZ-SIC. A smaller exchange enhancement factor can be used [27], bringing the exchange estimate closer to LDA, as illustrated by the fact that PZ-SIC gives an overcorrection when applied to PBE while it is an undercorrection when applied to LDA [24]. By developing an optimal exchange enhancement factor tailored to PZ-SIC, the scaling factor of 1/2 used here as well as in previous calculations based on the PBE functional [24, 26] could be dropped. The promising results that have been obtained here with the variational, self-consistent implementation of PZ-SIC show that this orbital density dependent functional form can give highly accurate results for both energetics as well as structure, the first time this is achieved for the Al–SiO2 system.
Acknowledgments
This work was supported by the Icelandic Research Fund, Nordic Energy Research and the Academy of Finland (grants 263294 and 278260). The calculations were carried on the Nordic High Performance Computer (NHPC) in Iceland.