Abstract
The frequencies of ambient vibrations are often low (below 30 Hz). A broadband (3 dB bandwidth is larger than 10 Hz at an acceleration amplitude of 9.81 m s−2) vibration based energy harvester is proposed for transducing mechanical energy at such low frequencies into electrical energy. The mechanical setup converts low frequency mechanical vibrations into high frequency resonance oscillations of the transducer. This conversion is done by mechanical impacts on two mechanical stoppers. The originality of the presented design is that both low-frequency and high-frequency oscillators are permanently mechanically coupled. In the equivalent mechanical circuit, this coupling is achieved by connecting the ends of the stiff spring to both seismic masses, whereas one seismic mass (collison member) is also attached to the soft spring used as the constitutive element of a low-frequency oscillator. Further, both mechanical oscillators are not realized as conventional cantilever beams. In particular, the high frequency oscillator with the natural frequency of 340 Hz is a disc-shaped diaphragm with attached piezoelectric elements and a seismic mass. It is shown that it is possible to convert mechanical vibrations with acceleration amplitude of 9.81 m s−2 in the region between approximately 7 and 25 Hz into electrical power larger than 0.1 mW with the maximum value of 0.8 mW. A simplified mathematical model based on piecewise linear coupled oscillators shows good agreement with experimental results. The ways to enhance the performance of the harvester and improve agreement with experiments are discussed.
Export citation and abstract BibTeX RIS
1. Introduction
Vibration energy harvesters (EHs) draw electric power from ambient vibrations. The crucial element of such an EH is an electromechanical transducer, e.g. a piezoelectric (PE) element exposed to ambient mechanical oscillations. The popularity of the PE transduction mechanism is explained by the larger energy density as compared to the alternative effects [1–3]. If ambient vibrations are strong, occur regularly and oscillations of a transducer are not severely damped, considerable alternating voltages can be generated [1, 2, 4]. The generated electrical energy should supply an electronic device that is wire-connected to the terminals of the transducer [5–7]. Unfortunately, the frequency of ambient mechanical vibrations, is often low (<30 Hz). This introduces a challenge for conventional PE EHs relying on PE ceramic materials and simple geometrical designs (cantilever beams and discs) [8]. A PE vibration EH generates its maximum power at its resonance frequency, where deformation of the PE layer is the largest. PE ceramics are usually selected because their PE properties are superior to polymers and composite materials [8]. The low frequency range differs considerably from the eigenfrequencies of typical configurations of PE ceramic transducers, thus preventing resonant oscillations thereof. This is due to relatively high elastic moduli of PE ceramic materials [8]. For example, the Young's modulus of lead zirconate titanate, PZT, is approximately two orders of magnitude larger than that of the polyvinylidene fluoride (≈7 × 1010 Pa versus ≈109 Pa). To be electromechanically effective, the PE resonant circuit must have a high quality factor [5, 9, 10]. This implies the narrow band behavior of a single circuit, because away from the resonant frequency, the power generation drops dramatically and is too low to be exploited [11]. To overcome this issue, Soliman et al proposed to replace a linear oscillator with a piecewise linear oscillator and utilize the frequency-range broadening upon impacts [10, 12]. Comprehensive reviews on available technologies and up-to-date advances in broadband vibration-based energy harvesting were published in 2010 by Tang et al and by Twiefel et al in 2013 [13, 14]. Since then, alternative concepts for broadband vibration energy harvesting employing magnetoelectric transduction mechanism [15, 16], triboelectric effect [17] or addition of a resonant electric circuit to the magnetic induction harvester [18] have been reported. The latter approach [18] can be considered as generalization of the earlier work [19].
An obvious solution for increasing the bandwidth is to use several PE cantilevers, whose mechanical resonance frequencies are distributed over the desired band in such a way that at any particular frequency there is at least one circuit operating close to its resonance frequency. The most general approach for designing an optimized mechanical bandpass filter has been provided by Shahruz [20, 21], who developed a mathematical model where the eigenfrequency of a single beam is adjusted both by the proof mass and the beam stiffness leading to the required dimensions of the beam. Xue et al [22] included into the calculations the PE properties of the beam elements and the electrical circuitry. It was shown that the frequency behavior of the entire system can be influenced by connecting the PE bimorphs either in series or parallel. Ferrari et al [23] combined three commercially available PE bimorph cantilevers into a single array improving the effectiveness of the overall energy conversion across a wideband frequency spectrum over the case of a single converter. The tuning of the resonant frequency was achieved by varying the tip mass. A broadband PE MEMS EH for low-frequency (≈30–47 Hz) vibrations was developed by Liu et al [24]. Their device consisted of several beams with different stiffness and the same tip mass. Al-Ashtari et al [3] proposed to detune the eigenfrequency of individual standard PE bimorphs by means of magnetic force acting on the small magnet positioned at the beams tip. By changing the magnetic force, the effective stiffness of the beam can be controlled.
In general, the oscillation frequency of the transducer stimulated by ambient mechanical vibrations may be low and the amplitude of transducer vibrations may be small, so that the AC power output of the transducer is not sufficient for supplying an electronic device. To reach the large amplitude of high-frequency vibrations of the transducer exposed to ambient low-frequency mechanical impulses, several techniques were proposed. Roundy [25] described a PE harvester comprising a PE beam that carries an additional weight on its free end for shifting the natural frequency of the beam towards lower frequencies. However, the disclosed technique achieves high efficiency only in a narrow operation region in the vicinity of the eigenfrequency. Gu and Livermore [26] investigated a PE EH with a low-frequency resonant circuit that impacts a high frequency energy harvesting resonant circuit, resulting in energy harvesting that occurs predominantly at the system's coupled vibration frequency. However, this arrangement is prone to mechanical wear out due to the friction between the low frequency resonator and the high frequency resonator. Liu et al [27] described a PE EH where the oscillation amplitude of a PE beam is limited by mechanical stoppers, thereby increasing the energy conversion bandwidth of the system. However, limitation of the oscillations of the PE beam by a stopper also decreases the power output. The latter two designs [26, 27] belong to the class of frequency up-conversion techniques because they rely on excitation of high-frequency oscillations in an electromechanical transducer by low-frequency mechanical impacts [28, 29] or non-impact magnetic interactions [30, 31]. The cited [26, 27] provide an extensive overview of up-conversion EH technologies.
Figure 1 compares schematically the mechanical part of the transducer proposed in this paper with previously published up-conversion concepts. Two mechanical oscillators (represented by spring k1, seismic mass (collision member) m1 and spring k2, seismic mass m2, respectively) are permanently connected to each other (see figure 1(a)). In previous designs, the coupling occurred only by collision of the two systems (see figure 1(b)). Kinetic energy of the mass m2 belonging to the high-frequency oscillator 2 is then transduced to electrical energy [26, 27, 32]. Additionally, kinetic energy of the mass m1 belonging to the low-frequency oscillator 1 can be converted to electric energy [27]. It is implied that (k1/m1) ≪ (k2/m2), what can be easily achieved if k1 ≪ k2 and m1 ≈ m2. Let us consider a number of simplified cases where the operation principle of the proposed EH can be easily understood. The masses of the spring elements are assumed to be negligibly small. For the sake of simplicity, the mass of the collision member m1 between the springs is first assumed to be negligible in comparison with the seismic mass m2, this limitation is not essential and will be overcome below. If two mechanical stoppers were not present, the resonance frequency of the entire (first) oscillator would be

If the mechanical stoppers are present and the collision member impacts on a stopper, the second oscillator comprising the second spring with the spring constant k2 and the mass m2 has the eigenfrequency

If k2 ≫ k1,
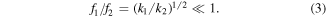
If the spring constant k2 is so large that the relative movement of masses m1 and m2 can be neglected in comparison with the movement of the mass m1 with respect to the base (casing), the eigenfrequency f1 of the first oscillator comprising the totality of mass elements m1 + m2 attached to the first spring would be
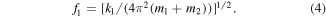
The eigenfrequency of the second oscillator is expressed by the same formula (2).
Figure 1. Functional principle of frequency up converting vibration energy harvesting. Comparsion of the present concept (a, left) with previously described concepts (b, right).
Download figure:
Standard image High-resolution imageObviously, the inequality

is fulfilled. Each impact of the collision member m1 on one of the mechanical stoppers excite oscillator 2. If the oscillator 2 is an electromechanical transducer, it vibrates at its eigenfrequency f2 allowing one to convert the mechanical kinetic energy into electric energy with the highest efficiency.
A mechanical design similar to figure 1(a) has been recently described by Liu et al [33], who used two cantilever beams, single mechanical stopper and scavenged energy from the low-frequency oscillator. Xiao et al analyzed multiple connected PE vibration EHs with close natural oscillation frequencies without mechanical stoppers present [34]. As far as particular realizations of EHs are concerned, two cantilevers were conventionally employed to convert low-frequency mechanical impulses (sub-system 1 in figure 1(b)) into high-frequency impulses (sub-system 2). However, if the acceleration amplitude of the excitation base is fixed, minimum usable frequency of a cantilever beam is limited at lower frequencies by the deflection limit of the beam. If the beam deflection is too large, the cantilever can be destroyed. Proposed realization of the EH does not employ cantilever beams. The design presented below contains a high frequency PE transducer in the form of a membrane and a low frequency mechanical spring member for excitation. With this mechanical set up, effective vibration energy harvesting can be achieved even at frequencies below 10 Hz.
The paper is organized as follows. The following section describes mechanical design of the harvester. The mathematical model of the harvester and its numerical solution are presented in section 3. Simulation results are compared with experiments in section 4. In section 5, the emphasis is made on the frequency dependences of the short-circuit output voltage and the output power at optimum resistive load. Conclusions are drawn in the final section.
2. Mechanical design
Figure 2 shows the schematic view of an experimental setup for converting low-frequency ambient mechanical impulses into high-frequency vibrations. Figure 3 presents the exploded view of the harvester. The top view of the brass diaphragm with the attached PE elements is depicted in figure 4. In figures 2–4, the same constitutive elements of the EH are given with the same color.
Figure 2. Schematic view of the mechanical design of the harvester. The drawing is not to scale.
Download figure:
Standard image High-resolution imageFigure 3. Exploded view of the harvester.
Download figure:
Standard image High-resolution imageFigure 4. Top view of the PZT element on the diaphragm. The geometrical dimensions and the thickness t are given.
Download figure:
Standard image High-resolution imageTo explain the operation principle, the constitutive elements are referred below to figure 1(a).
The mechanical setup comprises a spring mechanism (corresponding to spring k1 in figure 1(a)) which is comprised of a plurality of spring elements. One end of each spring is connected to the base while the other end is connected to the diaphragm holder (see figure 3). The holder supports a brass diaphragm having a disc-shaped form with the through hole in the middle. The diaphragm holder corresponds to the collision member m1 in figure 1(a). The brass diaphragm also plays the role of the second spring k2. It is seen that both spring elements are connected in series. The metallic diaphragm has two PE PZT rings glued to it and an additional seismic mass positioned in the center of the diaphragm. This additional mass serves to increase the amplitude of oscillations of the second oscillator. This seismic mass together with the fixing screw can be considered as the embodiment of the mass m2. An electromechanical transducer is a PE bimorph connected in series. The movement of the collision member is restricted by an upper impact member (lid) and a lower impact member (base), which are arranged around the collision member. The base and the lid are made of aluminum. Δ denotes the clearance of rattling space. In the present setup Δ = 1 mm. The holder (collision member) with the diaphragm can move by the distance Δ from its equilibrium position upwards or downwards without impact on the lid or the base. Figure 5 presents the photograph of the mechanical set up of the assembled harvester.
Figure 5. Photograph of the mechanical setup.
Download figure:
Standard image High-resolution image3. Mathematical model
The equivalent mechanical circuit of the harvester is presented schematically in figure 6. The vibration EH is phenomenologically described as the system of two coupled mechanical oscillators.
Figure 6. Picewise linear model of the system.
Download figure:
Standard image High-resolution imageIt consists of the following components: the spring-mass damped system k1, m1 and c1, where c1 is the viscous damping coefficient of the first oscillator, represents the mechanical components of the low-frequency oscillator, e.g. the spring mechanism and the plurality of masses attached to it. The high-frequency oscillator which utilizes the elasticity of the diaphragm element and the inertia of the seismic mass, is also represented by the spring-mass damped system k2, m2 and c2, where c2 is the viscous damping coefficient of the second oscillator. Both damped oscillators are connected in series. Further component is the plurality of mechanical stoppers, which can be simulated as a parallel spring-dashpot system (k3 and c3, respectively) [35]. This complete system is a piecewise linear system where different cases are distinguished. The first case is the free oscillation of the mass m1 characterized by the coordinate x1 without collision with a stopper. If the relative deflection of m1 with respect to the base (housing) exceeds a particular value Δ, the mass m1 collides with the upper or lower stopper. In this case, the spring k3 and the dashpot c3 of the stopper come into play. The base excitation of the entire system is assumed to be a sinusoidal function of time y(t) = Y0sin(2πft), where f is the excitation frequency. Obviously, the amplitude A0 of the base acceleration [ = −A0sin(2πft)] is equal to (2πf)2Y0.
= −A0sin(2πft)] is equal to (2πf)2Y0.
The coordinate x1 describes the position of the collision member m1 and the coordinate x2 gives the deflection of the seismic mass m2. The coordinates y, x1, x2 are measured with respect to the resting laboratory coordinate system. Their zero values correspond to those positions of the constitutive elements when the entire system is not excited (Y0 = 0), the elements m1 and m2 are in their equilibrium positions and do not move. The arrows in figure 6 designate the positive coordinate direction.
For the mathematical description of the system, the deflection of the mass m1 is divided into three regions. The first region corresponds to the collision with the upper stopper, second region describes the free oscillation without collisions and the third part specifies the collision with the lower stopper. These three specific cases can be described by the following differential equations:
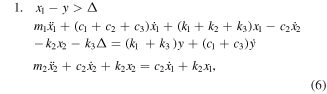
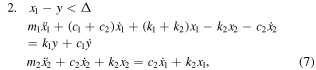
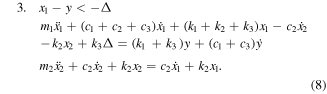
These equations are similar to those derived by Narimani et al for a pieceweise linear vibration isolator [36].
For simulations, mechanical parameters of the equivalent circuit were determined empirically. They are given in table 1.
Table 1. Mechanical parameters.
| Parameter | Value |
|---|---|
| k1 | 88.4 N m−1 |
| c1 | 0.0266 kg s−1 |
| m1 | 0.013 kg |
| k2 | 15 884 N m−1 |
| c2 | 0.26 kg s−1 |
| m2 | 0.0034 kg |
| k3 | 28 000 N m−1 |
| c3 | 27.0 kg s−1 |
The values of masses m1 and m2 were determined by weighing using precision scales (Kern PCB350, KERN and SOHN GmbH, Balingen, Germany). The seismic mass m1 comprised the brass diaphragm with the attached PE elements and the diaphragm holder. The mass m2 included the fixing screw. The corresponding spring constants k1 and k2 were then calculated from the experimentally determined natural frequencies of the low (4) and high-frequency (2) mechanical oscillators. The damping coefficients c1 and c2 were experimentally determined from the step response. The spring-dashpot parameters of the stoppers (k3, c3) were derived by fitting the simulated steady-state time dependences of  to experimental results. Notice that k1 ≪ k2 < k3, m2 < m1 and c1 ≪ c2 ≪ c3.
to experimental results. Notice that k1 ≪ k2 < k3, m2 < m1 and c1 ≪ c2 ≪ c3.
For numerical simulations, the system of equations (7)–(9) was supplemented by zero initial conditions:  The steady-state solutions were sought.
The steady-state solutions were sought.
4. Numerical solution
To solve piecewise linear differential equations of motion for the masses m1 and m2, commercially available MATLAB/Simulink software was used3 .
The Simulink model corresponds to the mathematical model in figure 6 and can be viewed in the supplementary information is available at stacks.iop.org/SMS/26/065021/mmedia. The numerical result for the motion of the mass m1 confirms the motion of the collision member between the two stoppers. The relative motion  of the mass m2 with respect to the collision member m1 corresponds to the deflection of the PZT disc. This movement can be transformed into electrical variables e.g. the output voltage by the electromechanical analogy [37]. The details can be found elsewhere [37–41]. It has been proven in earlier publications (see, e.g. [42, 43]) that clamped PE circular diaphragm can be modeled as a simple equivalent circuit with lumped elements. Despite achieved progress in theoretical analysis of PE circular diaphragms (see, e.g. [44]), calculation of these lumped elements from the geometry of the problem and material parameters still represents a challenge requiring advanced dynamic plate vibration theory or finite-element calculations [42]. However, experimental determination of lumped parameters is simple and straightforward as described in the preceding section and in the literature [37–41]. It will be shown below that simplified lumped element model gives in our case good agreement with experimental results.
of the mass m2 with respect to the collision member m1 corresponds to the deflection of the PZT disc. This movement can be transformed into electrical variables e.g. the output voltage by the electromechanical analogy [37]. The details can be found elsewhere [37–41]. It has been proven in earlier publications (see, e.g. [42, 43]) that clamped PE circular diaphragm can be modeled as a simple equivalent circuit with lumped elements. Despite achieved progress in theoretical analysis of PE circular diaphragms (see, e.g. [44]), calculation of these lumped elements from the geometry of the problem and material parameters still represents a challenge requiring advanced dynamic plate vibration theory or finite-element calculations [42]. However, experimental determination of lumped parameters is simple and straightforward as described in the preceding section and in the literature [37–41]. It will be shown below that simplified lumped element model gives in our case good agreement with experimental results.
In our Simulink model, the relative velocity  can be transformed into the output current of the PE transducer by an electromechanical transformer with the coupling factor α of 0.0085 A s m−1 (see figure 7). To simulate the output power of the PE transducer, the electromechanical transformer must be loaded by the total capacitance of the PE transducer CP = 32 nF connected in parallel to the load resistance RL. This parallel circuit has the following transfer function:
can be transformed into the output current of the PE transducer by an electromechanical transformer with the coupling factor α of 0.0085 A s m−1 (see figure 7). To simulate the output power of the PE transducer, the electromechanical transformer must be loaded by the total capacitance of the PE transducer CP = 32 nF connected in parallel to the load resistance RL. This parallel circuit has the following transfer function:
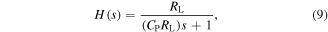
where s is the frequency parameter of the Laplace transform. With the help of the electromechanical analogy, the output voltage u(t) can determined directly from the solution to the differential equations of movement (6)–(8).
Figure 7. Electromechanical transformer.
Download figure:
Standard image High-resolution imageIn experiments, the harvester was driven by the shaker Modal Exciter 4826 manufactured by Brüel and Kjaer Sound and Vibration, Nærum, Denmark. As an example, figures 8 and 9 compare the steady-state time dependences of the open-circuit output voltage u0(t) and the coordinate of the collision member x1(t) obtained from simulation and experiment at the excitation frequency of 7 and 15 Hz, respectively. The open-circuit voltage u0(t) corresponds to u(t) if RL → ∞. The motion of the base y(t) and the collision member x1(t) is measured with the laser distance sensor ILD2300-100 from the company Micro-Epsilon, Ortenburg, Germany. The clearance Δ in the experiment and simulation was 1 mm. It can be seen that the peak output voltage of the PZT disc is roughly 15 V at both presented excitation frequencies (7 and 15 Hz). The double repetition frequency of the output voltage is caused by collisions with the upper and lower stoppers. After the collision, the output voltage oscillates at the eigenfrequency of about 340 Hz. The amplitude of the output voltage declines between the collisions. This process converts the low-frequency excitation into high-frequency oscillations of the PZT disc. At the higher excitation frequency of 15 Hz the output voltage declines less between the collisions, because the time between two collisions is smaller than the decay time.
Figure 8. Comparsion between the experimental measurments (left) and the numerical simulation (right) of the open-circuit voltage of the PE transducer (a), (b) and the displacement of the collision member (c), (d) obtained with the acceleration amplitude of 9.81 m s−2 and frequency of 7 Hz.
Download figure:
Standard image High-resolution imageFigure 9. Comparsion between the experimental measurments (left) and the numerical simulation (right) of the open-circuit voltage of the PE transducer (a), (b) and the displacement of the collision member (c), (d) obtained with the acceleration amplitude of 9.81 m s−2 and frequency of 15 Hz.
Download figure:
Standard image High-resolution imageTherefore, the root mean square (rms) output voltage is larger at 15 Hz than at 7 Hz as it is observed below in figure 11. Comparison between the simulation and the experiment shows very good results in the time domain. It can be seen that even fine specific features in temporal behavior of u0(t) and x1(t) are reproduced in the simulation. In particular, notice that x1(t) is not exactly a sinusoidal function of time but strongly resembles a triangle wave at the higher frequency of 15 Hz. In figures 8 and 9, the displacements x1(t) for the mass m1 in both 7 and 15 Hz cases are larger than the actual gaps between the stopper and the collision member. However, there is no discrepancy in the simulation or the experiment because the coordinate x1(t) is measured with respect to the resting laboratory coordinate system. The base is moving as well, i.e. y(t) is a function of time. The condition  determines the free movement of the collision member m1 between the stoppers (impact members).
determines the free movement of the collision member m1 between the stoppers (impact members).
5. Frequency dependencies
To determine the bandwidth of the developed EH, dependencies of the rms value of the open-circuit output voltage  and the electrical power Popt dissipated in the optimum load resistance RLopt = 16 kΩ on the excitation frequency f have been measured. T0 has been selected in such a way that the system was in a steady state. It has been experimentally verified that this optimum value of RL is valid for the entire frequency range of interest. As an example, figure 10 shows dependences of the average power Pavg on the resistance RL for the acceleration amplitude A0 = 9.81 m s−2 at excitation frequency f of 24 Hz and A0 = 5 m s−2 at excitation frequency f of 18 Hz. To calculate Pavg, the following equation was used:
and the electrical power Popt dissipated in the optimum load resistance RLopt = 16 kΩ on the excitation frequency f have been measured. T0 has been selected in such a way that the system was in a steady state. It has been experimentally verified that this optimum value of RL is valid for the entire frequency range of interest. As an example, figure 10 shows dependences of the average power Pavg on the resistance RL for the acceleration amplitude A0 = 9.81 m s−2 at excitation frequency f of 24 Hz and A0 = 5 m s−2 at excitation frequency f of 18 Hz. To calculate Pavg, the following equation was used:

To calculate the rms values, the averaging time interval T1 was about 30 periods of the sinusoidal function  for the experimental results and about 100 periods for the simulation. Popt is Pavg with RL = RLopt.
for the experimental results and about 100 periods for the simulation. Popt is Pavg with RL = RLopt.
Figure 10. Experimental determination of the optimal load resistance. Two cases are shown. The upper (blue) curve corresponds to A0 = 9.81 m s−2 and f = 24 Hz. The lower (red) curve is obtained with A0 = 5 m s−2 and f = 18 Hz.
Download figure:
Standard image High-resolution imageFigure 11 presents the dependencies U0(f) for different amplitudes A0 of the base acceleration. Figure 12 depicts the dependencies Popt(f) for different amplitudes A0 of the base acceleration. In general, it can be concluded that there is a semi-quantitative agreement between the simulation and experiment. Stronger vibrations or an increase in vibration frequency lead to more power output and higher output voltages since more mechanical energy is fed into the EH. The bandwidth of the harvester increases with growing amplitude of the excitation acceleration. The lower (≈5 Hz at A0 = 9.81 m s−2) and upper (≈25 Hz at A0 = 9.81 m s−2) onset frequencies, where the high-frequency oscillations of the PE transducer become appreciable, are determined by the bandwidth of the entire mechanical arrangement and the geometrical positions of the impact members. The growth of the electrical power Popt with the growing excitation frequency f can be at least partially attributed to the fact that with increasing frequency the collision member strikes the mechanical stoppers more often.
Figure 11. Comparsion between the experimental mesurments (left) and the simulation (right) of the frequency dependence of the open-circuit rms voltage.
Download figure:
Standard image High-resolution imageFigure 12. Comparsion between the experimental mesurments (left) and the simulation (right) of the frequency dependence of the output power at the optimum load of 16 kΩ.
Download figure:
Standard image High-resolution imageTable 2 compares the experimental and simulated values of bandwidth B for different values of A0. The bandwidth B is defined at fixed A0 as the frequency range where the output power Popt is above the half of its maximum value (see figure 12). Some discrepancies between simulations and measurements are observed. The simulations predict somewhat larger bandwidths as they are found in experiments. The lower frequency onset (≈5 Hz) is predicted rather well, there is good quantitative agreement with the increasing excitation frequency f but simulation predicts cessation of effective high-frequency transduction at lower frequency than detected in experiment. This is also an indication that there is significant retroactive effect of the load on the PE transducer at high excitation frequencies. The 3 dB bandwidth determined from the dependence U0(f) is smaller than B, what can be explained by additional losses introduced be the electrical resistive load. We believe that the observed differences between simulation and experiment can be partially attributed to nonlinearity of the electromechanical circuit which is more strongly expressed at higher excitation frequencies. Moreover, the variation of properties of home-made springs comprising a spring mechanism in figure 3 may lead to the broadening of frequency dependences. Figures 11 and 12 also present the experimental results for the up and down frequency sweeps. Similarly to previous works on PE EHs with mechanical stoppers, we observed some hysteresis in the output characteristics at higher boundary frequency for up and down frequency sweeps. For hardening springs, the bandwidth is wider for frequency up-sweeps [45]. In the presented design, the 'hardening' of the spring k1 effectively occurs upon impact on the mechanical stopper. However, in our case, this hysteresis is small (Δf is about 0.7 Hz what corresponds to roughly 6% of the resonance frequency (4) of the low-frequency oscillator). We did not observe the significant reduction of the hysteresis frequency width Δf width decreasing amplitude A0 what we also attribute to the variation of spring constants of three spring elements fabricated. In the simulation, the results for the up and down frequency sweeps are the same, because of the identical zero initial conditions for each frequency.
Table 2. Frequency bandwidth.
| A0 (m s−2) | B experiment (Hz) | B simulation (Hz) |
|---|---|---|
| 9.81 | 10.2 | 11.1 |
| 7 | 6.3 | 8.4 |
| 5 | 4.5 | 4.6 |
However, it should be emphasized that the qualitative behavior of the presented EH is well understood and predictive design on the basis of a simplified mathematical model is possible. It can be seen that the EH provides considerable output power (maximum is about 0.8 mW at A0 = 9.81 m s−2) over a wide region of low excitation frequencies.
6. Conclussion and outlook
In this paper, a new concept for low-frequency broadband EH with two mechanical stoppers is presented. The corresponding mathematical model is a piecewise linear system of two permanently coupled mechanical oscillators. The numerical solution and the experimental results compare well with each other and show very good agreement in the time domain. The mechanical design is presented and it is shown that it is possible to convert low frequency vibrations of the harvester's base into high frequency oscillations of a PE disc transducer in order to generate electrical energy in the low-frequency range of mechanical vibrations. In addition, presented concept allows one to generate electrical power over a wide bandwidth starting at few Hertz above the DC level.
Further improvements can be possibly achieved from the influence of the gap value Δ on the bandwidth. Figure 13 presents the calculations of the frequency dependence of the output power Popt with the given value of A0 = 9.81 m s−2 for different values of Δ. It can be expected that the reduction of distance Δ decreases the maximum output power but increases the bandwidth. This can be useful if the optimization of minimum power (worst-case scenario) is required for a particular application [46]. Moreover, the mathematical model can be enhanced by including more realistic nonlinear properties of the electromechanical transducer in order to get even better agreement between the numerical solution and experiment. More sophisticated theoretical approaches relying on the dynamic plate vibration theory and finite-element calculations may bring further advances by variation of structural parameters and material properties.
Figure 13. Frequency dependence of calculated output power Popt with amplitude A0 = 9.81 m s−2 for different values of gap Δ.
Download figure:
Standard image High-resolution imageAcknowledgments
The work of FF, DVC, LYF and YKF was supported by the Russian Foundation for Basic Research (RFBR grant No. 15-32-70006). ED and MS acknowledge financial support by Technologie- und Wissenschaftsnetzwerk Oberpfalz (TWO). FF and ED have also received allowance from the Bayerisches Hochschulzentrum für Mittel-, Ost- und Südosteuropa (BAYHOST).
Footnotes
- 3
Matlab® and Simulink® are registered trademarks of The MathWorks, Inc.














