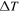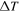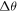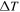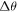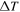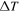Grain size effects on stability of nonlinear vibration with nanocrystalline NiTi shape memory alloy

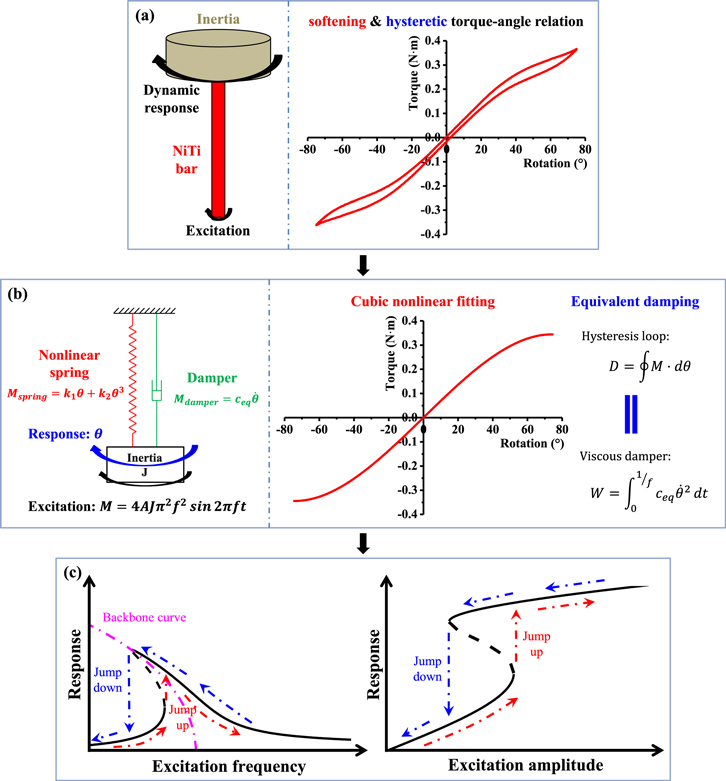
Due to the large recoverable deformation and damping capacity from the first-order martensitic phase transition, NiTi shape memory alloy (SMA) has been widely used in vibration control and energy absorption in civil engineering, aerospace engineering and automotive industry [1–5]. However, nonlinearity and hysteresis in stress–strain relation of the material during phase transition bring a critical issue of instability to the mechanical system as shown in figure 1.

When NiTi SMA is used as a nonlinear damping component, such instability manifests as the jump phenomena of thermomechanical responses from one branch of solution to the alternative branch in the frequency and amplitude domains as shown in figure 1(c) [6, 7]. When deformation of NiTi SMA is in softening nonlinear phase transition stage, the smooth and stable dynamic response along one branch of frequency response curve (FRC) or amplitude response curve (ARC) will gradually go into a metastable region and eventually become unstable and drastically switch to a contrasting alternative stable state along the other branch of FRC or ARC. These metastable regions between jump-up and jump-down must be well identified and excluded in the design and operation of mechanical system with phase transformable NiTi component. Over the past few decades, great theoretical and experimental efforts have been made to investigate such dynamic instability and affecting parameters in the nonlinear vibration system with NiTi SMA around the primary resonance frequency [8–20]. However, to enhance the dynamic stability of mechanical system remains a challenging task and effective methods to manipulate the undesired jump phenomenon are still not available so far.

Zoom In Zoom Out Reset image size

With the fast development of nanotechnology, severe plastic deformation (e.g. cold-rolling, high pressure torsion and equal-channel angular pressing) followed by annealing has been successfully used to control the grain size (GS) and manipulate the thermomechanical properties of nanocrystalline NiTi SMA. When the GS goes down below 100 nm, high density of grain boundary and amorphous phase in nanocrystalline NiTi brings unusual thermomechanical properties including Hall–Petch strengthening, linearized stress–strain relation with vanishing hysteresis, broadened superelasticity window and improved cyclic stability [21–27]. As the key microstructural factor, GS can significantly affect nonlinearity and damping capacity in the stress-strain relation of nanocrystalline NiTi. It is therefore very promising to manipulate the stability of thermomechanical responses for a nonlinear vibration system with NiTi SMA by tailoring the material properties through grain refinement.

This paper aims at investigating the grain size effects on stability of thermomechanical responses for a torsional vibration system with nanocrystalline NiTi bar in the frequency and amplitude domains. Section 2 describes the material fabrication, sample preparation and dynamic testing platform with thermomechanical measurements. The experimental results in the frequency and amplitude domains are reported and discussed in section 3. Finally, all the works in this paper are summarised in section 4.

In this paper, polycrystalline superelastic NiTi sheets (Ni-49.7 at.% Ti from Nitinol, USA) of 1.70 mm initial thickness were cold-rolled to 1.00 mm (42% thickness reduction) by multiple passes. To achieve a wide range of GS, the cold-rolled NiTi sheets were annealed at $485\,^\circ {\rm{C}}$ for 2 min, $520\,^\circ {\rm{C}}$ for 2 min, $520\,^\circ {\rm{C}}$ for 3 min, $520\,^\circ {\rm{C}}$ for 6 min and $520\,^\circ {\rm{C}}$ for 8 min respectively followed by water quenching [28, 29]. Average GS of the annealed materials were examined by bright field TEM (JEM 2010F from JEOL, Japan) as shown in figure 2 and summarised in table 1. Prismatic NiTi bars (thickness $a=1.00\,{\rm{mm}},$ width $b=1.50\,\mathrm{mm}$ and total length ${L}_{{\rm{t}}{\rm{o}}{\rm{t}}{\rm{a}}{\rm{l}}}=60.00\,{\rm{mm}}$) were wirecut from the annealed sheets along the rolling direction. Room temperature was maintained at $25\,^\circ {\rm{C}}$ during the experiments and superelasticity of the materials could be guaranteed.

Zoom In Zoom Out Reset image size

Table 1.  Thermomechanical properties of nanocrystalline NiTi bar with different grain size.

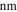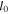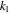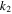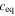Sample No.	Annealing condition	GS (${\rm{nm}}$)	${l}_{0}$ (${\rm{J}}\cdot {{\rm{g}}}^{-1}$)	${k}_{1}$ (${\rm{N}}\cdot {\rm{m}}$)	${k}_{2}$ (${\rm{N}}\cdot {\rm{m}}$)	${k}_{2}/{k}_{1}$	${c}_{{\rm{e}}{\rm{q}}}$ (${\rm{N}}\cdot {\rm{m}}\cdot {\rm{s}}$)
1	—	10	4.14	0.1867	−0.0019	−0.0102	0.00109
2	$485\,^\circ {\rm{C}}/2\,{\rm{\min }}$	27	8.32	0.1898	−0.0067	−0.0353	0.00196
3	$520\,^\circ {\rm{C}}/2\,{\rm{\min }}$	42	10.81	0.1709	−0.0091	−0.0533	0.00269
4	$520\,^\circ {\rm{C}}/3\,{\rm{\min }}$	68	11.74	0.1887	−0.0204	−0.1081	0.00352
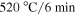
5	$520\,^\circ {\rm{C}}/6\,{\rm{\min }}$	80	13.40	0.1886	−0.0215	−0.1140	0.00354
6	$520\,^\circ {\rm{C}}/8\,{\rm{\min }}$	100	13.62	0.1452	−0.0189	−0.1302	0.00353

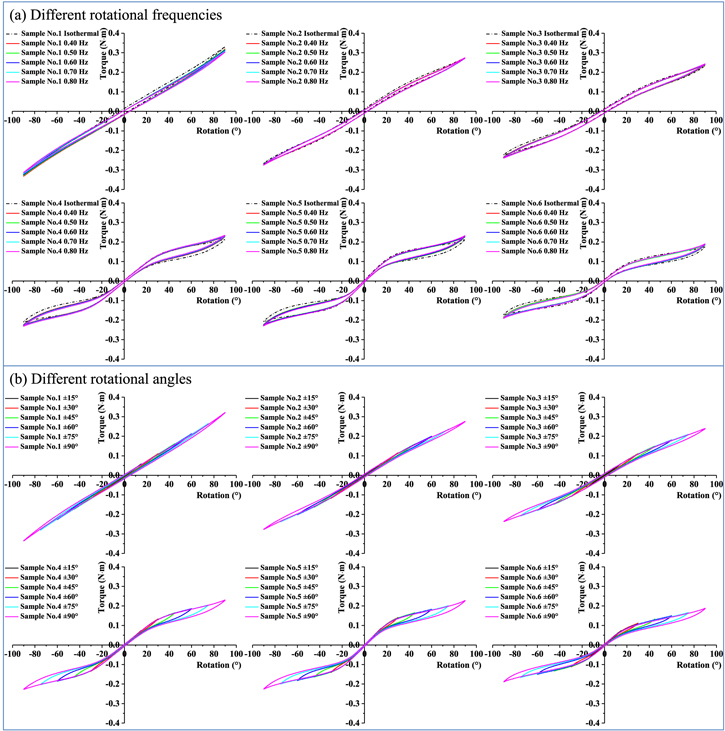
Before the torsional vibration tests, each NiTi bar was trained by quasi-isothermal torsion (rotational angle $\theta =90^\circ$ and rotational frequency $f=0.004\,{\rm{Hz}}$ for 200 cycles) to remove cyclic plasticity and ensure a repeatable torque-angle relation as shown in figure 3(a). After training, the NiTi bars were characterised by pure torsion at different rotational frequencies and the steady-state responses were summarised in figure 4(a). It is seen that the non-isothermal torque-angle relations significantly deviate from the isothermal case ($f=0.001\,{\rm{Hz}}$ by dashed line) in pure torsion. However, in the testing frequency range of $f\in [0.4\,{\rm{Hz}},\,0.8\,{\rm{Hz}}],$ the differences among these steady-state torque-angle relations are negligible and therefore rate effect can be neglected. At an intermediate frequency of $f=0.6\,{\rm{Hz}},$ pure torsion was performed at $\theta =15^\circ /30^\circ /45^\circ /60^\circ /75^\circ /90^\circ$ and all the steady-state responses collapsed onto a single curve as shown in figure 4(b). In order to check if there was any cyclic plasticity involved in the dynamic tests, each NiTi bar was examined by pure torsion before and after the tests. It is seen from the comparison in figure 3(b) that degradation of NiTi bar during the torsional vibration tests is indeed ignorable.

Zoom In Zoom Out Reset image size

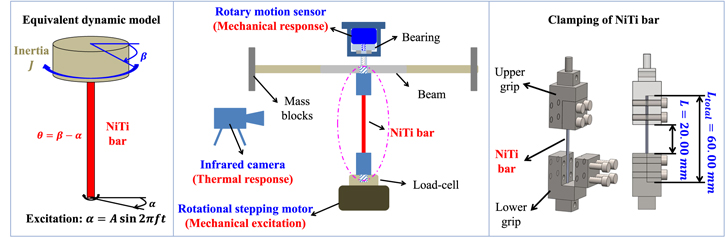
Zoom In Zoom Out Reset image size

The dynamic tests were performed on a single degree of freedom torsional vibration platform with base sinusoidal angular excitation provided by a rotational stepping motor (ElectroForce 3510 from TA Instruments, USA) as shown in figure 5. The NiTi bar was held by a pair of tungsten grips and the upper grip was plugged into a beam. A mass block was attached at each end of the beam to provide rotational momentum of inertia ($J=0.01875\,\mathrm{kg}\cdot \,{{\rm{m}}}^{2}$). The beam was held by a single direction thrust ball bearing so as to rotate freely without axial force. Primary resonance frequency of the vibration system in the linear elastic region is ${{f}}_{0}\,=\displaystyle {\textstyle \tfrac{1}{2{\pi }}}\sqrt{{\textstyle \tfrac{{Gab}({{a}}^{2}+{{b}}^{2})}{12{JL}}}}\approx 0.673\,{\rm{Hz}}$ with shear modulus $G\,=\,16.5\,{\rm{GPa}}.$

Zoom In Zoom Out Reset image size

Rotation of the NiTi bar ($\theta$) was calculated from synchronised measurements of external sinusoidal angular excitation ($\alpha =A\,\sin \,2\pi ft$) and rotation of the beam ($\beta$) by a rotary motion sensor (PS-2120A from PASCO, USA). Average temperature of the NiTi bar ($T$) was measured by an infrared camera (SC7700M from FLIR, USA) after matt black painted (TS-6 from Tamiya, Japan) to enhance the thermal emissivity. Peak-to-valley magnitudes of rotational angle and average temperature (${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$) in the steady-state oscillation were quantified as mechanical response and thermal response of the torsional vibration system (see [7] for more details).

For nanocrystalline NiTi investigated in this paper, both softening nonlinearity and dissipative property come from the martensitic phase transition and manifest macroscopically as the nonlinear hysteretic torque-angle relation of the bar. For the purpose of simplicity, softening nonlinearity and dissipative property of the nanocrystalline NiTi bar are effectively modelled by a softening nonlinear spring (${M}_{{\rm{s}}{\rm{p}}{\rm{r}}{\rm{i}}{\rm{n}}{\rm{g}}}={k}_{1}\theta +{k}_{2}{\theta }^{3}$ with ${k}_{1}\gt 0$ and ${k}_{2}\lt 0$) and a viscous damper (${M}_{{\rm{d}}{\rm{a}}{\rm{m}}{\rm{p}}{\rm{e}}{\rm{r}}}={c}_{{\rm{e}}{\rm{q}}}\dot{\theta }$) as shown in figure 1(b). ${k}_{1}$ and ${k}_{2}$ come from cubic nonlinear fitting of the steady-state torque-angle relation of the NiTi bar in figure 6(a). The significant change of torque-angle relation of the NiTi bar is due to the strong GS dependence of stressâ–strain relation of the nanocrystalline material. ${c}_{{\rm{e}}{\rm{q}}}$ is obtained by equalling the steady-state hysteresis loop area of the NiTi bar in cyclic pure torsion to the energy dissipation of an equivalent angular viscous damper in mechanical vibration system ($H=2{\pi }^{2}f{\theta }^{2}{c}_{{\rm{e}}{\rm{q}}}$). It is seen from figures 6(b) and (c) that damping capacity, softening nonlinearity and specific latent heat of the NiTi bar are significantly reduced as the GS decreases below 80 nm.

Zoom In Zoom Out Reset image size

To investigate the GS effects on the jump phenomena in the frequency domain, the excitation amplitude $A$ was fixed at $A=5^\circ$ and the excitation frequency $f$ varied in the range of $f\in [0.4\,{\rm{Hz}},\,0.8\,{\rm{Hz}}]$ so as to sweep through the primary resonance frequency ($f\approx 0.673\,{\rm{Hz}}$). For each nanocrystalline NiTi bar, a total of 82 independent vibration tests were performed following ascending frequency order (from $0.4\,{\rm{Hz}}$ up to $0.8\,{\rm{Hz}}$ at $0.01\,{\rm{Hz}}$ interval) and descending frequency order (from $0.8\,{\rm{Hz}}$ down to $0.4\,{\rm{Hz}}$ at $0.01\,{\rm{Hz}}$ interval). The obtained ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ are plotted against the excitation frequency as FRCs in figure 7.

• (1)  
  For sample No.1 (GS = 10 nm in black), as its torque-angle relation is almost linear with small hysteresis and latent heat (see figure 6(a) and table 1), the torsional vibration response is similar to that of a linear vibration system and the FRC only shows a symmetric peak without instability. The temperature oscillation ${\rm{\Delta }}T$ is quite small due to the significantly reduced latent heat with GS reduction.
• (2)  
  For sample No.2 (GS = 27 nm in red), the torque-angle relation is slightly softening nonlinear and hysteretic (see figure 6(a)). Therefore, FRCs of thermomechanical responses become steeper as shown in figure 7. Compared with sample No.1, though ${\rm{\Delta }}\theta$ is suppressed by the increased damping capacity ${c}_{{\rm{e}}{\rm{q}}},$ ${\rm{\Delta }}T$ still grows larger due to the doubled latent heat (see table 1).
• (3)  
  For sample No.3 (GS = 42 nm in green), as the torque-angle relation becomes more softening nonlinear and hysteretic, the peaks in FRCs become sharper at $f=0.50\,{\rm{Hz}}$ and clear jumps of thermomechanical responses are observed.
• (4)  
  For sample No.4 (GS = 68 nm in blue), jump phenomena of thermomechanical responses become more significant and FRCs further bend to the left, exhibiting typical features of softening nonlinear dynamic response.
• (5)  
  For sample No.5 (GS = 80 nm in cyan), simultaneous jump-ups and jump-downs of ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ following ascending and descending frequency orders are captured on the FRCs. The jump-up frequency and jump-down frequency become separated, showing a strong path-dependence of the thermomechanical responses.
• (6)  
  For sample No.6 (GS = 100 nm in magenta), due to the further increased nonlinearity and the same damping capacity, jumps of both ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ become much more significant and the frequency gap between jump-up and jump-down is also enlarged compared with sample No.5.

Zoom In Zoom Out Reset image size

To examine the GS effects on the dynamic stability in the amplitude domain, the excitation frequency $f$ was fixed at $f=0.5\,{\rm{Hz}}$ and the excitation amplitude $A$ was set in the range of $A\in [4.0^\circ ,\,8.0^\circ ].$ For each NiTi bar, 82 independent vibration tests were performed according to ascending amplitude order (from $4.0^\circ$ up to $8.0^\circ$ at $0.1^\circ$ interval) and descending amplitude order (from $8.0^\circ$ down to $4.0^\circ$ at $0.1^\circ$ interval). The obtained steady-state ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ are plotted against the excitation amplitude as ARCs in figure 8.

• (1)  
  For sample No.1 (GS = 10 nm in black), both ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ increase linearly with the excitation amplitude without jump phenomena in the testing range since the torque-angle relation is almost linear as shown in figure 6(a). ${\rm{\Delta }}T$ is quite small due to the greatly reduced latent heat of the cold-rolled material.
• (2)  
  For sample No.2 (GS = 27 nm in red), as the softening nonlinearity and hysteresis start to get involved in the torque-angle relation, the ARCs become slightly nonlinear but are still continuous, monotonic and one-to-one single-valued. The dynamic responses are stable though there is a significant variation of ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ in the intermediate region.
• (3)  
  For sample No.3 (GS = 42 nm in green), instability of the mechanical response starts to occur through the observed jump-up (following ascending order) and jump-down (following descending order) on the ARCs in figure 8. Simultaneous jump-up and jump-down of ${\rm{\Delta }}T$ at the same position are also captured in the experiments. The increased ${c}_{{\rm{e}}{\rm{q}}}$ suppresses the magnitude of ${\rm{\Delta }}\theta$ while the larger latent heat keeps ${\rm{\Delta }}T$ close to that of sample No.2.
• (4)  
  For sample No.4 (GS = 68 nm in blue) with further increased nonlinearity, jump phenomena become significant as shown by the larger amplitude gap between jump-up and jump-down.
• (5)  
  For sample No.5 (GS = 80 nm in cyan), the magnitudes of ${\rm{\Delta }}\theta$ and ${\rm{\Delta }}T$ keep increasing and jump amplitude gap is also enlarged.
• (6)  
  For sample No.6 (GS = 100 nm in magenta), as the nonlinearity increases and the damping capacity remains almost the same (see figure 6(a) and table 1), the ARCs become more softening nonlinear and the gap between jump-up and jump-down is further enlarged.

Zoom In Zoom Out Reset image size

In the following, we will briefly outline the theoretical modelling procedures to interpret the above experimental observations. Thermomechanical coupling effects of NiTi SMA are decoupled by separately considering the mechanical response and thermal response [6, 7]. Therefore, mechanical response can be obtained through an effective Duffing oscillation model consisting of a cubic nonlinear softening spring (${M}_{{\rm{s}}{\rm{p}}{\rm{r}}{\rm{i}}{\rm{n}}{\rm{g}}}={k}_{1}\theta +{k}_{2}{\theta }^{3}$) and an angular viscous damper (${M}_{{\rm{\text{damper}}}}={c}_{{\rm{e}}{\rm{q}}}\dot{\theta }$). Thermal response is then determined by the lumped heat transfer analysis using the mechanical response as input.

The equation of motion can be expressed as

$$\begin{eqnarray*}&&J\ddot{\beta }=-{c}_{{\rm{e}}{\rm{q}}}\dot{\theta }-{k}_{1}\theta -{k}_{2}{\theta }^{3}.\end{eqnarray*}$$

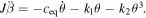
Replacing $\beta$ by $\theta$ and $\alpha$ ($\beta =\theta +\alpha =\theta +A\,\sin \,2\pi ft$), we have

$$\begin{eqnarray*}&&J\ddot{\theta }+{c}_{{\rm{e}}{\rm{q}}}\dot{\theta }+{k}_{1}\theta +{k}_{2}{\theta }^{3}=4AJ{\pi }^{2}{f}^{2}\,\sin \,2\pi ft.\end{eqnarray*}$$

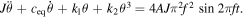
The steady-state response is obtained through the method of multiple scales

$$\begin{eqnarray*}&&{\left[({k}_{1}-4{\pi }^{2}{f}^{2}J)\displaystyle \frac{{\rm{\Delta }}\theta }{2}+\displaystyle \frac{3}{4}{k}_{2}{\left(\displaystyle \frac{{\rm{\Delta }}\theta }{2}\right)}^{3}\right]}^{2}\\ &&\,+\,{(\pi f{c}_{{\rm{e}}{\rm{q}}}{\rm{\Delta }}\theta )}^{2}={(4AJ{\pi }^{2}{f}^{2})}^{2}.\end{eqnarray*}$$

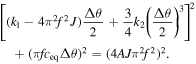
This is an implicit solution of rotational angle (${\rm{\Delta }}\theta$) as a function of external excitation ($f$ and $A$). For nanocrystalline NiTi bar with different GS, ${k}_{1}$ is almost the same (see table 1) and therefore ${k}_{2}$ and ${c}_{{\rm{e}}{\rm{q}}}$ will determine the mechanical response of the nonlinear vibration system.

Assuming the shear behaviour of NiTi bar during partial phase transition in torsion as ideal elastoplastic type, a lumped heat analysis (see [6, 7] for more details) is performed to establish the relationship between temperature oscillation (${\rm{\Delta }}T$) and rotation (${\rm{\Delta }}\theta$) of the NiTi bar,

$$\begin{eqnarray*}{\rm{\Delta }}T=\left\{\begin{array}{rr}0, & {\rm{\Delta }}\theta \leqslant \displaystyle \frac{4L{\gamma }_{s}}{d},\\ \left[\displaystyle \frac{d}{6L{\gamma }_{0}^{PT}}{\rm{\Delta }}\theta +\displaystyle \frac{16{L}^{2}{\gamma }_{s}^{3}}{3{d}^{2}{\gamma }_{0}^{PT}}\displaystyle \frac{1}{{({\rm{\Delta }}\theta )}^{2}}-\displaystyle \frac{{\gamma }_{s}}{{\gamma }_{0}^{PT}}\right]\displaystyle \frac{{l}_{0}}{\lambda }, & {\rm{\Delta }}\theta \gt \displaystyle \frac{4L{\gamma }_{s}}{d}.\end{array}\right.\end{eqnarray*}$$

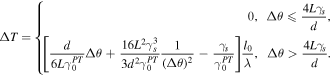
The above equation quantifies the temperature oscillation (${\rm{\Delta }}T$) at a given rotational angle (${\rm{\Delta }}\theta$). In addition to ${k}_{1},\,{k}_{2}$ and ${c}_{{\rm{e}}{\rm{q}}},$ thermal response of the nonlinear dynamic system further involves specific latent heat (${l}_{0}$) of the nanocrystalline material.

The effective Duffing oscillation model and lumped heat analysis are established based on the macroscopic torque-angle relation of nanocrystalline NiTi bar regardless of the microstructure. The theoretical analysis has shown that thermomechanical responses of the nonlinear vibration system with nanocrystalline NiTi bar are significantly influenced by the cubic nonlinear fitting parameters (${k}_{1}$ and ${k}_{2}$), equivalent damping coefficient (${c}_{{\rm{e}}{\rm{q}}}$) and specific latent heat (${l}_{0}$), all of which decrease sharply with the GS reduction in the nano-scale region below 100 nm. Therefore, it is through these fundamental parameters calculated from the macroscopic torque-angle relation that GS of nanocrystalline NiTi bar determines the stability of dynamic response in the frequency and amplitude domains.

Furthermore, recent research [30, 31] shows that with the decrease of GS below 100 nm, the low-cycle fatigue life of nanocrystalline NiTi increases but the fracture toughness is decreased. Therefore, stabilising the thermomechanical responses of nonlinear vibration system with nanocrystalline NiTi through GS reduction brings extra benefits of enhancing the fatigue life at the expense of fracture toughness reduction.

In summary, nanocrystalline NiTi bars with average GS from 10 nm to 100 nm were fabricated through severe plastic deformation followed by annealing. Torsional vibration tests were performed to investigate the GS effects on the stability of thermomechanical responses in the frequency and amplitude domains. It is found that as the GS of nanocrystalline NiTi decreases from 100 nm down to 10 nm, nonlinearity, damping capacity and latent heat of the material are sharply reduced in torsion. The GS effects on material's fundamental thermomechanical properties bring significant enhancement to the stability of dynamic responses: the FRC and ARC gradually evolve from softening nonlinear to linear and the undesired jump phenomena become less significant and eventually vanish with the decrease of GS. By controlling GS of the nanocrystalline NiTi in the vibration system, thermomechanical properties of the material and stability of the system can be effectively manipulated for different purposes, therefore opening up a new route in the applications.

The financial support from the Hong Kong Research Grants Council (Project No. N_HKUST 617/14) and the National Natural Science Foundation of China (Project No. 11532010) is gratefully acknowledged. Technical assistance from the Advanced Engineering Material Facility (AEMF), Materials Characterization and Preparation Facility (MCPF) and Design and Manufacturing Services Facility (DMSF) of the Hong Kong University of Science and Technology is highly appreciated.